Skip to main content
SpringerLink
Log in

A flow-based pattern recognition algorithm for rapid quantification of geologic uncertainty

  • Original Paper
  • Published:
Computational Geosciences Aims and scope Submit manuscript

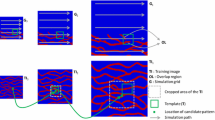
Abstract

Geologic uncertainties and limited well data often render recovery forecasting a difficult undertaking in typical appraisal and early development settings. Recent advances in geologic modeling algorithms permit automation of the model generation process via macros and geostatistical tools. This allows rapid construction of multiple alternative geologic realizations. Despite the advances in geologic modeling, computation of the reservoir dynamic response via full-physics reservoir simulation remains a computationally expensive task. Therefore, only a few of the many probable realizations are simulated in practice. Experimental design techniques typically focus on a few discrete geologic realizations as they are inherently more suitable for continuous engineering parameters and can only crudely approximate the impact of geology. A flow-based pattern recognition algorithm (FPRA) has been developed for quantifying the forecast uncertainty as an alternative. The proposed algorithm relies on the rapid characterization of the geologic uncertainty space represented by an ensemble of sufficiently diverse static model realizations. FPRA characterizes the geologic uncertainty space by calculating connectivity distances, which quantify how different each individual realization is from all others in terms of recovery response. Fast streamline simulations are employed in evaluating these distances. By applying pattern recognition techniques to connectivity distances, a few representative realizations are identified within the model ensemble for full-physics simulation. In turn, the recovery factor probability distribution is derived from these intelligently selected simulation runs. Here, FPRA is tested on an example case where the objective is to accurately compute the recovery factor statistics as a function of geologic uncertainty in a channelized turbidite reservoir. Recovery factor cumulative distribution functions computed by FPRA compare well to the one computed via exhaustive full-physics simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alpak, F.O., Barton, M.D., van der Vlugt, F.F., Pirmez, C., Prather, B.E.: Simplified modeling of turbidite channel reservoirs. In: SPE Annual Technical Conference and Exhibition, Denver, Colorado, 21–24 September 2008

  2. Alpak, F.O., Torres-Verdín, C., Habashy, T.M.: Estimation of in-situ petrophysical properties from wireline formation tester and induction logging measurements: a joint inversion approach. J. Pet. Sci. Eng. 63, 1–17 (2008)

    Article  Google Scholar 

  3. Barton, M., O’Byrne, C., Pirmez, C., Prather, B., van der Vlugt, F.,Alpak,O., Sylvester, Z.: Turbidite channel architecture: recognizing and quantifying the distribution of channel base drapes using core and dipmeter data. AAPGMemoir on Borehole Imaging (in press)

  4. Batycky, R.P., Blunt, M.J., Thiele, M.R.: A 3D field-scale streamline-based reservoir simulator, SPE 36726. SPE Reserv. Eng. 12(4), 246–254 (1997)

    Google Scholar 

  5. Borg, I., Groenen, P.J.F. (2005) Modern Multi-dimensional Scaling: Theory and Applications, 2nd edn. Springer, New York

    Google Scholar 

  6. Damsleth, E., Hage, A., Volden, R.: Maximum information at minimum cost: a north sea field development study with an experimental design, SPE 23139. J. Pet. Technol. 44(12), 1350–1356 (1992)

    Google Scholar 

  7. Datta-Gupta, A., King, M.J.: A semianalytic approach to tracer flow modeling in heterogeneous permeable media. Adv. Water Resour. 18(1), 9–24 (1995)

    Article  Google Scholar 

  8. Franc, V., Hlavac, V.: Statistical Pattern Recognition Toolbox for Matlab: User’s Guide, Center for Machine Perception, Department of Cybernetics, Faculty of Electrical Engineering, Czech Technical University, Prague (2004)

  9. Friedmann, F., Chawathe, A., Larue, D.K.: Assessing uncertainty in channelized reservoirs using experimental designs, SPE 85117. SPE Reserv. Evalu. Eng. 6(4), 264–274 (2003)

    Google Scholar 

  10. Gilman, J.R., Meng, H.-Z., Uland, M.J., Dzurman, P.J., Cosic, S.: Statistical ranking of stochastic geomodels using streamline simulation: a field application, SPE 77374. In: SPE Annual Technical Conference and Exhibition, San Antonio, Texas, 29 September–2 October 2002

  11. Kwok, J.T.-Y., Tsang, I.W.-H.: The pre-image problem in kernel methods. IEEE Trans. Neural Netw. 15(6), 1517–1525 (2004)

    Article  Google Scholar 

  12. Onyeagoro, K., Naruk, S., van der Vlugt, F., Barton, M., Pirmez, C., O’Byrne, C.: Impact of structural and stratigraphic heterogeneities in deepwater development, SPE 11190. In: Nigeria Annual International Conference and Exhibition, Abuja, Nigeria, 6–8 August 2007

  13. Peake, W.T., Abadah, M., Skander, L.: Uncertainty assessment using experimental design: Minagish Oolite reservoir, SPE 91820. In: SPE Reservoir Simulation Symposium, The Woodlands, TX, 31 January–2 February 2005

  14. Regtien, J.M.M., Por, G.J.A., van Stiphout, M.T., van der Vlugt, F.F.: Interactive reservoir simulation, SPE 29146. In: SPE Reservoir Simulation Symposium, San Antonio, Texas, 12–15 February 1995

  15. Samantray, A.K., Dashti, Q.M., Ma, E.D.C., Kumar, P.S.: Upscaling and 3D streamline screening of several multimillion-cell earth models for flow simulation, SPE 81496. SPE Reserv. Evalu. Eng. 9(1), 15–23 (2006)

    Google Scholar 

  16. Sarma, P., Durlofsky, L.J., Aziz, K., Chen, W.-H.: A new approach to automatic history matching using kernel PCA, paper SPE 106176. Presented at the SPE Reservoir Simulation Symposium, Houston, Texas, USA, 26–28 February 2007

  17. Scheidt, C., Caers, J.: Representing spatial uncertainty using distances and kernels. Math. Geosci. 41(4), 397–419 (2009)

    Article  MATH  Google Scholar 

  18. Scheidt, C., Caers, J.: Uncertainty quantification in reservoir performance using distances and kernel methods—application to a West-Africa deepwater turbidite reservoir. SPE J. (2009, in press)

  19. Schlumberger Information Solutions: Petrel Introduction Course. Houston, Texas (2006)

    Google Scholar 

  20. Schölkopf, B., Smola, A.J.: Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond. MIT Press, Cambridge (2002)

    Google Scholar 

  21. Schölkopf, B., Knirsch, P., Smola, A., Burges, C.: Fast Approximation of Support Vector Kernel Expansions, and an Interpretation of Clustering as Approximation in Feature Spaces, Mustererkennung 1998. In: 20 DAGM-Symposium, pp. 125–132, 29 September –1 October 1998

  22. Schölkopf, B., Smola, A., Muller, K-.R.: Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 10(5), 1299–1319 (1998)

    Article  Google Scholar 

  23. Tabachnick, B.G., Fidell, L.S.: Using Multivariate Statistics, 4th edn. Allyn and Bacon, Needham Heights (2001)

    Google Scholar 

  24. Wang, F., White, C.D.: Designed Simulation for a Detailed 3D Turbidite Reservoir Model, SPE 75515. In: SPE Gas Technology Symposium, Calgary, Alberta, Canada, 30 April–2 May 2002 2002

  25. Wen, R., Martinius, A.W., Næss, A., Ringrose, P.S.: Three-dimensional simulation of small-scale heterogeneity in tidal deposits—a process based stochastic method. In: Buccianti, A., Nardi, G., Potenza, A. (eds.) Proceedings of the 4th Annual Conference of the International Association of Mathematical Geology (IAMG), pp. 129–134. De Frede, Ischia (1998)

    Google Scholar 

  26. Weinberger, K.Q., Sha, F., Saul, L.K.: Learning a kernel matrix for nonlinear dimensionality reduction. In: Proceedings of the 21st International Conference on Machine Learning, Alberta, Canada (2004)

  27. White, C.D., Royer, S.A.: Experimental design as a framework for reservoir studies, SPE 79676. In: SPE Reservoir Simulation Symposium, Houston, Texas, 3–5 February 2003

  28. White, C.D., Willis, B.J., Narayanan, K., Dutton, S.P.: Identifying and estimating significant geologic parameters with experimental design, SPE 74140. SPE J. 6(3), 311–324 (2001)

    Google Scholar 

  29. Williams, C.K.I.: On a connection between kernel PCA and metric multi-dimensional scaling. Mach. Learn. 46(1–3), 11–19 (2002)

    Article  MATH  Google Scholar 

  30. Yang, T., Liu, J., McMillan, L., Wang, W.: A fast approximation to multidimensional scaling. In: Proceedings of the IEEE Workshop on Computation Intensive Methods for Computer Vision (2006)

Download references

Author information

Authors and Affiliations

  1. Shell International Exploration and Production Inc., 3737 Bellaire Blvd., Houston, TX, 77025, USA

    Faruk O. Alpak & Mark D. Barton

  2. Department of Energy Resources Engineering, Stanford University, 367 Panama Street, Green Earth Sciences 353, Stanford, CA, 94305, USA

    Jef Caers

Authors
  1. Faruk O. Alpak
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mark D. Barton
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jef Caers
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Faruk O. Alpak.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Alpak, F.O., Barton, M.D. & Caers, J. A flow-based pattern recognition algorithm for rapid quantification of geologic uncertainty. Comput Geosci 14, 603–621 (2010). https://doi.org/10.1007/s10596-009-9175-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10596-009-9175-5

Keywords

Search

Navigation