Abstract
With 40% of the European Black-tailed Godwit population breeding in The Netherlands, this country harbours internationally significant numbers of this species. However, ongoing agricultural intensification has resulted in the fragmentation of the population and drastic population declines since 1967. By establishing genetic diversity, genetic differentiation and gene flow on the basis of 12 microsatellites, we investigated whether the population genetic structure of the Dutch Black-tailed Godwit bears the marks of these changes. Genetic diversity appeared to be moderate, and Bayesian model-based analysis of individual genotypes revealed no clustering in the Dutch populations. This was supported by pairwise FST values and AMOVA, which indicated no differentiation among the nine breeding areas. Gene flow estimates were larger than “one migrant per generation” between sample locations, and no isolation by distance was demonstrated. Our results indicate the maintenance of moderate levels of genetic diversity and genetic connectivity between breeding sites throughout the Dutch Black-tailed Godwit breeding population. We suggest that the Dutch Black-tailed Godwit breeding areas should be managed as a single panmictic unit, much as it is presently done.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
For a long time, agriculture in Europe generated high bird species diversity. However, with the increasing intensification over the last 50 years many bird species breeding on farmland are now declining (Stoate et al. 2009; van Turnhout et al. 2007). A good example of a bird species that waxed and waned in response to agricultural land use changes is the Black-tailed Godwit Limosa limosa limosa (Birdlife International 2009). The Black-tailed Godwit was previously confined to raised bogs, moorlands, lake margins and damp grassy depressions in steppe. However, when wet grassland created for dairy farming increased in northwestern Europe, this species became very successful in this habitat (Beintema et al. 1995; Haverschmidt 1963). Close to half of the European Black-tailed Godwit population breeds in The Netherlands (Birdlife International 2004). However, continuing declines of 5% per year since the peak numbers of the late 1970s (Schroeder et al. 2009) have decreased Black-tailed Godwit breeding numbers. While 120,000 pairs (Mulder 1972) were estimated to breed in 1967, only 40,000 pairs remained in 2004 (Birdlife International 2004).
The most significant threats for this species include loss of nesting habitat owing to wetland drainage and agricultural intensification. The earliest modernization of farming enhanced food supply and thus increased population sizes of several wader species (Cramp and Simmons 1983). However, further intensification practices have resulted in reduced food availability, lower water tables, increased cattle densities, and increased early mowing (Benton et al. 2002; Schekkerman et al. 2008, 2009; Kleijn et al. 2010). Furthermore, predation risk has increased as a result of early mowing practices, mostly due to reduced coverage for nesting, and chick raising (Schekkerman et al. 2009). These agricultural adjustments have in turn culminated in impaired chick recruitment and decreasing habitat quality. Subsequently, the declining habitat quality has led to the fragmentation of suitable grassland (Zwarts et al. 2009). Schekkerman et al. (2008) documented a decline from 0.9 fledged chicks per godwit pair in 1985 to roughly 0.23 fledged chicks per pair in 2006.
Although Black-tailed Godwit habitat is becoming ever more fragmented and habitat quality decreasing, this species shows high breeding site fidelity and some degree of natal philopatry (Groen 1993; van den Brink et al. 2008). Groen (1993) showed that 90% of the adult breeding birds returned within 700 m of the previous nest site, whereas van den Brink et al. (2008) found that 100% of the adult Black-tailed Godwits returned within 3 km of the former nest site. In the former study, natal philopatry was demonstrated to be high as well, with 75% of the birds returning within 18 km of their previous hatching site. With such limited dispersal in a fragmenting landscape, breeding areas could become isolated from each other. This might affect population dynamics, resulting in a metapopulation structure including source-sinks dynamics and isolation by distance (Höglund 2009).
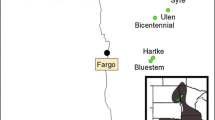
Here we describe gene flow indirectly by investigating genetic diversity and differentiation on a national scale covering the most important breeding areas of the Dutch Black-tailed Godwit breeding population (Fig. 1). Twelve microsatellite loci developed specifically for this species by Verkuil et al. (2009) were used, and their polymorphic nature verified to ensure that the assumptions made by several population genetic models were obeyed. Additionally, the population genetic structure of the Dutch Black-tailed Godwit breeding sites was assessed through genetic diversity, genetic differentiation, isolation by distance and gene flow calculations. Moreover, if genetic structure or the lack of it was portrayed, we tried to explain the underlying mechanism.
Materials and methods
Sample collection, DNA extraction and amplification
From 2004 to 2008, blood samples from freshly hatched chicks and dry egg shell remains (Trimbos et al. 2009) were collected in nine regions in The Netherlands separated by 7–135 km (Fig. 1). When a nest was found during incubation, the floating method of Liebezeit et al. (2007) was used to predict hatch date. Around the time of predicted hatch the nests were visited regularly to obtain either eggshell remains (if chicks had left the nest) or ca. 30 μl whole blood per chick (if they were found quickly after hatch, before leaving the nest). Egg shells were stored individually in plastic bags to minimize post-sampling contamination. Blood was stored in individual 1.5 ml Eppendorf tubes containing 97% alcohol buffer. Blood samples were stored at −70°C, while egg shells were stored dry at room temperature to get a good separation of the egg shell membranes from the outer shell. DNA samples of 140 individual Black-tailed Godwits were collected (Table 1). These 140 samples incorporated only one individual per nest to avoid pseudoreplication at the family-level.
DNA was extracted from 6–10 μl of blood using the ammonium acetate method as described by Richardson et al. (2001). DNA was extracted from eggshell membrane using Qiagen Dneasy Tissue Kit (Qiagen 2003), with minor modifications as described by Trimbos et al. (2009). DNA quality and quantity were checked twice, using the NanoDrop ND-1000 (Thermo Scientific) for 260/280 ratios and concentration values. For optimal PCR amplification, blood samples were diluted to concentrations below 10 ng/μl. Compared to blood derived DNA, DNA from eggshell membranes was of less purity occasionally. Consequently, eggshell derived DNA was diluted to concentrations below 50 ng/μl. We used 12 microsatellite loci (LIM3, LIM5, LIM8, LIM10, LIM11, LIM12a, LIM24, LIM25, LIM26, LIM30, LIM33) developed for Black-tailed Godwits (Verkuil et al. 2009). The final volumes of the PCR amplification mix were 11 μl and included 1–10 ng DNA for blood samples or 1–50 ng DNA for eggshell membrane samples, 1.65 mM MgCl2, 2.5 μM dNTPs, 0.5 μM forward primer with M13 extension, 0.5 μM reverse primer, 1 μM fluorescent-labelled M13 primer, 10× PCR buffer and 0.45 U Taq DNA Qiagen polymerase. The polymerase chain reaction program used was as described by Verkuil et al. (2009), except the final PCR step was extended to 20 min to minimize peak stutter patterns. PCR products were analyzed using a MegaBACE 1000 (Amersham Biosciences) and allele sizes were assigned using Fragment Profiler 1.2 (Amersham Biosciences 2003). Contamination of PCR pre-mix with exogenous DNA was minimized by carrying out pre- and post-PCR pipetting in different rooms. Additionally, to control for potential contamination problems, negative controls were included in every PCR reaction and MegaBACE runs.
Genetic marker validation
Microsatellite markers are expected to be independently distributed in the genome, as such linkage between loci would result in pseudo-replication (Selkoe and Toonen 2006). A Fisher’s exact test for linkage disequilibrium was carried out using the samples from the nine breeding areas, with 1,000 dememorization steps, 100 batches and 1,000 iterations per batch (GENEPOP; Raymond and Rousset 1995, web version 4.0). Deviations from Hardy–Weinberg, heterozygote excess and deficit were tested per locus and sample location separately using 1,000 dememorization steps, 100 batches and 1,000 iterations per batch (GENEPOP; Raymond and Rousset 1995). For multiple testing, Bonferroni corrections were applied (Rice 1989). Micro-Checker was used to test for scoring and amplification errors (stutter and null alleles) with a 95% confidence interval over 10,000 runs (van Oosterhout et al. 2004). To evaluate genotyping error, scoring was performed three times and the frequency of disagreement between different times of scoring was noted and averaged.
Genetic diversity, FIS and population structure analyses
Observed (Ho), expected heterozygosity (He), inbreeding values (FIS) per location and pairwise FST between locations were calculated using Arlequin 3.11 (Excoffier et al. 2005). Furthermore, an analyses of molecular variance (AMOVA) was performed, through which variance among sample locations (Va), among individuals within sample locations (Vb), and within all individuals could be computed (Vc), using Arlequin with 20,000 permutations. If significant values were obtained, Bonferroni corrections were applied. The number of private alleles was determined using Convert 1.31 (Glaubitz 2004). FSTAT 2.9.3.2 (Goudet 1995) was used to calculate allelic range, number of alleles per sample location and allelic richness per sample location. This program uses the rarefaction index described by Hurlbert (1971) to correct for sample size. Additionally, the levels of allelic richness and FIS among sample locations were compared using FSTAT with 10,000 permutations to obtain P-values.
The model based Bayesian cluster algorithm implemented in STRUCTURE 2.3.1 (Pritchard et al. 2000) was used to cluster from a pool of genotypes from all sampling locations. As recommended by Evanno et al. (2005) we determined the deltaK (Structure Harvester), the second order rate of change in log likelihood Ln P(X|K). Although this method was demonstrated to be more reliable in estimating the inferred amount of clusters in natural populations, K = 1 (a reasonable possibility here) can not be measured. Consequently, the most likely number of genetic clusters (K) in our sample set was also investigated by determining the maximum average log likelihood Ln P(X|K). Values computed with both methods were plotted using Structure Harvester 0.56.3 (Dent 2009, web version). The Structure model was run using admixture and correlated allele frequencies. Additionally, the LOCPRIOR model, incorporated into STRUCTURE 2.3.1, was used. This model assumes that individuals sampled close together are often from the same population and can assist in the clustering when population structure is weak. The program was run 5 times with a burn-in of 200,000 iterations and a length of 1,000,000 MCMC iterations for K (1–11). Convergence was checked by looking whether the graphs provided by the program reached equilibrium before the end of the burn-in phase.
The genetic structure profile within this dataset could display a historic situation of Black-tailed Godwit population dynamics. The Dutch Black-tailed Godwit breeding population is believed to have expanded from 1900 until the 1960s. The k test as implemented in the program Kgtests (Bilgin 2007) detects population expansion on the basis of allele size distributions. The method uses a one tailed binomial distribution to test for the number of loci with negative k values and if this represents a significant number of negative k values. Additionally, this software included the g test, which tests the notion that stable populations are reflected by large variances of allele sizes among loci, while in an expanding population this variance is smaller. Although Luikart et al. (1998) demonstrated that the g test was the more powerful of the two, both tests were performed here.
Gene flow patterns between sample locations
The number of migrants between the different sample locations was estimated using Slatkin’s (1985) private allele method, implemented in Genepop 4.0 (Raymond and Rousset 1995). This calculation assumes an approximately equilibrium distribution of allele frequencies among the demes comprising a population (Barton and Slatkin 1986). Most coalescent computer programs, developed to calculate gene flow between populations and effective population size, assume stable (sub) populations over time (Kuhner 2009). As the Dutch Black-tailed Godwit population is believed to have been rather variable in size over the last 100 years (Beintema et al. 1995; Schekkerman et al. 2008; Schroeder et al. 2009), we refrained from using these programs. Nevertheless, programs such as IMa2 (Hey and Nielsen 2007) allow testing of migration rates between different locations in populations with a probably unstable subpopulation structure over time. However, this program uses a tree string as a backbone to make coalescent inferences; the uncertainties in our dataset did not enable us to construct such a tree and therefore this program was not used. To explore dispersal limitation issues due to the confounding effect of geographic distance, a Mantel test (normally transformed and log transformed) with 9999 permutations was preformed using GENALEX 6.2 (Peakal and Smouse 2006) which calculates the correlation between a genetic and a geographic distance matrix (Smouse and Long 1992; Smouse et al. 1986).
Results
Genetic marker validation
A total of 140 birds from 9 breeding locations were genotyped. All 12 loci amplified no more that two alleles per individual and were polymorphic with 4–15 alleles per locus. In total we detected 126 alleles. Some loci in some locations exhibited significant deviations from Hardy–Weinberg. However, none of these values remained significantly different from zero after sequential Bonferroni correction. After Bonferroni corrections, no linkage-disequilibrium was found between any of the loci in any of the locations. The mean genotyping error, the averaged difference between the 1st and 2nd and 1st and 3rd time of scoring, was 1.5%. Micro-Checker showed no null alleles at any of the sample locations or loci.
Genetic diversity, FIS and population structure analysis
The mean number of alleles, absolute number of alleles, allelic richness, Ho, He, FIS, and private alleles, per sample location are assembled in Table 1. There was no relationship between genetic diversity values (Table 1) and sample location. FIS was not significantly different from zero in any location. Differences in allelic richness (N = 9, P = 0.079) and FIS (N = 9, P = 0.866) among sample locations were not significant either.
Nearly all pairwise FST values between locations were not significantly different from zero, except for those between ZWF and VIJF (Table 2). However, after Bonferroni correction, this difference was not upheld at the 5%-significance level. AMOVA calculations showed no significance for any of the calculated variances (0% Va = −0.0011, P = 1.000 ± 0.000, 0.3% Vb = 0.004, P = 0.37793 ± 0.00353 and 99.7% Vc = 0.004, P = 0.37903 ± 0.00358).
Structure analyses indicated that the most likely value for the amount of genetic clusters (K) was K = 1. Using the method as described by Evanno et al. (2005) and plotting delta K did not result in a ‘plateau’ and as such it was not clear what value for K was the most likely. Maximum average log likelihood Ln P(X|K) values plotted against number of inferred clusters (K) demonstrated that K = 1 best fit the data (Fig. 2), as the highest log likelihood was obtained with K = 1.
Kgtests indicated no population expansion in the dataset. The k test revealed that 9 out of 12 loci had a negative kurtosis, a bias that was close to significance (P = 0.06). The g test estimated that the variance of the allele sizes was 8.01. According to the fifth-percentile cutoff table given by Reich et al. (1999), this value was not significant.
Gene flow patterns between sample locations
Mantel tests detected no significant correlation between genetic distance and two measures of geographic distance (P = 0.157 normally transformed and log transformed P = 0.448). The estimated number of migrants (Nm) per generation (Table 3) showed a range from 4.96 (between ZWF and EAV) to 1.50 (between NOR and OVE). The average number of migrants per generation among the Dutch breeding locations, and corrected for sample size, was 2.79.
Discussion
The multi-locus microsatellite data presented here suggest the most likely explanation for the lack of genetic structure is that Black-tailed Godwit breeding areas in The Netherlands comprise a single panmictic unit. Gene flow estimates demonstrated an overall migration rate of three individuals per generation among Dutch breeding locations. Genetic connectivity between areas is maintained by dispersal of successfully reproducing animals among breeding areas, i.e., gene flow. Slatkin (1985, 1987) concluded that only one migrant per generation is needed to counter any disruptive effects of genetic drift. Mills and Allendorf (1996) suggest that this number should actually be larger than one in many natural populations and that the one migrant per generation rule should be considered as a minimum. Hence, according to both Mills and Allendorf (1996) and Slatkin (1985) the gene flow rate found in our study should be enough to minimize genetic differentiation. Subsequently, results of the Mantel test demonstrated no isolation by distance that would indicate restrictions on gene flow. This shows that dispersal movements have taken place well beyond the 18 km range, as far as 134 km, which demonstrates the high breeding mobility capabilities of this species. Groen (1993) and van den Brink et al. (2008) have most likely underestimated the dispersal distance of the Black-tailed Godwit. This is supported by unpublished observations of Kentie et al. which indicate that adult birds seek out new breeding sites up to 10 km from the previous breeding site.
Bayesian analysis in STRUCTURE showed that all individual Black-tailed Godwits could most likely be assigned to one genetic cluster. This was supported by pairwise FST calculations which demonstrated little (ranging from −0.0168 to 0.01337) or no significant differentiation between locations. Additionally, none of the FIS values was significantly different from zero for any of the locations, indicating an absence of inbreeding. Subsequently, AMOVA showed that more than 99% of the molecular variation was found across all individuals, while an insignificant proportion (0.3%) was attributable to variation between individuals from different locations. Interestingly, Höglund et al. (2009), using mitochondrial DNA from four Dutch Black-tailed Godwit breeding sites, did not detect any genetic structure either. This suggests that all subpopulations are affected by long term panmixis or that gene flow between different breeding areas ceased too recently for both marker types to detect geographical differences (Zink and Barrowclough 2008).
The level of genetic diversity in the Black-tailed Godwit in our study is higher (average of 6.3 alleles per locus) compared to that reported by Höglund et al. (2009) who found rather low genetic diversity (1 haplotype) within Dutch Black-tailed Godwits using mitochondrial DNA. However, the marker they used (the second domain of the control region, a part that is highly conserved) might be less suitable for detection of genetic variation. The Dutch samples in their study came from the western part of The Netherlands only, whereas 50% of the population resides in the northern part of the country, possibly holding a significant amount of the total population genetic variation. All together it appears that the Dutch Black-tailed Godwit population is not confronted with immediate genetic threats and we argue that according to these data Dutch Black-tailed Godwit populations should be managed as one panmictic unit, much as it is presently done.
References
Barton NH, Slatkin M (1986) A quasi-equilibrium theory of the distribution of rare alleles in a subdivided population. Heredity 56:409–415
Beintema A, Moedt O, Ellinger D (1995) Ecologische Atlas van de Nederlandse Weidevogels. Schuyt & Co, Haarlem
Benton TG, Bryant DM, Cole L, Crick HOP (2002) Linking agricultural practice to insect and bird populations: a historical study over three decades. J Appl Ecol 39:673–687
Bilgin R (2007) Kgtests: a simple Excel Macro program to detect signatures of population expansion using microsatellites. Mol Ecol Notes 7:416–417
Birdlife International (2004). Birds in Europe: population estimates, trends and conservation status. Birdlife International, Cambridge
BirdLife International (2009) Species factsheet: Limosa limosa. http://www.birdlife.org Accessed 29 Jan 2010
Cramp S, Simmons KEL (1983) The birds of the Western Palearctic. Volume III: waders to gulls. Oxford University Press, Oxford, UK
Dent EA (2009) STRUCTURE HARVESTER version 0.56.3 http://taylor0.biology.ucla.edu/struct_harvest/
Evanno G, Regnaut S, Goudet J (2005) Detecting the number of clusters of individuals using the software STRUCTURE: a simulation study. Mol Ecol 14:2611–2620
Excoffier L, Laval G, Schneider S (2005) Arlequin (version 3.0): an integrated software package for population genetics data analysis. Evol Bioinform Online 1:47–50
Glaubitz JC (2004) CONVERT: a user friendly program to reformat diploid genotypic data for commonly used population genetic software packages. Mol Ecol Notes 4:309–310
Goudet J (1995) FSTAT (version 1.2): a computer program to calculate F-statistics. J Heredity 86:485–486
Groen NM (1993) Breeding site tenacity and natal philopatry in the Black-tailed Godwit. Ardea 81:107–113
Haverschmidt F (1963) The black-tailed godwit. E.J. Brill, Leiden
Hey J, Nielsen R (2007) Integration within the Felsenstein equation for improved Markov chain Monte Carlo methods in population genetics. Proc Natl Acad Sci USA 104:2785–2790
Höglund J (2009) Evolutionary conservation genetics. Oxford University Press, Oxford
Höglund J, Johansson T, Beintema A, Schekkerman H (2009) Phylogeography of the Black-tailed Godwit Limosa limosa: substructuring revealed by mtDNA control region sequences. J Ornithol 150:45–53
Hurlbert SH (1971) The nonconcept of species diversity: a critique and alternative parameters. Ecology 52:577–586
Kleijn D, Schekkerman H, Dimmers WJ, van Kats RJM, Melman D, Teunissen WA (2010) Adverse effects of agricultural intensification and climate change on breeding habitat quality of Black-tailed Godwits Limosa l. limosa in the Netherlands. Ibis 152:475–486
Kuhner MK (2009) Coalescent genealogy samplers: windows into population history. Trends Ecol Evol 24:86–92
Liebezeit JR, Smith PA, Lanctot RB, Schekkerman H, Tulp I, Kendall SJ, Tracy DM, Rodriques RJ, Meltofte H, Robinson JA, Gratto-Trevor C, McCaffery BJ, Morse J, Zack SW (2007) Assessing the development of shorebird eggs using the flotation method: species-specific and generalized regression models. Condor 109:32–47
Luikart G, Sherwin WB, Steele BM, Allendorf FW (1998) Usefulness of molecular markers for detecting population bottlenecks via monitoring genetic change. Mol Ecol 7:963–974
Mills LS, Allendorf FW (1996) The one-migrant-per-generation rule in conservation and management. Conserv Biol 10:1509–1518
Mulder T (1972) De grutto (Limosa limosa (L)) in Nederland: aantallen, verspreiding terreinkeuze, trek en overwintering. Bureau van de KNNV, Hoogwoud
Peakal R, Smouse PE (2006) GENALEX 6: genetic analysis in Excel. Population genetic software for teaching and research. Mol Ecol Notes 6:288–295
Pritchard JK, Stphens M, Donnelly P (2000) Inference of population structure using multilocus genotype data. Genetics 155:945–959
Qiagen (2003) DNeasy tissue handbook. Protocol for isolation of total DNA from animal tissues. QIAGEN, Valencia, pp 18–20
Raymond M, Rousset F (1995) GENEPOP (version 1.2): population genetics software for exact tests and ecumenicism. J Hered 86:248–249
Reich DE, Feldman MW, Goldstein DB (1999) Statistical properties of two tests that use multilocus data sets to detect population expansions. Mol Biol Evol 16:453–466
Rice WR (1989) Analysing tables of statistical tests. Evolution 43:223–225
Richardson DS, Jury FL, Blaakmeer K, Komdeur J, Burke T (2001) Parentage assignment and extra-group paternity in a cooperative breeder: the Seychelles warbler (Acrocephalus sechellensis). Mol Ecol 10:2263–2273
Schekkerman H, Teunissen WA, Oosterveld E (2008) The effect of ‘mosaic management’ on the demography of black-tailed godwit Limosa limosa on farmland. J Appl Ecol 45:1067–1075
Schekkerman H, Teunissen WA, Oosterveld E (2009) Morality of Black-tailed Godwit Limosa limosa and Northern Lapwing Vanallus vanellus chicks in wet grasslands: influence of predation and agriculture. J Ornithol 150:133–145
Schroeder J, Hinsch M, Hooimeijer JCEW, Piersma T (2009) Faillissement dreigt voor Nederlands weidevogelbeleid. De Levende Nat 110:333–338
Selkoe KA, Toonen RJ (2006) Microsatellites for ecologists: a practical guide to using and evaluating microsatellite markers. Ecol Lett 9:615–629
Slatkin M (1985) Gene flow in natural populations. Annu Rev Ecol Syst 16:393–430
Slatkin M (1987) Gene flow and the geographic structure of natural populations. Science 236:787–792
Smouse PE, Long JC (1992) Matrix correlation analysis in anthropology and genetics. Yearb Phys Anthropol 35:187–213
Smouse PE, Long JC, Sokal RR (1986) Multiple regression and correlation extensions of the Mantel test of matrix correspondence. Syst Zool 35:627–632
Stoate C, Báldi A, Beja P, Boatman ND, Herzon I, van Doorn A, de Snoo GR, Rakosy L, Ramwell C (2009) Ecological impacts of early 21st century agricultural change in Europe—a review. J Environ Manag 91:22–46
Trimbos KB, Broekman J, Kentie R, Musters CJM, de Snoo GR (2009) Using eggshell membranes as a DNA source for population genetic research. J Ornithol 150:915–920
van den Brink V, Schroeder J, Both C, Lourenco PM, Hooijmeijer JCEW, Piersma T (2008) Space use by Black-tailed Godwits Limosa limosa limosa during settlement at a previous or a new nest location. Bird Study 55:188–193
van Oosterhout C, Hutchinson WF, Wills DPM, Shipley P (2004) MICRO-CHECKER: software for identifying and correcting genotyping errors in microsatellite data. Mol Ecol Notes 4:535–538
van Turnhout CAM, Foppen RPB, Leuven RSEW, Siepel H, Esselink H (2007) Scale-dependent homogenization: changes in breeding bird diversity in the Netherlands over a 25-year period. Biol Conserv 134:505–516
Verkuil YI, Trimbos K, Haddrath O, Baker AJ, Piersma T (2009) Characterization of polymorphic microsatellite DNA markers in the black-tailed godwit (Limosa limosa: Aves). Mol Ecol Res 9:1415–1418
Zink RM, Barrowclough GF (2008) Mitochondrial DNA under siege in avian phylogeography. Mol Ecol 17:2107–2121
Zwarts L, Bijlsma RG, van der Kamp J, Wymenga E (2009) Living on the edge. Wetlands and birds in a changing Sahel. KNNV Publishing, Zeist
Acknowledgments
We hereby declare that the experiments comply with the current laws of the country in which they were performed. Lida Kanters, David Kleijn, Rene Faber, Astrid Kant, Gerrit Gerritsen, Wim Tijssen and Dirk Tanger all helped to collect egg shell membrane samples. We thank Jos Hooijmeijer, Petra de Goeij, Pedro Lourenço and the rest of the University of Groningen Black-tailed Godwit team for their help in collecting eggshells and blood samples in South-west Fryslân, sharing their blood samples collected at other Dutch Black-tailed Godwit breeding sites, and providing laboratory space for DNA extractions, courtesy of Marco van der Velde. Klaas Vrieling and Rene Glas of the Leiden Institute of Biology (IBL) were helpful with PCR amplifications and providing laboratory space. Dick Groenenberg and Camiel Doorenweerd helped with the interpretation of the data.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Trimbos, K.B., Musters, C.J.M., Verkuil, Y.I. et al. No evident spatial genetic structuring in the rapidly declining Black-tailed Godwit Limosa limosa limosa in The Netherlands. Conserv Genet 12, 629–636 (2011). https://doi.org/10.1007/s10592-010-0167-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10592-010-0167-8