Abstract
Most native red foxes (Vulpes vulpes) in the western contiguous United States appear to be climatically restricted to colder regions in the major mountain ranges and, in some areas, have suffered precipitous declines in abundance that may be linked to warming trends. However, another population of unknown origin has occurred in arid habitats in the Sacramento Valley of California well outside this narrow bioclimatic niche since at least 1880. If native, this population would be ecologically distinct among indigenous North American red foxes. We used mitochondrial and microsatellite markers from historical and modern samples (modes: 1910–1930 and 2000–2008, respectively) obtained throughout the western United States to determine the origins of the Sacramento Valley red fox, and assess the historical and modern connectivity and genetic effective population sizes of Sacramento Valley and montane red foxes. We found clear and consistent evidence supporting the indigenous origin of the Sacramento Valley population, including the phylogenetic positioning of the dominant, endemic mtDNA clade and microsatellite clustering of the Sacramento Valley population with the nearest montane population. Based on both mitochondrial and microsatellite AMOVAs, connectivity among Western populations of red foxes declined substantially between historical and modern time periods. Estimates based on temporal losses in gene diversity for both marker types suggest that both the Sierra Nevada (including the Southern Cascades population) and the Sacramento Valley populations have small genetic effective population sizes. Significant heterozygote excesses also indicate the occurrence of recent bottlenecks in these populations. Both substitutions distinguishing the 2 endemic Sacramento Valley haplotypes from the dominant montane haplotype were in the coding region and nonsynonymous, consistent with adaptive differences. These findings along with previously reported body size distinctions between Sacramento Valley and montane red foxes argue for distinct subspecific status for the Sacramento Valley red fox, for which we propose the designation V. v. patwin n. subsp. The small genetic effective population size estimates for the Sierra Nevada red fox and Sacramento Valley red fox are cause for concern, as is the possibility of genetic introgression into the latter population from an adjacent, recently established nonnative population.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Multiple lineages of the red fox (Vulpes vulpes) occupy subalpine and alpine habitats in the Cascade Range (V. v. cascadensis), Sierra Nevada (V. v. necator), and Rocky Mountains (V. v. macroura) of the western contiguous United States (US), where they are believed to be restricted by specialized adaptations to cold climatic zones (Grinnell et al. 1937; Aubry 1983; Perrine 2005). These montane foxes are phylogenetically, morphologically, and ecologically distinct from red foxes native to eastern and northern North America (Roest 1977; Swanson et al. 2005; Perrine et al. 2007; Aubry et al. 2009). In the 1900s, North American red foxes of Eastern and Northern ancestry were introduced to and have thrived in several warm, lowland regions of Washington, Oregon, and California (Aubry 1984; Lewis et al. 1999; Kamler and Ballard 2002). Additionally, red foxes have occupied arid, lowland habitats in the Sacramento Valley of California since at least 1880, which predates both the earliest known fur farms and the establishment of other lowland and putatively introduced red fox populations in western North America (Grinnell et al. 1937; Kamler and Ballard 2002).
Owing in part to a paucity of information of the pre-European fauna of northern California, the origins of the Sacramento Valley population are unknown (Hall 1981). The anomalous nature of the semi-desert habitat conditions in the Sacramento Valley relative to the subalpine and alpine habitats occupied by native montane red foxes in the western contiguous US led to early speculation that this population may have been introduced (Grinnell et al. 1937). This belief later appeared to be supported by a morphometric study, which demonstrated that Sacramento Valley foxes were significantly larger than montane foxes but similar in size to Midwestern foxes (Roest 1977), suggesting that exotic red foxes could have been transported to the Valley via transcontinental railway, after it reached the city of Sacramento in 1869 (Roest 1977; Lewis et al. 1999; Kamler and Ballard 2002). However, recent mitochondrial analyses of historical and modern specimens from the Sacramento Valley indicated this population was distinct from other nonnative populations in California, which were clearly of Eastern and Northern origins (Perrine et al. 2007; Aubry et al. 2009). Moreover, the most common haplotype (D) in the Sacramento Valley differed by a single substitution from the dominant haplotype (A) of the Western mountains. However, the cytochrome b marker lacked sufficient resolution to rule out the possibility that the D haplotype was a rare Eastern haplotype. A more rapidly evolving portion of the mitochondrial genome, such as the D-loop, is needed to confidently determine the origins of the Sacramento Valley red fox. If native to the West, microsatellites would be needed to determine whether the founders came from California or elsewhere in the West along the transcontinental railway (e.g., Wyoming, Utah, or Nevada).
Resolving the origins of the Sacramento Valley population is especially important in light of contemporary indicators that this population could be at risk. Because it is presumed to be nonnative, this population currently receives no special protection. Anecdotal evidence suggests that in recent decades this population has declined in abundance within its historical range (Grinnell et al. 1937; Gray 1975; M. Wolder, US Fish and Wildlife Service, personal communication). Moreover, populations that occupy the adjacent San Joaquin Valley to the south, which presumably originated primarily from nonnative fur-farm stock, have recently expanded their range and may come into contact with the Sacramento Valley population (Lewis et al. 1999; Perrine et al. 2007). Hybridization with these inbred, admixed, and invasive foxes would compromise the genetic integrity of the Sacramento Valley population, and could reduce their fitness through the loss of locally adapted alleles or disruption of coadapted gene complexes. Lastly, if native, the Sacramento Valley red fox could represent the closest living relative to the endangered Sierra Nevada red fox (Perrine et al. 2007), which occurs within about 65 km, albeit in a vastly different habitat and climate.
The range of the Sierra Nevada red fox appears to have retracted precipitously in recent decades (Gould 1980; CDFG 1996, 2004; Perrine 2005; Perrine et al. 2007). As with other mammals restricted to high-elevation habitats in mid-latitude mountain ranges (Grayson 2005; Aubry et al. 2007), these montane red foxes could be experiencing the adverse effects of climatic warming (Perrine et al. in press). Little is known about the current status of the Cascade or Rocky Mountain red foxes, but indications of potential range losses in the Cascade Range are beginning to emerge (K. Aubry, unpublished data).
The primary objective of the present study was to determine the origins of the Sacramento Valley population and, if native, to evaluate its conservation status. These objectives necessitated a comprehensive analysis of both historical and modern genetic samples from throughout the range of native montane red foxes, which enabled us to also assess both historical and current connectivity among native red fox populations in the western contiguous US (hereafter, “Montane,” where capitalization is used to distinguish ancestry from habitat affinity). Thus, our overarching goals were to develop new understandings of the population genetic structure, taxonomy, and conservation status of Montane red foxes (including the Sacramento Valley population).
Materials and Methods
Samples
We sampled red fox specimens collected throughout the western contiguous US between 1880 and 2008, excluding populations likely or known to be nonnative (Aubry 1983, 1984; Perrine et al. 2007), and also included a sample of Eurasian red foxes as an outgroup. The specimens had a bimodal temporal distribution, which facilitated their division into historical (1880–1950) and modern (1951–2008) samples (Fig. S1, Table S1; Supplementary Information). Collection dates for historical and modern specimens were 75 years apart on average, and represent time periods that occurred either before or after the establishment of several putative nonnative populations (Kamler and Ballard 2002).
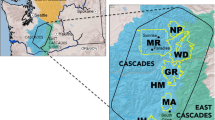
For analytical purposes, we classified our samples into the following geographical units (hereafter, populations): (1) San Joaquin Valley, (2) Rocky Mountains, (3) Northern Cascades, (4) Southern Cascades, (5) Sierra Nevada, and (6) Sacramento Valley. The San Joaquin Valley population was known to be nonnative (Perrine et al. 2007) and was included for reference because it was parapatric with the Sacramento Valley red fox along its southern range limits (Gould 1980; Perrine et al. 2007). The range of V. v. cascadensis is believed to encompass the breadth of the Cascade Range from Washington to northern California (Hall 1981). However, the Columbia River Gorge at the border of Washington and Oregon is a potentially significant barrier to gene flow (Gordon 1966), and a lack of connectivity between these populations could confound our results. Consequently, we analyzed samples collected north and south of the Columbia River separately (Northern Cascades and Southern Cascades, respectively). Additionally, we divided V. v. necator into populations occupying the Sierra Nevada proper and those to the north in the southern Cascades of California, which were grouped with the Southern Cascades population (i.e., extending into Oregon). Because of the large geographic area occupied by V. v. macroura, potential discontinuity among higher portions of ranges, and uncertainty of origin of samples in a recently colonized part of Nevada (in the intermountain zone), we divided the Rocky Mountains population into three subpopulations; use of subpopulations in some analyses also ensured similar extents among geographical units.
Mitochondrial sequences for many of the historical specimens used in our analyses were available from previous studies (Perrine et al. 2007; Aubry et al. 2009), but most of our modern samples were obtained for this study (Fig. S1). We included all known historical specimens of the red fox from the Sacramento Valley in our sample (Perrine et al. 2007). We sampled museum specimens with maxilloturbinal bones or skin snips (Wisely et al. 2004). Most modern specimens were salvaged road kills and foxes removed as part of animal-control activities, but also included 25 scat samples. For the modern sample of Sacramento Valley red foxes, we avoided sampling in the southernmost extent, to minimize the potentially confounding influence of genetic introgression from the San Joaquin Valley.
Laboratory procedures
We conducted DNA extraction, polymerase chain reaction (PCR) amplification, sequencing, and genotyping primarily at the Veterinary Genetics Laboratory of University of California, Davis; however, DNA extraction was also performed in other laboratories (Perrine et al. 2007; Aubry et al. 2009). We extracted DNA from muscle or ear-tissue samples using the DNeasy® tissue kit (Qiagen Inc.), from scats using the QiaAmp® Stool Kit (Qiagen, Inc.), and from maxilloturbinal bones or skin snips using a previously described phenol–chloroform protocol in a dedicated ancient DNA laboratory (Wisely et al. 2004; Perrine et al. 2007; Aubry et al. 2009). Primers, PCR chemistry and cycling condition for the mtDNA D-loop and cytochrome b loci were as previously reported (Perrine et al. 2007; Aubry et al. 2009) as were those for 14 microsatellite loci (Sacks and Louie 2008). We sequenced samples in both forward and reverse directions and purified PCR product using Millipore PCR purification plates and a sequencing reaction using the ABI big-dye-terminator cycle sequencing kit 2.0 (Applied Biosystems). We cleaned up sequencing product using Millipore SEQ96 plates and then electrophoresed on an ABI 3730 capillary sequencer (Applied Biosystems). We aligned sequences visually using Sequencher 4.5 software.
An inherent problem with the use of museum samples in genetic analyses is that they are more prone to sequencing or genotyping errors and contamination (Wandeler et al. 2007). One way to detect such errors is to compare independently determined portions of a clonally inherited marker such as mtDNA. Therefore, we compared cytochrome b to D-loop haplotypes and when haplotypes from these 2 portions of the mtDNA genome were incompatible, we re-amplified and re-sequenced them at least 2 more times. Due to the special significance of historical samples from the Sacramento Valley, we re-extracted and re-sequenced/genotyped them at all mtDNA and microsatellite loci. Additionally, we twice re-amplified and genotyped a subset of 22 historical (i.e., those with sufficient DNA) and 41 modern samples at the 14 microsatellite loci to assess genotyping error. Genotyping error associated with fecal DNA samples was previously estimated based on 170 replicated multilocus genotypes to include 2.3% allelic dropout and 1% false alleles (Moore 2009). We based all mtDNA analyses on a 696-bp portion of the mitochondrial genome composed of 354 bp of the cytochrome b gene and 342 bp of the D-loop, chosen to facilitate direct comparison with previous analyses (Perrine et al. 2007; Aubry et al. 2009).
mtDNA data analysis
We constructed a median-joining network using Network v4.111 with default parameters, except that polymorphisms in the cytochrome b region were conservatively weighted twice those in the D-loop region (Bandelt et al. 1999). We estimated gene and nucleotide diversity for each population in each time period (Nei 1987). We calculated Strobeck’s (1987) S statistic to test for admixture as might be expected in nonnative populations, particularly those derived from multiple source populations. We calculated summary statistics in DNasP v. 4 (Rozas et al. 2003).
We assessed connectivity separately in each time period using a Mantel test based on pairwise F ST to assess isolation-by-distance; if no such relationship was found, we used analysis of molecular variance (AMOVA) to assess overall connectivity among contemporaneous populations (Excoffier et al. 1992). We conducted these analyses and the computation of pairwise F ST estimates in Arlequin 3.1 (Excoffier et al. 2005). We used differences in historical and modern gene diversity to calculate estimates of local N e (Appendix S1). We also estimated the long-term genetic effective population size of the entire Montane group using a maximum-likelihood approach based on coalescent simulations conditioned on the data, as well as the traditional Watterson (1975) estimator, calculated using the program Fluctuate (Kuhner et al. 1995). To increase the accuracy of the maximum-likelihood estimate of θF (i.e., 2Neμ), we jointly estimated and parsed out population growth, g (1/μ per generation), because that is an independent process that would have affected the genealogical composition of the data set.
Microsatellite data analysis
We estimated observed and expected heterozygosity for each population in each time period using Arlequin 3.1 (Excoffier et al. 2005). We used a rarefaction procedure in program HP-rare to effectively equalize sample sizes for estimates of allelic richness and private alleles (Kalinowski 2005). To assess changes in genetic diversity over time within populations and between contemporaneous populations, we conducted a 1-way ANOVA with planned contrasts (Fisher’s LSD) of H e (arc-sin transformed; Zar 1999) on population-per-time-period samples using SYSTAT v. 9.0 (SPSS, Inc.). Because we sampled 2 of the 5 populations in only 1 time period, we could not use a 2-way ANOVA with time period and population as distinct factors.
Traditional moment-based and maximum-likelihood, coalescent-based parameter estimates have different strengths and weaknesses; consequently, we computed and presented both whenever possible. In general, the latter approach is less biased but tends to produce estimates with higher variance when sample sizes are small. For this reason, we replicated maximum-likelihood-based computations (3 times total), checked consistency (correlations between runs), and, if consistent, presented averages across runs. Because the 2 approaches use different characteristics of the data, the most robust conclusions were those supported by both approaches.
We calculated maximum-likelihood, coalescent-based estimates of gene flow for multiple populations in Migrate v. 2.1.3, assuming an infinite alleles model, variable mutation rates (varying according to a gamma distribution), and allowing for unequal population size and asymmetric gene flow (Beerli and Felsenstein 2001; Beerli 2004). We used default settings for the search strategy, except for the addition of a recommended adaptive-heating scheme (Beerli 2004).
We used both allele-frequency-based and genotype-based approaches to assess population divergence. The former approaches are more robust to allelic dropout or null alleles, whereas the latter methods use more information contained in the data. For the allele-frequency approach, we computed a matrix of pairwise genetic distance (Nei’s D A; Takezaki and Nei 1996) and used these values to generate a neighbor-joining tree, with bootstrap values calculated from 1,000 resampling (with replacement) cycles on loci using Populations 1.2.30 (O. Langella 1999, http://bioinformatics.org/~tryphon/populations/). We conducted this procedure both as an unrooted tree, including putative Montane populations, and rooted to the Eurasian sample.
For the genotype-based approach, we used a Bayesian model-based method implemented in Structure v. 2.0, using the admixture model with correlated allele frequencies (Pritchard et al. 2000; Falush et al. 2003). After 10 replicate runs of 20,000 MCMC cycles (first 10,000 discarded as burn-in) at each value of K = 2–7, we performed a final run at each K consisting of 1,100,000 cycles (the first 100,000 discarded).
Estimates of genetic effective population size (N e) using the temporal method tend to be overestimated when effects of gene flow are not parsed out (Palstra and Ruzzante 2008). Therefore, we computed maximum-likelihood estimates of N e and gene flow jointly based on temporally spaced samples using MLNE 1.0 (Wang and Whitlock 2003). For comparison between moment-based (Appendix S1) and maximum-likelihood estimates, we also used MLNE to estimate N e in each population assuming no gene flow between them. Replicate runs produced nearly identical results. Lastly, as a check on these estimates based solely on the modern samples, we used a linkage-equilibrium-based estimator with bias correction as implemented in LDNE (Waples 2006; Waples and Do 2008). We assumed a monogamous mating system, excluded alleles with frequencies < 0.05, and used jackknife-based confidence intervals (Waples and Do 2008).
To test for recent population declines, we assessed heterozygote excess relative to expectation under mutation-drift equilibrium among modern samples using program Bottleneck v 1.2.02 (Piry et al. 1999). When loci are highly polymorphic and have imperfect repeats, as was the case with most of our markers, the test has very low power to detect heterozygosity excess under assumptions of the stepwise mutation model (SMM) relative to the generally more powerful infinite alleles model (IAM; Cornuet and Luikart 1996). Therefore, we used the IAM model but also conservatively employed a 2-phase mutation model assuming 70% stepwise mutations. These tests were performed first using the same 14 loci used in all other analyses. Additionally, to increase power, we performed these tests on a subset of our modern samples (Rocky Mountains, Southern Cascades, and Sacramento Valley) genotyped at a total of 33 microsatellite loci, including 19 loci recently developed for red foxes (Moore et al. 2010). We used 1-tailed Wilcoxon rank sum tests (Piry et al. 1999) to assess statistical significance. The Sierra Nevada red fox (i.e., represented in this analysis by the Southern Cascades populations) was known a priori to have declined substantially (Perrine et al. in press) and served as a positive control.
Results
mtDNA analyses
The mtDNA samples used in our analyses were obtained from 229 foxes, resulting in 206 composite (i.e., cytochrome b and D-loop) haplotypes (Table S1). This sample included red foxes newly sequenced at cytochrome b (n = 106) and D-loop (n = 144) loci, mostly from the modern period (Fig. S1). Despite a substantial increase in sample sizes from previous studies (Perrine et al. 2007; Aubry et al. 2009), we found only 1 new cytochrome b haplotype (D2; Genbank Accession No. GU004541) and 6 new D-loop haplotypes (18, 20, 65, 66, 82, 83; Genbank Accession Nos. GQ911200–GQ911203; GU224186–GU224187), all of which were found only once, suggesting that the mtDNA diversity of the study region had been well sampled in previous studies. Re-extracting and re-sequencing samples with incompatible combinations of cytochrome b and D-loop portions resulted in 3 corrections to previously published sequences and the removal of 3 additional specimens for which we could not replicate or produce consistent sequences (Table S1).
Although a portion of the Sacramento Valley sample was previously sequenced at cytochrome b (Perrine et al. 2007), D-loop sequences from samples collected in this study revealed 3 new 696-bp composite haplotypes, D-19 (cytochrome b D, D-loop 19), D2-19, and A-18, which differed from the most common, most widely distributed, and basal Mountain subclade haplotype, A-19 (Aubry et al. 2009), by 1–2 substitutions. These haplotypes were exclusive to the Sacramento Valley and D-19 was the most common haplotype in both historical (75%, n = 8) and modern (97%, n = 34) samples (Table S1). Only 9 of 79 total substitutions observed previously in the composite haplotypes from a sample encompassing much of Europe, Asia, and North America were nonsynonymous (Aubry et al. 2009), yet both cytochrome b substitutions in the endemic Sacramento Valley haplotypes (D-19 and D2-19) were nonsynonymous, including one distinguishing them from each other (new in this study) and another distinguishing both of them from the basal Mountain haplotype (A-19). At the 308th position (i.e., of our 354 bases) of the D and D2 haplotypes, a C replaced a T in the A haplotype, thereby specifying a Threonine amino acid (D) instead of a Methionine amino acid (A). At the 298th position of the D2 haplotype, a C replaced the T in the D haplotype, thereby specifying a Histidine amino acid instead of a Tyrosene amino acid.
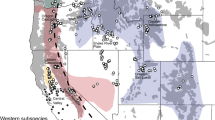
Previously, we identified a Holarctic clade and a Nearctic clade from a sample of historical museum specimens from Eurasia and North America (Aubry et al. 2009). Within North America, the Holarctic clade originated in Alaska and western Canada, whereas the Nearctic clade was subdivided into a Mountain subclade native to the West, an Eastern subclade native to the East, and a more ancient Widespread subclade with widely divergent haplotypes found in native populations of eastern North America or the western contiguous US (Fig. 1a). All haplotypes in both historical and modern samples from the Sacramento Valley, including the unique composite sequences (D-19, D2-19), belonged to the Mountain subclade (Fig. 1b; Table S1). In contrast, all samples from the nonnative population in the adjacent San Joaquin Valley had haplotypes originating from the phylogenetically distinct Eastern subclade or Holarctic clade (Fig. 1).
a Median-joining network of 696-bp composite cytochrome b and D-loop mtDNA haplotypes, with nodes color-coded by population composition. Cytochrome b substitutions were weighted 2× D-loop mutations. Branch lengths are proportional to the number of substitutions, with the shortest indicating a single substitution. b Geographic distribution of samples, color-coded according to composite cytochrome b and D-loop mtDNA clade or subclade (see inset). Multicolored samples indicate potential clades of incomplete sequences. We recognized one non-native population in the San Joaquin Valley (1), and 5 major Montane populations: the Rocky Mountains (2), Northern Cascades (3), Southern Cascades (4), Sierra Nevada (5), and Sacramento Valley (6). The “Rocky Mountains” were further divided into 3 subpopulations (dashed lines): Northern Rocky Mountains (2a), Eastern Rocky Mountains (2b), and Nevada (2c). Population breaks were finer than subspecies ranges in an attempt to resolve taxonomic uncertainties (Merriam 1900; Bailey 1936; Grinnell et al. 1937; Gordon 1966; Hall 1981; Aubry 1983). The shaded area represents one conception of the geographic range of native western red foxes (Hall 1981)
Although the historical haplotype diversity was slightly lower in the Sacramento Valley than in other populations, the most common haplotype was unique to the Sacramento Valley, suggesting this population was relatively isolated (Table 1). We found no significant evidence of admixture in the Sacramento Valley based on Strobeck’s (1987) S statistic (Table 1) or direct phylogenetic observations (Fig. 1). In contrast, Strobeck’s S statistic indicated a highly significant signature of admixture in the nonnative San Joaquin Valley population, where haplotypes clearly originated from phylogenetically divergent clades.
Haplotype diversity in the Sacramento Valley was higher in the historical sample (0.46) than in the modern sample, where it declined nearly to 0 (Table 1), reflecting a decline in the number of haplotypes from 3 (in a small sample) to 2 (in a large sample) between these time periods. Haplotype diversity also declined over time in the Southern Cascades population, from 0.86 historically to 0 in modern times, with numbers of haplotypes declining from a minimum of 5 to 1.
Mantel tests detected no significant isolation-by-distance relationships for historical or modern time periods (P > 0.10), enabling us to adopt an island model and use AMOVAs to quantify population structure. Although there was significant structure associated with both time periods, global AMOVA divergence estimates were higher for modern (F ST = 0.75; P < 0.001) than historical (F ST = 0.25; P < 0.001) time periods. Pairwise comparisons reflected this increase in divergence between time periods (Table 2).
To estimate the female genetic effective population sizes for both the Southern Cascades and Sacramento Valley populations, we used the decline in gene diversity between historical and modern times (Table 1) and conservatively assumed a 1-year generation time. The point estimate for the Southern Cascades (half a female) was meaningless, but the upper 95% confidence limit was 20 females (40 breeding adults, assuming an even sex ratio). The estimate for the Sacramento Valley was 19 females (38 breeding adults), with a 95% upper confidence limit of 49 females or 98 breeding individuals. We estimated long-term global genetic effective population size of the entire Montane group (including the Sacramento Valley population) using the 160 composite haplotypes from North American native populations (i.e., all but the Eurasian and nonnative San Joaquin Valley samples). The maximum-likelihood approach resulted in a higher estimate (θ F = 0.029; 95% CI = 0.026–0.032; Kuhner et al. 1995) than did the traditional Watterson estimator (θ W = 0.010), corresponding to long-term genetic effective population size estimates of 160,000 (95% CI = 161,700–181,300) versus 54,000 individuals, respectively, assuming a site-specific mutation rate of 1.02 × 10−7 (see Aubry et al. 2009). The maximum-likelihood estimate also accounted for population growth, which was low but significantly positive (g = 302 ± 95% CI = 204–399), corresponding to approximately 0.002% growth per generation.
Microsatellite analyses
We found 168 alleles among the 14 loci we genotyped in 211 red foxes, including 152 alleles in 192 individuals from 6 North American populations. Based on rarefaction (2n = 20 genes per population) to adjust for uneven sample sizes, we found no difference among populations in allelic richness (F 5,78 = 0.71, P = 0.62) or numbers of private alleles (F 5,78 = 1.25, P = 0.30) (Table 3). Deviations from Hardy–Weinberg were generally small in modern samples and somewhat larger in historical samples (Appendix S2). Correspondingly, we observed a 3.2% frequency of allelic dropout and a 0.7% frequency of false alleles in the replicated historical subsample (n = 432 allelic comparisons), compared to 0.8 and 0.4%, respectively, in the modern replicated subsample (n = 1,164 allelic comparisons). Information on the other 19 loci used in bottleneck analyses on a subset of the samples was presented elsewhere (Moore et al. 2010).
A 1-way ANOVA comparing H e among population-period groups indicated that significant differences were present (F 7,104 = 2.47, P = 0.02), and post-hoc tests revealed 4 significant pairwise differences (Fig. 2). In addition to the declines in heterozygosity from historical to modern times in the Southern Cascades and in the Sacramento Valley (P = 0.011 and 0.041, respectively), heterozygosity in these 2 populations was lower than in the Rocky Mountain population (P = 0.003 and 0.042, respectively) during modern times.
We detected no evidence of isolation-by-distance during either time period (P > 0.10), but we did find a general increase in divergence from historical to modern time periods (Fig. 3). As with mtDNA comparisons, this lack of isolation-by-distance was consistent with a rapid range expansion followed by isolation, enabling us to adopt the island model to estimate population-wide connectivity. The AMOVAs indicated a small historical global divergence estimate (F ST = 0.04; P = 0.04) and a relatively large one in modern times (F ST = 0.14; P < 0.001). Pairwise F ST values were also generally small among historical populations and larger among modern ones (Table 4). Maximum-likelihood F ST estimates were also higher on average in modern (F ST = 0.35, SE = 0.04) than historical (F ST = 0.27, SE = 0.03) comparisons, and indicated generally higher divergence than moment-based estimates. Particular pairwise F ST estimates in the historical data set were inconsistent across runs (average r < 0.05) likely due to small sample size, and were therefore not presented. Estimates for the modern data set, which had larger sample sizes, were reasonably well correlated across runs (average r = 0.89).
Estimates of F ST as a function of geographical distance (calculated from decimal degree coordinates) in historical and modern time periods (including the modern nonnative San Joaquin Valley population for reference). Pairwise F ST in both time periods between Southern Cascades (SCa) and both Northern Cascades (NCa) and the Sacramento Valley (SV) illustrate reductions in gene flow over time (arrows). The average F ST estimate between Eurasian and North American populations was 0.19, indicating saturation due to the high polymorphism of microsatellites
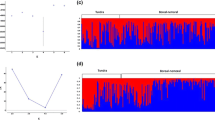
Within-population comparisons between historical and modern samples indicated non-significant F ST values for all populations except the Southern Cascades, for which historical and modern allele frequencies were significantly divergent (F ST = 0.19; P < 0.001). A tree of sampling sites indicated moderate bootstrap support for only a single cluster, the Sacramento Valley and historical Southern Cascades populations (Fig. 4a). When Rocky Mountain sampling sites were pooled and the tree rooted to Eurasian samples, bootstrap support was somewhat stronger for this cluster and also supported a cluster containing all but the Rocky Mountains population (Fig. 4b). Lastly, when historical and modern Southern Cascades populations were pooled, the cluster excluding the Rocky Mountains was strongly supported (Fig. 4c). Genotype-based analyses also suggested a hierarchical structure, with the Sacramento Valley and Southern Cascades populations clustered together at the most basal split (K = 2; Fig. 5).
Neighbor-joining tree describing Nei’s genetic distance (D A; Takezaki and Nei 1996) calculated using 14 microsatellite loci and bootstrapped on loci among populations or subpopulations of the Montane group pooled across time except in the Southern Cascades, and unrooted (a), or rooted to a Eurasian sample pooled across time for all samples except Southern Cascades (b) or including the Southern Cascades (c). Bootstrap support > 60% is indicated
Bayesian model-based clusters corresponding to 5 sample populations (and 3 subsamples within the “Rocky Mountains”, including Nevada [NV]) as determined for K = 2–6 clusters. Initial runs excluding 4 loci with the highest heterozygote deficits (Appendix S2) did not differ qualitatively from the one shown using 14 loci. Log probability of the data averaged across 10 runs for K = 2–6 were as follows: −6408, −6155, −6025, −5952, and −5894, respectively
Maximum-likelihood estimates of gene flow indicated generally low levels of migration among modern populations (Table 5). Only 1 estimate of migration exceeded 1 individual per generation, that from the Sacramento Valley into the Northern Cascades, which is likely an artifact of small sample size in the latter since gene flow between these populations seems exceedingly unlikely (and inconsistent with mtDNA). Estimates of recent gene flow also were low among the 3 modern California populations, and generally within the range seen in more distant populations. The low estimate for gene flow between the Sacramento Valley and San Joaquin Valley populations may simply reflect our lack of sampling in the potential contact zone; however, it does indicate that comparisons among native populations were not unduly biased by nonnative introgression into the modern Sacramento Valley population.
The ratios of modern-to-historical heterozygosity estimates in the Southern Cascades (H e(Mod)/H e(Hist) = 0.76) and Sacramento Valley (0.82) populations (Fig. 2a) result in estimates of N e = 140 (95% CI = 90–320) and N e = 188 (95% CI = 113–509), respectively, conservatively assuming a 1-year generation time. These estimates can be compared with the maximum-likelihood estimates of 142 (95% CI = 97–216) and 435 (95% CI = 271–808) for these populations, respectively, as calculated in MLNE assuming complete isolation. However, given the likely historical connections between these populations and the possibility of recent genetic introgression by males, we also jointly estimated N e and m between these populations using MLNE (Wang and Whitlock 2003), which indicated similar immigration into the 2 populations, m = 0.0256 (95% CI = 0.011–0.099) and m = 0.016 (95% CI = 0.007–0.045), respectively, along with considerably smaller estimates of N e: 45 (95% CI = 13–99) and 107 (95% CI = 42–227), respectively. The independent approach based on linkage disequilibrium within a single temporal sample produced somewhat lower estimates in the modern Southern Cascades (estimated N e = 21; 95% CI = 13–34) and Sacramento Valley populations (estimated N e = 49; 95% CI = 29–79). The 2-sample estimates would have been nearly identical to these estimates had we assumed a 2-year generation time. For comparative purposes, the linkage-disequilibrium method was also used with the historical Sierra Nevada sample, yielding an estimated N e of 62 individuals (95% CI = 35–163). The maximum-likelihood estimate of genetic effective population size for the entire Montane group that encompasses both historical and modern time periods (i.e., recent on an evolutionary timescale) (N e = 1,979; 95% CI = 1,290–3,421), was orders of magnitude smaller than the long-term genetic effective population size estimated from mtDNA data, which is consistent with a major population decline during the late Holocene.
Based on the entire data set with 14 loci, significant heterozygote excesses consistent with bottlenecks were detected in the modern Rocky Mountains (P < 0.001), Southern Cascades (P = 0.008), and Sacramento Valley (P = 0.016) populations under the IAM model. Interestingly, a heterozygote excess also was detected in the Sierra Nevada (historical only) under the IAM model (P = 0.039). Using the TPM model (70% SMM), heterozygote excess was only significant in the Rocky Mountains population (P < 0.001). Sample size was too small in the modern Northern Cascades population to assess heterozygote excess. Using the subset of modern samples genotyped at 33 loci, heterozygote excess was detected in all 3 tested populations—Rocky Mountains (n = 18), Southern Cascades (n = 20), and Sacramento Valley (n = 21)—under the IAM (all P < 0.001) and TPM models (P < 0.001, P = 0.02, and P = 0.02, respectively).
Discussion
The origin of the Sacramento Valley red fox
Our primary objective in this study was to determine whether the Sacramento Valley red fox was derived from individuals introduced by humans to the Valley in the mid to late 1800s (Roest 1977; Jameson and Peeters 1988; Lewis et al. 1999; Kamler and Ballard 2002), or was native to the Valley prior to European settlement, a possibility acknowledged by several earlier naturalists (Grinnell et al. 1937; Ingles 1965; Hall 1981). The dominant haplotype found in the Sacramento Valley during this study (D-19) appears endemic, as it has not been reported from other regions despite extensive surveys throughout North America and Eurasia (Frati et al. 1998; Valiere et al. 2003; Inoue et al. 2007; Aubry et al. 2009). The D-19 haplotype was phylogenetically nearest to (and likely derived from) the A-19 haplotype, which was the dominant haplotype in the Montane group. Second, the D2-19 haplotype (also likely endemic) was apparently derived from the D-19 haplotype, indicating molecular evolution within this population. Third, despite the substitution separating the D-19 and A-19 haplotypes, and the apparent lack of gene flow between these populations currently, nuclear microsatellites indicated that the Sacramento Valley population was most closely related to the Southern Cascades population (i.e., to the subspecies V. v. necator), based on both allele and genotype frequencies, as would be expected if the former arose naturally. In general, there was a comparable number of private alleles in the Sacramento Valley and other native populations, indicative of long-term residency.
In contrast, the nonnative California population that became established in the San Joaquin Valley by the late 1970s (Gould 1980) represented a phylogenetically diverse admixture of stock originating from both the Holarctic and Nearctic clades, including haplotypes naturally found in Alaska, western Canada, and eastern North America, but distinct from the nearby native montane populations (Aubry et al. 2009). This population was the only one to display a significant signature of admixture (Strobeck’s S). Microsatellite allele frequencies in the San Joaquin Valley population were no more similar to neighboring populations than to geographically distant ones, which is clearly inconsistent with its having arisen naturally. Although some nonnative arctic fox (Alopex lagopus) populations have been shown to exhibit low genetic diversity (i.e., no admixture) due to derivation from a small number of individuals from a single source, they were also characterized by unusual haplotypes from a distant location (Norén et al. 2006).
Because the dominant D-loop haplotype in the Sacramento Valley population is the basal Mountain subclade haplotype, our results clearly refute previous speculations that the Sacramento Valley population was of Midwestern origin (Roest 1977; Lewis et al. 1999). Additionally, the presence of an endemic mtDNA clade (2 haplotypes) and a moderate prevalence of private microsatellite alleles in the historical Sacramento Valley sample, which is comparable to other native populations, argue against this population having originated from a translocated sample of nearby montane red foxes. Thus, the genetic characteristics of the Sacramento Valley population met all expectations for a native, isolated population and none associated with a nonnative one, and strongly support the indigenous origin of the Sacramento Valley red fox.
Taxonomic implications for the Sacramento Valley red fox
Taxonomic designations at the subspecific level can significantly influence conservation efforts and their outcomes. Decisions about lumping versus splitting at this level also can be somewhat arbitrary, but criteria should be applied consistently within a taxon and should accurately reflect evolutionary relationships (Crandall et al. 2000; Fraser and Bernatchez 2001). Hall (1981) considered the Sacramento Valley red fox to belong to the same subspecies as those in the Sierra Nevada (V. v. necator), based presumably on proximity. Although our genetic analyses indicate a close phylogenetic relationship between these populations, substantial ecological differences exist between the Sacramento Valley and montane populations that probably reflect adaptations to varying local conditions, an important criterion in subspecies designation (Crandall et al. 2000). The Sacramento Valley differs substantially in climate and physiognomy from the montane habitat of V. v. necator, which might result in different selective pressures on body size, basal metabolic rate (BMR), and other attributes (Williams et al. 2004; Careau et al. 2007). Second, red foxes appear to be absent from the mid-elevation area (Fig. S2) that separates the Southern Cascades and Sacramento Valley populations by about 65 km; thus, these habitat conditions may have provided a barrier to gene flow that facilitated adaptive divergence. In addition, our estimates of mitochondrial and nuclear gene flow between these populations were low (e.g., Table 5).
Observed phenotypic and genetic differences between the Southern Cascades/Sierra Nevada and Sacramento Valley populations also are consistent with the hypothesis of adaptive divergence. For example, the larger average body size of the Sacramento Valley red fox compared to montane populations (Roest 1977; Aubry 1983; Aubry et al. 2009) contradicts predictions based on Bergmann’s Rule, and may instead reflect variation in the length of the growing season (e.g., Geist 1987) or character displacement associated with different carnivore assemblages in these 2 elevational zones (Fuentes and Jaksic 1979; Dayan et al. 1989). Additional research is needed to differentiate adaptive explanations from phenotypic plasticity in body size (Gortázar et al. 2000).
Our molecular findings also support the possibility of differential selection within the Sacramento Valley population on mitochondrial function. The only mtDNA substitutions separating the Sacramento Valley endemic haplotypes (D-19, D2-19) from the most common Mountain subclade haplotype (A-19) were in the coding region and were nonsynonymous. Only 8 other nonsynonymous substitutions (compared to 71 synonymous substitutions) were observed in composite haplotypes in our previous study (Aubry et al. 2009). Although genetic drift could account for the predominance of the D haplotype in the Sacramento Valley, the occurrence of 2 haplotypes with nonsynonymous mutations seem improbable results of chance alone, and point instead to the possibility of a selective sweep. Unfortunately, the low mitochondrial diversity of the Sacramento Valley population prevented the use of statistical tests for selection.
The mitochondria are involved in metabolism, which differs between cold and hot environments in other red fox populations (Careau et al. 2007). Others have found direct evidence of elevational selection in mammalian mitochondrial genes that may be related to the limits of thermoneutrality (Fontanillas et al. 2005). Altogether, these findings argue against assigning the Sacramento Valley population to one of the montane subspecies (i.e., V. v. necator, V. v. cascadensis, or V. v. macroura). Consequently, we propose that the Sacramento Valley red fox be designated a new subspecies, and propose the name V. v. patwin n. subsp. in recognition of the Native American group (along with the Nomlaki to the north) that occupied the central Sacramento Valley prior to European settlement. Information on the morphometrics, distribution, and other distinguishing characteristics of V. v. patwin is presented in the Appendix.
Temporal changes in the genetic structure of Montane red foxes
Previously, we used historical museum specimens to elucidate the broader phylogeographical structure of native North American red foxes (Aubry et al. 2009). Populations that occur in the Western mountains and in eastern North America comprise the Nearctic clade. This clade was highly divergent from the Holarctic clade, which includes populations of the red fox in northern North America and Eurasia. We also found strong evidence for population expansion by the Montane group at the end of the last glacial maximum (Aubry et al. 2009). Our findings in this study, which include modern samples, support these earlier conclusions and additionally elucidate the recent history of these populations. Geographic restriction of the more recently derived subclades suggests that the expansion was soon followed by a period of isolation among populations occurring in montane regions of the western contiguous US and in the Sacramento Valley. The temporal estimate of recent N e for the Montane group was an order of magnitude lower than the long-term estimate based on coalescent simulations, indicating a range-wide decline. Lastly, AMOVAs using both markers showed clear increases in isolation in the modern period relative to the historical period.
Although there is evidence of increasing fragmentation among montane populations and in the Sacramento Valley, we found little evidence that connectivity within the broad range of the Rocky Mountain population has declined over the past century. Moreover, although mitochondrial genetic diversity apparently declined in the Rocky Mountain population (including some lowland and montane regions of the intermountain West), red foxes apparently have expanded their range or increased in abundance in some areas (Fichter and Williams 1967). Until recently, it was presumed that these locations were invaded by nonnative red foxes from the East (Kamler and Ballard 2002, 2003). However, we found no genetic evidence to support the hypothesis of a wave of Eastern red foxes moving west. The small number of nonnative haplotypes we found in the Rocky Mountain region indicate that exotic genotypes were rare, although expanded sampling is required to assess the presence of local exotic populations where intensive farming of red foxes once occurred, such as on the margin of the Great Salt Lake in Utah (Westwood 1989). However, in general, modern populations of the Rocky Mountain red fox in both historical and expanded habitats are native to the region.
Taxonomic implications for the Cascade red fox
Our results support Grinnell et al.’s (1937) view that a single subspecies of montane red fox occurs in California, and also demonstrate that its range extends northward into Oregon. Based on both mtDNA and microsatellite data, the Southern Cascades and Sierra Nevada populations are very closely related, whereas the Northern Cascades population is not closely related to either. Thus, consistent with previous zoogeographic arguments (Gordon 1966), our results show that the Columbia River provides a barrier to gene flow among populations of red foxes that are currently classified in a single subspecies (V. v. cascadensis). Accordingly, we propose that the range of the Sierra Nevada red fox (V. v. necator) be modified to include the southern Cascade Range in California and Oregon, and that the range of the Cascade red fox (V. v. cascadensis) be limited to the Cascade Range in Washington (Table S1). Red foxes were known to occur throughout the northern Cascade Range as recently as the early 1980s (Aubry 1983, 1984). Since that time, however, neither broad-scale mesocarnivore surveys nor extensive research activities on Canada lynx (Lynx canadensis), wolverine (Gulo gulo), and other associated species have documented the continued presence of montane red foxes in the North Cascades (K. Aubry, unpublished data), consistent with ongoing range contraction. Otherwise, there is little empirical basis for assessing the current population status of montane red foxes in the Pacific Northwest. Given the critically endangered status of the Sierra Nevada red fox in California, a reliable assessment of the current distribution and abundance of montane red foxes in Oregon and Washington is urgently needed to adequately evaluate their conservation status.
Conservation status of the Sacramento Valley and Sierra Nevada red foxes
In California, montane populations of the red fox have declined in abundance over the past several decades to critically low numbers (Schempf and White 1977; Gould 1980; CDFG 1996; Perrine et al. in press). Our findings of (1) substantial declines in both mtDNA and nuclear genetic diversity, (2) estimates of contemporary genetic effective population sizes based on these markers, and (3) heterozygote excesses indicative of recent bottlenecks in the modern sample are consistent with this decline, and serve to validate our general approach. Thus, our findings also indicate that there may be cause for concern over the trajectory of the Sacramento Valley population. Both mtDNA and nuclear microsatellite diversity declined to a similar degree in the Southern Cascades and Sacramento Valley. Although our microsatellite-based estimates of contemporary genetic effective population size (and heterozygosity) were not as low in the Sacramento Valley as in the montane population, they were consistently low enough to raise concerns. For example, the International Union for the Conservation of Nature considers populations of breeding adults below 50 to be “critically endangered” and those below to 250 to be “endangered” (IUCN 2008). Although the genetic effective population size does not necessarily reflect the present number of breeding adults, it suggests that the population was very small recently and, thus, potentially vulnerable to extirpation. Thus, if our estimates are accurate, the Sacramento Valley red fox could require conservation measures to ensure its persistence.
Although the data we obtained from historical versus modern samples were of unequal quality, due to the higher prevalence of museum specimens in our historical sample, our findings cannot be explained on that basis alone. First, the lack of diversity in mtDNA in the modern period was based on large sample sizes. Second, the finding of 3 distinct haplotypes in the small historical sample was verified through re-extraction and re-sequencing, clearly demonstrating that genetic diversity was higher in the early 1900s than at present. Inferences drawn from microsatellite data generally agreed with those based on mtDNA data and, similarly, could not be explained by genotyping error. As is typically the case (Tableret et al. 1999; Wandeler et al. 2007), allelic dropout was more prevalent than false alleles among historical museum specimens. Thus, more frequent genotyping errors in the historical sample should have led to an underestimate of its heterozygosity relative to the modern sample, and therefore an underestimate of the decline in heterozygosity over time and an overestimate of historical N e. Most importantly, the method producing the lowest estimate of N e in both the Southern Cascades (21 individuals) and Sacramento Valley (45 individuals) populations was that based solely on the modern sample, thereby removing dependence of this conclusion on the historical sample. Third, in our temporal analyses, we conservatively assumed a generation time of 1 year, which would only be possible if this monestrous species was semelparous and always bred in the 1st year. If the true generation time were 2 years, all temporal estimates of genetic effective population size would be halved and become comparable to the more alarming estimates generated using the linkage-disequilibrium method. Lastly, the change in F ST estimates from historical to modern samples between the Sacramento Valley and Southern Cascades populations were consistent with these population size estimates based on simulations (Fig. S3).
There is little reliable information on the demographic characteristics of the Sacramento Valley population. Since the 1970s, biologists have observed increases in the distribution of low-elevation red foxes in California (Gray 1975; Gould 1980; Lewis et al. 1999). However, these assessments did not account for the distinction between native and nonnative lowland populations in California. It seems clear from our findings that most, if not all, of the observed increases in California red foxes represent range expansions or increasing densities of nonnative red foxes outside the Sacramento Valley. Anecdotal evidence suggests that the Sacramento Valley red fox has recently declined in abundance from at least some locations where it was abundant historically through the 1970s, coinciding with increases in coyote (Canis latrans) abundance following major restrictions in 1972 on the use of toxicants for predator control (Grinnell et al. 1937; Gray 1975; M. Wolder, US Fish and Wildlife Service, personal communication). Our own experiences interviewing residents and attempting to locate dens in the Sacramento Valley indicate that the distribution of red foxes in that region is highly discontinuous. Population monitoring designed to identify potential zones of hybridization between the Sacramento Valley red fox and non-native populations to the south may be an important first step for conserving this unique population of native red foxes.
References
Aubry KB (1983) The Cascade red fox: distribution, morphology, zoogeography and ecology. Dissertation, University of Washington, Seattle
Aubry KB (1984) The recent history and present distribution of the red fox in Washington. Northwest Sci 58:69–79
Aubry KB, McKelvey KS, Copeland JP (2007) Distribution and broadscale habitat relations of the wolverine in the contiguous United States. J Wildl Manag 71:2147–2158
Aubry KB, Statham MJ, Sacks BN, Perrine JD, Wisely SM (2009) Phylogeography of the North American red fox: vicariance in Pleistocene forest refugia. Mol Ecol 18:2668–2686
Bailey V (1936) The red fox in America. Nat Mag 28:269–272
Bandelt H-J, Forster P, Röhl A (1999) Median-joining networks for inferring intraspecific phylogenies. Mol Biol Evol 16:37–48
Beerli P (2004) Effect of unsampled populations on the estimation of population sizes and migration rates between sampled populations. Mol Ecol 13:827–836
Beerli P, Felsenstein J (2001) Maximum likelihood estimation of a migration matrix and effective population sizes in n subpopulations by using a coalescent approach. Proc Natl Acad Sci USA 98:4563–4568
Careau V, Morand-Ferron J, Thomas D (2007) Basal metabolic rate of Canidae from hot deserts to cold arctic climates. J Mammal 88:394–400
CDFG (1996) The status of rare, threatened and endangered animals and plants of California. California Department of Fish and Game, Sacramento
CDFG (2004) Special animals. California Department of Fish and Game, Sacramento
Cornuet JM, Luikart G (1996) Description and power analysis of two tests for detecting recent population bottlenecks from allele frequency data. Genetics 144:2001–2014
Crandall KA, Beninda-Emmonds ORP, Mace GM, Wayne RK (2000) Considering evolutionary processes in conservation biology. Trends Ecol Evol 15:290–295
Dayan T, Tchernov E, Yom-Tov Y, Simberloff D (1989) Ecological character displacement in Saharo-Arabian Vulpes: outfoxing Bergmann’s rule. Oikos 55:263–272
Excoffier L, Smouse PE, Quattro JM (1992) Analysis of molecular variance inferred from metric distances among DNA haplotypes: application to human mitochondrial DNA restriction data. Genetics 131:479–491
Excoffier L, Laval G, Schneider S (2005) Arlequin ver. 3.0: an integrated software package for population genetics data analysis. Evol Bioinform Online 1:47–50
Falush D, Stephens M, Pritchard JK (2003) Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics 164:1567–1587
Fichter E, Williams R (1967) Distribution and status of the red fox in Idaho. J Mammal 48:219–230
Fontanillas P, Depraz A, Giorgi MS, Perrin N (2005) Nonshivering thermogenesis capacity associated to mitochondrial DNA haplotypes and gender in the greater white-toothed shrew, Crocidura russula. Mol Ecol 14:661–670
Fraser DJ, Bernatchez L (2001) Adaptive evolutionary conservation: towards a unified concept for defining conservation units. Mol Ecol 10:2741–2752
Frati F, Hartl GB, Lovari S, Delibes M, Markov G (1998) Quaternary radiation and genetic structure of the red fox Vulpes vulpes in the Mediterranean Basin, as revealed by allozymes and mitochondrial DNA. J Zool 245:43–51
Fuentes ER, Jaksic FM (1979) Latitudinal size variation of Chilean foxes: tests of alternative hypotheses. Ecology 60:43–47
Geist V (1987) Bergmann’s rule is invalid. Can J Zool 65:1035–1038
Gordon K (1966) Mammals and the influence of the Columbia River Gorge on their distribution. Northwest Sci 40:142–146
Gortázar C, Travaini A, Delibes M (2000) Habitat-related microgeographic body size variation in two Mediterranean populations of red fox (Vulpes vulpes). J Zool Lond 250:335–338
Gould GI (1980) Status of the red fox in California. California Department of Fish and Game, Sacramento
Gray RL (1975) Sacramento Valley red fox survey. Nongame Wildl Invest Prog Rep, Job II-1.2. California Department of Fish and Game, Sacramento
Grayson DK (2005) A brief history of Great Basin pikas. J Biogeogr 32:2103–2111
Grinnell J, Dixon JS, Linsdale JM (1937) Fur-bearing mammals of California. University of California Press, Berkeley
Hall ER (1981) The mammals of North America, 2nd edn. Wiley, New York
Ingles LG (1965) Mammals of the Pacific states: California, Oregon, and Washington. Stanford University Press, Stanford
Inoue T, Nonaka N, Mizuno A, Morishima Y, Sato H, Katakura K, Okul Y (2007) Mitochondrial DNA phylogeography of the red fox (Vulpes vulpes) in northern Japan. Zool Sci 24:1178–1186
IUCN Standards and Petitions Working Group (2008) Guidelines for using the IUCN Red List categories and criteria. Version 7.0
Jameson EW Jr, Peeters HJ (1988) California mammals. California Natural History Guides 52. University of California Press, Berkeley
Kalinowski ST (2005) HP-Rare: a computer program for performing rarefaction on measures of allelic diversity. Mol Ecol Notes 5:187–189
Kamler JF, Ballard WB (2002) A review of native and nonnative red foxes in North America. Wildl Soc Bull 30:370–379
Kamler JF, Ballard WB (2003) Range expansion of red foxes in eastern Nevada and western Utah. J Ariz-Nev Acad Sci 36:18–20
Kuhner MK, Yamato J, Felsenstein J (1995) Estimating effective population size and mutation rate from sequence data using Metropolis-Hastings sampling. Genetics 140:1421–1490
Lewis JC, Sallee KL, Golightly RT Jr (1999) Introduction and range expansion of nonnative red foxes (Vulpes vulpes) in California. Am Midl Nat 142:372–381
Merriam CH (1900) Preliminary revision of the North American red foxes. Proc Wash Acad Sci 2:661–676
Moore M (2009) Impacts of encroaching nonnative red foxes on the Sacramento Valley red fox. Thesis, California State University, Sacramento
Moore M, Brown SK, Sacks BN (2010) Thirty-one short red fox (Vulpes vulpes) microsatellite markers. Mol Ecol Resour
Nei M (1987) Molecular evolutionary genetics. Columbia University Press, New York
Norén K, Dalén L, Kvaløy K, Angerbjörn A (2006) Detection of farm fox and hybrid genotypes among wild arctic foxes in Scandinavia. Conserv Genet 6:885–894
Palstra FP, Ruzzante DE (2008) Genetic estimates of contemporary effective population size: what can they tell us about the importance of genetic stochasticity for wild population persistence? Mol Ecol 17:3428–3447
Perrine JD (2005) Ecology of the red fox (Vulpes vulpes) in the Lassen Peak region of California, USA. Dissertation, University of California, Berkeley
Perrine JD, Pollinger JP, Sacks BN, Barrett RH, Wayne RK (2007) Genetic evidence for the persistence of the critically endangered Sierra Nevada red fox in California. Conserv Genet 8:1083–1095
Perrine JD, Campbell LA, Green GA (in press) Conservation assessment for the Sierra Nevada red fox. USDA For. Serv. Gen. Tech. Rep. PSW-GTR-XXX, Vallejo, California
Piry SG, Luikart G, Cornuet JM (1999) BOTTLENECK: a computer program for detecting recent reductions in the effective population size using allele frequency data. J Hered 90:502–503
Pritchard JK, Stephens M, Donnelly P (2000) Inference of population structure using multilocus genotype data. Genetics 155:945–959
Roest AI (1977) Taxonomic status of the red fox in California. Final Report, Job II-1.3. California Polytechnic State University, San Luis Obispo
Rozas J, Sánchez-De JC, Barrio I, Messeguer X, Rozas R (2003) DnaSP, DNA polymorphism analyses by the coalescent and other methods. Bioinformatics 19:2496–2497
Sacks BN, Louie S (2008) Using the dog genome to find SNPs in red foxes and other distantly related members of the Canidae. Mol Ecol Resour 8:35–49
Schempf PF, White M (1977) Status of six furbearer populations in the mountains of northern California. USDA Forest Service, Pacific Southwest Region, Berkeley
Strobeck C (1987) Average number of nucleotide differences in a sample from a single subpopulation: a test for subdivision. Genetics 117:149–153
Swanson BJ, Fuhrmann RT, Crabtree RL (2005) Elevational isolation of red fox populations in the Greater Yellowstone ecosystem. Conserv Genet 6:123–131
Tableret P, Waits LP, Luikart G (1999) Noninvasive genetic sampling: look before you leap. Trends Ecol Evol 14:324–327
Takezaki N, Nei M (1996) Genetic distances and reconstruction of phylogenetic trees from microsatellite DNA. Genetics 144:389–399
Valiere N, Fumagalli L, Gielly L, Miquel C, Lequette B, Poulle M-L, Weber J-M, Arlettaz R, Taberlet P (2003) Long-distance wolf recolonization of France and Switzerland inferred from non-invasive genetic sampling over a period of 10 years. Anim Conserv 6:83–92
Wandeler P, Hoeck PEA, Keller LF (2007) Back to the future: museum specimens in population genetics. Trends Ecol Evol 22:634–642
Wang JL, Whitlock MC (2003) Estimating effective population size and migration rates from genetic samples over space and time. Genetics 163:429–446
Waples RS (2006) A bias correction for estimates of effective population size based on linkage disequilibrium at unlinked gene loci. Conserv Genet 7:167–184
Waples RS, Do C (2008) LDNE: a program for estimating effective population size from data on linkage disequilibrium. Mol Ecol Resour 8:753–756
Watterson G (1975) On the number of segregating sites in genetical models without recombination. Theor Popul Biol 7:256–276
Westwood RE (1989) Early fur farming in Utah. Utah Hist Q 57:320–339
Williams JB, Munoz-Garcia A, Ostrowski S, Tieleman BI (2004) A phylogenetic analysis of basal metabolism, total evaporative water loss, and life-history among foxes from desert and mesic regions. J Comp Physiol B Biochem, Syst, Environ Physiol 174:29–39
Wisely SM, Madonado JE, Fleischer RC (2004) A technique for sampling ancient DNA that minimizes damage to museum specimens. Conserv Genet 5:105–107
Zar JH (1999) Biostatistical analysis, 4th edn. Prentice Hall, Upper Saddle River, NJ
Acknowledgments
We thank J. Bennett, M. Bodenchuk, M. Collinge, M. Jensen, E. McDonald, T. Pitlick, and J. Wiscomb of the USDA/Animal Plant Health Inspection Service/Wildlife Services and R. Beach, B. Chomel, B. Cypher, L. Dalén, P. Figura, M. Gilbert, R. Golightly, R. Jones, D. Kemner, and T. Schweitzer for donating modern red fox specimens. The following individuals graciously provided us access to museum specimens: R. Fisher and S. Peurach (National Museum of Natural History; USNM), C. Conroy and E. Lacey (Museum of Vertebrate Zoology; MVZ), J. Bradley (University of Washington Burke Museum), I. Torres and A. Engilis (University of California Davis Museum of Wildlife and Fish Biology), J. Bogiatto (California State University, Chico), J. Dines and I. Horovitz (Natural History Museum of Los Angeles County). H. Wittmer helped with sample collection and M. Moore provided technical assistance. We thank K. Helgen (USNM) for lengthy correspondence and advice on protocols for describing a new subspecies, J. Patton (MVZ) for help designating and describing the holotype, and R. Wayne and 2 anonymous reviewers for helpful suggestions on earlier drafts of this manuscript. Partial funding was provided by the Veterinary Genetics Laboratory and the Genetic Resources Conservation Program at the University of California, Davis; California Department of Fish and Game (Agreements Nos. P0780029, S0810020 and subcontract No. HBSDF12); UC Davis Center for Population Biology; USDA Forest Service, Pacific Northwest Research Station; and the Kansas State University Ecological Genomics Institute.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendix–Vulpes vulpes patwin, n. subsp. (Mammalia, Carnivora, Canidae) from the Sacramento Valley of California
Appendix–Vulpes vulpes patwin, n. subsp. (Mammalia, Carnivora, Canidae) from the Sacramento Valley of California
Holotype: MVZ-33550, subadult male, skin and skull, from 7 miles northeast of Maxwell, Colusa County, California, USA, 39.34832° −122.10165° (NAD 1927), collected November 7, 1923 by Joseph S. Dixon (field number 8359) and Sam Lamme. Standard body measurements taken by James L. Patton: 1055-390-70-104 = 10 ¾ lbs. Skull measurements (as per Aubry 1983): total length = 144.4 mm, condylobasal length = 137.4, zygomatic breadth = 71.0, palatal length = 66.2, post-palatal length = 63.1, palatal width = 17.5, braincase breadth = 47.4, interorbital breadth = 27.0, post-orbital breadth = 21.4, lyre breadth = 4.8, auditory bulla breadth = 18.0, rostral breadth = 23.9, maxillary tooth row = 64.4, length of first molar = 9.2, length of fourth premolar = 12.8, and (as per Roest 1977): nasal suture length = 50.3, nasal width = 10.5, and diastema length = 3.0.
Referred specimens: 22 accessioned specimens (deposited at the National Museum of Natural History [USNM], Washington, D.C.; Museum of Vertebrate Zoology, University of California at Berkeley; Museum of Wildlife and Fisheries Biology, University of California at Davis; California State University, Chico; see Table S1).
Diagnosis: Vulpes v. patwin occurs primarily in the red color phase, although 1 specimen with the cross phenotype is known (USNM 146294). It is typically similar in coloration to other North American subspecies in the red color phase. Preliminary morphometric comparisons indicate that, in combination, multiple skull measurements distinguish patwin from the Nearctic montane subspecies (V. v. necator, V. v. cascadensis, V. v. macroura) as well as the Nearctic eastern (V. v. regalis, V. v. rubricosa) and Holarctic (V. v. alascensis, V. v. abietorum) subspecies (Roest 1977; Aubry et al. 2009). Vulpes v. patwin is larger on average than V. v. necator (the geographically closest subspecies), although body mass and individual skull dimensions overlap between these subspecies (Roest 1977). Endemic mitochondrial haplotypes differentiate V. v. patwin from other subspecies for all specimens examined except 1 that was collected in 1906, which had a haplotype that also occurs in the Nearctic montane subspecies (Aubry et al. 2009; this study).
Distribution: Vulpes v. patwin occurs at elevations below 150 m in California’s Sacramento Valley, which is bordered to the west by the Coast Range, to the north by the Siskiyou Mountains, to the east by the southern Cascade Range and Sierra Nevada, and to the south by the Sacramento-San Joaquin River Delta.
Etymology: The name honors the Patwin, the Native American people who (along with the Nomlaki to the north) presumably shared the central Sacramento Valley with this subspecies prior to European colonization.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Sacks, B.N., Statham, M.J., Perrine, J.D. et al. North American montane red foxes: expansion, fragmentation, and the origin of the Sacramento Valley red fox. Conserv Genet 11, 1523–1539 (2010). https://doi.org/10.1007/s10592-010-0053-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10592-010-0053-4