Abstract
An innovative strategy for an optimal design of planar frames able to resist seismic excitations is proposed. The optimal design is performed considering the cross sections of beams and columns as design variables. The procedure is based on genetic algorithms (GA) that are performed according to a nested structure suitable to be implemented in parallel on several computing devices. In particular, this bi-level optimization involves two nested genetic algorithms. The first external one seeks the size of the structural elements of the frame which corresponds to the most performing solution associated with the highest value of an appropriate fitness function. The latter function takes into account, among other considerations, the seismic safety factor and the failure mode that are calculated by means of the second internal algorithm. The proposed procedure aims at representing a prompt performance-based design procedure which observes earthquake engineering principles, that is displacement capacity and energy dissipation, although based on a limit analysis, thus avoiding the need of performing cumbersome nonlinear analyses. The details of the proposed procedure are provided and applications to the seismic design of two frames of different size are described.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The structural design of a structure may be faced considering different aspects and strategies with increasing levels of complexity. The problem can be tackled accounting for static, seismic, or alternative load scenarios. Usually, in the case of seismic loads and for new structures, the codes [1] suggest the employment of global elastic analysis, performed according to an equivalent static load distribution or to a Response Spectrum Analysis (RSA) for seismic excitations, and then to singularly design each member. However, a local design does not ensure to have an effective global performance of the building, especially in seismic conditions. For the latter reason, modern design strategies of structures must observe the principles of global ductility that assure the capability to dissipate an adequate amount of energy before collapsing during an earthquake. To this aim, the behaviour factor to scale the design spectrum (evaluated on the basis of the structural typology and not calibrated on the specific structure) and the regulations associated with the strength hierarchy [2] of beams and columns, have been more recently introduced in the design process.
The adoption of a nonlinear approach for the assessment of structures, even in the case of design of new buildings, has been suggested by several authors both considering static [3, 4] and dynamic [5, 6] load conditions, for instance adopting pushover analyses within a performance-based approach [7]. Nonlinear analyses ensure a deeper knowledge of structures and are preferred in the study of existing structures; nevertheless, the required computational effort and the number of configurations that are usually needed to be analysed in a design process, make them usually unsuitable for a global speedy design of structures. A comparison between design algorithms adopting linear and nonlinear analyses is presented in [8], where a fast convergence is observed when the elastic optimization process is assumed, compared with the relatively slow but steady and smooth convergence of the inelastic optimization process.
In structural analysis, a fair compromise between linear and nonlinear (pushover and time-history) analyses in terms of computational effort is represented by the limit analysis. Plastic theory has been introduced since the early 1950 [9,10,11,12,13] and never stopped developing. Limit analysis is able to evaluate the global resistance of a structure subjected to a certain load condition with a reasonable computational cost, and was widely employed for design purposes since it also provides useful information in terms of failure mode [14, 15]. The latter aspect was taken into account in [16] where a failure mode control was introduced in the design process as well as the second order effects and the hierarchy strength principle. Comprehensive overviews of the performance-based plastic design methods and, more specifically, for the design of steel structures can be found in [17] and [18], respectively. Nevertheless, in the plastic design of a structure it is difficult to ensure meeting the desired global performance in terms of ductility demand.
The need to explore numerous structural configurations to reach a satisfactory design solution favoured the employment of evolutionary algorithms [19] to guide the design process and limit the number of configurations to be assessed. Under the simplified hypothesis of linear behaviour, evolutionary algorithms were widely employed in design problems [20,21,22,23,24]; alternative strategies based on the feasible direction method [25] on teaching–learning based [26] and ant colony [27] optimizations, or on the harmony search algorithm [28] were also proposed. The application of genetic algorithms in design contexts was also evaluated with reference to reinforced concrete structures [29], to steel frames with semi-rigid connections [30]. These procedures are often capable of accounting for different features, such as buckling effects [31], and different load scenarios besides gravity and seismic loadings, such as the effects of wind [32]. In the field of seismic analysis, dynamic simulations can also be employed and combined with evolutionary algorithms [33, 34]. Due to the needed computational effort, nonlinear analyses are rarely combined with evolutionary algorithms. Applications of pushover analyses in combination with genetic algorithms may be found in [35], for the retrofitting design of existing buildings, in [36] where geometric nonlinearities are also considered, and in [37] where structural configurations are selected by a genetic algorithm aiming at identifying a Pareto optimal design set.
The latter paper [37] is an example of combination of two different algorithms for structural optimization problems. Actually, evolutionary algorithms are often combined considering two different levels of accuracy for the same problem (rough selection of a set of approximate solutions with the first algorithm, and then identification of an optimal solution among those previously selected with the second one) or treating different aspects of the problem. Bi-level algorithms are very common in structural optimization or optimal shape design, where the minimization of the weight or cost of a structure is typically needed. Such minimization is considered as an upper-level objective, subjected to constraints involving bounds on displacements, stresses and contact forces, whose values are determined, in general, by solving the potential energy minimization problem at the lower level [38]. In the context of bi-level optimization strategies, nested evolutionary algorithms have been introduced since the early 1990s and include genetic algorithms, differential evolution, particle swarm or ant colony optimization methods, etc. (see [38] and references therein); however, only a few of them were applied to structural optimization along the years [39].
In terms of design criteria, the economic one (i.e. minimum weight) is often considered as the only variable to be minimized in the design process, as long as the structural requirements are satisfied. Within this context, the design problem consists in finding a set of variables, namely the cross section of the members, which minimize a certain function (weight of the structure) under some design constraints, which have to be evaluated following a structural analysis. The latter aspect usually prevents the formulation of explicit approaches for a comprehensive design of the structural members of buildings. Enrichments of such procedures led to including other performance objectives in the design process (e.g. the energy dissipation) to achieve an improved structural solution, that is the formulation of multi-objective design processes. The adoption of nonlinear static [40,41,42] and dynamic [43, 44] analyses was often combined with a multi-objective approach.
In the field of the limit analysis, some of the authors recently proposed a strategy for the evaluation of the ultimate load of frame structures in seismic conditions based on the application of evolutionary algorithms to the method of the combination of elementary mechanism [45]. The proposed methodology can be applied both to regular [46, 47] and irregular [48] frames. A further advance was then proposed in [49], where the second order effects [50] were introduced and a simplified capacity curve of a frame is derived to evaluate its seismic capacity. The results obtained by means of the procedure proposed in [49] allow evaluating the seismic vulnerability of an assigned frame and are here used as one of the needed steps in a bi-level optimal design strategy.
Precisely, a nested genetic algorithm (GA) for an optimal design of planar frames able to resist seismic excitations is here proposed. The optimal design is performed selecting the cross sections of beams and columns, here considered as the design variables, among a predefined set of profiles in order to satisfy structural safety and economic criteria. The procedure is composed of two levels: the upper algorithm (called “External GA”) assigns the cross sections to the members of the frame and provides the input data for the lower level routine (called “Internal GA”), which exploits the algorithm for the structural assessment of a specific configuration [49], able to evaluate the safety factor of the frame with respect to prescribed seismic load scenarios. Besides seismic safety factors, different design requirements are included in the evaluation of the fitness function of each frame such as economic cost (associated with the minimum weight) and strength hierarchy criterion privileging those frames associated with a more dissipative failure mode. The strategy is implemented in a dedicated software developed within the agent-based multiplatform environment Netlogo [51] and has been integrated into a cloud-based computational workflow built on top of the GARR Cloud Infrastructure, using modern and innovative strategies allowing to easily reproduce this work in accordance to the FAIR principles in OpenScience. The conceived approach is a multi-objective design strategy, compatible with the main modern concepts of earthquake engineering for an effective design of structures, which is keen to introduce additional design criteria and to vary the relative weights of the adopted criteria in the evaluation of the performance of a generic set of cross-sections distribution.
The novel contribution of the proposed methodology mainly involves the procedure itself rather than the capability of speeding up existing design strategies, and the comparison with already proposed methodologies should be made in terms of quality of the procedure. Precisely, to the best authors’ knowledge, a bi-level optimization algorithm with nested GA is here applied for the first time as a structural seismic design approach of frames. In addition, the design process not only avoids the employment of oversimplified linear analysis, but is able to include in the structural assessment the ductility resources of the structure although exploiting a limit analysis strategy. The presented procedure represents a fair compromise between accuracy and rapidity of the algorithm, since it avoids performing nonlinear static analyses, but is able to more accurately estimate the displacement capacity with respect to a linear approach, which requires assuming a priori the behaviour.
The procedure is validated against two significant case studies, which are duly analysed considering the needed computational effort, demonstrating how the designed frames are those which maximize the defined fitness and providing a discussion on the criteria included in the fitness function and how they affect the final outcome of the design procedure.
2 The proposed design strategy
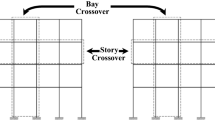
In the present study planar regular frames with columns clamped at the base are considered (Fig. 1). These are characterized by the number of floors Nf and the number of columns Nc. The length of all the beams is L and the height of the columns is H. Different constant cross sections for the beams within the same floor can be considered and the same assumption is made for the columns. The structural members are numbered starting from the base to the top of the frame and from left to right, first columns and then beams.
The frame may be loaded, at each floor, by permanent vertical distributed loads qk and concentrated horizontal forces Fk proportionally increased with a multiplier λ. With the aim of simulating seismic inputs, the horizontal forces are considered variable while the vertical loads are assumed to be distributed and of constant value within the same floor.
In the proposed design procedure, the geometry of the frame in terms of interstorey height and frame bays, is assigned. In addition, the vertical loads, and the horizontal ones, which depend on the weights, are considered known as well. The design variables are the cross sections associated with the members, that is their stiffness and resisting plastic moments.
The proposed design approach, consisting in the two nested genetic algorithms, is described in the following subsections. Specifically, in the first subsection, the External GA, devoted to the identification of the best set of cross sections to be assigned to the members of the frame, is described. Aiming at the evaluation of the fitness function for a certain set of cross sections investigated by the External GA, a procedure for the assessment of the corresponding seismic performance, according to the strategy proposed in [49], is run. The latter considers two load scenarios, each of which constitutes a procedure here addressed as Internal GA, briefly recalled in the second subsection. In the third subsection, the procedure for the definition and calculation of the fitness of the generic frame, which takes into account not only the seismic performance but also other meaningful criteria, and the considerations leading to the identification of the optimal design, are illustrated.
2.1 The external GA (design algorithm)
The main loop of the external algorithm is devoted to the definition of the cross sections to be assigned to the members of the frame. The cross sections of the structural members are assumed as design variables and can vary within a predefined list of commercial profiles for steel frames or, in the case of reinforced concrete structures, in a predefined list of conveniently chosen cross sections. Since the procedure adopted in the present paper, in order to identify the optimal set of profiles, makes use of genetic algorithms, a population of profile chromosomes is considered. Each individual of the population is coded as a string of integer numbers, where each number (called “gene”) identifies the considered commercial profile. Therefore, a generic profile chromosome \({C}_{k}^{ext}\) of the population (k = 1, …, Pext), being Pext the overall number of possible different external chromosomes, can be coded in the following string:
where
and \({c}_{i}\) represents the identification code of the cross section of the i-th structural element within the predefined list.
In the design of frames for engineering applications it is realistic to consider a vertical symmetry according to which the cross sections of both columns and beams within the same story can vary although respecting the symmetry condition. This consideration induces a drastic reduction of the number of independent genes as reported in Eq. (2).
It can also be interesting to consider the particular case in which a constant cross section for the beams within the same floor is taken into account and the same assumption is made for the columns. In this case it is easy to verify that the number of genes in the profile chromosome is equal to 2*Nf.
For each profile chromosome, and therefore for each generic frame, the correspondent seismic performance is evaluated by means of a limit analysis strategy procedure described in detail in [49], which represents the internal algorithm in the proposed nested strategy and is briefly recalled in the next Sect. 2.2. The seismic performance of the frame, together with other engineering requirements, contribute to the definition of the fitness of the profile chromosome and therefore to the identification of the optimal set of cross sections, as described in Sect. 2.3.
2.2 The internal GA (seismic assessment algorithm)
The inner level of the routine aims at evaluating the safety factor of the structural configurations selected by the upper level of the algorithm. Such inner procedure is able to reconstruct a capacity curve representing an equivalent single degree of freedom system, on which the verification suggested by the standards [1] are performed. The procedure, which was originally presented in [49], is able to account for geometric (second order effects) and constitutive nonlinearities and estimates the displacement capacity according to the main criteria suggested by the codes. The evaluation of the approximated capacity curve is here briefly recalled.
Specifically, the procedure exploits the estimation of the resistance of the structure, which is evaluated according to a limit analysis approach. Although a considerable number of possible approaches to compute the resistance of a frame through limit analysis could have been adopted, here the strategy proposed in a previous paper by the authors [46] is used. The adopted strategy makes use of the method of combination of elementary mechanisms [11, 45], following its combination with a genetic algorithm as proposed in [46]. This strategy has been extensively validated [46,47,48] with Finite Element nonlinear static analyses showing how fast and reliable it is. Given a profile chromosome \({C}_{k}^{ext}\), the load factor λo of the horizontal forces is calculated following an approach which takes into account the global collapse mechanisms obtained by means of linear combinations of three elementary ones: floor, beam and node mechanisms [11].
For each collapse mechanism, making use of the virtual work theorem, the value of the load multiplier λo is given by:
where \(\delta {W}_{extH}\) and \({\delta W}_{extV}\) represent the virtual work done by the horizontal forces and the vertical permanent load, respectively, and \({\delta W}_{int}\) is the internal virtual work concentrated in the plastic hinges. Analysing all the possible combinations of N elementary mechanisms, the minimum value of λo must be sought in order to obtain the real collapse load.
The optimization adopted within the inner level of the algorithm aims indeed at seeking the combination of elementary mechanisms which minimizes the load multiplier λo of the adopted load distribution, that is the correct collapse multiplier. The minimization procedure makes again use of genetic algorithms through the definition of the population of “internal chromosomes” \({C}_{h}^{int}\) (h = 1, …, Pint), being Pint the overall number of possible different internal chromosomes, defined as:
where \({c}_{j}\) = 1 or \({c}_{j}\) = 0 depending on fact that the j-th elementary mechanism is involved in the combination or not. For these internal algorithms, a number Nint of generations will be considered. Once the winning internal chromosome is sought through the procedure proposed in [46], the corresponding final collapse load \({\lambda }_{c}\) can be obtained by decreasing the load factor λo taking into account the second order effects of the work done by the vertical loads as follows:
where \(\delta\) is the horizontal displacement of the top of the frame purged of the elastic deformability, and \(\gamma\) is the slope of the linear post-elastic descending branch accounting for the second order effects [49].
An approximated bilinear capacity curve, referred to a monitored point conveniently chosen at the top floor of the frame is adopted. In Fig. 2 the construction of the proposed bilinear capacity curve (black line), which approximates the actual nonlinear one (red line) is depicted.
Approximated bilinear capacity curve [49]
It is worth highliting that, in order to take into account the progressive damage diffusion occurring in the frame during the collapse, the initial stiffness ki is an appropriate reduction of the elastic stiffness ke, by a reduction coefficient able to account for the ratio between the acting moment in correspondence of the global elastic load multiplier and the relevant plastic moment in all the sections involved in the collapse mechanism, as described in [49]. The resistance Vby is obtained as the cross point between the initial elastic branch associated with the stiffness \({k}_{i}\) and the inelastic one, with slope ks, departing from the point \(u=0, {V}_{b}={V}_{b,max}= {\lambda }_{o}\sum_{j=1}^{{N}_{f}}{F}_{j}\) (where the maximum base shear Vb,max is computed multiplying the summation of the horizontal forces Fj by the collapse load multiplier λo). The second branch of the capacity curve is identified considering the resistance of the structure obtained through a limit analysis and evaluating how the resistance of the structure reduces as the horizontal displacements increase. Precisely, the post-peak slope \({k}_{s}\) is evaluated considering the second order effects and is equal to
The capacity curve is then truncated considering as ultimate displacement uu the condition associated with the achievement of the ultimate conditions in the structure according to the adopted standard [1], namely the global base shear reduction and the achieving of ultimate chord rotations in beams.
The described approximated bilinear curve is representative of the Multi-Degrees of Freedom (MDOF) system and therefore of the whole frame. According to the procedure reported in [49], the properties of an equivalent Single-Degree of Freedom (SDOF) system and the demand and capacity associated with the Near Collapse (NC) Limit State are compared in order to evaluate the safety factor. The latter is defined as the ratio between the ultimate displacement of the equivalent elastic–plastic SDOF system and the seismic demand (displacement at the top floor of the frame) as recommended by the codes.
For seismic assessments of the worked examples presented in the following, the procedure proposed in Eurocode 8 [1] is employed. In particular, in order to define the seismic demand, the city of Catania (Italy) was chosen; correspondingly, the Italian annex [52] was considered to obtain the design spectrum, considering soil type B and modal damping equal to 5%.
For each profile chromosome \({C}_{k}^{ext}\) two internal genetic algorithms (“Internal GA A” and “Internal GA B”) are firstly launched for the determination of the collapse loads and failure mechanisms when mass proportional (A) or inverse triangular (B) horizontal load distributions are applied. The consequent two values of the collapse loads, say \({\lambda }_{c}^{A}\) and \({\lambda }_{c}^{B}\), are the minimum ones corresponding to the winning chromosomes \({C}_{A}^{int}\) and \({C}_{B}^{int}\), obtained for the considered load distributions after several runs of the algorithms (typically Nint = 10, in order to avoid local minima). When the two collapse loads are evaluated, the corresponding safety factors \({SF}_{k}^{A}\) and \({SF}_{k}^{B}\) of the profile chromosome \({C}_{k}^{ext}\) with respect to expected seismic demand are calculated. It is important to point out that configurations with safety factors lower than one are automatically discarded by the algorithm.
2.3 Fitness calculation
In the identification of the most performant frame many requirements must be considered. For example, as already said, both the safety factors described in the previous paragraph must be greater than one. Other considerations, involving the economic cost of the structural members (related to the weight of the frame) and further engineering design precautions, can be introduced in the definition of the following fitness value Fk of the profile chromosome \({C}_{k}^{ext}\):
where
-
\({f}_{1k}=1-0.5\left(\frac{1}{{SF}_{k}^{A}}+\frac{1}{{SF}_{k}^{B}}\right)\) is the fitness component related to the seismic safety factors;
-
\({f}_{2k}=1-\frac{{Mass}_{k}}{Max Mass}\) takes into account the ratio between the mass (Massk) of the frame associated with the profile chromosome \({C}_{k}^{ext}\) and the maximum one (Max Mass) which corresponds to a frame with all the structural members having the biggest cross section in the list of considered profiles;
-
\({f}_{3k}=\frac{1}{2N}{\left(\sum_{j=1}^{N}{c}_{j}^{A}+\sum_{j=1}^{N}{c}_{j}^{B}\right)}_{k}\), with \({c}_{j}^{A}\in {C}_{A}^{int}\) and\({c}_{j}^{B}\in {C}_{B}^{int}\), allows to control the failure mode privileging the frames for which more elementary mechanisms (and therefore more unitary values of \({c}_{j}^{A}\) or\({c}_{j}^{B}\)) are involved, that is the failure mode is global, which implies a large energy dissipation;
-
\({f}_{4k}=\frac{1}{Nc(Nf-1) }{\left[\sum_{h=0}^{Nf-2}{\sum }_{i=1+h({2N}_{c}-1)}^{{N}_{c}+h({2N}_{c}-1)}\mathcal{F}({c}_{i}-{c}_{i+(2{N}_{c}-1)})\right]}_{k}\), with \(\mathcal{F}\left(x-y\right)=1\) if\(x>y\), \(\mathcal{F}\left(x-y\right)=-1\) if \(x<y\) and\({{c}_{i}\in C}_{k}^{ext}\), is the fitness component that takes into account a resistance hierarchy according to which the cross section of the columns cannot increase with the height of the frame.
It is worth to note that the last two criteria are widely accepted and adopted in the plastic design of frames and were already accounted for in [16]. Here, the same criteria are also considered, and the relevant fitness components represent mathematical formulas to express the same concepts.
The definitions of the four components of the fitness imply that the four values range between 0 and 1, thus favouring the introduction of the relative weights \({\alpha }_{1,} {\alpha }_{2, } {\alpha }_{3},{\alpha }_{4},\) by means of which the designer can calibrate the above requirements. It is worth pointing out that in the design process there is not an absolute optimal solution and different configurations can be sought according to the criterion of choice the designer wants to privilege. For example a designer interested only on limiting the cost of the structure could adopt as relative weights \({\alpha }_{1}={\alpha }_{3 }={\alpha }_{4}=0,{ \alpha }_{2}=1\). A designer more attentive to the structural performance of the frame would increase the relative weights corresponding to the first, third and fourth criteria.
Once the fitness of all the profile chromosomes \({C}_{k}^{ext}\) (k = 1, …, Pext) have been evaluated by means of a parallel computing procedure, the fitness array is processed by the External GA which produces the next generation.
The process is repeated until the established number of iterations Next has been reached. The optimal design of the frame is finally achieved considering the set of cross sections for beams and columns associated with the highest fitness.
The whole nested procedure is summarized in the flow chart reported in Fig. 3.
The adoption of a weighting method, where the original multiobjective problem is converted into a single objective one through a linear combination of the objective functions is motivated by the fact that, provided that all weights are positive, this method should only generate Pareto-like solutions [53]. Actually, it presumably will generate a subset of these solutions. A modified algorithm for the exploration of the entire Pareto front will be explored in future works.
It is worth stressing that the design strategy entrusts two different tasks to the two levels of the algorithm. Namely, for each configuration of the frame explored by the external loop, the internal one identifies the expected collapse mechanism and the relevant load multiplier, which are employed to perform a prompt assessment of the seismic vulnerability; on the other hand, the external level of the algorithm explores the possible cross-section distribution in the frame, aiming at identifying a safe and optimized structural design of the frame. In this sense, the internal loop is at the service of the external one but cannot be faced simultaneously for two main reasons:
-
The safety multiplier, identified for each frame configuration by the external loop, is exploited by the fitness function reported in Eq. (7) implemented in the external loop.
-
The fitness functions of the internal and external loops cannot be mixed since they measure completely different aspects of the frame (minimization of the load multiplier as single optimization criterion in the case of the internal loop, four different parameters with different relative weights in the case of the external loop).
3 Algorithm implementation
The algorithm matches the classic case of a job workflow running Next • Pext times a direct acyclic graph (DAG) where Next expresses the number of the External GA generations and Pext the number of profile chromosomes to compute at each cycle. Although several commercial software products are available to implement this type of computational workflow, their use may be better justified in those cases where the process flow can vary during the computation.
In the case of the proposed nested genetic algorithm, the computational workflow ever has a static configuration so that it can be easily controlled by a dedicated set of shell scripts.
Recalling the algorithm workflow depicted in Fig. 3, a main script manages the NetLogo External GA and several worker scripts (whose number, in the presence of limited resources, may be lower than the number of profile chromosomes) are responsible for executing the necessary NetLogo Internal GA, A and B, algorithms. The worker script also computes the final fitness Fk value as soon as all \({\uplambda }_{\mathrm{c}}^{\mathrm{A}}\) and \({\uplambda }_{\mathrm{c}}^{\mathrm{B}}\) will be available for each chromosome Ckext. Once all fitness values have been determined, the main script wakes up the External GA and a new generation calculation will start until the maximum number Next of repetitions is reached.
The execution coordination among the main and the workers scripts is ensured by a database instance principally holding a task queue, a chromosomes table and relevant computed values such as the fitness evolution across External GA’ generations.
The computation of the two nested algorithms makes use of the virtualization based on containers. Since the earlier design phases, virtualization has been considered a key element, because it offers the possibility to run on a wide range of physical platforms, especially those provided by open and private Cloud infrastructures. This way to access computing infrastructures also becomes a key enabler to let this work be reproducible and reusable [54], two important factors in the incoming age of Open Science [55] and FAIR principles (www.go-fair.org/fair-principles/) compliant research data. For this reason, all source codes related to the running environment setup and the algorithm execution are publicly available in the INFN source code repository, (baltig.infn.it/brunor/optimal_design).
The decision of using containers to manage the virtualized resources has been made for principally two reasons. The first is associated with the simplicity to install, use, and maintain the execution environment. The second is related to the reached level of maturity and popularity since container images can be considered today a standard technology.
The software development, testing and the final data extraction were carried out executing the nested algorithm on top of the GARR Cloud Infrastructure (www.garr.it/en/garr-en/documents/documenti-tecnici/3474-garr-white-paper-maggio-2017) which reserved for the execution the following resources:
Cores: 100
RAM: 100 GB
Disk storage: 1 TB
To perform the data analysis of the present paper, these resources have been used to instantiate a virtual cluster made of 4 nodes having 24CPU and 24 GB of RAM, all of them accessing a common storage volume. The cluster used a container orchestration system to execute the following microservices:
Service | Instances | Description |
|---|---|---|
db | 1 | Database instance holding persistent data |
dbmgr | 1 | A tiny REST-API server to perform CRUD operations on the database |
master | 1 | Service controlling the External GA |
worker | 15 | Service executing Internal GA 1 and 2 and performing the final Fitness calculation |
web | 1 | Service exposing the algorithm execution dashboard and serving a file management to access computed data |
The External GA and the Internal GA, A and B, use a common directory storing all parameters inside different text files; the following Table 1 explains their meaning.
The overall architecture of the algorithm implementation is summarised in Fig. 4, which further specifies the flow chart presented in Fig. 3, explaining the role of all involved docker containers and showing how the External GA interconnects with the Internal GAs and the fitness calculation. Notice that the External GA will iterate the profile chromosomes generations till the maximum number of iterations have been reached or by user interruption.
4 Numerical applications
In the present paragraph the proposed design strategy is applied to two different steel frames having 2 spans and 2 storeys, and 3 spans and 5 storeys, respectively. Therefore, the profile chromosome size for the two frames is 10 and 35, respectively. Taking into account a vertical symmetry the number of independent genes decreases to 6 and 15 respectively while for frames in which the cross sections for beams and columns are constant within the same floor, the number of independent genes becomes 4 and 10 respectively. For both the frames two applications are developed respectively assuming a vertical symmetry or equal members within the same inter-floor. After a preliminary analysis, aimed at identifying sets of parameters for the GA algorithms that allowed to find stationary value for both the minimum collapse load of the internal chromosomes and the fitness of the profile chromosomes, the numbers of the external algorithm generations and of the chromosomes to compute at each cycle have been chosen respectively equal to Next = 30 and Pext = 100. The corresponding values for the internal (A and B) algorithms are Nint = 40 and Pint = 100. For both the external and internal algorithms the crossover rate and the mutation-rate are fixed, respectively, to 80% and 1% (see [46, 49] for more details about these parameters). In the following subsections, two worked examples are first described and analysed; then, the computational effort required by the proposed procedure is shortly discussed.
4.1 Two-storey frame
The considered frame, reported in Fig. 5, has 2 bays each one of length 4 m and 2 storeys with interstorey height equal to 3 m. The beams are subjected to a permanent distributed vertical load equal to 50 kN/m. According to standard seismic analyses two horizontal force distributions are considered, namely a mass proportional force distribution and an inverse triangular one. The relevant horizontal forces are summarized in Table 2
The objective of the design strategy is to select an optimal set of profiles for beams and columns among a predefined list (according to a chosen criterion). In the present application reference is made to steel profiles in the class HEA and 10 possible cross sections are considered as reported in Table 3 where, for each cross section the moment of inertia I, the area A and the plastic moment Mp are reported. Axial and shear deformability are neglected. The Young’s modulus adopted for the steel is equal to 210,000 MPa.
For the considered frame, the generic profile chromosome for the application of the external genetic algorithm has 10 genes corresponding respectively to the ID of the profile of the structural elements numbered in Fig. 5. Since each gene can assume ten different values, the overall number of possible different chromosomes in the population is Pmax = 1010.
Assuming a vertical symmetry for the frame the number of independent genes reduces to 6 which correspond respectively to the ID of profiles for: outer columns, inner column and beams for each floor. Also the case in which a constant cross section for the beams and columns within the same floor is considered; in this case the number of independent genes is 4. This means that, in these last two cases, the number of possible different chromosomes will be reduced to Pmax = 106 and Pmax = 104, respectively. However, for sake of clearness, the general form (1) of the profile chromosomes, with a size equal to the number of structural members, has been always maintained in reporting the simulation results.
The chosen relative weights are α1 = 0.2, α2 = 0.6, α3 = 0.1 and α4 = 0.1, which allow to reasonably balance the contribution of all the criteria introduced in the fitness function. Anyway, the designer can differently calibrate the design requirements privileging one of them or also add some new ones in the definition of the fitness of a profile chromosome.
Once reached the established number of iterations Next of the nested algorithm, the profile chromosomes of the last generation are analysed and the one with the highest fitness will be the winner. Table 4 shows three examples of winning chromosomes obtained for the vertically symmetric frame, together with their corresponding fitness components defined in Eq. (7). The analogous result related to the frame with a constant cross section for the beams and columns within the same floor are reported in Table 5.
It is worth to note that removing the assumptions of adopting the same cross-section for the columns at a given floor leads to a more optimized configurations (outer beams at the ground floor can accommodate a smaller section).
Aiming at a deeper insight on the differences between the above results, more details related to the two profile chromosomes with the best fitness in the two design configurations, having vertical symmetry or equal members within the same floor, are provided in the following. In particular, for each one of the two frames, the value of the collapse load multiplier λc, the correspondent collapse mechanism, the ultimate displacement of the equivalent elasto-plastic SDOF system dcu, the seismic demand dmax and the related safety factors SF for the two considered load conditions are reported in Table 6.
In the same table, in the bottom panels, a visual representation of the temporal spreading of the winning profiles among the population of chromosomes is reported for the two cases. After a certain amount of generations, the diversity in the population of chromosomes tends to vanish (except for the random mutations introduced at each generation). In particular, the population of Pext = 100 profile chromosomes, indicated by coloured cells (different colours correspond to different chromosomes), is reported in the x-axis, while in the y-axis (from bottom to top) the sequence of the Next = 30 generations of the external GA is shown: the temporal convergence towards a single colour expresses the diffusion of the winning chromosome among the population.
The single-coloured cells, randomly distributed in the top part of the figure, represent random mutations of the winning chromosome produced by the GA. It is interesting to highlight that the fitness of the profile chromosome [4 5 4 5 5 3 3 3 4 4], having the internal column at the first storey with cross section greater than the external ones at the same floor, turns out to be greater than that of [5 5 5 5 5 3 3 3 4 4] with equal columns at the first storey. In particular, the chromosome related to the frame with vertical symmetry has a higher value of the term f2 in the fitness definition being related to a more performant distribution of the masses and its realization is therefore economically more convenient. Furthermore the safety factors of the vertically symmetric frame turn out to be greater only in one of the two load conditions, anyway this has a small influence in the fitness function due to the assumed weight α1.. This consideration allows underlining that the provided results are deeply related to the weights introduced for each component of the fitness function, which can be conveniently calibrated according to desired requirements.
To focus on the dependency of fitness calculation on the choice of the main weights α1 and α2, in Table 7 the fitness of the two best profile chromosomes reported in Tables 4 and 5 evaluated for different couples of weights have been compared.
It immediately appears that the frame with vertical symmetry shows the highest fitness until the weight α2, related to the mass, overcomes the weight α1, related to the safety factors. Then, the fitness of the other frame becomes the best one. Bold characters help to recognize this effect.
4.2 Five-storey frame
The second application refers to a frame with three bays and five storeys. The storey height is equal to 3.2 m and the length of the bays is 4.5 m (Fig. 6). The beams are subjected to a permanent distributed vertical load equal to 25 kN/m while the horizontal forces in the two considered load conditions are reported in Table 8. Also for this frame, reference is made to the 10 steel profiles in the class HEA reported in Table 3. Since in this case, as previously stated, the number of structural elements is equal to 35, the size of the external GA population will be Pmax = 1035. Again, assuming a vertical symmetry or a constant cross section for the beams and columns within the same floor, the size of Pmax will be reduced to 1015 and 1010 respectively.
Table 9 reports the three profile chromosomes, obtained with the proposed design strategy for vertically symmetric frames, which correspond to the highest values of the fitness. Each rate of the fitness defined in Eq. (7) is also reported.
The results related to the three profile chromosomes correspondent to the highest values for the frame having a constant cross section for the beams and columns within the same floor are reported in Table 10.
Again, for this frame a comparison between the two best profile chromosomes in the two design configurations is performed and the details are reported in Table 11.
It is interesting to point out that, adopting in the design processes of the two and five storey frames the same values of the relative weights \({\alpha }_{1,} {\alpha }_{2, } {\alpha }_{3},{\alpha }_{4},\) the safety factors and the total mass play different roles in the identification of the winning profile chromosome. Actually, unlike the smaller frame described in the previous paragraph, in the case of the vertically symmetric five storey frame, the chromosome with the best fitness has greater safety factors with respect to those of the frame with constant cross sections at the same floor. This is due to the presence, in correspondent locations, of structural members having bigger cross sections. This “strengthening” of the frame produces evidently an increase of the safety factors and therefore of the term f1 in the fitness function. Although the weight \({\alpha }_{1,}\) attributed to this design parameter is smaller than \({\alpha }_{2,}\) which takes into account the mass of the frame, in this case the former has a prevalent effect in the fitness value. Anyway, as already pointed out, the selected frame does not represent an absolute optimal design since a small change in the relative weights leads to different final results in which other requirements can be privileged.
Finally, in order to appreciate the convergence of the external algorithm to the best profile chromosomes, in Fig. 7 the average fitness evolution of the profile chromosomes as function of the number of generations for both the two-storey (a) and the five-storey (b) frames with vertical symmetry is reported. It can be clearly seen, from the observation of the figure, that the number of generations selected in the numerical applications, equal to 30, guarantees a stable convergence of the algorithm, since a stationary state with a (local) maximum of average fitness is already reached just after 10–15 generations for both the considered frames. This last result also explain why the populations of profile chromosomes in the bottom panels of both Tables 6 and 11 seem to stagnate after 10–12 generations.
4.3 Computational effort analysis of the proposed strategy
In order to provide a computing time estimation for the two considered frames which would not depend on the number of available resources, the results summarized in Table 12 have been extracted for a single profile chromosome, considering the average computing time (expressed in seconds) of the internal algorithms (A and B) and the fitness calculation, extracted from the task queue.
In particular the partial times related to the different tasks of the algorithm have been separately specified as follows:
-
INT_1_A evaluates the collapse load for load condition 1 (mass proportional force distribution).
-
INT_1_B evaluates the collapse load for load condition 2 ( inverse triangular force distribution).
-
INT_2 evaluates the safety factors and the fitness of the profile chromosome.
In the table, for each frame, the total average computing time per chromosome is reported. Since each one of the Pext = 100 profile chromosomes is elaborated in parallel during a single generation (as well as the 10 runs of each internal algorithm), the total average computing time for the whole procedure can be obtained simply multiplying the previous total time for the Next = 30 generations of the external GA and is also reported in bold for both the cases.
It is clear that the required CPU time increases with the size of the frame and can assume significant values. However, the priority in this study was not maximizing performance but rather ensuring that the source codes were easily readable and maintainable. Thus, the significant amount of time requested by the code prototype has been somehow mitigated using a distributed computing environment as described in Sect. 3. The distributed code was prototyped as well and, in particular, a common relational database to manage the job queue has been used. This led to a trade-off in performance compared to more advanced but complex solutions.
It is also worth to note that the reported values hold for unlimited (and homogeneous) resources, but in real cases they depend on the number of cores effectively available in the virtual infrastructure and on their performance. Furthermore, it must be pointed out that computing time strongly depends also on the kind of physical resources beyond the virtualized ones, here provided by the GARR institute; this time can be different if other cloud providers are adopted or if physical resources are directly used.
5 Conclusions
The present paper proposes an original multi-objective strategy for the optimal plastic design of the cross-sections in frames subjected to seismic excitations. The procedure is based on the application of two different genetic algorithms launched in a nested structure. In particular, when the geometry (lengths of the beams and of the columns) and loads acting on the frame that must be designed are assigned, the external algorithm explores different configurations associated with different sizes of the cross sections of the structural members, whereas each selected configuration is evaluated by means of an internal algorithm that assigns a score based on the relevant performance. The bi-level strategy accommodates a multi-objective approach able to account for the modern concepts of seismic engineering (e.g. global ductility, strength hierarchy criterion, energy dissipation maximization in seismic conditions) as well as an economic criterion, through the assignments of relative weights associated with each design criterion.
The main advance of the proposed approach lies in the combination of a design process employing a standard parallelizable optimization procedure with a simplified methodology to evaluate the seismic performance of a generic frame, yet able to account dissipative resources and displacement capacity of the structure. The latter aspect leads to a fair compromise between accuracy and rapidity in obtaining results. More precisely, the proposed methodology provides new features with respect classic design algorithms based on linear models of the structure and is able to speed up those procedures that employ nonlinear static analyses thanks to an expeditious although approximated evaluation of the capacity curve.
Therefore, the proposed procedure must be considered as a new design strategy, which can be either enriched taking into account other fitness components or opportunely calibrated according to specific requirements. It is worth noticing that the software implementation has been conceived in order to let this work be reproducible and reusable, according to the Open Science paradigm and FAIR principles.
Data availability
Some or all data, models, or code that support the findings of this study are available from the corresponding author upon reasonable request.
References
EN 1998-3 (2005) (English): Eurocode 8: Design of structures for earthquake resistance—Part 3: assessment and retrofitting of buildings [Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC]
Sasmal, S., Ramanjaneyulu, K.: Evaluation of strength hierarchy of beam-column joints of existing RC structures under seismic type loading. J. Earthq. Eng. 16(6), 897–915 (2012)
Gholizadeh, S.: Performance-based optimum seismic design of steel structures by a modified firefly algorithm and a new neural network. Adv. Eng. Softw. 81, 50–65 (2015)
Mansouri, S.F., Maheri, M.R.: Performance-based seismic design of steel frames using constraint control method. Adv. Struct. Eng. 22(12), 2648–2661 (2019)
Málaga-Chuquitaype, C., Elghazouli, A.Y., Bento, R.: Rigid-plastic models for the seismic design and assessment of steel framed structures. Earthq. Eng. Struct. D 38(14), 1609–1630 (2009)
Mergos, P.E.: Efficient optimum seismic design of reinforced concrete frames with nonlinear structural analysis procedures. Struct. Multidiscip. Optim. 58, 2565–2581 (2018)
Ganzerli, S., Pantelides, C.P., Reaveley, L.D.: Performance-based design using structural optimization. Earthq. Eng. Struct. Dyn. 29, 1677–1690 (2000)
Chan, C.M., Zou, X.K., Hajirasouliha, I., Asadi, P., Pilakoutas, K.: Elastic and inelastic drift performance optimization for reinforced concrete buildings under earthquake loads. Earthq. Eng. Struct. Dyn. 33, 929–950 (2004)
Hill, R.: The Mathematical Theory of Plasticity. Oxford University Press, Oxford (1950)
Heyman, J.: Plastic Design of Frames. Cambridge University Press, Cambridge (1971)
Neal, B.G.: The Plastic Methods of Structural Analysis. Chapman and Hall, London (1977)
Livesley, R.K.: Linear programming in structural analysis and design. In: Gallagher, R.H., et al. (eds.) Optimum Structural Design. Wiley, New York (1977)
Horne, M.R., Morris, L.J.: Plastic Design of Low-Rise Frames Constrado Monographs. Collins, London (1981)
Kaneko, I., Maier, G.: Optimum design of plastic structures under displacement constraints. Comput. Method Appl. Mech. Eng. 27(3), 369–391 (1981)
Park, H.S., Adeli, H.: A neural dynamics model for structural optimization-Application to plastic design of structures. Comput. Struct. 57(3), 391–399 (1995)
Mazzolani, F.M., Piluso, V.: Plastic design of seismic resistant steel frames. Earthq. Eng. Struct. Dyn. 26(2), 167–191 (1997)
Goel, S.C., Liao, W.C., Bayat, M.R., Chao, S.H.: Performance-based plastic design (PBPD) method for earthquake-resistant structures: an overview. Struct. Des. Tall Spec. Build. 19(1–2), 115–137 (2010)
da Silva, L.S., Simões, R., Gervásio, H.: Design of Steel Structures. Wiley, New York (2014)
Mitsuo, G., Runwei, C.: Genetic Algorithms and Engineering Optimization, vol. 7. Wiley, New York (2000)
Erbatur, F., Hasançebi, O., Tütüncü, İ, Kılıç, H.: Optimal design of planar and space structures with genetic algorithms. Comput. Struct. 75(2), 209–224 (2000)
Kaveh, A., Talatahari, S.: Optimum design of skeletal structures using imperialist competitive algorithm. Comput. Struct. 88, 1220–1229 (2010)
Kaveh, A., Ghafari, M.H., Gholipour, Y.: Optimum seismic design of steel frames considering the connection types. J. Constr. Steel Res. 130, 79–87 (2017)
Kaveh, A., Biabani Hamedani, K., Milad Hosseini, S., Bakhshpoori, T.: Optimal design of planar steel frame structures utilizing meta-heuristic optimization algorithms. Structures 25, 335–346 (2020)
Maheri, M.R., Talezadeh, M.: An Enhanced Imperialist Competitive Algorithm for optimum design of skeletal structures. Swarm Evol. Comput. 40, 24–36 (2018)
Memari, A.M., Madhkhan, M.: Optimal design of steel frames subject to gravity and seismic codes’ prescribed lateral forces. Struct. Optim. 18, 56–66 (1999)
Toğan, V.: Design of planar steel frames using Teaching-Learning Based Optimization. Eng. Struct. 34, 225–232 (2012)
Camp, C.V., Bichon, B.J., Stovall, S.P.: Design of steel frames using ant colony optimization. J. Struct. Eng. 131(3), 369–379 (2005)
Degertekin, S.O.: Optimum design of steel frames using harmony search algorithm. Struct. Multidisc. Optim. 36, 393–401 (2008)
Camp, C.V., Pezeshk, S., Hansson, H.: Flexural design of reinforced concrete frames using a genetic algorithm. J. Struct. Eng. 129(1), 105–115 (2003)
Liu, D., Wang, Z., Pan, J., Zheng, Y., Hu, Z.: Optimum design of nonlinear semi-rigid steel frame based on performance-price ratio via genetic algorithm. J. Build. Eng. 61, 105287 (2022)
Benfratello, S., Giambanco, F., Palizzolo, L., Tabbuso, P.: Optimal design of steel frames accounting for buckling. Meccanica 48, 2281–2298 (2013)
Isenberg, J., Pereyra, V., Lawver, D.: Optimal design of steel frame structures. Appl. Numer. Math. 40(1–2), 59–71 (2002)
Kaveh, A., Zakian, P.: Optimal design of steel frames under seismic loading using two meta-heuristic algorithms. J. Constr. Steel Res. 82, 111–130 (2013)
Papadrakakis, M., Lagaros, N.D., Plevris, V.: Optimum design of space frames under seismic loading. Int. J. Struct. Stab. Dyn. 1(1), 105–123 (2001)
Di Trapani, F., Pio Sberna, A., Marano, G.C.: A new genetic algorithm-based framework for optimized design of steel-jacketing retrofitting in shear-critical and ductility-critical RC frame structures. Eng. Struct. 243, 112684 (2021)
Pezeshk, S., Camp, C.V., Chen, D.: Design of nonlinear framed structures using genetic. Optimization 126(3), 382–388 (2000)
Liu, M., Scott, A.B., Wen, Y.K.: Optimal seismic design of steel frame buildings based on life cycle cost considerations. Earthq. Eng. Struct. Dyn. 32, 1313–1332 (2003)
Sinha, A., Malo, P., Deb, K.: A review of bilevel optimization: from classical to evolutionary approaches and applications. IEEE Trans. Evolut. Comput. 22(2), 276–295 (2018)
Sarma, K.C., Adeli, H.: Bilevel parallel genetic algorithms for optimization of large steel structures. Comput.-Aided Civ. Infrastruct. 16(5), 295–304 (2001)
Fragiadakis, M., Lagaros, N.D., Papadrakakis, M.: Performance-based multiobjective optimum design of steel structures considering life-cycle cost. Struct. Multidiscip. Optim. 32, 1 (2006)
Xu, L., Gong, Y., Grierson, D.E.: Seismic design optimization of steel building frameworks. J. Struct. Eng. 132(2), 277–286 (2006)
Liu, M., Scott, A.B., Wen, Y.K.: Multiobjective optimization for performance-based seismic design of steel moment frame structures. Earthq. Eng. Struct. Dyn. 34, 289–306 (2005)
Hajirasouliha, I., Asadi, P., Pilakoutas, K.: An efficient performance-based seismic design method for reinforced concrete frames. Earthq. Eng. Struct. Dyn. 41, 663–679 (2012)
Basim, M.C., Estekanchi, H.E.: Application of endurance time method in performance-based optimum design of structures. Struct. Saf. 56, 52–67 (2015)
Neal, B.G., Symonds, P.S.: The calculations of collapse loads for framed structures. J. Inst. Civ. Eng. 35, 21–40 (1951)
Greco, A., Cannizzaro, F., Pluchino, A.: Seismic collapse prediction of frame structures by means of genetic algorithms. Eng. Struct. 143, 152–168 (2017)
Greco, A., Pluchino, A., Cannizzaro, F.: An improved ant colony optimization algorithm and its applications to limit analysis of frame structures. Eng. Optim. 51(11), 1867–1883 (2019)
Greco, A., Cannizzaro, F., Pluchino, A.: Automatic evaluation of plastic collapse conditions for planar frames with vertical irregularities. Eng. Comput. 35(1), 57–73 (2019)
Greco, A., Cannizzaro, F., Pluchino, A.: A novel procedure for the assessment of the seismic performance of frame structures by means of limit analysis. Bull. Earthq. Eng. 18, 4363–4386 (2020)
Challamel, N.: An application of large displacement limit analysis to frame structures. Struct. Eng. Mech. 33(2), 159–177 (2009)
Wilensky, U.: NetLogo, http://ccl.northwestern.edu/netlogo. Center for Connected Learning and Computer-Based Modeling. Northwestern University, Evanston, IL (1999)
Norme Tecniche per le Costruzioni (NTC2018) (2018) Gazzetta Ufficiale, n. 42 del 20/02/2018-Supplemento ordinario no. 8 (in Italian)
Xin-She, Y.: Nature-Inspired Optimization Algorithms, Elsevier Insights 2021, 2nd edn, chapter 15 pp. 221–237
Anagnostou, A., Taylor, S.J.E., Groen, D., Suleimenova, D., Anokye, N., Bruno, R., Barbera, R.: Building global research capacity in public health: the case of a science gateway for physical activity lifelong modelling and simulation. In: 2019 Winter Simulation Conference, WSC 2019, National Harbor, MD, USA, December 8-11, pp 1067–1078, IEEE, (2019). https://doi.org/10.1109/WSC40007.2019.9004845
Pontika, N., Knoth, P., Cancellieri, M., Pearce, S.: Fostering open science to research using a taxonomy and an eLearning portal. In: iKnow: 15th International Conference on Knowledge Technologies and Data Driven Business, 21–22 Oct 2015, Graz, Austria. https://doi.org/10.1145/2809563.2809571
Funding
Open access funding provided by Università degli Studi di Catania within the CRUI-CARE Agreement. This research was funded by the University of Catania, with the project "PIA.CE.RI 2020/2022" of the Department of Civil Engineering and Architecture and by the Italian Ministry of University and Research (MUR) with the projects “PRIN2017 linea Sud: Stochastic forecasting in complex systems” and PRIN2020 #20209F3A37. Part of the resources used in this work have been provided by the Cloud infrastructure at GARR, the Italian Research and Education Network.
Author information
Authors and Affiliations
Contributions
All the authors equally contributed to the drafting of the manuscript and to the data analysis.
Corresponding author
Ethics declarations
Conflict of interest
We do not have competing interests of financial or personal nature.
Ethical approval
This declaration is not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Greco, A., Cannizzaro, F., Bruno, R. et al. A nested genetic algorithm strategy for an optimal seismic design of frames. Comput Optim Appl 87, 677–704 (2024). https://doi.org/10.1007/s10589-023-00523-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-023-00523-x