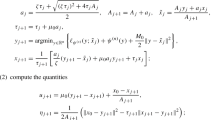Abstract
We design inexact proximal augmented Lagrangian based decomposition methods for convex composite programming problems with dual block-angular structures. Our methods are particularly well suited for convex quadratic programming problems arising from stochastic programming models. The algorithmic framework is based on the application of the abstract inexact proximal ADMM framework developed in [Chen, Sun, Toh, Math. Prog. 161:237–270] to the dual of the target problem, as well as the application of the recently developed symmetric Gauss-Seidel decomposition theorem for solving a proximal multi-block convex composite quadratic programming problem. The key issues in our algorithmic design are firstly in designing appropriate proximal terms to decompose the computation of the dual variable blocks of the target problem to make the subproblems in each iteration easier to solve, and secondly to develop novel numerical schemes to solve the decomposed subproblems efficiently. Our inexact augmented Lagrangian based decomposition methods have guaranteed convergence. We present an application of the proposed algorithms to the doubly nonnegative relaxations of uncapacitated facility location problems, as well as to two-stage stochastic optimization problems. We conduct numerous numerical experiments to evaluate the performance of our method against state-of-the-art solvers such as Gurobi and MOSEK. Moreover, our proposed algorithms also compare favourably to the well-known progressive hedging algorithm of Rockafellar and Wets.
Similar content being viewed by others
Data availability statement
The links of datasets from the literature that are used in this paper have been included where they are mentioned. For the other simulated data, they are available from the corresponding author on reasonable request.
References
Benders, J.F.: Partitioning procedures for solving mixed-variables programming problems. Numer. Math. 4(3), 238–252 (1962)
Berkelaar, A., Dert, C., Oldenkamp, B., Zhang, S.: A primal-dual decomposition-based interior point approach to two-stage stochastic linear programming. Oper. Res. 50, 904–915 (2002)
Birge, J.R.: Current trends in stochastic programming computation and applications. Technique Report 95-15, Department of Industrial and Operations Engineering, University of Michigan (1995)
Birge, J.R., Qi, L.: Computing block-angular Karmarkar projections with applications to stochastic programming. Manag. Sci. 34, 1472–1479 (1988)
Chatzipanagiotis, N., Dentcheva, D., Zavlanos, M.M.: An augmented Lagrangian method for distributed optimization. Math. Program. 152, 405–434 (2015)
Chen, L., Li, X.D., Sun, D.F., Toh, K.C.: On the equivalence of inexact proximal ALM and ADMM for a class of convex composite programming. Math. Program. 185, 111–161 (2021)
Chen, M., Mehrotra, S.: Self-concordance and decomposition based interior point methods for the two stage stochastic convex optimization problem. SIAM J. Optim. 21, 1667–1687 (2011)
Chen, L., Sun, D.F., Toh, K.C.: An efficient inexact symmetric Gauss–Seidel based majorized ADMM for high-dimensional convex composite conic programming. Math. Program. 161, 237–270 (2017)
Dantzig, G.: Upper bounds, secondary constraints and block triangularity in linear programming. Econometrica 23, 174–183 (1955)
Fischetti, M., Ljubić, I., Sinnl, M.: Redesigning Benders decomposition for large-scale facility location. Manag. Sci. 63(7), 2146–2162 (2017)
G\(\stackrel{..}{\rm u}\)nl\(\stackrel{..}{\rm u}\)k, O., Lee, J., Weismantel, R.: MINLP strengthening for separable convex quadratic transportation-cost UFL. Technical Report RC24213 (W0703-042), Research Division, IBM, Yorktown Heights, NY (2007)
Karmarkar, N.: A new polynomial time algorithm for linear programming. Combinatorica 4(4), 373–395 (1984)
Kontogiorgis, S., Meyer, R.: A variable-penalty alternating directions method for convex optimization. Math. Program. 83, 29–53 (1998)
Lam, X.Y., Sun, D., Toh, K.C.: Semi-proximal augmented Lagrangian-based decomposition methods for primal block-angular convex composite quadratic conic programming problems. Informs J. Optim. 3(3), 254–277 (2021)
Lau, K.K., Womersley, R.S.: Multistage quadratic stochastic programming. J. Comput. Appl. Math. 129, 105–138 (2001)
Li, M., Wu, Z.: On the convergence rate of inexact majorized sGS ADMM with indefinite proximal terms for convex composite programming. Asia-Pac. J. Oper. Res. 38(01), 2050035 (2021)
Li, X.D., Sun, D.F., Toh, K.C.: A highly efficient semismooth Newton augmented Lagrangian method for solving Lasso problems. SIAM J. Optim. 28, 433–458 (2018)
Li, X.D., Sun, D.F., Toh, K.C.: A block symmetric Gauss–Seidel decomposition theorem for convex composite quadratic programming and its applications. Math. Program. 175, 395–418 (2019)
Lubin, M., Hall, J.A.J., Petra, C.G., Anitescu, M.: Parallel distributed-memory simplex for large-scale stochastic LP problems. Comput. Optim. Appl. 55, 571–596 (2013)
Mehrotra, S., Özevin, M.: Decomposition-based interior point methods for two-stage stochastic semidefinite programming. SIAM J. Optim. 18, 206–222 (2007)
Mehrotra, S., Özevin, M.: Decomposition based interior point methods for two-stage stochastic convex quadratic programs with recourse. Oper. Res. 57, 964–974 (2009)
Rockafellar, R.T., Wets, R.: Scenarios and policy aggregation in optimization under uncertainty. Math. Oper. Res. 16, 119–147 (1991)
Ruszczyński, A.: On convergence of an augmented Lagrangian decomposition method for sparse convex optimization. Math. Oper. Res. 20, 634–656 (1995)
Ruszczyński, A.: Some advances in decomposition methods for stochastic linear programming. Ann. Oper. Res. 85, 153–172 (1999)
Sun, J., Xu, H.L., Zhang, M.: A new interpretation of the progressive hedging algorithm for multistage stochastic minimization problems. J. Ind. Manag. Optim. 16, 1655–1662 (2020)
Torres, J., Li, C., Apap, R., Grossmann, I.: A review on the performance of linear and mixed integer two-stage stochastic programming algorithms and software. Eprints for the optimization community (2019)
Van Slyke, R.M., Wets, R.: L-shaped linear programs with applications to optimal control and stochastic programming. SIAM J. Appl. Math. 17(4), 638–663 (1969)
Wollenberg, T.: Two-stage stochastic semidefinite programming: theory, algorithms, and application to AC power flow under uncertainty. Ph.D. Thesis, Universität Duisburg-Essen (2017)
Zhao, G.: Interior-point methods with decomposition for solving large-scale linear programs. J. Optim. Theory Appl. 102, 169–192 (1999)
Zhao, G.: A log-barrier method with Benders decomposition for solving two-stage stochastic programs. Math. Program. 90, 507–536 (2001)
Zverovich, V., Fábián, C.I., Ellison, E.F.E., Mitra, G.: A computational study of a solver system for processing two-stage stochastic LPs with enhanced Benders decomposition. Math. Program. Comput. 4, 211–238 (2012)
Acknowledgements
We would like to thank the two anonymous referees for their careful reading of this paper, and their insightful comments and suggestions which have helped to improve the quality of this paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Financial interest or Non-financial interest
The research of Kim-Chuan Toh is supported by the Ministry of Education, Singapore, under its Academic Research Fund Tier 3 Grant call (MOE-2019-T3-1-010). All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: two-stage stochastic programming datasets
-
assets.
This network model represents the management of assets. Its nodes are asset categories and its arcs are transactions. The problem is to maximize the return of an investment from every stage with the balance of material at each node.
-
env.
This model assists the Canton of Geneva in planning its energy supply infrastructure and policies. The main objective is to minimize the installation cost of various types of energy, while meeting all the supply–demand at each node and satisfying several realistic constraints such as the environmental constraints.
-
phone.
This is a problem which models the service of providing private lines to telecommunication customers, often used by large corporations between business locations for high speed, private data transmission. The goal is to minimize the unserved requests, while staying within budget.
-
AIRL.
This dataset is used to schedule monthly airlift operations. The airlift operation is scheduled so that the restriction on each aircraft such as the number of flight hours available during the month can be satisfied. The cost such as the available flight time to go unused, switching aircraft from one route to another and buying commercial flights is the main objective to be minimized.
-
4node.
This is a two stage network problem for scheduling cargo transportation. While the flight schedule is completely determined in stage one, the amounts of cargo to be shipped are uncertain and shall be determined in stage two.
-
pltexp.
This is a stochastic capacity expansion model that tries to allocate new production capacity across a set of plants so as to maximize profit subject to uncertain demand.
-
storm.
This is a two period freight scheduling problem described in Mulvey and Ruszczynski. In this model, routes are scheduled to satisfy a set of demands at stage 1, demands occur, and unmet demands are delivered at higher costs in stage 2 to account for shortcomings.
-
gbd.
This is the aircraft allocation problem where aircraft of different types are to be allocated to routes in a way that maximizes profit under uncertain demand, and minimizes the cost of operating the aircraft as well as costs associated with bumping passengers when the demand for seats outstrips the capacity.
Appendix 2: Derivation of solutions of (36) and (38)
We can rewrite the subproblem in (36) as follows:
where the last equality comes from the definition of Moreau-Yosida envelope, and the equality holds for \(z=-\mathop {\textrm{Prox}}_{\delta ^*_{{{\mathcal {K}}}}/\sigma }(A^*y-{\hat{c}}^k)\). By the property of Moreau-Yosida proximal mapping, \(\mathrm {{Prox}}_{\delta ^*_{{{\mathcal {K}}}}/\sigma }(A^*y-{\hat{c}}^k)=(A^*y-{\hat{c}}^k)-\mathrm {{Prox}}_{\sigma \delta _{{{\mathcal {K}}}}}(\sigma (A^*y-{\hat{c}}^k))\), therefore, \(z=\Pi _{{{\mathcal {K}}}}(\sigma (A^*y-{\hat{c}}^k))-(A^*y-{\hat{c}}^k)\), which gives (36). The derivation of (38) is similar, we omit the details.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ding, KY., Lam, XY. & Toh, KC. On proximal augmented Lagrangian based decomposition methods for dual block-angular convex composite programming problems. Comput Optim Appl 86, 117–161 (2023). https://doi.org/10.1007/s10589-023-00493-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-023-00493-0