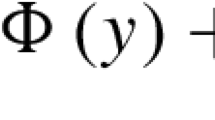Avoiding bad steps in Frank-Wolfe variants

Abstract

The study of Frank-Wolfe (FW) variants is often complicated by the presence of different kinds of “good” and “bad” steps. In this article, we aim to simplify the convergence analysis of specific variants by getting rid of such a distinction between steps, and to improve existing rates by ensuring a non-trivial bound at each iteration. In order to do this, we define the Short Step Chain (SSC) procedure, which skips gradient computations in consecutive short steps until proper conditions are satisfied. This algorithmic tool allows us to give a unified analysis and converge rates in the general smooth non convex setting, as well as a linear convergence rate under a Kurdyka-Łojasiewicz (KL) property. While the KL setting has been widely studied for proximal gradient type methods, to our knowledge, it has never been analyzed before for the Frank-Wolfe variants considered in the paper. An angle condition, ensuring that the directions selected by the methods have the steepest slope possible up to a constant, is used to carry out our analysis. We prove that such a condition is satisfied, when considering minimization problems over a polytope, by the away step Frank-Wolfe (AFW), the pairwise Frank-Wolfe (PFW), and the Frank-Wolfe method with in face directions (FDFW).

Appendix

1.1 KL property

We state here a result showing an implication between the (global) PL property used in [46] and (2.2). We first recall the PL property used in [46]:

$$\begin{aligned} \frac{1}{2}\Vert \nabla f(x)\Vert ^2 \ge \mu (f(x) - f^*) \, . \end{aligned}$$

(8.1)

with $f^*$ optimal value of f with non empty solution set $\mathcal {X}^*$.

Proposition 8.1

If f is convex, the optimal solution set $\mathcal {X}^*$ of f is contained in $\Omega$ and (8.1) holds, then (2.2) holds for every $x \in \Omega$.

Proof

By [46, Theorem 2] the PL property is equivalent, for convex objectives, to the unconstrained quadratic growth condition:

$$\begin{aligned} f(x) - f^* \ge \frac{\mu }{2}\text {dist}(x, \mathcal {X}^*)^2 \end{aligned}$$

(8.2)

In turn, given that by the assumption $\mathcal {X}^* \subset \Omega$ the set $\mathcal {X}^*$ is the solution set for $f_{\Omega }$ as well, (8.2) implies the global non smooth Holderian error bound condition from [26] with $\varphi (t) = \sqrt{\frac{2t}{\mu }}$, and by [26, Corollary 6] this is equivalent to the KL property (2.2) holding globally on $\Omega$. $\square$

Remark 4

We remark that without the assumption $\mathcal {X}^* \subset \Omega$ the implication is no longer true even for convex objectives, a counter example being $\Omega$ equal to the unitary ball and $f((x^{(1)},..., x^{(n)})) = (x^{(1)} - 1)^2$. At the same time, the KL property we used does not imply the PL property in general, since the latter only deals with unconstrained minima.

1.2 Proofs

We report here the missing proofs. We start with the proof of Lemma 3.2.

Proof

By the standard descent lemma [64, Proposition 6.1.2],

$$\begin{aligned} f(x_{k + 1}) = f(x_k + \alpha _k d_k) \le f(x_k) + \alpha _k \langle \nabla f(x_k), d_k \rangle + \alpha _k^2 \frac{L}{2}\Vert d_k\Vert ^2 \, , \end{aligned}$$

(8.3)

and in particular

$$\begin{aligned} f(x_{k}) - f(x_{k+1}) \ge - \alpha _k \langle \nabla f(x_k), d_k \rangle - \alpha _k^2 \frac{L}{2}\Vert d_k\Vert ^2 \ge \frac{L}{2}\alpha _k^2\Vert d_k\Vert ^2 = \frac{L}{2}\Vert x_{k + 1} - x_k\Vert ^2 \, , \end{aligned}$$

(8.4)

where we used $\alpha _k \le \bar{\alpha }_k$ in the last inequality. This proves (3.13). $\square$

We now state a preliminary result needed to prove Proposition 2.2:

Proposition 8.2

Let C be a closed convex cone. For every $y \in \mathbb {R}^n$

$$\begin{aligned} \text {dist}(C^*, y) = \sup _{c \in C} \langle \hat{c}, y \rangle \, . \end{aligned}$$

As stated in [65] this is an immediate consequence of the Moreau-Yosida decomposition:

$$ y = \pi (C, y) + \pi (C^*, y) \,. $$

Proposition 2.2

First, by continuity of the scalar product we have

$$\begin{aligned} \sup _{h\in \Omega /\{\bar{x}\}} \left( g, \frac{h-\bar{x}}{\Vert h - \bar{x}\Vert }\right) = \sup _{h\in T_{\Omega }(\bar{x}) \setminus \{0\}} (g, \hat{h}) \, . \end{aligned}$$

(8.5)

Since $N_{\Omega }(\bar{x}) = T_{\Omega }(\bar{x})^*$ the first equality is exactly the one of Proposition 8.2 if $g \notin N_{\Omega }(\bar{x})$, and it is trivial since both terms are clearly 0 if $g \in N_{\Omega }(\bar{x})$.

It remains to prove

$$\begin{aligned} \text {dist}(N_{\Omega }(\bar{x}), g)= \Vert \pi (T_{\Omega }(\bar{x}), g)\Vert \, , \end{aligned}$$

which is true by the Moreau - Yosida decomposition. $\square$

Proposition 4.1

Let $B_j = \bar{B}_{\langle g, \hat{d}_j \rangle /L}(x_k)$ and let T be such that $x_{k + 1} = y_T$.

Inequality (4.3) applied with $j = T$ gives (4.5). Moreover, by taking $\tilde{x}_k = y_{\tilde{T}}$ for some $\tilde{T} \in [0:T]$ the conditions

$$\begin{aligned} f(x_{k+1}) \le f(\tilde{x}_k) \le f(x_k) - \frac{L}{2} \Vert x_k - \tilde{x}_k\Vert ^2 \end{aligned}$$

(8.6)

are satisfied by Lemma 4.1 and (4.3).

Let now $p_j = \Vert \pi (T_{\Omega }(y_j), -\nabla f(y_j))\Vert$ and $\tilde{p}_j = \Vert \pi (T_{\Omega }(y_j), g)\Vert = \Vert \pi (T_{\Omega }(y_j), -\nabla f(x_k))\Vert$. We have

$$\begin{aligned} \vert p_j - \tilde{p}_j \vert \le L\Vert y_j-x_k\Vert \, , \end{aligned}$$

(8.7)

reasoning as for (3.17). We now distinguish four cases according to how the SSC terminates.

Case 1 $T = 0$ or $d_T = 0$. Since there are no descent directions $x_{k + 1} = y_T$ must be stationary for the gradient g. Equivalently, $\tilde{p}_T = \Vert \pi (T_{\Omega }(x_{k + 1}), g)\Vert = 0$. We can now write

$$\begin{aligned} \Vert x_{k + 1}-x_k\Vert \ge \frac{1}{L}( \vert p_T - \tilde{p}_T \vert ) = \frac{p_T}{L} > Kp_T \, , \end{aligned}$$

where we used (8.7) in the first inequality and $\tilde{p}_T = 0$ in the equality. Finally, it is clear that if $T = 0$ then $d_0 =0$, since $y_0$ must be stationary for $-g$.

Before examining the remaining cases we remark that if the SSC terminates in Phase II then $\alpha _{T- 1} = \beta _{T-1}$ must be maximal w.r.t. the conditions $y_T \in B_{T-1}$ or $y_T \in \bar{B}$. If $\alpha _{T-1} = 0$ then $y_{T-1} = y_T$, and in this case we cannot have $y_{T-1} \in \partial \bar{B}$, otherwise the SSC would terminate in Phase II of the previous cycle. Therefore necessarily $y_T = y_{T-1} \in \text {int}(B_{T-1})^c$ (Case 2). If $\beta _{T - 1} = \alpha _{T- 1} > 0$ we must have $y_{T-1}\in \Omega _{T-1} = B_{T-1} \cap \bar{B}$, and $y_T \in \partial B_{T - 1}$ (case 3) or $y_T \in \partial \bar{B}$ (case 4) respectively.

Case 2 $y_{T-1} = y_T \in \text {int}(B_{T-1})^c$. We can rewrite the condition as

$$\begin{aligned} \langle g, \hat{d}_{T-1} \rangle \le L\Vert y_{T-1} - x_k\Vert = L \Vert y_T - x_k\Vert \, . \end{aligned}$$

(8.8)

Thus

$$\begin{aligned} p_T = p_{T-1} \le \tilde{p}_{T-1} + L\Vert y_{T} - x_k\Vert \le \frac{1}{\tau }\langle g, \hat{d}_{T-1} \rangle + L\Vert y_T - x_k\Vert \le \left( \frac{L}{\tau } + L\right) \Vert y_T - x_k\Vert \, , \end{aligned}$$

(8.9)

where in the equality we used $y_{T} = y_{T-1}$, the first inequality follows from (8.7) and again $y_T = y_{T-1}$, the second from $\frac{\langle g, \hat{d}_T \rangle }{\tilde{p}_T} \ge \text {DSB}_{\mathcal {A}}(\Omega , y_{T}, g) \ge \text {SB}_{\mathcal {A}}(\Omega ) = \tau$, and the third from (8.8). Then $\tilde{x}_k = x_{k + 1} = y_T$ satisfies the desired conditions.

Case 3 $y_T = y_{T - 1} + \beta _{T - 1} d_{T-1}$ and $y_T \in \partial B_{T-1}$. Then from $y_{T-1} \in B_{T-1}$ it follows

$$\begin{aligned} L \Vert y_{T-1} - x_k\Vert \le \langle g, \hat{d}_{T-1} \rangle \, , \end{aligned}$$

(8.10)

and $y_T \in \partial B_{T-1}$ implies

$$\begin{aligned} \langle g, \hat{d}_{T-1} \rangle = L \Vert y_T - x_k\Vert \, . \end{aligned}$$

(8.11)

Combining (8.10) with (8.11) we obtain

$$\begin{aligned} L \Vert y_{T - 1} - x_k\Vert \le L \Vert y_T - x_k\Vert \, . \end{aligned}$$

(8.12)

Thus

$$\begin{aligned} p_{T - 1} \le \tilde{p}_{T - 1} + L\Vert y_{T - 1} - x_k\Vert \le \frac{1}{\tau }\langle g, \hat{d}_{T - 1} \rangle + L\Vert y_{T - 1} - x_k\Vert \le \left( \frac{L}{\tau } + L\right) \Vert y_T - x_k\Vert \, , \end{aligned}$$

where we used (8.11), (8.12) in the last inequality and the rest follows reasoning as for (8.9). In particular we can take $\tilde{x}_k = y_{T-1}$, where $\Vert \tilde{x}_k - x_k\Vert \le \Vert x_{k + 1} - x_k\Vert$ by (8.12).

Case 4 $y_T = y_{T - 1} + \beta _{T - 1} d_{T-1}$ and $y_T \in \partial \bar{B}$.

The condition $x_{k + 1} = y_T \in \bar{B}$ can be rewritten as

$$\begin{aligned} L\Vert x_{k + 1} - x_k\Vert ^2 - \langle g, x_{k + 1} - x_k \rangle = 0 \, . \end{aligned}$$

(8.13)

For every $j \in [0:T]$ we have

$$\begin{aligned} x_{k + 1} = y_j + \sum _{i=j}^{T-1} \alpha _i d_i \, . \end{aligned}$$

(8.14)

We now want to prove that for every $j \in [0:T]$

$$\begin{aligned} \Vert x_{k + 1} - x_k\Vert \ge \Vert y_j - x_k\Vert \, . \end{aligned}$$

(8.15)

Indeed, we have

$$\begin{aligned} \begin{aligned} L\Vert x_{k + 1} - x_k\Vert ^2 = \langle g, x_{k + 1} - x_k \rangle&= \langle g, y_j - x_k \rangle + \sum _{i=j}^{T-1} \alpha _i \langle g, d_i \rangle \\&\ge \langle g, y_j - x_k \rangle \ge L\Vert y_j - x_k\Vert ^2 \, , \end{aligned} \end{aligned}$$

where we used (8.13) in the first equality, (8.14) in the second, $\langle g, d_j \rangle \ge 0$ for every j in the first inequality and $y_j \in \bar{B}$ in the second inequality.

We also have

$$\begin{aligned} \begin{aligned} \frac{\langle g, x_{k + 1} - x_k \rangle }{\Vert x_{k + 1} - x_k\Vert }&= \frac{\langle g, \sum _{j=0}^{T-1}\alpha _j d_j \rangle }{\Vert \sum _{j=0}^{T-1}\alpha _j d_j\Vert } \ge \frac{\langle g, \sum _{j=0}^{T-1}\alpha _j d_j \rangle }{\sum _{j=0}^{T-1}\alpha _j \Vert d_j\Vert } \\&\ge \min \left\{ \frac{\langle g, d_j \rangle }{\Vert d_j\Vert } \ \vert \ 0 \le j \le T-1 \right\} \, . \end{aligned} \end{aligned}$$

(8.16)

Thus for $\tilde{T} \in \text {argmin}\left\{ \frac{\langle g, d_j \rangle }{\Vert d_j\Vert } \ \vert \ 0 \le j \le T-1 \right\}$

$$\begin{aligned} \langle g, \hat{d}_{\tilde{T}} \rangle \le \frac{\langle g, x_{k + 1} - x_k \rangle }{\Vert x_{k + 1} - x_k\Vert } = L\Vert x_{k + 1} - x_k\Vert \, , \end{aligned}$$

(8.17)

where we used (8.16) in the first inequality and (8.13) in the second.

We finally have

$$\begin{aligned} p_{\tilde{T}} \le \tilde{p}_{\tilde{T}} + L\Vert y_{\tilde{T}} - x_k\Vert \le \frac{1}{\tau }\langle g, \hat{d}_{\tilde{T}} \rangle + L\Vert y_{ \tilde{T}} - x_k\Vert \le \left( \frac{L}{\tau } + L\right) \Vert x_{k + 1} - x_k\Vert \, , \end{aligned}$$

where we used (8.15), (8.17) in the last inequality and the rest follows reasoning as for (8.9). In particular $\tilde{x}_k = y_{\tilde{T}}$ satisfies the desired properties, where $\Vert \tilde{x}_k - x_k\Vert \le \Vert x_{k + 1} - x_k\Vert$ by (8.15). $\square$

Proof of Proposition 4.3

Let T(k) be the number of iterates generated by the SSC at the step k in Phase II. For the AFW and the PFW, reasoning as in the proof of Proposition 4.2 we obtain that if the SSC does T(k) iterations, the number of active vertices decreases by at least $T(k) - 2$. Then on the one hand

$$\begin{aligned} \vert S^{(k)} \vert - \vert S^{(0)} \vert \ge 1 - \vert S^{(0)} \vert \, , \end{aligned}$$

(8.18)

while on the other hand

$$\begin{aligned} \begin{aligned} \vert S^{(k)} \vert - \vert S^{(0)} \vert&= \sum _{i = 0}^{k - 1} (\vert S^{(i + 1)} \vert - \vert S^{(i)} \vert ) \\&\le 2k - \sum _{i = 0}^{k - 1} T(i) \, . \end{aligned} \end{aligned}$$

(8.19)

Combining (8.18) and (8.19) and rearranging, we obtain:

$$\begin{aligned} \frac{1}{k}\sum _{i = 0}^{k - 1} T(i) \le 2 + \frac{\vert S^{(0)} \vert - 1}{k} \, , \end{aligned}$$

(8.20)

and the desired result follows by taking the limit for $k \rightarrow \infty$.

For the FDFW, notice that at every iteration the SSC performs a sequence of maximal in face steps terminated either by a Frank Wolfe step, after which $\mathcal {F}(y_j)$ can increase of at most $\Delta (\Omega )$, or by a non maximal in face step, after which $\mathcal {F}(y_j)$ stays the same. In both cases, we have

$$\begin{aligned} \dim (\mathcal {F}(x_{ k + 1})) - \dim (\mathcal {F}(x_k)) \le \Delta (\Omega ) - T(k) + 1. \end{aligned}$$

(8.21)

Then,

$$\begin{aligned} \dim \mathcal {F}(x_{k}) - \dim \mathcal {F}(x_0) \ge - \dim \mathcal {F}(x_0) \, , \end{aligned}$$

(8.22)

and

$$\begin{aligned} \begin{aligned} \dim \mathcal {F}(x_k) - \dim \mathcal {F}(x_0)&= \sum _{i = 0}^{k - 1} (\dim (\mathcal {F}(x_{i + 1}) - \dim (\mathcal {F}(x_i)))) \\&\le k\Delta (\Omega ) + k - \sum _{i = 0}^{k - 1} T(i) \, . \end{aligned} \end{aligned}$$

(8.23)

The conclusion follows as for the AFW and the PFW. $\square$

Theorem 4.1

The sequence $\{f(x_k)\}$ is decreasing by (4.5). Thus by compactness $f(x_k) \rightarrow \tilde{f} \in \mathbb {R}$ and in particular $f(x_k) - f(x_{k + 1}) \rightarrow 0$. So that by (4.5) also $\Vert x_{k + 1} - x_k \Vert \rightarrow 0$. Let $\{x_{k(i)}\} \rightarrow \tilde{x}^*$ be any convergent subsequence of $\{x_k\}$. For $\{\tilde{x}_k\}$ chosen as in the proof of Proposition 4.1 we have $\Vert \tilde{x}_k - x_k\Vert \le \Vert x_{k+1} - x_k\Vert$ because $\tilde{x}_k = y_T = x_k$ in case 1 and case 2, by (8.12) in case 3, and by (8.15) in case 4. Therefore

$$\Vert \tilde{x}_{k(i)} - x_{k(i)}\Vert \le \Vert x_{k(i)+ 1} - x_{k(i) }\Vert \rightarrow 0 \,.$$

Furthermore, $\Vert \pi (T_{\Omega }(\tilde{x}_{k(i)}), -\nabla f(\tilde{x}_{k(i)})))\Vert ~\le ~\frac{\Vert x_{k(i)+ 1} - x_{k(i) }\Vert }{K} \rightarrow 0$ again by Proposition 4.1, so that $\tilde{x}_{k(i)} \rightarrow \tilde{x}^*$ with $\Vert \pi (T_{\Omega }(\tilde{x}_{k(i)}), -\nabla f(\tilde{x}_{k(i)}))\Vert \rightarrow 0$. Then $\Vert \pi (T_{\Omega }(\tilde{x}^*), -\nabla f(\tilde{x}^*))\Vert =0$ and $\tilde{x}^*$ is stationary.

The first inequality in (4.9) follows directly from (4.6). As for the second, we have

$$\begin{aligned} \begin{aligned} \frac{k + 1}{K^2} (\min _{0 \le i \le k} \Vert x_{i + 1} - x_i\Vert )^2&= \frac{k + 1}{K^2} \min _{0 \le i \le k} \Vert x_{i + 1} - x_i\Vert ^2 \\&\le \frac{1}{K^2} \sum _{i= 0}^k \Vert x_{i} - x_{i + 1}\Vert ^2 \le \frac{2}{LK^2} \sum _{i = 0}^{k}(f(x_{i + 1}) - f(x_i)) \\&\le \frac{2(f(x_0) - \tilde{f})}{LK^2} \, , \end{aligned} \end{aligned}$$

where we used (4.5) in the first inequality, $\{f(x_i)\}$ decreasing together with $f(x_i) \rightarrow \tilde{f}$ in the second and the thesis follows by rearranging terms. $\square$

We now prove Lemma 4.3. We start by recalling Karamata’s inequality ([66, 67]) for concave functions. Given $A, B \in \mathbb {R}^N$ it is said that A majorizes B, written $A \succ B$, if

$$\begin{aligned} \begin{aligned} \sum _{i= 1}^j A_i&\ge \sum _{i= 1}^j B_i \ \text {for } j \in [1:N] \, , \\ \sum _{i = 1}^N A_i&= \sum _{i= 1}^N B_i \, . \end{aligned} \end{aligned}$$

If h is concave and $A \succ B$ by Karamata’s inequality

$$\begin{aligned} \sum _{i= 1}^N h(A_i) \le \sum _{i = 1}^N h(B_i) \, . \end{aligned}$$

In order to prove Lemma 4.3 we first need the following technical Lemma.

Lemma 8.1

Let $\{\tilde{f}_i\}_{i \in [0:j]}$ be a sequence of nonnegative numbers such that $\tilde{f}_{i + 1} \le q \tilde{f}_i$ for some $q < 1$. Then

$$\begin{aligned} \sum _{i = 0}^{j - 1} \sqrt{\tilde{f}_i - \tilde{f}_{i + 1}} \le \frac{\sqrt{\tilde{f}_0(1 - q)}}{1 - \sqrt{q}} \, . \end{aligned}$$

(8.24)

Proof

Let $\bar{j} = \max \{i \ge 0 \ \vert \ \tilde{f}_j \le q^{i} \tilde{f}_0 \}$, so that by (8.32) we have $\bar{j} \ge j$. Define $w^*, v \in \mathbb {R}^{\bar{j} + 1}_{\ge 0}$ by

$$\begin{aligned} \begin{aligned} v&= (\tilde{f}_0 - q \tilde{f}_0, ..., q^{\bar{j} - 1}\tilde{f}_0 - q^{\bar{j}} \tilde{f}_0, q^{\bar{j}} \tilde{f}_0 - \tilde{f}_{j}) \, , \\ w^*&= (\tilde{f}_0 - \tilde{f}_1, ..., \tilde{f}_{j - 1} - \tilde{f}_{j}, 0, ..., 0) \, . \end{aligned} \end{aligned}$$

(8.25)

Then for $0 \le l < \bar{j}$ we have

$$\begin{aligned} \sum _{i = 0}^l v_i = \tilde{f}_0 - q^{l + 1} \tilde{f}_0 \le \tilde{f}_{0} - \tilde{f}_{\min (l+1, j)} = \sum _{i = 0}^l w^*_i \, , \end{aligned}$$

(8.26)

where we used $q^{l + 1}\tilde{f}_0 \ge \tilde{f}_{l + 1}$ for $l \le j - 1$ and $q^{l + 1}\tilde{f}_0 \ge \tilde{f}_{j}$ for $j \le l < \bar{j}$ in the inequality. Furthermore, for $l = \bar{j}$ we have

$$\begin{aligned} \sum _{i= 0}^l v_i = \tilde{f}_{0} - \tilde{f}_{j} = \sum _{i=0}^{l} w^*_i \, . \end{aligned}$$

(8.27)

Now if w is the permutation in descreasing order of $w^*$, clearly thanks to (8.26), and (8.27) we have $w \succ v$. Then

$$\begin{aligned} \begin{aligned} \sum _{i = 0}^{j - 1} \sqrt{\tilde{f}_i - \tilde{f}_{i +1}} =&\sum _{i= 0}^{\bar{j} + 1} \sqrt{w^*_i} = \sum _{i= 0}^{\bar{j} + 1} \sqrt{w_i} \le \sum _{i= 0}^{\bar{j} + 1} \sqrt{v_i} \\ \le&\sqrt{\tilde{f}_0} \sum _{i= 0}^{+ \infty }\sqrt{q^i - q^{i + 1}} = \frac{\sqrt{\tilde{f}_0(1 - q)}}{1 - \sqrt{q}} \, , \end{aligned} \end{aligned}$$

(8.28)

where the first inequality follows from Karamata’s inequality. $\square$

Proof of Lemma 4.3

If the sequence $\{x_k\}$ is finite, with $x_m =\tilde{x}$ stationary for some $m \ge 0$, we define $x_k = x_{m}$ for every $k \ge m$, so that we can always assume $\{x_k\}$ infinite. Notice that with this convention the sufficient decrease condition (4.5) is still satisfied for every k. Let $f_k = f(x_k) - f(x^*)$. $\{f_k\}$ is monotone decreasing by (4.5), and nonnegative since (2.2) holds for every $x_k$.

We want prove $f_{k + 1} \le q f_k$. This is clear if $f_{k + 1} = 0$. Otherwise using the notation of Proposition 4.1 we have

$$\begin{aligned} f_k - f_{k+1} \ge \frac{L}{2}\Vert x_k - x_{k+1}\Vert ^2 \ge \frac{LK^2}{2}\Vert \pi (T_{\Omega }(\tilde{x}_k), -\nabla f(\tilde{x}_k))\Vert \, , \end{aligned}$$

(8.29)

where we used (4.5) in the first inequality, (4.6) in the second. Since $\tilde{x}_k \in \{y_j\}_{j = 0}^T$ by Proposition 4.1, we can apply (2.2) in $\tilde{x}_k$ to obtain

$$\begin{aligned} \frac{LK^2}{2}\Vert \pi (T_{\Omega }(\tilde{x}_k), -\nabla f(\tilde{x}_k))\Vert ^2 \ge \mu L K^2(f(\tilde{x}_k) - f(x^*)) \ge \mu L K^2f_{k+1}. \end{aligned}$$

(8.30)

Concatenating (8.29), (8.30) and rearranging we obtain

$$\begin{aligned} f_{k+1} \le (1 + \mu LK^2)^{-1}f_k = q f_k \, . \end{aligned}$$

(8.31)

Thus by induction for any $i \ge 0$

$$\begin{aligned} f_{k + i} \le q^i f_k \, , \end{aligned}$$

(8.32)

which implies in particular (4.12).

We can now bound the length of the tails of $\{x_k\}$:

$$\begin{aligned} \sum _{i = 0}^{+\infty } \Vert x_{k + i} - x_{k + i + 1}\Vert \le \sqrt{\frac{2}{L}} \sum _{i = 0}^{+ \infty } \sqrt{f_{k + i} - f_{k + i + 1}} \le \frac{\sqrt{2f_k(1 - q)}}{\sqrt{L}(1 - \sqrt{q})} \le \frac{\sqrt{2f_0(1 - q)}}{\sqrt{L}(1 - \sqrt{q})} q^{\frac{k}{2}} \, , \end{aligned}$$

(8.33)

where we used (4.5) in the first inequality, Lemma 8.1 with $\{\tilde{f}_i\} = \{f_{k + i}\}$ and for $j \rightarrow +\infty$ in the second inequality, and (8.32) in the third. In particular $x_k \rightarrow \tilde{x}^*$ with

$$\begin{aligned} \Vert x_k - \tilde{x}^*\Vert \le \sum _{j = 0}^{+\infty } \Vert x_{k + j} - x_{k + j + 1}\Vert = \frac{\sqrt{2f_0(1 - q)}}{\sqrt{L}(1 - \sqrt{q})} q^{\frac{k}{2}} \end{aligned}$$

(8.34)

by (8.33). $\square$

Proof of Theorem 4.2

By continuity, for $\tilde{\delta } \rightarrow 0$ and $f_0 = f(x_0) - f(x^*)$ we have that

$$\begin{aligned} \max _{x_0 \in B_{{\tilde{\delta }}}(x^*) \cap [f \ge f(x^*)]} f_0 \rightarrow 0 \, , \end{aligned}$$

(8.35)

so we can take $\tilde{\delta } < \delta /2$ small enough in such a way that

$$\begin{aligned} \max _{x_0 \in B_{{\tilde{\delta }}}(x^*) \cap [f \ge f(x^*)]} \frac{\sqrt{2f_0(1 - q)}}{L(1 - \sqrt{q})} + \sqrt{\frac{2}{L}}\sqrt{f_0} < \frac{\delta }{2} \, . \end{aligned}$$

(8.36)

Let now $x_0 \in B_{{\tilde{\delta }}}(x^*) \cap [f \ge f(x^*)]$, so that

$$\begin{aligned} {\tilde{\delta }}< \frac{\delta }{2} < \delta - \frac{\sqrt{2f_0(1 - q)}}{L(1 - \sqrt{q})} - \sqrt{\frac{2}{L}}\sqrt{f_0} \, , \end{aligned}$$

(8.37)

where we use (8.36) in the second inequality. We now want to prove, by induction on k, $\{x_i\}_{i \in [0:k]} \subset B_{\delta }(x^*)$ with $f(x_{i + 1}) \le qf(x_i)$ for every $i \in [0:k]$ and $k \in \mathbb {N}$. To start with,

$$\begin{aligned} \sum _{i = 0}^{k - 1} \Vert x_i - x_{i + 1}\Vert \le \sqrt{\frac{2}{L}} \sum _{i = 0}^{k - 1} \sqrt{f_{i} - f_{i + 1}} \le \frac{\sqrt{2f_0(1 - q)}}{\sqrt{L}(1 - \sqrt{q})} \end{aligned}$$

(8.38)

where we used (4.5) in the first inequality, and Lemma 8.1 (which we can apply thanks to the inductive assumption) in the second. But then

$$\begin{aligned} \begin{aligned} \Vert x_{k + 1} - x^*\Vert&\le \Vert x_0 - x^*\Vert + \left( \sum _{i = 0}^{k - 1} \Vert x_i - x_{i + 1}\Vert \right) + \Vert x_k - x_{k + 1}\Vert \\&\le {\tilde{\delta }}+ \frac{\sqrt{2f_0(1 - q)}}{L(1 - \sqrt{q})} + \sqrt{\frac{2}{L}}\sqrt{f_k - f_{k + 1}} \\&< {\tilde{\delta }}+ \frac{\sqrt{2f_0(1 - q)}}{L(1 - \sqrt{q})} + \sqrt{\frac{2}{L}}\sqrt{f_k} < \delta \, , \end{aligned} \end{aligned}$$

(8.39)

where we used (8.38) together with (4.5) in the second inequality, the assumption $x_k \in B_{\delta }(x^*) \Rightarrow f_{k + 1} \ge 0$ in the third inequality, and (8.37) together with $f_0 \ge f_{k}$ in the last inequality.

We now have

$$\begin{aligned} \begin{aligned} \Vert \tilde{x}_{k} - x^*\Vert&\le \Vert x_0 - x^*\Vert + \left( \sum _{i = 0}^{k - 1} \Vert x_i - x_{i + 1}\Vert \right) + \Vert x_k - \tilde{x}_{k}\Vert \\&\le \Vert x_0 - x^*\Vert + \left( \sum _{i = 0}^{k - 1} \Vert x_i - x_{i + 1}\Vert \right) + \Vert x_k - x_{k + 1}\Vert < \delta \, , \end{aligned} \end{aligned}$$

(8.40)

where we use $\Vert \tilde{x}_k - x_k\Vert \le \Vert x_{k + 1} - x_k\Vert$ in the second inequality and the last inequality follows as in (8.40). Thus $\tilde{x}_k \in B_{\delta }(x^*)$ as well, which is enough to prove (8.31) and complete the induction. We have thus obtained $\{\tilde{x}_k\}, \{ x_k \} \subset B_{\delta }(x^*)$, and the conclusion follows exactly as in the proof of Lemma 4.3. $\square$

Proof of Corollary 4.2

Let $x^*$ be a limit point of $\{x_k\}$, and let $\tilde{\delta }$ be as in Theorem 4.2. First, for some $\bar{k} \in \mathbb {N}$ we must have $x_{\bar{k}} \in B_{\tilde{\delta }}(x^*)$. Furthermore, for every $k \in \mathbb {N}$ we have $f(x_k) \ge f(x^*)$ because $f(x_k)$ is non increasing and converges to $f(x^*)$. Thus we have all the necessary assumptions to obtain the asymptotic rates by applying Theorem 4.2 to $\{y_k\}=\{x_{\bar{k} + k}\}$. $\square$

Lemma 8.2

Let x be a proper convex combination of atoms in $A' \subset A$, and $d \ne 0$ feasible direction in x. Then, for some $y \in \text {conv}(A')$, we have

$$\begin{aligned} \hat{\alpha }^{\max }(y, d) \ge \frac{\text {PWidth}(A)}{\Vert d\Vert } \, . \end{aligned}$$

(8.41)

Proof

Let $y\in \text {argmax}_{z \in \text {conv}(A')} \hat{\alpha }^{\max }(z, d)$, and let $A'' \subset A'$ be such that y is a proper convex combination of elements in $A''$. Furthermore, let $\mathcal {F}_y$ be the minimal face containing the maximal feasible step point $\bar{y}:= y + \hat{\alpha }^{\max }(y, d)$. We claim that $\mathcal {F}_y \cap A'' = \emptyset$. In fact, for $p \in A'' \cap \mathcal {F}_y$ we can consider an homothety of center p and factor $1 + \epsilon$ mapping y in $y_{\epsilon } \in \text {conv}(A'')$ and $\bar{y}$ in $\bar{y}_{\epsilon } \in \mathcal {F}_y$ with

$$\bar{y}_{\epsilon } = y_{\epsilon } + (1 + \epsilon ) \hat{\alpha }^{\max }(y, d) d \,.$$

But then we would have $\hat{\alpha }(\bar{y}_{\epsilon }, d) \ge (1 + \epsilon ) \hat{\alpha }(\bar{y}, d)$, in contradiction with the maximality of $\hat{\alpha }(\bar{y}, d)$. Therefore

$$\begin{aligned} \hat{\alpha }^{\max }(y, d) \ge \text {dist}(A'', \mathcal {F}_y) \ge \min _{\mathcal {F}\in \text {pfaces}(\Omega )} \text {dist}(\mathcal {F}, \text {conv}(A\setminus \mathcal {F})) = \text {PWidth}(A) \, , \end{aligned}$$

(8.42)

where we used $A'' \cap \mathcal {F}= \emptyset$ in the second inequality, and [53, Theorem 2] in the equality. $\square$