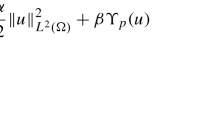Efficient scalarization in multiobjective optimal control of a nonsmooth PDE

Abstract

This work deals with the efficient numerical characterization of Pareto stationary fronts for multiobjective optimal control problems with a moderate number of cost functionals and a mildly nonsmooth, elliptic, semilinear PDE-constraint. When “ample” controls are considered, strong stationarity conditions that can be used to numerically characterize the Pareto stationary fronts are known for our problem. We show that for finite dimensional controls, a sufficient adjoint-based stationarity system remains obtainable. It turns out that these stationarity conditions remain useful when numerically characterizing the fronts, because they correspond to strong stationarity systems for problems obtained by application of weighted-sum and reference point techniques to the multiobjective problem. We compare the performance of both scalarization techniques using quantifiable measures for the approximation quality. The subproblems of either method are solved with a line-search globalized pseudo-semismooth Newton method that appears to remove the degenerate behavior of the local version of the method employed previously. We apply a matrix-free, iterative approach to deal with the memory and complexity requirements when solving the subproblems of the reference point method and compare several preconditioning approaches.

1 Problem formulation

The prevailing notion of optimality in multiobjective optimization is that of optimal compromises or Pareto optimal points, see Definition 1. Evaluating the quality of Pareto optimal points typically involves interpreting the set of function values of all Pareto optimal points – the Pareto front. The aim of this paper is the efficient numerical characterization of the Pareto fronts of nonsmooth multiobjective optimal control problems with few objectives and an elliptic PDE-constraint with $\max$-type nonsmoothness using generalized stationarity conditions, and the comparison of the numerical performance of a weighted-sum approach and a reference point method in terms of efficiency and discretization quality. For ease of presentation, we restrict this exposition to the case of two objectives only – though the scope of this paper can readily be extended to moderately many objective functions using hierarchical approaches, see [3, 4, 15]. Hence, we consider bicriterial problems of the form

$$\begin{aligned}&\min _{(y,u)}\mathcal {J}(y,u)= \left( \begin{aligned} \mathcal {J}_1(y, u)\\ \mathcal {J}_2(y, u) \end{aligned} \right) = \left( \begin{aligned} j_1(y) + \frac{\sigma _1}{2} \left\Vert u\right\Vert _{U}^2\\ j_2(y) + \frac{\sigma _2}{2} \left\Vert u\right\Vert _{U}^2 \end{aligned} \right) \\&\text {s.t. }(y,u)\in {V}\times {U}\text { satisfies }- \varDelta y + \kappa \max \{0,y\} ={{\mathcal {B}}}(u)\text { in } {V}'.\end{aligned}$$

(P)

In (P), the symbols y and u denote the state and control variables in the corresponding state space ${V}$ and (possibly finite dimensional) control space ${U}$, respectively, the $j_i$ denote suitably well behaved scalar cost functionals, the $\sigma _i$ are nonnegative regularization parameters and ${{\mathcal {B}}}:{U}\rightarrow {L^2}(\varOmega )$ denotes a control-to-right-hand-side mapping. For the detailed assumptions on the problem, we refer to Assumption 1.

Multicriterial optimization problems with nonsmooth PDE-constraints like (P) arise in various physical applications with conflicting objectives, see, e.g., [13, 16, 19, 21]. The combination of generally only (Hadamard) directionally differentiable Nemytski operators in the constraint and the inherently nonsmooth structure of multiobjective optimization makes sensitivity and stationarity analysis as well as the numerical solution of these problems rather delicate. Their treatment typically requires specialized stationarity concepts and approaches that do not follow standard procedure for Gâteaux differentiable problems. The particular case of the PDE-constraint in (P) is rather well understood in terms of existence and regularity of solutions and differentiability properties of the solution operator and has previously been addressed as a constraint in optimization problems in, e.g., [6, 7]. The specific structure of the PDE even allows for the derivation of strong stationarity systems when the control space is sufficiently rich, which has been considered in both scalar and multiobjective optimization with an arbitrary number of objectives, see [6, 7]. Stationarity conditions of intermediate strength based on the characterization of the subdifferentials of the solution operator to the constraining PDE have been addressed in [6] and the considerations in [7] show that C-stationarity and strong stationarity in fact coincide for ample controls.

Numerically, the Pareto stationary front of problem (P) has been characterized for two and three cost functionals and ${{L^2}(\varOmega )}$ controls [7] by combining a first-optimize-then-discretize approach and a pseudo-semismooth Newton (PSN) method, and by using a regularization approach. With multiple objectives, computation times can quickly become large with increased fineness of discretizations of the domain and the Pareto front, making efficient numerics a vital component to these simulations. In [5], the authors discussed a standard offline/online greedy reduced-basis approach for (P) with a single scalar objective function and both low and high dimensional control/parameter space and compared the results to an adaptive way of generating the reduced basis along the solution process of the PSN.

In this paper, our goal is the efficient characterization of the Pareto stationary front of the bicriterial problem (P) for both ${{L^2}(\varOmega )}$-controls as well as finite-dimensional controls with specific structure to allow for a combination with the reduced-basis approaches from [5] mentioned above. In the case of the ${{L^2}(\varOmega )}$-controls, where strong stationarity conditions were derived in [7], this is essentially a refinement of the numerical techniques employed in the same paper. For finite dimensional controls, which are typically insufficiently “rich” to obtain strong stationarity conditions, however, this requires revisiting the optimality conditions and how they can be used to characterize the Pareto stationary fronts. Following the approaches in [7], we show that, in the case of finite dimensional controls, a sufficient stationarity system can still be obtained. Though a sufficient system for a necessary optimality condition is unfavorable in general, it turns out that the system we obtain is essentially a strong stationarity system for the optimization problems corresponding to the weighted-sum method and the Euclidean reference point method and therefore a somewhat reasonable system to use for characterization of the Pareto stationary fronts. The nonlinear structure in the sets that are involved there, introduced by the nonsmoothness of the PDE, however, does not lend itself to use for characterization of the front directly. Instead, a linearization of the same system will be solved by a line-search stabilized PSN approach and combined with a sign condition that is checked a-posteriori. The line-search essentially eliminates the rare, mesh-dependent non-convergence issue observed for the undamped PSN in [5, 7]. We will compare the efficiency and the approximation quality of the front of the weighted-sum and the reference point approach using quantifiable quality measures.

The structure of this paper is as follows: We will shortly comment on the assumptions for this paper in Subsect. 1.1. Then, we recall the required notions of Pareto optimality and Pareto stationarity and state the respective first order systems for (non-)ample controls in Sect. 2. In the case ${U}= {{L^2}(\varOmega )}$, the analytical results are analogous to those in [7] and the strong stationarity results are simply restated, whereas similar conditions in the case ${U}= {\mathbb {R}}^p$ are shown to remain sufficient only. In Sect. 3, we will shortly recall the weighted-sum method and the reference point method, and show that the sufficient system from the multiobjective setting is equivalent to strong stationarity systems for the scalarized systems. We explain how these methods can therefore be used to characterize the Pareto stationary front. The numerical implementation is explained in detail in Sect. 4, where we present a matrix-free preconditioned limited-memory generalized minimal residual (L-GMRES) method for the line-search globalized pseudo-semismooth Newton (gPSN) method that will be used to handle the density of the discretization matrices in the reference point method and the convergence issues arising from the nonsmoothness of the PDE-constraint, respectively. We further present two numerical examples – one with (FE-discretized) $L^2(\varOmega )$-controls and one with inherently finite dimensional controls in Sect. 5. The interpretation of the numerical results is specifically focused on the effects of different preconditioning strategies for the reference point method. We introduce two quantities to measure the approximation quality of the two methods and use them as a basis for a performance comparison of the two scalarization approaches.

1.1 Notation and assumptions on the data

We endow ${V}= H_0^1(\varOmega )$ with the inner product ${{\langle \varphi ,\phi \rangle }_{V}=\int _\varOmega \nabla \varphi \cdot \nabla \phi +\varphi \phi \,\mathrm d{\varvec{x}}}$ for $\varphi ,\phi \in {V}$ and the induced norm $\Vert \cdot \Vert _{V}=\langle \cdot \,,\cdot \rangle _{V}^{1/2}$. Its topological dual space is written as ${V}' = H^{-1}(\varOmega )$. The space ${Y}$ denotes $V\cap H^2(\varOmega )$ with topological dual space ${Y}'$. We also set $H=L^2(\varOmega )$. For functions in Y, the Laplacian is understood in the non-variational sense and the Dirichlet Laplacian $\varDelta :H \rightarrow {Y}'$ is understood in the very weak sense (see [12], Section 1.9). Our assumptions on the data are as follows:

Assumption 1

• 1) $\varOmega \subset \mathbb {R}^d$ for $d \in {\mathbb {N}}\setminus \{0\}$ is a bounded domain that is convex or possesses a $C^{1,1}$-boundary (cf. [10, Section 6.2]),

• 2) $j_1, j_2 :{Y}\rightarrow {\mathbb {R}}$ are weakly lower semicontinuous, twice continuously Fréchet-differentiable and bounded from below,

• 3) $\sigma _1 \ge 0$, $\sigma _2 > 0$, $\kappa \ge 0$,

• 4) ${U}= {\mathbb {R}}^p$ for $p \in {\mathbb {N}} \setminus \{0\}$ and $\Vert \cdot \Vert _{U}$ denotes the Euclidean norm or ${U}= H$ and $\Vert \cdot \Vert _{U}$ denotes the $L^2$-norm,

• 5) ${{\mathcal {B}}}:{U}\rightarrow H$ possesses the following property:

  • 5a) If ${U}= \mathbb {R}^p$ the operator ${{\mathcal {B}}}:{U}\rightarrow H$ is linear (and therefore automatically bounded) and the pairwise intersection of the sets $\{b_i\ne 0\}\subset \varOmega$ of $b_i{:}{=}{{\mathcal {B}}}(e_i) \in H$, where $e_i,\, i=1,\dots ,p$ denote the unit vectors in ${U}$, are Lebesgue nullsets and none of the $b_i$ are zero.

  • 5b) If ${U}= H$ the operator ${{\mathcal {B}}}:{U}\rightarrow H$ is unitary.

2 A sufficient condition for pareto stationarity

Structurally, this section follows [7] closely, where the case ${U}= H = {{L^2}(\varOmega )}$ is dealt with and carries over immediately, yielding strong stationarity conditions for the Pareto stationary points. For the case where ${U}= {\mathbb {R}}^p$, however, the same reasoning does not hold up – specifically, the system obtained by similar arguments will only be sufficient in general. The main issue in the analysis is the well-known fact that strong stationarity conditions typically require ample controls. Note that the results presented in this section can readily be generalized to an arbitrary finite number of objective functionals.

We start by summarizing the main properties of the solution operator $\mathcal {S}$ to the PDE-constraint in the next lemma as a minor extension to [7, Lemma 4.2]. Note that, since we will mostly focus on the case ${U}= {\mathbb {R}}^p$, we do not obtain analogous results to all the results stated in [7, Lemma 4.2] for the case ${U}= H$.

Lemma 1

(Properties of the solution operator $\mathcal {S}$) Let $u \in U$ be a control with associated state $y=\mathcal {S}(u)$. Then:

• 1) There is a solution operator $\mathcal {S}:{U}\rightarrow {Y}$ that is Lipschitz continuous and Hadamard directionally differentiable, where the derivative $\mathcal {S}'(u;h) = w \in {Y}$ for given direction $h\in U$ is the unique solution to

  $$\begin{aligned} - \varDelta w + \kappa \mathbbm {1}_{\{y = 0\}} \max \{0, w\} + \kappa \mathbbm {1}_{\{y > 0\}} w = {{\mathcal {B}}}(h) \quad \text { in } {V}'. \end{aligned}$$

  (1)

  This especially implies the Y-regularity of the state variable y.

• 2) If ${U}= {\mathbb {R}}^p$, then the map

  $$\begin{aligned}&\tilde{{{\mathcal {B}}}^\dagger } :H\rightarrow {U},\quad v \mapsto \nu =(\nu _i)_{1\le i\le p}\quad \text {with }\nu _i = \frac{\langle v, b_i\rangle _H}{\Vert b_i\Vert _H^2} \end{aligned}$$

  (2)

  is a linear and bounded left inverse of ${{\mathcal {B}}}:{U}\rightarrow H$.

• 3) The map $\mathcal {S}'(u;\cdot ):{U}\rightarrow {Y}$ is Lipschitz continuous and allows for a Lipschitz continuous left inverse given by

  $$\begin{aligned} \mathcal {S}'(u;\cdot )^\dagger :{Y}\rightarrow {U},\quad w \mapsto {{{\mathcal {B}}}^\dagger } \big ( \underbrace{- \varDelta w + \kappa \mathbbm {1}_{\{y = 0\}} \max \{0,w\} + \kappa \mathbbm {1}_{\{y > 0 \}} w}_{\in\, H} \big ), \end{aligned}$$

  where ${{{\mathcal {B}}}^\dagger }$ is any linear, bounded left inverse of ${{\mathcal {B}}}$.

• 4) There exists a linear and bounded left inverse ${{{\mathcal {B}}}^\dagger }$ of ${{\mathcal {B}}}$ that does not depend on u such that

  $$\begin{aligned} \big \langle u, \mathcal {S}'(u;\cdot )^\dagger (w)\big \rangle _{{U}} = \big \langle ( - \varDelta + \kappa \mathbbm {1}_{\{y > 0\}}){{{\mathcal {B}}}^\dagger }^*(u), w \big \rangle _{{Y}',{Y}} \end{aligned}$$

  for every $w \in {Y}$, where ${{{\mathcal {B}}}^\dagger }^*:U\rightarrow H$ is the Hilbert adjoint of the left inverse ${{{\mathcal {B}}}^\dagger }$.

Proof

Let $u\in U$ be arbitrarily given and $y={\mathcal {S}}(u)\in Y$. Notice that the ${Y}$-regularity also follows from Proposition 2.1 in [6].

• 1) The linearity and boundedness of ${{\mathcal {B}}}$ imply Lipschitz continuity and Hadamard differentiability analogously to Proposition 2.1 and Theorem 2.2 in [6] and due to the chain rule, the directional derivative of the solution operator $w = \mathcal {S}'(u;h)$ solves

  $$\begin{aligned} - \varDelta w + \kappa \mathbbm {1}_{\{y = 0\}} \max \{0, w\} + \kappa \mathbbm {1}_{\{y > 0\}} w = {{\mathcal {B}}}(h) \quad \text { in } {V}'. \end{aligned}$$

• 2) Note that the operator $\tilde{{{\mathcal {B}}}^\dagger }$ is well defined due to Assumption 1-5). Clearly, the operator is linear and bounded. The left inverse quality remains to be proved. Let ${\tilde{u}}\in {U}= {\mathbb {R}}^p$ and $v = {{\mathcal {B}}}{\tilde{u}}= \sum _{j=1}^p b_j {\tilde{u}}_j\in H$. For every $i\in \{1,\dots ,p\}$, we have that

  $$\begin{aligned} \big (\tilde{{{\mathcal {B}}}^\dagger }(v )\big )_i&=\frac{\langle v ,b_i\rangle _H}{\Vert b_i\Vert _H^2} =\sum _{j=1}^p{\tilde{u}}_j\frac{\langle b_j, b_i\rangle _H}{\Vert b_i\Vert _H^2} ={\tilde{u}}_i\frac{\langle b_i, b_i\rangle _H}{\Vert b_i\Vert _H^2}={\tilde{u}}_i, \end{aligned}$$

  where the second to last equality holds due to the H-orthogonality of the $b_i$’s induced by Assumption 1-5).

• 3) The Lipschitz continuity of the linearized solution operator is implied by the form of the linearization (1). Existence of a left inverse is clear due to part 1 if ${U}= {\mathbb {R}}^p$ and since ${{\mathcal {B}}}$ is unitary if ${U}= H$. Thus existence of a left inverse of $\mathcal {S}'(u;\cdot )$ and its Lipschitz continuity are obvious from the explicit definition.

• 4) First assume that ${U}=H$ and that ${{\mathcal {B}}}$ is a unitary operator. Then, by definition, we obtain that ${{{\mathcal {B}}}^\dagger }^*={{\mathcal {B}}}.$ Consequently, for $u\in {U}$ and $y=\mathcal {S}(u)$,

  $$\begin{aligned} \begin{aligned}&{\langle {{{\mathcal {B}}}^\dagger }^*(u), \kappa \mathbbm {1}_{\{y = 0\}} \max \{0,w\}\rangle }_H={\langle {{\mathcal {B}}}(u), \kappa \mathbbm {1}_{\{y = 0\}} \max \{0,w\}\rangle }_H\\&\qquad = \langle \underbrace{-\varDelta y + \kappa \max \{0,y\}}_{=\, 0 \text { a.e. on } \{y\, =\, 0\}}, \kappa \mathbbm {1}_{\{y = 0\}} \max \{0,w\}{\rangle }_H = 0, \end{aligned} \end{aligned}$$

  (3)

  where $\varDelta y = 0$ a.e. on $\{y = 0\}$ is a consequence of [7, Lemma 4.1]. Thus, using part 3) and (3), we find that

  $$\begin{aligned}&\big \langle u,\mathcal {S}'(u;\cdot )^\dagger (w)\big \rangle _{{U}}=\big \langle u, {{{\mathcal {B}}}^\dagger }\big ( - \varDelta w + \kappa \mathbbm {1}_{\{y = 0\}} \max \{0,w\} + \kappa \mathbbm {1}_{\{y> 0 \}} w \big )\big \rangle _{{U}}\\&\quad =\big \langle {{{\mathcal {B}}}^\dagger }^*(u),\big (-\varDelta + \kappa \mathbbm {1}_{\{y> 0\}}\big )w\big \rangle _H+\big \langle {{{\mathcal {B}}}^\dagger }^*(u), \kappa \mathbbm {1}_{\{y = 0\}} \max \{0,w\} \big \rangle _H\\&\quad =\big \langle {{{\mathcal {B}}}^\dagger }^*(u),\big (-\varDelta + \kappa \mathbbm {1}_{\{y> 0\}}\big )w\big \rangle _H\\&\quad =\big \langle \big (-\varDelta + \kappa \mathbbm {1}_{\{y > 0\}}\big ){{{\mathcal {B}}}^\dagger }^*(u),w\big \rangle _{{Y}',{Y}} \end{aligned}$$

  for every $w\in Y$, where the last line follows due to the definition of the very weak Dirichlet Laplacian.Now assume that ${U}= {\mathbb {R}}^p$. We show that $\tilde{{{\mathcal {B}}}^\dagger }$ is the desired left inverse. For $u\in {U}$, $y=\mathcal {S}(u)$ and any $i\in \{1,\ldots ,p\}$, we have that ${\{y = 0\}}\cap \{ b_i u_i \ne 0\}$ is a nullset, because

  $$\begin{aligned} \{b_i u_i \ne 0\} \cap \{y = 0\}\subset \{b_i u_i \ne 0 \} \cap \{{{\mathcal {B}}}(u) = 0\} \subset \{b_i u_i \ne 0\} \cap \{ b_i u_i = 0\}, \end{aligned}$$

  where the first inclusion is again a consequence of [7, Lemma 4.1] and the second inclusion is due to Assumption 1-5). Thus, for any $i\in \{1,\ldots ,p\}$, we infer

  $$\begin{aligned} \frac{\langle \mathbbm {1}_{\{y = 0\}} \max \{0,w\}, b_i u_i\rangle _H}{\Vert b_i\Vert _H^2}=0. \end{aligned}$$

  Due to part 2), we obtain that

  $$\begin{aligned}&\big \langle u,\tilde{{{\mathcal {B}}}^\dagger } \big (\kappa \mathbbm {1}_{\{y = 0\}}\max \{0,w\}\big )\big \rangle _{U}\\&\quad =\sum _{i=1}^pu_i\,\frac{\langle \kappa \mathbbm {1}_{\{y = 0\}}\max \{0,w\},b_i\rangle _H}{\Vert b_i\Vert _H^2}= \kappa \sum _{i=1}^p\frac{\langle \mathbbm {1}_{\{y = 0\}}\max \{0,w\},u_ib_i\rangle _H}{\Vert b_i\Vert _H^2} =0 \end{aligned}$$

  for every $w \in {Y}$. Consequently,

  $$\begin{aligned} {\langle u,\mathcal {S}'(u;\cdot )^\dagger (w) \rangle }_{{U}}&=\big \langle u,\tilde{{{\mathcal {B}}}^\dagger }\big (-\varDelta w+ \kappa \mathbbm {1}_{\{y = 0\}} \max \{0,w\}+ \kappa \mathbbm {1}_{\{y> 0 \}}w\big )\big \rangle _{U}\\&=\big \langle \big (-\varDelta + \kappa \mathbbm {1}_{\{y > 0\}}\big )\tilde{{{\mathcal {B}}}^\dagger }^*(u),w\big \rangle _{{Y}',{Y}}, \end{aligned}$$

  for every $w \in {Y}$.

$\square$

As usual, we denote the well-defined reduced cost functional as $\hat{\mathcal {J}}:{U}\rightarrow {\mathbb {R}}^2,\, \hat{\mathcal {J}}(u)=\mathcal {J}(\mathcal {S}(u),u)$. Having established the properties of the solution operator, we are ready to review the different notions of Pareto optimality and the optimality conditions that will play a role later on.

Definition 1

(Pareto Optimality) Let $\bar{y}, \bar{u}$ with $\bar{y}= \mathcal {S}(\bar{u})$ and $\bar{u}\in {U}$. The control $\bar{u}$ is called:

• 1) a local weak Pareto optimal point of (P) if an $r > 0$ exists such that there is no $u \in {U}$ satisfying

  $$\begin{aligned}&{\Vert u - \bar{u}\Vert }_{U}< r,&\mathcal {J}_i\left( \mathcal {S}(u), u\right) < \mathcal {J}_i\left( \bar{y}, \bar{u}\right) \text { for }i = 1,2; \end{aligned}$$

• 2) a local Pareto optimal point of (P) if an $r > 0$ exists such that there is no $u \in {U}$ satisfying

  $$\begin{aligned}&{\Vert u - \bar{u}\Vert }_{U}< r,&\mathcal {J}_i\left( \mathcal {S}(u), u\right) \le \mathcal {J}_i\left( \bar{y}, \bar{u}\right) \text { for }i = 1, 2, \end{aligned}$$

  where the latter inequality is strict for at least one i;

• 3) a local proper Pareto optimal point of (P) if there are $r, C > 0$ such that for every $u \in {U}$ satisfying $\Vert u - \bar{u}\Vert _{U}< r$ and $\mathcal {J}_i\left( \mathcal {S}(u), u\right) \le \mathcal {J}_i\left( \bar{y}, \bar{u}\right)$ for some index $i \in \{ 1,2 \}$, there exists an index $m \in \{1,2\} \setminus \{i\}$ with

  $$\begin{aligned} \mathcal {J}_i(\bar{y},\bar{u}) - \mathcal {J}_i(\mathcal {S}(u),u) \le C( \mathcal {J}_m(\mathcal {S}(u),u) - \mathcal {J}_m(\bar{y},\bar{u})); \end{aligned}$$

• 4) a global (weak/proper) Pareto optimal point of (P) if the previous conditions hold with $r = \infty$;

The image sets of all controls that are (local/global) (weak/proper) Pareto optimal under the cost functional are called the Pareto fronts corresponding to the respective sense of optimality.

Analogously to [7], we obtain the following corresponding primal optimality conditions.

Theorem 1

(Optimality Conditions – Primal Form)

• 1) If $\bar{u}\in {U}$ with associated state $\bar{y}= \mathcal {S}(\bar{u})$ is a local weak Pareto optimal point of (P), then there exists no direction $h \in {U}$ satisfying

  $$\begin{aligned} {\langle j_i'(\bar{y}), \mathcal {S}'(\bar{u};h)\rangle }_{{Y}',{Y}} + \sigma _i\,{\langle \bar{u}, h\rangle }_{{U}} < 0\quad \text {for }i = 1,2. \end{aligned}$$

  (4)

• 2) If $\bar{u}\in {U}$ with associated state $\bar{y}= \mathcal {S}(\bar{u})$ is a local proper Pareto optimal point of (P) with constants $r, C > 0$, then for every $h \in {U}$ with $\langle j_i'(\bar{y}), \mathcal {S}'(\bar{u};h)\rangle _{{Y}',{Y}} + \sigma _i \langle \bar{u},h\rangle _{U}< 0$ for some $i \in \{1,2\}$, there exists an $m \in \{1,2\} \setminus \{i\}$ with

  $$\begin{aligned}&- \big ({\langle j_i'(\bar{y}),\mathcal {S}'(\bar{u};h)\rangle }_{{Y}',{Y}} + \sigma _i\,{\langle \bar{u},h\rangle }_{U}\big )\\&\quad \le C \big ( \langle j_m'(\bar{y}),\mathcal {S}'(\bar{u};h)\rangle _{{Y}',{Y}} + \sigma _m\,{\langle \bar{u},h\rangle }_{U}\big ). \end{aligned}$$

Proof

See [7, Theorem 3.1]. $\square$

Accordingly, we obtain the corresponding notions of Pareto stationarity.

Definition 2

(Pareto Stationarity) Let $\bar{u}\in {U}$ and $\bar{y}= \mathcal {S}(\bar{u})$. The control $\bar{u}$ is called:

• 1) a weak Pareto stationary point of (P) if there is no $h \in {U}$ satisfying

  $$\begin{aligned} {\langle j_i'(\bar{y}), \mathcal {S}'(\bar{u};h)\rangle }_{{Y}',{Y}}+\sigma _i\,{\langle \bar{u}, h \rangle }_{U}< 0\quad \text {for }i = 1,2; \end{aligned}$$

• 2) a Pareto stationary point of (P) if there is no $h \in {U}$ satisfying

  $$\begin{aligned} {\langle j_i'(\bar{y}), \mathcal {S}'(\bar{u};h) \rangle }_{{Y}',{Y}} + \sigma _i\,{\langle \bar{u}, h \rangle }_{U}\le 0\quad \text {for }i = 1,2, \end{aligned}$$

  where the latter inequality is strict for at least one i;

• 3) a proper Pareto stationary point of (P) if there is a $C > 0$ such that for all $h \in {U}$ with $\langle j_i'(\bar{y}),\mathcal {S}'(\bar{u};h)\rangle _{{Y}',{Y}} + \sigma _i \langle \bar{u},h\rangle _{U}< 0$ for some $i \in \{1,2\}$, there exists an $m \in \{1,2\} \setminus \{i\}$ with

  $$\begin{aligned}&-\big ({\langle j_i'(\bar{y}),\mathcal {S}'(\bar{u};h)\rangle }_{{Y}',{Y}} + \sigma _i\,{\langle \bar{u},h\rangle }_{U}\big )\\&\quad \le C \big ({\langle j_m'(\bar{y}),\mathcal {S}'(\bar{u};h)\rangle }_{{Y}',{Y}} + \sigma _m\,{\langle \bar{u},h\rangle }_{U}\big ). \end{aligned}$$

Remark 1

By definition, all proper Pareto optima are Pareto optima, which in turn all are weak Pareto optima. The same holds locally. As a consequence of Theorem 1, all local weak Pareto optima are weakly Pareto stationary and all local proper Pareto optima are properly Pareto stationary. However, Pareto stationarity is generally not necessary for local Pareto optimality. $\Diamond$

In the case of ${{L^2}(\varOmega )}$-controls, the version of Tucker’s/Motzkin’s theorem of the alternative in infinite dimensions in [7, Lemma 4.4] provides the existence of the multipliers appearing in the system of strong stationarity conditions. In the case of finite dimensional controls, we unfortunately have to deal with generally nonlinear subsets of the spaces involved, and, as it turns out, an extension of the existence results to arbitrary subsets does not hold. Hence, we can only recover one of the implications when the result is generalized to potentially nonlinear subsets of Hilbert spaces.

Lemma 2

Suppose ${\mathcal{W}}$ is a nonempty subset of a real Hilbert space ${\mathcal{V}}$ and $v_1',\ldots , v_N' \in {\mathscr {V}}'$ are given. Assume that there exists $\lambda \in {\mathbb {R}}^N$ with $\lambda _i \ge 0$ for $i = 1,\ldots ,N$ such that

$$\begin{aligned}&\sum \limits _{i = 1}^N \lambda _i = 1&\text {and}&&\sum \limits _{i = 1}^N \lambda _i \,\langle v_i',w\rangle _{\mathscr {V}} \ge 0&&\text {for all } w \in {\mathcal{W}}. \end{aligned}$$

Then there exists no $z \in {\mathcal{W}}$ such that

$$\begin{aligned}&\langle v_i',z\rangle _{{\mathscr {V}}} < 0&\text {for all } i = 1,\ldots , N. \end{aligned}$$

Furthermore, if $\lambda _i > 0$ for all $i = 1,\ldots ,N$, then there exists no $z \in {\mathcal{W}}$ such that

$$\begin{aligned}&\langle v_i',z\rangle _{{\mathscr {V}}} \le 0&\text {for all } i = 1,\ldots , N, \end{aligned}$$

with the inequality holding strictly for at least one i.

Proof

Assume that there exists a $z \in {\mathcal{W}}$ with $\langle v_i',z\rangle _{{\mathscr {V}}} < 0$ for all $i = 1,\ldots ,N$. This would imply that

$$\begin{aligned} \sum \limits _{i = 1}^N \lambda _i\,{\langle v_i',z\rangle }_{\mathscr {V}} < 0, \end{aligned}$$

which is a contradiction. Analogously, if $\lambda _i > 0$ for all $i = 1,\ldots , N$, then there exists no $z \in {\mathcal{W}}$ such that $\langle v_i',z\rangle _{{\mathcal{V}}} \le 0$ for all $i = 1,\ldots , N$ with the inequality holding strictly for at least one i, which shows the claim. $\square$

It follows that the technique used to show [7, Theorem 4.5] now yields a sufficient system only, i.e., we obtain the following sufficient adjoint-based optimality system.

Theorem 2

(Sufficient adjoint-based system)

• 1. Assume that there exists an adjoint state $\bar{p}$ and a multiplier $\bar{\alpha }$ such that $\bar{u}, \bar{y}, \bar{p}, \bar{\alpha }$ satisfy the coupled system

  $$\begin{aligned} \bar{u}\in {U}, \quad \bar{y}&\in {Y},&\bar{p}\in {H}, \quad \bar{\alpha }\in {\mathbb {R}}^2, \end{aligned}$$

  (5a)
  $$\begin{aligned} \bar{\alpha }_i \ge 0 \quad \text {for } i&= 1,2,&\sum \limits _{i = 1}^2 \bar{\alpha }_i = 1,\end{aligned}$$

  (5b)
  $$\begin{aligned} - \varDelta \bar{y}+ \kappa \max \{0, \bar{y}\}&= {{\mathcal {B}}}(\bar{u})\quad \text { in } {V}',\\ \big \langle - \varDelta \bar{p}+ \kappa \mathbbm {1}_{\{\bar{y}> 0 \}} \bar{p},w{\big \rangle }_{{Y}', {Y}} \nonumber &\le \sum \limits _{i = 1}^2 \bar{\alpha }_i {\langle j_i'(\bar{y}),w\rangle }_{{Y}',{Y}}\nonumber \text { for all } w\in {\text {Im}}(\mathcal {S}'(\bar{u};\cdot )), \end{aligned}$$

  (5c)
  $$\begin{aligned} \bar{p}+ \sum \limits _{i = 1}^2 \bar{\alpha }_i\sigma _i{{{\mathcal {B}}}^\dagger }^* (\bar{u})&= 0&\text { in } H. \end{aligned}$$

  (5d)

  Then $\bar{u}\in {U}$ is a weak Pareto stationary point of (P).

• 2. Assume that $\bar{u}, \bar{y}, \bar{p}, \bar{\alpha }$ satisfy the system (5), where the inequality in (5b) is strict, i.e. $\bar{\alpha }_i > 0$ for $i = 1,2$. Then $\bar{u}$ is a proper Pareto stationary point of (P) (and thus also a Pareto stationary point).

Proof

Let $\bar{u}, \bar{y}, \bar{p}, \bar{\alpha }$ that solve (5) be given. Inserting (5d) into (5c), yields

$$\begin{aligned} \sum \limits _{i = 1}^2 \bar{\alpha }_i\,{\langle j_i'(\bar{y}) + \sigma _i(-\varDelta + \kappa \mathbbm {1}_{\{\bar{y}> 0\}}){{{\mathcal {B}}}^\dagger }^*(\bar{u}),w\rangle }_{{Y}',{Y}} \ge 0 \quad \text {for all } w \in {\text {Im}}(\mathcal {S}'(\bar{u};\cdot )). \end{aligned}$$

According to Lemma 2, this implies that

$$\begin{aligned} {\langle j_i'(\bar{y}),w\rangle }_{{Y}',{Y}} + \sigma _i\,{\langle (-\varDelta + \kappa \mathbbm {1}_{\{\bar{y}> 0\}}) {{{\mathcal {B}}}^\dagger }^*( \bar{u}),w\rangle }_{{Y}',{Y}} < 0 {\quad \text {for }i = 1,2} \end{aligned}$$

is valid for no $w \in {\text {Im}}(\mathcal {S}'(\bar{u};\cdot ))$. Since $\mathcal {S}'(\bar{u};\mathcal {S}'(\bar{u};\cdot )^\dagger (w)) = w$ for all $w \in {\text {Im}}(\mathcal {S}'(\bar{u};\cdot ))$ and due to the explicit form of $\mathcal {S}'(\bar{u};\cdot )^\dagger$ provided by Lemma 1-1, we have that

$$\begin{aligned} {\langle j_i'(\bar{y}),\mathcal {S}'(\bar{u};\mathcal {S}'(\bar{u};\cdot )^\dagger (w))\rangle }_{{Y}',{Y}} + \sigma _i\,{\langle \bar{u},\mathcal {S}'(\bar{u};\cdot )^\dagger (w)\rangle }_{U}< 0\quad \text {for }i = 1,2 \end{aligned}$$

is valid for no $w \in {\text {Im}}(\mathcal {S}'(\bar{u};\cdot )) \subset {Y}$. Since ${\text {Im}}(\mathcal {S}'(\bar{u};\cdot ))$ under the map $\mathcal {S}'(\bar{u};\cdot )^\dagger$ is ${U}$, this is equivalent to weak Pareto stationarity. For part 2, ordinary Pareto stationarity immediately follows from Lemma 2 and we will show that this implies proper Pareto stationarity analogously to [7, Theorem 4.5 iii)]. To that end, assume that there is $h \in {U}$ such that $\langle j_i'(\bar{y}),\mathcal {S}'(\bar{u};h)\rangle _{{Y}',{Y}} + \sigma _i \langle \bar{u},h\rangle _{U}< 0$ for some $i \in \{1,2\}$. Just like in the proof of part 1, we obtain that

$$\begin{aligned} \sum \limits _{i = 1}^2 \bar{\alpha }_i\,{\langle j_i'(\bar{y}) + \sigma _i(-\varDelta + \kappa \mathbbm {1}_{\{\bar{y}> 0\}}){{{\mathcal {B}}}^\dagger }^*(\bar{u}),w\rangle }_{{Y}',{Y}} \ge 0 \quad \text {for all } w \in {\text {Im}}(\mathcal {S}'(\bar{u};\cdot )). \end{aligned}$$

and applying the form of ${\mathcal {S}'(\bar{u};\cdot )^\dagger }$ provided by Lemma 1-4) again, this implies that

$$\begin{aligned} \sum \limits _{i = 1}^2 \bar{\alpha }_i\, ( {\langle j_i'(\bar{y}),\mathcal {S}'(\bar{u};\mathcal {S}'(\bar{u};\cdot )^\dagger (w))\rangle }_{{Y}',{Y}} + \sigma _i {\langle \bar{u}, \mathcal {S}'(\bar{u};\cdot )^\dagger w \rangle } _{{Y}',{Y}} ) \ge 0 \end{aligned}$$

for all $w \in {\text {Im}}(\mathcal {S}'(\bar{u};\cdot ))$ and therefore

$$\begin{aligned} \sum \limits _{i = 1}^2 \bar{\alpha }_i\, ( {\langle j_i'(\bar{y}),\mathcal {S}'(\bar{u};v)\rangle }_{{Y}',{Y}} + \sigma _i {\langle \bar{u}, v \rangle } _{{Y}',{Y}} ) \ge 0 \end{aligned}$$

for all $v \in {U}$. Hence

$$\begin{aligned} \begin{aligned} 0&< - \langle j_i'(\bar{y}),\mathcal {S}'(\bar{u};h)\rangle _{{Y}',{Y}} + \sigma _i \langle \bar{u},h\rangle _{U}\\&\le \frac{1}{\min \limits _{l=1,2}\alpha _l}\langle j_k'(\bar{y}),\mathcal {S}'(\bar{u};h)\rangle _{{Y}',{Y}} + \sigma _k \langle \bar{u},h\rangle _{U}\end{aligned} \end{aligned}$$

for $k\in \{1,2\}\setminus \{i\}$. $\square$

Additionally, we make the following observations.

Corollary 1

Consider the setting of Theorem 2 with ${U}= {\mathbb {R}}^p$. If (5d) is replaced by

$$\begin{aligned} {{\mathcal {B}}}^* (\bar{p}) + \sum \limits _{i = 1}^2 \bar{\alpha }_i \sigma _i \bar{u}= 0 \quad \text { in } {U}. \end{aligned}$$

(6)

in Theorem 2-1) or -2) and the sign condition

$$\begin{aligned} {\langle \mathbbm {1}_{\{\bar{y}= 0\}}\max \{0,w\},\bar{p}\rangle }_H \le 0 \quad \text {for all } w \in {\text {Im}}(\mathcal {S}'(\bar{u};\cdot )), \end{aligned}$$

(7)

is added, then the resulting system is sufficient (but generally not necessary) for weak/proper Pareto stationarity.

Proof

Assume that $\bar{u}, \bar{y}, \bar{p}, \bar{\alpha }$ satisfy the system (5a)-(5c), (6) and (7) with $\bar{\alpha }_i \ge 0$ for $i = 1,2$. For arbitrary $h \in {U}$ set $w = \mathcal {S}'(\bar{u};h)$. It follows that

$$\begin{aligned}&- \sum \limits _{i = 1}^2 \bar{\alpha }_i \sigma _i \langle \bar{u}, h\rangle _{U}= \langle {{\mathcal {B}}}^*(\bar{p}), h\rangle _{U}= {\langle \bar{p}, {{\mathcal {B}}}(h)\rangle }_H\\&\quad = {\langle - \varDelta w + \kappa \mathbbm {1}_{\{\bar{y}> 0\}} w + \kappa \mathbbm {1}_{\{\bar{y}= 0\}} \max \{0,w\},\bar{p}\rangle }_H\\&\quad \le {\langle - \varDelta w + \kappa \mathbbm {1}_{\{\bar{y}> 0\}} w, \bar{p}\rangle }_H= {\langle - \varDelta \bar{p}+ \kappa \mathbbm {1}_{\{\bar{y}> 0\}} \bar{p}, w\rangle }_{{Y}',{Y}}\\&\quad \le \sum \limits _{i = 1}^2 \bar{\alpha }_i\,{\langle j_i'(\bar{y}),w\rangle }_{{Y}',{Y}}. \end{aligned}$$

Thus since $\bar{\alpha }_i \ge 0$ and $\sum \limits _{i = 1}^2 \bar{\alpha }_i = 1$ the inequality

$$\begin{aligned} {\langle j_i'(\bar{y}),w\rangle }_{{Y}',{Y}} + \sigma _i\,{\langle \bar{u},h\rangle }_{{U}} < 0 \end{aligned}$$

cannot be true for all $i = 1,2$. This implies the desired weak Pareto stationarity. (Proper) Pareto stationarity can be shown analogously. $\square$

3 Connection to scalarization methods

As shown in Sect. 2, we can obtain an adjoint based system that is sufficient for Pareto stationarity. When we base numerical characterizations of the Pareto stationary front on this system, since it is potentially not necessary for Pareto stationarity, we may lose out on points on the front. In this section, we want to show that the adjoint system from Theorem 2 is a strong stationarity system for problems arising in two well-known scalarization methods – i.e., using the adjoint multiobjective stationarity system is not a worse approach than straight forward scalarization. We will briefly explain the scalarization methods – the weighted-sum method (cf., e.g., [8]) and the reference point method (cf., e.g., [14, 17]) – and how we intend to use them to characterize the Pareto stationary front.

3.1 Weighted-sum method (WSM)

For weights $\alpha _1, \alpha _2 \ge 0$ with $\alpha _1 + \alpha _2 = 1$, the optimization problem

$$\begin{aligned} \begin{aligned}&\min _{(y,u)} \alpha _1 \mathcal {J}_1(y, u) + \alpha _2 \mathcal {J}_2(y, u) \\&\text {s.t. }(y,u)\in {V}\times {U}\text { satisfies }- \varDelta y + \kappa \max \{0,y\} ={{\mathcal {B}}}(u)\text { in } {V}', \end{aligned} \quad \quad \quad \quad \quad \quad ({{\textbf {P}}_\alpha }) \end{aligned}$$

is called the weighted-sum problem (with non-negative weights $\alpha _1, \alpha _2$) corresponding to (P). The weighted-sum method is based on solving (P$_{\alpha }$) for varying $\alpha$. The primal optimality conditions for the WSM are given in the following theorem.

Theorem 3

Let $\alpha _1, \alpha _2 \ge 0$ with $\alpha _1 + \alpha _2 = 1$ and denote $\alpha = (\alpha _1, \alpha _2)$. Let the control $\bar{u}\in {U}$ be locally optimal for (P$_{\alpha }$) and let $\bar{y}= \mathcal {S}(\bar{u}) \in {Y}$ be the associated state. Then

$$\begin{aligned} \sum _{i = 1}^2 \alpha _i \big (\langle j_i'(\bar{y}),\mathcal {S}'(\bar{u};h)\rangle _{{Y}',{Y}} + \sigma _i \langle u, h\rangle _{{U}}\big ) \ge 0 \quad \text { for all } h\in {U}. \end{aligned}$$

(8)

Proof

The claim follows analogously to [7, Theorem 3.1]. $\square$

A control $\bar{u}\in {U}$ with associated $\bar{y}= \mathcal {S}(\bar{u})$ is called a stationary point of (P$_{\alpha }$) if (8) is satisfied.

Corollary 2

Let $\alpha _1, \alpha _2 \ge 0$ with $\alpha _1 + \alpha _2 = 1$ and denote $\alpha = (\alpha _1, \alpha _2)$. Then the following statements are equivalent:

• 1. A control $\bar{u}\in {U}$ with associated state $\bar{y}= \mathcal {S}(\bar{u}) \in {Y}$ is a stationary point of (P$_{\alpha }$).

• 2. There exists $\bar{p}$ such that $\bar{u}, \bar{y}, \bar{p}$ satisfy the system (5) with $\bar{\alpha }= \alpha$.

Proof

The corollary follows analogously to the proof of Theorem 2. However, since the problem is inherently scalar, the reverse implication of Lemma 2 is obtained for free and we obtain equivalence. $\square$

Corollary 2 especially implies that the adjoint system (5) is a strong stationarity system for the weighted-sum problem (P$_{\alpha }$), i.e., that it is equivalent to the primal necessary stationarity conditions (8) of the weighted-sum problem. Accordingly, it is reasonable to characterize the stationary points of the weighted-sum problems using the system (5). However, system (5) may have multiple solutions, and (in the case of the finite dimensional controls) we cannot solve it numerically because of the variational inequality (5c) on the possibly unknown and nonlinear set ${{\text {Im}}(\mathcal {S}'(\bar{u};\cdot ))}$. In practice, we therefore modify (5c)-(5d) and instead consider the system

$$\begin{aligned} \bar{u}\in {U}, \quad \bar{y}&\in {Y}, \quad&\bar{p}\in {H}, \quad \bar{\alpha }\in {\mathbb {R}}^2 \end{aligned}$$

(9a)

$$\begin{aligned} \bar{\alpha }_i \ge 0 \quad \text {for } i&= 1,2, \quad&\sum \limits _{i = 1}^2 \bar{\alpha }_i = 1,\end{aligned}$$

(9b)

$$\begin{aligned} - \varDelta \bar{y}+ \kappa \max \{0, \bar{y}\}&= {{\mathcal {B}}}(\bar{u})&\text { in } {V}', \end{aligned}$$

(9c)

$$\begin{aligned} - \varDelta \bar{p}+ \kappa \mathbbm {1}_{\{\bar{y}> 0 \}} \bar{p}&= \sum \limits _{i = 1}^2 \bar{\alpha }_i j_i'(\bar{y})&\text { in } {V}', \end{aligned}$$

(9d)

$$\begin{aligned} {{\mathcal {B}}}^* (\bar{p}) + \sum \limits _{i = 1}^2 \bar{\alpha }_i \sigma _i \bar{u}&= 0&\text { in } {U}, \end{aligned}$$

(9e)

which coincides with the strong stationarity system in the case ${U}=H$. If ${U}= {\mathbb {R}}^p$, we additionally check the sign condition

$$\begin{aligned} \bar{p}\le 0\quad \text {a.e. in } \{\bar{y}= 0\} \end{aligned}$$

(10)

for $\bar{p}$ a posteriori. If the condition is satisfied, then the solution is still a solution to (5) and therefore a weak Pareto stationary point, see Corollary 2. In the weighted-sum algorithm, we can now set $\alpha _1 = 1 - \alpha _2$ and solve the stationarity system of the WSM for varying $\alpha _2 \in [0,1]$, where $\alpha _2\ne 0$ is required to guarantee well-posedness of the problems. Specifically, we introduce an additional small parameter $\alpha _\mathrm{{tol}}> 0$ and choose $\alpha _2$ in $[\alpha _\mathrm{{tol}}, 1 - \alpha _\mathrm{{tol}}]$. The final procedure of the WSM is summarized in Algorithm 1.

The result of Algorithm 1 is a discrete approximation of the set of weakly Pareto stationary points and the corresponding front.

3.2 Reference point method (RPM)

The reference point problem with Euclidean norm $\left\Vert \cdot \right\Vert _2$ for a reference point $z \in {\mathbb {R}}^2$ is given by

$$\begin{aligned} \begin{aligned}&\min _{(y,u)} \mathcal {F}_z(y, u) = \frac{1}{2} \left\Vert \mathcal {J}(y, u) - z\right\Vert _{2}^2 \\&\text {s.t. }(y,u)\in {V}\times {U}\text { satisfies }- \varDelta y + \kappa \max \{0,y\} ={{\mathcal {B}}}(u) \text { in } {V}'. \end{aligned}\quad \quad \quad \quad \quad \quad \quad ({{\textbf {P}}_{z}}) \end{aligned}$$

The reference point method is based on solving (P$_{z}$) for varying reference points. As the next theorem shows, optimizers to the reference point problems are Pareto optimal.

Theorem 4

Every local (global) solution to (P$_{z}$) such that $z \in {\mathbb {R}}^2$ with $\hat{\mathcal {J}}(u)-z > 0$ holds, is also a local (global) Pareto optimal point of (P).

Proof

We assume that $\bar{u}\in {U}$ with $\bar{y}= \mathcal {S}(\bar{u})$ is a local solution to (P$_{z}$), i.e., there exists an $r_1 > 0$ such that for all $u \in {U}$ with $\Vert \bar{u}- u \Vert _{U}< r_1$ the inequality $\mathcal {F}_z(\bar{y}, \bar{u}) \le \mathcal {F}_z(\mathcal {S}(u), u)$ is satisfied. Now, we assume that $\bar{u}$ is not locally Pareto optimal, which implies that for every $r_2 > 0$ there exists $u_\mathrm{end} \in {U}$ with $\Vert u_\mathrm{end} - \bar{u}\Vert < r_2$ and $\mathcal {J}_i(\mathcal {S}(u_\mathrm{end}), u_\mathrm{end}) \le \mathcal {J}_i(\bar{y}, \bar{u})$ for $i = 1,2$, where the latter inequality is strict for at least one i. Since we can choose $r_2$ arbitrarily small, $\mathcal {S}$ and $\mathcal {J}_i$ are continuous and $\mathcal {J}_i(\bar{y},\bar{u}) - z_i > 0$ holds for $i=1,2$ by assumption, this implies that

$$\begin{aligned} z_i \le \mathcal {J}_i(\mathcal {S}(u_\mathrm{end}), u_\mathrm{end}) \le \mathcal {J}_i(\bar{y}, \bar{u}), \quad i = 1,2, \end{aligned}$$

where the second inequality is strict for at least one i. Since the Euclidean norm is strictly monotone [8, Definition 4.19], this implies the contradiction $\mathcal {F}_z(\mathcal {S}(u_\mathrm{end}), u_\mathrm{end}) < \mathcal {F}_z(\bar{y}, \bar{u})$ and proves the first inclusion. The statement for global solutions follows immediately from the first statement by choosing $r_1 = \infty$. $\square$

Primal stationarity conditions for (P$_{z}$) are shown in the next theorem.

Theorem 5

Let the control $\bar{u}\in {U}$ with associated state $\bar{y}= \mathcal {S}(\bar{u}) \in {Y}$ be locally optimal for (P$_{z}$). Then, we have for all $h \in {U}$

$$\begin{aligned} \sum \limits _{i = 1}^2 \left( \mathcal {J}_i(\bar{y},\bar{u}) - z_i \right) \left( \langle j_i'(\bar{y}),\mathcal {S}'(\bar{u};h)\rangle _{{Y}',{Y}} + \sigma _i \langle \bar{u}, h\rangle _{{U}}\right) \ge 0. \end{aligned}$$

(11)

Proof

Due to the chain rule for Hadamard differentiable functions, this follows analogously to [7, Theorem 3.1]. $\square$

A control $\bar{u}\in {U}$ with associated state $\bar{y}= \mathcal {S}(\bar{u})$ is called a stationary point of (P$_{z}$) for $z\in {\mathbb {R}}^2$ if (11) is satisfied.

Corollary 3

Let the control $\bar{u}\in {U}$ with associated state $\bar{y}= \mathcal {S}(\bar{u})$ be given.

• 1) The following are equivalent:

  • (a) The control $\bar{u}$ is a stationary point of (P$_{z}$).

  • (b) There exists an adjoint state $\bar{p}$ such that $\bar{u}, \bar{y}, \bar{p}$ satisfy

    $$\begin{aligned} \bar{u}\in {U}, \quad \bar{y}&\in {Y},&\bar{p}\in {H}\end{aligned}$$

    (12a)
    $$\begin{aligned} - \varDelta \bar{y}+ \kappa \max \{0, \bar{y}\}&= {{\mathcal {B}}}(\bar{u})&\text { in } {V}', \end{aligned}$$

    (12b)
    $$\begin{aligned} \langle - \varDelta \bar{p}+ \kappa \mathbbm {1}_{\{\bar{y}> 0 \}} \bar{p},w\rangle _{{Y}', {Y}}&\le \sum \limits _{i = 1}^2\left( \mathcal {J}_i(\bar{y},\bar{u}) - z_i \right) \langle j_i'(\bar{y}),w\rangle _{{Y}',{Y}}\nonumber \\&\text { for all } w\in {\text {Im}}(\mathcal {S}'(\bar{u};\cdot )), \end{aligned}$$

    (12c)
    $$\begin{aligned} \bar{p}+ \sum \limits _{i = 1}^2 \left( \mathcal {J}_i(\bar{y},\bar{u}) - z_i \right) \sigma _i {B^\dagger }^* (\bar{u})&= 0&\text { in } {H}. \end{aligned}$$

    (12d)

• 2) The following are equivalent:

  • (a) There exists $z \in {\mathbb {R}}^2$ such that the control $\bar{u}$ is a stationary point of (P$_{z}$) with $0 \ne \mathcal {J}(\bar{y},\bar{u}) - z \ge 0$ (or $\mathcal {J}(\bar{y},\bar{u}) - z > 0$).

  • (b) There exists $\alpha \in {\mathbb {R}}^2$ with $\alpha \ge 0$ for $i = 1,2$ (or $\alpha > 0$) and $\alpha _1 + \alpha _2 = 1$ such that the control $\bar{u}$ is a stationary point of (P$_{\alpha }$).

Proof

Part 1) follows analogously to the proof of Corollary 2.

To show part 2), let $\bar{u}$ be a stationary point of (P$_{z}$) with associated state $\bar{y}= \mathcal {S}(\bar{u})$ such that $0 \ne \mathcal {J}(\bar{y},\bar{u}) - z \ge 0$. Then part 1) implies that there exists an adjoint state $\bar{p}$ such that $\bar{u}, \bar{y}, \bar{p}$ solve (12). Accordingly, with normalized weight $\alpha$ and adjoint $\tilde{p}$ given by

$$\begin{aligned} \alpha _i = \tilde{\alpha }_i \big / \sum \limits _{j = 1}^2 \tilde{\alpha }_j \text { with } \tilde{\alpha }_i = \mathcal {J}_i(\bar{y}, \bar{u}) - z_i \ge 0,\quad \tilde{p}&= \bar{p}\big / \sum \limits _{i = 1}^2 \tilde{\alpha }_i, \end{aligned}$$

system (5) is also satisfied. Thus Corollary 2 implies that $\bar{u}$ is a stationary point of (P$_{\alpha }$) with $\alpha \ge 0$ and $\alpha _1 + \alpha _2 = 1$. The other implication follows analogously without normalization by choosing the reference point $z = \mathcal {J}(\bar{y},\bar{u}) - \alpha$, since then $0 \ne \mathcal {J}(\bar{y}, \bar{u}) - z = \alpha \ge 0$. The cases with strict inequalities follow analogously. $\square$

Corollary 3 shows that primal stationarity in the two scalarization methods is essentially equivalent. Also note that, except for rather degenerate choices of reference points, system (12) is equivalent to the adjoint multiobjective system (5), i.e., (5) is a strong stationarity condition for the reference point problem (P$_{z}$). Again, we generally cannot solve (12) directly in the implementation when ${U}={\mathbb {R}}^p$ because of the variational inequality on a possibly unknown and nonlinear image set. We proceed analogously to the modifications in the WSM, cf. (9), and instead solve

$$\begin{aligned} \bar{u}\in {U}, \quad \bar{y}&\in {Y}, \quad \bar{p}\in {H}, \end{aligned}$$

(13a)

$$\begin{aligned} - \varDelta \bar{y}+ \kappa \max \{0, \bar{y}\}&= {{\mathcal {B}}}(\bar{u}) \quad&\text { in } {V}', \end{aligned}$$

(13b)

$$\begin{aligned} - \varDelta \bar{p}+ \kappa \mathbbm {1}_{\{\bar{y}> 0 \}} \bar{p}&= \sum \limits _{i = 1}^2 \left( \mathcal {J}_i(\bar{y},\bar{u}) - z_i \right) j_i'(\bar{y}) \quad&\text { in } {V}', \end{aligned}$$

(13c)

$$\begin{aligned} {{\mathcal {B}}}^* (\bar{p}) + \sum \limits _{i = 1}^2 \left( \mathcal {J}_i(\bar{y},\bar{u}) - z_i \right) \sigma _i \bar{u}&= 0 \quad&\text { in } {U}{.} \end{aligned}$$

(13d)

For ${U}={{L^2}(\varOmega )}$, this again coincides with the strong stationarity system from [7]. For ${U}= {\mathbb {R}}^p$ we test for the sign condition (10) a posteriori. If it is satisfied as well, $\bar{u}$ is a weak Pareto stationary point of (P).

Another central question for the RPM is how suitable reference points can be chosen in the numerical implementation. To this end, we follow the approach presented in [2]. Let $k_{\mathrm{max}}$ denote the maximal number of Pareto stationary points in the numerical implementation and let $(y^1, u^1)$ denote an initial starting point with $u^1$ being a stationary point of the weighted-sum problem with weights $\alpha _1 = 1 - \alpha _\mathrm{{tol}}$ and $\alpha _2 = \alpha _\mathrm{{tol}}\ll 1$. Then the first reference point $z^2$ (corresponding to the second point on the front) is chosen as

$$\begin{aligned} z^2 = \mathcal {J}(y^1, u^1) - \begin{pmatrix} h^\perp \\ h^\parallel \end{pmatrix}, \end{aligned}$$

(14)

where $h^\perp , h^\parallel > 0$ are scaling parameters. For $i = 2, \ldots , k_{\mathrm{max}}- 2$ the reference point $z^{i + 1}$ is chosen as

$$\begin{aligned} z^{i + 1} = \mathcal {J}(y^i, u^i) + h^\parallel \cdot \frac{\varphi ^\parallel }{\Vert \varphi ^\parallel \Vert } + h^\perp \cdot \frac{\varphi ^\perp }{\Vert \varphi ^\perp \Vert }, \end{aligned}$$

(15)

with $\varphi ^\perp = z^i - \mathcal {J}(y^i, u^i)$ and $\varphi ^\parallel = (- \varphi ^\perp _2, \varphi ^\perp _1)^T$. Note that due to the strong weighting of $\mathcal {J}_1$ at $(y^1, u^1)$, the Pareto front is approximately vertical in the area of the first reference point. This motivates the initial choice $\varphi ^\parallel = (0, -1)^T$ and $\varphi ^\perp = (-1, 0)^T$.

Using this update technique, we end up with the reference point method stated in Algorithm 2.

Note that the stopping criterion implies that if $k_{\mathrm{max}}$ is large enough, then the upper left as well as the lower right corner points of the Pareto front coincide with those of the WSM. If $0\ne \mathcal {J}(\mathcal {S}(\bar{u}), \bar{u}) - z \ge 0$ holds for all $\bar{u}\in {\tilde{{{\mathscr {P}}}}}_s^{sw}{}$, then the result of Algorithm 2 is a discrete approximation of the set of weak Pareto stationary points and the corresponding Pareto front. If one wants to ensure this condition a priori, it is possible to, e.g., choose fixed reference points on shifted coordinate axes. The shift has to be performed such that all reference points are below the lower bounds on $\mathcal {J}_i$, cf. [3].

4 Numerical implementation

For the numerical realization and tests of the algorithms, we will assume that $j_1(y) = \frac{1}{2} \Vert y - y^{d}\Vert _{{H}}^2$, $j_2(y) = 0$ and $\sigma _1 = 0$. We fix the domain $\varOmega = (0,1)^2$ and consider $P_1$-type finite elements (FE) on a Friedrichs-Keller triangulation of the domain. The measure of fineness of the grids will be $h>0$, which denotes the inverse number of square cells per dimension – i.e., the grid will have $2/h^2$ triangles. We write the coefficient vector of the piecewise linear interpolant of a function $w:\varOmega \rightarrow {\mathbb {R}}$ on the grid vertices in sans-serif font (i.e., $\mathsf {w} \in {\mathbb {R}}^N$) and use the same font for the matrices in the discretized settings. We resort to mass lumping for the nonlinear max-term in order to be able to evaluate it componentwisely. Inevitably, this introduces a numerical discretization error. Its effects decrease with increasing fineness of the discretization but increase with the coefficient $\kappa$ that scales the nonlinearity. The corresponding stiffness matrix ${{\mathsf {K}}}\in {\mathbb {R}}^{N\times N}$, mass matrix ${{\mathsf {M}}}\in \mathbb R^{N\times N}$ and lumped mass matrix ${\tilde{{\mathsf {M}}}}\in {\mathbb {R}}^{N\times N}$ are given from the FE ansatz functions $\varphi _i,\, i=1,\dots ,N$, as

$$\begin{aligned} {{\mathsf {K}}}_{ij} = \langle \nabla \varphi _i,\nabla \varphi _j\rangle _{H},\, {{\mathsf {M}}}_{ij} = \langle \varphi _i, \varphi _j \rangle _{H},\, {\tilde{{\mathsf {M}}}}=\mathrm {diag} \left( \frac{|\mathrm {supp}(\varphi _i)|}{3}:i = 1,\ldots ,N\right) . \end{aligned}$$

Thus the FE approximation of (9c, e) introduced for the WSM is

$$\begin{aligned} \begin{pmatrix} {{\mathsf {K}}}\bar{ \mathsf {y}}_{ h } + \kappa {\tilde{{\mathsf {M}}}}\max \{0,\bar{ \mathsf {y}}_{ h } \} - {{\mathsf {B}}}\bar{u}\\ {{\mathsf {K}}}\bar{ \mathsf {p}}_{ h } + \kappa {\tilde{{\mathsf {M}}}}\varTheta (\bar{ \mathsf {y}}_{ h } ) \bar{ \mathsf {p}}_{ h } - \alpha _1 {{\mathsf {M}}}(\bar{ \mathsf {y}}_{ h } - {\mathsf {y}}^{d})\\ {{\mathsf {B}}}^T \bar{ \mathsf {p}}_{ h } + \alpha _2 \sigma _2 {\mathsf {A}} \bar{u}\end{pmatrix} = 0 \end{aligned}$$

(16)

for some given $\alpha \in {\mathbb {R}}^2$ that satisfies (9a, b), where ${{\mathsf {B}}}$ is the FE-discretized version of the linear operator ${{\mathcal {B}}}$ and $\varTheta {:}{=}\varTheta _0$ where $\varTheta _x:{\mathbb {R}}^N\rightarrow {\mathbb {R}}^{N\times N}$ maps a vector to the diagonal matrix that takes the Heaviside function with functional value x at 0 evaluated for each entry of the vector as its diagonal entries. The matrix ${\mathsf {A}} = {\mathsf {I}}_p \in {\mathbb {R}}^{p \times p}$ is the identity if ${U}= {\mathbb {R}}^p$, and ${\mathsf {A}} = {{\mathsf {M}}}$ is the mass matrix if ${U}= {H}$. Note that this means that, depending on the space ${U}$, sometimes sans-serif notation would be appropriate for the (discretized) control u. To avoid any misunderstandings, we will always denote u without sans-serif style. These finite dimensional systems are solved with a globalized version of a pseudo-semismooth Newton (PSN) method (which essentially ignores the indicator functions’ dependence on the state in the continuous system, i.e. the Heaviside functions’ dependence in the discretized system, when the linearization of the systems is computed). For more details on the PSN without globalization, we refer to [5, 7]. The FE system matrix at iterates $({ \mathsf {y}_{ h } }, { \mathsf {p}_{ h } }, u)$ reads as:

$$\begin{aligned} \begin{pmatrix} {{\mathsf {K}}}+ \kappa {\tilde{{\mathsf {M}}}}\varTheta ({ \mathsf {y}_{ h } }) &{} 0 &{} -{{\mathsf {B}}}\\ - \alpha _1 {{\mathsf {M}}}&{} {{\mathsf {K}}}+ \kappa {\tilde{{\mathsf {M}}}}\varTheta ({ \mathsf {y}_{ h } }) &{} 0\\ 0 &{} {{\mathsf {B}}}^T &{} \alpha _2 \sigma _2 {\mathsf {A}} \end{pmatrix}. \end{aligned}$$

(17)

We proceed analogously for the RPM and discretize (13 b, d) using finite elements, which yields

$$\begin{aligned} \begin{pmatrix} {{\mathsf {K}}}\bar{ \mathsf {y}}_{ h } + \kappa {\tilde{{\mathsf {M}}}}\max \{0,\bar{ \mathsf {y}}_{ h } \} - {{\mathsf {B}}}\bar{u}\\ {{\mathsf {K}}}\bar{ \mathsf {p}}_{ h } + \kappa {\tilde{{\mathsf {M}}}}\varTheta (\bar{ \mathsf {y}}_{ h } ) \bar{ \mathsf {p}}_{ h } - \left( \frac{1}{2}(\bar{ \mathsf {y}}_{ h } - {\mathsf {y}}^{d})^T {{\mathsf {M}}}(\bar{ \mathsf {y}}_{ h } - {\mathsf {y}}^{d}) - z_1\right) {{\mathsf {M}}}(\bar{ \mathsf {y}}_{ h } - {\mathsf {y}}^{d})\\ {{\mathsf {B}}}^T \bar{ \mathsf {p}}_{ h } + \left( \frac{\sigma _2}{2} \bar{u}^T {\mathsf {A}} \bar{u}- z_2\right) \sigma _2 {\mathsf {A}} \bar{u}\end{pmatrix} = 0. \end{aligned}$$

(18)

These discretized systems are solved with a PSN method as well. The FE system matrix at iterates $({ \mathsf {y}_{ h } }, { \mathsf {p}_{ h } }, u)$ reads as:

$$\begin{aligned} \begin{pmatrix} {{\mathsf {K}}}+ \kappa {\tilde{{\mathsf {M}}}}\varTheta ({ \mathsf {y}_{ h } }) &{} 0 &{} -{{\mathsf {B}}}\\ {\mathsf {C}}({ \mathsf {y}_{ h } }) &{} {{\mathsf {K}}}+ \kappa {\tilde{{\mathsf {M}}}}\varTheta ({ \mathsf {y}_{ h } }) &{} 0 \\ 0 &{} {{\mathsf {B}}}^T &{} {\mathsf {D}}(u) \end{pmatrix} \end{aligned}$$

(19)

with

$$\begin{aligned} {\mathsf {C}} ({ \mathsf {y}_{ h } })&{:}{=}({{\mathsf {M}}}({\mathsf {y}}^{d}-{ \mathsf {y}_{ h } })) ({{\mathsf {M}}}({ \mathsf {y}_{ h } }- {\mathsf {y}}^{d}))^T - \big ({\textstyle \frac{1}{2}}({ \mathsf {y}_{ h } }- {\mathsf {y}}^{d})^T {{\mathsf {M}}}({ \mathsf {y}_{ h } }- {\mathsf {y}}^{d})-z_1\big ) {{\mathsf {M}}}, \end{aligned}$$

(20)

$$\begin{aligned} {\mathsf {D}} (u)&{:}{=}(\sigma _2 {\mathsf {A}} u) (\sigma _2 {\mathsf {A}} u)^T + \left( \frac{\sigma _2}{2} u^T {\mathsf {A}} u - z_2\right) \sigma _2 {\mathsf {A}}. \end{aligned}$$

(21)

Remark 2

For both methods, the sign condition (10) is not added into the discretized stationarity system and instead verified a posteriori if ${U}= {\mathbb {R}}^p$. $\Diamond$

Compared to the system matrix of the single objective case presented in [5], especially the system matrix of the RPM is more complicated and possesses a non-sparse substructure. This is due to the matrices ${\mathsf {C}}({ \mathsf {y}_{ h } })$ and ${\mathsf {D}}(u)$, which possess the dense terms ${{\mathsf {M}}}({ \mathsf {y}_{ h } }- {\mathsf {y}}^{d}) ({{\mathsf {M}}}({ \mathsf {y}_{ h } }- {\mathsf {y}}^{d}))^T$ and $(\sigma _2 {\mathsf {A}} u) (\sigma _2 {\mathsf {A}} u)^T$. These can cause severe memory and runtime problems when the reference point problem is solved on fine finite element grids with a linear solver. Due to these restrictions, the reference point method’s subproblems will generally take longer to solve than the WSM, also on coarser grids.

One thing to keep in mind when applying the PSN method is that there is no guarantee of convergence as seen in the numerical examples in [7]. The method in fact shows failure to converge in practice, with the rate of failed attempts over the subproblems decaying as the grid discretization’s fineness is increased. This suggest some sort of degeneration of the undamped search directions that could be countered with a globalization mechanism.

Accordingly, the two questions that we will address in the remainder of this section are the following:

• 1) Can the non-convergence issue of the PSN method itself be removed?

• 2) Is it possible to reduce computation times and memory problems of the (linear) PSN steps in the reference point method to make it competitive in terms of computation times?

4.1 Globalized PSN

The numerical experiments in [7] indicate that non-convergence of the PSN is an issue that strongly depends on (insufficiently fine) discretizations. As a stabilization approach independently of the grid fineness, we will present and test a line-search globalization of the PSN based on results for semismooth Newton methods as in, e.g., [9] and [11], which will be referred to as the gPSN method. Let us assume that we want to find a root of a function $F : \mathbb {R}^{2 N + p} \rightarrow \mathbb {R}^{2 N + p}$ with system matrix $G : \mathbb {R}^{2 N + p} \rightarrow \mathbb {R}^{(2 N + p) \times (2 N + p)}$. This will either be (16) with system matrix (17) for the subproblems in the WSM or (18) with system matrix (19) for the subproblems in the RPM. We will employ a line-search globalization with the merit function $\Lambda : \mathbb {R}^{2 N + p} \rightarrow \mathbb {R},\, x \mapsto \frac{1}{2} \Vert F(x) \Vert ^2$.

Remark 3

Note that the norm in the merit function $\Lambda$ is the discrete equivalent of the norm in ${V}' \times {V}' \times {U}$. Hence it is generally expensive to evaluate, since we need to compute a Riesz representative. However, we will precompute the necessary factorizations to speed-up the computations to some extent. $\Diamond$

The gPSN method is summarized in the following algorithm. Note that we cannot conclude – e.g., from theory on globalized semismooth Newton methods – that the algorithm converges without introducing a maximum number $k_{\mathrm{max}}$ of PSN steps and a minimum step length $\epsilon _2 > 0$.

It turns out that there are examples, where Algorithm 3 converges while a refinement of the grid does not yield convergence, see Sect. 5. However, it can still happen that the gPSN method does not converge. Obviously, it would not be a good idea to add the final iterate of the gPSN method to the Pareto set nonetheless. Instead, if within the RPM the PSN does not converge, we update the reference point as follows: If no previous solution to the reference point problem is available, we choose

$$\begin{aligned} z^{i + 1} = z^{i} - \begin{pmatrix} 0 \\ h^\parallel \end{pmatrix}. \end{aligned}$$

If previous solutions to the reference point problem are available, we choose

$$\begin{aligned} z^{i + 1} = z^{i} + h^\parallel \frac{\varphi ^\parallel }{\Vert \varphi ^\parallel \Vert }. \end{aligned}$$

Essentially, previous information is used repeatedly to find a new reference point by going into the same parallel direction. If the gPSN is used within the WSM and does not converge, we can simply proceed to the next discretized weight.

4.2 A Preconditioned Matrix-Free L-GMRES Method

We will now focus on how to speed-up the computation and how to overcome the difficulties arising from the dense terms in the RPM. Notice that both dense terms are rank-1-matrices. Therefore it is easy to implement the matrix-vector-product for some $w \in {\mathbb {R}}^N$ and $v \in {\mathbb {R}}^N$ with $v = {{\mathsf {M}}}({ \mathsf {y}_{ h } }- {\mathsf {y}}^{d})$ or $v = \sigma _2 {\mathsf {A}} u$:

$$\begin{aligned} \left( v v^T\right) w = \left( v^T w\right) v. \end{aligned}$$

This motivates the use of an iterative solver that only relies on matrix-vector-products in each PSN step for solving the reference point subproblem. Since the system is not symmetric positive definite, the CG method is not an alternative and we will use L-GMRES instead. As the performance heavily depends on the condition number of the system matrix (see [18]), which might be very large, especially for very small values of the regularization parameter $\sigma _2$, we will precondition the method with one of the following preconditioners:

• 1. a: The dense terms ${{\mathsf {M}}}({ \mathsf {y}_{ h } }- {\mathsf {y}}^{d}) ({{\mathsf {M}}}({ \mathsf {y}_{ h } }- {\mathsf {y}}^{d}))^T$ and $(\sigma _2 {\mathsf {A}} u) (\sigma _2 {\mathsf {A}} u)^T$ are omitted in an approximated system matrix that is used as a preconditioner.

• 2. aBJ: A block Jacobi preconditioner is applied with the approximation described for the preconditioner a.

• 3. aBGS: A block Gauss-Seidel preconditioner is applied with the approximation described for the preconditioner a.

• 4. aILU: An incomplete LU factorization together with the approximation described for the preconditioner a is applied.

Of course the same iterative, preconditioned approach can be implemented for the WSM, with the only difference being that no approximation – by ignoring dense terms – is necessary for the preconditioner. Note that also standard Jacobi, Gauss-Seidel, block Jacobi and block Gauss-Seidel and incomplete LU factorization preconditioners were tested. But the first two did not give any speed-up and the last four were still significantly less effective than the preconditioners above due to the dense terms still remaining. As expected, it is quite important to use the block structure of the problem as much as possible and to avoid the dense terms.

Remark 4

As long as $\sigma _2u^T {\mathsf {A}} u/2 - z \ne 0$, the invertibility of the aBJ preconditioner is ensured for the RPM, since the first two block diagonal elements are symmetric positive definite and the last block diagonal element is symmetric and either positive or negative definite (see (19)). Analogously in case of the WSM, the invertibility is always ensured. $\Diamond$

For the four different preconditioners above, we propose three different update strategies. Those strategies are:

• 1. Never update: Only one preconditioner is generated for the first iteration of the first subproblem and then this preconditioner is used for all subproblems and all gPSN iterations.

• 2. Update once: One preconditioner is generated for each subproblem and then used for all gPSN iterations.

• 3. Always update: The preconditioner is generated for each gPSN iteration of each subproblem.

5 Numerical examples

In this section, we present numerical results for two examples – one with finite and one with infinite dimensional control space. First, the focus of our exposition will be on the performance of the RPM and the different preconditioning strategies. After the best update strategy is identified, we will compare RPM and WSM method.

In order to reasonably quantify the quality of the approximation of the respective Pareto (stationary) fronts, we employ two quality measures. The maximal distance between neighboring points on the Pareto front

$$\begin{aligned} \varDelta _\mathrm{max} := \max \limits _{a \in {\tilde{{\mathscr {P}}}}_f} \min \limits _{b \in {\tilde{{\mathscr {P}}}}_f \setminus \{a\}} \Vert a - b \Vert _2 \end{aligned}$$

(22)

will be our first measure. As a second measure of approximation quality, we will consider

$$\begin{aligned} \varDelta _\mathrm{clust} = \frac{|{\tilde{{\mathscr {P}}}}_f| \varDelta _\mathrm{max}}{\sum \limits _{a \in {\tilde{{\mathscr {P}}}}_f} \min \limits _{b \in {\tilde{{\mathscr {P}}}}_f \setminus \{a\}} \Vert a - b \Vert _2}, \end{aligned}$$

(23)

which is the maximum shortest distance between points on the front divided by the average shortest distance and therefore bounded from below by one. If this quantity is small, this indicates that the approximation quality is somewhat uniform across the entire Pareto front, while a large value indicates that some parts of the Pareto front are approximated better than others are, i.e., a localized clustering.

Note that in all results presented here, the sign condition (see Remark 2) is satisfied and the gPSN method always converges.

Our code is implemented in Python3 and uses FEniCS [1] for the matrix assembly. Sparse memory management and computations (especially L-GMRES) are implemented with SciPy [20]. All computations below were run on an Ubuntu 20.04 notebook with 32 GB main memory and an Intel Core i7-8565U CPU.

5.1 The numerical examples

First we introduce the two examples. The parameters listed in Table 1 are fixed for the rest of this work.

Table 1 Fixed parameters for the two numerical examples

5.1.1 Example 1 – Infinite dimensional controls

For the first numerical example the desired state is chosen as $y^d = \mathbbm {1}_{\varOmega _1} - \mathbbm {1}_{\varOmega _2}$ with $\varOmega _1 = \{(x_1, x_2) \in \varOmega : x_1, x_2 > 1/3\}$ and $\varOmega _2 = \{(x_1, x_2) \in \varOmega : x_1, x_2 < 2/3\}$. This desired state is chosen to promote nonsmoothness. The control space ${U}$ is chosen as ${H}=L^2(\varOmega )$, the operator ${{\mathcal {B}}}$ as the identity on ${U}$ and ${\mathsf {A}}$ is the mass matrix.

5.1.2 Example 2 – finite dimensional controls

For the second numerical example, we choose $y^d(x) = \left( \frac{1}{2} - x_1\right) \sin (\pi x_1) \sin (\pi x_2)$. The space ${U}$ is chosen as ${\mathbb {R}}^2$, ${\mathsf {A}} = {\mathsf {I}}_2$ is the identity matrix in ${\mathbb {R}}^{2\times 2}$ and the operator ${{\mathcal {B}}}$ is set to

$$\begin{aligned} \left( {{\mathcal {B}}}(u)\right) ({\varvec{x}})=10\cdot {\left\{ \begin{array}{ll} u_1 x_1 x_2, &{} \text {for }{\varvec{x}}=(x_1,x_2)\text { and }x_1 \le \frac{1}{2},\\ u_2 x_1^2 x_2^2, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

where the definition is to be understood as $L^2$-functions mapping ${\varvec{x}}\in \varOmega$ to ${\mathbb {R}}$ that are embedded into ${V}'$. For plots of the operator ${{\mathcal {B}}}$ and the desired state we refer to [5, Fig. 1 and 4].

5.2 Preconditioning the reference point method

In this section, we consider the different preconditioning approaches for the RPM. Therefore, we additionally choose the parameter $\sigma _2 = 5 \cdot 10^{-3}$ and the parameters $h^\perp = 10$, $h^\parallel = 0.1$ in the RPM and $\epsilon _1 = 1 \cdot 10^{-4}$ for the gPSN. Note that the arguably large value of $\epsilon _1$ is necessary for the L-GMRES method to converge without preconditioner, because the (sometimes badly conditioned) problem is numerically difficult to solve. The results for Example 1 are given in Table 2.

Table 2 Example 1. Comparison of average L-GMRES iterations (av. it.) and speed-up (s.-up) of the RPM for different preconditioning approaches and different step sizes h for $\sigma _2 = 5 \cdot 10^{-3}$

First of all, we can see that the computation time decreases for all preconditioning approaches. Also the average number of L-GMRES iterations is very small (between 2 and 3.5) and increases only slightly for smaller step sizes h. The latter observation is in contrast to the performance of the non-preconditioned solving, which starts out with a large number of average L-GMRES iterations that nonetheless significantly increases for smaller step sizes h. Furthermore, we can see that cheaper preconditioners lead to a larger speed-up if the preconditioner is updated more often, i.e. with the preconditioning strategy always update the preconditioner aBJ still gives a significant speed-up of about 35, but all other preconditioners cannot give a speed-up above 9. Nonetheless, the best preconditioning approach surprisingly is the never update strategy combined with the preconditioner aBJ. This indicates that the problem structure does not change significantly with respect to the current reference point and thus a computationally expensive update of the preconditioner is unnecessary.

Next, we consider the results for Example 2, which can be found in Table 3.

Table 3 Example 2. Comparison of average L-GMRES iterations (av. it.) and speed-up (s.-up) of the RPM for different preconditioning approaches and different step sizes h for $\sigma _2 = 5 \cdot 10^{-3}$

We basically observe the same behavior as previously and again never update and aBJ is the best preconditioning approach. Note that this finite dimensional example is inherently better conditioned and thus combinations of more expensive preconditioners such as a, aBGS and aILU and expensive preconditioning strategies such as update once and always update often lead to larger computation times compared to the performance in the absence of a preconditioner. Furthermore, the preconditioner aILU seems to behave unstably, since the number of average L-GMRES iterations increases significantly for smaller step sizes h. Note that aILU includes some parameters which could be varied and might improve this behavior, but we will not go into details here.

Next we consider a fixed step size $h = 1/100$ and investigate the behavior of the different preconditioning approaches for varying $\sigma _2$. We expect larger condition numbers for smaller values of $\sigma _2$ and therefore problems which are harder to solve numerically. Since the strategies update once and always update and the preconditioner aILU did not prove useful, they are excluded from this considerations. The results can be found in Table 4 for Example 1 and in Table 5 for Example 2.

Table 4 Example 1. Comparison of average L-GMRES iterations (av. it.) and speed-up (s.-up) of the RPM for different preconditioning approaches and different values of $\sigma _2$ for fixed step size $h = 1/100$

Table 5 Example 2. Comparison of average L-GMRES iterations (av. it.) and speed-up (s.-up) of the RPM for different preconditioning approaches and different values of $\sigma _2$ for fixed step size $h = 1/100$

In both examples the average number of L-GMRES iterations increases slightly for smaller values of $\sigma _2$. This increase is stronger for the first example. If, on the other hand, no preconditioner is used, there is a significant increase for smaller values of $\sigma _2$. This is especially true for the first example, which starts with an average number of 18.75 iterations for $\sigma _2 = 1$ and ends with an average number of 501.07 iterations for $\sigma _2 = 10^{-3}$. In the second example there is only an increase from 10.48 to 52.10. Nonetheless in both examples preconditioning pays off and again the preconditioner aBJ is the best. It results in a speed-up of 62.84 in the first example and a speed-up of 12.64 in the second example for $\sigma _2 = 10^{-3}$.

5.3 Comparison of the RPM and the WSM

In this section, we want to compare the performance of the reference point method and the weighted-sum method both in terms of computation times and discretization quality. We choose a step size of $h = 1/100$, a tolerance $\epsilon _1 = 10^{-5}$ in the gPSN and $h^\perp = 1$, $h^\parallel = 0.2$ in the RPM. We will consider $\sigma _2 = 1$ for both examples. This means that the problems are relatively well conditioned, but the Pareto fronts are harder to approximate than for smaller values of $\sigma _2$.

In order to make the results of the RPM and the WSM qualitatively comparable, we first run the RPM, which yields a number of discretization points on the front. Afterwards we run the WSM with $k_{\mathrm{max}}$ (the number of Pareto points) chosen as the number of discretization points generated by the RPM. At this point we have the same number of discretization points on the respective approximated fronts. However, the WSM tends to cluster the discretization points. In order to obtain comparable approximation quality, we then double the number of points in the WSM until the maximal distance for points on the Pareto front (see (22)) is below the maximal distance for the RPM. Afterwards, the parameter $h^\parallel$ is halved as often as $k_{\mathrm{max}}$ in the WSM was doubled before to compare the evolution of the quality measures $\varDelta _\mathrm{max}$ and $\varDelta _\mathrm{clust}$ for an increasing size of the approximated Pareto front.

The Pareto fronts are shown in Fig. 1.

Fig. 1

Pareto fronts from WSM and RPM for step size $1/h = 100$ and $\sigma _2 = 1$

We can see that both methods approximate the same curve. But the WSM shows a clustering behavior in the lower right corner whilst giving only a poor approximation in the remainder of the Pareto front. This already indicates that some refinement of the weights’ distribution is generally well advised for the WSM. In Fig. 2, the evolution of the quality measures for the WSM and RPM for the procedure described above is shown.

Fig. 2

Evolution of measures of approximation quality ($\varDelta _\mathrm{max}$ and $\varDelta _\mathrm{clust}$) for the WSM with respect to doubling the number of discretization points on the Pareto front and for the RPM with respect to halving $h^\parallel$ with $\sigma _2 = 1$ and step size $1/h = 100$

In the left figures, we can see that for the WSM the number of points on the Pareto front needs to be doubled seven times in order to reach a maximal distance of points on the Pareto front that is smaller than that of the RPM. Furthermore the approximation quality decreases every time the size of the Pareto front is doubled. This is due to the clustering behavior in the lower right corner. As a result, an unnecessarily large number of points on the Pareto front is needed to reach a desired maximal distance $\varDelta _\mathrm{max}$. On the other hand, with the RPM, the approximation quality even decreases whilst $h^\parallel$ is halved. This behavior can be seen in the right figures and is even better than expected. Note that the size of the Pareto front is approximately doubled when $h^\parallel$ is halved.

The question remains, which method performs better in terms of computational cost. A comparison of the results from the RPM and the first and last result from the WSM in the procedure of doubling the number of discretization points is shown in Table 6.

Table 6 Comparison of computation time and approximation quality for RPM and WSM with $\sigma _2 = 1$. WSM (first) indicates WSM with the size of RPM. WSM (last) indicates WSM after doubling the size until a maximal distance on the Pareto front below that of RPM is reached. The step size is chosen as $h = 1/100$

The observation for both examples are similar with respect to sizes of the Pareto fronts and the measures of approximation quality. Also whilst the RPM is slightly slower than the WSM if the same size for the Pareto front is used, it is about 28 times faster than the WSM when an at least equally good approximation quality is desired.

6 Conclusion

If the controls on the right-hand-side of the constraining PDE to (P) are finite dimensional, then conditions that imply primal stationarity can be found. Those conditions can be interpreted as strong stationarity systems of scalarization methods. They are, however, not usable numerically because they contain unknown nonlinearities in the spaces that the conditions are formulated in. Modifying the conditions, we ended up with linear systems as in the case of ample controls. We have shown that both WSM and RPM can be applied to characterize the front of Pareto stationary points for this nonsmooth problem. The reference point method performs significantly better when both approximation quality and computation time are considered, as long as preconditioning is used intelligently in GMRES. In our tests, the preconditioning strategy aBJ without updates performs the best. We also saw that the line-search globalized version of the PSN method leads to better performance and convergence of the method over the basic version with uncontrolled step lengths. A simple reduction of the step size numerically does not appear to guarantee this behavior.