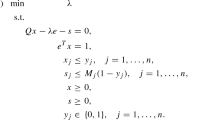1 Introduction

Piecewise linear function fitting, also known as linear-spline regression, is a classical problem of determining a piecewise-linear function \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\), with a given number of pieces m, that best fits the given predictor data \(x\in {\mathbb {R}}^n\) and response data \(y_i=f(x_i)+\epsilon _i\) for unbiased and independent error terms \(\epsilon _i\) where \(i=1,\ldots ,n\). The problem has been mostly addressed in the case that the candidate breakpoints are given as a part of the input. A dynamic program (DP) given such a fixed set of candidate breakpoints has been proposed in [1]. The regression problem becomes more challenging if the breakpoints are themselves variables and are not fixed to a choice from a finite set. Historically, in this more general setting, solutions have been computed by heuristics.

Goldberg et al. [5] propose exact computation schemes using mixed-integer nonlinear programming (MINLP) and a sophisticated adaptive-refinement DP-based heuristic as a more tractable approach for handling larger problems. We show below that their MINLP model can result in a piecewise linear curve that is not a graph of a function (i.e., there is an x that is associated with more than one expected response value). We start by presenting the model from [5]. In the next section we present two counterexamples that illustrate that this model is incomplete, and we develop three alternative MINLP models that overcome this defect and study their theoretical relationship. In Sect. 3 we present numerical results suggesting that one formulation is superior.

Given data \(x,y\in {\mathbb {R}}^n\), with \(x_1< x_2< \ldots < x_n\), the incomplete model in [5] aims to determine the piecewise linear function, given by breakpoint horizontal coordinates \(b_0,b_1,\ldots ,b_m\in {\mathbb {R}}\), by solving the following nonconvex MINLP, where \(b_0=x_1\) is fixed and \({\mathbf {b}}=(b_1,\ldots ,b_m)\) is a tuple of decision variables,

$$\begin{aligned}&\underset{b,c,\beta ,\xi ,\phi }{\text {minimize}}&\sum _{i=1}^n \xi _i^p \end{aligned}$$
(1a)
$$\begin{aligned}&\text {subject to}&\left| y_i - c_{j} - \beta _j x_i\right| \le \xi _i + {{\hat{M}}}_i\phi _{ij}\,&i=1,\ldots ,n, \quad j=1,\ldots ,m \end{aligned}$$
(1b)
$$\begin{aligned}&\sum _{j=1}^m \phi _{ij} = m-1&i=1,\ldots ,n \end{aligned}$$
(1c)
$$\begin{aligned}&-M_i\phi _{ij} \le b_{j}-x_i&i=1,\ldots ,n, \quad j=1,\ldots ,m \end{aligned}$$
(1d)
$$\begin{aligned}&-M_i\phi _{ij} \le x_i-b_{j-1}&i=1,\ldots ,n, \quad j=2,\ldots ,m \end{aligned}$$
(1e)
$$\begin{aligned}&b_{j}(\beta _j-\beta _{j+1}) = c_{j+1}-c_{j}&j=1,\ldots ,m-1 \end{aligned}$$
(1f)
$$\begin{aligned}&\phi _{ij}\in \{0,1\}&i=1,\ldots ,n, \quad j=1,\ldots ,m \end{aligned}$$
(1g)
$$\begin{aligned}&x_1 \le b_j \le x_n&j=1,\ldots ,m. \end{aligned}$$
(1h)

The constraints (1h) are simple bounds that tighten the original formulation. The problem is typically solved with the least squares objective, where (1a) has \(p=2\), but minimizing the absolute value of the deviations using \(p=1\) (or “\(L_1\)-loss”) is also possible. The decision variables of (1) are described in Table 1.

Table 1 Description of problem variables
Full size table

The constraints (1c) ensure that each data point is assigned (when \(\phi _{ij}=0\)) to exactly one line segment, which together with constraints (1b) ensures that the error \(\xi _i\) for data point i is evaluated with respect to the line segment j to which it is assigned. The jth (nonconvex) constraint (1f) is used to ensure that consecutive line segments j and \(j+1\) intersect at the breakpoint \(b_j\). There are several constraints that can be appended to (1) to make its solution more tractable; see [9]. Here, the big-M constants are set to depend on \(i=1,\ldots ,n\), similar to [9] in order to strengthen the formulation compared with a global setting of \(M_i=M\) and \({{\hat{M}}}_i={{\hat{M}}}\) for all \(i=1,\ldots ,n\), as proposed in [5]. In particular, these constants satisfy \(M_i\ge \max _{i'=1,\ldots ,n}\left| x_{i'}-x_i\right|\) and \({{\hat{M}}}_i\ge \max _{j=1,\ldots ,m}\left| y_i - c_{j} - \beta _j x_i\right|\) for every \(c,\beta\) that may be a part of an optimal solution (see the analysis in the following sections as well as [9] for details and bounds in terms of the input data for \({{\hat{M}}}_i\)).

Special Cases of (1). In [5], the authors apply (1) only in the special case of concave (or convex) data fitting. In that case, the slopes of the segments are constrained to be decreasing (or increasing), which ensures that the resulting curve is the graph of a concave (or convex) function. In particular, it can be shown that the slope inequalities imply some of the inequalities that are proposed in order to correct formulation (1) in the following section. Similar arguments are used to prove the correctness of the convex MINLP for convex function fitting that appears in [10], which is also studied in [9]. In that paper, the authors also propose another (convex) mixed integer linear program (MILP) formulation for the case where \(p=1\) for fitting general piecewise linear functions. In the general case, however, the MINLP (1) is incomplete, and so we present counterexamples and remedies in the next section.

2 Counterexample and correction of (1)

The MINLP (1) is incomplete, and we now present two illustrating examples where it fits a polygonal curve that is not a graph of a function. We begin with a small synthetic example.

Example 1

Consider the data \(x=(1, 1.01, 1.02,1.03,1.04)\) and \(y=(0,0,1,0,1)\) and \(p=2\). The optimal solution of (1), with \(m=3\) is illustrated in the Figure 1(a), where it is evident that it has a zero optimal objective value by fitting a polygonal curve, which is not a graph of a function, and whose breakpoints are given by \(b_0=1.00\) and \({\mathbf {b}}=(1.04, 1.00, 1.03)\). This curve’s second segment, from (1.04, 1.0) to (1.0, 0.0), is not assigned to any of the data points (i.e., \(\phi _{12}=\cdots =\phi _{52}=1\)). An optimal piecewise linear function that best fits the data, obtained by requiring that the breakpoint horizontal coordinate values are in increasing order. It is depicted in Figure 1(b), with a nonzero optimal objective value of 0.167.

Fig. 1
figure 1

A small example in which formulation (1) results in fitting a polygonal curve with three segments (\(m=3\)) that is not a piecewise linear function. Note that the dashed line segment is not assigned any of the data points

Full size image

In many real datasets including all of those experimented with in [5] and [9], the relaxed formulation (1) coincidentally computes a correct solution that does correspond to a piecewise linear function. An exception is the next real data example that shows that the defect in MINLP (1) can affect a real problem in fitting a curve that may not be graph of a continuous piecewise linear function.

Example 2

This example is based on the classic (scaled) Titanium data set from [3] and [6] with \(n=49\) data points. The number of segments \(m=3\) and applying formulation (1) with \(p=2\). The optimal objective value is 1.003 and an optimal solution found has \({\mathbf {b}}=(1075.0,731.2,945.0)\). The segment from \(b_1=1075\) to \(b_2=731.2\) (the dashed line segment) is not assigned any data points. An optimal piecewise linear function found, when the breakpoints are required to maintain an increasing order as shown in Figure 2(b), has \(b=(850.2, 885.0,1075.0)\) and the corresponding optimal objective value is 2.129.

Fig. 2
figure 2

The Titanium dataset example where formulation (1) with \(m=3\) results in fitting a curve with three segments (\(m=3\)) that is not a piecewise linear function. Note that the dashed line segment is not assigned any of the data points

Full size image

We next describe three alternative formulations that correct MINLP (1) and ensure that the solution curve is a function, by either implicitly or explicitly maintaining an increasing order of the breakpoints:

  1. 1.

    We can include the missing assignment-type constraints requiring that each segment is assigned to at least one data point,

    $$\begin{aligned} \sum _{i=1}^n \phi _{ij} \le n-1\,\,&j=1,\ldots ,m . \end{aligned}$$
    (2)

    These are referred as assignment-type constraints because they require that \(\phi _{ij}=0\) for some \(i=1,\ldots ,n\), and, if satisfied, then segment j is assigned to at least one data point.

  2. 2.

    We can explicitly enforce the order of the breakpoints by adding constraints,

    $$\begin{aligned} b_j \le b_{j+1} \qquad j = 1, \dots ,m-1. \end{aligned}$$
    (3)

    These constraints are similar to ones used in the piecewise linear function approximation model proposed in [8].

  3. 3.

    We can also use a set of constraints proposed for the convex MILP reformulation in [9], which in the current setting amount to requiring that

    $$\begin{aligned}&\phi _{i,j} + \phi _{i,j+1}-1 \le \phi _{i+1,j+1}&i=1,\dots ,n-1, \quad j=2,\dots ,m-1 \end{aligned}$$
    (4a)
    $$\begin{aligned}&\phi _{i,1} \le \phi _{i+1,1}&i = 1, \dots , n-1 \end{aligned}$$
    (4b)
    $$\begin{aligned}&\phi _{i+1,m} \le \phi _{i,m}&i = 1, \dots , n-1. \end{aligned}$$
    (4c)

    These inequalities, in particular (4a), require that for each data point i, if it is not assigned to one of two consecutive line segments j and \(j+1\), then the next data point \(i+1\) cannot be assigned to segment \(j+1\). It follows that segment j is not assigned any data points only if segment \(j+1\) is not assigned any data points.

The following theorem establishes the correctness of the formulation (1) together with inequality (3) in estimating a continuous piecewise linear function with m line segments and minimum sum of (pth power) errors.

Theorem 1

(Correctness) Formulation (1) together with (3) is correct for sufficiently large finite constants \(M_i\) and \({{\hat{M}}}_i\)  for \(i=1,\ldots ,n\).

Proof

First we establish that every feasible solution of (1) with (3) corresponds to a continuous piecewise linear function with m segments and that the sum of (pth power) errors is given by (1a).

Let \(b^*,c^*,\beta ^*,\xi ^*,\phi ^*\) be an optimal solution to (1) with (3). Constraints (1c) ensure that each data point i is assigned to exactly one line segment j. Together with constraints (1d) and (1e) it is ensured that for each \(j=1,\ldots ,m\), all \(i=1,\dots ,n\) satisfying \(b^*_{j-1}\le x_i < b^*_{j}\), or for \(j=m\), all i with \(x_i\ge b^*_{m-1}\), are assigned if and only if \(\phi ^*_{ij}=0\). The constraints (3) ensure that the breakpoints are nondecreasing and that accordingly the estimated f is a function (and none of the intervals \([b_{j-1},b_j)\) overlap for \(j=0,\ldots ,m\). Finally, the constraints (1f) ensure that for each \(j=1,\ldots ,m-1\), pair of line segments j and \(j+1\) must intersect at \((b^*_j,c^*_j+\beta ^*_jb^*_j)\) so the estimated function is continuous. To see that the sum of (pth power) errors is given by (1a) first note that constraints (1b) must hold as equalities by optimality of \(b^*,c^*,\beta ^*,\xi ^*,\phi ^*\). Then, for each pair \((i,j)\in \{1,\ldots ,n\}\times \{1,\ldots ,m\}\), \(\xi ^*_i\) equals i’s deviation absolute value if and only if segment j is assigned to point i, that is if \(\phi ^*_{ij}=0\).

Now we establish that every continuous piecewise linear function on \(D\subseteq {\mathbb {R}}\), where \(L=\inf D\) and \(U=\sup D\), , with \(m'\) line segments, corresponds to a solution that is feasible for (1) with (3) for some \(m\le m'\). Suppose that \(f: D\rightarrow {\mathbb {R}}\) is a continuous piecewise linear function with \(m'\) line segments and \(m'-1\) corresponding breakpoints \({{\tilde{b}}}_j\), for \(j=1,\ldots ,m-1\), each of which joining two segments, satisfying

$$\begin{aligned} L< {\tilde{b}}_1< \ldots< {\tilde{b}}_{m'-1} < U, \end{aligned}$$
(5)

and that minimizes the sum of squared (pth power) errors for input data \(x,y\in {\mathbb {R}}^n\). Let \(q=\min \left\{ j=1,\ldots ,m' \; \left| \;\; \tilde{b}_j>x_1 \right. \right\}\) assign

$$\begin{aligned}&& b_0=x_1,\; b_m=x_n,\quad & b_j = {\tilde{b}}_{j+q}&j=1, \ldots , m-1 \end{aligned}$$
(6a)
$$\begin{aligned}&&c_j= {\tilde{c}}_{j+q}, \quad &\beta _j = {\tilde{\beta }}_{j+q}&j=1, \ldots , m \end{aligned}$$
(6b)
$$\begin{aligned} \phi _{ij} = {\left\{ \begin{array}{ll}0 &{}\quad i=1, \ldots , n,\quad j=1, \ldots , m-1:\quad {b}_{j-1} \le x_i < {b}_{j} \\ 0 &{}\quad i=1, \ldots , n,\quad j=m:\quad {b}_{m-1} \le x_i \\ 1 &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$
(7)

The construction (7) together with the fact that f is a function on \(D\supseteq [x_1,x_n]\) and setting \(b_0=x_1\) and \(b_m=x_n\), assures that each data point \(i\in \{1,\ldots ,n\}\) is assigned to exactly one segment, implying that constraints (1c) are satisfied and that letting

$$\begin{aligned} \xi _i = {\left\{ \begin{array}{ll} \left| y_i - {c}_{j} - {\beta }_{j} x_i\right| &{}\quad i=1,\ldots ,n,\quad j=1,\ldots ,m:\quad \phi _{ij}=0\\ 0 &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$
(8)

is well defined. For \(i=1,\ldots ,n\) and \(j=1,\ldots ,m\), if \(\phi _{ij}=0\) then (1b) follows from (8) and (1d) and (1e) follow from (7). Otherwise if \(\phi _{ij}=1\), then by construction the constraints (1d) and (1e) hold for \(M_i=\max _{i'}\left| x_{i'}-x_i\right| \ge \left| b_j-x_i\right|\). Then, for each \(i=1,\ldots ,n\), constraints (1b) are satisfied also for j such that \(\phi _{ij}=1\), as long as

$$\begin{aligned} {{\hat{M}}}_i \equiv \max _{\begin{array}{c} k,l\in \{1,\ldots ,n\}:\\ l>k \end{array}}\left| y_{i}-y_k-\frac{y_l-y_k}{x_l-x_k} (x_i-x_k)\right| \ge \left| y_{i}-c_j-\beta _jx_{i}\right| . \end{aligned}$$

The last inequality followed from the optimality of f; the converse would imply that there is no line connecting any pair k, l that crosses line segment j implying the suboptimality of f. (8) implies that the solution \(b,c,\beta ,\xi ,\phi\) has an objective value that equals the sum of (pth power) errors. Further, by the definitions (6a) together with (5), constraints (1h) and (3) are satisfied. Constraints (1f) follow from the continuity of f; for each \(j=1,\ldots ,m-1\), the pair of consecutive line segments j and \(j+1\) must intersect at \((b_j,c_j+\beta _jb_j)\). So \(b,c,\beta ,\xi ,\phi\) corresponds to f, in particular it is a function whose graph coincides with that of f restricted to \([x_1,x_n]\subseteq D\), and it is feasible for (1) with (3). \(\square\)

We now derive relationships between the resulting optimization problems when the different constraints (2), (3) and (4) are added to (1). The obtained results enables us to prove the correctness of formulation (1), extended by either of these constraints. To this end, let

  • \(z_R\) denote an optimal objective function value of (1),

  • \(z_S\) denote an optimal objective function value of (1) with (2),

  • \(z_3\) denote an optimal objective function value of (1) with (3),

  • \(z_4\) denote an optimal objective function value of (1) with (4).

Finally, let \(X_R, X_3, X_4, X_S\subseteq {\mathbb {R}}^{3m}\times {\mathbb {R}}^n\times \{0,1\}^{nm}\) denote the feasible regions corresponding to these formulations with optimal objective values \(z_R, z_3, z_4\) and \(z_S\), respectively. The following proposition establishes the relations between the feasible regions and objective function values of these formulations.

Theorem 2

Suppose that \(M_i, {{\hat{M}}}_i\), for \(i=1,\ldots ,n\), are sufficiently large constants satisfying the hypothesis of Theorem 1. Then, feasible regions \(X_R, X_3, X_4, X_S\) satisfy \(X_R\supset X_3, X_4 \supset X_S\). Further, suppose that \(m\le n\). Then, these formulations’ optimal objective values satisfy \(z_R\le z_3 =z_4 = z_S\).

Proof

\(X_R\supset X_3,X_4\) is straightforward given that (1) is a relaxation of the formulations with either constraints (3) or (4), which require the breakpoints to be ordered. Further, \(X_3\), which admits only solutions whose breakpoints are ordered as feasible, is a relaxation of the formulation (1) with (2), which requires each segment to be assigned at least one data point, and whose constraints (1d) and (1e) together with (2), imply (3). To see that \(X_S\subset X_4\), observe that the constraints (4) enforce that for each \(i=1,\ldots ,n-1\) and \(j=2,\ldots ,m\) a data point \(i+1\) can be assigned to segment j only if i is assigned to either j or to \(j-1\). Evidently, constraints (4) are satisfied if there exists some integer \(1\le j'\le m\) for which all segments in \(\{1,\ldots ,j'\}\) are each assigned at least one data point and segments \(\{j'+1,\ldots ,m\}\) are not assigned any data points. In particular, constraints (2) being satisfied imply that \(j'=m\). Otherwise, a solution in \(X_4\) with \(m>j'\) is also a solution in \(X_S\) where \(m=j'\). It follows that \(z_4\ge z_S\) since the optimal solutions using \(m\ge j'\) line segments cannot have an objective value that is worse than optimal solutions using only \(j'\) line segments. Equality follows from the fact that \(X_4\) is a relaxation, that is \(X_4\supset X_S\) implies \(z_4\le z_S\).

To see that \(z_3=z_4=z_S\) consider an optimal solution of (1) with (3) having optimal objective \(z_3\) and a minimal number of line segments that is not assigned any data points. Then, consider a line segment along \([b_{j-1}, b_{j}]\) that is not assigned any data points for some \(j=1,\ldots ,m\), where \(b_0=\min _{i=1,\ldots ,n}x_i\), and a closest data point (for convenience suppose from the right) with horizontal coordinate \(x^*\) (note that if no such line segment exists then clearly \(z_3=z_S\)). Then, consider a solution with \(b_{j}\) replaced by \(x^*\) (so that segments j and \(j+1\) now intersect at horizontal coordinate \(x^*\) and only the slope of line segment j that is previously not assigned any data points is adjusted accordingly). Evidently, this solution is feasible for (1) with (2) and has the same objective value. This shows that \(z_3=z_S\) and the proof of the equality with \(z_4\) is similar. \(\square\)

Now, Theorems 1 and 2 immediately imply the following

Corollary 1

Suppose that \(M_i\) and \({{\hat{M}}}_i\), for \(i=1,\ldots ,n\), are sufficiently large finite constants, and that \(m\le n\). Then, formulation (1) together with either constraints (2), (3) or (4), is correct.

Note that all of the proposed formulations require the breakpoints to be ordered, so they satisfy the requirement that the fitted curve is a graph of a function (including the formulations that require each line segment to be assigned at least one data point). We next compare the performance of a MINLP solver in solving the different alternative formulations.

3 Computational experiments

In our computational experiments we solve the formulation (1) with \(p=2\) and appending one of the constraints (2), (3) and (4), all or none of them—a relaxation of the intended problem. All formulations have been implemented using the Julia optimization package JuMP [4] and the state-of-the-art MINLP solver Couenne [2] version 0.5.6 run on a machine with a 2.5 GHz 4 MB cache CPU. The results of the experiments are shown in Table 2. In these experiments the time limit is set to 2 h. We experimented with the Titanium (\(n=49\)) dataset [3], a dataset based on the Concrete data [11] and the NHTemp dataset [7]. For the Concrete data we selected fly ash as the predictor variable and averaged the response variable value for entries with the same predictor variable value (so following that it had \(n=58\)). NHTemp [7] is a dataset containing New Haven’s average annual temperatures between the years 1912–1971 (\(n=60\)).

Table 2 Computational experiments with the alternative/different formulations using one or more of the constraints (2)–(4) and the given number of line segments m.
Full size table

The results of Table 2 indicate that the formulation (1) with constraints (3) is usually solved faster and with the fewest number of branch-and-bound nodes compared with the other formulations. This is despite the fact that this formulation admits many feasible solutions that would otherwise be infeasible (but with a similar objective value) for the formulations that append the constraints (2) or (4). A close second in the computational performance is the formulation (1) with (4). On the other hand, the formulation (1) with (2) failed to determine an optimal solution in many cases within the given 2-h time limit. Interestingly, formulation (1) by itself, which amounts to a relaxation of the other formulations, usually takes even longer to solve than (1) with (2), other than in the case of the Concrete instance with \(m=2\).

4 Conclusions

We have pointed out an error in the nonconvex MINLP for fitting piecewise linear functions proposed in [5]. This error may result in some cases in fitting a polygonal curve that is not the graph of a function. We present three different formulations that add inequalities in order to correct the MINLP. Formulations with constraints that explicitly enforce the ordering of breakpoints appear to perform better than assignment-type constraints that require that each line segment is assigned a data point. These assignment constraints implicitly imply the ordering of breakpoints when combined with other inequalities of the model, and they are shown to preserve at least one solution that is optimal for the function-fitting problem (which requires the breakpoints to be ordered but does not require each line segment to be assigned a data point).

Finally, the study of these inequalities and alternative formulations may also suggest and support the use of particular ordering-based constraints rather than assignment-type constraints for other formulations have been recently modeled to effectively solve larger problems such as the one proposed in [9].