1 Introduction

There is a variety of methods for unconstrained optimization calculations, where in general the following problem is studied: given an at least twice continuously differentiable objective function f in n unknowns, we seek its minimum for x on a domain or the whole n dimensional space

$$\begin{aligned} x^* :=\mathrm{argmin}f(x). \end{aligned}$$

As an important step towards this, we seek a stationary point \(x^*\) where f’s gradient vanishes. This stationary point is approached iteratively, by sequence of points \(x^k\) in n dimensions, beginning with an initial point \(x^0\). We go from step to step along a so-called search direction without using a Hesse matrix of the objective function.

However, in the so-called quasi-Newton algorithms for large scale unconstrained optimization calculations, an approximation \(B^k=(H^k)^{-1}\) to the second derivative matrix is used successfully for the computation of the search direction \(d^k\).

A superior method for nonlinear optimization is the DFP (Davidon–Fletcher–Powell) algorithm (a “variable metric method”, and such methods had a huge impact on optimization) a predecessor to the BFGS scheme we use in this article. It contains Mike Powell’s name and that scheme uses derivative information (Fletcher and Powell [2], Powell [6,7,8,9,10,11,12]).

We use the condition as a stopping criterion in our algorithms that the gradient at \(x^k\) that we shall denote by \(g^k\) has length at most \(\epsilon\) after only finitely many steps.

Algorithm 1

Step 0 :

Let any starting vector \(x^{0}\) and any positive definite symmetric matrix \(H^{0}\) be given, often the identity matrix. Set \(k:=0\).

Step 1 :

If the stopping criterion \(\Vert g^k\Vert _2\le \epsilon\) for a small positive \(\epsilon\) is satisfied then stop. Else: calculate the search direction from the formula

$$\begin{aligned} d^{k}:= - H^k g^k. \end{aligned}$$
(1.1)
Step 2 :

Compute the vectors

$$\begin{aligned} {\delta ^{k}}:= \alpha ^{k}d^{k}, \quad x^{k+1}:= x^{k}+ {\delta ^{k}},\quad {\gamma ^{k}}:= g^{k+1}- g^k, \end{aligned}$$
(1.2)

where \(\alpha ^{k}\) is determined by a line search that reduces the value of the objective function f and provides \({{\delta ^{k}}}^{T}{\gamma ^{k}}> 0\) (e.g., the Wolfe conditions).

Step 3 :

Form the matrix \(H^{k+1}\) by applying the usual Broyden class update formula where its parameter \(\psi ^{k}\) is chosen so that \(H^{k+1}\) is positive definite: it is of the form

$$\begin{aligned} H^{k+1}:= & {} \left( I - \frac{{\delta ^{k}}{{\gamma ^{k}}}^{T}}{{\delta ^{k}}^{T} {\gamma ^{k}}} \right) H^{k}\left( I - \frac{{\gamma ^{k}}{{\delta ^{k}}}^{T}}{{\delta ^{k}}^{T} {\gamma ^{k}}} \right) + \frac{{\delta ^{k}}{{\delta ^{k}}}^{T}}{{\delta ^{k}}^{T} {\gamma ^{k}}} \nonumber \\&-\, \psi ^{k}({{\gamma ^{k}}}^T H^{k}{\gamma ^{k}}) \left( \frac{H^{k}{\gamma ^{k}}}{{{\gamma ^{k}}}^{T} H^{k}{\gamma ^{k}}} - \frac{{\delta ^{k}}}{{\delta ^{k}}^{T} {\gamma ^{k}}} \right) \left( \frac{H^{k}{\gamma ^{k}}}{{{\gamma ^{k}}}^{T} H^{k}{\gamma ^{k}}} - \frac{{\delta ^{k}}}{{\delta ^{k}}^{T} {\gamma ^{k}}} \right) ^{T} \end{aligned}$$
(1.3)

where I is the identity matrix. Then increase k by one and go back to Step 1.

In Step 3 we restrict the parameter \(\psi ^k\) to choices giving a positive definite matrix \(H^{k+1}\) since this ensures that the search directions calculated in Step 1 are downhill.

For large scale problems, that is to say, large n, the standard method of Algorithm 1 has the unfavourable feature of requiring \(O(n^2)\) operations per iteration and storage for \({\frac{1}{2}}n^2 + O(n)\) numbers.

The limited memory updating technique presented by Nocedal [4] computes a second derivative approximation by updating a simple matrix (usually the identity or some other diagonal matrix) using the \(\delta ^k\) and \(\gamma ^k\) vectors from the most recent m iterations, where m is a prescribed integer. Nocedal’s method stores \(2nm + O(n)\) numbers and calculates \(4nm + O(n) + O(m)\) multiplications per iteration.

In Sect. 2 of this paper we present an implementation of Broyden class updates that, for \(H^0 = I\), stores only one new n vector per iteration. Our approach differs from the work quoted above by following a geometrical motivation based on Lemma 1 below—which uses the span of the first k gradient vectors to show certain invariance properties with respect to multiplications by \(H^k\) for our following algorithms—rather than relying on algebraic simplifications and by applying to the entire Broyden class.

This algorithm is the basis for the investigations of this paper. We demonstrate that it is computationally efficient [requiring only \(2nk + O(k^2) + O(n)\) multiplications on the kth iteration] and leads in a natural way to a modification by a scaling technique that, in our test cases, substantially reduces the number of functions calls required to find the solution within given accuracy. These numerical results are presented in Sect. 3. The mentioned reduction is as much as close to 60 percent.

Section 4 offers a number of limited memory modifications of the algorithms presented in Sect. 2. The numerical results presented in Sect. 5 indicate that these methods are superior to Nocedal’s method. In Sect. 6 we apply a scaling technique to both Nocedal’s method and the ones developed in Sect. 4 arriving at the surprising result that scaling is so beneficial to Nocedal’s method that it closes the performance gap observed in Sect. 5.

2 A new implementation of Broyden class updates

The algorithm presented in this section relies on the simplifications that occur if the initial second derivative approximation \(B^0\) is the identity matrix. We note that due to the invariance properties of the Broyden class updates with respect to diagonal scaling (which cancel), the choice \(B^0 = D\), where D is a diagonal matrix, is equivalent to setting \(B^0 = I\) and scaling the axes by the transformation

$$\begin{aligned} x' := D^{{\frac{1}{2}}} x , \end{aligned}$$
(2.1)

so that such choices of \(B^0\) can be treated within our framework. We note that other choices of \(B^0\) are uncommon in practical large scale calculations.

The following lemma and the ensuing comments form the basis for our implementation.

Lemma 1

Let Algorithm 1with \(H^0 = I\) be applied to a twice continuously differentiable function f. Define the subspace

$$\begin{aligned} S^k := \text{ span } \{ g^0, g^1, \ldots , g^k \} . \end{aligned}$$
(2.2)

Then, for all k, the inclusion

$$\begin{aligned} {\delta ^{k}}\in S^k \end{aligned}$$
(2.3)

is satisfied. Let in addition the vectors s and t belong to \(S^k\) and the orthogonal complement of \(S^k\), respectively. Then we have the relations

$$\begin{aligned}&B^{k}s \in S^k , \qquad H^{k}s \in S^k \quad \text{ and } \quad \end{aligned}$$
(2.4)
$$\begin{aligned}&B^{k}t = H^{k}t = t . \end{aligned}$$
(2.5)

Proof

We prove the lemma by induction over k, noting that for \(k = 0\) the statements (2.3)–(2.5) follow directly from \(\delta ^0\) being parallel to \(d^0 := - g^0\) and \(B^0 = H^0 = I\). We now assume that the Eqs. (2.3)–(2.5) hold for k and consider them for \(k+1\). By the induction hypothesis we have the inclusions

$$\begin{aligned} {\delta ^{k}}\in S^k,\quad B^k {\delta ^{k}}\in S^k \subset S^{k+1} , \end{aligned}$$
(2.6)

and by definition the vector in (1.2) is also contained in \(S^{k+1}\). Using \(B^k {\delta ^{k}}, \; {\gamma ^{k}}\in S^{k+1}\), we find \(B^{k+1}t = B^{k}t = t\) for any vector t belonging to the orthogonal complement of \(S^{k+1}\) which is equivalent to \(H^{k+1}t = t\).

Hence, since \(B^{k+1}\) is symmetric, orthogonality yields (2.4) with k replaced by \(k+1\) for any vector \(s \in S^{k+1}\). Finally the definition

$$\begin{aligned} \delta ^{k+1}:= - \alpha ^{k+1}H^{k+1}g^{k+1} \end{aligned}$$
(2.7)

and the second inclusion of (2.4) with k replaced by \(k+1\) give \(\delta ^{k+1}\in S^{k+1}\). \(\square\)

Let the conditions of Lemma 1 be satisfied, where we begin with the identity matrix as a start matrix by assumption. This is an essential feature of our method.

We define \(\ell ^k := \text{ dim } S^k\) and let \(Q^k\) be an orthogonal matrix whose first \(\ell ^k\) columns span the subspace \(S^k\). Consider the change of variables

$$\begin{aligned} x' := {Q^k}^T x , \end{aligned}$$
(2.8)

which suggests the definitions

$$\begin{aligned} {{\delta ^{k}}}' := {Q^k}^T {\delta ^{k}},\quad {g^k}' := {Q^k}^T {g^k}, \quad {H^{k}}' := {Q^k}^T H^{k}Q^k . \end{aligned}$$
(2.9)

Thus, using Lemma 1 we find

$$\begin{aligned} {H^{k}}' = \left( \begin{array}{cc} {\hat{H}}^k &{}\quad 0 \\ 0 &{}\quad I \\ \end{array} \right) , \end{aligned}$$
(2.10)

where \({\hat{H}}^k\) is an \(\ell ^k \times \ell ^k\) matrix, and we apply these updates to \(\hat{H}^k\) from now on. We notice as well that the last \(n - \ell ^k\) components of \({{\delta ^{k}}}'\) and \({g^k}'\) are zero. Let us now assume that \({g^{k+1}}\in S^k\), implying \(S^{k+1} = S^k\) and \(\ell ^{k+1} = \ell ^k\). Then the last \(n - \ell ^k\) components of \({g^{k+1}}'\) and hence also those of \({{\gamma ^{k}}}'\) are zero. It thus follows that, in transformed variables, the updated matrix is

$$\begin{aligned} {H^{k+1}}' = \left( \begin{array}{cc} {\hat{H}}^{k+1} &{}\quad 0 \\ 0 &{}\quad I \\ \end{array} \right) , \end{aligned}$$
(2.11)

where \({\hat{H}}^{k+1}\) is obtained by updating the \(\ell ^k \times \ell ^k\) matrix \({\hat{H}}^k\) instead of \(H^k\), resulting in \({\hat{H}}^{k+1}\) in place of \({H}^{k+1}\), and the \(\ell ^k\) vectors \({\hat{\delta }}^k\) and \({\hat{\gamma }}^k\) containing the first \(\ell ^k\) components of \({{\delta ^{k}}}'\) and \({{\gamma ^{k}}}'\), respectively. These choices come once more from Lemma 1.

We now turn to \({g^{k+1}}\notin S^k\) giving \(\ell ^{k+1} = \ell ^k + 1\) and consider the change of variables

$$\begin{aligned} x'' := {Q^{k+1}}^T x , \end{aligned}$$
(2.12)

where the first \(\ell ^k\) columns of \(Q^{k+1}\) agree with those of \(Q^k\) and the \((\ell ^k + 1)\)st column is the normalized component of \({g^{k+1}}\) orthogonal to \(S^k\). Because the first \(\ell ^k\) columns are the same, we have the identities

$$\begin{aligned} {{\delta ^{k}}}'' = {{\delta ^{k}}}' , \qquad {g^k}'' = {g^k}', \qquad {H^{k}}'' = {H^{k}}' . \end{aligned}$$
(2.13)

In addition, the last \(n - (\ell ^k + 1)\) components of \({g^{k+1}}''\), and therefore also those of \({{\gamma ^{k}}}''\), are zero. Hence

$$\begin{aligned} {H^{k+1}}'' = \left( \begin{array}{cc} {\hat{H}}^{k+1} &{}\quad 0 \\ 0 &{}\quad I \\ \end{array} \right) , \end{aligned}$$
(2.14)

where \({\hat{H}}^{k+1}\) is now the \((\ell ^k + 1) \times (\ell ^k + 1)\) matrix obtained by updating

$$\begin{aligned} {\tilde{H}}:= \left( \begin{array}{cc} {\hat{H}}^k &{}\quad 0 \\ 0 &{}\quad 1 \\ \end{array} \right) , \end{aligned}$$
(2.15)

using the vectors \({\hat{\delta }}^k\) and \({\hat{\gamma }}^k\) formed by the first \(\ell ^k + 1\) components of \({{\delta ^{k}}}''\) and \({{\gamma ^{k}}}''\).

The following new algorithm applies the above observations, exploiting the fact that all the information that is required from the \(n \times n\) matrix \(H^{k}\) is contained in the first \(\ell ^k\) columns of \(Q^k\) and in the \(\ell ^k \times \ell ^k\) matrix \({\hat{H}}^k\).

We shall take

$$\begin{aligned} d^{k}= - {\hat{Q}}^k {\hat{H}^k} {\hat{Q}}^{k^{{ T}}}{g^k}. \end{aligned}$$
(2.16)

We decompose the current approximation to the inverse of the Hesse matrix into \({\hat{Q}}^k {\hat{H}^k} {\hat{Q}}^{k^{{ T}}} + RR^T\), where the columns of R span the orthogonal complement of the space spanned by the columns of \({\hat{Q}}^k\). Then \(-H^k{g^k}\) gives the above \(d^{k}\) where we use \(R^Tg^k=0\).

Algorithm 2

Step 0 :

Let any starting vector \(x^{0}\) be given. If \(g_0 = 0\) then stop, else set \(k:=0\), \(\ell ^0 := 1\) and let \({\hat{H}}^0={\hat{H}}^0_{11}\) be the \(1 \times 1\) unit matrix. Let the column of the \(n \times 1\) matrix \({\hat{Q}}^0\) be the vector \(g^0 / \Vert g^0 \Vert\). End.

Step 1 :

If the stopping criterion is satisfied then End. Else: calculate the search direction by (2.16).

Step 2 :

As in Algorithm 1.

Step 3a :

Compute the vector

$$\begin{aligned} \eta ^k := {g^{k+1}}- {\hat{Q}}^k {\hat{Q}}^{k^{{ T}}} {g^{k+1}}. \end{aligned}$$
(2.17)

If \(\eta ^k = 0 \;\), then set \(\; \ell ^{k+1} := \ell ^k \;\) and \(\; {\hat{Q}}^{k+1} := {\hat{Q}}^k\).

Else: set \(\; \ell ^{k+1} := \ell ^k + 1 \;\) and \(\; {\hat{Q}}^{k+1} := ({\hat{Q}}^k \; | \; \eta ^k / \Vert \eta ^k \Vert )\).

End. Always calculate the vectors \({\hat{\delta }}^k := {\hat{Q}}^{k+1^{{ T}}} {\delta ^{k}}\), \({\hat{\gamma }}^k := {\hat{Q}}^{k+1^{{ T}}} {\gamma ^{k}}\).

Step 3b :

If \(\eta ^k = 0\), then, using the vectors \({\hat{\delta }}^k\) and \({\hat{\gamma }}^k\), apply the Broyden class update to \({\hat{H}}^k\). Else apply the Broyden class update to the matrix \({\tilde{H}}\). End. Increase k by one and go back to Step 1.

The algorithm requires storage for \(n\ell ^k + O((\ell ^k)^2) + O(n)\) numbers, where k is the total number of iterations and \(\ell ^k \le k+1\).

By storing appropriate intermediate results, the kth iteration of Algorithm 2 can be done in \(3n\ell ^k + O((\ell ^k)^2) + O(n)\) multiplications in total, where \(\ell ^k \le k+1\). In fact, we note that the temporary \(\ell ^k\) vectors defined by

$$\begin{aligned} t^k_1 := {\hat{Q}}^{k^{{ T}}} {g^k},\quad t^k_2 := {\hat{Q}}^{k^{{ T}}} {g^{k+1}},\quad t^k_3 := {\hat{H}}^k t^k_1, \end{aligned}$$
(2.18)

can be computed from the identities (\(\Vert \cdot \Vert\) meaning the Euclidean norm)

$$\begin{aligned} t^k_1= & {} t_2^{k-1} \quad \text{ if }\ \ell ^k = \ell ^{k-1} , \end{aligned}$$
(2.19)
$$\begin{aligned} {t^k_1}^T= & {} \biggl ({t^{k-1}_2}^T \; | \; \frac{{\eta ^{k-1}}^T {g^k}}{\Vert \eta ^{k-1}\Vert }\biggr ) \nonumber \\= & {} \biggl ({t^{k-1}_2}^T \; | \; \Vert \eta ^{k-1} \Vert \biggr ) \quad \text{ if }\ \ell ^k = \ell ^{k-1} + 1, \end{aligned}$$
(2.20)

and from the definitions (2.18) in \(n \ell ^k + O(n) + O ((\ell ^k)^2)\) multiplications. Given \(t^k_1\), \(t^k_2\) and \(t^k_3\), the calculations of \(d^k\) and of \(\eta ^k\) in Eqs. (2.16) and (2.17), respectively, can each be done in \(n\ell ^k\) multiplications via the definitions

$$\begin{aligned} d^k := {\hat{Q}}^k t^k_3 ,\qquad \eta ^k := g^{k+1} - {\hat{Q}}^k t^k_2. \end{aligned}$$
(2.21)

Moreover we observe that computing the transformed vectors \({\hat{\delta }}^k\) and \({\hat{\gamma }}^k\) requires only \(O((\ell ^k)^2) + O(n)\) operations. In fact, we have the identities

$$\begin{aligned} {\hat{\delta }}^k= & {} - \alpha ^{k}{\hat{Q}}^{k+1^{{ T}}} {\hat{Q}}^k {\hat{H}^k} {\hat{Q}}^{k^{{ T}}} {g^k}\nonumber \\= & {} \; - \alpha ^{k}{\hat{Q}}^{k+1^{{ T}}} {\hat{Q}}^k {\hat{H}^k} t^k_1 \end{aligned}$$
(2.22)
$$\begin{aligned}= & {} \; - \alpha ^{k}{\hat{Q}}^{k+1^{{ T}}} {\hat{Q}}^k t^k_3, \end{aligned}$$
(2.23)

where the elements of the \(\ell ^{k+1} \times \ell ^k\) matrix \({\hat{Q}}^{k+1^{{ T}}} {\hat{Q}}^k\) are zero except for the diagonal elements which are one. We thus have: If \(\ell ^{k+1} = \ell ^k\), \({\hat{\delta }}^k = - \alpha ^{k}t^k_3\),

$$\begin{aligned} {\hat{\gamma }}^k = {\hat{Q}}^{k+1^{{ T}}} \gamma ^k = t^k_2 - t^k_1, \end{aligned}$$

else (i.e., if \(\ell ^{k+1} = \ell ^k+1\)),

$$\begin{aligned} {\hat{\delta }}^{k^{{ T}}}= & {} - \alpha ^{k}({t^k_3}^T \; | \; 0), \\ {\hat{\gamma }}^{k^{{ T}}}= & {} \biggl ({t^k_2}^T \; | \; \frac{{\eta ^{k}}^T {g^{k+1}}}{\Vert \eta ^k \Vert }\biggr ) - \biggl ({t^k_1}^T \; | \; \frac{{\eta ^{k}}^T {g^k}}{\Vert \eta ^k \Vert }\biggr ) = ({t^k_2}^T - {t^k_1}^T \; | \; \Vert \eta ^k \Vert ) , \end{aligned}$$

the last equation being a consequence of the following identities:

$$\begin{aligned} \bigl (\eta ^k \bigr )^T\gamma ^{k}= & {} \Vert g^{k+1}\Vert ^2-\bigl (g^{k+1}\bigr )^T{\hat{Q}}^k\bigl ({\hat{Q}}^k\bigr )^Tg^{k+1}{}-\bigl (\eta ^k \bigr )^Tg^{k}\\= & {} \Vert \eta ^k\Vert ^2-\bigl (g^{k+1}\bigr )^Tg^k+\bigl (g^{k+1}\bigr )^T{\hat{Q}}^k\bigl ({\hat{Q}}^k\bigr )^Tg^{k} \end{aligned}$$

by (2.17). The value \((\eta ^k )^Tg^{k}\) need not be zero. Finally we note that the update of \({\hat{H}}^k\) itself is only an \(O((\ell ^k)^2)\) process.

Equation (2.17) shows that the columns of the matrix \({\hat{Q}}^k\) are calculated by applying the Gram-Schmidt process to the gradients \(\{g^0, \ldots , {g^k}\}\). It is well known that the calculation of \(\eta ^k\) is ill-conditioned if the gradients are almost linearly dependent, which due to rounding leads to a loss of orthogonality in the columns of \({\hat{Q}}^k\). In the following paragraphs we present a technique overcoming this.

Let at the kth iteration of Algorithm 2 the columns of the \(n \times \ell ^k\) matrix \(G^k\) be from

$$\begin{aligned} \left\{ g^{j} \; | \; \left[ j = 0 \right] \; \vee \; \left[ (1 \le j \le k) \; \wedge \; (\ell ^{j} = \ell ^{j-1} + 1) \right] \right\} . \end{aligned}$$
(2.24)

By construction of \({\hat{Q}}^k\) there exists a nonsingular upper triangular \(\ell ^k \times \ell ^k\) matrix, \(R^k\) say, so that the identity

$$\begin{aligned} {\hat{Q}}^k R^k = G^k \end{aligned}$$
(2.25)

is satisfied, the elements of \(R^k\) being the coefficients of the Gram-Schmidt process that has just been described. We exploit this relation by storing \(G^k\) and \(R^k\) instead of \({\hat{Q}}^k\), noting that the work for computing products of the form

$$\begin{aligned} {\hat{Q}}^{k^{{ T}}} v = {R^k}^{-T} {G^k}^T v,\quad {\hat{Q}}^k w = G^k (R^k)^{-1} w , \end{aligned}$$
(2.26)

where \(v \in {\hbox {I}\hbox {R}}^n\) and \(w \in {\hbox {I}\hbox {R}}^{\ell ^k}\), increases only by \(O({\ell ^k}^2)\) multiplications. The update of \(R^k\) and \(G^k\) is done as follows:

If \(\Vert \eta ^k \Vert = 0\) we do not change \(R^k\) and \(G^k\), otherwise we let \(G^{k+1}\) and \(R^{k+1}\) be

$$\begin{aligned} G^{k+1}:= & {} (G^k \; | \; g^{k+1}) , \end{aligned}$$
(2.27)
$$\begin{aligned} R^{k+1}:= & {} {\hat{Q}}^{k+1^{{ T}}} G^{k+1} = \biggl ({\hat{Q}}^k \; | \; \frac{\eta ^k}{\Vert \eta ^k \Vert }\biggr )^T (G^k \; | \; g^{k+1}) = \left( \begin{array}{cc} R^k &{} {\hat{Q}}^{k^{{ T}}} g^{k+1} \\ 0 &{} \Vert \eta ^k \Vert \\ \end{array} \right) . \qquad \end{aligned}$$
(2.28)

We note that the computation of the Cholesky factorisation in this fashion using orthogonality does not worsen condition numbers. We also note from (2.17) and (2.18) that

$$\begin{aligned} \Vert \eta ^k \Vert = \sqrt{ \Vert g^{k+1} \Vert ^2 - \Vert t^k_2 \Vert ^2} , \end{aligned}$$
(2.29)

because

$$\Vert g^{k+1}\Vert ^2-\Vert t_2^k\Vert ^2=\Vert g^{k+1}\Vert ^2-{g^{k+1}}^T{{{\hat{Q}}}{^{k}}}^T {{\hat{Q}}^k}g^{k+1}. $$

We also note that the argument of the square root is nonnegative in exact arithmetic as \({\hat{Q}}^k\) contains orthogonal vectors.

The ill-conditioned calculation of the vector \(\eta ^k\) is thus avoided. This also saves \(n \ell ^k\) multiplications. Cancellation will, however, occur in the computation of the difference \(\Vert g^{k+1} \Vert ^2 - \Vert t^k_2 \Vert ^2\), if \({g^{k+1}}\) is almost contained in the column span of \(G^k\). In our practical implementation we will, therefore, ignore the component of \(g^{k+1}\) orthogonal to the column span of \(G^k\) and thus keep \(G^k\) and \(R^k\) unchanged, if

$$\begin{aligned} \Vert \eta ^k \Vert \le C \; \Vert g^{k+1} \Vert \end{aligned}$$
(2.30)

holds, where \(C\ge 0\) (the value \(C := 0.1\) gave good results in our numerical experiments). With this choice, inequality (2.30) failed on most iterations, so the above modification was hardly ever invoked. We also noticed that choosing \(C := 0.2\) or \(C := 0.05\) led to only very minor changes in the number of function evaluations or iterations required for the solution of our test problems. Since rounding errors could cause the argument of the square root in (2.29) to become negative we replace (2.30) by

$$\begin{aligned} \Vert t_2^k \Vert ^2 \ge (1 - C^2) \; \Vert g^{k+1} \Vert ^2 , \end{aligned}$$
(2.31)

which are equivalent in exact arithmetic.

Algorithm 3 incorporates the changes suggested above. It thus requires only \(2 n \ell ^k + O((\ell ^k)^2) + O(n)\) multiplications on iteration k, where \(\ell ^k \le k + 1\).

Algorithm 3

Step 0 :

Let any starting vector \(x^{0}\) be given. If \(g^0 = 0\) then End. Else: set \(k:=0\), \(\ell ^0 := 1\) and let \({\hat{H}}^0\) and \(R^0\) be given by \({\hat{H}}^0_{11} = 1\) and \(R^0_{11} = \Vert g^0 \Vert\), respectively. Let the column of the \(n \times 1\) matrix \(G^0\) be the vector \(g^0\) and let the real component \(t^0_1\) be given by \((t^0_1)_1 = \Vert g^0 \Vert\).

Step 1 :

If the stopping criterion is satisfied then stop. Else: calculate the search direction from the formulae (2.18) and

$$\begin{aligned} d^{k}:= - G^k (R^k)^{-1} t_3^k . \end{aligned}$$
(2.32)
Step 2 :

As in Algorithm 1.

Step 3a :

Compute the vector

$$\begin{aligned} t_2^k := {R^k}^{-T} {G^k}^T g^{k+1} . \end{aligned}$$
(2.33)

If inequality (2.31) does not hold, set

$$\begin{aligned} {{\underline{\eta }}^k}& :=\, \sqrt{ \Vert g^{k+1} \Vert ^2 - \Vert t^k_2 \Vert ^2} , \end{aligned}$$
(2.34)
$$\begin{aligned} \ell ^{k+1}& :=\, \ell ^k+1 , \end{aligned}$$
(2.35)
$$\begin{aligned} G^{k+1}& := \,(G^k \; | \; g^{k+1}) , \end{aligned}$$
(2.36)
$$\begin{aligned} R^{k+1}& := \,\left( \begin{array}{cc} R^k &{}\quad t_2^k \\ 0 &{}\quad {{\underline{\eta }}^k} \\ \end{array} \right) , \end{aligned}$$
(2.37)
$$\begin{aligned} {\hat{\delta }}^k:=\, - \alpha ^{k}({t^k_3}^T \; | \; 0)^T , \end{aligned}$$
(2.38)
$$\begin{aligned} {\hat{\gamma }}^k:=\, ({t^k_2}^T - {t^k_1}^T \; | \; {{\underline{\eta }}^k})^T , \end{aligned}$$
(2.39)
$$\begin{aligned} t^{k+1}_1:= \,({t^k_2}^T \; | \; {{\underline{\eta }}^k})^T , \end{aligned}$$
(2.40)

else

$$\begin{aligned} \ell ^{k+1}:= \,\ell ^k , \end{aligned}$$
(2.41)
$$\begin{aligned} G^{k+1}:=\, G^k , \end{aligned}$$
(2.42)
$$\begin{aligned} R^{k+1}:= \,R^k , \end{aligned}$$
(2.43)
$$\begin{aligned} {\hat{\delta }}^k:=\, - \alpha ^{k}t^k_3 , \end{aligned}$$
(2.44)
$$\begin{aligned} {\hat{\gamma }}^k:=\, t^k_2 - t^k_1 , \end{aligned}$$
(2.45)
$$\begin{aligned} t^{k+1}_1:=\, t^k_2 . \end{aligned}$$
(2.46)

End.

Step 3b :

If \(\ell ^{k+1} = \ell ^k\) then use the vectors \({\hat{\delta }}^k\) and \({\hat{\gamma }}^k\) and apply the Broyden class update to \({\hat{H}}^k\). Else (i.e., \(\ell ^{k+1} = \ell ^k + 1)\) apply the Broyden class update to the matrix \({\tilde{H}}\). End. Increase k by one and go back to Step 1.

The following observations will lead to an alternative formulation of Algorithm 3. This is relevant to the next section, where we present a limited memory update. Let us assume that on iteration k the gradient \(g^{k+1}\) has been included into the matrix \(G^{k+1}\). We note that, because of (2.32), the vector \(\delta ^{k+1}= \alpha ^{k+1}d^{k+1}\) is contained in the column span of \(G^{k+1}\). Moreover, we find \({\delta ^{k+1}}^T {g^{k+1}}\ne 0\) as \(d^{k+1}\) is a downhill search direction, thus the columns of the matrices \(G^{k+1}\) and \((G^k \; | \; \delta ^{k+1})\) span identical subspaces. One could replace the last columns of \(G^{k+1}\) and \(R^{k+1}\) by \(\delta ^{k+1}\) and

$$\begin{aligned} {\hat{Q}}^{{k+1}^{{ T}}} \delta ^{k+1}= - \alpha ^{k+1}{\hat{H}}^{k+1}{\hat{Q}}^{{k+1}^{{ T}}} {g^{k+1}}= - \alpha ^{k+1}{\hat{H}}^{k+1} t^{k+1}_1 = - \alpha ^{k+1}t^{k+1}_3 , \end{aligned}$$
(2.47)

respectively, without changing the underlying matrix \({\hat{Q}}^{k+1}\). Employing this exchange of columns whenever \(\ell ^k\) is increased gives an equivalent algorithm, in which the vectors \({\delta ^{k}}\) rather than the gradients \(g^k\) are stored. Note that \(\delta ^{k+1}\) cannot be included into \(G^{k+1}\) directly, as it is available only at the beginning of iteration \(k+1\).

Now Algorithm 4 is obtained from Algorithm 3 by inserting Step 2a below after Step 2.

Algorithm 4

As in Algorithm 3, but insert after Step 2 the following

Step 2a:

If \(\ell ^k = \ell ^{k-1} + 1\), then replace the last columns of \(G^{k}\) and \(R^{k}\) by \({\delta ^{k}}\) and \(-\alpha ^{k}t^k_3\), respectively.

As indicated, Algorithm 4 will be important in Sect. 4. Nonetheless, we do not recommend its general use, since inequality (2.30) whose purpose is to make sure that no cancellation occurs in the \(g^k\) vectors, does not guarantee this for the corresponding \({\delta ^{k}}\) vectors, which may lead to a loss of orthogonality in Gram-Schmidt.

Due to the structure given in (2.10), the new algorithms provide full information on the subspace for which the second derivative information is based on the gradient information gathered so far and on the orthogonal subspace on which it is still the identity matrix. In the final algorithm of this section we intend to enhance the performance of Algorithm 3 by a scaling technique (as suggested in a similar setting for instance in Powell [11] and Siegel [14]) aimed at not distorting the second derivative information already gained on the previous iterations.

This is achieved by multiplying the identity matrix in (2.10) by a scalar, which we shall denote by \(\tau\), thus changing the curvature of our second derivative approximation on the subspace orthogonal to the gradients from 1 to \(\tau ^{-1}\).

Of course, reasoning for choosing \(\tau\) is heuristic; it applies to a subspace on which no curvature information has been gathered so far. Our approach is \(\frac{{\delta ^k}^T \gamma ^k}{{\delta ^k}^T \delta ^k}\) as in Oren and Luenberger [5] as an approximation of the one dimensional curvature encountered on iteration k and choose \((\tau ^k)^{-1}\) to be the geometric mean

$$\begin{aligned} \tau ^k=\prod _{j=0}^k\left( \frac{{\delta ^j}^T \gamma ^j}{{\delta ^j}^T \delta ^j}\right) ^{1/(k+1)},\quad k>0, \end{aligned}$$
(2.48)

recursively computed of all such curvature approximations encountered so far, thus implementing the assumption that the average curvature encountered so far should be a reasonable indicator for the curvature on the not yet discovered subspace. For such a curvature approximation it is reasonable to take geometric averages as weights to balance between the subspaces as all updates are essentially products in these method. No particular subspace is however emphasised.

The resulting Algorithm 5 is obtained from Algorithm 3, using the well-known recursive expression for the geometrical mean in (2.48), as follows:

Algorithm 5

Step 0–2 :

As in Algorithm 3, but add the definition \(\tau ^0 := 1 \;\)

and \(\tau ^k\) by (2.48).

Step 3a :

As in Algorithm 3 .

Step 3b :

As in Algorithm 3, but: If \(\ell ^{k+1} = \ell ^k + 1\) then update \(\left( \begin{array}{cc} {\hat{H}}^{k} &{} 0 \\ 0 &{} \tau ^k \\ \end{array} \right) ,\) instead of \({\tilde{H}}.\) End.

3 Numerical results—full BFGS implementations

In this section we compare the performances of Algorithms 3 and 3HH (Alg. 3 with Householder factorisation) and 5, all using \(\psi ^k = 0\) in the Broyden H updates.

Our test problems, motivated by the need to be able to create problems for both small and very large values of n, are derived from the physical situation described in (Siegel [13]). Our stopping condition is the inequality

$$\begin{aligned} \Vert g^k \Vert < \epsilon , \end{aligned}$$
(3.1)

where \(\epsilon >0\) (in our work we chose \(\epsilon =10^{-2}, 10^{-4}, 10^{-6}, 10^{-8}\)).

All algorithms were implemented in double precision. Our line search routine finds steplengths \(\alpha ^{k}\) that satisfy Wolfe’s [15] conditions with the choice of constants \({c_{1}}= 0.01\) and \({c_{2}}= 0.9\). It uses function gradients as well as function values, and is a slightly modified version of the line search used in the TOLMIN Fortran package (see Powell [11]). We implemented the algorithms so that they were compatible (see the first paragraph of Sect. 2) with choosing the initial second derivative approximation

$$\begin{aligned} ({H^0})^{-1}= B^0 = \frac{{\delta ^0}^T \gamma ^0}{{\delta ^0}^T \delta ^0} \; I , \end{aligned}$$
(3.2)

noting that this initial scaling is often used in practice (Oren and Luenberger [5]). Moreover, it is compatible with the choice of \(\tau ^0\) in Algorithm 5.

For Algorithm 3 and Algorithm 5 we use \(C := 0.1\). Anticipating the well-known robustness of the Householder approach we use \(C := 0.0\) in Algorithm 3HH.

Table 1 gives the results of 20 runs for each pair of n and \(\epsilon\), where the first column entry gives the average number of function evaluations and the second the average number of iterations. We draw the following conclusions:

  • Generally the performance of the native BFGS algorithm is very similar to both Algorithm 3 with \(C := 0.1\) and Algorithm 3HH (with Householder factorisation). We view this as an indication that the measures introduced to retain stability in the orthogonalization process required by the new algorithms are successful. In fact, in the course of our numerical tests we continuously monitored the orthogonality of the \(Q^k\) matrices implied by the matrices \(R^k\) and \(G^k\) for Algorithm 3 and by the Householder factorization for Algorithm 3HH instead of Gram-Schmidt to ascertain this point.

  • The scaling introduced by Algorithm 5 is indeed highly beneficial in our examples for the Siegel test, typically reducing the number of function calls by 25% to 60% and the number of iterations even further.

Table 1 Average no. of function evaluations and iterations/Performance of the BFGS method compared to Algorithm 3, Algorithm 3HH and Algorithm 5 on Siegel’s problem with 20 random values for \(x^0\)
Full size table

4 Derivation of limited memory algorithms

In this section we consider the case when, due to limitations in the storage available on the computer, the number of columns of \(G\) is restricted by a number m, say.

We therefore have to devise a procedure for removing a column from G and making corresponding changes to R and \(\hat{H}\). Our strategy will be to delete the gradient or \(\delta\)-vector with the smallest iteration index. As a consequence of this procedure the column spaces of the matrices G will no longer agree, so now \(G\) usually changes the search directions of the algorithm even in exact arithmetic. For the deleting procedure it will turn out to be advantageous if the gradient or \(\delta\)-vector to be removed is the last column of G.

We therefore replace the Gram-Schmidt process used so far by the “inverse” Gram-Schmidt procedure, which is outlined below. First we consider an algorithm in which gradients are stored.

When we add a column to \(G^k\) we define the matrix \(G^{k+1} := (g^{k+1} \; | \; G^k)\) and the preliminary matrix

$$\begin{aligned} R_{{\text{ prel }}{}}^{k+1} := \left( \begin{array}{cc} t_2^k &{}\quad R^k \\ \Vert \eta ^k \Vert &{}\quad 0\\ \end{array} \right) . \end{aligned}$$
(4.1)

Thus the equation \({\hat{Q}}_{{\text{ prel }}{}}^{k+1} R_{{\text{ prel }}{}}^{k+1} = G^{k+1}\) implies the same underlying preliminary basis matrix

$$\begin{aligned} {\hat{Q}}_{{\text{ prel }}{}}^{k+1} = ({\hat{Q}}^k \; | \; \eta ^k / \Vert \eta ^k \Vert ) , \end{aligned}$$
(4.2)

as before. The matrix \(R_{{\text{ prel }}{}}^{k+1}\) possesses the sparsity structure

$$\begin{aligned} \left( \begin{array}{ccccc} \times &{}\quad \times &{}\quad \times &{}\quad \ldots &{}\quad \times \\ \times &{}\quad 0 &{}\quad \times &{}\quad \ldots &{}\quad \times \\ \times &{}\quad 0 &{}\quad 0 &{}\quad \ldots &{}\quad \times \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \times &{}\quad 0 &{}\quad 0 &{}\quad \ldots &{}\quad 0 \\ \end{array} \right) . \end{aligned}$$
(4.3)

Therefore we can obtain an upper triangular matrix \(R^{k+1}\) by premultiplying \(R_{{\text{ prel }}{}}^{k+1}\) by an orthogonal matrix

$$\begin{aligned} X^k := X^k_1 \cdots X^k_{\ell ^{k+1} -1} , \end{aligned}$$
(4.4)

where \(X^k_i\) is a Givens rotation that is different from the identity matrix only in its ith and \((i+1)\)st rows, which is defined by making the \((i+1)\)st and ith components of the first column of the matrix

$$\begin{aligned} X^k_i X^k_{i+1} \cdots X^k_{\ell ^{k+1} -1} \; R_{{\text{ prel }}{}}^{k+1} \end{aligned}$$
(4.5)

zero and positive, respectively. Therefore the equation \({\hat{Q}}^{k+1} {R}^{k+1} = G^{k+1}\) defines the new basis matrix using the definition

$$\begin{aligned} {\hat{Q}}^{k+1} := {\hat{Q}}_{{\text{ prel }}{}}^{k+1} {X^k}^T . \end{aligned}$$
(4.6)

We note that we have to take into account this change to \({\hat{Q}}^{k+1}\) when calculating the vectors \({\hat{\delta }}^k\) and \({\hat{\gamma }}^k\) and updating the matrix \({\hat{H}}^k\), see Steps 3a and 3b of Algorithm 6.

In case \(\delta\)-vectors are stored we proceed as above obtaining the matrices \(G^{k+1} = (g^{k+1} \; | \; G^k)\) and \(R^{k+1}\). We replace the first columns of \(G^{k+1}\) and \(R^{k+1}\) by \(\delta ^{k+1}\) and \(-\alpha ^{k}{\hat{H}}^{k+1} t^{k+1}_1\) once these vectors are available. By premultiplying \(R^{k+1}\) by an orthogonal matrix, \(Y^{k+1}\) say, we restore \(R^{k+1}\) to upper triangular structure, again keeping in mind that this operation changes the underlying basis matrix \({\hat{Q}}^{k+1}\), see Step 2a of Algorithm 7 below.

As required the updates of G have the property that the last columns of G contain the gradient or \(\delta\)-vector with the smallest iteration number. We outline our deleting procedure. We give a description for the case that gradients are stored.

Consider the case \(\ell ^{k+1} = m + 1\) and denote by \(G^{k+1}_{{\text{ del }}{}}\) the matrix formed by the first m columns of \(G^{k+1}\) and by \(R^{k+1}_{{\text{ del }}{}}\) the mth principal minor of \(R^{k+1}\), noting that \(R^{k+1}_{{\text{ del }}{}}\) is upper triangular and that the matrix

$$\begin{aligned} {\hat{Q}}^{k+1}_{{\text{ del }}{}} := G^{k+1}_{{\text{ del }}{}} \; (R^{k+1}_{{\text{ del }}{}})^{-1} \end{aligned}$$
(4.7)

is formed by the first m columns of \({\hat{Q}}^{k+1} = G^{k+1} (R^{k+1})^{-1}\). We therefore let \({\hat{H}}^{k+1}_{{\text{ del }}{}}\) be the matrix obtained by deleting the last row and column from \({\hat{H}}^{k+1}\). We note that for any two vectors \(v_1\) and \(v_2\) in the column space of \({\hat{Q}}^{k+1}_{{\text{ del }}{}}\) we have the identity

$$\begin{aligned} v_1^T H^{k+1} v_2 = v_1^T H_{{\text{ del }}{}}^{k+1} v_2 , \end{aligned}$$
(4.8)

where

$$\begin{aligned} H^{k+1}:= & {} Q^{k+1} \left( \begin{array}{cc} {\hat{H}}^{k+1} &{}\quad 0 \\ 0 &{}\quad I \\ \end{array} \right) {Q^{k+1}}^T , \end{aligned}$$
(4.9)

\(H^{k+1}_{{\text{ del }}{}}\) is the same with \({\hat{H}}^{k+1}_{{\text{ del }}{}}\) replacing \({\hat{H}}^{k+1}\), and \(Q^{k+1}\) is any orthogonal \(n \times n\) matrix, whose first \(m+1\) columns agree with those of \({\hat{Q}}^{k+1}\). Our deleting procedure thus leaves the approximation to the inverse Hessian unchanged on the column space of \({\hat{Q}}^{k+1}_{{\text{ del }}{}}\). Moreover, assuming that \({\hat{H}}^{k+1}\) is positive definite, the matrices \({\hat{H}}^{k+1}_{{\text{ del }}{}}\) and thus \(H^{k+1}_{{\text{ del }}{}}\) inherit this property as any principal minor of a positive definite matrix is itself positive definite.

Algorithm 6 employs the inverse Gram-Schmidt process and the deleting procedure outlined above.

Algorithm 6

Step 0 :

Let an integer \(m \ge 2\) and a starting vector \(x^{0}\) be given. If \(g^0 = 0\) then stop. Else set \(k:=0\), \(\ell ^0 := 1\) and let \({\hat{H}}^0\) and \(R^0\) be the \(1 \times 1\) matrices given by \({\hat{H}}^0_{11} = 1\) and \(R^0_{11} = \Vert g^0 \Vert\), respectively. Let the column of the \(n \times 1\) matrix \(G^0\) be the vector \(g^0\) and let \(t^0_1 \in {\hbox {I}\hbox {R}}^1\) be given by \((t^0_1)_1 = \Vert g^0 \Vert\). End.

Step 1 :

As in Algorithm 3.

Step 2 :

As in Algorithm 3.

Step 3a :

Compute the vector

$$\begin{aligned} t_2^k := \, {R^k}^{-T} {G^k}^T g^{k+1} . \end{aligned}$$
(4.10)

If (2.31) does not hold (i.e., \(\Vert t_2^k \Vert ^2 < (1 - C^2) \; \Vert g^{k+1} \Vert ^2)\), set

$$\begin{aligned} {{\underline{\eta }}^k}:= \sqrt{ \Vert g^{k+1} \Vert ^2 - \Vert t^k_2 \Vert ^2} , \end{aligned}$$
(4.11)
$$\begin{aligned} \ell ^{k+1}:=\, \ell ^k+1 , \end{aligned}$$
(4.12)
$$\begin{aligned} G^{k+1}:= \,(g^{k+1} \; | \; G^k) , \end{aligned}$$
(4.13)
$$\begin{aligned} R^{k+1}:= \,X^k \; \left( \begin{array}{cc} t_2^k &{}\quad R^k \\ {{\underline{\eta }}^k} &{}\quad 0 \\ \end{array} \right) , \end{aligned}$$
(4.14)
$$\begin{aligned} {\hat{\delta }}^k:= \,- \alpha ^k X^k \; ({t_3^k}^T \; | \; 0)^T , \end{aligned}$$
(4.15)
$$\begin{aligned} {\hat{\gamma }}^k:=\, X^k \; ({t^k_2}^T - {t^k_1}^T \; | \; {{\underline{\eta }}^k})^T , \end{aligned}$$
(4.16)
$$\begin{aligned} t^{k+1}_1:= \,X^k \; ({t^k_2}^T \; | \; {{\underline{\eta }}^k})^T , \end{aligned}$$
(4.17)

where \(X^k\) is the product of Givens rotations defined in the paragraph containing equation (4.4).

Else set the variables as in (2.42)–(2.46). End.

Step 3b :

If \(\ell ^{k+1} = \ell ^k\) then use the vectors \({\hat{\delta }}^k\) and \({\hat{\gamma }}^k\) and apply the Broyden class update to \({\hat{H}}^k\). Else (i.e., \(\ell ^{k+1} = \ell ^k + 1\)) apply the Broyden class update to the matrix \(X^k{\tilde{H}} {X^k}^T\), where \({\tilde{H}}\) is given by (2.15). End.

Step 4 :

If \(\ell ^{k+1} = m + 1\), then delete the last component of the vector \(t^{k+1}_1\), the last column of \(G^{k+1}\), the last row and column of \(R^{k+1}\) and \({\hat{H}}^{k+1}\) which is the updated \({\hat{H}}^{k}\), and set \(\ell ^{k+1} := m\). End.

Increase k by one and go back to Step 1.

Algorithm 7 below (the algorithm that stores delta-vectors rather than gradients) is obtained form Algorithm 6 by replacing the variable name G by \(\Delta\) and inserting Step 2a after Step 2.

Algorithm 7

As in Algorithm 6, except:

Step 2a:

If \(\Delta\) was changed on the previous iteration, then replace the first columns of \(\Delta ^{k}\) and \(R^{k}\) by \({\delta ^{k}}\) and \(-\alpha ^{k}{\hat{H}}^{k} t^{k}_1\), respectively, and let the resulting matrices overwrite the original matrices. Let \(Y^k\) be an orthogonal matrix such that \(Y^k R^k\) is upper triangular and redefine the variables

$$\begin{aligned} R^k:= & {} Y^k R^k \end{aligned}$$
(4.18)
$$\begin{aligned} t_1^k:= & {} Y^k t_1^k \end{aligned}$$
(4.19)
$$\begin{aligned} {\hat{H}}^k:= & {} Y^k {\hat{H}}^k {Y^k}^T \end{aligned}$$
(4.20)
$$\begin{aligned} t_3^k:= & {} Y^k t_3^k . \end{aligned}$$
(4.21)

End.

  • As the additional Givens rotations are applied to m vectors and \(m \times m\) matrices they require only \(O(m^2)\) multiplications. The total number of multiplications per iteration is thus \(2nm + O(m^2) + O(n)\) both for Algorithms 6 and 7.

  • Consider Algorithm 6 and assume that on iterations \(k-1\) and k the test \(\Vert {\eta ^k}\Vert \ge C \Vert g^{k+1} \Vert\) is satisfied, this being the usual case. Then the vector \({\gamma ^{k}}\) is contained in the column span of the matrix \(G^{k+1}\) defined in (4.13) as \({g^{k+1}}\) and \({g^k}\) are the first two columns of \(G^{k+1}\). Moreover \({\delta ^{k}}\) is also in the vector-space spanned by the columns of \(G^{k+1}\) since \(d^k\) is calculated from (2.32). The update of \({\hat{H}}^k\) in Step 3b is thus compatible with a Broyden update of the underlying matrix \(H^k\). Hence the resulting matrix \(H^{k+1}\) satisfies the quasi-Newton equation. Unfortunately, however, \(d^{k+1}\) is not calculated until the deleting procedure of Step 4 has changed the underlying matrix \(H^{k+1}\). A “standard” proof of quadratic termination is thus not possible.

  • We now turn to Algorithm 7 and note that by design of Step 1, \(d^{k}\), and thus \({\delta ^{k}}\), are contained in the column span of \(G^{k}\). Thus the replacement taking place in Step 2a does not change the subspace spanned by the columns of \(G^{k}\).

  • By design of Algorithm 7 the vectors \({\delta ^{k}}\) and \({g^{k+1}}\) are linear combinations of the columns of \(G^{k+1}\). However, the gradient \({g^k}\) and thus the vector \({\gamma ^{k}}\) will in general not be contained in this space. Thus the update in Step 3b does not correspond to applying the Broyden formula to \(H^k\), \({\delta ^{k}}\) and \({\gamma ^{k}}\), but we can enforce that the vector will be in the mentioned space: we replace it by \(\gamma ^k_P\), where \(\gamma ^k_P\) is the projection of \({\gamma ^{k}}\) onto the column space of \(G^{k+1}\). Note that the update gives a positive definite matrix \(H^{k+1}\) too, since the relation

    $$\begin{aligned} {{\delta ^{k}}}^T \gamma ^k_P = {{\delta ^{k}}}^T \gamma ^k > 0 \end{aligned}$$
    (4.22)

    is a consequence of \({\delta ^{k}}\) being in the span of the columns of \(G^{k+1}\).

  • If we use the BFGS update in Step 3b, corresponding to \(\psi ^k = 0\), Algorithm 7 has the quadratic termination property, which is the following result:

Theorem 1

Let Algorithm 7with \(\psi ^k = 0\) in the updating formula employed in Step 3b be applied to a strictly convex quadratic function f, and let the line searches be exact. Then the algorithm finds the minimum of f in at most L iterations, where L is the number of distinct eigenvalues of the Hessian matrix, A say, of f.

Proof

By induction we will show that the search directions \(d^k\) generated by Algorithm 7 satisfy the equations

$$\begin{aligned} \left. \begin{array}{rclll} d^k &{} = &{} - g^k &{} \quad \text{ for }\ k = 0 , \\ d^k &{} = &{} - g^k + {\displaystyle \frac{{g^k}^T A d^{k-1}}{{d^{k-1}}^T A d^{k-1}}} \; d^{k-1} &{} \quad \text{ for }\ k \ge 1 . \qquad \\ \end{array} \right\} \end{aligned}$$
(4.23)

Under the assumptions made in the statement of the theorem, Algorithm 7 is thus equivalent to the conjugate gradient method, for which quadratic termination in at most L steps is a well known result.

By definition (4.23) holds for \(k=0\). We now assume that (4.23) has been established for all search directions with iteration index less than or equal to k and consider iteration k. From the theory of the conjugate gradient method we have

$$\begin{aligned} {g^{k+1}}^T g^{j} = {g^{k+1}}^T d^{j} = 0 \quad \text{ for }\ 0 \le j \le k . \end{aligned}$$
(4.24)

Thus \(t^k_2\) formed in Step 3a is the zero vector as

$$\begin{aligned} t_2^k=\bigl (R^k\bigr )^{-T}\bigl (G^k\bigr )^{T}g^{k+1} \end{aligned}$$

and

$$\begin{aligned} \bigl (d^k\bigr )^{T}=-(t_3^k)^T\bigl (R^k\bigr )^{-T}\bigl (G^k\bigr )^T. \end{aligned}$$

This gives

$$\begin{aligned} \bigl (d^k\bigr )^{T}g^{k+1}=0=-(t_3^k)^T\bigl (R^k\bigr )^{-T}\bigl (G^k\bigr )^Tg^{k+1}, \end{aligned}$$

since otherwise \(d^k\) would have to vanish. This implies \({ \eta ^k } = \Vert g^{k+1} \Vert\), so the test Not (2.31) [i.e., \(\Vert t_2^k \Vert ^2 < (1 - C^2) \; \Vert g^{k+1} \Vert ^2\)] holds. From the structure of (4.1) and the definition of \(X^k\) in the paragraph containing Eq. (4.4) we deduce that \(X^k\) is the permutation matrix defined by the equations

$$\begin{aligned} X^k e_i= & {} e_{i+1} \quad \text{ for }\ 1 \le i \le n - 1 , \end{aligned}$$
(4.25)
$$\begin{aligned} X^k e_n= & {} e_1 , \end{aligned}$$
(4.26)

the \(e_i\) being the ith unit vector. Therefore we obtain in the Steps 3a and 3b

$$\begin{aligned} {\hat{\gamma }}^k= & {} ( \Vert {g^{k+1}}\Vert \; | \; {t^k_1}^T)^T , \end{aligned}$$
(4.27)
$$\begin{aligned} t^{k+1}_1= & {} ( \Vert {g^{k+1}}\Vert \; | \; 0^T)^T , \end{aligned}$$
(4.28)
$$\begin{aligned} R^{k+1}= & {} \left( \begin{array}{cc} \Vert {g^{k+1}}\Vert &{}\quad 0 \\ 0 &{}\quad R^k \\ \end{array} \right) , \qquad \end{aligned}$$
(4.29)
$$\begin{aligned} X^k \left( \begin{array}{cc} {\hat{H}}^{k} &{}\quad 0 \\ 0 &{}\quad 1 \\ \end{array} \right) {X^k}^T= & {} \left( \begin{array}{cc} 1 &{}\quad 0 \\ 0 &{}\quad {\hat{H}}^{k} \\ \end{array} \right) . \end{aligned}$$
(4.30)

The first row of both sides of (4.29) implies that the first two columns of \({\hat{Q}}^{k+1} = G^{k+1} (R^{k+1})^{-1}\) are the vectors \(\Vert {g^{k+1}}\Vert ^{-1} {g^{k+1}}\) and \(\Vert {\delta ^{k}}\Vert ^{-1} {\delta ^{k}}\), giving the formula

$$\begin{aligned} {\hat{\delta }}^k = {\hat{Q}}^{{k+1}^{{ T}}} {\delta ^{k}}= (0 \; | \; \Vert {\delta ^{k}}\Vert \; | \; 0^T)^T . \end{aligned}$$
(4.31)

Applying the update with \(\psi ^k = 0\) to the matrix (4.30) and to the vectors \({\hat{\delta }}^k\) and \({\hat{\gamma }}^k\) given by (4.31) and (4.27), respectively, we obtain a matrix \({\hat{H}}^{k+1}\) whose first column is

$$\begin{aligned} {\hat{H}}^{k+1} e_1 = \biggl (1 \; | - \frac{\Vert {g^{k+1}}\Vert \; \Vert {\delta ^{k}}\Vert }{{{\delta ^{k}}}^T {\gamma ^{k}}} \; | \; 0^T\biggr )^T . \end{aligned}$$
(4.32)

The deletion process of Step 4 changes neither the nonzero elements of the first column of \({\hat{H}}^{k+1}\) nor the first two columns of \({\hat{Q}}^{k+1}\). Thus, recalling (4.28), the new search direction \(d^{k+1}\) formed in Step 1 of the next iteration is

$$\begin{aligned} d^{k+1}= & {} - {\hat{Q}}^{k+1} {\hat{H}}^{k+1} t^{k+1}_1 \end{aligned}$$
(4.33)
$$\begin{aligned}= & {} - {g^{k+1}}+ \frac{\Vert {g^{k+1}}\Vert ^2}{{{\delta ^{k}}}^T {\gamma ^{k}}} \; {\delta ^{k}}, \end{aligned}$$
(4.34)

which, because of the identities

$$\begin{aligned} \frac{\Vert {g^{k+1}}\Vert ^2}{{{\delta ^{k}}}^T {\gamma ^{k}}} \; {\delta ^{k}}= & {} \frac{{{g^{k+1}}}^T ({g^{k+1}}- {g^k})}{{{\delta ^{k}}}^T ({g^{k+1}}- {g^k})} \; {\delta ^{k}}\; = \; \frac{{{g^{k+1}}}^T A {\delta ^{k}}}{{{\delta ^{k}}}^T A {\delta ^{k}}} \; {\delta ^{k}}\end{aligned}$$
(4.35)
$$\begin{aligned}= & {} \frac{{{g^{k+1}}}^T A d^{k}}{{d^{k}}^T A d^{k}} \; d^{k}\end{aligned}$$
(4.36)

is equivalent to (4.23) postdated by one iteration, as required. \(\square\)

It is interesting to observe that Algorithm 7 can be seen as a generalization of the conjugate gradient algorithm.

In the limited memory setting we have—unlike in the classic Quasi-Newton case—an additional option of dealing with the situation in which the test \(\Vert t_2^k \Vert ^2 < (1 - C^2) \; \Vert g^{k+1} \Vert ^2\) fails: We can re-start the entire algorithm since (given that usually \(m \ll n\)) the loss of second derivative information caused by the re-start is acceptable. Moreover, failure of the above test may be an indicator of ill-conditioning, in which case a re-start would be appropriate anyway.

We build in this modification into Algorithm 7 to arrive at the following Algorithm 8 which, due to its importance, we spell out in full detail. We note that it also has the quadratic termination property since the test Not (2.31) [i.e., \(\Vert t_2^k \Vert ^2 < (1 - C^2) \; \Vert g^{k+1} \Vert ^2\)] cannot fail if the objective function is a strictly convex quadratic function.

In order to avoid too many restarts we have also introduced the condition that no restart is carried out unless at least m steps have been performed without a restart.

Algorithm 8

Step 0 :

As in Step 1 in Algorithm 3 with \(m\ge 2\).

Step 1 :

If the stopping criterion is satisfied then stop. Else: calculate the search direction from the formula (2.18), (2.32). End.

Step 2 :

As in Algorithm 5.

Step 2a :

As in Algorithm 7. End.

Step 3a :

Compute the vector \(t_2^k\) given by (2.33). If Not (2.31) \((\Vert t_2^k \Vert ^2 < (1 - C^2) \; \Vert g^{k+1} \Vert ^2)\) then set the variables as in (4.11)–(4.17) where \(X^k\) is the product of Givens rotations defined in the paragraph containing equation (4.4) and where the argument of the square-root defining \({{\underline{\eta }}^k}\) is nonnegative by the properties of \(R^k\). End.

If (2.31) holds and if at least m iterations have been carried out without restart, then restart the algorithm by increasing k by one, setting \(\ell ^k := 1\) and letting \({\hat{H}}^k={\hat{H}}^k_{11} = 1\) and \(R^k=R^k_{11} = \Vert g^k \Vert\). Moreover, let the column of the \(n \times 1\) matrix \(G^k\) be the vector \(g^k\) and let \(t^k_1 \in {\hbox {I}\hbox {R}}^1\) be given by \((t^k_1)_1 = \Vert g^k \Vert\). End. Go to Step 1.

Step 3b :

If \(\ell ^{k+1} = \ell ^k\), then use the vectors \({\hat{\delta }}^k\) and \({\hat{\gamma }}^k\) and apply the Broyden class update to \({\tilde{H}}\). Else \((\ell ^{k+1} = \ell ^k + 1)\), use the vectors \({\hat{\delta }}^k\) and \({\hat{\gamma }}^k\) and apply the Broyden class update to \({\tilde{H}}\) given by (2.15). End.

Step 4 :

If \(\ell ^{k+1} = m + 1\), then delete the last component of the vector \(t^{k+1}_1\), the last column of \(G^{k+1}\), the last row and column of \(R^{k+1}\) and \({\hat{H}}^{k+1}\) and set \(\ell ^{k+1} := m\). End.

Increase k by one and go back to Step 1.

5 Numerical results—limited memory case

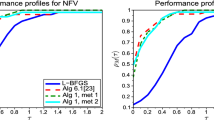
In this section we first compare the performance of Algorithms 6, 7 and 8 all using \(\psi ^k = 0\) with Nocedal’s [4] limited memory BFGS update.

Given the poor performance of Algorithm 6 we constrain the comparison for very large problems to Nocedal’s method and the generalized conjugate gradient Algorithms  7 and 8.

We use the test problems introduced in Sect. 3, implemented all algorithms in double precision and used the same line search as in Sect. 3. Again we implemented all algorithms so that they were compatible with choosing the initial second derivative approximation given by (3.2). When Algorithm 8 re-starts, it also updates this initial scaling. For Algorithms 6, 7 and 8 we used \(C := 0.1\).

Table 2 gives the results obtained from 20 (for \(n \le 1000\)) and 10 (for \(n \ge 2000\)) runs for \(m=10\) and \(\epsilon =10^{-6}\), where the first column entry gives the average number of function evaluations, the second the average number of iterations and the third the percentage of cases in which the solution was not found within 10,000 function calls (those runs not being included in the averages stated in the first two columns). We observe the following:

  • We note that Algorithm 6 performs poorly, which is why we excluded it from the test of \(n \ge 2000\). Therefore we do not recommend its use.

  • Algorithm 7 and Nocedal’s algorithm exhibit comparable performance.

    Algorithm 8 clearly outperforms Nocedal’s [4] approach, \(\tau ^k\) given by \({\gamma ^k}^T\gamma ^k\over {\delta ^k}^T\gamma ^k\) as in Liu and Nocedal [3], often reducing the number of function calls by more than two thirds—whilst at the same time requiring only half the storage for the same choice of m.

Table 2 Comparison of Nocedal’s limited memory method with the generalized conjugate gradient methods A6, A7 and A8
Full size table

6 Scaling techniques for limited memory methods

In this section we ask the question in how far scaling techniques can be used—in analogy to their positive effect shown in Sect. 3—to improve further the performance of both the generalized conjugate gradient method Algorithm 7 and Nocedal’s limited memory method. It is well known that scaling techniques can offer substantial improvements for Nodedal’s method (Liu and Nocedal [3]); we are referring to the L-BFGS method, see also Al-Baali et al. [1]. However, the updating technique in Step 3 of their Algorithm 2.1 is different from the one we use.

Following the line of reasoning of Sect. 2 we obtain the scaling version of Algorithm 7 which we shall refer to as Algorithm 9 by using a geometric average for scaling.

Algorithm 9

Step 0–3a :

As in Algorithm 7, but add the statements \(\tau ^0 := 1 \;\) and (2.48).

Step 3b :

As in Algorithm 7, but—for the case \(\ell ^{k+1} = \ell ^k + 1\)—apply the update to \(\left( \begin{array}{cc} {\hat{H}}^{k} &{} 0 \\ 0 &{} \tau ^k \\ \end{array} \right) ,\) instead of \({\tilde{H}}\), given by (2.15).

Step 4 :

as in Algorithm 7.

For Nocedal’s method the idea is to replace the identity matrix as the initial second derivative approximation by \(\tau I\), where we calculate the series of \(\tau ^k\) in the same way as above. The final Table 3 gives a comparison of Nocedal’s Algorithm with and without scaling with Algorithms 7, 8 and 9 for a number of test problem from CUTEst.

7 Conclusions/observations

In line with the results of Liu und Nocedal, applying the scaling approach to Nocedal’s limited memory method provides a significant improvement. Algorithm 9 is indeed superior to the original generalized conjugate gradient Algorithm 7. However, the improvement is comparatively small—and it performs worse than Algorithm 8. There is little to choose between Nocedal’s method with scaling and Algorithm 8 (generalized conjugate gradient with restarts).

We also tried the obvious idea of applying the scaling approach to the generalized conjugate gradient method with restarts of Algorithm 8. Unfortunately this did not give any improvements. In fact, we observed that scaling removes the need for restarts in most cases, so the resulting algorithm performs almost identically to Algorithm 9.

In summary, in this paper we introduced a new way of looking at the Broyden class of Quasi Newton methods for the case in which the initial second derivative approximation is the identity matrix. We exploited the resulting computational simplifications to derive several new algorithms (both quasi-Newton and Limited Memory) that are particularly efficient in housekeeping cost (storage and number of multiplications per iteration) and number of iterations and function calls required to find the solution within a given accuracy. Of particular interest is an algorithm that can be viewed as a generalized conjugate gradient method. Similarly to what is the case for Nocedal’s Limited Memory algorithm, restart and scaling modifications offer improvements for this generalized conjugate gradient method as well.

Table 3 Comparison of Nocedal’s limited memory method with the generalized conjugate gradient methods and A8, A7, A9, \(\epsilon =10^{-6}\), \(m=10\)
Full size table