1 Introduction

In the conventional facility location problem each customer is associated with a single point in the space. Often in applications, the number of points is too large to consider them individually and the clients are combined in demand regions, see Dinler et al. [6]. In the basic problem considered in the present paper, we assume the transportation costs to a demand region are proportional to the shortest distance between any point in the region and the facility, also referred to as a center. The transportation costs within the demand region are negligible. While Brimberg and Wesolowsky [3] have used the same cost function with the regions being polytopes, we consider a special case where the demand regions are disks (balls) of radius \(R\ge 0\) and the distances are measured by a rectilinear norm, e.g., \(\ell _1\) or \(\ell _\infty \). Notice, under \(\ell _1\)- and \(\ell _\infty \)-norm a disk shape is not a conventional disk but a diamond and a square, respectively.

A special case of the problem with \(R=0\) and distances defined by the Euclidean norm \(\ell _2\) is the well-known geometric 1-median problem. It has been shown that for the geometric 1-median problem, neither a closed form formula, nor an exact algorithm involving only ruler and compass can be constructed, see Bajaj [1]. Kumar et al. [9] presented a randomized sampling algorithm, which for any \(\varepsilon >0\) with probability at least 1 / 2 finds a \((1+\varepsilon )\)-approximation to the geometric k-median problem in \(O(2^{{(k/\varepsilon )}^{O(1)}}dn)\) time, where d is the space dimension and n is the number of points. Very recently, Cohen et al. [5] presented a deterministic algorithm computing the geometric median to arbitrary precision in nearly linear time. For \(R=0\) and under \(\ell _1\)- or \(\ell _\infty \)-norm, Kalcsics et al. [7] constructed an algorithm solving the 1-median problem in \(O(n\log ^d n)\) time. In that work the authors utilized a general framework of Cohen and Megiddo [4] developed for minimization of a broad class of convex functions over polytopes.

In this paper we develop an exact algorithm for the single facility location problem with disk-shaped demand regions in \(\mathbb {R}^d\) under rectilinear distance measures. The running time of our exact algorithm matches the running time of the algorithm by Kalcsics et al. [7], but solves the problem for arbitrary \(R\ge 0\). Then, we generalize the algorithm to generic polyhedral norms.

2 Problem definition

First, we derive the results for the \(\ell _1\) norm. Let \(\rho (x) = \left\| x \right\| _1\) be the \(\ell _1\)-norm. Since a disk in \(\mathbb {R}^d\) under \(\ell _1\)-norm has a diamond shape, we refer to the disk-shaped demand regions as the diamond-shaped regions.

Given an input set \(X=\{ x_1,x_2, \ldots , x_n\}\subseteq \mathbb {R}^d\) and \(R\ge 0\), the single facility location problem (SFLP) with diamond-shaped regions is to find a center \(c \in \mathbb {R}^d\), which minimizes

$$\begin{aligned} f(c) = \sum _{i=1}^n \left( \rho (x_i-c) - R\right) _+, \end{aligned}$$
(1)

where \((x)_+ = \max \{0,x\},\ x\in \mathbb {R}\). This problem can be reformulated as a linear program as follows. Let index \(j\in \{1,2,\ldots ,d\}\) specify the jth coordinate of a point. Then, the linear program reads

$$\begin{aligned} \min _{c,y,z} \displaystyle \sum _{i=1}^n z_i \end{aligned}$$

subject to

$$\begin{aligned} y_{i,j}\ge & {} x_{i,j} - c_j, \quad \forall i\in \{1,2,\ldots ,n\},\ j\in \{1,2,\ldots ,d\}\\ y_{i,j}\ge & {} -x_{i,j} + c_j, \quad \forall i\in \{1,2,\ldots ,n\},\ j\in \{1,2,\ldots ,d\}\\ z_i\ge & {} \displaystyle \sum _{j=1}^n y_{i,j}-R, \quad \forall i\in \{1,2,\ldots ,n\},\\ z_i\ge & {} 0, \quad \forall i\in \{1,2,\ldots ,n\}, \end{aligned}$$

where for each data point \(i\in \{1,2,\ldots ,n\}\), variable \(y_{i,j}\) is the distance between c and \(x_i\) projected on the jth coordinate, and \(z_i\) is the distance between c and \(x_i\) minus R if this value is non-negative, otherwise it equals 0.

This linear program has \(nd+n+d\) variables and \(2nd+n\) constraints. Vaidya [14] have shown that the time needed to solve such a linear program is \(O((nd)^{2.5}L)\), where L is a parameter characterizing the constraint matrix. In this paper we introduce a simple combinatorial algorithm as an alternative to the solution of the above linear program. Moreover, our algorithm outperforms the classical linear programming algorithm.

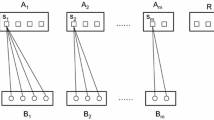
The idea of the algorithm is purely geometrical. First, we observe, that the objective function f(c) is convex and piecewise linear. Second, we can define polynomially many polytopal regions, such that the objective function is linear in each region; see Fig. 1 for an illustration of a two-dimensional case with four data points.Third, the algorithm runs a binary search in each dimension over these polytopal regions and finds an optimal solution.

Fig. 1
figure 1

Linear regions for \(d=2, n=4\)

Full size image

3 A two-dimensional \(\ell _1\) case

To simplify the presentation, we first describe the algorithm for the planar case, i.e. for \(d=2\). For one data point x, the basic division of the space into regions, where f is linear, is depicted in Fig. 2a. This basic drawing is centered at x. For the case of more than one data point, say for \(x_1, x_2,\dots , x_n\), we embed such basic drawings in the plane centering them at points \(x_1, x_2,\dots , x_n\) (Fig. 1), respectively. Similar to the graph drawing terminology, we call the union of the basic drawings an embedding. For simplicity of further calculations, we extend the line segments to the straight lines; see Fig. 2b. This creates a complex grid with two types of lines: vertical-horizontal and turned by 45\(^\circ \). Let a cell be an inclusion maximal polyhedron in the plane, not crossed by any line of the embedding. This is similar to a face of a planar graph embedding. Finally, we refer to the union of cells between any two consecutive parallel grid lines as a block of cells, see Fig. 2d.

Fig. 2
figure 2

Division of the space in linearity regions. a Linear regions, b Grid, c cell and d block of cells

Full size image

Notice, division of the space into the regions where the objective function is linear is very well-known approach in Location Theory, see e.g. [10,11,12,13]. These regions are often referred to as linearity regions, domains of linearity, or cells, see the above references. For simplicity, in this paper we follow the latter notion of cells introduced in Nickel et al. [12]. The most important property of the problem is that within any cell of the embedding the function f is linear. Therefore the evaluation of the function in any point of a cell takes only O(n) time.

In the two-dimensional case there are only four different line directions and, therefore, any cell has at most eight facets and eight vertices. Thus the evaluation of the function in all corner points of a cell takes O(n) time and finding a minimum in a cell also takes linear time. Despite the fact that there are in general \(O(n^2)\) cells and naive brute force would take cubic time, we are able to construct an almost linear time algorithm to the problem. Instead of enumerating over a quadratic number of cells, we run binary searches along four possible line directions, corresponding to four different types of blocks. Since the function f is convex, binary search correctly determines a cell containing a minimizer of the function. Binary search requires at most \(O(\log n)\) steps per line direction, making the total number of steps \(O(\log ^4 n)\) for the four line directions of any two-dimensional case. At each step of this high dimensional binary search, the function f is evaluated, making the overall computation time of the algorithm at most \(O(n\log ^4 n)\). Details on the algorithm are deferred to the next section where we discuss the more general high dimensional case.

4 Higher dimensions and polyhedral norms

4.1 Notation and definitions

Notice that under the \(\ell _1\)-norm for any \(x\in \mathbb {R}^d\) we have \(\rho (x) = \max _{a \in \{-1,1\}^d} a^T x\), where \(\{-1,1\}^d\) is the set of d-dimensional vectors consisting entries 1 and \(-1\). Therefore, we rewrite the objective function f as follows:

$$\begin{aligned} f(c) = \sum _{i=1}^n \left( \max _{a \in \{-1,1\}^d} a^T (x_i-c) - R\right) _+. \end{aligned}$$

Similar to the two-dimensional case, we define the notions of grid, cells and blocks in \(\mathbb {R}^d\). We first define the set of directions A, which is the set of orthogonal vectors to the norm defining hyperplanes. Let

$$\begin{aligned} A = \left\{ a \in \{ -1,0,1\}^d \ | \ a \ne \{0\}^d \text { and the first non-zero entry of } a \text { is }1 \right\} . \end{aligned}$$
(2)

Notice, \(|A|=(3^d-1)/2\). For simplicity of notations we assume all vectors in A are indexed: \(A=\{ a_1, a_2, \dots , a_{|A|}\}\). Let us remind that \(X=\{ x_1,x_2, \ldots , x_n\}\). For every vector \(a_k\in A\), we define

$$\begin{aligned} B_k = \left\{ b^k_1,b^k_2,\ldots ,b^k_{\left| B_k \right| }\right\} = \left\{ \begin{array}{ll} \left\{ a_k^T x \pm R \ | \ x \in X\right\} , &{}\quad \text {if } a_k \in \{-1,1\}^d; \\ \left\{ a_k^T x \ | \ x \in X\right\} , &{}\quad \text {otherwise,} \end{array}\right. \end{aligned}$$
(3)

being the set of positions/levels of the hyperplanes orthogonal to \(a_k\in A\). The intuition for the set \(B_k\) is that the hyperplanes \(a_k^T x = b_j^k,\ x\in \mathbb {R}^d,\ b_j^k\in B_k\), are the delimiters of the linearity regions (cells) in the space, and these hyperplanes will be used in the construction of the high dimensional grid, blocks and cells, similarly to the two-dimensional case in Sect. 3. Again, without loss of generality, assume \(b^k_1 \le b^k_2 \le \cdots \le b^k_{\left| B_k \right| }\), otherwise we sort the positions in the preprocessing step in \(O(n\log n)\) time. For convenience, let us introduce \(b_0^k = -\infty \) and \(b_{\left| B_k \right| +1}^k = + \infty \). Now, we define the grid, cells and blocks of cells for a general high dimensional case.

Definition 1

The hyperplanes \(\left\{ x \in \mathbb {R}^d\ |\ a_k^T x = b_j^k,\ a_k\in A,\ b_j^k\in B^k \right\} \) form the grid. A cell is an inclusion maximal polyhedron in \(\mathbb {R}^d\) not crossed by a grid hyperplane. A set of indices \(\{j_1,j_2,\dots ,j_{\left| A \right| }\}\), where \(j_k\in \{0,1, \ldots , \left| B_k \right| +1\}\) for any \(k\in \{1, 2, \ldots , |A|\}\), completely specifies the cell:

$$\begin{aligned} C(0;j_1,j_2,\dots ,j_{\left| A \right| }) = \left\{ x \in \mathbb {R}^d\ | \ b_{j_k}^k \le a_k^T x \le b_{j_k+1}^k,\ a_k\in A \right\} . \end{aligned}$$
(4)

Leaving out l constraints in the definition of a cell, we arrive at the definition of a block of cells parameterized by l:

$$\begin{aligned} C(l;j_{1},j_2,\dots ,j_{\left| A \right| -l})= & {} \left\{ x \in \mathbb {R}^d \ | \ b_{j_k}^k \le a_k^T x \le b_{j_{k+1}}^k\text { for any }\right. \nonumber \\&\left. k \in \{ 1,2,\dots , \left| A \right| -l\} \right\} . \end{aligned}$$
(5)

4.2 Observations

The following observations are necessary ingredients of the algorithm and its further analysis. First of all, notice that for any cell C and for any \(x\in X\), either the cell is within the range R from x and then

$$\begin{aligned} \left( \max _{a \in \{ -1,1\}^d} a^T (c-x)-R\right) _+ = 0,\quad \forall c \in C, \end{aligned}$$
(6)

or there exists a vector \(a_0 \in \{ -1, 1\}^d\) such that

$$\begin{aligned} \left( \max _{a \in \{ -1,1\}^d} a^T (c-x)-R\right) _+ = {a_0}^T (c-x)-R,\quad \forall c \in C. \end{aligned}$$
(7)

In other words, every individual contribution of a data point \(x\in X\) to the objective function f is linear in any cell C. As the sum of linear functions is a linear function, f is linear in any cell C.

The second observation is that every individual contribution of a data point \(x\in X\) to the objective function f is convex as it is a maximum of two linear functions. Since the sum of convex functions is convex, the function f is convex.

The third observation is that for any cell C the minimum of f over C can be found in \(O(d n + d^{4.5} 3^d)\) time. By linearity of the function f within a cell, we have to compute d coefficients of that linear function. Computation of any coefficient requires at most O(n) time. Thus, specification of the linear objective function in a cell is obtained in O(dn) time. Then, solving the linear program minimizing f on polyhedron cell C takes at most \(O(d^{4.5} 3^d)\) time, e.g., using Karmarkar’s Algorithm [8].

4.3 High dimensional recursive binary search algorithm

Now, we are ready to present the algorithm and to analyze its running time.

figure a

Theorem 1

Algorithm 1 returns an optimal solution \(c^* \in \mathbb {R}^d\) to the single facility location problem with diamond-shaped regions in \(O\left( d n\log ^{3^d} n+d^{4.5} 3^d\log ^{3^d} n \right) \) time.

Proof

By convexity of the function f, the binary search correctly computes the minimum objective function values and the corresponding solution points in the blocks of cells. Given that the binary search for a single parameter q takes at most \(O(\log n)\) time and the recursion depth in the algorithm is at most \(3^d\), we have that the binary search takes \(O(\log ^{3^d} n)\) steps in total. In every leaf of the binary search tree, the algorithm evaluates a minimum of the function f in a cell. By the observation above, this evaluation is done by solving a linear program in \(O(d n + d^{4.5} 3^d)\) time. Hence, the claimed time complexity follows. \(\square \)

Algorithm 1 works also for \(l_\infty \) and for more general polyhedral norms. We use the definition of a polyhedral norm as in Barvinok et al. [2]. Let P be a centrally symmetric bounded polyhedron in \(\mathbb {R}^d\) with the origin in its center. By symmetry, the number of facets is even. Let the number of facets be 2m. Then, there is a set \(H_P=\{h_1,h_2,\ldots ,h_m\}\) of points in \(\mathbb {R}^d\) such that P is the intersection of a collection of half-spaces defined by \(H_P\):

$$\begin{aligned} P=\left( \bigcap _{i=1}^m\{x\in \mathbb {R}^d|\ h_i^T x\le 1\}\right) \cap \left( \bigcap _{i=1}^m\{x\in \mathbb {R}^d|\ h_i^T x\ge -1\}\right) . \end{aligned}$$

Then, the polyhedral norm is defined by \(\rho (x)=\max _{1\le i\le m}|h_i^T x|\). For instance, for \(\ell _1\) in \(\mathbb {R}^2\) we can take \(H_P=\{(1,1),(-1,1)\}\) and for \(\ell _\infty \) in \(\mathbb {R}^2\) we can take \(H_P=\{(0,1),(1,0)\}\).

For a polyhedral norm, the only adjustment we have to make in the Algorithm 1 is to generalize sets A and B in the definition of the grid. For this generalization, let

$$\begin{aligned} A_1 = \left\{ \pm h_i|\ h_i\in H_P,\ 1\le i\le m\right\} , \end{aligned}$$
(8)
$$\begin{aligned} A_2= \left\{ h_i-h_j|\ h_i,h_j\in H_P,\ 1\le i,j\le m,\ i\ne j\right\} , \end{aligned}$$
(9)
$$\begin{aligned} A=A_1\cup A_2. \end{aligned}$$
(10)

Again, we assume all vectors in A are indexed: \(A=\{ a_1, a_2, \dots , a_{|A|}\}\). For every vector \(a_k\in A\), we define

$$\begin{aligned} B_k = \left\{ b^k_1,b^k_2,\ldots ,b^k_{\left| B_k \right| }\right\} = \left\{ \begin{array}{ll} \left\{ a_k^T x \pm R \ | \ x \in X\right\} , &{}\quad \text {if } a_k\in A_1; \\ \left\{ a_k^T x \ | \ x \in X\right\} , &{}\quad \text {if } a_k\in A_2. \end{array} \right. \end{aligned}$$
(11)

Now, to adjust Algorithm 1 to a generic polyhedral norm we define the grid by the sets A and \(B_k,\ a_k\in A\), according to the definitions (10) and (11). The rest of the algorithm remains intact.

Finally, let us estimate the run-time of Algorithm 1 adjusted to a polyhedral norm. The new set A determines the types of the grid hyperplanes. For each \(a_k\in A\) the set \(B_k\) determines all hyperplanes of type \(a_k\). Notice, \(|A|=O(m^2)\) as the size of \(A_2\) is quadratic in the number of facets. By definition, for every \(a_k\in A\), the size of the set \(B_k\) is at most 2n. Thus, the number of grid cells created in this construction is \(n^{O(m^2)}\). Using the adjusted number of grid cells and following literally the same arguments as in Theorem 1, we generalize the result as follows.

Theorem 2

Under a polyhedral norm determined by a polyhedron with 2m facets, the adjusted Algorithm 1 returns an optimal solution \(c^* \in \mathbb {R}^d\) to the single facility location problem with disk-shaped demand regions in \(O\left( (d n+d^{4.5} m^2)\log ^{O(m^2)}n\right) \) time.

Since \(2m\ge d+1\) for any bounded polyhedron in \(\mathbb {R}^d\), we have the following straightforward corollary:

Corollary 1

Under a polyhedral norm determined by a polyhedron with 2m facets, the adjusted Algorithm 1 returns an optimal solution to the single facility location problem with disk-shaped demand regions in \(O\left( (m n+m^{6.5})\log ^{O(m^2)}n\right) \) time.