Comparative study of RPSALG algorithm for convex semi-infinite programming

Abstract

The Remez penalty and smoothing algorithm (RPSALG) is a unified framework for penalty and smoothing methods for solving min-max convex semi-infinite programing problems, whose convergence was analyzed in a previous paper of three of the authors. In this paper we consider a partial implementation of RPSALG for solving ordinary convex semi-infinite programming problems. Each iteration of RPSALG involves two types of auxiliary optimization problems: the first one consists of obtaining an approximate solution of some discretized convex problem, while the second one requires to solve a non-convex optimization problem involving the parametric constraints as objective function with the parameter as variable. In this paper we tackle the latter problem with a variant of the cutting angle method called ECAM, a global optimization procedure for solving Lipschitz programming problems. We implement different variants of RPSALG which are compared with the unique publicly available SIP solver, NSIPS, on a battery of test problems.

Appendix: performance profiles

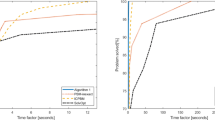
The benchmark results are generated by running the three solvers to be compared on the collection of problems gathered in the SIPAMPL database and recording the information of interest, in this case the number of function evaluations (as it is independent of the available hardware). In this paper we use the notion of performance profile due to Dolan and Moré [14]) as a tool for comparing the performance of a set of solvers $\mathcal {S}$ on a test set $\mathcal {P}$. For each couple $({ p}, { s})\in \mathcal {P\times S}$ we define

$$\begin{aligned} f_{{ p},{ s}}:= \text {number of function evaluations required to solve problem}\; p\; \text {by solver}\; s. \end{aligned}$$

Let ${ p}\in \mathcal {P}$ be a problem solvable by solver ${ s}\in \mathcal {S}$. We compare the performance on problem ${ p}$ of solver ${ s}$ with the best performance of any solver on the same problem by means of the performance ratio

$$\begin{aligned} r_{{ p},{ s}}:=\frac{f_{{ p},{ s} }}{\min \{f_{{ p},{ s}}:~{ s}\in \mathcal {S} \}}\ge 1, \end{aligned}$$

with $r_{{ p},{ s}}=1$ if and only if $s$ is a winner for $p$ (i.e. it is at least as good, for solving $p,$ as any other solver of $\mathcal {S}$). We also define $r_{{ p},{ s}}=r_{M}$ when solver ${ s}$ does not solve problem ${ p},$ where $r_{M}$ is some scalar greater than the maximum of the performance ratios$r_{{ p},{ s}}$ of all couples $( { p},{ s})\in \mathcal {P\times S}$ such that ${ p}$ is solved by solver ${ s}.$ The choice of $r_{M}$ does not affect the performance evaluation.

The performance of solver ${ s}$ on any given problem may be of interest, but we would like to obtain an overall assessment of the performance of the solver. To this aim, we associate with each ${ s}\in \mathcal {S}$ a function $\rho _{{ s}}:\mathbb {R} _{+}\rightarrow [0,~1],$ called performance profile of $s,$ defined as the ratio

$$\begin{aligned} \rho _{{ s}}(t)=\frac{\text { size}\{{ p}\in \mathcal {P} :~r_{{ p},{ s}}\le t\}}{\text { size}\mathcal {P}}, \text { }t\ge 0. \end{aligned}$$

Obviously, $\rho _{{ s}}$ is a stepwise non-decreasing function such that $\rho _{{ s}}\left( t\right) =0$ for all $t\in [ 0,1[$ and $\rho _{{ s}}(1)$ is the relative frequency of wins of solver $s$ over the rest of the solvers. If $p$ is taken at random from $\mathcal {P},$ then $r_{{ p},{ s}}$ can be interpreted as a random variable and $\rho _{{ s}}(1)$ as the probability of solver $s$ to win over the rest of the solvers while, for $t>1,$ $\rho _{{ s}}(t)$ represents the probability for solver ${ s}\in \mathcal {S}$ that a performance ratio $r_{{ p}, { s}}$ is within a factor $t\in \mathbb {R}$ of the best possible ratio. So, in probabilist terms, $\rho _{{ s}}$ can be seen as a distribution function.

The definition of the performance profile for large values requires some care. We assume that $r_{{ p},{ s}}\in [1,r_{M}]$ and that $r_{{ p},{ s}}=r_{M}$ only when problem ${ p}$ is not solved by solver ${ s}$. As a result of this convention, $\rho _{{ s}}(r_{M})=1$, and the number

$$\begin{aligned} \rho _{{ s}}^{*}:=\lim _{t\searrow r_{M}}\rho _{{ s} }(t) \end{aligned}$$

is the probability that the solver ${ s}\in \mathcal {S}$ solves problems of $\mathcal {P}$.

Choosing a best solver for $\mathcal {P}$ is a bicriteria decision problem, the objectives being the probability of winning and the probability of solving a problem, i.e.

$$\begin{aligned} ``{\min }\hbox {''} \left\{ \left( \rho _{{ s}}(1),\rho _{{ s}}^{*}\right) :s\in \mathcal {S }\right\} . \end{aligned}$$

Performance profiles are relatively insensitive to changes in results on a small number of problems. Additionally, they are also largely unaffected by small changes in results over many problems.