A linear-time approximate convex envelope algorithm using the double Legendre–Fenchel transform with application to phase separation

Abstract

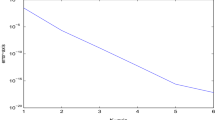
We study the double discrete Legendre–Fenchel transform (LFT) to approximate the convex envelope of a given function. We analyze the convergence of the double discrete LFT in the multivariate case based on previous convergence results for the discrete LFT. We focus our attention on the grid on which the second discrete LFT is computed (dual grid); its choice has great impact on the accuracy of the resulting approximation of the convex envelope. Then, we present an improvement (both in time and accuracy) to the standard algorithm based on a change in the factorization order for the second discrete LFT. This modification is particularly beneficial for bivariate functions. Moreover, we introduce a method for handling functions that are unbounded outside sets of general shape. We also present some situations in which the selection of the dual grid is crucial, and show that it is possible to choose a dual grid of arbitrary size without increasing the memory requirements of the algorithm. Finally, we apply our algorithm to the study of phase separation in non-ideal ionic solutions.

Appendix: Treatment of non-rectangular domains

The double discrete LFT algorithms operate naturally on rectangular computational domains discretized by a Cartesian grid. But since every function can be extended by setting its value to $+\infty$ where it is not defined, we should be able to treat inside this framework functions defined on sets of arbitrary shape. Unfortunately, as observed in Remark 1, the double discrete LFT is always finite everywhere and thus every information about the domain shape is lost.

The problem lies in the fact that the information about the domain shape is encoded in the behavior at infinity of the LFT. Consider for example a one-dimensional function $f$ which is finite on the interval $[l,r]$ and $+\infty$ elsewhere. Its discrete LFT $f^*_{X_N}$ is a piecewise linear function whose domain is the whole real line and whose first and last slopes, which extend all the way to $\mp \infty$, are respectively $l$ and $r$. If we apply the continuous LFT to $f^*_{X_N}$, we obtain again a function which is defined on $[l,r]$ and $+\infty$ elsewhere. On the other hand, by applying a discrete LFT to $f^*_{X_N}$, we use its values in only a finite number of points and suppose that it is $+\infty$ elsewhere, which produces again a function defined on the whole real line. In order to reconstruct the correct domain, it is sufficient to keep in memory the values of the external slopes of $f^*_{X_N}$.

In the two-dimensional case, we similarly have to preserve the external slope information of the first discrete LFT in order to obtain the correct domain after the second discrete LFT. Using the modified algorithm simplifies the matter because we only have one set of slopes to consider since there are only two passes of one-dimensional discrete LFTs; however, because of the pass of convex envelopes between them, these slopes change before the last pass. This is reasonable since the convex envelope can make the domain of finiteness of a function grow.

Using the notation of Sect. 4.2, in order to compute the slopes after the convex envelope pass, we have to determine which points of $Y_N$ belong asymptotically for $\xi \rightarrow \pm \infty$ to the convex envelope ${{\mathrm{conv}}}\left[ \left( -g(\xi ,\cdot )\right) _{Y_{N}}\right]$. This can be done in a similar way to the computation of the standard one-dimensional convex envelope by taking into account also the slopes obtained in the first pass of discrete LFTs. We explain explicitly only the case $\xi \rightarrow \infty$; the other case can be treated in exactly the same way by inverting the $\xi$-axis. Let $y_{i}$, $i=1,\ldots ,N$ be the points of the grid $Y_{N}$. Fixed $i$, the function $-g(\cdot ,y_{i})$ is a piecewise linear function whose slope has a constant value $s_{i}$ after a certain value $\xi _{i}$ on the $\xi$-axis. Take $\xi _{0}=\max _{i}\xi _{i}$. For simplicity, given $\xi >\xi _{0}$, denote the value $-g(\xi ,y_{i})$ by $z_{i}(\xi )$; we have that $z_{i}(\xi )=z_{i}(\xi _{0})+s_{i}(\xi -\xi _{0})$ and that the slopes $c_{ij}(\xi )$ between the nodes $x_{i}$ and $x_{j}$ are

$$\begin{aligned} c_{ij}(\xi )=\frac{z_{j}(\xi )-z_{i}(\xi )}{x_{j}-x_{i}}=\frac{z_{j} (\xi _{0})-z_{i}(\xi _{0})+(s_{j}-s_{i})(\xi -\xi _{0})}{x_{j}-x_{i}}. \end{aligned}$$

(5)

The convex hull of the piecewise linear function having nodes $y_{i}$ and values $z_{i}(\xi )$ with $i=1,\ldots ,N$ is given by interpolating only a subset of the nodes. This subset depends on $\xi$, but we will now show that there exists $\xi _{r}\ge \xi _{0}$ such that the subset remains constant for $\xi \ge \xi _{r}$; we will denote by $i_{k}^{*}$, $k=1,\ldots ,M$, with $M\le N$, these nodes.

We have that $i_{1}^{*}=1$ since the first node always belongs to the convex hull nodes for every $\xi$ (similarly we also have $i_{M}^{*}=N$). Given $i_{k}^{*}$, the next value $i_{k+1}^{*}$ can be computed in the following way. Neglecting the grid points $x_{i}$ with $i<i_{k}^{*}$ and supposing that $x_{i_{k}^{*}}$ is in the convex hull, the next node in the convex hull at $\xi$ is ${{\mathrm{arg\ min}}}_{j=i_{k}^{*}+1,\ldots ,N}c_{i_{k}^{*}j}(\xi )$. Since $c_{i_{k}^{*}j}(\xi )$ are affine as functions of $\xi$, there is $\xi _{k+1}^{*}\ge \xi _{0}$ such that the minimizer will be the same for all $\xi >\xi _{k+1}^{*}$. This value is $i_{k+1}^{*}$ and from (5) we have that $i_{k+1}^{*}={{\mathrm{arg\ min}}}_{j=i_{k}^{*}+1,\ldots ,N}\frac{s_{j}-s_{i_{k}^{*}}}{x_{j}-x_{i_{k}^{*}}}$. In the case of the minimum being assumed by more than one value of $j$ we choose the one for which $\frac{z_{j}(\xi _{0})-z_{i_{k}^{*}}(\xi _{0})}{x_{j}-x_{i_{k}^{*}}}$ is the smallest; in case of a further draw, we can take the point for which $x_{j}$ is larger. If $i_{k+1}^{*}=N$, then $M=k+1$ and all values have been computed.

The value $\xi _{k+1}^{*}$ is the first value of $\xi$ for which

$$\begin{aligned} c_{i_{k}^{*}i_{k+1}^{*}}(\xi )\le c_{i_{k}^{*}j}(\xi )\quad \text {for every }j>i_{k}^{*}; \end{aligned}$$

by substituting (5) and solving these linear inequalities we obtain that

$$\begin{aligned} \xi _{k+1}^{*}=\xi _{0}+\max _{\begin{array}{c} j>i_{k}^{*}\\ j\ne i_{k+1}^{*} \end{array}}\frac{\frac{z_{i_{k+1}^{*}}(\xi _{0}) -z_{i_{k}^{*}}(\xi _{0})}{x_{i_{k+1}^{*}}-x_{i_{k}^{*}}} -\frac{z_{j}(\xi _{0})-z_{i_{k}^{*}}(\xi _{0})}{x_{j} -x_{i_{k}^{*}}}}{\frac{s_{j}-s_{i_{k}^{*}}}{x_{j} -x_{i_{k}^{*}}}-\frac{s_{i_{k+1}^{*}} -s_{i_{k}^{*}}}{x_{i_{k+1}^{*}}-x_{i_{k}^{*}}}}. \end{aligned}$$

Taking $\xi _{r}=\max _{k=1,\ldots ,M}\xi _{k}^{*}$ (where we put $\xi _{1}^{*}=\xi _{M}^{*}=\xi _{0}$), we have that the convex hull nodes are given by $(i_{k}^{*})_{k=1,\ldots ,M}$ for all $\xi >\xi _{r}$. The functions ${{\mathrm{conv}}}\left[ \left( -g(\xi ,\cdot )\right) _{Y_{N}}\right] (y_{i})$, $i=1,\ldots ,N$, when $\xi >\xi _{r}$ are given by the formulas

$$\begin{aligned} {\left\{ \begin{array}{ll} z_{i}(\xi ) &{}\quad \text {if }i=i_{k}^{*}\text { for some }k,\\ \alpha z_{i_{k}^{*}}(\xi )+(1-\alpha )z_{i_{k+1}^{*}}(\xi ) &{}\quad \text {if }i_{k}^{*}<i<i_{k+1}^{*}\text { for some }k; \end{array}\right. } \end{aligned}$$

by substituting the $z_{i}$, we can easily get their slopes as functions of $s_{i}$.

In this way we obtain the interval $[\xi _l,\xi _r]$ outside which the points of $Y_N$ belonging to the convex envelope do not change anymore and we obtain the external slopes of ${{\mathrm{conv}}}\left[ \left( -g(\xi ,\cdot )\right) _{Y_{N}}\right] (y)$ as a function of $\xi$ for every $y\in Y_N$. Then, by discretizing $[\xi _l,\xi _r]$ and using the obtained slopes, we can compute the final pass of discrete LFTs recovering the correct shape of the domain. We finally observe that this improvement to the algorithm can also be seen as a further enlargement of the dual set; in particular, the function we are computing is $\left( f_{\varOmega _{N}}^{*}\right) _{(]-\infty ,\xi _l[\cup C_{M} \cup ]\xi _r,+\infty [)\times \mathbb {R}}^{*}$, where $C_M$ is a discretization of $[\xi _l,\xi _r]$; by applying the symmetrization, we can then compute the double LFT with a dual set $S_M$ such that $\mathbb {R}^2\setminus S_M$ is bounded.