1 Introduction

The classical conjugate gradient (CG) method with line search is as follows:

$$ x_{k+1} = x_k + \alpha_k d_k, $$
(1)

where the directions d k is given by

$$ \left \{ \begin{array}{l@{\quad}l} d_1=-g_1,\\ d_{k+1}=-g_{k+1}+\beta_k d_k, & \forall k \ge1 , \end{array} \right . $$
(2)

where g k =g(x k )=∇f(x k ). The different choices for the parameter β k correspond to different CG methods, such as HS method [15], FR method [7], PRP method [22, 23], LS method [16], PRP+ method [8], DY method [5] and so on. On the history of the conjugate gradient method, there are several survey articles, such as [11].

In [17], the Perry conjugate gradient algorithm [21] was generalized and the line search directions were formulated as follows:

$$ \left \{ \begin{array}{l@{\quad}l} d_1=-g_1,\\ d_{k+1}= - P_{k+1}g_{k+1}=-g_{k+1}+\frac{y_k^{\mathrm {T}}g_{k+1}}{s_k^{\mathrm{T}}y_k}s_k -\sigma\frac{s_k^{\mathrm{T}}g_{k+1}}{y_k^{\mathrm{T}} u_k}u_k, & \forall k>1 , \end{array} \right .$$
(3)

where s k =x k+1−x k =α k d k , y k =g k+1−g k , α k is the steplength of the line search and σ is a preset parameter,

$$ P_{k+1}= \biggl(I- \frac{s_ky_k^{\mathrm{T}}}{s_k^{\mathrm{T}}y_k}+\sigma\frac {u_k s_k^{\mathrm{T}}}{y_k^{\mathrm{T}} u_k} \biggr), $$
(4)

which is called Perry iteration matrix, and the vector u k is any vector in \(\mathbb{R}^{n}\) such that \(y_{k}^{T}u_{k}\ne0\). In the paper [17], the case u k =y k was discussed. When u k =s k , the CG_DESCENT algorithm [10–12] can be deduced and the D-L method [4] can be derived from the restriction σ>0. Recently, we also studied the case u k =s k in [19] and presented a RSPDCGs algorithm.

In this paper, a family of symmetric Perry conjugate gradient methods is proposed, that is, the line search directions are formulated by

$$ \left \{ \begin{array}{l@{\quad}l} d_1 =-g_1,\\ \begin{aligned} d_{k+1} &= -Q_{k+1}g_{k+1} = -g_{k+1}+\beta_k d_k+\gamma_k y_k,& \forall k\ge1 \\ &= -g_{k+1} +\tfrac{s_k^{\mathrm{T}}g_{k+1}}{s_k^{\mathrm{T}}y_k}y_k + \bigl[\tfrac{y_k^{\mathrm{T}}g_{k+1}}{s_k^{\mathrm{T}}y_k}- \bigl( \sigma+\tfrac{y_k^{\mathrm{T}}y_k}{s_k^{\mathrm{T}}y_k} \bigr) \tfrac{s_k^{\mathrm{T}}g_{k+1}}{s_k^{\mathrm{T}}y_k} \bigr]s_k,&\forall k\ge1 \end{aligned} \end{array} \right . $$
(5)

where \(\beta_{k}=\frac{y_{k}^{\mathrm{T}}g_{k+1}}{d_{k}^{\mathrm{T}}y_{k}}- ( \alpha_{k}\sigma+\frac{y_{k}^{\mathrm{T}}y_{k}}{d_{k}^{\mathrm {T}}y_{k}} ) \frac{d_{k}^{\mathrm{T}}g_{k+1}}{d_{k}^{\mathrm{T}}y_{k}}\), \(\gamma _{k}=\frac {d_{k}^{\mathrm{T}}g_{k+1}}{d_{k}^{\mathrm{T}}y_{k}}\) and

(6)

which is called the symmetric Perry iteration matrix. When \(\sigma y_{k}^{\mathrm{T}} s_{k}>0\), for any line search, the directions defined by (5) satisfy the descent property [1]

$$ d_{k+1}^{\mathrm{T}}g_{k+1} < 0, $$
(7)

or the sufficient descent property [8]

$$ d_{k+1}^{\mathrm{T}}g_{k+1} \le-c_0 \|g_{k+1}\|^2\quad (c_0 >0). $$
(8)

This paper is organized as follows. In Sect. 2, first, the family of the symmetric Perry conjugate gradient methods is deduced. Then the spectra of the iteration matrix are analyzed, so, its sufficient descent property is proved and several concrete algorithms are proposed. In Sect. 3, the scaling technology and the restarting strategy are applied to the symmetric Perry conjugate gradient methods, thus, a family of scaling Perry conjugate gradient methods with restarting procedures is developed. In Sect. 4, the global convergence of the two families of the new methods with the Wolfe line searches is proven by the spectral analysis of the conjugate gradient iteration matrix. In Sect. 5, the preliminary numerical results are reported. A remark for further research is given in Sect. 6.

2 The symmetric Perry conjugate gradient method

In [21], A. Perry changed the CG update parameter β k of the HS conjugate gradient method [15] into \(\beta_{k}^{P}=\frac{(y_{k}-s_{k})^{\mathrm{T}}g_{k+1}}{y_{k}^{\mathrm{T}} d_{k}}\), and formulated the line search directions

$$ d_{k+1} =-g_{k+1}+\beta_k^P d_k= -Q_{k+1}g_{k+1},\quad k=1,2,\ldots, $$

and

$$ y_k^{\mathrm{T}} d_{k+1} = -s_k^{\mathrm{T}} g_{k+1}, $$
(9)

where

$$ Q_{k+1} =D_{k+1}+\frac{s_ks_k^{\mathrm {T}}}{y_k^{\mathrm{T}} s_k} \quad \mbox{and}\quad D_{k+1} = \biggl(I-\frac{s_ky_k^{\mathrm {T}}}{s_k^{\mathrm{T}}y_k} \biggr). $$
(10)

In [17], (10) and (9) were substituted by

$$ Q_{k+1}= D_{k+1}+uv^{\mathrm{T}} $$
(11)

and

$$ y_k^{\mathrm{T}} d_{k+1} = -\sigma s_k^{\mathrm{T}} g_{k+1}, $$
(12)

respectively, where \(u,v\in\mathbb{R}^{n}\) and σ is a parameter. Thus, it is follows from (11), (12) and d k+1=−Q k+1 g k+1 that \((\sigma s_{k} - vy_{k}^{\mathrm {T}}u)^{\mathrm{T}} g_{k+1}=0\), which yields \(v= \frac{\sigma s_{k}}{y_{k}^{\mathrm{T}}u} \). So,

$$ Q_{k+1}= \biggl(I-\frac {s_ky_k^{\mathrm{T}}}{s_k^{\mathrm{T}}y_k}+ \sigma\frac{u s_k^{\mathrm{T}}}{y_k^{\mathrm{T}} u} \biggr), $$
(13)

from which the generalized Perry conjugate gradient method ((1) and (3)) can be obtained [17].

In this paper, we choose a suitable u such that Q k+1 is a symmetric matrix, thus the line search directions d k may satisfy (7) or (8). Let \(Q_{k+1}=Q_{k+1}^{\mathrm{T}}\), then

$$ \biggl(\frac{y_k}{s_k^{\mathrm{T}}y_k}+\sigma\frac{u}{y_k^{\mathrm{T}} u} \biggr)s_k^{\mathrm{T}} = s_k \biggl(\frac{y_k}{s_k^{\mathrm{T}}y_k}+\sigma\frac {u}{y_k^{\mathrm {T}} u} \biggr)^{\mathrm{T}}. $$

Therefore, the vector u can be taken as

$$ u =a \biggl( \frac{\sigma s_k^{\mathrm{T}}y_k+y_k^{\mathrm{T}}y_k}{(s_k^{\mathrm {T}}y_k)^2}s_k-\frac{1}{s_k^{\mathrm{T}}y_k}y_k \biggr)\quad (a\ne0), $$
(14)

and u T y k =aσ. We note that the matrix Q k+1 defined by (13) is independent of the nonzero constant a, so, we can choose a=1. Thus, from (13) and (14) we can obtain the matrix Q k+1 defined by (6).

The method formulated by (1) and (5) is called the symmetric Perry conjugate gradient method, denoted by SPCG. And the directions generated by (5) are called the symmetric Perry conjugate gradient directions, which will be proven to be descent directions in Sect. 2.2.

From the above discussions, a family of new nonlinear conjugate gradient algorithms can be obtained as follows:

Algorithm 1

(SPCG)

Step 1.:

Give an initial point x 1 and ε≥0. Set k=1.

Step 2.:

Calculate g 1=g(x 1). If ∥g 1∥≤ε then stop, otherwise let d 1=−g 1.

Step 3.:

Calculate steplength α k with line searches.

Step 4.:

Set x k+1=x k +α k d k .

Step 5.:

Calculate g k+1=g(x k+1). If ∥g k+1∥≤ε then stop.

Step 6.:

Calculate the directions d k+1 via (5) with different σ.

Step 7.:

Set k=k+1, then go to step 3.

Remark 1

In this paper, to ensure the convergence of the algorithm, we adopt the Wolfe line search strategies:

$$ f(x_k+\alpha_kd_k) \leq f(x_k)+b_1\alpha_k d_k^{\mathrm{T}}g_k $$
(15)

and

$$ d_k^{\mathrm{T}}g(x_k+ \alpha_kd_k) \ge b_2d_k^{\mathrm{T}}g_k, $$
(16)

where 0<b 1<b 2<1. The stopping criterion, ∥g k ∥≤ε, can be changed into other forms. For the different choices of σ, several concrete forms of the algorithm will be discussed in the Sect. 2.2.

2.1 Spectral analysis

Here, we analyze the spectra of the Perry matrix and the symmetric Perry matrix.

Theorem 1

Let P k+1 be defined by (4). Then when \(\sigma (y_{k}^{\mathrm{T}} s_{k})\ne0\), P k+1 is a nonsingular matrix and the eigenvalues of P k+1 consist of 1 (n−2 multiplicity), \(\lambda_{\,1}^{k+1}\) and \(\lambda_{2}^{k+1}\), where

(17)

and

(18)

Proof

From the fundamental algebra formula

$$ \det\bigl(I+xy^{\mathrm{T}}+uv^{\mathrm{T}}\bigr)= \bigl(1+y^{\mathrm {T}}x\bigr) \bigl(1+v^{\mathrm{T}}u\bigr)- \bigl(x^{\mathrm{T}}v\bigr) \bigl(y^{\mathrm{T}}u\bigr), $$

it follows that

$$ \det(P_{k+1})=\det\biggl(I-\frac{s_ky_k^{\mathrm {T}}}{s_k^{\mathrm {T}}y_k}+ \frac{\sigma u_ks_k^{\mathrm{T}}}{y_k^{\mathrm{T}} u_k} \biggr) = \sigma\frac{s_k^{\mathrm{T}}s_k}{y_k^{\mathrm{T}} s_k}. $$
(19)

Therefore, the Perry matrix (4) is a nonsingular matrix when \(\sigma y_{k}^{\mathrm{T}} s_{k} \ne0\).

Since \(\forall\xi\in\mathrm{span} \{s_{k},y_{k}\}^{\perp}\subset \mathbb{R}^{n}\),

the matrix P k+1 has the eigenvalue 1 (n−2 multiplicity), corresponding to the eigenvectors ξ∈span{s k ,y k }⊥.

By the relationships between the trace and the eigenvalues of matrix and between the determinant and the eigenvalues of matrix, the other two eigenvalues are the roots of the following quadratic polynomial

$$ \lambda^2 - \biggl(1+\sigma\frac {s_k^{\mathrm{T}}u_k}{y_k^{\mathrm{T}} u_k} \biggr)\lambda+ \sigma\frac{s_k^{\mathrm{T}}s_k}{y_k^{\mathrm {T}} s_k}=0. $$
(20)

Thus, the other two eigenvalues are determined by (17) and (18), respectively. □

According to Theorem 1, the following theorem for the symmetric Perry matrix Q k+1 defined by (6) can be deduced.

Theorem 2

Let \(\lambda_{\mathrm{min}}^{(k+1)}\) and \(\lambda_{\mathrm{max}}^{(k+1)}\) be the minimum and maximum eigenvalues of Q k+1, respectively, where Q k+1 is defined by (6). If \(\sigma(y_{k}^{\mathrm{T}} s_{k})> 0\), then

(21)
(22)
(23)

and

$$ \lambda_{\mathrm{min}}^{(k+1)}\le\sigma \frac{s_k^{\mathrm{T}}s_k}{s_k^{\mathrm {T}}y_k}\le\max\biggl\{\omega_k,\omega_k+\sigma \frac{s_k^{\mathrm {T}}s_k}{s_k^{\mathrm{T}}y_k}-1\biggr\}\le\lambda_{\mathrm{max}}^{(k+1)}, $$
(24)

where \(\omega_{k}=\frac{y_{k}^{\mathrm{T}}y_{k}s_{k}^{\mathrm {T}}s_{k}}{(s_{k}^{\mathrm{T}}y_{k})^{2}}\). Moreover, Q k+1 is a symmetric positive definite matrix when \(\sigma (y_{k}^{\mathrm{T}} s_{k})>0\).

Proof

When \(\sigma(y_{k}^{\mathrm{T}} s_{k})> 0\), from (14), (17), (18) and the following relations:

$$ \biggl(\omega_k+\sigma \frac{s_k^{\mathrm{T}}s_k}{s_k^{\mathrm {T}}y_k} \biggr)^2 -4\sigma\frac{s_k^{\mathrm{T}}s_k}{y_k^{\mathrm {T}} s_k}= \biggl( \omega_k-\sigma\frac{s_k^{\mathrm{T}}s_k}{s_k^{\mathrm{T}}y_k} \biggr)^2+4\sigma( \omega_k-1)\frac{s_k^{\mathrm{T}}s_k}{s_k^{\mathrm{T}}y_k}\ge0, $$
(25)

it can be proven that \(\lambda_{\mathrm{min}}^{(k+1)}\) and \(\lambda _{\mathrm{max}}^{(k+1)}\) are formulated by (21) and (22), respectively.

Simple calculation claims that

and

(26)

So, the inequality (26) implies that

In addition, it follows from (25) that

$$ \lambda_{\mathrm{max}}^{(k+1)} \ge\frac{1}{2} \biggl( \omega_k+\sigma\frac{s_k^{\mathrm {T}}s_k}{s_k^{\mathrm{T}}y_k} +\biggl \vert \omega_k- \sigma\frac{s_k^{\mathrm{T}}s_k}{s_k^{\mathrm {T}}y_k}\biggr \vert \biggr)\ge\omega_k. $$

Therefore, \(\lambda_{\mathrm{max}}^{(k+1)}\ge \max\{\omega_{k},\omega_{k}+\sigma\frac{s_{k}^{\mathrm {T}}s_{k}}{s_{k}^{\mathrm {T}}y_{k}}-1\} \ge\sigma\frac{s_{k}^{\mathrm{T}}s_{k}}{s_{k}^{\mathrm{T}}y_{k}}\).

Similarly,

and

In the end, it follows from (20) that \(\lambda_{\mathrm{min}}^{(k+1)}\lambda_{\mathrm{max}}^{(k+1)}=\sigma\frac {s_{k}^{\mathrm {T}}s_{k}}{y_{k}^{\mathrm{T}} s_{k}}\), which implies that

$$ \lambda_{\mathrm{min}}^{(k+1)}=\bigl(\lambda_{\mathrm{max}}^{(k+1)} \bigr)^{-1}\sigma\frac {s_k^{\mathrm{T}}s_k}{y_k^{\mathrm{T}} s_k} \ge\biggl(\omega_k+ \sigma\frac{s_k^{\mathrm{T}}s_k}{y_k^{\mathrm{T}} s_k} \biggr)^{-1} \sigma\frac{s_k^{\mathrm{T}}s_k}{y_k^{\mathrm {T}} s_k} = \frac{\sigma y_k^{\mathrm{T}} s_k}{ y_k^{\mathrm{T}}y_k+\sigma y_k^{\mathrm{T}} s_k}. $$

Hence, (23) and (24) hold, which implies that Q k+1 is a symmetric positive definite matrix when \(\sigma(y_{k}^{\mathrm{T}} s_{k}) > 0\). □

From the above theorem, we can easily obtain the following corollary.

Corollary 1

Let Q k+1 be defined by (6) and \(\sigma (y_{k}^{\mathrm{T}} s_{k}) > 0\). The spectral condition number of Q k+1, κ 2(Q k+1), is formulated by

$$ \kappa_2(Q_{k+1}) = \biggl[ \omega_k+\sigma\frac{s_k^{\mathrm {T}}s_k}{s_k^{\mathrm{T}}y_k}+ \sqrt{\biggl( \omega_k+\sigma\frac{s_k^{\mathrm{T}}s_k}{s_k^{\mathrm {T}}y_k} \biggr)^2 -4\sigma \frac{s_k^{\mathrm{T}}s_k}{y_k^{\mathrm{T}} s_k}} \biggr]^2\bigg /4\sigma\frac{s_k^{\mathrm{T}}s_k}{y_k^{\mathrm{T}} s_k}. $$
(27)

Especially, κ 2(Q k+1) arrives at the minimum, \((\sqrt {\omega_{k}} + \sqrt{\omega_{k}-1} )^{2}\), when \(\sigma=\frac{y_{k}^{\mathrm {T}}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\).

Proof

According to Theorem 2, (21) and (22) imply that (27) holds. Let

$$ t= \biggl(\omega_k+\sigma\frac{s_k^{\mathrm {T}}s_k}{s_k^{\mathrm {T}}y_k} \biggr) \bigg/ \biggl(2\sqrt{\sigma\frac{s_k^{\mathrm {T}}s_k}{y_k^{\mathrm {T}}s_k}} \biggr), $$
(28)

then, according to (27), κ 2(Q k+1) can be rewritten as follows:

$$ \kappa_2(Q_{k+1}) =\psi(t) = \bigl(t + \sqrt{t^2-1}\bigr)^2, $$
(29)

where ψ(⋅) is a strictly increasing function on [1,+∞). Note that

$$t\ge\biggl(2\sqrt{\omega_k}\sqrt{\sigma\frac{s_k^{\mathrm {T}}s_k}{s_k^{\mathrm{T}}y_k}} \biggr) \bigg/ \biggl(2\sqrt{\sigma\frac{s_k^{\mathrm {T}}s_k}{y_k^{\mathrm {T}}s_k}} \biggr) = \sqrt{\omega_k}\ge1 $$

and the above first inequality takes “=” if and only if \(\omega_{k}=\sigma\frac{s_{k}^{\mathrm{T}}s_{k}}{s_{k}^{\mathrm{T}}y_{k}}\), namely, \(\sigma=\frac{y_{k}^{\mathrm{T}}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\). Hence, the minimum of κ 2(Q k+1) is \((\sqrt{\omega_{k}} + \sqrt{\omega_{k}-1} )^{2}\) when \(\sigma=\frac{y_{k}^{\mathrm{T}}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\). □

2.2 Descent property

For the SPCG method, Theorem 2 shows that the symmetric Perry conjugate gradient directions defined by (5) satisfy the descent property (7), when \(\sigma y_{k}^{\mathrm{T}} s_{k}>0\). In fact,

$$ d_{k+1}^{\mathrm{T}} g_{k+1} = -g_{k+1}^{\mathrm{T}} Q_{k+1}g_{k+1} \le- \lambda_{\mathrm{min}}^{(k+1)}\|g_{k+1}\|^2 \le- \frac{\sigma y_k^{\mathrm{T}} s_k \|g_{k+1}\|^2}{ y_k^{\mathrm{T}}y_k+\sigma y_k^{\mathrm{T}} s_k} <0. $$
(30)

When σ=1, Q k+1, defined by (6), becomes

(31)

Thus, the method defined by (1) and (5) with σ=1 is the famous memoryless BFGS quasi-Newton method [25], denoted by mBFGS.

According to (30), we let \(\sigma= c \frac{y_{k}^{\mathrm{T}}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\), c>0 and \(s_{k}^{\mathrm{T}}y_{k}\ne0\), then it follows from (6) and (30) that

$$ Q_{k+1}^{\mathrm{SPD}} = \biggl(I- \frac{s_ky_k^{\mathrm{T}}}{s_k^{\mathrm {T}}y_k} \biggr) \biggl(I-\frac{y_ks_k^{\mathrm{T}}}{s_k^{\mathrm {T}}y_k} \biggr)+c \frac {y_k^{\mathrm{T}}y_k}{s_k^{\mathrm{T}}y_k}\frac{s_ks_k^{\mathrm {T}}}{s_k^{\mathrm{T}}y_k} $$
(32)

and

$$ d_{k+1}^{\mathrm{T}}g_{k+1} \le- \frac{c}{1+c}\|g_{k+1}\|_2^2, $$
(33)

which shows that the directions defined by (5) with \(\sigma=c \frac{y_{k}^{\mathrm{T}}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\) satisfy the sufficient descent property (8) for any functions and any line searches. Thus, the method defined by (1) and (5) with \(\sigma=c \frac{y_{k}^{\mathrm{T}}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\) is called symmetric Perry descent conjugate gradient algorithm, denoted by SPDCG, or by SPDCG(c), to indicate the dependence on the positive constant c. Especially, due to Corollary 1, when c=1, the method is called symmetric Perry descent conjugate gradient algorithm with optimal condition number, denoted by SPDOC. The corresponding iteration matrix is denoted by \(Q_{k+1}^{\mathrm{SPDOC}}\), i.e.

$$ Q_{k+1}^{\mathrm{SPDOC}} = \biggl(I- \frac{s_ky_k^{\mathrm{T}}}{s_k^{\mathrm {T}}y_k} \biggr) \biggl(I-\frac{y_ks_k^{\mathrm{T}}}{s_k^{\mathrm {T}}y_k} \biggr) + \frac{y_k^{\mathrm{T}}y_k}{s_k^{\mathrm{T}}y_k}\frac {s_ks_k^{\mathrm {T}}}{s_k^{\mathrm{T}}y_k}. $$
(34)

In addition, when σ=0, then it follows from (6) and (30) that

$$ H_{k+1}^{\mathrm{SHS}} = \biggl(I- \frac{s_ky_k^{\mathrm{T}}}{s_k^{\mathrm {T}}y_k} \biggr) \biggl(I-\frac{y_ks_k^{\mathrm{T}}}{s_k^{\mathrm {T}}y_k} \biggr) $$
(35)

and \(d_{k+1}^{\mathrm{T}}g_{k+1} \le0\). Thus, the method defined by (1) and (5) with σ=0 is the symmetric Hestenes-Stiefel method [18], denoted by SHS, which does not satisfy the descent property (7).

3 Scaling technology and restarting strategy

According to S.S. Oren and E. Spedicato’s idea [20], D.F. Shanno applied the scaling technology to the memoryless BFGS update formula (31) and developed a self-scaling conjugate gradient algorithms [25], i.e., he translated the memoryless BFGS update formula (31) into

(36)

Thus, the symmetric Perry matrix Q k+1 defined by (6) can be scaled as follows:

We substitute σ in Q k+1(ρ) with ρσ, then Q k+1(ρ)=ρQ k+1, where

(37)

Thus, the line search directions defined by (5) are rewritten as

$$ \left \{ \begin{array}{l@{\quad}l} d_1=-g_1,\\ \begin{aligned} d_{k+1}&=-\rho Q_{k+1}g_{k+1}\\ &=-\rho g_{k+1} +\rho\frac{s_k^{\mathrm{T}}g_{k+1}}{s_k^{\mathrm{T}}y_k}y_k +\rho\bigl[\tfrac{y_k^{\mathrm{T}}g_{k+1}}{s_k^{\mathrm{T}}y_k}- \bigl( \sigma+\tfrac{y_k^{\mathrm{T}}y_k}{s_k^{\mathrm{T}}y_k} \bigr) \tfrac{s_k^{\mathrm{T}}g_{k+1}}{s_k^{\mathrm{T}}y_k} \bigr]s_k, &\forall k>1, \end{aligned} \end{array} \right . $$
(38)

from which a family of scaling Perry conjugate gradient methods can be deduced.

Based on Beale-Powell restarting strategy [24] (see also [2, 3, 25, 26]), we define the following scheme to compute the directions. When

$$ \bigl|g_{r+1}^{\mathrm{T}}g_r\bigr|\ge0.2 \|g_{r+1}\|^2 $$
(39)

at r-th step, we use the directions defined by (38). For k>r, the directions d k+1 are computed by the following double update scheme:

$$ d_{k+1}=-H_{k+1}g_{k+1} $$
(40)

with

$$ H_{k+1}= H_{r+1}-\frac{s_ky_k^{\mathrm{T}}H_{r+1} + H_{r+1}y_ks_k^{\mathrm{T}}}{s_k^{\mathrm{T}}y_k}+ \biggl(\widetilde{\sigma}+\frac{ y_k^{\mathrm{T}}H_{r+1}y_k}{s_k^{\mathrm{T}}y_k} \biggr)\frac {s_ks_k^{\mathrm{T}}}{s_k^{\mathrm{T}}y_k} $$
(41)

and

$$ H_{r+1}=\widehat{\rho}Q_{r+1}=\widehat{ \rho} \biggl[I-\frac {s_ry_r^{\mathrm{T}} + y_rs_r^{\mathrm{T}}}{s_r^{\mathrm{T}}y_r}+ \biggl(\widehat{\sigma} +\frac{y_r^{\mathrm{T}}y_r}{s_r^{\mathrm{T}}y_r} \biggr)\frac {s_rs_r^{\mathrm{T}}}{s_r^{\mathrm{T}}y_r} \biggr], $$
(42)

where \(\widetilde{\sigma}\), \(\widehat{\rho}\) and \(\widehat{\sigma }\) are three preset parameters.

Since

$$ H_{r+1}^{-1/2}H_{k+1}H_{r+1}^{-1/2}= I-\frac{\widetilde{s}_k\widetilde {y}_k^{\mathrm{T}} + \widetilde{y}_k\widetilde{s}_k^{\mathrm{T}}}{\widetilde {s}_k^{\mathrm {T}}\widetilde{y}_k}+ \biggl(\widetilde{\sigma}+\frac{\widetilde {y}_k^{\mathrm{T}}\widetilde {y}_k}{\widetilde{s}_k^{\mathrm{T}}\widetilde{y}_k} \biggr) \frac{\widetilde{s}_k\widetilde{s}_k^{\mathrm{T}}}{\widetilde {s}_k^{\mathrm{T}}\widetilde{y}_k}, $$
(43)

where \(\widetilde{s}_{k}=H_{r+1}^{-1/2}s_{k}\), \(\widetilde{g}_{k+1}=H_{r+1}^{1/2}g_{k+1}\) and \(\widetilde{y}_{k}=H_{r+1}^{1/2}y_{k}\), Corollary 1 asserts that \(\kappa_{2}(H_{r+1}^{-1/2}H_{k+1}H_{r+1}^{-1/2})\) arrives at the minimum if \(\widetilde{\sigma} = \frac{\widetilde{y}_{k}^{\mathrm{T}}\widetilde{y}_{k}}{\widetilde {s}_{k}^{\mathrm{T}}\widetilde{y}_{k}} =\frac{y_{k}^{\mathrm{T}}H_{r+1}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\). According to (42), Corollary 1 shows that κ 2(H r+1) is minimal when \(\widehat{\sigma}=\frac{y_{r}^{\mathrm{T}}y_{r}}{s_{r}^{\mathrm {T}}y_{r}}\). We also note that the matrix \(H_{r+1}^{-1/2}H_{k+1}H_{r+1}^{-1/2}\) is similar to the matrix \(H_{r+1}^{-1}H_{k+1}\), thus

$$ \kappa_2(H_{k+1}) \le \kappa_2(H_{r+1})\kappa_2\bigl(H_{r+1}^{-1}H_{k+1} \bigr)=\kappa_2(H_{r+1})\kappa_2 \bigl(H_{r+1}^{-1/2}H_{k+1}H_{r+1}^{-1/2} \bigr), $$
(44)

which implies that the optimal choices for \(\widetilde{\sigma}\) in (41) and \(\widehat{\sigma}\) in (42) are

$$ \widetilde{\sigma} =\frac{y_k^{\mathrm {T}}H_{r+1}y_k}{s_k^{\mathrm {T}}y_k} \mbox{ and } \widehat{\sigma}=\frac{y_r^{\mathrm{T}}y_r}{s_r^{\mathrm{T}}y_r}, $$
(45)

respectively, such that κ 2(H k+1) is optimal.

Let \(\widehat{g}_{k+1}=H_{r+1}g_{k+1}\) and \(\widehat {y}_{k}=H_{r+1}y_{k}\), namely,

$$ \widehat{g}_{k+1}=\widehat{\rho}g_{k+1} - \widehat{\rho}\frac {s_r^{\mathrm{T}}g_{k+1}}{s_r^{\mathrm{T}}y_r}y_r+ \widehat{\rho} \biggl[ \biggl( \widehat{\sigma} +\frac{y_r^{\mathrm{T}}y_r}{s_r^{\mathrm{T}}y_r} \biggr)\frac {s_r^{\mathrm{T}}g_{k+1}}{s_r^{\mathrm{T}}y_r} - \frac{y_r^{\mathrm{T}}g_{k+1}}{s_r^{\mathrm{T}}y_r} \biggr]s_r $$
(46)

and

$$ \widehat{y}_k=\widehat{\rho}y_k- \widehat{\rho}\frac{s_r^{\mathrm {T}}y_k}{s_r^{\mathrm{T}}y_r}y_r+ \widehat{\rho} \biggl[ \biggl( \widehat{\sigma} +\frac{y_r^{\mathrm{T}}y_r}{s_r^{\mathrm{T}}y_r} \biggr)\frac {s_r^{\mathrm{T}}y_k}{s_r^{\mathrm{T}}y_r} - \frac{y_r^{\mathrm{T}}y_k }{s_r^{\mathrm{T}}y_r} \biggr]s_r, $$
(47)

then the directions d k+1 defined by (40) can be reformulated by

$$ d_{k+1} =-\widehat{g}_{k+1}+ \frac{s_k^{\mathrm{T}}g_{k+1}}{s_k^{\mathrm {T}}y_k}\widehat{y}_k - \biggl[ \biggl(\widetilde{\sigma}+ \frac{ \widehat{y}_k^{\mathrm{T}}y_k}{s_k^{\mathrm{T}}y_k} \biggr)\frac {s_k^{\mathrm{T}}g_{k+1}}{s_k^{\mathrm{T}}y_k} -\frac{\widehat {y}_k^{\mathrm{T}}g_{k+1} }{s_k^{\mathrm{T}}y_k} \biggr]s_k. $$
(48)

Hence, we can introduce the following scaling symmetric Perry conjugate gradient method with restarting procedures (SSPCGRP).

Algorithm 2

(SSPCGRP)

Step 1.:

Give an initial point x 1 and ε≥0. Set k=1 and Nrestart=0.

Step 2.:

Calculate g 1=g(x 1). If ∥g 1∥≤ε, then stop, otherwise, let d 1=−g 1.

Step 3.:

Calculate steplength α k using the Wolfe line searches (15) and (16) with initial guess α k,0, where α 1,0=1/∥g 1∥ and α k,0=α k−1∥d k−1∥/∥d k ∥ when k≥2.

Step 4.:

Set x k+1=x k +α k d k .

Step 5.:

Calculate g k+1=g(x k+1). If ∥g k+1∥≤ε then stop.

Step 6.:

If the Powell restarting criterion (39) holds, then calculate the directions d k+1 via (38) with different σ and ρ, let y r =y k and s r =s k (store y r and s r ), set Nrestart=Nrestart+1 and k=k+1, go to step 3. Otherwise, go to step 7.

Step 7.:

If Nrestart=0, then calculate the directions d k+1 via (38) with different σ and ρ, otherwise, calculate d k+1 via (48), where \(\widehat{y}_{k}\) and \(\widehat{g}_{k+1}\) are computed by (46) and (47), respectively, \(\widetilde{\sigma}\), \(\widehat{\sigma}\) and \(\widehat{\rho}\) are preset parameters.

Step 8.:

Set k=k+1, go to step 3.

In Algorithm 2, k and Nrestart record the number of iterations and the number of restarting procedures, respectively.

When ρ=1 and \(\sigma=c_{1}\frac{y_{k}^{\mathrm {T}}y_{k}}{s_{k}^{\mathrm {T}}y_{k}}\) in (38), and \(\widehat{\rho}=1\), \(\widetilde{\sigma} =c_{2}\frac{y_{k}^{\mathrm{T}}H_{r+1}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\) and \(\widehat{\sigma}=c_{2}\frac{y_{r}^{\mathrm{T}}y_{r}}{s_{r}^{\mathrm {T}}y_{r}}\) in (46)–(48), then the SSPCGRP algorithm is denoted by SPDRP, or SPDRP(c 1,c 2) to indicate the dependence on the positive constants c 1 and c 2. Especially, when they are equal to 1, i.e., \(\sigma=\frac{y_{k}^{\mathrm{T}}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\) in (38), \(\widetilde{\sigma}\) and \(\widehat{\sigma}\) are computed by (45), the condition numbers κ 2(Q k+1)=κ 2(ρQ k+1), κ 2(H k+1) and κ 2(H r+1) are optimal, where Q k+1 is defined by (6) with \(\sigma=\frac{y_{k}^{\mathrm{T}}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\). So, the SSPCGRP algorithm is called the symmetric Perry descent conjugate gradient method with optimal condition numbers and restarting procedures, denoted by SPDOCRP.

When ρσ=1, \(\rho=\frac{s_{k}^{\mathrm {T}}s_{k}}{y_{k}^{\mathrm {T}}s_{k}}\), \(\widehat{\rho}\ \widehat{\sigma}=1\), \(\widehat{\rho}=\frac{s_{r}^{\mathrm{T}}s_{r}}{y_{r}^{\mathrm{T}}s_{r}}\) and \(\widetilde{\sigma}=1\), these formulas (38), (46), (47) and (48) were used by N. Andrei in [2], the SSPCGRP algorithm becomes the SCALCG algorithm with the spectral choice for θ k+1 [2], it is also called Andrei-Perry conjugate gradient method with restarting procedures.

4 Convergence

In this section, we analyze the convergence of the symmetric Perry conjugate gradient method (Algorithm 1) and the scaling symmetric Perry conjugate gradient method with restarting procedures (Algorithm 2). For this, we assume that the objective function f(x) satisfies the following assumptions:

H1.:

f is bounded below in \(\mathbb{R}^{n}\) and f is continuously differentiable in a neighborhood \(\mathcal{N}\) of the level set \(\mathcal{L} \stackrel{def}{=}\{x : f(x)\le f(x_{0})\}\), where x 0 is the starting point of the iteration.

H2.:

The gradient of f is Lipschitz continuous in \(\mathcal{N}\), that is, there exists a constant L>0 such that

$$ \bigl\|\nabla f(\bar{x})-\nabla f(x)\bigr\| \leq L\| \bar{x}-x \|, \quad \forall\bar{x},x \in\mathcal{N}. $$
(49)

Next, we introduce the spectral condition lemma of the global convergence for an objective function satisfying H1 and H2, which comes from [18], Theorem 4.1.

Lemma 1

Let the objective function f(x) satisfy H1 and H2. Assume that the line search directions of a nonlinear conjugate gradient method satisfy

$$ d_1 = -g_1, d_{k} = - M_{k}g_{k} \quad \forall k > 1 , $$
(50)

where M k is the conjugate gradient iteration matrix, which is a symmetric positive semidefinite matrix. For a nonlinear conjugate gradient method (1) and (50) satisfying the sufficient descent condition (8), if its line search satisfies the Wolfe conditions (15) and (16), and

$$ \sum_{k=1}^{\infty}( \varLambda_{k})^{-2}= + \infty, $$
(51)

where Λ k is the maximum eigenvalue of M k , then lim inf k→∞∥g k ∥=0. Moreover, if \(\varLambda_{k} \le\widetilde{\varLambda}\) for all k, where \(\widetilde{\varLambda}\) is a positive constant, then lim k→∞∥g k ∥=0.

Remark 2

If M k is a symmetric positive definite matrix, then the spectral condition (51) can be rewritten as

$$ \sum_{k=1}^{\infty}\bigl( \kappa_2(M_{k})\bigr)^{-2}= + \infty. $$
(52)

In fact, by (50), it can be derived that

$$ \cos^2\theta_k = \frac{\displaystyle(g_k^{\mathrm {T}}d_k)^2}{\displaystyle\|d_k\|^2\|g_k\|^2} = \frac{(g_k^{\mathrm{T}}M_kg_k)^2}{g_k^{\mathrm{T}} M_k^{\mathrm {T}}M_kg_k\|g_k\|^2} \ge\frac{\lambda_k^2\|g_k\|^4}{\varLambda _{k}^2\|g_k\|^4} =\bigl(\kappa_2(M_{k}) \bigr)^{-2}, $$
(53)

where θ k is the angle between d k and −g k , λ k and Λ k are the minimum eigenvalue and maximum eigenvalue of M k , respectively. The Zoutendijk’s condition (Theorem 2.1 of [8]) asserts that (52) implies that the results of Lemma 1 are true.

In what follows, the convergence of these resulting algorithms is proved by evaluating the spectral boundary of the iteration matrix and Lemma 1. The proof method is called the spectral method. It should be pointed out that the proof method also can be applied to the non-symmetric conjugate gradient methods, if the positive square root of the maximum eigenvalue \(M_{k}^{\mathrm{T}}M_{k}\) substitutes for with the one of M k in Lemma 1, that is, the maximum singular value of M k substitutes for the maximum eigenvalue of M k (see Theorem 3.1 in [17]).

4.1 The convergence for uniformly convex functions

Here, we first prove the global convergence of the symmetric Perry conjugate gradient method (SPCG), the scheme (1) and (5) with Q k+1 defined by (6), for uniformly convex functions. For this, we introduce the following basic assumption, which is an equivalent condition for a uniformly convex differentiable function.

H3.:

There exists a constant m>0 such that

$$ \bigl(\nabla f(\bar{x})-\nabla f(x) \bigr)^{\mathrm{T}}(\bar{x}-x)\ge m \|\bar{x}-x\|^2 \quad \forall\bar{x},\ x \in\mathcal{N}. $$
(54)

Theorem 3

Assume that H1, H2 and H3 hold. Let ν 0 and ν 1 be two positive constants. For the symmetric Perry conjugate gradient method (1) and (5) with ν 0≤σ≤ν 1, the Wolfe line searches (15) and (16) are implemented. If g 1≠0 and steplength α k >0 for k≥1, then g k =0 for some k>1, or lim k→∞∥g k ∥=0.

Proof

Assume that g k ≠0, \(\forall k\in\mathbb{N}\). Below, by induction, we first prove that the line search direction d k , defined by (5), satisfies the sufficient descent property (8).

When k=1, \(d_{1}^{\mathrm{T}}g_{1}=-\|g_{1}\|^{2}<0\). From (16), it follows that \(s_{1}^{\mathrm{T}}y_{1}\ge-(1-b_{2})\alpha_{1} d_{1}^{\mathrm{T}}g_{1}>0\).

Now, assume that \(d_{k}^{\mathrm{T}} g_{k} \le-\frac{\nu_{0} m}{L^{2} +\nu_{0} m}\|g_{k}\|^{2}\). Then, it follows from (16) that \(s_{k}^{\mathrm {T}}y_{k}\ge -(1-b_{2})\alpha_{k} d_{k}^{\mathrm{T}}g_{k}>0\). So, (30) and the assumptions H2 and H3 imply that

$$ d_{k+1}^{\mathrm{T}} g_{k+1} \le-\frac{\sigma y_k^{\mathrm{T}} s_k}{ y_k^{\mathrm{T}}y_k+\sigma y_k^{\mathrm{T}} s_k} \|g_{k+1}\|^2 \le-\frac{\nu_0 m}{L^2 +\nu_0 m} \|g_{k+1} \|^2. $$

Hence, by induction, the sufficient descent property (8) holds.

Next, we prove that \(\lambda_{\mathrm{max}}^{(k+1)}\), the maximum eigenvalue of Q k+1 defined by (6), is uniformly bounded above. From the above analysis, it can be derived that \(s_{k}^{\mathrm{T}}y_{k}>0\). So, from (23) in Theorem 2, it can be deduced that

(55)

Therefore, Lemma 1 claims that lim k→∞∥g k ∥=0. □

Remark 3

Theorem 3 shows that the memoryless BFGS quasi-Newton method and the method SPDCG are convergent for uniformly convex functions under the Wolfe line searches. In fact, the global convergence of the method SPDCG and the method mBFGS results from the following inequalities

$$ m\le\frac{y_k^{\mathrm{T}}s_k}{s_k^{\mathrm {T}}s_k}\le\frac {y_k^{\mathrm{T}}y_k}{s_k^{\mathrm{T}}y_k} \le \frac{L^2}{m}. $$
(56)

Next, we prove the global convergence of the SSPCGRP method for uniformly convex functions.

Theorem 4

Assume that H1, H2 and H3 hold, and that ν 0 and ν 1 are two positive constants. Let the sequence {x k } be generated by the SSPCGRP algorithm (Algorithm 2), where the five different parameters σ, ρ, \(\widetilde{\sigma}\), \(\widehat{\sigma}\) and \(\widehat{\rho}\) satisfy \(\nu_{0}\le\sigma, \rho, \widetilde{\sigma},\widehat{\sigma },\widehat {\rho}\le \nu_{1}\). If g  1≠0, and steplength α k >0 for k≥1, then g k =0 for some k>1, or lim k→∞∥g k ∥=0.

Proof

First, we note that \(\widetilde{y}_{k}^{\mathrm{T}}\widetilde {s}_{k}=y_{k}^{\mathrm{T}}s_{k}\) for all k≥1. If \(\widetilde{y}_{k}^{\mathrm{T}}\widetilde{s}_{k}>0\), we can denote the minimum and the maximum eigenvalues of the matrix \(H_{r+1}^{-1/2}H_{k+1}H_{r+1}^{-1/2}\) by \(\widetilde{\lambda}_{\mathrm{min}}^{(k+1)}\) and \(\widetilde{\lambda}_{\mathrm{max}}^{(k+1)}\), respectively. We also denote the minimum and the maximum eigenvalues of the matrix H r+1 by \(\widehat{\lambda}_{\mathrm{min}}^{(r+1)}\) and \(\widehat{\lambda}_{\mathrm{max}}^{(r+1)}\), respectively. Thus, (42), (43), Theorem 2 and the assumptions H2 and H3 imply that

$$ \widetilde{\lambda}_{\mathrm{max}}^{(k+1)}\le \widetilde{\omega}_k +\widetilde{\sigma} \frac{\widetilde {s}_k^{\mathrm{T}}\widetilde{s}_k}{ \widetilde{s}_k^{\mathrm{T}}\widetilde{y}_k}, \widetilde{\lambda}_{\mathrm{min}}^{(k+1)}\ge\frac{\widetilde{\sigma} \widetilde{y}_k^{\mathrm{T}} \widetilde{s}_k}{ \widetilde{y}_k^{\mathrm{T}}\widetilde{y}_k+\widetilde{\sigma} \widetilde{y}_k^{\mathrm{T}} \widetilde{s}_k} \ge \frac{\nu_0 y_k^{\mathrm{T}}s_k}{y_k^{\mathrm {T}}H_{r+1}y_k+\nu_0 y_k^{\mathrm{T}}s_k} $$
(57)

and

$$ \widehat{\lambda}_{\mathrm{max}}^{(r+1)} \le\widehat{\rho}\omega_r +\widehat{\rho}\ \widehat{\sigma} \frac{s_r^{\mathrm{T}}s_r}{s_r^{\mathrm {T}}y_r} \le\nu_1\frac{L^2+\nu_1 m}{m^2}, \widehat{ \lambda}_{\mathrm{min}}^{(r+1)}\ge\frac{\widehat{\rho}\ \widehat{\sigma} y_r^{\mathrm{T}} s_r}{ y_r^{\mathrm{T}}y_r+\widehat{\sigma} y_r^{\mathrm{T}} s_r}\ge \frac {\nu_0^2 m}{ L^2+\nu_0 m}, $$
(58)

where \(\widetilde{\omega}_{k}=\frac{\widetilde{y}_{k}^{\mathrm{T}} \widetilde{y}_{k}\widetilde{s}_{k}^{\mathrm{T}}\widetilde{s}_{k}}{ (\widetilde{s}_{k}^{\mathrm{T}}\widetilde{y}_{k})^{2}}\) and \(\omega_{r}= \frac{y_{r}^{\mathrm{T}}y_{r} s_{r}^{\mathrm{T}}s_{r}}{(s_{r}^{\mathrm{T}}y_{r})^{2}}\).

In what follows, by induction, we prove that \(\widetilde{y}_{k}^{\mathrm{T}}\widetilde{s}_{k}>0\) and the sufficient descent property (8) is true for all k.

If the Powell restarting criterion (39) never holds for all k≥1, the iteration matrix is ρQ k+1. Thus, similar to Theorem 3, it can be easily shown that the results of Theorem 4 are true.

Suppose that k 0 is the first natural number such that the Powell restarting criterion (39) is true, then Nrestart≥1. Similar to Theorem 3, it can be obtained that for k=1,2,…,k 0, \(\widetilde{y}_{k}^{\mathrm{T}}\widetilde{s}_{k}=y_{k}^{\mathrm {T}}s_{k}>0\) and

So, it follows from (16) and the above inequality that

$$s_{k+1}^{\mathrm{T}}y_{k+1}\ge-(1-b_2) \alpha_{k+1} d_{k+1}^{\mathrm {T}}g_{k+1}>0. $$

If the Powell restarting criterion (39) holds for k+2, d k+2 is calculated by (38). Thus, Theorem 2 and the assumptions H2 and H3 claim that

If the Powell restarting criterion (39) does not hold for k+2, d k+2 is calculated by (48) with (46) and (47) (i.e., (40)–(42)). Since Nrestart≥1, from (40)–(42) and Theorem 2, it can be obtained that

By (57), (58), the assumptions H2 and H3, it is yielded that

Therefore,

$$ d_{k+2}^{\mathrm{T}}g_{k+2} \le- \frac{\nu_0^3 m^4\|g_{k+2}\|^2}{ (L^2+\nu_0 m) ((L^2+\nu_1m)\nu_1L^2+\nu_0m^3 )} $$

which, together with (16), implies that

$$s_{k+2}^{\mathrm{T}}y_{k+2}\ge-(1-b_2) \alpha_{k+2} d_{k+2}^{\mathrm {T}}g_{k+2}>0. $$

By induction, it follows that \(s_{k}^{\mathrm{T}}y_{k}>0\) for all k and the directions generated by the SSPCGRP algorithm (Algorithm 2) satisfy the sufficient descent property (8) with

$$ c_0=\min\biggl\{\frac{\nu_0^2 m }{ L^2 +\nu_0 m },\frac{\nu_0^3 m^4}{ (L^2+\nu_0 m) ((L^2+\nu_1m)\nu_1L^2+\nu_0m^3 )} \biggr\}. $$

Next, we prove that κ 2(H k+1) is bounded above. Since \(\widetilde{s}_{k}=H_{r+1}^{-1/2}s_{k}\) and \(\widetilde{y}_{k}=H_{r+1}^{1/2}y_{k}\), from (57), (58) and the assumptions H2 and H3, it can be derived that

and

Thus, it follows from (44), (58) and above two inequalities that

$$\kappa_2(H_{k+1}) \le\frac {\widehat{\lambda}_{\mathrm{max}}^{(r+1)}\widetilde{\lambda}_{\mathrm{max}}^{(k+1)}}{ \widehat{\lambda}_{\mathrm{min}}^{(r+1)}\widetilde{\lambda}_{\mathrm{min}}^{(k+1)}} \le \bigl(L^2+\nu_1 m\bigr)^3\frac{ ((L^2+\nu_1 m)\nu_1 L^2+\nu_1 m^3 )^2}{ \nu_0^5 m^{11}}. $$

If d k+1 is calculated by (38), the iteration matrix is defined by (37). So, Corollary 1, (28), (29) and the assumptions H2 and H3 imply that

$$ t= \biggl(\omega_k+\sigma\frac{s_k^{\mathrm{T}}s_k}{s_k^{\mathrm {T}}y_k} \biggr) \bigg/ \biggl(2\sqrt {\sigma\frac{s_k^{\mathrm{T}}s_k}{y_k^{\mathrm {T}}s_k}} \biggr) \le\sqrt{\frac{m}{\sigma}} \frac{L^2+\sigma m}{2m^2}\le\sqrt{\frac{m}{\nu_0}}\frac{L^2+\nu_1 m}{2m^2} $$

and

$$ \kappa_2(\rho Q_{k+1})=\kappa_2(Q_{k+1}) =\psi(t)\le\psi\biggl(\sqrt{\frac{m}{\nu_0}}\frac{L^2+\nu_1 m}{2m^2} \biggr), $$

where ψ(⋅) is defined by (29).

Hence, the spectral condition number of the iteration matrix of Algorithm 2 is uniformly bounded above, which claims that the results of Theorem 4 are true according to Remark 2. □

From (56) and this theorem, it can be shown that the SPDRP algorithm and the SCALCG algorithm with the spectral choice [2] are global convergence for uniformly convex functions under the Wolfe line searches.

4.2 The convergence for general nonlinear functions

For general nonlinear functions, we first have following result for the symmetric Perry conjugate gradient method.

Theorem 5

Assume that H1 and H2 hold. For the symmetric Perry conjugate gradient method (1) and (5) with \(\sigma=c\frac{y_{k}^{\mathrm{T}}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\), where c is a positive constant, if the line searches satisfy the Wolfe conditions (15) and (16), then lim k→∞∥y k ∥=0 implies that lim inf k→∞∥g k ∥=0.

Proof

Denote the maximum eigenvalue of the iteration matrix Q k+1 by \(\lambda_{\mathrm{max}}^{(k+1)}\). The Wolfe condition (16) leads to \(s_{k}^{\mathrm{T}}y_{k}\ge-(1-b_{2}) s_{k}^{\mathrm{T}}g_{k}\), which, together with (33), implies that

$$ \omega_k\le\frac{y_k^{\mathrm{T}}y_k s_k^{\mathrm{T}}s_k}{(1-b_2)^2( -s_k^{\mathrm{T}}g_k)^2} = \frac{y_k^{\mathrm{T}}y_kg_kQ_k^2g_k}{ (1-b_2)^2(g_kP_kg_k)(-d_k^{\mathrm{T}}g_k)} \le\frac{(1+c)\lambda _{\mathrm{max}}^{(k)}\|y_k\|^2}{(1-b_2)^2c\|g_k\|^2}. $$
(59)

Thus,

$$ \lambda_{\mathrm{max}}^{(k+1)} \le\omega_k+\sigma \frac{s_k^{\mathrm{T}}s_k}{s_k^{\mathrm {T}}y_k}=(1+c)\omega_k\le\frac{(1+c)^2\lambda_{\mathrm{max}}^{(k)}\|y_k\| ^2}{ (1-b_2)^2c\|g_k\|^2}= \lambda_{\mathrm{max}}^{(k)}c_5^2 \frac{\|y_k\|^2}{\| g_k\|^2}, $$

where \(c_{5}=\frac{1+c}{(1-b_{2})\sqrt{c}}\). So,

$$ \lambda_{\mathrm{max}}^{(k+1)} \le \lambda_{\mathrm{max}}^{(k-1)}c_5^4 \frac{\|y_{k-1}\|^2}{ \|g_{k-1}\|^2}\frac{\|y_k\|^2}{\|g_k\|^2} \le\cdots\le\lambda _{\mathrm{max}}^{(1)}c_5^{2k} \prod_{j=1}^k\frac{\|y_j\|^2}{ \|g_j\|^2}. $$
(60)

Now assume that lim k→∞∥y k ∥=0, lim inf k→∞∥g k ∥=ε>0. Then there exists a positive integer N 0 such that for j>N 0, \(\frac{\|y_{j}\|}{\|g_{j}\|}\le c_{5}^{-1}\). Let \(C_{N}=\lambda_{\mathrm{max}}^{(1)}\prod_{j=1}^{N_{0}}c_{5}^{2}\frac{\|y_{j}\|^{2}}{\| g_{j}\|^{2}}\), thus,

$$ \lambda_{\mathrm{max}}^{(k+1)}\le\lambda_{\mathrm{max}}^{(1)} \prod_{j=1}^{N_0}c_5^2 \frac {\|y_j\|^2}{\|g_j\|^2} \prod_{j=N_0+1}^kc_5^2 \frac{\|y_j\|^2}{\|g_j\|^2}\le C_N. $$

Therefore, Lemma 1 and (33) claim that lim k→∞∥g k ∥=0, which contradicts the above assumption. So, lim k→∞∥y k ∥=0 implies that lim inf k→∞∥g k ∥=0. □

Next, we prove the global convergence of the SSPCGRP algorithm (Algorithm 2) for general nonlinear functions.

Theorem 6

Assume that H1 and H2 hold. Let the sequence {x k } be generated by the SSPCGRP algorithm with \(\sigma=c\frac{y_{k}^{\mathrm{T}}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\) and ν 0≤ρ≤ν 1 in (38), where c, ν 0 and ν 1 are positive constants. If the line searches satisfy the Wolfe conditions (15) and (16), then lim k→∞∥y k ∥=0 implies that lim inf k→∞∥g k ∥=0.

Proof

If lim inf k→∞∥g k ∥≠0 as ∥y k ∥→0, then, for some ε>0, there exists a positive integer N 1 such that ∥g k+1∥>ε and ∥y k ∥≤0.8ε as k≥N 1. Thus,

So, \(g_{k+1}^{\mathrm{T}}g_{k}\ge0.2\|g_{k+1}\|^{2}\) for k≥N 1, which means that the directions d k+1 are calculated by (38) for k≥N 1, that is,

$$ d_{k+1} = -\rho Q_{k+1}g_{k+1}, $$

where Q k+1 is defined by (6). Since \(\sigma=c\frac{y_{k}^{\mathrm{T}}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\) and ν 0≤ρ≤ν 1, from Theorem 2, it follows that

$$ d_{k+1}^{\mathrm{T}} g_{k+1} = - \rho g_{k+1}^{\mathrm{T}} Q_{k+1}g_{k+1} \le- \frac{\rho\sigma y_k^{\mathrm{T}} s_k}{ y_k^{\mathrm{T}}y_k+\sigma y_k^{\mathrm{T}} s_k} \|g_{k+1}\|^2 \le -\frac{c\nu_0}{1+c} \|g_{k+1}\|^2. $$
(61)

For convenience, we also denote the maximum eigenvalue of ρQ k+1 by \(\lambda_{\mathrm{max}}^{(k+1)}\). Analogous to (60), it can be derived that

where \(c_{5}=\frac{1+c}{(1-b_{2})\sqrt{c}}\). We substitute \(\lambda _{\mathrm{max}}^{(N_{1})}\) and N 1 for \(\lambda_{\mathrm{max}}^{(1)}\) and 1 in (60), respectively, then, similar to Theorem 5, it can be obtain from Lemma 1 and (61) that lim k→∞∥y k ∥=0 implies that lim inf k→∞∥g k ∥=0. □

The above two theorems show that the SPDCG(c) algorithm and the SPDRP(c 1,c 2) algorithm are global convergence for the nonconvex functions under the Wolfe line searches, as lim k→∞∥y k ∥=0. The condition for the global convergence, lim k→∞∥y k ∥=0, was used by J.Y. Han, et al. in [14].

5 Numerical experiments

In this section, we demonstrate our algorithms: SPDCG and SPDRP, and compare them with the CG_DESCENT algorithm [12], the SCALCG algorithm with the spectral choice [2], the mBFGS algorithm (a special form of the SPCG algorithm with σ=1) and the RSPDCGs algorithm [19] whose line search directions are formulated by

$$ d_1= -g_1,\qquad d_{k+1} =-g_{k+1}+\beta_k d_k,\quad k\ge1, $$

where

$$ \beta_k =\frac{1}{ \eta^d_k} \biggl(y_k -\frac{\|y_k\|^2}{\eta^d_k} d_k \biggr)^{\mathrm {T}}g_{k+1} \quad \mbox{with } \eta^d_k=\left \{ \begin{array}{l@{\quad}l} y_k^{\mathrm{T}} d_k, & \hbox{if } \|g_k\|^2 \ge\eta\alpha_k\| d_k\| ^2,\\ \alpha_k\|d_k\|^2, & \hbox{otherwise.} \end{array} \right . $$
(62)

In numerical experiments, we let η=10−5. The RSPDCGs algorithm is fully detailed in [19].

The numerical experiments use two groups test functions, one group (145 test functions) is taken from the CUTEr [9] library, referring to website:

http://www.cuter.rl.ac.uk/,

which is only used to test mBFGS, SPDCG, RSPDCGs and CG_DESCENT algorithms. In order to compare with the SCALCG algorithm, the second group consists of the 73 unconstrained problems but the 71-st in SCALCG Fortran software package coded by N. Andrei, referring to website:

http://camo.ici.ro/forum/SCALCG/.

For the second group, each test function is made ten experiments with the number of variable 1000,2000,…,10000, respectively. The starting points used are those given in the code, SCALCG.

The SPDCG, mBFGS and RSPDCGs algorithms are coded according to the package, CG_DESCENT (C language, Version 5.3), with minor revisions and implement the approximate Wolfe line searches with the default parameters in CG_DESCENT [10, 12]. The package, CG_ DESCENT, can be got from Hager’s web page at

http://www.math.ufl.edu/~hager/.

In addition, in order to compare with the SCALCG algorithm, all subroutines of the SPDRP algorithm are written in Fortran 77 with the double precision, and the SPDRP algorithm uses the Wolfe line searches in the SCALCG Fortran code.

The termination criterion of all algorithms is that ∥g∥∞<10−6, where ∥⋅∥∞ is the infinity norm of a vector. The maximum number of iterations is 500n, where n is the number of variables. The tests are performed on PC (Dell Inspiron 530), Intel® Core™ 2 Duo, E4600, 2.40 GHz, 2.39 GHz, RAM 2.00 GB, with the gcc and g77 compilers.

The SPDCG algorithm is a special form of the SPCG algorithm (Algorithm 1) with \(\sigma=c\frac{y_{k}^{\mathrm{T}}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\) in (5) (see also step 6 in Algorithm 1). Thus the line search directions are formulated by

$$ d_1=-g_1, \qquad d_{k+1} = -g_{k+1} +\beta_k d_k +\gamma_k y_k,\quad \forall k\ge1 $$
(63)

with \(\beta_{k}=\frac{y_{k}^{\mathrm{T}}g_{k+1}}{d_{k}^{\mathrm{T}}y_{k}}- (1+c)\frac{y_{k}^{\mathrm{T}}y_{k}}{d_{k}^{\mathrm{T}}y_{k}} \frac{d_{k}^{\mathrm{T}}g_{k+1}}{d_{k}^{\mathrm{T}}y_{k}}\), \(\gamma_{k}= \frac{d_{k}^{\mathrm{T}}g_{k+1}}{d_{k}^{\mathrm{T}}y_{k}}\), and the iteration matrix is defined by (32). For the SPDCG algorithm, we test several different values of c in β k of (63) on the first group of test functions and find that the performance [6] is slightly better when c=1 (SPDOC algorithm) than that when c is taken other values.

For the first group of test functions, to compare the algorithms: mBFGS and SPDOC with the RSPDCGs and CG_DESCENT algorithms. we divide the group into two parts: large scale problems, whose numbers of variables are not less than 100 (72 test functions), and small scale problems, whose numbers of variables are less than 100 (73 test functions).

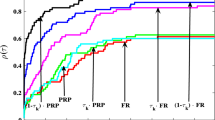
Figures 1 and 2 present that their Dolan-Moré performance profiles for large scale problems based on Nite (the number of iterations) and CPU time, respectively. Figures 3 and 4 present the Dolan and Moré performance profiles of these algorithms for small scale problems with relative to Nite and CPU time, respectively. Figures 1 and 2 show that for large scale problems, the performance of the SPDOC algorithm is similar to that of the CG_DESCENT algorithm and their performances are better than that of the others; the performance of the RSPDCGs algorithm is better than that of the mBFGS algorithm. For small scale problems, Figs. 3 and 4 show that the mBFGS algorithm is best, which means that SPDOC and CG_DESCENT algorithms are more suitable for solving large scale problems. It should be pointed out that although mBFGS algorithm give better results on the small problems, it fails to solve three problems of the CUTEr test set. In the recent paper [13], it is observed that for the small ill-conditioned quadratic PALMER test problems in CUTEr, the gradients generated by the conjugate gradient method quickly lose orthogonality due to numerical errors. See Hager and Zhang’s paper [13] for a strategy for handling these ill-conditioned problems.

Fig. 1
figure 1

Performance based on Nite of SPDOC, mBFGS, CG_DESCENT and RSPDCGs for large scale problems

Full size image
Fig. 2
figure 2

Performance based on CPU time of SPDOC, mBFGS, CG_DESCENT and RSPDCGs for large scale problems

Full size image
Fig. 3
figure 3

Performance based on Nite of SPDOC, mBFGS, CG_DESCENT and RSPDCGs for small scale problems

Full size image
Fig. 4
figure 4

Performance based on CPU time of SPDOC, mBFGS, CG_DESCENT and RSPDCGs for small scale problems

Full size image

The SPDRP algorithm is a special case of the SSPCGRP algorithm (Algorithm 2) with ρ=1 and \(\sigma=c_{1}\frac{y_{k}^{\mathrm {T}}y_{k}}{s_{k}^{\mathrm {T}}y_{k}}\) in (38), and \(\widehat{\rho}=1\), \(\widetilde{\sigma} =c_{2}\frac{y_{k}^{\mathrm{T}}H_{r+1}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\) and \(\widehat{\sigma}=c_{2}\frac{y_{r}^{\mathrm{T}}y_{r}}{s_{r}^{\mathrm {T}}y_{r}}\) in (46)–(48). For the SPDRP algorithm, we also test several different values of c on the second group of test functions, we find the performance is slightly better when c 1=c 2=1 (i.e., the SPDOCRP algorithm) than that when c 1 and c 2 are taken other values. Next, we compare the SPDOCRP algorithm with the SCALCG algorithms, using the second group of test functions. Figures 5 and 6 present that their Dolan-Moré performance profiles based on Nite and CPU time, respectively. The SPDOCRP algorithm and the SCALCG algorithm use the restarting strategy and the double update scheme, but the SPDOCRP algorithm has the optimal spectral condition number of the iteration matrix, so the SPDOCRP algorithm displays better numerical performance than the SCALCG algorithm.

Fig. 5
figure 5

Performance based on Nite of SPDOCRP and SCALCG algorithms for the second group of test functions

Full size image
Fig. 6
figure 6

Performance based on CPU time of SPDOCRP and SCALCG algorithms for the second group of test functions

Full size image

So, the preliminary numerical experiments show that SPDOC and SPDOCRP are very effective algorithms for the large scale unconstrained optimization problems.

In addition, for the SPDCG algorithm, the inequality (33) shows that the descent degree of the line search directions of the algorithm becomes higher and higher as the value of c increases, but the performance of the algorithm is not directly proportional to c. In fact, the line search directions generated by the SPDCG algorithm vary with the value of c. What kind of criterion can be used to evaluate the performance of an algorithm? Does the criterion exist? These are still open problems. Of course, the condition number and the descent property are two important factors.

In the end, it should be pointed out that the version 5.3 of CG_ DESCENT (C code) uses a new formula for β k ,

$$ \beta_k =\frac{1}{ y_k^{\mathrm{T}} d_k} \biggl(y_k - \frac{\|y_k\|^2}{y_k^{\mathrm{T}} d_k} d_k \biggr)^{\mathrm{T}}g_{k+1}, $$
(64)

i.e., η≡0 in (62), instead of

$$ \beta_k =\frac{1}{y_k^{\mathrm{T}} d_k} \biggl(y_k - \frac{2\|y_k\|^2}{y_k^{\mathrm{T}} d_k} d_k \biggr)^{\mathrm {T}}g_{k+1}, $$

presented in [10]. In [19], we proved that β k formulated by (64) makes the spectral condition number of the iteration matrix defined by (4) with u=s k optimal.

6 Conclusion

In [18], we presented a rank one updating formula for the iteration matrix of the conjugate gradient methods:

$$ M_{k+1} = M_{k+1}^{shs}+\frac{s_k\xi_k^{\mathrm{T}}}{y_k^{\mathrm {T}}\xi_k}, \quad \forall \xi_k\in\mathbb{R}^n, $$

where the symmetric Hestenes-Stiefel matrix \(M_{k+1}^{shs}\) is defined by

$$ M_{k+1}^{shs} = \biggl(I-\frac{s_ky_k^{\mathrm{T}}}{s_k^{\mathrm {T}}y_k} \biggr) \biggl(I- \frac{y_ks_k^{\mathrm{T}}}{s_k^{\mathrm{T}}y_k} \biggr). $$

If we replace D k+1 with \(M_{k+1}^{shs} \) in (11), the symmetric Perry matrix (6) can be rewritten as

$$ Q_{k+1} = M_{k+1}^{shs}+\sigma\frac{s_ks_k^{\mathrm {T}}}{s_k^{\mathrm{T}}y_k}, $$

that is, if we apply the Powell symmetric technique to D k+1 in (11), we can obtain \(M_{k+1}^{shs}\), then we add a rank one update \(\sigma\frac{s_{k}s_{k}^{\mathrm{T}}}{s_{k}^{\mathrm{T}}y_{k}}\) to \(M_{k+1}^{shs} \), we can also deduce the symmetric Perry matrix (6).

For the parameter σ in SPCG algorithm, besides the cases mentioned above, there also exist other choices, such as \(\sigma =c^{2}\frac{s_{k}^{\mathrm{T}}s_{k}}{s_{k}^{\mathrm{T}} y_{k}}\), \(\sigma =c\frac {s_{k}^{\mathrm{T}} y_{k}}{s_{k}^{\mathrm{T}}s_{k}}\), \(\sigma=c \frac{s_{k}^{\mathrm {T}}y_{k}}{y_{k}^{\mathrm{T}}y_{k}}\), \(\sigma=c \frac{s_{k}^{\mathrm{T}}s_{k}}{y_{k}^{\mathrm{T}}y_{k}}\), \(\sigma=c \frac{y_{k}^{\mathrm{T}}y_{k}}{s_{k}^{\mathrm{T}}s_{k}}\), and so on, where c>0.

For the SSPCGRP algorithm, when ρσ=1, \(\sigma=\frac{y_{k}^{\mathrm{T}}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\), \(\widehat{\sigma}=\frac{y_{r}^{\mathrm{T}}y_{r}}{s_{r}^{\mathrm{T}}y_{r}}\), \(\widehat{\rho}\ \widehat{\sigma}= \widetilde{\sigma}=1\), these formulas (38), (46), (47) and (48) were suggested by D. F. Shanno in [25] and [26]. When \(\rho=\sigma=\widehat{\rho}=\widetilde{\sigma}=\widehat {\sigma }=1\), the SSPCGRP algorithm becomes the memoryless BFGS conjugate gradient method with restarting procedures. Therefore, it is worthy of studying further how the parameters σ and ρ are chosen to construct more effective nonlinear conjugate gradient algorithms.

The condition number of Q k+1 defined by (6) only depends on the parameter σ and the condition number of ρQ k+1 is the same as the one of Q k+1 (see (37)), so, we let ρ=1 and \(\widehat{\rho}=1\) in SSPCGRP algorithm. That is to say, σ can scale the symmetric Perry iteration matrix Q k+1. Therefore, the symmetric Perry conjugate gradient methods have the self-scaling property, Similarly, σ can also alter the maximum and minimum eigenvalues of the Perry iteration matrix P k+1 defined by (4), and P k+1 is a self-scaling matrix. Thus, the parameter σ in the condition (12) is a self-scaling factor, which can alter the condition number of the iteration matrix of the conjugate gradient method.

From (30) and (23), we find that if we restrict that

$$ \bigl|y_k^{\mathrm{T}} s_k\bigr|> \delta \|s_k\|^2, \quad 0<\delta<1, $$
(65)

then under Lipschitz condition, \(|y_{k}^{\mathrm{T}} s_{k}|>\delta\|s_{k}\| ^{2}\ge\delta/L \|s_{k}\|\|y_{k}\|\), i.e., the angle between y k and s k is less than π/2. Thus,

$$ d_{k+1}^{\mathrm{T}} g_{k+1} \le- \lambda_{\mathrm{min}}^{(k+1)} \|g_{k+1}\|^2 \le-\frac{\sigma\delta}{ L^2+\sigma\delta} \|g_{k+1} \|^2<0 $$

and

$$ \lambda_{\mathrm{max}}^{(k+1)} \le\omega_k+\sigma \frac{s_k^{\mathrm {T}}s_k}{s_k^{\mathrm{T}}y_k} =\frac{y_k^{\mathrm{T}}y_k s_k^{\mathrm{T}}s_k}{ (s_k^{\mathrm{T}}y_k)^2}+\sigma\frac{s_k^{\mathrm {T}}s_k}{s_k^{\mathrm {T}}y_k} \le \frac{L^2}{\delta^2}+\frac{\sigma}{\delta}. $$

Therefore, according to Lemma 1, if a descent algorithm satisfies the condition (65), then it is globally convergent for nonconvex functions. So, (65) is also an interesting restarting strategy [19]. In fact, (65) is a uniformly convex condition.

Based on (6) and the relationship between the conjugate gradient method and quasi-Newton method, we let

(66)

where

$$ H_{k+1}^{\mathrm{BFGS}}= H_k-\frac{s_ky_k^{\mathrm{T}}H_k + H_ky_ks_k^{\mathrm {T}}}{s_k^{\mathrm{T}}y_k}+ \biggl( 1 +\frac{y_k^{\mathrm{T}}H_ky_k}{s_k^{\mathrm{T}}y_k} \biggr)\frac {s_ks_k^{\mathrm{T}}}{s_k^{\mathrm{T}}y_k}. $$

So, a new family of quasi-newton method can be obtained from (66), which belongs to Huang’s family, but does not belongs to Broyden’s family. Hence, it is worth probing further to develop new and more effective unconstrained optimization algorithms. For example, we let \(\sigma=c \frac{y_{k}^{\mathrm{T}}H_{k}y_{k}}{s_{k}^{\mathrm{T}}y_{k}}\) in (66).