Quantitative cost comparison of on-premise and cloud infrastructure based EEG data processing

Abstract

High-density, high-sampling rate EEG measurements generate large amounts of measurement data. When coupled with sophisticated processing methods, this presents a storage, computation and system management challenge for research groups and clinical units. Commercial cloud providers offer remote storage and on-demand compute infrastructure services that seem ideal for outsourcing the usually burst-like EEG processing workflow execution. There is little available guidance, however, on whether or when users should migrate to the cloud. The objective of this paper is to investigate the factors that determine the costs of on-premises and cloud execution of EEG workloads, and compare their total costs of ownership. An analytical cost model is developed that can be used for making informed decisions about the long-term costs of on-premises and cloud infrastructures. The model includes the cost-critical factors of the computing systems under evaluation, and expresses the effects of length of usage, system size, computational and storage capacity needs. Detailed cost models are created for on-premises clusters and cloud systems. Using these models, the costs of execution and data storage on clusters and in the cloud are investigated in detail, followed by a break-even analysis to determine when the use of an on-demand cloud infrastructure is preferable to on-premises clusters. The cost models presented in this paper help to characterise the cost-critical infrastructure and execution factors, and can support decision-makers in various scenarios. The analyses showed that cloud-based EEG data processing can reduce execution time considerably and is, in general, more economical when the computational and data storage requirements are relatively low. The cloud becomes competitive even in heavy load case scenarios if expensive, high quality, high-reliability clusters would be used locally. While the paper focuses on EEG processing, the models can be easily applied to CT, MRI, fMRI based neuroimaging workflows as well, which can provide guidance to the wider neuroimaging community for making infrastructure decisions.

Introduction

Electroencephalography (EEG) is a non-invasive, portable and cost-effective measurement technology that can provide a view with sub-millisecond resolution into the activity of the brain. It is routinely used in experimental and clinical neuroscience and in neuropsychology when information is sought about the brain activity with high temporal resolution. Due to advances in measurement technology and analysis methods, the size of data in EEG measurements as well as processing time have been increasing steadily. Theoretical studies [1,2,3] established that at least 64 EEG electrodes were required to avoid spatial aliasing caused by inadequate spatial sampling [4, 5]; therefore, high-density EEG systems with 128 or 256 electrodes and high sampling rates (up to 4 kHz) [6,7,8] are now common. When used with sophisticated processing methods (e.g. ICA-based artefact removal [9], time–frequency and spatiotemporal analysis methods [10,11,12], source localisation based on realistic head models [13,14,15,16], dynamic connectivity analysis [17] or spike and seizure detection [18,19,20], etc.), the execution time of multi-subject analyses may easily increase beyond acceptable limits.

Local compute clusters have been used with success to speed up EEG computations. The majority of EEG experiments are group studies in which individual subject data can be analysed simultaneously, independently from others. Such style of parallel job execution is ideal for multi-node clusters and require no modification in the existing analysis programs. Execution in the cluster can be managed automatically, e.g. using the Parallel Toolbox in MATLAB, a dedicated job management system (e.g. SLURM [21]) or similar in-house solutions. In clinical environments, cluster infrastructure is mainly used for very fast data storage [22] and, optionally, for computational purposes (epilepsy surgery) [23]. Another purpose of using multi-processor clusters is the execution of sophisticated single subject analyses, whose exceptionally time-consuming processing can only be reduced by highly parallel algorithms [24,25,26]. These parallel implementations typically use specialised multi-core or distributed parallel programming technologies such as OpenMP [27] or Message Passing Interface (MPI) [28]. In most developed countries, research groups can have access to large-scale campus or institutional computing facilities, local or national HPC resources (e.g. XSEDE¹ and NIH Biowulf² systems in the US, or EOSC³ in Europe), although this is less common in clinical environments. When these HPC facilities can be accessed free or at a small nominal flat rate, the research group can expect to work without computational or storage resource problems. This paper focuses on situations where the use of local IT resources incur cost.

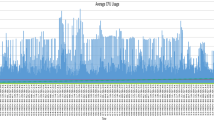
A common problem with on-premises compute resources is utilisation. Depending on whether the required resource capacity during analysis is below or above the one set out during system planning, the cluster might become over-utilised (presenting a performance bottleneck) or under-utilised (leaving valuable resources unused), as illustrated in Fig. 1. On-premises systems perform best when the computation load is uniform. Since EEG data analysis is typically performed unpredictably and in a burst-like fashion, clusters dedicated to processing EEG jobs only will sit idle most of the time.

Fig. 1

Typical resource requirements of EEG data processing in a fixed-size compute cluster. The resource usage varies from zero through under-utilised to over-utilised periods

With the arrival of commercial cloud service providers, outsourcing hardware infrastructure and software operation to third parties have become a viable and inviting alternative. As the generated data volume increases steadily and obtaining funding for local computing equipment becomes ever more difficult, interest in cloud-based techniques is rising rapidly in the neuroscience and neuroimaging communities [29,30,31,32,33]. Cloud systems allow flexible, on-demand scaling of resources that seems as an ideal solution for computations with hard-to-predict execution patterns. A very appealing use case for “EEG clouds” is storing and sharing large collections of EEG data generated by various groups in order to perform large cohort studies, as data sharing is not easily achieved if local clusters or HPC facilities are used. Interest in using cloud computing in EEG-related workflows manifested first in the development of various cloud EEG software frameworks [34,35,36,37], and analysis methods for various application areas, such as seizure detection [38, 39], health monitoring [40, 41], BCI and mobile applications [42, 43].

Interestingly, the question of whether using the cloud is indeed a cost-effective solution in neuroscience has not been addressed to date in a satisfactory manner. Before neuroscientists commit to a long-term cloud service plan or purchase a local cluster system, they should be able to answer questions such as, for instance, the followings:

• Given an estimated monthly compute load in hours, which infrastructure is less expensive for a given number of years, an on-premises cluster or a cloud system?

• What is the cost of a data processing job of a given size on a cluster and in the cloud?

• Does the cluster-to-cloud cost ratio depend on the length of the intended usage period?

• What will be the cost of storing data locally or in the cloud?

• Will a local cluster of a given size provide sufficient resources for executing all data processing tasks and at the same time reduce execution times?

The author is not aware of published cost models that could be used easily to analyse and compare the cost of EEG/ERP data processing tasks executed on a cloud or on-premises compute infrastructure. Since the decision to migrate to the cloud or invest in a local computing infrastructure has long-lasting effects on any research group, it is of prime importance that these decisions are backed by careful analysis. This paper presents cluster and cloud cost models that can form the basis of this process. It also illustrates how the models can be used to explore system alternatives and answer questions such as the ones listed above. While the focus of this work is on EEG/ERP applications, the cost models are general enough to give guidance for the broader neuroimaging community [44] as well.

Related work

The question of buying vs leasing IT infrastructure is not new. Using the net present value, Walker developed hardware level buy-or-lease decision models for CPU [45], and storage system costs [46] and found that lease, in general, is better for single users and medium enterprises operating clusters with tens to hundred nodes, whereas buying is preferred for large organisations. Armbrust et al. gave a comprehensive overview of the cloud computing scene in [47] highlighting three fundamental novelties of cloud systems: (i) the illusion of infinite resources available on demand, (ii) no upfront commitment by users, and (iii) the ability to pay for use on short term basis. They also introduced a simple trade-off cost model that can be used to compare cloud and datacentre costs. In addition, they identified new applications that can greatly benefit from cloud technology. Most of these have important use cases in EEG-related research and clinical systems, e.g. mobile interactive applications: neurofeedback-based rehabilitation, stroke or epilepsy monitoring; parallel batch processing: group EEG data analysis as discussed in this paper; data analytics: EEG time-series analysis and classification; or extending compute-intensive desktop apps: integrating cloud-based HPC resources into compute-intensive EEG processing pipelines. Chen and Sion [48] present a cost model for single and multi-user application classes. The model can be used to make decisions whether or not to outsource to the cloud, but the models are based on CPU cycles that are difficult to generalise for high-level data processing execution steps. Tak et al. developed a comprehensive cloud vs. on-premises cost analysis framework focusing on workload intensity and growth [49, 50]. Their approach is comparable to the one used in this paper but their model seems to be too detailed and complex to be easily applied by researchers in the EEG field. Madhyastha et al. [51] approached the problem from the application scientist’s point of view. They studied the use of the Amazon cloud infrastructure for executing neuroimaging workflows and presented a collection of best practices and cost comparison of cloud vs cluster approaches. Unfortunately, cost estimation was performed based on empirical data without a detailed cost model. Other researchers working on cost models either created models that help setting the price at the service provider end [52, 53], or provided cost analyses of highly specialised genomics [54] or imaging workflows [55] that make their findings hard to generalise.

Methods

EEG research groups typically employ local, on-premises computer equipment of various sizes to process EEG/ERP data. This section develops cost models for such clusters to quantify their cost of installation and operation (Total Cost of Ownership, TCO). A cloud cost model is then presented that characterises the cost of computation, storage and networking in a given cloud environment. While there can be found several sophisticated vendor-specific TCO calculators for large data centre and compute facility cost calculations [56] and even for cloud infrastructures [57], the focus here is on the development of a simple yet reliable model for the neuroscience community that can be used by practicing researchers who need efficient and cost-effective EEG data analysis systems. The overall goal of the model development process is to quantitatively describe the cost of both the local clusters and their cloud alternatives at an easily applicable level, yet with sufficient accuracy, in order to determine the cost of computation and storage in both types of infrastructure, and to be able to compare these computing systems objectively.

On-premises compute cluster cost model

We start the cost model development with local, on-premises clusters. These may include any computing system (computers of a given research group, departmental and campus clusters or national HPC resources) if their users must pay for their use. Free computational resources are ignored in this paper.

The total cost ${C}_{cluster}$ of a local compute cluster can be broken down into fixed and variable cost components. Fixed cost represents capital expenditure that does not change with usage time, whereas variable cost describes operational costs that depend on the duration for which the cluster is in use.

$$C_{cluster} = C_{fixed} + C_{variable}$$

(1)

The fixed cost term covers the cost of hardware equipment (computers, storage servers, cluster networking equipment) and facilities cost (cooling equipment, building alterations):

$$C_{fixed} = N \cdot C_{node} + C_{storage} + C_{network} + C_{facilities}$$

(2)

where $N$ is the number of nodes/computers in the cluster, ${C}_{node}$, ${C}_{storage}$ and ${C}_{networking}$ represent the hardware equipment cost of each cluster building block, and ${C}_{facilities}$ cover the costs of creating a suitable server room for the cluster. If proper location is already available, facilities cost can be left out from the calculations. If the cluster is placed into a leased facility, the rental fee can be incorporated into the variable cost below. Clusters with fewer than approximately 30 (core count 120) desktop computers can be installed in a computing lab room, and may be operated without dedicated cooling if the compute load is small to moderate. In such cases, ${C}_{facilities}$ can also be dropped from (2). If rack-mounted servers are used, smaller rooms will suffice but adequate cooling is required.

The term ${C}_{variable}$ includes operational costs, such as electricity, parts replacement, depreciation, software license and technical staff costs. These are easy to forget but evidence shows that up to two third of the overall cost is attributable to variable cost [58]. Assuming a uniform monthly operational cost (the same average computing load, staff working hours and replacements each month), the following linear model describes the variable cost for the entire lifetime of the system:

$$C_{variable} = m \cdot \left( {C_{electricity} + C_{replacement} + C_{staff} + C_{depreciation} } \right) + C_{software} ,$$

(3)

where $m$ is the lifetime of the cluster system in months. The individual cost terms in (3) are given as follows. Electricity cost includes the cost of running the computers, storage units, cooling system and the networking equipment. In the simplest case, if the cluster operates in a 24/7 mode and computers are not under an energy saving operating scheme, the monthly cost of electricity is calculated from the average power consumption of the hardware devices.

$$C_{electricity} = \frac{24 \cdot 365}{{12 \cdot 1000}}\left( {N \cdot P_{node} + P_{storage} + P_{network} + P_{cooling} } \right) \cdot c_{electricity} ,$$

(4)

where ${P}_{node}$, ${P}_{storage}$, ${P}_{network}$, and ${P}_{cooling}$ represent the power consumption of the hardware components in Watts, and ${c}_{electricity}$ is the unit electricity cost given in USD/kWh. When data is stored on the internal hard disks of the cluster computers (no specialised storage server), storage power consumption is already included in ${P}_{node}$, hence ${P}_{storage}$ can be dropped. If idle and peak compute power values are significantly different and computers can go into sleep mode automatically, a more sophisticated power calculation is required that reflects peak, idle and sleep operating modes as well as the execution time of the EEG/ERP processing jobs. The same applies to storage units if they that can also go into low-power mode. Since EEG processing is normally not a 24/7 operation, processing is performed in batches with longer breaks in-between, cluster nodes operate alternately in peak and idle/sleep mode. In idle mode, only the network is active, compute nodes and storage units consume less power. If sleep mode is enabled, nodes can switch into low-power mode after a predefined time is spent in idle mode. In peak mode, compute nodes execute jobs and CPU power usage is at maximum. Assuming $h$ hours spent with processing EEG jobs each month, the power mode-aware electricity cost formula is as follows.

$$C_{electricity} \left( h \right) = \left[ {\frac{24 \cdot 365}{{12 \cdot 1000}}\left( {N \cdot P_{node}^{idle} + P_{storage}^{idle} + P_{network} + P_{cooling} } \right) + h\left( {\left( {P_{node}^{peak} - P_{node}^{idle} } \right) - \left( {P_{storage}^{peak} - P_{storage}^{idle} } \right)} \right)} \right] \cdot c_{electricity}$$

(5)

If the system is enabled for sleep mode, ${P}_{node}^{idle}$ and ${P}_{storage}^{idle}$ should be replaced with ${P}_{node}^{sleep}$ and ${P}_{storage}^{sleep}$ to reflect the correct power consumption.

Replacement cost is the average monthly cost of hardware parts replaced or repaired in order to keep the cluster operational. A first order estimate of the cost of repair per year can be given as a percentage $r$ (e.g. 0.1–10%) of the total cluster hardware cost

$$C_{replacement} = r\left( {N \cdot C_{node} + C_{storage} + C_{network} } \right).$$

(6)

Staff cost covers all the personnel costs associated with operating the cluster. Since small clusters can be operated and maintained without employing full-time technical support staff, monthly staff cost is calculated on an hourly basis using the hourly wage ${c}_{staff}^{hour}$.

$$C_{staff} \left( h \right) = h \cdot c_{staff}^{hour} {.}$$

(7)

Cost components (hardware, salary and electricity costs) should be adjusted to the local rates and hardware energy consumption characteristics when the model is used for actual calculations.

The calculation of depreciation cost may vary by institutions and countries. Readers are encouraged to substitute their depreciation model complying with regulations into (3). In the rest of this paper, depreciation cost is ignored on the basis that it is a non-cash expense that will not increase the capital expenditure of resources for the user.

Cloud cost model

This section develops a cost model for performing EEG data processing in the cloud. The model development is simpler than for local clusters since all major cloud service providers operate under similar pricing schemes; they offer resources on pay-as-you-go, usage-based, on-demand fix-rate price [35, 59, 60]. Using long-term reserved instances, up to 75% discount is available but since EEG processing is rather unpredictable, this option is not considered in the developed cost model. Resources accounted for in the cloud model are the main cloud infrastructure elements; i.e. compute, storage, and networking services. There is a rich set of services offered on top of these infrastructure components, e.g. MapReduce/Spark data processing, containers, various database solutions, serverless Function/Lambda execution, and so on, but all of these can be incorporated into the proposed cloud model as trivial adjustments.

Tables 1, 2 and 3 list the unit price of the resources of the major cloud providers. Table 1 includes the hourly cost of virtual machine (VM) instances (compute nodes). Since vendors offer a wide selection of general, compute, memory or storage optimised hardware configurations (Amazon⁴: over 160, Microsoft⁵: over 240, Google⁶: over 60), only a representative set is included in Table 1. For up-to-date configurations and pricing information, the reader should consult the cloud vendor websites.

Table 1 Cloud compute instance costs at the major service providers

Table 2 Cost of storage at the major cloud providers

Table 3 Cost of networking at the major cloud providers

Each vendor offers a wide variety of structured and non-structured storage options. Typical unstructured storage service types and their cost is listed in Table 2. Network costs are given in Table 3.

The cost of performing data processing in the cloud is the sum of the compute instance, storage and network usage prices. Formally, the total cost of the cloud for a period of $m$ months is given as

$$C_{cloud} \left( {m,h} \right) = C_{compute} \left( {m,h} \right) + C_{storage} \left( {m,v, d} \right) + C_{network}$$

(8)

Parameters $h$, $v$ and $d$ are explained below. The compute cost is calculated from the hourly VM instance rate $c\_VM$ assuming $h$ hours per month average data processing time.

$$C_{compute} \left( {m,h} \right) = m \cdot h \cdot c_{VM}$$

(9)

To illustrate higher cloud service cost modelling, if, for instance, the compute node will run a container service, such as Kubernetes, ${c}_{VM}$ should be increased by the hourly cost of the container (e.g. 0.05 USD/h per container on Google Cloud). Similarly, if a MapReduce job will be executed, ${c}_{VM}$ should reflect the hourly cost of the job execution cluster.

The storage cost model is slightly more complex. Assuming that a research group follows a uniform experimental regime, in which approximately the same number of EEG measurements are performed each month and the measured data ($d$ GBs) is uploaded to cloud storage monthly, the amount of stored data will grow with monthly increments of $d$. For instance, performing 60 measurements each month with an estimated 600 MB file size per measurement, approximately 35 GB new data will be added to the cloud storage every month. Since storage is billed monthly based on the total amount of data stored, in each month we will pay more due to the increasing data volume. The total cost of storing data cumulatively over $m$ months is the sum of the following arithmetic series

$$C_{storage} \left( {m,v, d} \right) = \frac{m}{2}\left[ {2v + \left( {m - 1} \right)d} \right]c_{st} ,$$

(10)

where $v$ is the initial data volume (existing data measured in the past and uploaded to the cloud), $d$ is the monthly data increment in GBytes and ${c}_{st}$ is the unit cost of storage in USD/GB per month. If $v>0$, existing data should be migrated to the cloud to create a central data repository. If a non-uniform measurement schedule is used, the average monthly data size should be estimated and used in the model to approximate the storage costs.

The model for network cost is straightforward. Ingress network traffic (data upload) is free at each network providers. Egress traffic (data download) is charged based on the amount of data transferred, but our assumption is that the output of EEG processing is largely reduced in size compared to the input, and will be downloaded to local computers infrequently. Consequently, egress traffic cost can be ignored, thus ${C}_{network}=0$. In exceptional cases, where downloading large amounts of data is unavoidable, the extra networking cost must be added to the formula; $D$ is the size of data downloaded per month in GBs. Accessing cloud services from the Internet requires an external IP address for the VM instance. Starting with 1 January 2020, Google sets a charge for external IP addresses ${c}_{IP}$ on an hourly basis. In this case, the second network cost formula of (11) should be used.

$$\begin{gathered} C_{network} \left( D \right) = D \cdot c_{egress } \hfill \\ C_{network} \left( {D,m,h} \right) = D \cdot c_{egress } + m \cdot h \cdot c_{IP} \hfill \\ \end{gathered}$$

(11)

Multi-instance and multi-core cloud compute cost model

Cloud technology is used not only to store large amount of data and reduce operation costs but also to access additional compute resources on-demand in order to complete data analysis faster than on a local computer system. EEG/ERP group studies typically require the repeated execution of the same processing pipeline for the subjects in a group. For instance, using only one computer, processing 60 subjects takes 60 times longer than 1 subject. Using multiple cloud virtual machine instances, the processing time can be greatly reduced; 60 cloud virtual machines can complete the 60-subject job in the same time as for 1 subject. More generally, using $p$ VM instances, $1\le p\le K$ where $K$ is number of subjects in the group, the overall EEG processing time can be reduced from ${T}_{seq}=K\cdot h$ to ${T}_{par}=K\cdot h/p$, where $h$ is the execution time for one subject in hours. The cost of processing the group on single cloud VM is $(K\cdot h)\cdot {c}_{VM}$, whereas the cost of processing the subjects in parallel using $p$ instances is $K\cdot \frac{h}{p}\cdot (p\cdot {c}_{VM})$. The two costs are identical; therefore, execution time can be reduced for independent parallel jobs by using multiple instances at no increase in cost.

In addition to using multiple virtual machines, VMs with higher number of cores are also available. This can provide a further reduction in execution time if single subject jobs can benefit from multi-core parallelism. As illustrated in Fig. 2, the cost of multi-core VMs increases linearly with core count. As in the multi-instance case, this also results in time reduction with no increase in cost, if ideal speedup ${S}_{p}=p$ can be achieved. In this case, job execution cost is given as $\frac{h}{p}\cdot ({c}_{VM}^{1}\cdot p)$ where $p$ designates the number of cores and ${c}_{VM}^{1}$ is the cost of a single-core instance given by a linear regression model fitted to the multi-core VM instance cost data.

Fig. 2

Multi-core Google Compute Engine VM costs in function of core count with fitted linear models (dotted lines) onto N1 VM types

Cluster and cloud comparison: break-even analysis

While the cost models are useful in their own right in estimating the cost of a cluster or execution in the cloud, they can be more usefully employed in break-even analysis, i.e. to decide whether a local cluster or the cloud is the economically more feasible execution environment for a given type of processing task. This comparison is elaborated in the rest of this section. Using the proposed cluster and cloud cost models, the following inequality is set:

$$C_{cluster} \left( {m,h} \right) < C_{cloud} \left( {m,h} \right).$$

(12)

Solving it for month $m$, one can determine whether there is a break-even point, beyond which the cost of the cloud is higher than that of a local cluster. By expanding Eqs. (1) an (8), the inequality (12) becomes

$$N \cdot C_{node} + C_{storage} + C_{network} + C_{facilities} + m\left( {C_{electricity} + C_{replacement} + C_{staff} } \right) + C_{software} < C_{compute}^{cloud} \left( {m,h} \right) + C_{storage}^{cloud} \left( {m,d} \right) + C_{network}^{cloud} .$$

(13)

After substituting the detailed formulae for the terms in (13), we arrive at

$$N \cdot C_{node} + C_{storage} + C_{network} + C_{facilities} + m\left( {\left[ {2 \cdot 365\left( {N \cdot P_{node}^{idle} + P_{storage}^{idle} + P_{network} + P_{cooling} } \right) + h\left( {\left( {P_{node}^{peak} - P_{node}^{idle} } \right) + \left( {P_{storage}^{peak} - P_{storage}^{idle} } \right)} \right)} \right]c_{electricity} + C_{replacement} + C_{staff} } \right) + C_{software} < m \cdot h \cdot c_{VM} + \frac{m}{2}\left[ {2v + \left( {m - 1} \right)d} \right]c_{st} + C_{network}^{cloud} ,$$

(14)

which, after rearrangement, becomes

$$0 < \frac{{dc_{st} }}{2}m^{2} + \left( {h \cdot c_{VM} + vc_{st} - \frac{d}{2}c_{st} - \left[ {730\left( {N \cdot P_{node}^{idle} + P_{storage}^{idle} + P_{network} + P_{cooling} } \right) + h\left( {\left( {P_{node}^{peak} - P_{node}^{idle} } \right) + \left( {P_{storage}^{peak} - P_{storage}^{idle} } \right)} \right)} \right]c_{electricity} - C_{replacement} - C_{staff} } \right)m + C_{network}^{cloud} - N \cdot C_{node} - C_{storage} - C_{network} - C_{facilities} - C_{software} .$$

(15)

Inequality (15) then can be solved for $m$ with different values of $N, h, d$ and $v$ as input parameters. The roots are given as

$$y_{1,2} = - b \pm \sqrt {b^{2} - 2dc_{st} c} /dc_{st} ,$$

where

$$b = h \cdot c_{VM} + vc_{st} - \frac{d}{2}c_{st } - \left[ {730\left( {N \cdot P_{node}^{idle} + P_{storage}^{idle} + P_{network} + P_{cooling} } \right) + h\left( {\left( {P_{node}^{peak} - P_{node}^{idle} } \right) + \left( {P_{storage}^{peak} - P_{storage}^{idle} } \right)} \right)} \right]c_{electricity} - C_{replacement} - C_{staff}$$

and

$$c = C_{network}^{cloud} - N \cdot C_{node} - C_{storage} - C_{network} - C_{facilities} - C_{software} .$$

The solution of the inequality ($m>max({y}_{1},{y}_{2})$) describes after how many months a cloud solution becomes more expensive than an on-premises cluster infrastructure for executing data processing jobs.

Results and discussion

This section illustrates how the cluster and cloud cost models can be used to determine the cost of EEG computations and data storage. For cluster cost calculations, three hypothetical cluster configurations will be used, whose parameters are listed in Table 4. The first, “BUDGET”, configuration is based on entry-level desktop computers. It is assumed that the BUDGET cluster will use the existing network infrastructure at no additional cost, and no replacements or cluster administrator staff costs are planned over the lifespan of the cluster. The second, “NORMAL”, configuration, which is built from more powerful desktop computers, includes its own dedicated cluster network. As before, no replacement, staff and cooling costs are considered. The third configuration is a HIGH_END cluster, built from server-grade computers using a dedicated high-speed network and large-capacity network storage device. Replacement, staff and cooling costs are also included in this configuration.

Table 4 Cost model parameters for three different cluster configurations

Cost of a computing job

Execution cost on a local cluster

The cost of a particular EEG processing job on a cluster infrastructure can be calculated using Eq. (1) after substituting the terms defined in Eqs. (2)-(7). Using the parameters in Table 4, and assuming 100% cluster utilisation and a 4-year lifespan, the cost of 1 cluster CPU-hour, ${C}_{hour}={C}_{cluster}(N)/(N\cdot 30\cdot 24)$, of the three clusters are ${C}_{hour}^{A}=0.0273$ USD, ${C}_{hour}^{B}=0.0614$ USD, and ${C}_{hour}^{C}=0.6623$ USD. Assuming an EEG experiment with 2 × 30 subjects and 1-h per-subject processing times, the cost of the 60-h total job is thus ${C}_{job}^{A}=60{\cdot C}_{hour}^{A}=1.64$ USD, and similarly, ${C}_{job}^{B}=3.68$ USD, ${C}_{job}^{C}=39.74$ USD for clusters A, B and C, respectively. As shown in Fig. 3, increasing the size of the cluster reduces the overall execution time and, as discussed in Sect. 3.2.1, the cost of the job is independent of the number of cluster nodes used during the computation if subject processing can be performed independently.

Fig. 3

Execution time of a 60-subject (1 h per subject) data processing job in function of cluster size

The above hourly rates are computed at 100% cluster utilisation. This level of utilisation can only be achieved if all nodes of the cluster compute analysis jobs continuously, in 24/7 mode. If, on the other hand, the cluster is used only by one research group or shared by a small number of groups with intermittent, burst-like usage pattern, a much lower utilisation rate is achieved in practice. As the utilisation level falls, both the hourly and the final job costs will increase significantly. The utilisation factor $U$ of the cluster is the ratio of the actual CPU hours used for computation to the total available cluster CPU hours. When a cluster is used ${h}_{total}$ CPU-hours per month for job processing, the utilisation factor becomes

$$U = \frac{{h_{total} }}{N \cdot 30 \cdot 24},$$

which is inverse proportional to cluster size $N$. To account for the effect of utilisation on the CPU-hour cost, a utilisation-corrected cluster CPU-hour cost ${C}_{hour}^{*}$ should be used, defined as

$$C_{hour}^{*} = \frac{{C_{cluster} \left( N \right)}}{U \cdot N \cdot 30 \cdot 24} = \frac{{C_{cluster} \left( N \right)}}{{h_{total} }}.$$

(16)

From this, the cost of the compute jobs can be expressed as ${C}_{jobs}^{*}={{h}_{jobs}\cdot C}_{hour}^{*}.$ Note that if the cluster is not shared with other groups, i.e., ${h}_{jobs}={h}_{total}$, the job cost reduces to ${C}_{jobs}^{*}={C}_{cluster}(N)$, demonstrating that the cost of a monthly job unit is equal to the monthly cost of the cluster, regardless of how many hours the cluster is in use. Figure 4 illustrates the cost of a cluster CPU-hour in function of cluster utilisation when the cluster is used 240 h a month for EEG data processing tasks. These results explain why a centralised cluster facility shared with several other user groups is preferable as this has the potential to achieve higher utilisation rates and lower unit cost.

Fig. 4

Effective cluster CPU-hour costs for the three cluster types in function of cluster utilisation

Figure 5 compares the CPU-hour costs of non-shared (dedicated) clusters with shared centralised clusters and cloud virtual machines. Shared cluster utilisation levels are set to 90, 50 and 25%. The results show that the CPU-hour cost of the non-shared, dedicated clusters (Cluster A and C in Fig. 5) increases quickly with the cluster size. The CPU cost of the shared clusters decreases with cluster size and converges to a constant value. This is demonstrated especially for Cluster C 90%, 50% and 25% in Fig. 5 (right panel). Note that the CPU cost in the cloud is constant and whether this cost is lower or higher than the local cluster CPU cost depends on the cluster configuration. In Fig. 5, the shared cluster CPU cost is always lower than the cloud cost for Cluster A, but always higher for Cluster C. Since cloud providers use enterprise-grade servers that are comparable to Cluster C type nodes of our hypothetical cluster configurations, it is not surprising that the 90% percent utilisation Cluster C approaches the cloud CPU-cost. It can be concluded, that using a cluster solely by a single group is clearly a bad economical decision; it results in orders of magnitude higher CPU-hour costs than other alternatives. Shared, centralised clusters are preferable as on-premises facilities but if high-quality equipment is used, higher than 90% utilisation rate must be maintained for achieving cloud-competitive cost.

Fig. 5

The per-job and fix-utilisation cluster CPU-hour costs compared to CPU-hour cost of the three major cloud providers. Per-job compute load is 240 h, the fixed utilisation rates are 90, 50 and 25%. The left plot shows the cost curves for the BUDGET, while the right for the HIGHEND cluster configurations

Execution cost in the cloud

The cost of executing $h$ hours per month for EEG analysis jobs in the cloud using $p$ virtual machine instances is simply the product of the cost of the virtual machine instance and the time it is used for during job execution, which is expressed as

$$C_{job}^{cloud} = \frac{h}{p} \cdot \left( {p \cdot c_{VM} } \right) = h \cdot c_{VM}$$

(17)

The cluster and cloud job cost models allow us to compare the cost of the two types of systems for actual EEG data processing tasks. Figure 6 compares the cost of processing in our hypothetical Cluster A, B and C configurations to that of the cloud, in function of the computational load given in number of hours per month. As before, a 4-year lifespan is assumed for the clusters. The figure shows that the cluster-cloud break-event point depends on the cluster size and the processing load. For our initial 240-h per month target computing load, Cluster A is cheaper than the cloud only for p = 1; clusters B and C are more expensive than the cloud irrespective of cluster size at this target load. Large compute loads give different results. For cluster A, the cloud becomes more expensive at h > 800 (p = 10, 8-core VM) and h > 1500 (p = 10, 4-core VM) or h > 2200 (p = 30, 8-core VM). The thresholds for cluster B are h > 1200 (p = 10, 8-core VM) and h > 2200 (p = 10, 4-core VM). For cluster C, the cloud is a cheaper option if p > 5 and h < 3000. If, however, our goal is to reduce execution time considerably (p > 10), the cloud is the best alternative for moderate loads. As we increase the number of compute nodes (p > 30), the load threshold after which the cloud becomes more expensive is increasing accordingly.

Fig. 6

Comparison of job execution costs of different cluster configurations /BUDGET (a), NORMAL (b) and HIGHEND (c)/ with 4 and 8-core Google Cloud virtual machines in function of computing load

Cost of storage

Local cluster

If a local cluster uses the built-in hard disks of the nodes (e.g. 1 TB/computer) and a distributed file system for storing data (e.g. in cluster configurations A and B) provides sufficient storage capacities for the analyses, the cost of data storage is already part of the operational cost of the cluster. If more storage is required, additional hard disks can be installed in the cluster nodes. The price of 1 GB hard disk storage is approximately 0.02 USD at current HDD prices. Using 4–6 TB disks per node, large clusters can provide storage capacity in the range of 200 TBs, which is more than sufficient for an EEG research group.

In clusters that use a dedicated network storage, the price is increased by the cost of the storage hardware. These systems normally operate with redundant RAID storage schemes, so the achieved storage capacity can be as low as 50% of the raw disk capacity, practically doubling the per-gigabyte cost. Depending on the hardware chosen, the number of disks in a storage unit can vary from 4 to 24, resulting in an overall storage capacity of (assuming 6 TB disks and 50% storage rate) 12 to 72 terabytes. Assuming EEG files of size 0.5 GB, and that a group is generating 240 files a month for 4 years, at least 6 TB storage capacity is required, which will be provided by this storage option.

The actual per-gigabyte storage cost depends on the chosen HDD models, but practically it varies between 0.01 and 0.1 USD. It is important that the per-gigabyte cost in a local cluster is projected to the entire lifetime of the cluster, unlike in the case of cloud storage options. Thus, storing e.g. 10 TB data for 1 or 4 years at 0.02 USD/GB base price will cost the same amount, 200 USD.

Cloud storage

Cloud providers charge for storage on a gigabyte-per-month basis. The cost of storing 1 GB data for one month is approximately 0.02 USD at each major cloud providers. Archival storage with infrequent access can be accessed cheaper. In this analysis, the cost of cloud storage is examined in three different scenarios; (i) storing an existing set of data without adding new measurements (e.g. for archival or sharing data with others), (ii) uploading a new set of measurement data each month, and (iii) the combination of the first two cases, i.e. first uploading existing datasets then adding new measurements monthly. The cost of these cases are calculated next using the general cloud storage cost formula given in Eq. (10).

Storing existing data Assuming an existing data set of size $v$ gigabytes, the cost of storing the data in the cloud for $m$ months is ${C}_{storage}\left(m\right) = m\cdot v\cdot {c}_{st} .$ As an example, storing e.g. 500 GB or 10 TB data in the cloud at c_st = 0.026 USD GB/month base price for 4 years would cost 624 or 12,480 USD, respectively. Note that these prices are significantly higher than the cluster storage prices that are based on HDD-only cost. If data are uploaded for archival purposes and accessed infrequently, significantly reduced prices are available. Using backup options (nearline: 0.010 USD and coldline: 0.007 USD), the cost of storing the same amount of data can be reduced to 240 and 4800 USD (nearline) or 158 and 3360 USD (coldline), respectively.

Monthly upload only If only new measurements of size $d$ gigabytes are uploaded to the cloud each month in a uniform manner over a period of $m$ months, and stored accumulatively, the cost of storage is calculated as ${C}_{storage}\left(m,d\right)=m\left(m-1\right)d\cdot {c}_{st}/2 .$ As an illustration, assuming 2 × 30 subjects measured weekly (or monthly), the amount of data to upload is approx. 13.2 GB (52.8 GB) at f_s = 512 Hz or 52.8 GB (211 GB) at f_s = 2048 Hz. Calculating with d₁ = 50 GB and d₂ = 200 GB per month, the cost of cumulative data storage for 4 years is 1466.4 and 5865.6 USD, respectively. Figure 7 plots the cost function for different monthly upload values in the range of 1 to 500 GB/month using standard ‘hot’ as well as ‘coldline’ storage rates.

Fig. 7

Cost of incremental storage in the cloud in function of storage duration. Coldline storage cost is plotted with dotted line

Combined accumulated data storage When the previous two options are combined, the general cloud storage cost calculation formula (10) should be used. Figure 8 shows how the upload of an initial 1 TB data effects to overall monthly accumulated storage cost. It is important to highlight that the above storage cost estimation is based on using 16 bit/sample datafile formats. If data is stored in 3-byte per sample file format (e.g. BDF), or 4-byte (single, float) or 8-byte (double) data formats, the cost of storage will increase considerably. Storing intermediate data files will also increase storage costs.

Fig. 8

Cost of combined storage in the cloud in function of storage duration. Initial upload size is 1 TB. Note the initial cost increase at the start. Coldline storage cost is plotted with dotted line

If data is accessed infrequently after processing, the cost of long-term storage can be decreased considerably if data is moved from standard storage to coldline once processing is complete. This strategy will use the expensive ‘hot’ storage only for the time of processing. The cost function for this cost-optimised version is

$$C_{storage}^{*} \left( {m,d} \right) = mdc_{st}^{hot} + \frac{m}{2}\left[ {2v + \left( {m - 1} \right)d} \right]c_{st}^{coldline} .$$

(18)

Figures 7 and 8 also illustrate to what extent coldline storage can reduce the overall storage cost (dotted line). The cost-optimised version is within the price range of the cost of a network attached storage system with a capacity of 32–64 terabytes.

Having discussed the cost of storage in the cloud, we should take a step back and assess whether data can be stored in the cloud safely. Medical data storage is governed by strict legal regulations. Their storage and transfer can be limited to an institute, a country or a higher entity, such as EU countries. If data can be stored in a cloud storage system, there need to be guarantees that data is stored securely. Data by default is stored encrypted when written to disks. If required, encryption keys can be managed by customers (customer-managed encryption keys) or if keys must be stored locally, by customer-supplied encryption keys. Data communication is also protected by default Encryption in Transit methods that can be strengthened, if necessary, by the use of IPsec, Virtual Private Network to cloud resources. Shielded virtual machines are normally available at no extra cost that provide stronger protection against tampering with during execution. Cloud vendors also comply with several regulatory requirements, e.g. with the Health Insurance Portability and Accountability Act of 1996 (HIPAA) in case of medical data. All these measures result in highly secure data storage systems that might be more secure and trusted than an on-premises data storage system.

Infrastructure selection

After the preceding, individual analyses of the computation and data storage costs, we now turn to comparing the cost of a local on-premises cluster with the cloud in terms of the total cost of ownership (TCO). As seen in the preceding sections, cluster cost is close to constant whereas cloud cost increases with usage, i.e. as the compute load and size of the stored data increase. The goal of the TCO analysis is to determine after how many months the cloud solution would become more expensive than a local cluster. Using the break-even model defined in Eq. (15), the three hypothetical clusters introduced earlier are compared with the cloud infrastructure, using a representative set of processing workflow parameters. Equation (15) is solved for $m$ (months) at varying input parameter values for $h$ (workload size in hours) and $d$ (monthly upload in GBs). Table 5 presents the results for the break-even values for different cluster types and sizes, expressed in years. Values highlighted in bold indicate that for the parameter combinations of that cell, the cloud is more cost-effective than an on-premises cluster when a 4-year useful lifetime is planned for the clusters.

Table 5 Results of the cluster-cloud break-even analysis

The range of the input parameters is established based on common EEG measurement and processing settings. Assuming that the number of electrodes vary from 19 to 256, the sampling frequency from 256 to 2048 Hz, and data stored as 2 bytes/sample, the size of 1-min measurement varies between 570 kB and 60 MB. Assuming an average experiment duration of 10 min, the average data file size is between 5.6 and 600 MBs. If the number of subjects measured each month varies between 20 and 100, the total uploaded data is in the range of 112 MB–58.6 GB. In order to incorporate longer measurements, the final range for $d$ is from 1 to 300 GB. The compute load is varied from 50 h (approximately 1 h/subject) up to 3000 h. For the one and 5-node clusters, the maximum is 720 and 1300 h. The maximum is set to represent computational problems requiring tens of compute hours per subject. The cost of the cloud virtual machine instance ${c}_{VM}$ is set to 0.2 USD/h whereas the cost of storage ${c}_{st}$ is 0.02 GB/month.

The financial analysis indicates that using the cloud for short term is an economically justifiable alternative to running a local cluster system. If a team does not want to commit long term to a local infrastructure, the cloud option should be preferred. High-end clusters are always more expensive than the cloud. Budget and normal cluster systems are only cost-efficient if operate under very high compute load and store large amounts of data. To conclude the analysis, assuming the typical usage characteristics of an EEG research group, any cluster consisting of more that 10–15 nodes will be more expensive than the cloud solution.

Note that the calculations in this paper rely on data obtained at the time of writing and the model only serves to indicate major cost trends. For making real decisions, calculations should be carried out using up-to-date hardware cost and cloud pricing data and specific local operational factors (utility and staff cost) should be taken into consideration.

Budget planning

In addition to finding out when a cloud infrastructue is more expensive, another important question is to determine how much data one can process in the cloud from the budget originally allocated for creating an on-premises cluster. In this scenario, we are interested in the hours $h$ we can process and data $d$ we can upload each month during the lifespan $m$ of the cluster. Changing the direction of the inequality in (15) we are now searching for values of $h$ and $d$ that satisfy

$$C_{cluster} \left( {m,h} \right) > m \cdot h \cdot c_{VM} + \frac{m}{2}\left[ {2v + \left( {m - 1} \right)d} \right]c_{st} + C_{network}^{cloud}$$

(19)

Fortunately, $h$ and $d$ are related, since the processing time $h$ depends on the data size $d$

$$h = A \cdot d$$

The exact value of $A$ can be determined with trial runs, after which the inequality can be solved for $d$.

If, instead of the processed data size, one is interested in calculating the number of experiments that can be analysed from the cost of the target cluster, $h$ and $d$ should be replaced by $k\cdot {h}_{exp}$ and $k\cdot {d}_{exp}$, where $k$ is the number of experiments, ${h}_{exp}$ is the processing time of the experiment of size ${d}_{exp}$. The experiment data size is dependent of the the number of electrodes, sampling rate, bytes-per-sample, and the measurement length. If these parameters are known, the inequality can be solved for $k$.

$$C_{cluster} \left( {m,h} \right) - C_{network}^{cloud} > m \cdot k \cdot h_{\exp } \cdot c_{VM} + \frac{m}{2}\left[ {2v + \left( {m - 1} \right)k \cdot d_{\exp } } \right]c_{st}$$

$$k < \frac{{C_{cluster} \left( {m,h} \right) - C_{network}^{cloud} - m \cdot v \cdot c_{st} }}{{m\left( {h_{exp} \cdot c_{VM} + \frac{{\left( {m - 1} \right)}}{2}d_{exp} \cdot c_{st} } \right)}}$$

Finally, we look at how the model can be used in project budgeting. Assuming that the cloud infrastructure has already been decided upon, the next step in the planning process is the calculation of the amount required in total and each month for carrying out the necessary data analysis tasks. By replacing ${C}_{cluster}(m,h)$ with the unknown budgeted cost $B$, the following equation provides the solution. From $B$, the monthly cloud budget can be derived easily.

$$B = m \cdot k \cdot h_{\exp } \cdot c_{VM} + \frac{m}{2}\left[ {2v + \left( {m - 1} \right)k \cdot d_{\exp } } \right]c_{st} + C_{network}^{cloud}$$

(20)

The aforementioned results illustrate that choosing between a local cluster infrastructure and the cloud is a complex task. The outcome depends on the complex interaction of a number of input parameters as well as EEG measurement settings and workload characteristics. In general, it can be observed that if very high computational capacity is required, an adequately sized local cluster may be more cost-effective, provided the efficiency of the cluster is kept high (e.g. shared with other groups). Similarly, if large amount of measurement data should be stored accumulatively in a frequently accessible manner, a local storage option might be more advisable. On the other hand, if EEG processing is characterised by relatively light compute and storage requirements, cloud execution is expected to be more cost effective. The presented models can help in the detailed analysis of these parameters within the specific data processing context of the given research group.

In those cases, for which cloud processing is more cost effective, there are additional benefits as well. The elastic scaling of the cloud can drastically decrease job execution times. These can be especially important in large cohort studies (e.g. groups with beyond 100 subjects or in large clinical studies); execution speed can increase up to two orders of magnitude without additional cost. The models in this paper assumed that the programs are executed in the cloud the same way as locally, without modification. Using parallel algorithms, execution time can be decreased considerably, even for individual subject analysis. This opens up new opportunities both for further reduction in execution time and for using more sophisticated models and analysis methods that would otherwise be too time-consuming when executed the traditional way. Every cloud vendor offers high-performance GPUs (graphics processing units) that can provide several orders of magnitude higher computational performance than multi-core CPUs. While GPU hourly costs (1.46–2.48 USD/h) are typically higher than CPU rates (0.1–4 USD/h), an execution speedup of, say, 300x, can reduce both the execution time and the overall cost of the compute resource to a fraction of the original price. The downside is that GPU execution is a disruptive technology, code must be modified substantially to efficiently execute on GPUs. With increasing support for GPUs in existing EEG execution frameworks and the implementation of new, efficient GPU data processing algorithms, this mode of execution has the potential to revolutionise EEG processing.

Conclusion

As cloud technology turns ubiquitous and equipment grants become ever more scarce, the neuroimaging community is actively investigating how cloud solutions could decrease the cost of research, while at the same time reduce execution time, increase productivity, promote data and computer program sharing across research groups. This paper attempted to contribute to this effort by developing and presenting a cost model that can aid researchers who need to process large amounts of EEG data in deciding whether a local cluster or a cloud infrastructure is the more economical solution for their data analysis needs. The proposed cluster and cloud cost models incorporate all the important cost factors encountered during the procurement and operation of these systems. The models can be used for calculating the cost of EEG data processing workflows in various configurations and thus provide a sound basis for decision-making. They can also be used for comparing the cost of alternative cluster and cloud infrastructures, or computing the cost of cloud usage for given data processing tasks. The analysis also showed that the underlying infrastructures have special usage and operational characteristics. Clusters should be operated at high utilisation rate to keep costs low; in the cloud, careful management of virtual machine instances and data transfer between frequent and infrequent-access storage services are necessary for minimising cost. In addition, extensive use of parallel technology will be required in the future to further reduce execution time and cost, which would enable researchers to use more complex models and/or more sophisticated analysis methods (requiring more computation resources). Although this paper focused solely on cluster and cloud usage from the point of view of EEG data processing, the presented models are sufficiently general to be applicable for estimating the cost of other neuroimaging workflows based on MRI, fMRI, CT, PET, MEG, etc. imaging modalities.