Abstract
Epilepsy is a neurological disease condition in which one experience seizures. These can be recorded using Electroencephalogram which is by nature long term recordings. A lot of work has been done towards automatic detection of these seizures in the literature with both short term and long term recordings. In this work, we have used the standard database of University of Bonn for a four different two class classification problem as addressed by various others in the literature. We have used novel single feature namely Tsallis entropy along with five different classifiers. Comparing with other literatures, we find that our method has the least computation time as low as 0.9 ms. We achieved a highest accuracy of 92.67–100% with Decision tree classifier for the four types of two class classification problem considered. Our method being very simple and also has fastest computation time in comparison with other features in the literature and thus can form as a software tool that can be installed easily and also opens future opportunities towards real time detection and prediction of epileptic seizures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Epilepsy is common disease experienced by at least 50 million people in the world, which surmounts about 1% of the world’s population [1, 2]. One with epilepsy as disease is not well received by the society. People from south India hide this disease in relation to marriage on the fear that they will be rejected or prohibited from marring. Factually the disease itself does not prompt threat, but it can become hazardous if the individual is swimming or driving as one loses control and consciousness during certain types of epilepsy.
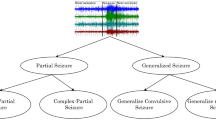
Seizures are of different types. They are classified primarily based on the source of the seizure within the brain namely localized or distributed. The localized seizures are named as partial or focal seizures. Partial seizures are further classified as simple partial seizure and complex partial seizure. If ones awareness is unaffected then it is called as simple partial seizure and if ones awareness is affected it is called as complex partial seizure. And generally seizures are classified according to the effect on the body but all of them involve loss of consciousness. These include absence (petit mal), myoclonic, clonic, tonic, tonic–clonic (grand mal), and atonic seizures. In general they have an ictal period during which the patient experiences the seizures and a period preceding that called pre ictal period. Epileptic seizures can be recorded along with recording of the Electroencephalogram (EEG).
Volumes of work are done towards automatic detection of epileptic seizures. In a broad way, researchers have used long term EEG data or EEG data segments for detecting the epileptic seizures. Here we are considering EEG data segments for the classification of epileptic seizures. Bonn University database [3] has EEG segments of a fixed duration of three different categories namely normal, ictal and preictal. A lot of work has been done using this database for classification of epileptic seizures.
In terms of techniques, starting from the 1970s different methods has been employed. Initially heuristic and descriptive methods were used for the detection of epileptic seizures [4]. Later time domain methods, frequency domain methods, time frequency domain methods and other nonlinear methods were all attempted for seizure detection [5]. Linear discriminant analysis (LDA), histogram methods were also used for automatically detecting the epileptic seizures [6, 7]. Seizure termination was identified using sample entropy [8]. Differential operation was also used to identify the seizures [9]. Recurrence quantification Analysis (RQA) [10], Higher order spectra (HOS) [11], Hurst exponent (H) [12], different entropies [1] were all employed for the identification of epileptic seizures. There are also works where they have employed wavelet transforms with single level analysis for detecting the epileptic seizures [13, 14]. Multilevel wavelet approach was also employed by Indiradevi et al. [15] for automatically detect the epileptic spikes. Sharma et al. [16] has used Fast Fourier transform(FFT) for extracting features from EEG as a first step and employed these features to the neural network for identifying the seizure.
Different methods of machine learning algorithms with pattern recognition such as neural networks [17,18,19,20,21,22,23], support vector machines [24, 25], KNN classifier [26], Bayesian classifier [27] have been implemented. Features such as correlation dimension [28], correlation density [29], Lyapunov exponent [30], Kolmogorov entropy [31] have been used for onset detection. Fourier transform was also implemented for onset detection of epileptic seizures [32,33,34]. Some researchers have also used wavelet transforms [35,36,37] to detect the seizure onsets [61].
Fundamentally, the researchers have used this database as a two class or three class problem [38–40]. We are going to use this database for a two class classification problem. Various methods which use the same database for a two class classification namely normal and abnormal are shown in the Table 8. It can be noted that few works have led to 100% classification accuracy [41–45]. It can also be seen that expect a few, no one talks about the computation time that is involved in these works [46–49]. Here, in this work, we are bringing the importance of computation time and accuracy towards real time detection or classification of epileptic seizures [50–55].
The paper is sorted out as it takes after. Section 2 exhibits the subtle elements of the information database, brief data about the feature that we have utilized and classifier which we have utilized as a part of this work. Segment 3 introduces the outcomes acquired in this work. Section 4 exhibits a discourse on related investigations of this database and contrasts our outcomes and different techniques and results in the writing. The conclusion is given in segment 5.
2 Methods and materials
In this section, we describe the methods that we have employed for automatic classification of the epileptic seizures.
2.1 Data
We have used the artefact free EEG data available at the Bonn University [see Ref. 38 for more details]. The dataset contains three classes namely normal (Set A (eyes open) and Set B(eyes closed)), pre-ictal (Set C and Set D) and seizure (Set E) each with 200, 200 and 100 data respectively. Each of the data is a single channel EEG signals with the duration of 23.6 s. In this work, we are taking the first 6 s of duration of the data from all the sets. Thus the normal class comprises of EEG data Set A and Set B. Thus the normal class contains 200 data. Similarly the pre-ictal class (Set C and Set D) contains 200 data. The seizure class (Set E) consists of 100 cases with same subjects when they were having epilepsy. Thus it forms a database of 500 datasets with 6 s of the data with size of 1024 samples. All these segments of EEG were recorded using 128 channel system with the sampling rate of 173.61 Hz and digitized with 12 bit A/D resolution. Further it was filtered with a band pass filter with 0.5340 Hz at 12 dB/octave [3]. A sample of these data under three classes namely normal, preictal and ictal is shown in Fig. 1. As in the literature, we are constructing 4 different types of 2 class problem from the data considered, which is described as follows. I Type: Set A versus Set E, II Type: Set A, B versus Set E, III Type: Set C, D versus Set E, and IV Type: Set A, B, C, D versus Set E.
2.2 Tsallis entropy as the feature
The idea of entropy was started in 1803 by a mathematician Lazare Carnot as he found that vitality is lost because of scattering and friction [56, 57]. This thermodynamic entropy was later brought into the field of data hypothesis with the name data entropy just in 1948 by Shannon [58]. Since at that point there are part of assortments of entropies have come in the writing like approximate entropy, sample entropy, permutation entropy etc. A short blueprint with only one entropy called Tsallis entropy (TsE) as a single feature. A short blueprint of this entropy is given below.
2.2.1 Tsallis-entropy(TsE)
Constantino Tsallis introduced this entropy in 1988 as a basis for generalizing standard statistical mechanics [59]. For a given discrete set of probabilities, {pi} with sum of their probabilities equal to one and q any real number, the Tsallis entropy (TsE) is given by
From the mathematical equation, we can see that it has only a summation part and thereby the computation time for this must be significantly low in comparison with other methods.
Table 1 shows the computation time of TsE for a single data. From this it can be noticed that the calculation time for TsE is very low which in this way opens the gate towards ongoing preparing. It can be observed that TsE has a computation time of 0.0009 s in a 1.6 GHz, 4 GB Ram computer with MATLAB 2008. Table 2 shows the computation time of various other features in the literature used for classification of epileptic seizures. The computation time shown in Tables 1 and 2 are average values over various single EEG data considered.
In this work, we have used five classifiers to be specific Naïve Bayes classifier (NBC), Radial basis function neural network classifier (RBF), Decision tree—Decision tree classifier (DT), K nearest neighbourhood classifier (KNN) and Support vector machines (SVM) which are briefly explained as follows.
2.2.2 Naive Bayes Classifier (NBC)
This classifier is based on Bayes theorem. It accept that factors are autonomous irregular factors. With this presumption, it registers the probabilities required by the Bayes hypothesis for the given information.
2.2.3 Radial basis function (RBF)
These are again probabilistic neural systems having outspread premise initiation works in its first layer and focused layer tailing it for arrangement.
2.2.4 Decision trees: functional tree (DTFT)
Functional trees [60] are one type of multivariate trees, which are classification trees that have logistic regression functions at the inner nodes and/or leaves. They can deal with multiclass target variables, nominal and numeric attributes and missing values.
2.2.5 K-nearest neighbour classifier (KNN)
This is a supervised learning technique where a new coming instance is classified based on the closest training samples present in feature space. It does not have any model for fitting the new instance. When the test data is given, it is mapped to the class that is most common among the K neighbors. In this work, various values of k ranging from 2 to 6 were considered and the distance were computed using Euclidean distance. We got the highest accuracy when k was 5.
2.2.6 Adaboost
Adaboost is short of Adaptive boosting. This classification algorithm was formulated by Yoav Freund. It is a machine learning meta algorithm. It can be used in conjunction with the other weak learners to enhance their performance. Here Adaboost is used independently.
2.3 Performance measures
The performance of these classifiers is assessed using the accuracy. Accuracy is given by the ratio of the number of correctly classified segments to the total number of segments [61].
3 Results
The TsE values are calculated for the EEG data. The mean and variance of these entropy values for the data of 4 different two class problems considered is shown in the Tables 4, 5, 6 and 7. Students T test is performed for each of them with TsE feature. The determined p value is also shown in the table which is very less than 0.00001 suggesting that TsE has high discriminating capacity for each of the problems considered.
TsE being the single feature in our work is given as input to the five different classifiers. Tenfold cross validation technique was used for evaluating the classifiers. In this system, the whole dataset is partitioned into 10 sets, each having same proportions of instances in each class. Nine sets are utilized for preparing and the staying one set is utilized for testing and evaluating the performance of the classifier. This system is rehashed ten times using new training and testing set each time. The average of all these ten performance measures is considered as the resultant final value. The performance measures thus obtained for each of the classifiers for various entropies considered are shown in Tables 4, 5, 6 and 7.
From the Tables 4, 5, 6 and 7 we can observe that the following. For the problem Type I: All the classifiers considered gave 100% accuracy. This shows the robustness and versatile nature of the TsE as feature that we have considered. For the problem Type II: DT classifier gave the highest classification accuracy of 98% accuracy. It can also be noted that the other classifiers also gave accuracies above 97%. This again proves the robust and versatile nature of the TsE feature across all the classifiers yielding consistent accuracies irrespective of the classifier used. For the problem Type III: It can be observed that the DT classifier gave the highest accuracy of 92.67%, whereas other classifiers gave accuracies above 88%. The reduction in the accuracy for this type is because we are classifying between preictal type and ictal type. Preictal stage is the region that comes before the onset of epileptic seizure. This is a transition period from normal to the ictal. Nevertheless we can see that TsE as a single feature has the ability to discriminate fairly well with the highest accuracy of 92.67%. For the problem Type IV: It can be observed that decision tree classifier achieved the highest classification accuracy of 95.8% with other classifiers accuracies being above 94%. This again shows that TsE as a single feature has a good discrimination capacity with fair good accuracy across all classifiers. Thus in a overall way, it can be pointed out that TsE as a single feature has the capacity for classifying all these four types of problems with fairly good levels of accuracies and with its significantly very less computation time, it is all capable for building towards a real time epilepsy detection system. The various accuracies obtained with different methods in the literature for these three classes are discussed in the following section.
4 Discussion
In this section, we present the various techniques used in the literature towards classification of the EEG data. We have only reviewed those studies which used Bonn University dataset towards classification of two classes and hence our results are comparable. A summary of the previous studies towards classification of various two class problems along with the accuracies obtained is listed in the Table 8.
Primarily it can be seen from Table 8 that TsE as single feature was not used by anyone and we are first to use this as a feature towards the four different types of two class problems for this database, as done earlier in various papers in the literature.
From the initial observation from the Table 3, we can see that the TsE feature values for four different types of problems considered are visibly having a contrast between the two classes. It has also been found in the literature that entropy value changes for ictal and normal EEG [1, 5]. This is also confirmed in our study.
Earlier permutation entropy (PE) was also used for epileptic detection [2]. In their work, they split the 23.6 s duration of EEG data into non overlapping windows of 1 s duration length and PE is calculated for that. They calculated PE for m = 3 and m = 4. Although they calculated the PE values to be a feature for classification, they used it only for 4 different two class classification problem. They used SVM classifier and achieved an accuracy of 86.1%.
Recently G. Chen [62] used dual tree complex wavelet with Fourier features and achieved 100% accuracy for these 4 different types of 2 class problem. He achieved a computation time fairly less as 5.7 ms as shown in the Table 8. In this work, we have used only TsE as feature whose calculation time is significantly very less as 0.9 ms.
In addition to the above, we have shown different algorithms in literature in the Table 8 showing the different levels of accuracies they obtained. It can be seen that the authors have not given their computation time. To have some comparison for the computation time of ours with other methods in the literature, we have calculated some of the computation time of different algorithms in the literature with the same computer configuration and it is shown in the Table 2 and Table 8. For the wavelet based features and Fourier features we have not given the computation time and we take those values to be definitely larger than computation time of TsE—the reason being the mathematical equation for TsE calculation in comparison to the wavelet transform and Fourier transform. Moreover we can see from G. Chen’s work where the minimum computation time given is to be 5.7 ms. We have marked ‘NA’ in Table 8 meaning that the corresponding authors have not given the computation time or we have not specifically calculated the computation time of their features in our computer. We take for granted from G. Chen’s work in general for those works that involves wavelet and Fourier features. From all of the above, it can be noted that our feature TsE has the least computation time. Although our accuracies achieved are not 100% for problem of Type II, III and IV, our computation time is significantly very less comparing with other methods in the literature, thereby opening the window towards real time detection. More appropriate features are planned to be added to increase the accuracies without further increasing the computation time.
Our method has the following specific significance and novelty.
- (a)
We are the first one to use TsE for this dataset and also towards epileptic seizure detection.
- (b)
The computation time for this TsE feature considered in this work is significantly very less as shown in the Table 1 in comparison with the computation time of other features used in the literature as shown in the Table 2. It should also be noted that our method did not involve any preprocessing of the data.
- (c)
We have used only a single feature i.e., TsE for the classification of 4 different types of two class classification problem. Also we would like to bring out that we have used tenfold cross validation technique for the accuracy calculation, which is not the case with the study of G. Chen.
- (d)
Having the least computation time, our strategy opens the window towards continuous detection which is one of important need of hour of this area of research.
In any case, it ought to be noticed that this technique is executed just to a restricted size of information. The method needs to be checked with other large databases for consistent results. Additionally it ought to be noticed that the EEG information considered here for arrangement are commotion and ancient rarity free information portions and they are not the constant running EEG. As stated by Acharya et al. [5]., such strategies should be additionally tried and checked with substantial database gathered at various focuses of clinical trials for the consistency in the outcomes, previously they can be actualized for reasonable social purpose.
5 Conclusion
EEG signals can be used to differentiate between the two different states namely normal and ictal. In this work, we have proposed novel single feature TsE along with five classifiers for classification of four different types of two class problems. It can be seen our work achieved a highest accuracy of 92.67–100% for the different types of problems considered as described earlier. More importantly, our method has the least computation time of 0.9 ms in solving these four different types of classification problem. Thus proposed method is simple yet fastest and therefore can be planned towards real time detection. More selective new features need to be appended to increase the accuracy without further increase of the computation time. It can also form as a software tool and be installed in the epileptic diagnostic centres. However before such installations, the method has to be tested thoroughly with various databases for consistency in the accuracy.
References
Acharya, U.R., Molinari, F., Sree, S.V., Chattopadhyay, S., Ng, K.H., Suri, J.S.: Automated diagnosis of epileptic EEG using entropies. Biomed. Signal Process. Control 7(4), 401–408 (2012)
Nicolaou, N., Georgiou, J.: Detection of epileptic electroencephalogram based on permutation entropy and support vector machines. Expert Syst. Appl. 39(1), 202–209 (2012)
Andrzejak, R.G., Lehnertz, K., Mormann, F., Rieke, C., David, P., Elger, C.E.: Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: dependence on recording region and brain state. Phys. Rev. E 64(6), 061907 (2001)
Callaway, E., Harris, P.R.: Coupling between cortical potentials from differentareas. Science 183(4127), 873–875 (1974)
Acharya, U.R., et al.: Automated EEG analysis of epilepsy: a review. Knowl. Based Syst. (2013). https://doi.org/10.1016/j.knosys.2013.02.014
Murro, A.M., King, D.W., Smith, J.R., Gallagher, B.B., Flanigin, H.F., Meador, K.: Computerized seizure detection of complex partial seizures. Electroencephalogr. Clin. Neurophysiol. 79, 330–333 (1991)
Harding, G.W.: An automated seizure monitoring system for patients with indwelling recording electrodes. Electroencephalogr. Clin. Neurophysiol. 86(6), 428–437 (1993)
Yoo, C.S., Jung, D.C., Ahn, Y.M., Kim, Y.S., Kim, S.G., Yoon, H., Yi, S.H.: Automatic detection of seizure termination during electroconvulsive therapy using sample entropy of the electroencephalogram. Psychiatry Res. 195(1), 76–82 (2012)
Majumdar, K.: Differential operator in seizure detection. Comput. Biol. Med. 42(1), 70–74 (2012)
Acharya, U.R., VinithaSree, S., Chattopadhyay, S., Wenwei, Y.U., Alvin, A.P.C.: Application of recurrence quantification analysis for the automated identification of epileptic EEG signals. Int. J. Neural Syst. 21(3), 199–211 (2011)
Acharya, U.R., VinithaSree, S., Suri, J.S.: Automatic detection of epileptic EEG signals using higher order cumulant features. Int. J. Neural Syst. 21(5), 1–12 (2011)
Acharya, U.R., Sree, S.V., Ang, P.C.A., Yanti, R., Suri, J.S.: Application of non-linear and wavelet based features for the automated identification of epileptic EEG signals. Int. J. Neural Syst. 22(02), 1250002 (2012)
Sartoretto, F., Ermani, M.: Automatic detection of epileptic form activity by single level analysis, clin. Neurophysiol. 110, 239–249 (1999)
Subashi, A.: Automatic detection of epileptic seizure using dynamic fuzzy neural networks. Expert Syst. Appl. 31, 320–328 (2006)
Indiradevi, K.P., Elias, E., Sathidevi, P.S., Nayak, S.D., Radhakrishnan, K.: A multi-level wavelet approach for automatic detection of epileptic spikes in the electroencephalogram. Comput. Biol. Med. 38, 805–816 (2008)
Sharma, A., Wilson, S.E., Roy, R: EEG classification for estimating anesthetic depth during halothane anesthesia. In: Proceedings of the 14th annual International Conference IEEE engineering in medicine and biology society. New York. IEEE, pp. 2409–2410 (1992)
Gabor, A.J., Leach, R.R., Dowla, F.U.: Automated seizure detection using a self-organizing neural network. Electroencephalogr. Clin. Neurophysiol. 99(3), 257–266 (1996)
Ubeyli, E.D., Guler, I.: Features extracted by eigenvector methods for detecting variability of EEG signals. Pattern Recognit. Lett. 28, 592–603 (2007)
Ghosh-Dastidar, S., Adeli, H.: Improved spiking neural networks for EEG classification and epilepsy and seizure detection. Integr. Comput.-Aided Eng. 14(3), 187–212 (2007)
Ghosh-Dastidar, S., Adeli, H.: Spiking neural networks. Int. J. Neural Syst/ 19(4), 295–308 (2009)
Ghosh-Dastidar, S., Adeli, H.: A new supervised learning algorithm for multiple spiking neural networks with application in epilepsy and seizure detection. Neural Netw. 22, 1419–1431 (2009)
Postnov, D.E., Ryazanova, L.S., Zhirin, R.A., Mosekilde, E., Sosnovtseva, O.V.: Noise controlled synchronization in potassium coupled neural networks. Int. J. Neural Syst. 17(2), 105–113 (2007)
Chen, M., Jiang, C.S., Wu, Q.X., Chen, W.H.: Synchronization in arrays of uncertain delay neural networks by decentralized feedback control. Int. J. Neural Syst. 17(2), 115–122 (2007)
Shoeb, A., Edwards, H., Connolly, J., Bourgeois, B., Treves, S.T., Guttag, J.: Patient- specific seizure onset detection. Epilepsy Behav. 5(4), 483–498 (2004)
Guler, I., Ubeyli, E.D.: Multiclass support vector machines for EEG signals classification. IEEE Trans. Inf Technol. Biomed. 11(2), 117–126 (2007)
Qu, H., Gotman, J.: A patient-specific algorithm for the detection of seizure onset in long-term EEG monitoring: possible use as a warning device. IEEE Trans. Biomed. Eng. 44(2), 115–122 (1997)
Saab, M.E., Gotman, J.: A system to detect the onset of epileptic seizures in scalp EEG. Clin. Neurophysiol. 116(2), 427–442 (2005)
Elger, C.E., Lehnertz, K.: Seizure prediction by non-linear time series analysis of brain electrical activity. Eur. J. Neurosci. 10, 786–789 (1998)
Martinerie, J., Adam, C., Le Van Quyen, M., et al.: Epileptic seizures can be anticipated by non-linear analysis. Nat. Med. 4, 1173–1176 (1998)
Iasemidis, L.D., et al.: Phase space topography and the Lyapunov exponent of electrocorticograms in partial seizures. Brain Topogr. 2(3), 187–201 (1990)
Van Drongelen, W., Nayak, S., Frim, D.M., et al.: Seizure anticipation in pediatric epilepsy: use of Kolmogorov entropy. Pediatr. Neurol. 29, 207–213 (2003)
Khan, Y.U., Gotman, J.: Wavelet based automatic seizure detection in intracerebral electroencephalogram. Clin. Neurophysiol. 114, 898–908 (2003)
Guler, I., Ubeyli, E.D.: Adaptive neuro-fuzzy inference system for classification of EEG signals using wavelet coefficients. J. Neurosci. Methods 148, 113–121 (2005)
Hopfengartner, R., et al.: An efficient, robust and fast method for the offline detection of epileptic seizures in long-term scalp EEG recordings. Clin. Neurophysiol. 118, 2332–2343 (2007)
Adeli, H., Ghosh-Dastidar, S., Dadmehr, N.: A wavelet-chaos methodology for analysis of EEGs and EEG sub-bands to detect seizure and epilepsy. IEEE Trans. Biomed. Eng. 54(2), 205–211 (2007)
Ghosh-Dastidar, S., Adeli, H., Dadmehr, N.: Mixed-band wavelet-chaos-neural network methodology for epilepsy and epileptic seizure detection. IEEE Trans. Biomed. Eng. 54(9), 1545–1551 (2007)
Adeli, H., Ghosh-Dastidar, S., Dadmehr, N.: A spatio-temporal wavelet-chaos methodology for EEG-based diagnosis of Alzheimer’s disease. Neurosci. Lett. 444(2), 190–194 (2008)
Bandt, C., Pompe, B.: Permutation entropy: a natural complexity measure for time series. Phys. Rev. Lett. 88(17), 174102 (2002)
Ouyang, G., Li, X., Dang, C., Richards, D.A.: Deterministic dynamics of neural activity during absence seizures in rats. Phys. Rev. E 79(4), 041146 (2009)
Ouyang, G., Dang, C., Richards, D.A., Li, X.: Ordinal pattern based similarity analysis for EEG recordings. Clin. Neurophysiol. 121, 694–703 (2010)
Bruzzo, A.A., Gesierich, B., Santi, M., Tassinari, C., Birbaumer, N., Rubboli, G.: Permutation entropy to detect vigilance changes and preictal states from scalp EEG in epileptic patients: a preliminary study. Neurol. Sci. 29, 3–9 (2008)
Rényi, A.: On measures of information and entropy. In: Proceedings of the fourth Berkeley Symposium on Mathematics, Statistics and Probability 1960. pp. 547–561 (1961)
Press, W.H., Teukolsky, S.A., Vetterling, W.T., Flannery, B.P.: Section 16.5. Support Vector Machines. Numerical Recipes: The Art of Scientific Computing, 3rd ed. Cambridge University Press, New York. ISBN 978-0-521-88068-8 (2007)
Chen, Guangyi: Automatic EEG seizure detection using dual-tree complex wavelet-fourier features. Expert Syst. Appl. 41(5), 2391–2394 (2014)
Guler, N.F., Ubey, E.D., Guler, I.: Recurrent neural network employing Lyapunov exponents for EEG signals classification. Expert Syst. Appl. 29(3), 506–514 (2005)
Ghosh-Dastidar, S., Adeli, H., Dadmehr, N.: Principal component analysis-enhanced cosine radial basis function neural network for robust epilepsy and seizure detection. IEEE Trans. Biomed. Eng. 55(2), 512–518 (2008)
Faust, O., Acharya, U.R., Min, L.C., Sputh, B.H.: Automatic identification of epileptic and background EEG signals using frequency domain parameters. Int. J. Neural Syst. 20(2), 159–176 (2010)
Chua, K.C., Chandran, V., Acharya, U.R., Lim, C.M.: Automatic identification of epileptic EEG signals using higher order spectra. J. Eng. Med. 223(4), 485–495 (2009)
Chua, K.C., Chandran, V., Acharya, U.R., Lim, C.M.: Application of higher order spectra to identify epileptic EEG. J. Med. Syst. 35(6), 1563–1571 (2011)
Sharma, R., Pachori, R.B.: Classification of epileptic seizures in EEG signals based on phase space representation of intrinsic mode functions. Expert Syst. Appl. 42(3), 1106–1117 (2015)
Acharya, U.R., Chua, K.C., Lim, T.C., Dorithy, J.S.Suri: Automatic identification of epileptic EEG signals using nonlinear parameters. J. Mech. Med. Biol. 9(4), 539–553 (2009)
Kolmogorov, A.N.: Three approaches to the definition of the concept of quantity of information. Probl. Inf. Transm. 1(1), 1–7 (1965)
Lempel, A., Ziv, J.: On the complexity of finite sequence. IEEE Trans. Inf. Theory 22, 75–81 (1976)
Fu-Zen, Shaw, Ruei-Feng, Chen, Hen-Wai, Tsao, Chen-Tung, Yen: Algorithmic complexity as an index of cortical function in awake and pentobarbital-anesthetized rats. J. Neurosci. Methods 93, 101–110 (1999)
Rapp, P.E., Zimmermean, I.D., Vining, E.P., Cohen, N., Albano, A.M., et al.: The algorithmic complexity of neural spicke trains increases during focal seizures. J. Neurosci. 14, 4731–4739 (1995)
Naterer, G.F., Camberos, J.A.: Entropy Based Design and Analysis of Fluids Engineering Systems. CRC Press, Boca Raton (2008)
Muller, I.: A History of Thermodynamics: The Doctrine of Energy and Entropy. Springer, New York (2007)
Shannon, C.E.: A mathematical theory of communication. Bell Syst. Tech. J. 27(3), 379–423 (1948)
Tsallis, C.: Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 52, 479–487 (1988)
Book Section 2001@ 978-3-540-42956-2 Discovery Science 2226 Lecture Notes in Computer Science E Jantke, Klaus P. Shinohara, Ayumi 10.1007/3-540-45650-3_9 Functional Trees, Springer, Berlin (2001)
Acharya, U.R., Sree, S.V., Alvin, A.P.C., Suri, J.S.: Use of principal component analysis for automatic classification of epileptic EEG activities in wavelet framework. Expert Syst. Appl. 39(10), 9072–9078 (2012)
Chen, G.: Automatic EEG seizure detection using dual-tree complex wavelet-fourier features. Expert Syst. Appl. 41, 2391–2394 (2014)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Thilagaraj, M., Pallikonda Rajasekaran, M. & Arun Kumar, N. Tsallis entropy: as a new single feature with the least computation time for classification of epileptic seizures. Cluster Comput 22 (Suppl 6), 15213–15221 (2019). https://doi.org/10.1007/s10586-018-2549-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10586-018-2549-5