Abstract
Apache Cassandra is an highly scalable and available NoSql datastore, largely used by enterprises of each size and for application areas that range from entertainment to big data analytics. Managed Cassandra service providers are emerging to hide the complexity of the installation, fine tuning and operation of Cassandra virtual data centers (VDCs). This paper address the problem of energy efficient auto-scaling of Cassandra VDC in managed Cassandra data centers. We propose three energy-aware autoscaling algorithms: Opt, LocalOpt and LocalOpt-H. The first provides the optimal scaling decision orchestrating horizontal and vertical scaling and optimal placement. The other two are heuristics and provide sub-optimal solutions. Both orchestrate horizontal scaling and optimal placement. LocalOpt consider also vertical scaling. In this paper: we provide an analysis of the computational complexity of the optimal and of the heuristic auto-scaling algorithms; we discuss the issues in auto-scaling Cassandra VDC and we provide best practice for using auto-scaling algorithms; we evaluate the performance of the proposed algorithms under programmed SLA variation, surge of throughput (unexpected) and failures of physical nodes. We also compare the performance of energy-aware auto-scaling algorithms with the performance of two energy-blind auto-scaling algorithms, namely BestFit and BestFit-H. The main findings are: VDC allocation aiming at reducing the energy consumption or resource usage in general can heavily reduce the reliability of Cassandra in term of the consistency level offered. Horizontal scaling of Cassandra is very slow and make hard to manage surge of throughput. Vertical scaling is a valid alternative, but it is not supported by all the cloud infrastructures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
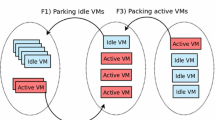
Today, data storage or serving systems such as Apache Cassandra and Hbase, Amazon SimpleDB and Dynamo, Google BigTable are playing an important role in the cloud and big data industry because the unprecedented high scalability and availability they achieve by means of data replication. Resource management for those data storage platforms is a challenging task and the complexity increase when multi-tenancy is considered. Human assisted control for such platforms is unrealistic and there is a growing demand for autonomic solutions. In this paper we consider the auto-scaling problem for providers of a managed Cassandra service (cf. Fig. 1). The goal of the service providers is always to minimise operational costs under the constraints imposed by service level agreements (SLAs) contracted with the customers. Minimisation of energy consumption is one of the strategies adopted to reduce costs, particularly when the service providers run their own data centers. To address this problem we propose three energy-aware auto-scaling algorithms (Opt, LocalOpt and LocalOpt-H) specifically designed for Cassandra virtual data centers (VDC) running on a cloud infrastructure and we compare their performance with two energy-blind auto-scaling algorithms (BestFit and BestFit-H).
Auto-scaling does not only mean to automatically increase/decrease the amount of resources. Auto-scaling implies to adapt, over time, the configuration of the Cassandra VDC and of the cloud infrastructure. To realize an optimal auto-scaling, the service provider could adopt three strategies: Vertical scaling, which means to change the Cassandra virtual nodes (vnodes) capacity at runtime, e.g. adding computing power (e.g. virtual cpu) and/or memory; Horizontal scaling, which means to add/remove, at runtime, Cassandra vnodes to/from the Cassandra VDC; Optimal placement, which means to instantiate the vnodes on the physical nodes in a way such that the usage of resources is optimised with respect to some objective function. In our specific case the objective function is the energy consumed by the datacenter and should be minimized.
The Opt and LocalOpt auto-scaling algorithms orchestrate those three adaptation strategies, while the LocalOpt-H does only horizontal scaling and optimal placement. The BestFit is based on the classical Best Fit decreasing algorithm to approximate the solution of the bin packing problem. The algorithm is capable to do both horizontal and vertical scaling. The BestFit-H is a variant that does only horizontal scaling. All the algorithms are designed to be integrated in the planning phase of a MAPE-K controller (cf. Fig. 1). The scaling decisions are based on three parameters that can be easily collected: the vnodes throughput, the CPU usage, and the memory usage.
The optimal energy-aware autoscaling is an algorithm that does an overall system reconfiguration at each scaling action needed to accommodate the resources for a specific tenant. That allow to have always a system configuration that minimize the energy consumed by the datacenter. The rational to introduce energy-aware heuristics is twofold: first, the heuristics are applied locally, for the specific tenant the need to scale, and that reduces the perturbation of the performance for the tenants that do not need to scale. Second, the Opt has a complexity of the order \(O((N\times H)^{3/2})\) for N tenants and H physical nodes, while the heuristics have a complexity of the order \(O(H^{3/2})\) and \(O(H^2)\) for (localOpt) and (BestFit) respectively (more details are provided in Sect. 6). The not optimised Matlab code implementing the heuristics finds the suboptimal solution in a range \(10^{-1}\), 10 s (when running on an Intel Core i5). The average time to find the optimum using the Matlab MILP solver is about 50 s with a maximum of about \(2 \times 10^3\) s.
1.1 Research contribution
With respect to the literature on QoS and energy-aware adaptation (e.g. [2, 3, 10, 17, 19, 24, 26]) and data center consolidation (e.g. [1, 5, 13, 14, 16]) and with respect to our previous results [4] we introduce the following novelties:
-
we compare the optimal energy aware allocation proposed in [4] with two new auto-scaling heuristics BestFit-H and LocalOpt-H
-
we provide a discussion on the issues related to auto-scaling in Cassandra virtual data centers and we give guidelines on how to best use the proposed algorithms, i.e. for medium/long term capacity planning and at run-time
-
we provide a detailed evaluation of the computational cost of the optimal autoscaling algorithms and of all the heuristic algorithms.
-
we provide a simple model to asses how the consistency level of a Cassandra VDC is impacted by the auto-scaling and specifically by the placement of vnodes on physical machines.
-
we analyse the performance of the proposed algorithms in case of surge of requests and failure of physical nodes
Our main findings are here summarized: First, the penalty in using an heuristic adaptation that does not hurt the system stability is between +25% and +50% for highly loaded systems. Second, energy efficient VDC allocations can heavily reduce the reliability of Cassandra in term of the consistency level offered. Third, horizontal scaling of Cassandra is very slow and make hard to manage surge of throughput. Vertical scaling is a valid alternative, but it is not supported by all the cloud infrastructures.
1.2 Paper organization
The paper is organised in the following way. The next section discusses related work. The reference scenario we consider is presented in Sect. 3. Section 4 introduces the system model and the optimal adaptation problem formulation. The auto-scaling algorithms are presented and discussed in Sect. 5. In Sect. 6 we provide the computational cost analysis. Issues on Cassandra auto-scaling and recommendations on the use of the algorithms are discussed in Sect. 7. The experimental methodology (analysis cases, metrics and experimental setup) is described in Sect. 8, while the experimental results are described in Sect. 9. Finally, Sect. 10 provides concluding remarks.
2 Related works
The problem we are addressing has been partially covered in literature by research paper in different fields: QoS and energy-aware datacenter management; VM placement; autonomic adaptation of cloud infrastructures; performance evaluation, management and adaptation of cassandra-based systems.
Examples of research works on measuring and managing the performance of NoSql distributed data stores such as Cassandra are [9, 23]. Chalkiadaki and Magoutis [6], Dede et al. [11], Kuhlenkamp et al. [18], Rabl et al. [25], Shankaranarayanan et al. [28], Shi et al. [30] are studies focusing on the horizontal scalability feature offered by such databases. Few studies consider vertical scaling, e.g. [6, 18], and configuration tuning [6, 12, 22, 28]. While Horizontal scaling, vertical scaling and configutation tuning approaches are somentime mixed, optimal placement (e.g. [1, 5, 13, 14, 16]) is never considered in combination with the other adaptation strategies.
In [9] and [23] the authors presented YCSB and YCSB++, the reference benchmarking frameworks for facilitating the comparison of cloud based data-serving systems. YCSB allows to simulate five different workloads and is compliant with BigTable, HBase, Cassandra, MongoDB, DynamoDB and more. In our work we decided to not to use YCSB because we are mainly interested in working with Ericssonn datasets and applications. However, our solution is based on a heuristic throughput model that is independent from the specific type of query and application.
In [30] has been evaluated the horizontal scalability of Cassandra and Hbase for a mix of sequential and random read and write operations, scan operations and structured queries. No report and consideration are provided on how and if the Cassandra and Hbase configuration impact the performance.
In [25] the authors evaluate the performance of six SQL and no-SQL databases under the pressure of 5 different workloads. These benchmarking experiments has been extended in [18] with a performance evaluation of Cassandra on different Amazon EC2 infrastructure configurations. In comparison with those researches we consider only read, write and read and write requests because of interest for our industrial case. However, our model is independent from the specific type of query. In [18] the authors explore both horizontal and vertical scalability. Their results confirms the experience we had with Cassandra performance on a virtualized environment. That is, a reduction of the Cassandra throughput up to 50% compared with Cassandra performance in non virtualized clusters.
Concerning self adaptation, few work has been presented. In [6] the authors propose a QoS controller for a Cassandra cluster that aims to guarantee system performance by means of coordinating horizontal scalability (bootstrap of new nodes) and cache size (i.e. configuration tuning). The proposed solution has been evaluated by means of YCSB benchmark. In [28] the authors consider the problem of optimizing geographically distributed cloud data stores with respect to latency under failure scenarios. The authors adapt the system tuning three main factors: R and W quorum, location of replicas and number of replicas. On the basis of experimental results the authors concludes that quorum-based data store could benefit from an adaptable and fine grain replica configuration. Indeed not only different applications could need different replication strategies, but also for the same application different group of object could need different replication strategies. This work motivates our assumption on the need for application specific Cassandra configurations. However, while [28] is mainly interested in the optimal configuration of the quorum mechanism and of the replication strategies, we are focused on the application specific scaling actions (Vertical and Horizontal) and on energy-aware optimal placement. Like [28], CADRE [31] shows that carefully distinguishing R + W queries in geographically distributed setting affects response time and carbon footprint. They propose an online algorithm to reduce carbon footprint while keeping response time low. The online algorithm is similar to our BestFit approach. Katsak et al. modify Cassandra for time varying resources by sending writes to vNodes and carefully maintaining a “working” set of available nodes. The choice of working set site and placement policies affects performance.
In [22] the authors propose AutoPlacer a mechanisms to self-tune the placement of replicas in distributed key-value stores. Their goal is to minimize the cost of replicas in term of overall latency. In [12] the authors propose a multidimensional indexing techniques for supporting complex queries using multiple object attributes. Such technique requires a complex system configuration and the authors propose a model and techniques to automatically and dynamically re-configure the system in dynamic workload environments.
A model for provisioning multi-tier applications in a cloud environment has been proposed by [29]. The authors proposed a simple and effective approach for resource provisioning to achieve a percentile bound on the end to end response time of a multi-tier application. The authors find that fewer high-capacity servers are preferable for high percentile provisioning. We leverage and verified this finding, but the solution can not be applied as it is for a Cassandra-based systems.
In [8] that authors consider the placement problem of virtual machines (VMs) of applications with intense bandwidth requirements. The proposed model fit in centralized storage scenarios like storage area networks and not in distributed storage scenarios like Cassandra.
The agility issue in scaling distributed storage systems as been addressed in [7]. The authors propose an elastic storage system, called JackRabbit, that can quickly change its number of active servers. JackRabbit is based on HDFS. Out paper confirm the agility issue.
3 Reference scenario
We consider a provider of a managed Apache Cassandra service offered to support enterprise applications. There are many examples of Cassandra-as-a-Service providers: Rackspace (http://rackspace.com), Instaclustr (http://instaclustr.com/) and Seastar (http://seastar.io/), just to mention a few.
The tenants of the service are independent applications each using its own Cassandra VDC (in what follow we will interchangeably use the terms application and tenant). A Cassandra VDC is a set of Cassandra virtual nodes (vnodes), i.e. an instance of Cassandra software running on a virtual machine (VM). All the Cassandra VDCs are tenants in a cloud infrastructure (no matter if on a public or private cloud), or data center in what follows.
Applications submit NoSql queries (called operations in what follows) at a specific rate. Each application requires a minimum throughput, a certain level of data replication to cope with node failures, and has a dataset of a specific size. To satisfy these customer’s requirements the service provider has to properly plan the capacity and the configuration of each Cassandra VDC. On the other side, the service provider wants to minimise its power consumption. The Cassandra-as-a-service provider has a typical scalability issue when: a new tenant subscribes to a service; and/or when existing tenants variate their requirements by modifying the target throughput, the data replication factor, and/or the dataset size; and/or there is a surge in the throughput.
The scenario is schematised in Fig. 1. The figure shows three applications, each with a data replication factor of three, that means each application has three copies of each data item. Applications could be served by Cassandra vnodes with diverse capacity in term of supported throughput. This can be achieved, for example, by running the Cassandra vnodes on VMs with different CPU power and memory size and allocating the proper number of Cassandra vnodes. To maximise the utilization, the provider decided to compact the Cassandra vnodes only on three out of four servers. The auto-scaler module is as a MAPE-K controller. The auto-scaling actions are based on data collected from the cluster infrastructure (the physical nodes and the hypervisor), from the Cassandra VDCs and from the applications. The executor controls the VMs and the Cassandra configuration parameters, as well as start and stop VMs and add/remove to/from Cassandra VDC the Cassandra vnodes.
4 Adaptation model
In this section we present the adaptation model that is behind the auto-scaling algorithms. In this respect, we first define models for: the workload and SLA; the system architecture; the throughput and the utility function. Those models are used to define the constraints and the objective function of an optimization problem. The solution of the optimisation problem provides the optimal (or suboptimal) auto-scaling decisions that, for each tenant, specify:
-
the number of vnodes of the Cassandra VDC (horizontal scaling)
-
the configuration of vnodes, e.g. in terms of CPU capacity and memory (vertical scaling)
-
the placement of vnodes (of the VDCs) on the physical infrastructure (optimal placement)
The periodic or event based evaluation of the optimisation problem provides an auto-scaling policy for the Cassandra service provider.
4.1 Workload and SLA model
The workload of a Cassandra VDC can be characterised by the following features: the type of requests, e.g. read only, write only, read & write, scan, or a combination of those; the rate of the operation requests; the size of the dataset; and the data replication_factor. Depending on the size of the dataset managed, a Cassandra VDC is classified as disk-bound if the dataset does not fit the memory offered by all the vnodes in the VDC. Otherwise, CPU-bound (see Eq. 1). Disk-bound installations have a performance degradation of two order of magnitude compared to CPU bound configurations [25].
Our workload model is based on the following assumptions.
Assumption 1
The system workload consist of a set \(\mathcal {L}\) of read (R), write (W) and read & write (RW) operation requests: \(\mathcal {L}=\{R, W, RW\}\). Such operation requests are generated by the N independent applications and we assume that application i generates only requests of type \(l_i \in \mathcal {L}\). If \(l_i=R\) or \(l_i=W\) we have 100% R or W requests. In case \(l_i=RW\) we have \(\alpha \%\) read requests and (\(100-\alpha \)) write requests (for example in our experiments \(\alpha =75 \%\)).
Assumption 2
Requests of type \(l_i\) are generated at a given rate measured in operations per second.
Assumption 3
The dataset size for application i is \(r_i\) GByte and the data are replicated with a factor \(D_i\)
Assumption 4
The workload is only CPU bound, hence the memory requirements are met.
Assumption 5
The internal/external network latency does not impact the auto-scaling decisions. Hence it is not considered in the SLA.
According with Assumptions 1–5, the SLA for the tenant i is modelled by the tuple:
that includes information on the agreed workload (\(l_i\) and \(r_i\)) and on the service level objectives (\(T_i^{min}\) and \(D_i\)). \(T_i^{min}\) is the minimum throughput the service provider must guarantee to process the requests from application i. The SLA parameters \(D_i\) and \(r_i\) are used to determine the number of vnodes to be instantiated, as discussed in the next section.
Concerning Assumption 1, we limit the study to the set \(\mathcal {L}=\{R, W, RW\}\). However, the model we propose can deal with any type of operation requests, as clarified later in Sect. 4.3. Assumption 4 implies that the service provider has to set up, during the application on-boarding phase, and to maintain, at runtime, the right number of vnodes for tenant i. Dealing only with CPU bound workloads exempt us from considering the workload consolidation problem (e.g. [32]). Besides, it is of interest for the customer to have CPU bound VDC in order to achieve the desired performance.
4.2 Architecture model
We consider a data center consisting of H homogeneous physical machines (PMs), installed at the same geographical location, and a set of V VM configurations. For example, Table 1 describes the characteristics of three different VM types (\(V=3\)). Each Cassandra vnode runs on a VM of type j and a Cassandra VDC is composed of \(n_i\) homogeneous Cassandra virtual nodes where \(n_i \ge D_i\) and at least \(D_i\) out of \(n_i\) vnodes must run on different physical machines (as suggested by Cassandra management best practices).
The configuration of the data center running N independent applications is defined by the vector \(\mathbf {x}=\left[ x_{i,j,h} \right] \), where \(x_{i,j,h}\) is the number of Cassandra vnodes serving application i and running on VMs with configuration j allocated on PM h, \(\forall i \in \mathcal{I}=[1,N]\), \(j\in \mathcal{J}=[1,V]\), \(k\in \mathcal{H}=[1,H]\) and \(\mathcal{I}, \mathcal{J}, \mathcal{H} \subset \mathbb {N}\).
We assume that each PM h has a nominal CPU capacity \(C_h\), measured in number of available cores, and a RAM of \(M_h\) GByte. A VM of type j is configured with \(c_j\) virtual cores, \(m_j\) GB of memory and a maximum JVM heap size \(heapSize_j\) (GB). The heap size is an important parameter in our case because it determines the size of the data a Cassandra vnode can store in the main memory for fast retrieval and processing. The relationship between the size of the RAM of the heap size is described in [15] and summarised in Table 2. Hence, to make the VDC instantiated for application i CPU bound we need a number \(n_{i,j}\) of nodes defined by the following empirical rule:
In case \(r_i > heapSize_j\) Eq. 1 holds, otherwise, the constraint \(n_{i,j} \ge D_i\) holds. Considering that the number \(n_{i,j}\) of vnodes can be defined as
and considering that in our industrial case is always \(r_i \ge heapSize_j\) for all configurations j, the above introduced constraints are modelled by the following equations:
where: \(y_{i,j}\) is equal to 1 if application i uses a VM configuration j to run Cassandra vnodes, otherwise \(y_{i,j}=0\); \(s_{i,h}\) is equal to 1 if a Cassandra vnode serving application i run of PM h. Otherwise \(s_{i,h}=0\).
To model vertical scaling actions, that is a change from configuration \(j_1\) to \(j_2\), we replace a VM of type \(j_1\) with a VM of type \(j_2\). However, in a real setting, hypervisors (e.g. VMWare) make it possible to resize, at runtime, the number of cores associated to a VM and the size of memory used without the need to shut down the VM. We do not consider the case of over-allocation, that is the maximum number of virtual cores allocated on PM h is equal to \(C_h\).
Finally we assume that the local network latency do not impact the performance of the VDC and the system reconfiguration (Assumption 5).
4.3 Throughput model
We model the actual throughput \(T_i\) offered by the provider to application i as a function of \(x_{i,j,h}\)
From the analysis of the experimental data and of the literature we conclude that, for CPU bound workloads, the throughput for a Cassandra VDC serving requests of type \(l_i\) and running on a VM of type j (on top of a PM h) can be approximated with a set of linear segment with slope \(\delta ^k_{l_i,j}\). \(\delta ^k_{l_i,j}\) is the slope of the kth segment and it is valid for a number of Cassandra vnodes \(n_i\) between \(n_{k-1}\) and \(n_k\). Therefore, for \(n_{k-1} \le n_{i} \le n_k\), we can write the following expression:
where \(k\ge 1\), \(n_0=1\) and \(t(1)=t^0_{l_i,j}\) is the value of the throughput supported by a specific Cassandra vnode configuration. An example of values for \(t^0_{l_i,j}\) is reported in Table 1.
Finally, for a configuration \(\mathbf {x}\) of a VDC, and considering Eq. 2 we define the overall throughput \(T_i\) as:
4.4 Power consumption model
As service provider utility we chose the power consumption which is directly related with the provider revenue (and with IT sustainability).
Many ways of reducing the power consumption in cloud systems have been proposed the literature; two interesting survey are [24] and [19]. Different approaches can be used for the sustainable operation of data centers. If we focus on cloud management systems the techniques typically used are: scheduling, placement, migration, and reconfiguration of virtual machines. The ultimate goal is to optimise the use of resources to reduce power consumption. Optimisation depends on the context, it could mean minimising PM utilisation or to balance the utilisation level of physical machine with the use of network devices for data transfer and storage. Independently from the configuration or adaptation policy adopted all these techniques are based on power and/or energy consumption models (in [24] a detailed surveys). Power consumption models usually define a linear relationship between the amount of power used by a system as function of the CPU utilisation (e.g. [2, 3, 10]), or processor frequency (e.g. [17]) or number of core used (e.g. [26]).
In this work we chose a linear model [3] where the power \(P_h\) consumed by a physical machine h is a function of the CPU utilization and hence of the system configuration \(\mathbf {x}\):
where \(P_h^{max}\) is the maximum power consumed when the PM h is fully utilised (e.g. 500W), \(k_h\) is the fraction of power consumed by the idle PM h (e.g. 70%), and the CPU utilisation for PM h is defined by
The overall energy consumption \(P(\mathbf {x})\) is defined by
where \(r_h=1\) if \(x_{i,j,h} > 0\) for some \(i \in \mathcal {I}\) and \(j \in \mathcal {J}\). Otherwise \(r_h=0\)
5 Auto-scaling algorithms
5.1 The optimal auto-scaling
The optimal auto-scaling algorithm is based on the solution of the optimization problem defined in Fig. 2 and based on the models presented in Sect. 4.

The pseudo code is listed in Algorithm 1. Opt simply invokes the solver for the optimization problem and returns: the optimal configuration of the system \(\mathbf {x}_{opt}\), that inform about the scaling actions; the remaining CPU and memory capacity (\(C^a\) and \(M^a\)) available after the adaptation; the type \(j^*\) of VM selected by the algorithm. The parameter e is an exit code flag that is true if a solution exist and false otherwise. The optimal configuration \(\mathbf {x}_{opt}\) indicates the necessary actions to perform (c.f. beginning of Sect. 4): horizontal scaling, vertical scaling and optimal placement. \(\mathbf {x}_{opt}\) is the solution \(\mathbf {x}\) to the optimization problem defined in Fig. 2, where: the set of constraints defined by Eq. 11 guarantee that the SLA is satisfied in terms of minimum throughput for all the tenants. For the sake of clarity we keep these constraints non linear, but they can be linearised using standard techniques from operational research if the throughput is modelled using Eq. 6. Eq. 12 introduces a set of constraints to guarantee that the number of vnodes allocated is enough to guarantee that the portion of the dataset handled by each node fits in the main memory and that the replication factor \(D_i\) specified in the SLAs is implemented. Equations 13 and 14 model the assumption that homogeneous VMs must be allocated for each tenant. \(\Gamma \) is an extremely large positive number. Equation 15 controls that the maximum capacity of the physical machine is not exceeded. A relaxation of this constraint would make it possible to model over-allocation. In the same way, 16 controls that the memory allocated for the vnodes do not exceed the main memory capacity of the physical nodes. Equation 17 guarantee that the Cassandra vnodes are instantiated on at least \(D_i\) different physical machines. Equations 18 and 19 force \(s_{i,h}\) to be equal to 1 if the physical machine h is used by application i and to be zero otherwise. In the same way, the set of constraints 20 and 21 force \(r_h\) to be equal to 1 if the physical machine is used and zero otherwise. Finally, expressions 22 and 23 are structural constraints of the problem.
5.2 Heuristics
In a real scenario it is reasonable that new tenants subscribe to a service and/or that existing tenants change their SLAs (for example requesting the support for an higher throughput, for a different replication factor or for a different dataset size). In such dynamic scenarios, in order to satisfy the SLAs, the auto-scaler should perform adaptation actions without perturbing the performance of the other tenants, that is for example avoiding vnodes migration.
A limitation of the Opt algorithm is that the scaling of a virtual data center or the instantiation of a new one can lead to an uncontrolled number of adaptation actions that involve all the tenants’ VDC and that could hurt the performance of the whole data center [4]. To solve that issue we propose four heuristic autoscaling algorithms that work locally allocating/deallocating resources only for the specified Cassandra VDC without re-configuring VDCs of other tenants. The first heuristic is called LocalOpt and is energy-aware. It applies locally the optimisation problem listed in Fig. 2, that is solve the optimization problem for only the one tenant. This implies that the configurations of the other Cassandra VDCs are not changed.
The second heuristic, BestFit, is a bin packing best-fit descending algorithm, widely used in practice, and it is applied locally. BestFit is energy-blind. The third and forth heuristics are modified versions of the first two and take only horizontal scaling and optimal placement decisions. They are called LocalOpt-H (energy-aware) and BestFit-H (energy-blind) respectivelly.

LocalOpt (the code is listed in Algorithm 2) receives as input the subset \(\mathcal {H}_{a} \subset \mathcal {H} \) of available physical resources, the available CPU and memory capacity for each PM in \(\mathcal {H}_{a}\), \(\{ C^a_h, M^a_h | h \in \mathcal {H}_{a}\}\), the SLA \(sla = \left<l_i,T^{min}_i, D_i, r_i \right>\) for a current or new tenant i (\(\mathcal{I} = \{ i \}\)) and \(\mathcal{J}\). The set \(\mathcal {H}_{a}\) is determined by observing the health state of the physical servers in the data center, and it accounts for hardware and software failure at infrastructure level. The output produced is the sub-optimal allocation \(\mathbf {x}_{sub}\), the new values for \(C^a\) and \(M^a\), and the error status e. At line 2 the algorithm evaluates the sub-optimal solution solving the optimisation problem optSol for the subset of available resources. If no optimal or sub-optimal solution exist (\(e =\) false) the request is rejected (line 3).

The pseudocode for the BestFit heuristic is reported in Algorithm 3. As for LocalOpt it requires as input \(\mathcal {H}_{a}\), \(C^a\) \(M^a\), the SLA sla for a current or new tenant i (\(\mathcal {I} = \{ i \}\)) and \(\mathcal {J}\). The code on lines 2-8 evaluates the number of vnodes required to satisfy throughput, dataset size, and data replication constraints, for each VM type. Line 9 selects the VM type that maximises the ratio between the requested throughput and the throughput achievable with the number of vnodes instantiated. That is, we try to minimise the over provisioning effect due to dataset constraints and, as result, the energy consumption is minimised. Lines 10-15 check if the selected VM type satisfies available CPU and memory constraints. Otherwise, the second VM type that minimises the over provisioning of resources is selected and so on, until all the VM types are analysed. Line 16 returns \(\mathbf {x}_{sub} = \emptyset \) because no feasible solutions were found. Lines 19 - 30 place the vnodes on the PMs minimising the number of PMs used, packing as many vnodes as possible in a PM, of course considering the \(D_i\) constraint. That also minimise the energy consumption. The function any(\(c_{j^*} \le C^a\)) compares \(c_{j^*}\) with all the element of \(C^a\) and it returns true if at least one element of \(C^a\) is greater than or equal to \(c_{j^*}\). Otherwise, if no PMs satisfy the constraint it returns false. The same behaviour is valid for any(\(m_{j^*} \le M^a\)). The function sortDescendent(\(\mathcal {H}_{a}\)) sorts the \(\mathcal {H}_{a}\) in descending order. The function popRR(\(\mathcal {H}_{a}\),\(D_i\)) extracts, in round-robin order, a PM from the first \(D_i\) in \(\mathcal {H}_{a}\). At Line 28, if there is no more room in the selected PMs h the set \(\mathcal {H}_{a}\) is updated removing the PMs h. At line 32, if not all the \(n^*_{i,j^*}\) vnodes could be allocated the empty set is returned because no feasible solutions for the allocation could be found. Otherwise, the suboptimal solution \(\mathbf {x}_{sub}\) is returned.
LocalOpt-H and BestFit-H are modified versions of the LocalOpt and BestFit algorithms that restrict the adaptation actions to horizontal scaling and optimal placement. The pseudo code is listed in Algorithm 4 and Algorithm 5 respectively. We omit the description of these algorithms, which is straightforward. We point out that LocalOpt-H and BestFit-H receive as input a specific VM type \(j^*\) rather then receiving the whole set \(\mathcal{J}\). In the Sect. 7 we give directions on how and when it is appropriate to use these algorithms.


6 Computational cost
There are several algorithms to solve LP problems, including the well-known simplex and interior points algorithms [20]. Widely used software packages (CPLEX®, MATLAB®) adopt variants of the well-known interior point Mehrothra’s predictor-corrector primal-dual algorithm [21], which has \(O(n^{\frac{3}{2}}\log \frac{(x^0)^Ts^0}{\epsilon })\) worst case iterations, where \(\epsilon \) is the accuracy and \((x^0)^Ts^0\) the starting point for the Mehrothra algorithm, and such that \(\epsilon \ge x^Ts\), where \(x^Ts\) is the final point in the algorithm. Hence, for a fixed \(\epsilon \) the Mehrothra algorithm has a complexity of \(O(n^{\frac{3}{2}})\), where n is the number of variables of the LP problem [27]. The complexity in our problem arises from the potentially large value of n, corresponding to the number of variables that is given by the following expression: \(n=N\times V \times H + N\times V + 3\times N + H\). This means that the worst-case complexity of our LP problem using Mehrothra’s predictor-corrector primal-dual algorithm is \(O((N\times V \times H)^{\frac{3}{2}})\).
The LocalOpt call of the optSol, which is solved with the Mehrothra algorithm. Because optSol is executed only for one tenant, the complexity of LocalOpt is \(O(( V \times H)^{\frac{3}{2}})\).
The complexity of the BestFit adaptation algorithm (Algorithm 3) can be determined in the following way. The first loop (lines 3-8) and the second loop (lines 12-15) run at most V iterations each. This means that the computational complexity of lines 1-18 is O(V). We then need to sort the list of available PMs, which has complexity \(O(H \log H)\). The third loop (lines 19-30) may run for at most H iterations. In each iteration the two functions any \((c_j* \le C_a)\) and any \((m_j* \le M_a)\) are called; these functions both have complexity O(H). As a consequence, the worst-case complexity of the third loop is \(O(H^2)\). The complexity of Algorithm 2 is thus \(O(V) + O(H^2)\). In real scenarios V is much less then H, therefore the complexity is \(O(H^2)\).
The variants BestFit-H and LocalOpt-H have the same complexity of the BestFit-H and LocalOpt-H respectively.
Figure 3 compares the number of iterations for the five autoscaling algorithms and for different values of N, V and H.
7 Recommendations on the use of the auto-scaling algorithms
Although all the proposed auto-scaling algorithms can be used at run-time, it is crucial to discuss their limitations and to give guidelines on how and when is appropriate to use them. Table 3 shows four typical use cases and what policy is best for each of them.
As mentioned before the Opt algorithm produces too many reconfigurations of the whole data center. Moreover, for large-scale systems, the polynomial complexity of the Opt is a limitation, especially if the workload changes at high frequency. Hence, the optimal auto-scaling algorithm is more suitable to support capacity planning decisions and for periodical mid term consolidation actions.
All the heuristic auto-scaling algorithms proposed are suitable for run-time adaptation decisions. Although, there are two cases that should be carefully considered: the algorithm recommend horizontal scaling actions and the algorithms recommend vertical scaling actions.
Horizontal scaling is seamlessly supported by the whole cloud stack, from application level, Cassandra in our case, to the hypervisor. The only limitation is the responsiveness of the scaling actions, that is bounded by the time needed to start a VM (about 2min) and by the time needed to add a Cassandra vnode to an existing VDC, scaling delay hereafter. Best practices for Cassandra cluster management suggest that, to preserve data consistency, vnodes should be added sequentially (one at time) and that the scaling delay is at least 2 min. While the VMs activation delay can be eliminated using a pool of warm VMs, the second could not be eliminated. In Fig. 4 we show an example of horizontal scaling for Cassandra.
The serialization of the horizontal scaling actions is a hot spot in case of throughput surges: the throughput increase (\(\Delta T_i^{min} / \Delta t\)) that can be supported is bounded by the capacity of the vnodes (\(t_{i,j,h}\)), by the scaling delay and by the configuration of the Cassandra VDC before the surge. Vertical scaling can help in managing surges of throughput (cf. Sect. 9.2).
Temporal sequence of horizontal scaling actions. At time \(t_0=4\) the throughput demanded from application i increase to \(T^{min}_i=16\). The increase takes place in 1 min. The autoscaling algorithm decision is to add three nodes. Let us suppose the SLA variation is forecasted at \(t_1\le t_0 - 2\) min, e.g. \(t_1=2\). If immediately a new Cassandra vnode is added to the VDC (relying on an VM in the warm pool) and 3 new VM are started, the 1st Cassandra vnode is in the VDC approximately at \(t_0\). At the same time the new VMs are ready to be used, and the 2nd Cassandra vnode can be started. At time \(t=6\) two new Cassandra nodes are in the VDC and the 3rd can be started. At time \(t=8\) all the required Cassandra vnodes are in the VDC. Between \(t=4.45\) and \(t=8\) the supposed amount of requests to be served is \(2.886\times 10^3\) and the amount of requests served is \(2.705\times 10^3\). Hence, the number of request that are delayed is about 182 that is the 6.31% (Color figure online)
Vertical scaling is partially supported by the cloud stack. For example, Open Stack supports live instance resizing, but not all the hypervisors do: VMWare support seamless vertical scaling, but with Xen and KVM the vertical scaling implies to shutdown and to restart the VMs. As before mentioned and as practically shown in Sect. 9.2 vertical scaling can help in managing surges of throughput. Let us consider the example in Fig. 4: if at time \(t_1\), rather than starting the horizontal scaling sequence, we operate a vertical scaling of the running nodes, we can manage a throughput surge by the deadline of \(t=5\).
Hence, we give the following recommendations for the use of the algorithms:
-
1.
The workload must be carefully characterized to properly size the vnodes capacity, that is \(t_{i,j,h}\)
-
2.
Workload prediction and proactive auto-scaling should be combined. The forecasting windows should be at least scaling delay time units ahead
-
3.
For horizontal scaling, the activation of the Cassandra vnodes should be pipelined (cf. Fig. 4) and maintaining a pool of warm VMs helps in reducing the scaling delay
-
4.
Vertical scaling can help in managing throughput surges, reducing the time to scale the capacity of the cluster (versus the horizontal scaling).
In case the vertical scaling is not seamlessly supported, what we recommend is:
-
1.
To use Opt, LocalOpt or BestFit algorithms for the first VDC configuration
-
2.
To run, at run time, LocalOpt-H or BestFit-H
-
3.
To run, periodically, LocalOpt or BestFit for VDC consolidation.
8 Performance evaluation methodology
In this section we describe the performance evaluation scenarios, the performance evaluation metrics and the setup of the experiments.
8.1 Scenarios
We selected three cases that are representative of real scenarios:
-
Increase of the throughput (SLA variation). Customer needs and service level objectives can change over time. This scenario considers a planned increase of the throughput demand.
-
Surge in the throughput. This scenario considers an unpredicted increase in the throughput demand of a specific tenant i.
-
Physical node failures. This scenario contemplate the failure of physical machines, that implies the loss of a given number of Cassandra vnodes. In this context, we analyze how the placement of the vnodes (operated by the auto-scaling algorithms) impact the consistency level reliability.
8.2 Performance metrics
Performance will be quantified using the following metrics:
-
\(P(\mathbf {x})\) the overall power consumption defined by equation 10;
-
The Scaling Index for application i \(SI(t_1,t_2)_{i,j}\) is defined as the variation in the number and type of Cassandra vnodes when the system change its configuration at time \(t_1\) (\(\mathbf {x}(t_1)\)) into a new configuration at time \(t_2\) (\(\mathbf {x}(t_2)\)).
$$\begin{aligned} SI(t_1,t_2)_{i,j}=\sum _{\mathcal {H}} \left( x(t_2)_{ijh} - x(t_1)_{ijh} \right) . \end{aligned}$$SI represents a gap and not an absolute value of the number of VMs used. Positive values for SI means that new VMs are allocated. Negative value represent the number of VMs deallocated. SI allows to quantify both vertical and horizontal scaling actions.
-
The Migration Index for application i. \(MI(t_1,t_2)_i\) is defined as the number of Cassandra vnodes migrations that application i experienced when the system change its configuration at time \(t_1\) into a new configuration at time \(t_2\).
$$\begin{aligned} MI(t_1,t_2)_i=\sum _{\mathcal {H}} \Delta _{i,h} \end{aligned}$$where \(\Delta _{i,h}=1\) if \((s(t_2)_{i,h} - s(t_1)_{i,h}) > 0\) and \(\Delta _{i,h}=0\) otherwise. \(s(t)_{i,h}\) is the value of \(s_{i,h}\) at time t.
-
Number of delayed requests \(Q_i( \tau )\) for tenant i in a time interval \(\tau = t_{end} - t_{start}\). Assuming that \(T_i (t)\) is the actual throughput observed and that \(T^{min}_i(t ) \ge T_i (t )\) \(\forall t\in \tau \) we define
$$\begin{aligned} Q_i( \tau ) = \int _{t_{start}}^{t_{end}} \left( T^{min}_i(t) - T_i (t) \right) dt . \end{aligned}$$ -
Consistency level reliability \(\mathcal {R}\) defined as the probability that the number of healthy replicas in the Cassandra VDC is enough to guarantee a specific level of consistency over a fixed time interval (c.f. Sect. 9.3 for details). We recall that, assuming independence of failures in the components, the reliability of K nodes working in parallel is defined as \(\mathcal {R}=1-(1-\rho )^{K}\), where \(\rho \) is the reliability of a single node and \((1-\rho )^{K}\) is the probability that K nodes fail.
8.3 Setup of the experiments
To measure the maximum Cassandra throughput achievable (\(t^0_{l_i,j}\)) for each type of workload and VM type and to compute also the values for \(\delta _{l_i,j}^k\) we use a real cluster and a workload generator provided by Ericsson to reproduce their application behaviour. The cluster is composed of nodes with 16 cores and 128 GB of memory (RAM). The nodes are connected with a high speed LAN. We run VMware ESXi 5.5.0 on top of Red Hat Enterprise Linux 6 (64-bit) and we use Cassandra 2.1.5. We use VMs with three different configurations, as reported in Table 1. The values obtained for \(t^0_{l_i,j}\) are reported in Table 1, while the values for \(\delta _{l_i,j}^k\) are reported in Table 4.
The performance of the proposed adaptation algorithms are assessed using Monte Carlo simulation for the Physical node failure scenario, while numerical evaluation is used for the SLA variation and Throughput surge scenarios. Experiments have been carried out using Matlab R2015b 64-bit for OSX running on a single Intel Core i5 processor with 16GB of main memory. The model parameters we used for simulation are reported in Table 4.
9 Experimental results
9.1 Increase of the throughput (SLA variation)
In this scenario we investigate how the adaptation policies react to an increase of the throughput specified in the SLA. We consider three tenants running a R, W and RW workload respectively and we increase, once at a time, the throughput for each tenant: the increment range from \(T^{min}_i=10.000\) ops/s to 70.000 ops/s. The replication factor and the dataset size is the same for all the applications: \(D_i = 3\) and \(r_i = 8\) GB. We assume that such SLA variations are planned, which means that the provider has time to allocate the right amount of resources and therefore there are no SLA violations.
Figure 5 shows the Scaling Index for the tenant generating a RW workload. The bars represent the scaling actions. There is one bar color for each VM type. An observation reporting both positive and negative bars means that the adaptation policy switches between two VM configurations (vertical scaling). The negative bar is for the VM type dismissed and the positive for the new VM type allocated. Observations with only positive bars correspond to horizontal scaling adaptation actions. For example, for the Optimal policy there is a change from VM type 3 (yellow bar) to VM type 2 (green bar) for the observation \(T^{min}_i = 30.000\) ops/s. The number of new allocated VMs is smaller because each new VM offers a higher throughput. The optimal adaptation policy always starts allocating VMs of Type 3 (cf. Table 1) and, if needed progressively moves to more powerful VM types. The Opt policy performs only one vertical scaling and when the VM type if changed from type 3 to type 2; after that it always does horizontal scaling actions (this is a particularly lucky case). The two heuristics LocalOpt and BestFit show a very unstable behaviour performing both vertical and horizontal scaling. Both first scale to VM type 1 from VM type 3 and then they scale back to VM type 2. When the variant of the above algorithm is used, that is LocalOpt-H and BestFit-H respectively, the VM type is fixed to type 1 and the only action taken is horizontal scaling.
Throughput increase: Migration Index for the optimal policy. The heuristic policies have a MI equal to zero by definition. For each box the central mark indicates the median (50th percentile), and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the maximum and the minimum value observed. Outlier are represented by red points (Color figure online)
The power consumption is plotted in Fig. 6. For throughput higher than \(40 \times 10^3\) ops/s, with the optimal scaling is possible to save about 50% of the energy consumed by the heuristic allocation. For low values of the throughput (\(10 - 20 \times 10^3\) ops/s) the BestFit and BestFit-H show a very high energy consumption compared to the LocalOpt and LocalOpt-H. When the throughput increase, the LocalOpt-H behave as the BestFit. For high throughput (\(60 - 70 \times 10^3\) ops/s), the energy consumed by the LocalOpt is less than all the other heuristics.
Figure 7 shows the Migration Index. Each box plot is computed over the data collected for the three tenants. We can observe that each application experiences between 0 and 3 vnode migrations depending on the infrastructure load state.
Considering the low values for the migration index for the Opt allocation and the high saving in the energy consumed compared with the other algorithms, it makes sense to perform periodic VDC consolidation using the Opt policy, as recommended in Sect. 7.
9.2 Throughput surge
In this set of experiments we analyse how fast the scaling is, with respect to the throughput variation rate, and what is the number of delayed requests. We assume the throughput requested by an application generating a RW workload increase a shown in Fig. 8. Differently from the previous set of experiments we assume what follow: the throughput increase is not agreed in advance, it is a surge; the throughput is forecasted 2 min ahead; the requested throughput, after the increase, remains stable for a relatively long period; the horizontal scaling of the Cassandra vnodes is serialized and the activation delay is 2 min; vertical scaling is supported by the cloud stack and can be done in parallel for all the interested vnodes.
The first case (Case A) uses VMs with the capacity specified in Table 1). The Opt auto-scaling starts allocating four vnodes of Type 3 (\(3.3 \times 10^3\) ops/s) and then five. At time \(t=8\) the algorithm did a vertical scaling action allocating five vnodes of Type 2 (\(8.3 \times 10^3\) ops/s). Than, at time \(t=10\), twelve vnodes are allocated. Considering the serialization of the horizontal scaling actions (cf. Sect. 7) the seven Cassandra vnodes are added in 14 min. The LocalOpt behaves like the Opt in terms of scaling decisions. The BestFit auto-scaling start allocationg 4vnodes of Type 3, than it scale-up to seven vnodes (at time \(t=8\)) and finally it did two vertical scaling actions: the first from vnodes Type 3 to Type 2, and the second from Type 2to Type 1 vnodes.
The number of delayed requests \(Q_i\) and the percentage with respect the total number of received requests (tot.req.) are reported in Table 5. \(Q_i\) and tot.req. are computed over the time interval the requested throughput \(T_{RW}^{min}\) exceed the actual throughput.
Intuitively, with Cassandra vnodes capable to handle a higher workload it should be possible to better manage the surge in the throughput. Hence, we have analyzed a Case B where we configure three new types of Cassandra vnodes capable to handle the following RW throughput: type 4, \(20\times 10^3\) ops/s; type 5, \(15\times 10^3\) ops/s; and type 6, \(7\times 10^3\)ops/s. Fig. 8 shows the behaviour of the Opt and BestFit auto-scaling algorithms. The LocalOpt behaves as the Opt. From the plots, it is evident that with more powerful vnodes the auto-scaling algorithms are capable to satisfy the requested throughput with a delay of only 2 min. The Opt starts allocating 3 vnodes of type 6, at time \(t=4\) a new node of type 6 is added and at time \(t=6\) the algorithm did a vertical scaling allocating 4 vnodes of type 5. At \(t=8\) the algorithm decided to add 2 more nodes of type 5, that are allocated in the next two time slots. The BestFit starts allocating vnodes of type 6 and scales from 4 to 6 nodes. After that, at \(t=10\) it performs a vertical scaling from type 6 to type 5. The values for delayed requests are reported in Table 5.
The take home message is that having a pool of vnodes type capable to handle from low throughput to very high throughput allow to manage throughput surges.
9.3 Physical node failures
Cassandra offers three main levels of consistency (both for Read and Write): ONE, QUORUM and ALL. Consistency level of ONE means that only one replica node is required to reply correctly, that is it contains the replica of the portion of the dataset needed to answer the query. Consistency level QUORUM means that \(Q=\left\lfloor \frac{D}{2} \right\rfloor +1 \) replicas nodes are available to reply correctly (where D is the replication factor). Consistency level ALL means that all the replicas are available.
In the following, we assess the Consistency level reliability \(\mathcal {R}\) for a consistency level of ONE and of QUORUM when the replication factor is \(D=3\) and \(D=5\) for all \(i\in \mathcal {I}\) and when the different autoscaling algorithms are applied.
In case the Cassandra VDC has a number of physical nodes H equal to the number of vnodes n, and there is a one-to-one mapping between vnodes and physical nodes, the consistency level of ONE is guaranteed if one replica is up. Hence, the Consistence reliability is the probability that at least one vnode is up and a replica is on that node:
where: \(\rho \) is the resiliency of a physical node, and \( \frac{D}{n}\) is the probability that a replica is on a Cassandra vnode when the data replication strategy used is the SimpleStrategy (cf. the Datastax documentation for Cassandra). In the same way, we can define the reliability of the Cassandra VDC to guarantee a consistency level of QUORUM as the probability that at least Q vnodes are up and that Q replicas are on them:
Table 6 shows the values of \(\mathcal {R}_{O}\) and \(\mathcal {R}_{Q}\) for \(D=3\) and 5 and for \(\rho =0.9\) and \(\rho =0.8\).
In a managed Cassandra data center, a Cassandra VDC is rarely allocated using a one-to-one mapping of vnodes on physical nodes. The resource management policies adopted by the provider usually end-up with a many-to-one mapping, that is h physical nodes run n Cassandra vnodes: \(D \le h < n\). In that case we can generalise Eqs. 24 and 25 to the following:
where: \(K_O\) is the number of failed physical nodes that causes a failure of n vnodes; and \(K_Q\) is the number of failed physical nodes that causes a failure of \(n-Q +1\) vnodes. Because the distribution of the vnodes on the physical nodes is unknown, we have heuristically computed the values of \(K_O\) and \(K_Q\) for \(D=3\) and 5. While the value for \(K_O\) is equal to the number of physical nodes used, the values for \(K_Q\) depend on the specific allocation and on the nodes that fail. Observing a VDC allocation, we could have a set of values \(\{ K_Q^1, K_Q^2, \ldots \}\) where the \(\max \{ K_Q^1, K_Q^2, \ldots \}\) represents the best case and the \(\min \{ K_Q^1, K_Q^2, \ldots \}\) represents the worst case. For example, if 8 vnodes are distributed on 5 PMs in the following way \(\{ 1, 1, 2, 1, 3 \}\) and \(D=3\), we have: \(Q=2\), \(n-Q +1=7\), \(K_O=5\), \(K^{best}_Q=5\), \(K^{worst}_Q=4\).
Table 6 reports the values of \(\mathcal {R}_{O}\) and \(\mathcal {R}_{Q}\) for \(D=3\) and \(D=5\), \(\rho =0.9\). The evaluation is done in the following way. We consider 5 customers that request for a randomly generated SLA: \(l_i\) is distributed as 10% RW, 15%W and 75% R; \(T_{min}\) is uniformly distributed in the interval [10.000, 18.000] ops/s; \(D_i= 3\) (5) and \(r_i\) is constant (8GB). The number of vnodes used by each tenant is \(n=6\) for the case \(D=3\) and \(n=10\) for the case \(D=5\). We run 10 experiments and we assess the best and worst case over all the allocated VDC.
In the first set of experiments we consider \(\rho =0.9\). The one-to-one mapping offers a consistency level of ONE and QUORUM with a very high reliability of six 9 s and five 9 s respectively if \(D=3\) and if the replication factor increase to 5 the reliability increases to ten 9 s and eight 9 s for consistency ONE and QUORUM respectively.
Unfortunately, when a n-to-one mapping is adopted the reliability of the consistency level drops down 3–4 orders of magnitude. In the case \(D=3\), we observed that all the auto-scaling policies offer a consistency level ONE with a reliability of three 9 s. If the replication factor increases to 5 the reliability increase to five 9 s. For the consistency level QUORUM, we have a dependency on both the replication factor and the auto-scaling policy. When the replication factor is three, Opt, LocalOpt and LocalOpt-H offer a consistency level of QUORUM with a reliability that ranges between two 9 s and three 9 s, while the BestFit and BestFit-H offer a reliability level of three 9 s. When the replication factor increase to five, the reliability level offered by Opt, LocalOpt and LocalOpt-H increase to three 9 s in the worst case and five 9 s in the best case. The BestFit and BestFit-H provide a reliability of four 9 s.
When we decrease the reliability of the physical machines to \(\rho =0.8\) the reliability decreases of two or three order of magnitude for the one-to-one mapping and of one or two order of magnitude for the heuristics.
10 Concluding remarks
In this paper we explored the problem of energy-aware autoscaling of Cassandra VDC in a multi-tenants environment. We presented an optimisation model that find the optimal auto-scaling actions. The system model we propose relies only on the measure or estimate of the relationship between the throughput achievable and the number of Cassandra vnodes. This information is easy to be collected and maintained up to date at execution time. The performance of the optimal auto-scaling is compared against two energy-aware heuristics and two energy-blind heuristics. The advantage of using heuristics is twofold: first, the heuristics are applied locally, and that reduces the perturbation of the performance of the tenants that do not need to scale. Second, the Opt has a complexity of the order \(O((V\times N\times H)^{3/2})\) for N tenants, H physical nodes and V Cassandra vnode Types, while the heuristics have a complexity of the order \(O((V\times H)^{3/2})\) and \(O(H^2)\) for (localOpt) and (BestFit) respectively (a details analysis has been provided in Sect. 6).
The lesson learned from that study is the following.
Planned variations of the throughput (increase and/or decrease) can be managed in an energy efficient way by the LocalOpt. For intense workload and for high utilized data centers the energy consumed by a LocalOpt allocation is comparable with the allocation determined by the BestFit. But for low throughput and/or low utilized data centers, the BestFit produces allocations that consume between the 48% and the 100% more energy than the LocalOpt.
The agility of Cassandra in scaling up is limited by the need to serialize the allocation of vnodes and by the scaling delay. Our experiments show that vertical scaling of vnodes is the only adaptation action capable to manage surges in the throughput.
Finally, a Cassandra cluster that use a one-to-one mapping of vnodes on physical nodes offer the consistency level of ONE and of QUORUM with a very high level of reliability (between five and ten 9 s) in case of physical node failures and a node reliability of 0.9. On the contraty, when a n-to-one mapping is implemented, the reliability for consistency level of ONE and QUORUM drop down of three - four order of magnitudes.
Hence, we have identified two open challenges. First, there is the need for energy-efficient auto-scaling algorithms that hide the structural limitation of Cassandra to scale fast. Such algorithms should prioritize vertical scaling actions and should take into consideration the state of the system (the algorithm we have proposed are memoryless). Second, there is the need for energy-efficient and consistency-aware algorithms that do not impact the reliability of the consistency level offered by Cassandra when configured using a one-to-one mapping.
References
Almeida Morais, F., Vilar Brasileiro, F., Vigolvino Lopes, R., Araujo Santos, R., Satterfield, W., Rosa, L.: Autoflex: service agnostic auto-scaling framework for IaaS deployment models. In: 2013 13th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing (CCGrid), pp. 42–49 (2013). doi:10.1109/CCGrid.2013.74
Borgetto, D., Maurer, M., Da-Costa, G., Pierson, J., Brandic, I.: Energy-efficient and SLA-aware management of IaaS clouds. In: 2012 Third International Conference on Future Energy Systems: Where Energy, Computing and Communication Meet (e-Energy), pp. 1–10 (2012)
Buyya, R., Beloglazov, A., Abawajy, J.H.: Energy-efficient management of data center resources for cloud computing: a vision, architectural elements, and open challenges. CoRR (2010). http://arxiv.org/abs/1006.0308
Casalicchio, E., Lundberg, L., Shirinbab, S.: Energy-aware adaptation in managed Cassandra datacenters. In: 2016 International Conference on Cloud and Autonomic Computing (ICCAC), pp. 60–71 (2016). doi:10.1109/ICCAC.2016.12
Casalicchio, E., Silvestri, L.: Mechanisms for SLA provisioning in cloud-based service providers. Computer Networks 57(3), 795–810 (2013). http://dx.doi.org/10.1016/j.comnet.2012.10.020. http://www.sciencedirect.com/science/article/pii/S1389128612003763
Chalkiadaki, M., Magoutis, K.: Managing service performance in NoSQL distributed storage systems. In: Proceedings of the 7th Workshop on Middleware for Next Generation Internet Computing, MW4NG ’12, pp. 5:1–5:6. ACM, New York, NY, USA (2012). doi:10.1145/2405178.2405183. http://doi.acm.org/10.1145/2405178.2405183
Cipar, J., Xu, L., Krevat, E., Tumanov, A., Gupta, N., Kozuch, M.A., Ganger, G.R.: Jackrabbit: improved agility in elastic distributed storage (2012)
Cohen, R., Lewin-Eytan, L., Naor, J.S., Raz, D.: Almost optimal virtual machine placement for traffic intense data centers. In: 2013 Proceedings IEEE INFOCOM, pp. 355–359 (2013). doi:10.1109/INFCOM.2013.6566794
Cooper, B.F., Silberstein, A., Tam, E., Ramakrishnan, R., Sears, R.: Benchmarking cloud serving systems with YCSB. In: Proceedings of the 1st ACM Symposium on Cloud Computing, SoCC ’10, pp. 143–154. ACM, New York, NY, USA (2010). doi:10.1145/1807128.1807152. http://doi.acm.org/10.1145/1807128.1807152
Dalvandi, A., Gurusamy, M., Chua, K.C.: Time-aware vmflow placement, routing, and migration for power efficiency in data centers. IEEE Trans. Netw. Serv. Manage. 12(3), 349–362 (2015). doi:10.1109/TNSM.2015.2443838
Dede, E., Govindaraju, M., Gunter, D., Canon, R.S., Ramakrishnan, L.: Performance evaluation of a MongoDB and Hadoop platform for scientific data analysis. In: Proceedings of the 4th ACM Workshop on Scientific Cloud Computing, Science Cloud ’13, pp. 13–20. ACM, New York, NY, USA (2013). doi:10.1145/2465848.2465849. http://doi.acm.org/10.1145/2465848.2465849
Diegues, N., Orazov, M., Paiva, J.A., Rodrigues, L., Romano, P.: Optimizing hyperspace hashing via analytical modelling and adaptation. SIGAPP Appl. Comput. Rev. 14(2), 23–35 (2014). doi:10.1145/2656864.2656866. http://doi.acm.org/10.1145/2656864.2656866
Ghanbari, H., Simmons, B., Litoiu, M., Barna, C., Iszlai, G.: Optimal autoscaling in a IaaS cloud. In: Proceedings of the 9th international conference on Autonomic computing, ICAC ’12, pp. 173–178. ACM, New York, NY, USA (2012). doi:10.1145/2371536.2371567. http://doi.acm.org/10.1145/2371536.2371567
Grozev, N., Buyya, R.: Multi-cloud provisioning and load distribution for three-tier applications. ACM Trans. Auton. Adapt. Syst. (TAAS) 9(3), 13 (2014)
Intel: Configuration and deployment guide for the Cassandra NoSQL data store on Intel architecture. Tech. rep., Intel Corporation (2013)
Jiang, Y., Perng, C.S., Li, T., Chang, R.N.: Cloud analytics for capacity planning and instant vm provisioning. IEEE Trans. Netw. Serv. Manage. 10(3), 312–325 (2013). doi:10.1109/TNSM.2013.051913.120278
Kliazovich, D., Bouvry, P., Audzevich, Y., Khan, S.: Greencloud: a packet-level simulator of energy-aware cloud computing data centers. In: Global Telecommunications Conference (GLOBECOM 2010), 2010 IEEE, pp. 1–5 (2010). doi:10.1109/GLOCOM.2010.5683561
Kuhlenkamp, J., Klems, M., Röss, O.: Benchmarking scalability and elasticity of distributed database systems. Proc. VLDB Endow. 7(12), 1219–1230 (2014). doi:10.14778/2732977.2732995. http://dx.doi.org/10.14778/2732977.2732995
Mastelic, T., Oleksiak, A., Claussen, H., Brandic, I., Pierson, J.M., Vasilakos, A.V.: Cloud computing: Survey on energy efficiency. ACM Comput. Surv. 47(2), 33:1–33:36 (2014). doi:10.1145/2656204. http://doi.acm.org/10.1145/2656204
Megiddo, N.: On the complexity of linear programming. In: Bewley, T (ed.) Advances in Economic Theory: 5th World Congress, pp. 225–268. Cambridge University Press, Cambridge (1987)
Mehrotra, S.: On the implementation of a (primal-dual) interior point method. SIAM J. Optim. 2, 575–601 (1992)
Paiva, J.A., Ruivo, P., Romano, P., Rodrigues, L.: Autoplacer: Scalable self-tuning data placement in distributed key-value stores. ACM Trans. Auton. Adapt. Syst. 9(4), 19:1–19:30 (2014). doi:10.1145/2641573. http://doi.acm.org/10.1145/2641573
Patil, S., Polte, M., Ren, K., Tantisiriroj, W., Xiao, L., López, J., Gibson, G., Fuchs, A., Rinaldi, B.: Ycsb++: benchmarking and performance debugging advanced features in scalable table stores. In: Proceedings of the 2nd ACM Symposium on Cloud Computing, SOCC ’11, pp. 9:1–9:14. ACM, New York, NY, USA (2011). doi:10.1145/2038916.2038925. http://doi.acm.org/10.1145/2038916.2038925
Priya, B., Pilli, E., Joshi, R.: A survey on energy and power consumption models for greener cloud. In: 2013 IEEE 3rd International Advance Computing Conference (IACC), pp. 76–82 (2013). doi:10.1109/IAdCC.2013.6514198
Rabl, T., Gómez-Villamor, S., Sadoghi, M., Muntés-Mulero, V., Jacobsen, H.A., Mankovskii, S.: Solving big data challenges for enterprise application performance management. Proc. VLDB Endow. 5(12), 1724–1735 (2012). doi:10.14778/2367502.2367512. http://dx.doi.org/10.14778/2367502.2367512
Rocha, L.A., Cardozo, E.: A hybrid optimization model for green cloud computing. In: Proceedings of the 2014 IEEE/ACM 7th International Conference on Utility and Cloud Computing, UCC ’14, pp. 11–20. IEEE Computer Society, Washington, DC, USA (2014). doi:10.1109/UCC.2014.9. http://dx.doi.org/10.1109/UCC.2014.9
Salahi, M., Terlaky, T.: Mehrotra-type predictor-corrector algorithm revisited. Optimization Methods Software 23(2) (2008)
Shankaranarayanan, P., Sivakumar, A., Rao, S., Tawarmalani, M.: Performance sensitive replication in geo-distributed cloud datastores. In: 2014 44th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), pp. 240–251 (2014). doi:10.1109/DSN.2014.34
Sharma, U., Shenoy, P., Towsley, D.F.: Provisioning multi-tier cloud applications using statistical bounds on sojourn time. In: Proceedings of the 9th International Conference on Autonomic Computing, ICAC ’12, pp. 43–52. ACM, New York, NY, USA (2012). doi:10.1145/2371536.2371545. http://doi.acm.org.miman.bib.bth.se/10.1145/2371536.2371545
Shi, Y., Meng, X., Zhao, J., Hu, X., Liu, B., Wang, H.: Benchmarking cloud-based data management systems. In: Proceedings of the Second International Workshop on Cloud Data Management, CloudDB ’10, pp. 47–54. ACM, New York, NY, USA (2010). doi:10.1145/1871929.1871938. http://doi.acm.org/10.1145/1871929.1871938
Xu, Z., Deng, N., Stewart, C., Wang, X.: Cadre: carbon-aware data replication for geo-diverse services. In: 2015 IEEE International Conference on Autonomic Computing (ICAC), pp. 177–186 (2015). doi:10.1109/ICAC.2015.15
Ye, K., Wu, Z., Wang, C., Zhou, B.B., Si, W., Jiang, X., Zomaya, A.Y.: Profiling-based workload consolidation and migration in virtualized data centers. IEEE Trans. Parallel Distrib. Syst. 26(3), 878–890 (2015). doi:10.1109/TPDS.2014.2313335
Acknowledgements
This work is funded by the research project “Scalable resource-efficient systems for big data analytics”—Knowledge Foundation Grant No. 20140032, Sweden.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Casalicchio, E., Lundberg, L. & Shirinbab, S. Energy-aware auto-scaling algorithms for Cassandra virtual data centers. Cluster Comput 20, 2065–2082 (2017). https://doi.org/10.1007/s10586-017-0912-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10586-017-0912-6