1 Introduction

Although reducing greenhouse gas (GHG) emissions in all economic sectors is necessary to achieve climate goals cost-efficiently and on time (Wollenberg et al. 2016; Rogelj et al. 2018), many sectors still lag behind in most national climate policies; for example, most countries exclude transport and agricultural sectors from their carbon pricing systems (World Bank 2020, p. 45). One reason for this is carbon leakage risk: when climate policies regulate sectors, they face the risk that their GHG emissions relocate to unregulated jurisdictions (Grosjean et al. 2018; Efthymiou and Papatheodorou 2019; Dray and Doyme 2019; Isermeyer et al. 2021).Footnote 1Footnote 2 Besides entailing economic losses for domestic sectors, carbon leakage could seriously reduce the effectiveness of unilateral mitigation policies and cause reductions in production, employment, and tax revenue (Martin et al. 2014b).

How considerable is carbon leakage risk in unregulated sectors compared to regulated sectors? How different is the risk of a specific sector across different countries? Knowing the answer to these questions could be helpful in many ways. Firstly, if carbon leakage risk is relatively unsubstantial in a particular sector, this risk should no longer be accepted as a valid excuse to opt out of national mitigation policy. However, this risk must be analyzed considering all the possible configurations of climate policy and their possible impacts. Second, knowing which unregulated sectors are at high carbon leakage risk is essential for governments to develop anti-leakage mechanisms for them (Metcalf and Weisbach 2009). Although it would be ideal to have these mechanisms in place for all sectors, the implementation feasibility of some mechanism types might require only applying them to the most vulnerable sectors (Mehling et al. 2019, p. 465). Third, knowing if carbon leakage risk for a specific sector differs between countries would be particularly informative for supranational carbon jurisdictions or climate clubs. In particular, if this risk varied significantly between countries, it would not be appropriate to aid sectors from different countries equitably (Sato et al. 2015).

Unfortunately, the existing literature is limited in several respects. On the one hand, we are unaware of studies comparing carbon leakage risk between sectors and countries comprehensively. Instead, existing studies focus on particular economic sectors, mainly energy-intensive, and analyze this risk in one country or among a few countries (Sugino et al. 2013; Sato et al. 2015; Martin et al. 2014b; Dray and Doyme 2019; Frank et al. 2021; Santos et al. 2019). Moreover, because these studies focus on different policies and use different methodologies, it is challenging to compare results across them. On the other hand, most studies ignore carbon leakage risk in downstream sectors; however, because indirect GHG emissions, i.e., emissions associated with a sector’s production inputs, often make up the largest share of organizations’ footprints (Li et al. 2020), downstream sectors might also face significant impacts due to carbon costs passed through higher input prices (Bushnell and Humber 2017; Stede et al. 2021).

To fill this literature gap, our paper calculates and compares potential carbon leakage risk across sectors and OECD countries. To measure this risk, we use an emission intensity and trade exposure (EITE) metric similar to phase 4 of the European Union Emissions Trading System (EU-ETS): the product of an emission intensity (EI) and a trade exposure (TE) component (European Commission 2019). The EI component, a proxy for a sector’s relative carbon cost burden, is equal to the volume of the sector’s regulated GHG emissions multiplied by the domestic carbon price divided by its gross value added (GVA). The TE component, a proxy for the risk that a sector’s products are replaced by foreign products from unregulated countries, is equal to a sector’s international trade value divided by its domestic market value. To calculate the EITE metric, we use Global Trade Analysis Project (GTAP) 10A data (Aguiar et al. 2019): the multiregional input–output (MRIO) (Carrico et al. 2020), the carbon dioxide (CO2) (Lee 2008), and non-CO2 (Chepeliev 2020) emissions databases, which contain harmonized data for 141 countries and 65 sectors in 2014. To estimate indirect GHG emissions, we use a global environmentally extended (EE) MRIO model, a popular model for estimating emissions along global value chains (Hertwich and Wood 2018; Li et al. 2020).

To include all the possible ways unilateral climate policies could affect sectors, we consider three climate policy scenarios: in the first, domestic climate policies imply carbon costs on all domestic sectors’ direct GHG emissions. Such a situation could occur if the domestic climate policy targets a sector’s GHG emissions, but carbon costs are not passed through via production inputs; in the second, domestic climate policies imply carbon costs on sectors’ indirect GHG emissions only. This scenario represents the situation downstream sectors face, which suffer from carbon cost increases via more expensive production inputs; in the third, domestic climate policies imply carbon costs on sectors’ total GHG emissions. This scenario represents the maximum potential carbon cost burden faced by a sector; it would be possible if carbon prices target this sector’s direct GHG emissions, those of the products it uses as inputs, and its imports.Footnote 3 To make the risk estimates comparable across sectors and countries, we assume the same carbon price in every country across all scenarios.

Our article contributes to the literature in several ways. First, it provides the first cross-country cross-sector carbon leakage risk analysis under varying climate policy scenarios. As such, it complements other more specific analyses. Second, our results are highly relevant for policy-makers; for example, while inter-sectoral differences indicate which sectors should receive special attention, cross-country differences inform them if anti-leakage policies should be developed by measuring risk on a country-by-country basis. Third, our results are also relevant to other researchers; for example, because GTAP databases are often employed to analyze climate policies, researchers can compare our results with alternative approaches to estimate carbon leakage. Fourth, due to the popularity of the EITE metric, our results are relevant in an international climate policy context.

Our work is organized as follows: the next section gives additional information about carbon leakage and the EITE metric. Section 3 formally introduces the EE-MRIO model, the EITE metric, and presents the climate policy scenarios. Section 4 describes the data and provides a brief overview of it. Section 5 presents results. Section 6 discusses the implications. Finally, Sect. 7 concludes by briefly summarizing the results, mentioning limitations, and opportunities for future research.

2 Background

2.1 Carbon leakage and consequences

A characteristic feature of climate policy is its high level of international fragmentation (World Bank 2020), implying divergent carbon prices across countries and sectors. In a highly integrated world through international trade and foreign direct investments, asymmetric carbon prices can seriously undermine the effectiveness of unilateral climate mitigation policies (Elliott et al. 2013). This phenomenon, known as policy-induced carbon leakage, happens when GHG emissions increase unintendedly in countries with less stringent climate policies due to GHG emission reductions in countries with more ambitious climate policies. These GHG emissions can neutralize or, even worse, exceed any GHG emission savings, leading to a net increase in global GHG emissions.

In theory, carbon leakage occurs through four main channels (Burniaux 2001; Elliott et al. 2013; Jakob 2021). First, under the “competitiveness” channel, the domestic climate policy raises the production costs of regulated domestic firms, who see their products lose competitiveness in domestic and export markets. As a result, the unregulated foreign product replaces the more expensive domestic variety, increasing GHG emissions in other countries. Second, under the “world energy price” channel, if the regulating country is large enough, policy-induced domestic demand reductions of fossil fuels cause world prices of these to fall. This, in turn, increases fossil fuel demand and GHG emissions in other countries. Third, under the “capital reallocation” channel, the domestic climate policy induces agents to invest in third countries, increasing their growth and related GHG emissions. Finally, under the “free-riding” channel, the domestic climate policy disincentivizes emission mitigation in third countries, who increase their GHG emissions hoping to profit from other countries’ mitigation efforts at the expense of the climate.

Carbon leakage can bring several negative consequences. On the one hand, when economic agents expect future carbon leakage, they oppose mitigation measures. For instance, the USA used carbon leakage as an excuse for delaying mitigation action (Elliott et al. 2013). Similarly, the agricultural sector has used it to justify its exclusion from carbon pricing policies (Murray and Rivers 2015; Grosjean et al. 2018). On the other hand, if carbon leakage were to materialize, besides reducing firms’ competitiveness and the effectiveness of unilateral mitigation policies, it could bring about additional costs, including reductions in production, employment, and tax revenue (Martin et al. 2014b).

2.2 Sectoral carbon leakage risk assessment

Assessing carbon leakage risk is difficult. On the one hand, there is a severe data shortage problem. This forces many studies to focus on specific sectors or countries, often ignoring several GHG emissions (Sato et al. 2015; Aldy and Pizer 2015). On the other hand, countries’ limited experience in mitigation policy hinders the ex-post analysis of carbon leakage. While the exclusion of some sectors from mitigation policies prevents any ex-post assessment on these sectors, anti-leakage programs mask carbon leakage happening in regulated sectors (Joltreau and Sommerfeld 2019). This is aggravated by historically low GHG emission prices and their short duration (Fischer and Fox 2018). Because of this, ex-post studies estimate carbon leakage with the help of energy or transportation cost differentials instead of true carbon cost differences (Aldy and Pizer 2015; Fischer and Fox 2018; Fowlie et al. 2016).

Given the above limitations, there are two main quantitative approaches for evaluating sectoral carbon leakage risk ex-ante. The first is based on economic simulation models, mostly partial and computable general equilibrium (CGE) models. Despite their ability to capture an industry’s technological characteristics accurately, main drawbacks of the former include their focus on a specific sector and the exclusion of market mechanisms influencing carbon leakage. While CGE models capture complex market mechanisms, they also face several problems, such as high data requirements. Unfortunately, many economic models lack transparency, and their estimates depend on many exogenous parameters and theoretical assumptions, both affecting carbon leakage magnitudes (Burniaux and Martins 2012). The second refers to the EITE metric; compared to economic models, it offers policymakers a simple, transparent, and easy to interpret carbon leakage risk indicator. Naturally, these advantages come at the cost of ignoring the theory of economic models and several factors driving carbon leakage, such as coalition size or abatement opportunities.

2.3 A closer look at the EITE metric

To the best of our knowledge, the EITE metric was used for the first time to assess sectors’ potential competitiveness impacts from the EU-ETS at the country level (Sato et al. 2007; Hourcade et al. 2007; Graichen et al. 2008). These studies used the EITE metric as a proxy for the potential international competitiveness losses faced by domestic sectors in particular countries. While the authors used the EI component to estimate the “maximum value at stake,” they introduced the TE component to measure the ability of a sector to pass through EU-ETS costs to downstream prices, which also depends on a sector’s exposure to international trade. Recognizing that the EITE components ignore information on additional factors also affecting competitiveness, the authors justify its use due to the scarcity and unreliability of trade and demand elasticities (Graichen et al. 2008, p. 30).

Over time, the EITE metric has become an official carbon leakage risk indicator in many carbon jurisdictions, including phases 3 and 4 of the EU-ETS, California’s Cap-and-Trade System (CC&T), the Australian Carbon Pricing Mechanism (ACPM), the South Korean ETS, and New Zealand’s ETS (Sun et al. 2019; Santos et al. 2019). Although we could not get the details of all of these versions, comparing the first four reveals several differences.Footnote 4 On the one hand, while the EI component remains practically the same across versions, there are differences in the TE component: while both phases of the EU-ETS and the CC&T use production and imports in the denominator, the ACPM uses only the former.Footnote 5 On the other hand, EITE components are used differently to identify high carbon leakage risk sectors; for example, while in phase 4 of the EU-ETS and the CC&T both components are used simultaneously, in phase 3, these are also used individually. These differences lead to different results: for example, Sugino et al. (2013) and Santos et al. (2019) find considerable differences in eligibility after applying different EITE metrics to Japanese and Brazilian data, respectively. Unfortunately, neither of these papers specifies the source of these differences.

Naturally, given its popularity and limitations, the EITE metric has been scrutinized. On the one hand, several studies criticize the EITE metric as a whole. As a proxy for potential competitiveness losses, the EITE metric also offers a risk measure for carbon leakage through the competitiveness channel. However, as captured by the EITE metric, competitiveness losses are necessary but not sufficient for carbon leakage to happen (Clò 2010, p. 2427): even if subject to carbon costs and absent any support, a sector could not experience carbon leakage, e.g., if transport costs are so high that they hinder substituting domestic output by imports (Næss-Schmidt et al. 2019, p. 24), or if foreign GHG emission intensities are lower than domestically. Furthermore, competitiveness losses say nothing about carbon leakage happening through other channels; however, since known anti-leakage mechanisms only address the competitiveness channel (Martin et al. 2014b; Monjon and Quirion 2011), identifying vulnerable sectors based on a metric of carbon leakage risk through the competitiveness channel seems justified.

On the other hand, some authors criticize its components and its use for identifying vulnerable sectors. Concerning the former, e.g., Fowlie and Reguant (2018) and Martin et al. (2014b) find that the TE component (phase 3 EU-ETS) shows substantial differences with trade elasticity estimates and a carbon leakage risk indicator based on interviews with firm managers, respectively. Concerning the latter, several authors show that, under phase 3 of the EU-ETS, most of the sectors enter the list of vulnerable sectors through the TE component alone (Clò 2010; De Bruyn et al. 2013; Martin et al. 2014b; Creason et al. 2021). This is problematic since several vulnerable sectors have a very low emission intensity. Clò (2010) also criticizes the thresholds under phase 3 of the EU-ETS as lacking an economic rationale and being politically influenced.

Some of the previous studies also suggest how to improve the EITE metric. Martin et al. (2014b), e.g., suggest only including trade flows with developing countries in the calculation of the TE component; the intuition is that, because a developed country is likely to have a more ambitious climate policy than the average country, it would be unlikely that this country serves as the source of carbon leakage of climate policy implemented in another developed country. Also, all studies almost unanimously recommend using the two components simultaneously, as in phase 4 of the EU-ETS. This recommendation is also in line with Fowlie et al. (2016), who, comparing econometric estimates of carbon leakage with EITE components, find that leakage risk only increases when both components increase together.

Finally, further studies assessing carbon leakage risk with the EITE metric also offer important insights. For instance, Sato et al. (2015) highlight the importance of assessing carbon leakage risk at the country level after comparing results for Germany, the UK, and the EU. De Bruyn et al. (2013) show that the number of vulnerable sectors would be considerably reduced from 60 to 33% if the EITE metric (phase 3 of EU-ETS) would be applied to more updated data, particularly concerning carbon prices, benchmarks, and geographical coverage. Creason et al. (2021) conducts a retrospective analysis of the Waxman-Markey Bill EITE metric; under a static version, the authors find that the number of eligible industries decreases over time, highlighting the importance of updating the list of vulnerable sectors.

3 Methodology

3.1 EE-MRIO model

To calculate sectors’ EITE metric, we use an environmentally extended (EE) multiregional input–output (MRIO) model. On the one hand, the input–output (IO) framework has been extended since the late 1960s to account for environmental pollution generation from interindustry activity (Miller and Blair 2009). On the other hand, many-region IO models improve single-region IO analysis by explicitly recognizing the interconnections between regions. EE-MRIO models combine these two features. Particularly because they relax the single-region models’ assumption that the carbon content of imports is equal to that of domestic production, they are helpful attribution models to estimate GHG emissions along global supply chains (Hertwich and Wood 2018; Li et al. 2020).

Let the global economy be composed of \(o,d=\left\{1,\dots ,P\right\}\) countries, where o are origin and d destination countries, and \(i,j=\left\{1,\dots ,N\right\}\) sectors, where \(i\) denotes rows and \(j\) columns. Equation 1 illustrates a full MRIO system of this economy, where each sector’s sales to other economic sectors and final consumers (sums across columns in Eq. 1a) is equal to its total payments for production inputs and value added (sums across rows in Eq. 1b).Footnote 6 In it, \(\mathbf{x}=[{x}_{j}^{d}]\) is a (NP × 1) vector of output, \(\mathbf{Z}=[{z}_{ij}^{od}]\) a (NP x NP) matrix of intermediate demand, \(\mathbf{Y}=[{y}_{i}^{od}]\) a (NP x P) matrix of final demand (e.g., household consumption), \(\mathbf{v}=[{v}_{j}^{d}]\) a (1 × NP) vector of value added (e.g., labor and capital), \(\mathbf{1}_{\mathbf{N}\mathbf{P}}\) and \(\mathbf{1}_{\mathbf{P}}\) (NP × 1) and (P × 1) summation vectors of ones, respectively, the apostrophe a transpose operator, and \(\times\) denotes matrix multiplication.Footnote 7 Note that these vectors and matrices are usually expressed in monetary terms, e.g., dollars for a particular year. Note also that while the block-diagonal matrices in \(\mathbf{Z}\) contain domestic inter-sectoral intermediate demand flows (from producing sector \(i\) to consuming sector \(j\)) within the same country, its block-off-diagonal matrices contain international inter-sectoral intermediate demand flows (from sector \(i\) in country \(o\) to sector \(j\) in country \(d\)). For example, an off-diagonal element of \(\mathbf{Z}\) could be the value of vegetable oils produced in Malaysia and used as input by the food industry in Germany. Further, note that, for simplicity, we assume an MRIO model with exogenous international transport services, i.e., the latter is part of the \(\mathbf{Y}\) vector (Peters et al. 2011, p. 140); this assumption implies that the calculation of indirect GHG emissions ignores international transportation emissions.

$$\mathbf{x}=\mathbf{Z}\times \mathbf{1}_{\mathbf{N}\mathbf{P}}+\mathbf{Y}\times \mathbf{1}_{\mathbf{P}}$$
(1a)
$${{\mathbf{x}}}^{\boldsymbol{^{\prime}}}=\mathbf{1}_{{\mathbf{N}}{\mathbf{P}}}^{\boldsymbol{^{\prime}}}\times \mathbf{Z}+{\mathbf{v}}^{\mathbf{^{\prime}}}$$
(1b)

Let us represent a sector’s total production GHG emissions by the (1 × NP) vector \({\mathbf{t}}=\left[{t}_{j}^{d}\right]\), its direct GHG emissions by the (1 × NP) vector \({\mathbf{d}}=\left[{d}_{j}^{d}\right]\), and its indirect GHG emissions by the (1 × NP) vector \({\mathbf{i}}=\left[{i}_{j}^{d}\right]\). By definition, a sector’s total production GHG emissions equal the sum of its direct and indirect GHG emissions, as represented by the left side of the equivalence in Eq. 2.Footnote 8 Letting \({\mathbf{r}}=\left[{r}_{j}^{d}\right]\) be a (1 × NP) vector of total GHG emissions coefficients (total emissions per dollar’s worth of sector \(j\)’s output in country \(d\)), \({\mathbf{c}}=\left[{c}_{j}^{d}\right]\) a (1 × NP) vector of direct GHG emission coefficients (direct emissions per dollar’s worth of sector \(j\)’s output in country \(d\)), and \({\mathbf{m}}=\left[{m}_{i}^{o}\right]\) a (1 × NP) vector of indirect GHG emission coefficients (indirect emissions per dollars’ worth of input \(i\) from country \(o\)), the previous balance can be equivalently represented in IO terms by the right side of the equivalence in Eq. 2. According to it, a sector’s total production GHG emissions (\(\mathbf{t}=\mathbf{r}\times \widehat{\mathbf{x}}\)) equal GHG emissions occurring inside of its plant (farm) due to its production process (\(\mathbf{d}=\mathbf{c}\times \widehat{\mathbf{x}}\)) plus GHG emissions embodied in the sector’s production inputs (\(\mathbf{i}=\mathbf{m}\times \mathbf{Z}\)), e.g., the emissions generated to produce its used energy.Footnote 9 Note that a hat over a vector denotes a diagonal matrix with the vector’s elements along its main diagonal.

$$\mathbf{t}\equiv \mathbf{d}+\mathbf{i}\leftrightarrow \mathbf{r}\times \widehat{\mathbf{x}}\equiv \mathbf{c}\times \widehat{\mathbf{x}}+\mathbf{m}\times \mathbf{Z}$$
(2)

Assuming one has only data on direct GHG emissions, it is possible to use an EE-MRIO model to estimate the remaining GHG emissions in Eq. 2. Following Hertwich and Wood (2018), we do so by assuming that \({m}_{i}^{o}={r}_{j}^{d}\) for all \(i=j\) and \(o=d\). This assumption implies that each sector in each country produces a good with the same cradle-to-gate GHG emissions regardless of whether it enters intermediate or final demand. Thus, replacing \(\mathbf{r}\) and \(\mathbf{m}\) by a new (1 × NP) vector \(\widetilde{\mathbf{m}}\) in Eq. 2, post-multiplying both sides of it by \({\widehat{\mathbf{x}}}^{-1}\), and re-arranging yields \(\widetilde{\mathbf{m}}=\mathbf{c}{\times (\mathbf{I}-\mathbf{A})}^{-1}\), which we use to estimate total and indirect GHG emissions. As usual in IO analysis, \({\widehat{\mathbf{x}}}^{-1}\) denotes the inverse of \(\widehat{\mathbf{x}}\) such that \(\widehat{\mathbf{x}}\times {\widehat{\mathbf{x}}}^{-1}=\mathbf{I}\), \(\mathbf{A}=\mathbf{Z}\times {\widehat{\mathbf{x}}}^{-1}\) is a (NP x NP) global coefficient matrix, I is a (NP x NP) identity matrix, and \({(\mathbf{I}-\mathbf{A})}^{-1}\) is the (NP x NP) Leontief inverse matrix. Equation 3 shows the estimated indirect GHG emissions, with the right most term splitting these emissions by origin, i.e., domestic (dom) and foreign (for). As far as we know, this approach, according to which multipliers are applied to intermediate instead of final demand, has only recently been used in the IO literature to estimate upstream emissions along supply chains (Huang et al. 2009; Hertwich and Wood 2018; Li et al. 2020).

$$\mathbf{i}=\widetilde{{\mathbf{m}}}\times \mathbf{Z}=\mathbf{c}\times {(\mathbf{I}-\mathbf{A})}^{-1}\times \mathbf{Z}={\mathbf{i}}^{(\mathbf{d}\mathbf{o}\mathbf{m})}+{\mathbf{i}}^{(\mathbf{f}\mathbf{o}\mathbf{r})}$$
(3)

3.2 EITE metric

Equation 4 shows the EI component for sector \(j\) in country d, which serves to assess a sector’s relative potential carbon cost increase due to climate policy. The nominator gives the potential carbon cost increase, which is equal to the volume of each sector’s regulated GHG emissions multiplied by a carbon price \(p\). Equation 4 assumes all sector’s GHG emissions as regulated, that is, direct and indirect GHG emissions, irrespective of origin. The denominator contains sectoral GVA, represented by \({v}_{j}^{d}\). Besides being a popular option, Sato et al. (2015) recommend using GVA over other alternatives due to its temporal stability and sectors’ direct control over it. Hence, other things equal, the larger a sector’s absolute GHG emissions or the smaller sector’s GVA, the larger the EI component.

$${ei}_{j}^{d (\mathrm{TOT})}= \frac{\left({d}_{j}^{d}+{i}_{j}^{d (\mathrm{dom})}+{i}_{j}^{d (\mathrm{for})}\right) \cdot p}{{v}_{j}^{d}}$$
(4)

Note that three assumptions are implicit in Eq. 4, which let us compare sectors and countries on an equal “footing.” First, it assumes a uniform carbon price covering the same GHG emissions in each sector and country. Hence, different values of the EI component are only caused by differences between sectors in terms of their economic emissions intensities, i.e., their volume of GHG emissions divided by GVA. Note that the magnitude of \(p\) does not matter for our comparative analysis since it scales \({ei}_{j}^{d}\) s linearly. Second, it assumes that producers incur full carbon costs for their production inputs (full carbon cost pass-through rate), which in reality might not always hold for every sector (De Bruyn et al. 2013, p. 59). Naturally, departures from this assumption would lead to an overestimation of the actual carbon costs increase (Stede et al. 2021, p. 6). Third, it also assumes that a sector’s GVA (capital and labor inputs) is invariable to carbon price variations, something that could not hold if companies take measures in the face of them (Fowlie and Reguant 2018, p. 126).

Equation 5 shows the TE component, a proxy for the trade responsiveness due to domestic climate policy.Footnote 10 The larger this indicator, the higher the risk that domestically produced goods get substituted by goods from countries with laxer climate policies. More specifically, the nominator gives the value of international trade, i.e., the value of exports plus imports. The denominator gives total domestic market value, which is equal to the value of domestic production plus imports. Similarly to Graichen et al. (2008) and in line with the suggestion by Martin et al. (2014b), we exclude intra-OECD trade, i.e., we only consider trade to/from less developed countries: countries outside of the OECD area.

$${te}_{j}^{d}= \frac{{\mathrm{exp}}_{j}^{d (\mathrm{non}-\mathrm{OECD})}+{\mathrm{imp}}_{j}^{d (\mathrm{non}-\mathrm{OECD})}}{{x}_{j}^{d}+{\mathrm{imp}}_{j}^{d (\mathrm{non}-\mathrm{OECD})}}$$
(5)

Finally, following the approach adopted by phase 4 of the EU-ETS (European Commission 2019), we measure carbon leakage risk by multiplying the two EITE components to construct a carbon leakage indicator, as shown in Eq. 6. Finally, note that, in the forthcoming analysis, we refrain from using thresholds because they lack an economic base and depend on the carbon price level (Clò 2010).

$${eite}_{j}^{d (\mathrm{TOT})}={ei}_{j}^{d (\mathrm{TOT})}\cdot {te}_{j}^{d}$$
(6)

3.3 Climate policy scenarios

Which GHG emissions to include in the EI component depend on the scope of the climate policy. Equation 4 considers the extreme situation in which a sector has carbon costs due to all its GHG emissions. However, given that the scope of climate policies might differ between sectors, we consider two additional scenarios (Table 1). Under the “direct” scenario, a sector has carbon costs due to its direct GHG emissions only. In such case, the EI component is \({ei}_{j}^{d (\mathrm{DIR})}\), which only includes direct GHG emissions. Under the “indirect” scenario, a sector has carbon costs due to its indirect GHG emissions only. Similarly, the corresponding EI component is \({ei}_{j}^{d (\mathrm{IND})}\), which only includes indirect GHG emissions. These different EI components lead to different EITE metrics: \({eite}_{j}^{d (\mathrm{DIR})}={ei}_{j}^{d (\mathrm{DIR})}\cdot {te}_{j}^{d}\), and \({eite}_{j}^{d (\mathrm{IND})}={ei}_{j}^{d (\mathrm{IND})}\cdot {te}_{j}^{d}\).

Table 1 Description of the climate policy scenarios
Full size table

Note that, because, climate policy might affect sectors heterogeneously, considering different climate policy scenarios makes this work’s results relevant for a larger number of sectors. For example, under the current climate legislation, Germany’s agricultural sectors have interest in the potential carbon leakage risk under the “indirect” scenario; while the EU-ETS already increases the price of domestically produced inputs (e.g., fertilizers), the recently approved EU’s Carbon Border Adjustment Mechanism (CBAM) would impose additional carbon costs on their imports (Lehmann 2021).Footnote 11 Finally, note that these policy scenarios are hypothetical; in reality, the mitigation policy will likely imply carbon costs due to a portion of all direct GHG emissions, a part of all indirect GHG emissions, or a mix of the two. Because of this, under each of these cases, our estimates represent an upper bound of carbon leakage risk estimated using the same EITE metric and carbon price as in this paper.

4 Data and overview

Our analysis uses GTAP data. Economic data comes from the GTAP-MRIO database (Carrico et al. 2020), which extends the GTAP 10A database (Aguiar et al. 2019) by providing a richer depiction of international trade flows; it distinguishes origin and destination countries and users for each trade flow. As such, this database provides a fully compatible dataset with the information requirements of a global MRIO model. More specifically, we use these database’s tables on domestic purchases, imports, and exports to construct our MRIO model (supp. Table S1). These tables are valued at US dollar market prices, i.e., prices paid by purchasers, including domestic margins but excluding commodity taxes. Environmental data comes from GTAP’s CO2 and non-CO2 databases (Lee 2008; Chepeliev 2020), which provide sector and country-level GHG emissions, except for land-use and land-use change (LULUC) emissions. The non-CO2 emissions database reports these emissions in CO2 equivalents (CO2eq) using global warming potentials (GWPs) from the IPCC’s Fourth Assessment Report. Table S1 also describes the tables we use to construct the d vector; because they do not affect industries’ production costs, we use all tables in these databases except those related to final consumption.

The above GTAP databases contain 141 regions, 37 of which are OECD countries, and 65 sectors (supp. Tables S2-S3).Footnote 12 These tables also contain GTAP sectors’ short names that we use throughout the analysis and concordances with the seven sector groups in Hertwich and Wood (2018) and Li et al. (2020): agriculture, forestry and other land use (AFOLU +), buildings, energy, industry, materials, transport, and services. The AFOLU + group includes all agri-food plus forestry-related GTAP sectors. GTAP’s manufacturing sectors are split between the industry and materials groups. Importantly, the materials group contains GTAP’s energy-intensive trade-exposed sectors, which receive particular attention in climate policy analyses due to their high carbon leakage risk (Böhringer et al. 2012, 2022; Fischer and Fox 2018).

Our calculations show that the volume of global direct GHG emissions from production adds up to 38.41 billion tCO2eq, of which 67.5% and 32.5% correspond to CO2 and non-CO2 emissions, respectively. The volume of global indirect GHG emissions from the EE-MRIO model adds up to 71.42 billion tCO2eq.Footnote 13 In the OECD area, direct and indirect GHG emissions add up to 12.60 and 23.22 billion tCO2eq, respectively. While energy is the sector group with the largest volume of total GHG emissions, mainly due to the electricity sector, services has the highest total GVA, with the trade sector standing out among other sectors (supp. Figs. S1-S4).

Finally, to make our results comparable to other studies (Clò 2010; Juergens et al. 2013; Stede et al. 2021), we use a benchmark carbon price of $30/tCO2eq. After calculating the EITE components (37 OECD countries × 65 sectors), we noticed several observations with extremely high values for the EI component. Although very high values of the EI component for certain sector-country combinations can be legitimate, we removed these observations to avoid our results depending on extreme values. For doing so, we used the inter-quartile range (IQR) method at the sector level, according to which observations above (below) the third (first) quartile of the data plus (minus) 1.5 times the IQR are removed. Furthermore, we also removed one observation containing negative direct GHG emissions (coal sector in Slovakia).Footnote 14 This process reduces the dataset to a total of 2236 observations.

5 Results

5.1 Sector groups

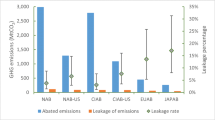
Our results show marked differences in average EITE values between sector groups under all climate policy scenarios. Figure 1 shows these values for the “total” scenario: the highest EITE values are for energy (0.12), followed by transportation (0.05), materials (0.02), AFOLU + (0.02), industry (0.01), services (0.00), and buildings (0.00).Footnote 15 Except for the “direct” scenario, where AFOLU + and materials switch relative positions, this ranking is the same across the other scenarios (supp. Fig. S5 and Table S4). Although the relative position of the energy, services, and buildings sectors with respect to the other sector groups is possibly not surprising, the high EITE value for transport and the similarity between AFOLU + and materials are remarkable. Importantly, the EITE value under “indirect” climate policy scenario is higher than under the “direct” scenario for AFOLU + , industry, materials, and services.

Fig. 1
figure 1

Average value of the EITE metric and its components in OECD countries, by sector group. Note: Averages are calculated by taking the mean of the EITE (component) value across all sectors belonging to the sector group and all OECD countries. For each OECD country and GTAP sector, the EI component based on indirect (national) emissions only considers emissions from domestic inputs. The EI component based on indirect (OECD) emission considers emissions from inputs of OECD origin but excludes emissions from domestic inputs

Full size image

Figure 1 also shows how the EITE components contribute to the previous EITE values. At both ends of the plot, we see that, while energy has the highest EI and TE values across all sector groups, these are very small for services and buildings. In between, we see a negative relationship between the EI and TE components. In particular, a fairly high total EI value more than makes up the relatively low TE value of transport. In contrast, we see that, despite AFOLU + , materials, and industry not having a high total EI value, they all have a relatively high TE value. This figure also shows the composition of the EI component values. Potential carbon cost due to indirect GHG emissions is substantial for all sector groups. Besides services and buildings, this contribution is also high for AFOLU + , materials, and industry. Furthermore, most carbon costs due to indirect GHG emissions are domestic. An exception is energy, whose EI value based on embodied GHG emissions from non-OECD countries is the highest among all sector groups. This high value is driven by the petroleum and coal products sector (supp. Table S5).Footnote 16

Figure 2 shows how sector groups’ EITE values vary across OECD countries under the “total” climate policy scenario. All sector groups except for services and buildings have a relatively high absolute cross-country variation, with energy, transport, and AFOLU + being the sector groups with the highest variation. For instance, while the EITE value in AFOLU + is similar in the USA (0.01) and Japan (0.01), in Estonia (0.05) it is about five times larger than in these countries.Footnote 17 Importantly, AFOLU + and transport have a higher EITE value than materials in 18 and 29 OECD countries, respectively. However, note that cross-country variation differs under the other climate policy scenarios (supp. Figs. S12-S13). Under the “direct” scenario, cross-country variation in industry and materials sectors drops considerably. Under the “indirect” scenario, this drop is less strong and also includes transport sectors. Under the “direct” climate policy scenario, AFOLU + and transport have a higher EITE value than materials in 30 and 34 OECD countries, respectively. In contrast, under the “indirect” climate policy scenario, these values drop to 11 and 21, respectively.

Fig. 2
figure 2

Average EITE value under the “total” scenario, by OECD country. Notes: to ease visualization, this figure omits the following values belonging to energy: Slovenia (1.45), Luxemburg (0.73), Latvia (0.56), France (0.30), Netherlands (0.26), and Greece (0.23). Averages are calculated by taking the mean of the EITE value over sectors belonging to the sector group

Full size image

5.2 Sectors

Table 2 presents the 10 sectors with the highest average EITE value across OECD countries across climate policy scenarios. Under the “total” scenario (left panel), four sectors belong to energy, three to AFOLU + , two to materials, and one to transport. It is remarkable that many non-energy-intensive and non-energy sectors make this list. This table also shows that alternative climate policy scenarios lead to different sectoral rankings. Interestingly, compared to the “total” climate policy scenario, the other scenarios include a larger number of sectors belonging to AFOLU + . Equally interesting is to see that, under the “direct” scenario, four AFOLU + sectors have a higher potential carbon leakage risk than bovine animals. Note that the EITE values under the “direct” and “indirect” scenarios are comparable in magnitude: considering only the top 10 rankings, they rank from 0.02 to 0.26 and 0.02 to 0.16, respectively.

Table 2 Top 10 sectors according to average EITE value in OECD countries under different climate policy scenarios. Note: values in parenthesis give standard deviations in the OECD area. The acronym n.e.c. stands for “not elswhere classified”
Full size table

Figure 3 shows how the EI and TE components contribute to the previous results under the "total" climate policy scenario. In it, the different colors indicate membership to one of the seven sector groups, and the circles’ sizes cross-country variation (standard deviation). Starting with energy, we see marked differences. On the one hand, petroleum and coal products are, by far, the sector with the highest EI value and variation.Footnote 18 Footnote 19 In contrast, the oil and gas sectors have the highest TE value but a fairly low EI value. On the other hand, although electricity, gas manufacturing, and coal have a similar EI, the former has a low TE value, which takes it out of the top 10 list. Concerning non-energy sectors, AFOLU + sectors are more spread in the plot than industry and materials sectors. The high EI values for the air transport and bovine animals also stand out. Naturally, the relative position of several sectors changes under the other climate policy scenarios (supp. Figs. S9-S10); for example, because many indirect emissions of bovine meat are the direct emissions of bovine animals, the former and latter sectors have the second highest EI value under the “indirect” and “direct” scenarios, respectively. Furthermore, we find that AFOLU + sectors have higher absolute differences between the “direct” and “indirect” scenarios than industry and materials (supp. Fig. S11).

Fig. 3
figure 3

Emission intensity vs. trade exposure under the “total” climate policy scenario, OECD country averages by sector. Notes: The circles’ area is proportional to the cross-country variation (standard deviation) of the EITE metric in the OECD area. To improve visualization, we omit service sector names

Full size image

Finally, for the interested reader, suppl. Figs. S14-S16 present sectors’ EITE value distributions across OECD countries under each climate policy scenario. These figures show which sectors have the greatest variation between countries and which are above and below their sector group average. For example, in the transport sector group, air transport has an average above the sector group and the largest variation across countries across all climate policy scenarios. Specific values for each sector in each country can be found in Online Resource 2.

5.3 Sensitivity analysis

This section shows how our findings change under different assumptions about the TE component, calculated based on trade with developing countries. In the baseline scenario, we have considered these as not belonging to the OECD area. We consider three sensitivity scenarios: the first includes seven OECD countries within the developing countries; the second includes intra-OECD trade; and the third exclude imports from the TE component’s denominator, as done by the ACPM’s EITE metric version.Footnote 20 Our calculations show average EITE values increases of 31%, 357%, and 2027% across these sensitivity scenarios, respectively. Although the sector groups with the highest increase are AFOLU + , materials, and energy across all sensitivity scenarios (supp. Tables S7-S8), the latter has a more than proportional increase under the third scenario because many countries only import but do not produce energy products.

Importantly, these changes do not change this paper’s main findings. On the one hand, the relative carbon leakage risk between sector groups remains almost equal with the exception of the third sensitivity scenario, where AFOLU + and materials (transport) switch their relative positions under the “total” (“indirect”) scenario (supp. Figs. S17-S19). Furthermore, while some sectors change position in the top 10 list under the second sensitivity scenario, several transport and AFOLU + sectors are still part of these lists (supp. Tables S9-S11). On the other hand, the materials, AFOLU + , and industry sectors continue to have a higher EITE value under the “indirect” climate policy scenario across all sensitivity scenarios.

6 Discussion

The previous results suggest that transport and AFOLU + sectors could suffer from considerable potential carbon leakage risk in the OECD area; we find that this risk is, on average, similar or higher than that of energy-intensive (material) sectors and that many of these sectors are in the list of sectors with the highest carbon leakage risk. These results are in line with studies reporting high carbon leakage risk in agriculture (e.g., Frank et al. 2021) and transport (e.g., Dray and Doyme 2019). These results highlight the need to develop anti-leakage mechanisms for these sectors, such as output-based rebates or CBAMs (Fischer and Fox 2012). Ideally, these anti-leakage mechanisms should be part of the mitigation policy from the beginning to foster sectors’ participation in national mitigation efforts (Metcalf and Weisbach 2009).

Our results also suggest that carbon leakage risk could be a concern in some downstream sectors: AFOLU + , materials, and industry sectors have, on average, a higher carbon leakage risk under the “indirect” than under the “direct” climate policy scenario. This means that even if these sectors are excluded from climate policy, they could still be considerably affected by carbon leakage. Importantly, tackling this issue through known anti-leakage mechanisms seems more complicated; for example, since carbon cost pass-through rates vary between (downstream) sectors, a cost-effective CBAM must consider this during its calculation.

Finally, we find that the results for many sector groups are highly variable across OECD countries, particularly for AFOLU + , transport, and energy sectors. This result is line with Sato et al. (2015), who find that industrial sectors’ carbon leakage risk substantially vary between Germany, the UK, and the EU. This result implies that supranational carbon jurisdictions, such as the EU, should be careful when extrapolating carbon leakage risk values from one jurisdiction to another.

7 Conclusion

Stopping global warming in time requires the contribution of more sectors beyond energy and energy-intensive ones. However, due to the high degree of fragmentation of climate policies across countries, there is concern about the effects that increasing national climate policies stringency could have on these sectors. The evidence presented in this article suggests that agri-food and transport sectors, usually lagging in countries’ national climate mitigation policies, could have an even higher carbon leakage risk than energy-intensive industries. Furthermore, this risk could be higher in many downstream sectors compared to directly regulated sectors and is highly heterogenous across OECD countries.

Admittedly, our work has several limitations. The first is the high sectoral aggregation of the data; the higher the within-sector heterogeneity, the stronger the confounding effect of analyses using aggregated data (Juergens et al. 2013; Steen-Olsen et al. 2014). Unfortunately, a comprehensive comparison of sectors and countries would not have been possible using more disaggregated data, only available for particular sectors and countries (Sato et al. 2015). Future studies should shed light on this confounding effect, such as Fischer and Fox (2018) do for energy-intensive sectors. Furthermore, the GHG emissions data in this work excludes LULUC emissions, which make a significant part of global GHG emissions: only global land-use GHG emissions for 2014 equal 9.3% of the global GHG emissions considered in this study (Chepeliev 2020). Future studies should analyze how including these emissions affects our findings, likely underestimated for land-based sectors such as agriculture.

Finally, future studies should provide additional evidence on the robustness of the EITE metric to measure carbon leakage adequately. An accurate carbon leakage risk assessment is necessary to guarantee the efficiency and legality of anti-leakage instruments (Mehling et al. 2019). In the context of the EU-ETS, for example, some authors argue that carbon leakage risk calculations based on the EITE metric may have led to overcompensation of sectors that received free emission permits according to these calculations (Martin et al. 2014a; Joltreau and Sommerfeld 2019). Overcompensation reduces the credibility of carbon pricing, its cost-efficiency, and the incentives for mitigating emissions (Martin et al. 2014b; Sato et al. 2015).