1 Introduction

Existing erosion and inundation problems at many of the world’s sandy coasts will be exacerbated due to global warming, mainly because of mean sea level rise (MSLR) and associated coastal hazards (Ranasinghe 2016; Luijendijk et al. 2018; Mentaschi et al. 2018; Vousdoukas et al. 2020; Hinkel et al. 2021). Although fully natural beaches with accommodation space are expected to adapt to MSLR by slowly migrating landward (Cooper et al. 2020), a significant part of the world’s beaches contain man-made structures in the backshore that limit that possibility. This is particularly the case in densely populated urban regions. As a consequence, the socio-economic and environmental effects of MSLR along the coast will become one of the costliest consequences of global warming, although mitigation strategies could significantly reduce projected losses (Hinkel et al. 2014; Brown et al. 2021). The low elevations of delta planes make them particularly vulnerable. An example is the southern part of the Dutch coast, a densely populated area of great socio-economic value that also concentrates important ecosystems. Beach nourishments can be used as a nature-based climate change adaptation strategy in such sand-rich, wave-dominated coasts (de Schipper et al. 2021). A pioneer mega-nourishment called Sand Engine, an artificial sandy peninsula, was constructed at the Dutch Delfland coast in 2011. Mega-nourishments rely on the concept that they tend to diffuse alongshore and hence feed the adjacent beaches. This has been verified during the initial years of the Sand Engine evolution (Fig. 1b; de Schipper et al. (2016); Rutten et al. (2018); Roest et al. (2021)). However, given the multi-decadal evolution of mega-nourishments, their long-term dynamics under projected climate change conditions are unknown. Thereby, modelling studies that anticipate their regional-scale evolution in the 21st century under different climate change scenarios, with the uncertainties, are essential to design future interventions for the needed adaptation to global warming (Ranasinghe 2020).

Fig. 1
figure 1

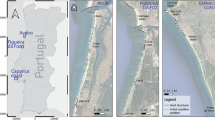
Panel a: Directional distribution of significant wave height at the Europlatform (\(52^{o}00^{\prime }\)N, \(3^{o}17^{\prime }\)E, 26.5-m depth) during the validation period (January 2010 - December 2019). Panels b-e: images of the Sand Engine mega-nourishment (\(52^{o}3^{\prime }10^{\prime \prime }\)N, \(4^{o}11^{\prime }25^{\prime \prime }\)E) in May 2012 (b), July 2013 (c), August 2016 (d), and March 2020 (d), extracted from Google Earth (images provided by Maxar Technologies and Landsat/Copernicus). Panels f-g: Sand Engine bathymetry measured in January 2012 (f) and adapted to Q2Dmorfo model input (g)

Full size image

The long-term (decades and beyond) morphological evolution of open sandy coasts is caused by gradients in wave-induced sediment transport that change bed level and shoreline position, which in turn affect wave transformation. This can produce strong feedback processes and a rich nonlinear dynamical behaviour (Coco & Murray 2007; van den Berg et al. 2011; Ribas et al. 2015). Waves propagate over the mean sea surface, which in turn changes due to astronomical tides, storm surges and MSLR. Given the long spatio-temporal scales involved, most of existing scientific contributions estimating the shoreline evolution under MSLR are performed with modified versions of the highly idealized Bruun Rule (Vousdoukas et al. 2020; Athanasiou et al. 2020; D’Anna et al. 2021b). However, the severe underlying simplifications of the Bruun method prevent obtaining accurate predictions even at locations that met the restrictive conditions of applicability of this rule (Cooper & Pilkey 2004; Cooper et al. 2020; Ranasinghe 2020). Therefore, more detailed morphodynamic models are essential predictive tools, despite the inherent uncertainties and present limitations (D’Anna et al. 2020; Montaño et al. 2020; Ranasinghe 2020). The most detailed 2DH models (e.g., Roelvink et al. 2009) describe dynamically the full surf-zone morphodynamic evolution, and have been applied to model the Sand Engine initial evolution (Luijendijk et al. 2017; Tonnon et al. 2018). However, their high computational cost hampers their applicability for long-term periods unless model input reduction techniques and acceleration factors are applied, which can compromise accuracy (Walstra et al. 2013; Luijendijk et al. 2019). The morphological evolution of mega-nourishments has also been modelled with 1D coastline models (Tonnon et al. 2018; Roelvink et al. 2020; Kroon et al. 2020; Whitley et al. 2021). They are less detailed and computationally much faster because only the dynamic evolution of the shoreline is described. Although the sediment transport along the coast is computed in a rather realistic way, they still rely on the Bruun Rule to include the cross-shore sediment transport linked to MSLR (e.g., Vitousek et al. 2017; Robinet et al. 2020).

Finally, there exists a reduced-complexity model called Q2Dmorfo (van den Berg et al. 2011; Arriaga et al. 2017). It is more sophisticated than existing 1D coastline models because it describes the dynamic evolution of the full bathymetry and the wave propagation over it, and it includes longshore and cross-shore transports. This provides both a more accurate description and a better understanding on the sediment dynamics because the alongshore diffusion of a mega-nourishment affects not only the shoreline but the whole profile. At the same time, it is simpler and hence faster than 2DH models, by paying the price of not-resolving the complete surf-zone hydrodynamics. Instead, sediment transport is directly estimated from wave transformation and the evolving bathymetry. In this way, the Q2Dmorfo model captures feedback mechanisms and can reproduce long-term coastal evolution quite accurately, as illustrated for the Sand Engine in Arriaga et al. (2017, 2020). In these applications the mean sea level was assumed to be constant, even though Luijendijk et al. (2017) found in a 2DH model study that including the daily sea level variability due to vertical tides could affect the Sand Engine dynamics substantially. We thus anticipate that projected MSLR induced by global warming will also influence the morphodynamics of the system in the long term and this has not yet been explored with any model. Moreover, studies on long-term coastal projections must attempt to quantify the uncertainties in the predictions, not only those associated to the MSLR scenarios and the intrinsic uncertainties in wave forcing but also those due to the epistemic model uncertainties (Kroon et al. 2020; D’Anna et al. 2021).

The aim of this study is to quantify the effect of mean sea-level rise on the evolution of the Sand Engine mega-nourishment in the 21st century, including an assessment of some of the associated uncertainties. To this end, the Q2Dmorfo model was chosen for being more realistic than 1D coastline models since it describes the dynamics of the full bathymetry, including longshore and cross-shore transport processes, it ensures sediment conservation and it does not require from the highly-idealized Bruun rule to incorporate the effects of MSLR. The model was first extended to allow for a variable mean sea level (Section 2). Before performing long-term simulations, the new model version was calibrated with measured bathymetries of the Sand Engine area from January 2012 until April 2013. The calibrated model was subsequently validated with measured bathymetries available until August 2019 (Section 3). The model was then applied to simulate the evolution of the mega-nourishment and its adjacent beaches (17-km of coast, Section 4) up to 2100, forcing it with wave and sea level series constructed from historical data and including projected MSLR under different Representative Concentration Pathways (RCP2.6, RCP4.5 and RCP8.5). The processes underlying the predicted morphological changes were also investigated. Section 5 contains a quantification of the uncertainties associated with this modelling exercise, related to model parameters and forcing scenarios. Also, an assessment of the widely-used Bruun rule performance is included. The conclusions are outlined in Section 6.

2 Model description

Q2Dmorfo is a reduced-complexity coastal morphodynamic model especially designed for large spatio-temporal scales (up to tens of km and decades). Its most important equations are described in this section, focusing on those related with sediment transport and bed evolution. A full description can be found in Arriaga et al. (2017). The model uses a Cartesian coordinate system, with the x-axis pointing seaward (\(x=0\) being located at the backshore), the y-axis pointing alongshore (from right to left in Fig. 1g) and the z-axis pointing upward. The dynamic mean sea level is at \(z=z_{s}(x,y,t)\). The sea bed is located at \(z=z_{b}(x,y,t)\) and evolves following the sediment mass conservation equation

$$\begin{aligned} (1-p)\frac{\partial z_{b}}{\partial t} + \frac{\partial q_{x}}{\partial x} + \frac{\partial q_{y}}{\partial y} = 0 \ , \end{aligned}$$
(1)

where t is time, \(\textbf{q}=(q_{x},q_{y})\) is the depth-integrated volumetric sediment flux and the sediment porosity has been set to \(p=0.4\). This is the main governing equation and it is solved throughout the whole domain using an explicit second order Adams-Bashforth scheme in time and standard finite difference methods in space. The rectangular domain is discretized with a regular spacial grid. The shoreline \(x_{s}(y)\) is computed from the water depth, \(D=z_{s}-z_{b}\), by interpolating in the cross-shore direction between the last wet cell (\(D>0\)) and the first dry cell (\(D<0\)).

Sediment transport \(\textbf{q}\) is assumed to be composed of longshore \(\mathbf {q_{L}}\), cross-shore \(\mathbf {q_{C}}\) and diffusive \(\mathbf {q_{D}}\) components,

$$\begin{aligned} \textbf{q}=\mathbf {q_{L}}+\mathbf {q_{C}}+\mathbf {q_{D}} \ . \end{aligned}$$
(2)

The meaning of cross-shore and alongshore directions in an undulating coast like that of the Sand Engine can be recovered from the averaged trends of the bathymetric contours (i.e., by filtering out the bathymetric features of, e.g., less than 100 m). Therefore, an averaged bathymetry is defined by using a running average in a rectangular window of O(100m). The local mean cross-shore direction is then defined by a unit vector \(\hat{{\textbf {n}}}\) perpendicular to the averaged bathymetry and directed offshore, and the local mean alongshore direction \(\hat{{\textbf {t}}}\) is defined so that the system is orthonormal and right-handed.

The first term in Eq. (2) is the sediment transport related with the wave-induced longshore current and it is based on the CERC formula (Komar 1998)

$$\begin{aligned} \mathbf {q_{L}}=\mu H_{b}^{5/2}\sin (2\alpha _{b}) f(x^{\prime })\hat{{\textbf {t}}} \ , \end{aligned}$$
(3)

where \(H_{b}\) is the root-mean-square (RMS) wave height at breaking, \(\alpha _{b}=\theta _{b}-\phi _{s}\) is the angle between wave fronts at breaking and the local coastline, and \(\mu\) is a calibration parameter. The relation of this parameter with the standard CERC constant K can be found in Eq. (8) of Arriaga et al. (2017). Finally, \(f(x^{\prime })\) is a normalized cross-shore shape function, assumed to follow the longshore current profile (Eq. (9) in Arriaga et al. (2017)). Here, \(x^{\prime }\) is the distance from the closest shoreline location to the point.

The second term in Eq. (2) parameterises the cross-shore transport by assuming a bathymetric tendency to evolve to a prescribed equilibrium profile, with \(\mathbf {q_{C}}\) being proportional to the difference between the equilibrium slope \(\beta _{e}\) and the actual local slope in the local cross-shore direction,

$$\begin{aligned} \mathbf {q_{C}}=-\gamma (\nabla z_{b} \cdot \hat{{\textbf {n}}}+ \beta _{e})\hat{{\textbf {n}}} \ . \end{aligned}$$
(4)

The first term describes the downslope transport and the second term simulates the net wave-induced onshore transport (Falqués et al. 2021). The third term in Eq. (2) represents the tendency of small bumps to be flattened in the alongshore direction due to wave stirring if there is no positive feedback,

$$\begin{aligned} \mathbf {q_{D}}=-\gamma (\nabla z_{b} \cdot \hat{{\textbf {t}}})\hat{{\textbf {t}}} \ . \end{aligned}$$
(5)

The stirring factor \(\gamma\) in both \(\mathbf {q_{C}}\) and \(\mathbf {q_{D}}\) accounts for sediment resuspension produced by orbital wave velocity and turbulence. The magnitude of the horizontal momentum mixing given by Battjes (1975) is used as scaling factor,

$$\begin{aligned} \gamma =\nu \gamma _{b}^{-1/6} H_{b}^{11/6}X_{b}^{\prime -1/3} g^{1/2} \psi (D) \ , \end{aligned}$$
(6)

where \(\gamma _{b}\) is the saturation ratio of H/D inside the surf zone (here, \(\gamma _{b}=0.5\)), \(X_{b}^{\prime }\) is the surf zone width (computed in the \(x^{\prime }\) direction), g is gravity acceleration and the constant of proportionality \(\nu\) is the second calibration parameter. The shape function \(\psi\) (Eq. (13) and Fig. 2 in Arriaga et al. (2017)) is assumed to have a maximum value near the shoreline and to decay both seaward (toward the closure depth, \(D_{c}\)) and shoreward (across the narrow swash zone). The instantaneous value of \(D_{c}\) is computed as a fraction of the depth at which the sediment particles are first mobilized by the waves. This fraction is called \(f_{c}\) and is the third calibration parameter. Given that the value of \(D_{c}\) is computed for each wave condition, a minimum \(D_{c}\) value must be imposed to have a non-negligible \(\gamma\) (i.e., a minimum morphodynamic diffusivity) during calm wave conditions. This minimum \(D_{c}\) is assumed to be proportional to the largest value of the breaking depth along the domain and the proportionality constant, called \(f_{m}\), is the fourth calibration parameter.

The sediment transport computation requires the wave characteristics at breaking. The model incorporates a wave module that takes into account refraction and shoaling over the evolving curvilinear depth contours. Incident monochromatic waves with \(T=T_{p}\) (peak period), \(H=H_{s}\) (significant wave height) and a wave angle \(\theta\) are considered at the offshore boundary. The waves are propagated inside the domain up to breaking point using the geometric optics approximation, i.e., applying the dispersion relation, the wave number irrotationality and the wave energy conservation (Arriaga et al. 2017). From the computed wave field, the breaker wave height, \(H_{b}\), and the corresponding wave angle, \(\theta _{b}\), are extracted. The breaking point is defined as the most onshore position where \(H\le \gamma _{b} D\).

In this study, the model was extended to include sea-level variability. First, a proxy for wave-induced set-up was incorporated by estimating it locally inside the surf zone using the highly-idealized formula of Bowen et al. (1968), derived from a cross-shore balance between the gradient of radiation stresses and the pressure force due to wave set-up. Second, sea-level variability induced by astronomical and barometric tides and wind stress was considered to be spatially uniform in the entire domain and was included as a time-series at the offshore boundary.

Different boundary conditions for \(\textbf{q}\) and \(z_{b}\) can be prescribed at the lateral boundaries (\(y=0\) and \(y=L_{y}\)): solid wall conditions (\(q_{y}=0\)) or open conditions. In the latter case, the longshore transport is computed assuming that the profile relaxes to the equilibrium profile, with a certain alongshore decay distance. Even when \(q_{y}=0\) at the lateral boundaries, wave diffraction into the wave shadow zone induced by the solid walls is not accounted for, which is a reasonable assumption if the area where those diffraction effects take place is much smaller than the study domain. Zero cross-shore sediment transport is imposed at \(x=0\), i.e., it is considered negligible at the backshore. Two different boundary conditions for the cross-shore transport can be imposed at the offshore boundary (\(x=L_{x}\)): no transport (\(q_{x}=0\)) or a value of \(q_{x}\) computed by linear extrapolation of its values in the last domain points (details in Arriaga et al. (2017)).

3 Model application to the Sand Engine site

3.1 Study site and available data

The Sand Engine mega-nourishment is located between Hoek van Holland and Scheveningen harbours (the Netherlands), which delimit a 17 km long coastline oriented at \(42^{o}\) with respect to North (Fig. 1). Initially, the Sand Engine measured 2.5 km in the alongshore direction and extended 1 km into the sea (de Schipper et al. 2016). The median grain size of the region between harbours is of 242 \(\mu\)m, whereas the median grain size of sediments used to construct the Sand Engine is 278 \(\mu\)m (Luijendijk et al. 2017). Waves mainly approach this area from southwest and north (Fig. 1a), with an average significant wave height of 1.3 m and a mean period of about 6 s. The tide in this region is semi-diurnal with a mean tidal range of 1.7 m (de Schipper et al. 2016). Observations up to 2016 showed that the mega-nourishment was slowly diffusing and feeding the adjacent beaches (de Schipper et al. 2016; Roest et al. 2021), as can be also seen in Fig. 1b. It barely migrated in the alongshore direction due to the nearly bimodal wave climate (Fig. 1a); however, alongshore feeding during the first few years was asymmetric, with the north-eastern beaches receiving 30-40% more sand than the south-western beaches (de Schipper et al. 2016; Arriaga et al. 2017; Roest et al. 2021).

After the Sand Engine construction, bathymetric measurements were performed every month during the first year, and every two months in the subsequent years (de Schipper et al. 2016). These bathymetries extended 1.5 km and 4.5 km with grid resolution of 2 m and 25 m in the cross-shore and alongshore directions, respectively. The survey from 17 January 2012 (Fig. 1f) was the basis of the initial bathymetry for the model simulations and bathymetries measured up to August 2019 were used to calibrate and validate the model parameters. Annual (1990-2009) cross-shore (JarKus) profiles measured before the Sand Engine construction over the studied region were used to complete the bathymetries in the region outside the mega-nourishment and to compute the equilibrium profile required by the model. Wave conditions from January 2010 until December 2019 were obtained once every hour from the Europlatform, located 40 km from the mega-nourishment in the southwestern direction, which is considered to be representative of the studied area because offshore wave climate is mainly alongshore uniform in this region (Wijnberg & Terwindt 1995). Hourly sea-level data in the same period was obtained from a tidal gauge in Scheveningen harbour (7 km north-east from the Sand Engine).

3.2 Model setup

The region of study for the long-term simulations (period 2012-2100) included the 17 km in the alongshore direction between Scheveningen and Hoek van Holland harbours (with the y-axis pointing into the latter, hence the SW direction), and extended 3 km in the cross-shore direction up to a water depth of 15 m. Part of this domain and the coordinate system is shown in Fig. 1g. In this large domain, solid wall conditions in the lateral boundaries (\(q_{y}=0\)) were assumed to represent the existing piers. Neglecting wave diffraction by the piers is a reasonable assumption in this application given that the lateral boundaries are located far away from the Sand Engine. The simulations for model calibration and validation (period 2012-2019) were performed with the smaller domain specifically shown in Fig. 1g to speed them up. In this smaller domain, lateral boundaries were assumed to be open, with the alongshore decay distance being of 4 km (details in Section 2). The shoreline outside the domain was imposed to be equal to the averaged shoreline position along 2 km inside the domain near the lateral boundaries (avoiding the influence of both the boundaries and the Sand Engine). In fact, in a preliminary analysis we verified that there were no significant differences in the results when using different types of lateral boundary conditions. At the offshore boundary, we computed \(q_{x}\) though linear extrapolation because this allows for a certain small transport in the offshore boundary in case of strong storms. Simulations imposing \(q_{x}=0\) were also performed and results did not change significantly. A grid spacing \(\Delta x=6\) m and \(\Delta y=50\) m was used in the present study, as a compromise between accuracy and computational cost. This choice followed from previous Q2Dmorfo studies with similar spatio-temporal scales (van den Berg et al. 2011, 2012; Arriaga et al. 2017, 2020). The adopted time step, \(\Delta t= 95\) s, was the largest value that ensured numerical stability. Waves were transformed from the Europlatform to the offshore model boundary with the geometric optics approximation.

JarKus data were used to obtain the cross-shore equilibrium profile (\(\beta _{e}\) in Eq. 4) by time and spatial averaging beach profiles from 1990-2009 over a region of 10 km. The averaged data were adjusted to a double slope profile

$$\begin{aligned} z_{be} = -a_{1}\left( 1-\frac{\beta _{2}}{\beta _{1}}\right) \tanh \left( \frac{\beta _{1}x}{a_{1}}\right) \ , \end{aligned}$$
(7)

from which \(\beta _{e}\) was finally computed. This adjustment allowed filtering the presence of sandbars since the model assumes a monotonic equilibrium profile (see Fig. 3c in Arriaga et al. (2017)). The bathymetries with the Sand Engine were reconstructed out of bathymetries measured from 2012 to 2019 (Fig. 1f shows the one in January 2012) following different steps. First, bars were filtered out obtaining a monotonic profile and conserving the initial volume, following the method by Kaergaard et al. (2012). The surveyed dry beach area was then added, with the inner water bodies (a lake and a lagoon) treated as dry beach region of 0.1 m high above the initial MSL. The submerged bathymetric contours outside the mega-nourishment were constructed following the equilibrium profile (Eq. 7) and assuming a straight shoreline corresponding to the conditions prior to the Sand Engine. The dry beach topography outside the Sand Engine region was built based on regional data of the sub-aerial beach (de Schipper et al. 2016) and the dune area (Nolet et al. 2018). In particular, the dune area was assumed to start 160 m inland from the shoreline, at a height of \(z_{b} = 4.0\) m, and to extend 40 m with \(z_{b}\) increasing inland up to 6.5 m at x=0, following a logarithmic profile. The final bathymetries were obtained by interpolating the different data (example in Fig. 1g).

3.3 Calibration and validation

Arriaga et al. (2017) previously calibrated Q2Dmorfo with Sand Engine data. The model was re-calibrated here because of the extension with sea-level variability due to set-up, tides, storm surges and MSLR. The first calibration parameter \(\mu\) controls the magnitude of the longshore sediment transport (Eq. 3). The range of values tested were \(\mu =0.01-0.07\) m\(^{1/2}\)s\(^{-1}\). Regarding the parameter fixing the magnitude of the cross-shore and diffusive sediment transport terms (4-5), the tested values were \(\nu =0.03,0.05,0.07\). The third calibration parameter \(f_{c}\) controls the value of the depth of closure and was varied as \(f_{c}=0.1,0.15,0.2\). Finally, the values \(f_{m}=0.1,1,2\) were tested for the calibration parameter fixing the minimum value of the closure depth. The model was run for 110 combinations of these values using the measured wave and sea-level conditions from January 2012 until August 2019.

Following Arriaga et al. (2017), calibration was performed for simulations covering the first 465 d, with a bathymetry on 25 April 2013, but the validation period was extended four more years compared with the previous studies, up to 25 August 2019. Model performance was assessed by comparing modelled and measured bathymetries using the root-mean-square skill score, \(RMSSS=1-RMSE(Y,X)/RMSE(B,X)\), where RMSE stands for root-mean-square error, Y represents the bathymetric predictions, X corresponds to the bathymetric measurements and B is the no-change prediction (i.e., the initial bathymetry). In the RMSSS computation, bed levels were weighted by a factor \(0.95^{-z_{b}}\), with \(z_{b}\) ranging from 0 to \(-8\) m, to amplify the role of the coastline behaviour because, regarding the bathymetry, Q2Dmorfo is intended to resolve just the overall trends but not the details. A value of \(RMSSS=1\) means perfect model-data agreement and negative values mean that the error in the prediction is greater than the magnitude of the observed changes.

In agreement with the calibration results obtained using constant sea level (Arriaga et al. 2017), the best-fit parameter values when comparing modelled and measured bathymetries in April 2013 were \(\mu =0.04\) m\(^{1/2}\)s\(^{-1}\), \(\nu =0.05\), \(f_{c}=0.15\) and \(f_{m}=1\) (maximum of purple line with stars in Fig. 2a). Results hardly changed when varying \(f_{m}\). Thus, including sea-level variability did not change the parameter values that better reproduced the observed dynamics. As quantified and discussed in section 6.1 of Arriaga et al. (2017), the best-fit value \(\mu =0.04\) m\(^{1/2}\)s\(^{-1}\) corresponds to a value of the standard CERC non-dimensional constant of \(K=0.14\), which is not contradictory with existing knowledge despite being in the lower range of published values. The best-fit value \(f_{c}=0.15\) corresponds to an effective closure depth of \(D_{c}=9.5\) m, consistent with the observed values in the Sand Engine area (Roest et al. 2021).

Fig. 2
figure 2

Root-mean-square skill score, RMSSS, between modelled and measured bathymetric lines for different values of the calibration parameters for the period up to 25 April 2013 (a), 12 March 2015 (b) and 25 August 2019 (c)

Full size image
Fig. 3
figure 3

Bathymetric lines of observations (green) and model (black) using the best-fit parameter values (\(\mu =0.04\), \(\nu =0.05\), \(f_{c}=0.15\), \(f_{m}=1\)) in 25 April 2013 (a), 12 March 2015 (b) and 25 August 2019 (c)

Full size image
Fig. 4
figure 4

Time-evolution from 2012 to 2019 (calibration and validation period) of the RMSSS between modelled and measured bathymetric lines with the best-fit parameter setting (\(\mu =0.04\) m\(^{1/2}\)s\(^{-1}\), \(\nu =0.05\), \(f_{c}=0.15\) and \(f_{m}=1\), panel a), and of the best-fit \(\mu\) value (panel b, where the rest of parameters take the best-fit values)

Full size image

The best-fit parameter values up to April 2013 also provided excellent results during the validation period up to 2019 (see examples in March 2015 and August 2019 in Fig. 2c,d). Thus, they were chosen as default parameter setting in the rest of the study. It is important to note that similar RMSSS values were obtained for various combinations of \(\mu\), \(\nu\) and \(f_{c}\) values. In particular, focusing on the last available measured bathymetry (Fig. 2c) there were 8 combinations of model parameters, including the default one, that gave similar RMSSS values (they differed by \(1.7\%\) at most). They corresponded to \(\mu =0.03,0.04\) m\(^{1/2}\) s\(^{-1}\), \(\nu =0.03,0.05\) and the two best values of \(f_{c}\) for each \(\nu\) value (\(f_{c}=0.15,0.2\) for \(\nu =0.03\) and \(f_{c}=0.1,0.15\) for \(\nu =0.05\)). These were all used in the long-term simulations to test the uncertainty related with model parameters (Section 5.1). Fig. 3 illustrates how measured bathymetric lines compare with the modelled ones using the default parameter setting in April 2013 (calibration moment), March 2015 and August 2019. Note that Q2Dmorfo modelled bathymetric contours were much smoother than the observed ones as a result of the idealizations behind the model (e.g., neglecting surf-zone and nearshore bar dynamics). The RMSSS was not high in April 2013 but it increased in time reaching values up to 0.6 for the default parameter setting (Figs. 2c and 4a). The initial bathymetry (January 2012) was strongly perturbed with respect to its equilibrium due to the presence of the Sand Engine mega-nourishment. Due to the simplified cross-shore transport, Q2Dmorfo gives an initially too fast cross-shore dynamics compared to reality, as discussed already by Arriaga et al. (2017), and this explains the initially negative values of RMSSS in Fig. 4a. Finally, given the importance of the longshore transport in the Q2Dmorfo model and for the Sand Engine natural evolution, the time dependence of the best-fit \(\mu\) value (with the rest of parameters taken as the best-fit value) was obtained using all available bathymetries in 2012-2019 (Fig. 4b). The default parameter value, \(\mu =0.04\) m\(^{1/2}\)s\(^{-1}\), indeed provides the best results most of the time, changing only slightly in some years.

Fig. 5
figure 5

Time evolution from 2012 to 2100 of the mean sea level (MSL) in the 6 scenarios (panel a), where a smoothing window of 1 yr has been applied to filter out the fast tidal oscillations and facilitate visualization. Example of projected sea level (panel b), wave height (panel c), wave period (panel d) and wave angle with respect to north (panel e) around December 2083 for the reference scenario (RCP8.5)

Full size image

3.4 Long-term forcing projections and model runs

In this study, only the projected changes in climatic conditions during the 21st century related to MSLR were included, following Kopp et al. (2014). Existing studies (de Winter et al. 2012; Bricheno & Wolf 2018; Amores & Marcos 2020; Lobeto et al. 2021) do not show statistically significant changes in future wave conditions in the Dutch coast. They systematically obtain a tiny decrease in mean wave heights and they disagree on the forecast of extreme heights. Moreover, they all acknowledge the uncertainty of these projections since future changes in waves in that coast cannot be separated from the natural variability and model differences are often larger than projected changes. Besides, Sterl et al. (2009) found no statistically significant changes in storm surge heights on our study site, either. Therefore, wave conditions (height, period and angle) and fast sea-level variability (including tides and storm surges) until 2100 were built by repeating the measured hourly data from January 2010 to December 2019 every decade.

In particular, in order to build the long-term sea-level projections, measured sea-level data from 2010-2019 (Section 3.1) was first linearly detrended to remove the corresponding MSLR and keep only tides and storm surges. Repeating these detrended data until 2100, a scenario without MSLR (sea-level baseline) was obtained, and was included also for comparison. Second, four MSLR projections by Kopp et al. (2014) for Hoek van Holland harbour (10 km south-west from the Sand Engine) were used from three different Representative Concentration Pathways. These correspond to the multi-model ensemble median projected MSLR under RCP2.6, RCP4.5 and RCP8.5. The fourth projection was taken as the 83rd percentile (median+\(\sigma\)) of RCP8.5. Then, these MSLR decadal projections were added to the sea-level baseline. The resulting forcing curves are shown in Fig. 5a, which only displays MSLR and inter-annual variability, since a low-pass filter of 1 yr has been applied to remove fast tidal and storm surge oscillations (only to make this figure) to facilitate visualisation. The three standard scenarios (RCP2.6, 4.5 and 8.5) give a similar sea-level increase until 2050, after which they start to diverge, especially in the higher scenario cases. In the present study, the RCP8.5 (sometimes called business as usual) was used as reference scenario, a common practise in Dutch coastal studies. An example of constructed time series (here, in December 2083) of sea level in the RCP8.5 scenario, wave height, wave period and wave angle is shown in Fig. 5b.

Table 1 Summary of the performed long-term model simulations
Full size table

The performed model simulations can be grouped into different sets (Table 1). The first set used the default parameter setting (best-fit values of the calibration of Section 3.3) and all the MSLR projections (RCP2.6, RCP4.5, RCP8.5, RCP8,5+\(\sigma\) and no MSLR) to analyse the role of MSLR. The second set of simulations were defined to assess the relevance of the different processes driving the Sand Engine morphological evolution. A case with a bathymetry constant in time (so equal to 2012 bathymetry) was analysed to characterize the pure inundation effect of MSLR (also called passive-flooding effect). A simulation of the morphological evolution of this coastal stretch without the mega-nourishment was also done to better understand the cross-shore dynamics and quantify the effect of the Sand Engine. These two cases were studied separately and using only the default parameter values and the RCP8.5. A third set of simulations was done to test the uncertainty related to model parameters and compare it with the uncertainty related to the MSLR projections. The chosen parameter values were those providing similar RMSSS than the default ones in the last validation point (Fig. 2c), as explained in Section 3.3. Finally, a fourth set of simulations was performed using sea-level and wave projections built using baseline data from a five year period, 2010-2015, to perform a preliminary test of the uncertainty related to the chosen time period.

3.5 Metrics for quantifying morphological evolution

Apart from looking at the full bathymetric evolution, it was often useful to compare the Sand Engine evolution in the different simulations using a few simplified morphological characteristics. The high-tide shoreline for calm wave conditions (\(x_{s}(t)\), defined at \(+0.8\) m above mean sea level, MSL) was used as the limit between the dry and submerged beach in all figures, for being a good indicator of the alongshore changes. Two other aggregated quantities were used. The first one is the dry beach area, defined as the total horizontal area from the current high-tide shoreline \(x_{s}(t)\) until the initial dune base (\(z_{b}=4\) m), including the entire alongshore domain (17 km between the two harbours). The second one is the feeding asymmetry, which quantifies the difference in the feeding capacity that the Sand Engine has towards the NE and the SW sides. Following Arriaga et al. (2020), this parameter was computed by defining two fixed monitoring areas of 2.5 alongshore km at both sides of the mega-nourishment, starting where the mega-nourishment perturbation initially affects the shoreline. The shoreline beach gain in each area was then computed as the alongshore-averaged mean change in shoreline position, \(\overline{\Delta x}_{s}(t)\). The feeding asymmetry is the relative difference of the shoreline gain in the two sides,

$$\begin{aligned} FA=2\frac{\overline{\Delta x}_{s1}-\overline{\Delta x}_{s2}}{ \overline{\Delta x}_{s1}+\overline{\Delta x}_{s2} } \ . \end{aligned}$$
(8)

Here, 1 and 2 refer to the two areas, and a positive feeding asymmetry implies an accumulated asymmetry towards NE.

The model results were also used to monitor the shoreline position during events with higher sea-levels caused by storm surges. For this, moderate and extreme inundation episodes in this region were first characterized using data from historical storm surge reports (Rijkswaterstaat 2021), including all the maximum sea levels reported from 2000 until present in Hoek van Holland. According to this analysis, moderate inundations, defined as those with a present-day 3-month recurrence period, correspond to a maximum \(z_{s}=+2.1\) m above present-day MSL, and extreme inundations, those with a present-day 10-yr recurrence period, have maximum \(z_{s}=+3\) m above current MSL. The modelled shorelines corresponding to these two types of inundations events were also tracked.

4 Results of long-term evolution

Fig. 6
figure 6

High-tide shorelines (\(+0.8\) m above MSL) in different years from 2012 to 2100 for the RCP8.5 scenario at the central part of the Sand Engine (panel a), at the SW area (panel b) and at the NE area (panel c). A zoom in the y axis has been implemented in panels b and c (compared to panel a) to facilitate visualization and the initial dune base (\(z_{b}=4\) m) is shown in dashed lines

Full size image

4.1 Morphodynamic evolution under RCP8.5 scenario

In the reference MSLR scenario (RCP8.5), the Sand Engine will continue to diffuse and feed the adjacent beaches but these processes fade with time, being less noticeable from 2050 onward (Fig. 6). The behaviour is not uniform along the domain. The shoreline retreats substantially in the SW area (\(y=11-17\) km, Fig. 6b), especially from 2050 onward, up to 80 m at \(y=14-16\) km in 2100. The NE coastline remains approximately stable (\(y=0-3\) km, Fig. 6c). Also, the Sand Engine initial asymmetric shape becomes symmetric during the first years, in agreement with observations (Roest et al. 2021).

Fig. 7
figure 7

Initial full bathymetry (2012, panel a) showing the model domain for the long-term simulations. Modelled full bathymetry in 2050 (panel b) for the RCP8.5 scenario with zooms to facilitate visualization at \(y=15\) km (panel c), \(y=12\) km (panel d) and \(y=2\) km (panel e). Modelled full bathymetry in 2100 (panel f) for the RCP8.5 scenario with zooms at \(y=15\) km (panel g), \(y=12\) km (panel h) and \(y=2\) km (panel i). In all panels, the black solid line is the initial high-tide shoreline (\(+0.8\) m above MSL), the black dashed line is the initial dune base (\(z_{b}=4\) m) and the red solid line is the current high-tide shoreline

Full size image

Figure 7 shows the bed level in the whole domain in 2012 (panel a, initial bathymetry), 2050 (panel b) and 2100 (panel f) with zooms around \(y=2\) km (NE side of the Sand Engine, panels e and i), \(y=12\) km (SW side, panels d and h) and \(y=15\) km (SW area further from the mega-nourishment, panels c and g). The cross-shore profiles of the bed level corresponding to these alongshore positions, together with that of \(y=7\) km (Sand Engine initial crest) are shown in Fig. 8, with zooms of the first 500 cross-shore metres to allow visualizing the active area. The loss of sand in the mega-nourishment (Fig. 8b) comes with a clear seaward profile progression at the NE side (Fig. 8a) and a more subtle progression at the SW side (Fig. 8c). The SW side experiences a net loss of sand on the dry beach (above high tide) and at the dune base, because of the storm surges of up to \(2-3\) m above mean sea level. Finally, the profile of the more SW located beaches shows an overall erosive trend (Fig. 8d): not only the submerged and dry beach areas experience a net loss of sand but the whole dune part included in the domain is lost by 2100.

Fig. 8
figure 8

Cross-shore bathymetric profiles in 2012, 2050 and 2100 for the RCP8.5 scenario at \(y=2\) km (NE side of the Sand Engine, panel a), \(y=7\) km (crest position, panel b), \(y=12\) km (SW side, panel c), \(y=15\) km (SW area further from the mega-nourishment, panel d). A zoom of the shallowest part is included in each panel

Full size image
Fig. 9
figure 9

High-tide shorelines (\(+0.8\) m above MSL) in 2100 for the 5 scenarios at the central part of the Sand Engine (panel a), at the SW area (panel b) and at the NE area (panel c). A zoom in the y axis has been implemented in panels b and c (compared to panel a) to facilitate visualization and the initial dune base (\(z_{b}=4\) m) is shown in dashed lines

Full size image

4.2 Role of climate change scenario on the morphodynamic evolution

The main tendencies described for the RCP8.5 scenario are also obtained with the other MSLR scenarios, the shoreline receding more with a higher rate of mean sea level, as shown in Fig. 9 for 2100. The 2100 coastline in the RCP2.6 and 4.5 scenarios is located fairly close to the RCP8.5 one, and substantially more landward than in the scenario without MSLR. This is clear not only in Fig. 9 but also in Fig. 10, where solid lines show the time evolution of the high-tide shoreline for all the scenarios in four cross-shore positions (those of the four panels of Fig. 8). In the three RCP scenarios, the NE coastline (\(y=2\) km, Fig. 10a) hardly changes in 2100 with respect to 2012, and only in the most extreme scenario RCP8.5\(+\sigma\) the shoreline recedes here. The situation is different in the SW region since, even in the part closest to the Sand Engine (\(y=12\) km, Fig. 10c), shoreline retreats substantially in the high-emission scenarios (green and blue lines), especially following the acceleration of MSLR from 2050 onward. The further SW region (\(y=15\) km) retreats continuously in all MSLR scenarios, indicating that the effect of the mega-nourishment does not reach this area.

To illustrate the conditions during storms and to understand their effect on the morphodynamic evolution, Fig. 10 also shows the shoreline position that would correspond to moderate and extreme inundation episodes (defined in Section 3.5) in dashed and dotted lines, respectively. Due to the large initial beach width of 118 m, in most of the domain there is enough space to accommodate moderate inundations (\(z_{s}=+2.1\) m above MSL): in the NE (\(y=2\) km, panel a, dashed lines) and SW (\(y=12\) km, panel c, dashed lines) sides of the Sand Engine, the shorelines under such events display a behaviour similar to the high-tide shoreline, only displaced some 70 m landward but without reaching the dune base. However, extreme inundation episodes (\(z_{s}=+3\) m above MSL, dotted lines) would reach the dune base by 2070 in both sides. In the further and more vulnerable SW beaches (Fig. 10d, dashed and dotted lines) moderate surges would reach the dune base by 2070 and extreme surges by 2040. This explains the complete erosion of the part of the dune included in the model domain that is observed in this area by 2100 (Fig. 8d).

To better compare the effect of MSLR in the morphodynamic evolution, the two aggregated bathymetric parameters defined in Section 3.5 were used. The dry beach area (Fig. 11a, solid lines) already experiences a small decrease (of 8% by 2100) in the baseline case (without MSLR, orange line). This is strongly exacerbated by projected MSLR, with a total area loss ranging from 28% to 48% by 2100 depending on the scenario. The initial feeding asymmetry (FA in Eq. 8) of some \(50\%\) towards NE (Fig. 11b) decreases to some \(30\%\) by 2060 and then remains relatively stable. This asymmetry slightly increases with sea-level rise, being smallest for the baseline scenario. Such feeding asymmetry, largest at the beginning but sustained in time, provides a partial explanation to the differences between the morphodynamic evolution of the NE side (which maintains its position by 2100) and the SW side next to the Sand Engine (which experience a recession, as shown in Figs. 6-10). As proven by Arriaga et al. (2020), this feeding asymmetry is due to both the initial asymmetric shape of the mega-nourishment, tilted towards the NE side (Fig. 1f), and the slight asymmetry in the bimodal offshore wave climate (Fig. 1a).

Fig. 10
figure 10

Time evolution from 2012 to 2100 of high-tide shoreline positions (\(+0.8\) m above MSL) for the 5 scenarios at \(y=2\) km (NE side of the Sand Engine, panel a), \(y=7\) km (initial crest position, panel b), \(y=12\) km (SW side, panel c), \(y=15\) km (SW area further from the mega-nourishment, panel d). Solid line is the high-tide shoreline during calm weather (\(+0.8\) m above MSL), dashed line is the high-tide shoreline during a moderate storm surge (3-month recurrence period, \(+2.1\) m above MSL) and dotted line is the high-tide shoreline during a extreme storm surge (10-yr recurrence period, \(+3\) m above MSL). The initial dune base (\(z_{b}=4\) m) is shown in black lines

Full size image
Fig. 11
figure 11

Time evolution from 2012 to 2100 for the 5 scenarios of the horizontal dry beach area (panel a) and the feeding asymmetry FA (panel b, \(FA>0\) meaning asymmetry towards NE). The description of these two quantities can be found in the main text. The areas corresponding to the solid lines are computed from the current high-tide shoreline (\(+0.8\) m above MSL) until the initial dune base (\(z_{b}=4\) m). The dotted lines quantify the area reduction by the pure inundation effect (passive flooding), related only to MSLR without sediment transport. The dashed lines quantify the area reduction associated only to bathymetric recession linked to net sediment loss, i.e., areas computed with the modelled bathymetries from the bathymetric line \(z_{b}=+0.8\) m (initial high-tide) until the initial dune base. See Section 4.3 for more details on these two latter lines

Full size image

4.3 Processes affecting shoreline recession

The morphological evolution of the Sand Engine results from longshore and cross-shore sediment transport processes. The former is responsible for the sediment transport from the central mega-nourishment area towards the nearby beaches while the overall area recession is mainly driven by MSLR and cross-shore transport. In fact, since in the modelled long-term evolution we imposed zero longshore sediment transport in the lateral boundaries and zero cross-shore transport at the backshore, the overall predicted shoreline recession is linked to sediment moving offshore. MSLR can produce a shoreline retreat due to two completely different processes. On the one hand, there is a pure inundation effect (also called passive flooding or bath-tube effect). This is the shoreline recession purely due to the sea level rise without any change in the morphology, thereby illustrating the situation if there was no sediment transport. It was here quantified applying MSLR but keeping the bathymetry fixed in the 2012 configuration. As shown by the dotted lines in Fig. 11a, this turns out to be responsible for about \(50\%\) of area reduction. On the other hand, MSLR can induce morphological changes because, as sea level rises, the new bed slope for a certain water depth is larger than the corresponding equilibrium slope (if the profile shows the typical concave-up shape). As a result, the downslope cross-shore transport, described by the first term in Eq. (4), exceeds the net wave-induced onshore transport (second term of that equation), transporting sediment seaward. This causes an additional shoreline recession that was called wave reshaping by D’Anna et al. (2021b). Its role was here quantified by following the bed level contour of the evolving bathymetry corresponding to the initial high-tide shoreline, \(z_{b}=+0.8\) m, instead of the current high-tide shoreline. As shown with the dashed lines of Fig. 11a, the wave reshaping effect explains the other \(50\%\) area decrease in the Sand Engine case.

The run simulating the hypothetical situation without mega-nourishment (made for the reference case) allowed us to better quantify both the effect of the Sand Engine construction and the cross-shore transport processes. The evolution of four representative profiles is shown in Fig. 12, which can be compared with Fig. 8. The two panels d) in these figures are alike and a similar shoreline retreat in 2100 is found (of 86 m in this case, see also Fig. S1 of the Supplementary Information), evidencing again that southern beaches are not affected by the Sand Engine presence. In contrast, the other three sectors would recede significantly more without its presence (Figs. 12a-c). Changes are most dramatic in the dry beach, with the dunes being partially eroded by 2100. Remarkably, the behaviour is slightly alongshore variable even without the mega-nourishment presence, the shoreline retreat increasing southward (Fig. 12 and Fig. S1 of the Supplementary Information). The explanation could be that this coastal area has a net longshore transport to the NE, as quantified by van Rijn (1997). Since the sediment flux is zero at the pier of Hoek van Holland, there must be a significant NE transport gradient along the southern section which would explain this erosive trend. However, given the bimodal nature of the wave climate (Fig. 1) the net longshore transport has a strong inter-annual variability, even with changes in direction (see Fig. 16 of Arriaga et al. (2017) and van Rijn (1997)). It seems that the net annual transport in this area is the result of subtracting large numbers where the result is small and can be dramatically affected by the uncertainties. Thereby, more observations would be needed to clarify this trend.

This simulation without Sand Engine, thereby with less alongshore variability, also illustrates better the offshore sediment transport process. The profile retreat obtained in 2100 compared with 2012 is restricted to about 7 m depth whilst the profile accretes from there to about 12 m depth (compare the lighter and darker lines in Fig. 12). This confirms the net offshore transport from the dry beach and the shallower sectors towards deeper waters. This effect is more noticeable from 2050 onward, indicating that the modelled net offshore sediment transport is linked to MSLR. As explained before, this offshore flux occurs because, under a rising sea level, the slope at a particular water depth is larger than the equilibrium one that would correspond to that depth and thereby gravity effect overcomes wave-induced onshore transport.

Fig. 12
figure 12

Cross-shore bathymetric profiles in 2012, 2050 and 2100 in a hypothetical situation without the Sand Engine for the RCP8.5 scenario at \(y=2\) km (panel a), \(y=7\) km (panel b), \(y=12\) km (panel c), \(y=15\) km (panel d). A zoom of the shallowest part is included in each panel to facilitate visualization

Full size image
Fig. 13
figure 13

Uncertainty in the modelled time evolution from 2012 to 2100 of the horizontal dry beach area (panel a) and the feeding asymmetry (panel b). The values corresponding to the solid lines are computed for the four MSLR scenarios and the default parameter setting (equal to solid lines in Fig. 11). The values corresponding to the shadowed areas are obtained for the four MSLR scenarios using the other parameter values that give equal RMSSS as the default ones in the last validation point (cases \(\mu =0.03, 0.04\) m\(^{1/2}\)s\(^{-1}\) in Fig. 2c). See Section 5.1 for more details

Full size image

5 Discussion

5.1 Analysis of uncertainty sources in this modelling exercise

In addition to fundamental model assumptions and choices (see the SI for a list of limitations of this modelling exercise), the most important uncertainty sources in long-term morphodynamic modelling are those related with climate change scenarios and intrinsic wave climate variability and those regarding the values of model free parameters (Kroon et al. 2020; D’Anna et al. 2021). As explained in Section 3.4, three MSLR RCP projections were used in this study (RCP2.6, 4.5, 8.5) together with a more extreme scenario (RCP8.5\(+\sigma\)), covering the potential range of future sea level values. Inherent uncertainty in climate projections was reflected in a difference of 1.5% in the dry beach area by 2050 between RCP4.5 and RCP8.5, reaching 5% if the two most extreme MSLR projections (RCP2.6 and RCP8.5+sigma) are considered. By 2100, the range of uncertainty increased up to 11% and 32% for the two intermediate and the two most extreme projections, respectively (Fig. 11a, solid lines).

As explained in Section 3.4, the hourly series of wave conditions (and sea level detrended baseline) were constructed by repeating past data (2010-2019), on the basis that present studies do not show clear projected changes in storms in the North Sea due to global warming (Sterl et al. 2009; de Winter et al. 2012; Bricheno & Wolf 2018; Amores & Marcos 2020; Lobeto et al. 2021). To explore the uncertainty related with the specific time period chosen as representative from the past, a second set of projections was generated with data from 2010-2015. The obtained results were very similar to the reference ones, the beach area being about \(1\%\) smaller by 2100 in all scenarios (Fig. S2 of the Supplementary Information). Thereby, the choice of time period to represent past conditions did not affect our results significantly. However, this is not a quantification of the uncertainty related with future wave conditions and climate variability, which has not been included in this contribution. First, there are many unknowns about how global warming will affect wave conditions and, second, chronology effects could play a certain role (Karunarathna et al. 2014; D’Anna et al. 2021; Vitousek et al. 2021) and have not been considered. However, since the Sand Engine evolution is gradual and not directly coupled to individual storm events, it is likely that chronology effects are of minor importance (Walstra et al. 2013).

To evaluate model parameter uncertainty, the long-term simulations were repeated for the four MSLR scenarios using 8 combinations of parameter values different from the default ones (described in Section 3.4). Figure 13 displays the results of the default parameter setting (in solid lines, which correspond to those in Fig. 11) surrounded by shadowed areas plotting the results attained with the other possible parameter values. The model-parameter uncertainty produced differences in dry beach area projections of 2-3% by 2050 and of 6-8% by 2100 (scenarios RCP4.5 and 8.5). Kroon et al. (2020) also found that model parameter uncertainty was important when modelling the first years of Sand Engine evolution with a 1D coastline model.

The comparison between the two tested sources of uncertainties is also illustrated in Fig. 13. Uncertainties in beach area projections until about 2050 related with model free parameters are larger or comparable to those associated to sea-level projections, whilst the latter become dominant from 2050 to 2100 (Fig. 13a). This result is consistent with the study by D’Anna et al. (2021), in which the shoreline evolution in the Truc Vert beach (French Atlantic coast) was studied. On the other hand, the large uncertainties in feeding asymmetry projections, of the order of 20-30%, are mainly due to model parameter uncertainty (Fig. 13b).

5.2 Assessment of Bruun rule performance

Despite its many limitations, the Bruun rule is a widespread method to estimate beach recession under MSLR due to cross-shore processes only and its use is increasing (D’Anna et al. 2021b). Our model computations of the coastal response without the Sand Engine (presented in Section 4.3) provided an interesting opportunity of assessing the performance of the Bruun Rule for the Delfland coast.

The Bruun Rule states

$$\begin{aligned} \Delta X =\frac{MSLR}{\tan {\alpha }} \ , \end{aligned}$$
(9)

where \(\Delta X\) is the shoreline retreat and \(\tan {\alpha }\) is the mean slope of the active coastal zone, running from a stable emerged beach location (e.g., berm, dune base or crest) until the depth of closure, \(D_{c}\). To apply the Bruun Rule to the Delftland coast we assumed \(D_{c} = 9\) m, corresponding to the time-averaged closure depth applied in the present simulations, which is at the upper limit of the 5-10 m range obtained from the first 5-yr Sand Engine observations by Roest et al. (2021). Then, \(\tan {\alpha }\) in a typical profile of this stretch of coast without the mega-nourishment is about 0.013, 0.014 or 0.016, depending on which point is chosen as stable beach location (berm, dune base or dune crest, respectively). Since in the RCP8.5 scenario the MSLR in 2100 was of 0.74 m, the shoreline retreat given by Eq. (9) was \(\Delta X \approx 45-55\) m. In the Q2Dmorfo simulation without the Sand Engine for the RCP8.5 scenario, the shoreline recession in 2100 was larger, from 47 m in the northernmost sector to 86 m in the southernmost sector (Fig. S1 of the Supplementary Information). Thus, the Bruun Rule estimate matches the Q2Dmorfo prediction in the northern section while it is smaller by a factor 2 in the southern section.

There are a number of reasons why the Bruun Rule deviates from the Q2Dmorfo predictions. First of all, even in the hypothetical situation without the Sand Engine, the Dutch Delfland coast still undergoes a significant effect of the longshore transport, as illustrated by the alongshore variability of Figs. 12 and S1. Another source of discrepancy might be the depth of closure, \(D_{c}\), which is assumed constant for the Bruun Rule while it is dynamic for Q2Dmorfo, depending on the instantaneous wave energy. In fact, this makes the choice of \(D_{c}\) to be somehow arbitrary in the Bruun method (D’Anna et al. 2021b), whilst it determines the value of \(\tan {\alpha }\) and shoreline recession (with Eq. 9). For example, \(\tan {\alpha }\) could be considered lower (\(\sim 0.008\)) in the Delfland coast if a larger value of the closure depth of, e.g., 12 m was chosen (given the long time scales involved). This would yield a Bruun Rule shoreline retreat \(\Delta X \approx 80-100\) m, becoming larger than that obtained by the Q2Dmorfo model. Finally, the application of the Bruun Rule is always done assuming an instantaneous adaptation of the whole bathymetry to the equilibrium profile for the actual sea level whilst Q2Dmorfo considers that the bathymetry tends gradually to this equilibrium at a rate that depends on the wave energy and decreases seaward, being negligible at \(D_{c}\). Also, due to tidal oscillations and storm surges, the profile in Q2Dmorfo is never exactly in equilibrium with the instantaneous sea level. Then, due to the strong non-linearity in the system, the average beach profile may differ from the equilibrium corresponding to the average sea level. Overall, the Bruun rule can provide at its best just the order of magnitude of shoreline recession under MSLR and a more accurate quantitative evaluation certainly requires the use of morphodynamic models (such as Q2Dmorfo).

6 Conclusions

The role of mean sea level rise (MSLR) on the evolution of the Sand Engine up to 2100 has been studied with Q2Dmorfo, a reduced-complexity morphodynamic model designed for large spatio-temporal scales. It includes both longshore and cross-shore sediment transport processes, thereby modelling the effect of MSLR in a more realistic manner than the commonly-used Bruun rule. The calibrated version of the model successfully reproduced the observed bathymetric evolution of the mega-nourishment from 2012 to 2019, the obtained values for the calibration parameters being robust as time evolves, proving the model adequacy for decadal morphodynamic projections.

According to the obtained long-term projections, the Sand Engine will continue to diffuse and feed the adjacent beaches, its effect fading in time from 2050 onward. Superimposed to these alongshore processes, the total dry beach area will diminish due to MSLR, the recession trends being significantly stronger in the higher-emission climate change scenarios. Half of the retreat is due to passive flooding and the other half to net offshore sediment transport, produced by wave reshaping in combination with gravity. The net sediment transported offshore accumulates at depths from 7 to 12 m. All this illustrates that in long-term coastal evolution, MSLR-driven shoreline recession associated to morphological change, despite being much harder to predict, can be as important as that produced by the simpler passive-flooding effect. The morphological evolution is predicted to be strongly alongshore variable, mainly due to the presence of the mega-nourishment. The asymmetries in both its initial shape and the bimodal wave climate produces a Sand Engine feeding higher to the NE side than to the SW side. On the former, the feeding counteracts the MSLR-induced retreat and the shoreline is stable up to 2100, with the profile showing an accretive tendency. On the SW side, the feeding is smaller and the shoreline recedes from 2050 onward, although the profile is rather stable on average. The effect of the mega-nourishment does not reach the beaches located further south (at more than 6 km alongshore from its initial crest) and, as a result, both the shoreline and the profile retreat substantially. Even the dunes of this vulnerable region could experience significant erosion because common moderate inundation episodes would reach their base by 2070. Results of dry beach area decrease are qualitatively robust, the uncertainties linked to the model parameters being most important up to 2050 and those related with the MSLR scenarios dominating from 2050 to 2100, in agreement with existing literature. This study shows that mega-nourishments like the Sand Engine can be a highly efficient measure to protect many km of coastline from the effect of MSLR during the 21st century. It also reveals that the protection efficiency can differ along the coast and this must be assessed with the use of morphodynamic models.