Abstract
Importance of evaluation of global hydrological models (gHMs) before doing climate impact assessment was underlined in several studies. The main objective of this study is to evaluate the performance of six gHMs in simulating observed discharge for a set of 57 large catchments applying common metrics with thresholds for the monthly and seasonal dynamics and summarize them estimating an aggregated index of model performance for each model in each basin. One model showed a good performance, and other five showed a weak or poor performance in most of the basins. In 15 catchments, evaluation results of all models were poor. The model evaluation was supplemented by climate impact assessment for a subset of 12 representative catchments using (1) usual ensemble mean approach and (2) weighted mean approach based on model performance, and the outcomes were compared. The comparison of impacts in terms of mean monthly and mean annual discharges using two approaches has shown that in four basins, differences were negligible or small, and in eight catchments, differences in mean monthly, mean annual discharge or both were moderate to large. The spreads were notably decreased in most cases when the second method was applied. It can be concluded that for improving credibility of projections, the model evaluation and application of the weighted mean approach could be recommended, especially if the mean monthly (seasonal) impacts are of interest, whereas the ensemble mean approach could be applied for projecting the mean annual changes. The calibration of gHMs could improve their performance and, consequently, the credibility of projections.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The projection of climate change impacts on river discharge is usually done by following a modelling chain, starting with several scenarios of future radiative forcing (representative concentration pathways, RCPs). After that, climate projections generated by general circulation models (GCMs) or regional climate models are collected, and often, statistical bias correction methods are applied. Then, hydrological impact models are driven by climate scenarios under certain RCPs to perform impact assessment. Nowadays, it is common to apply not only ensembles of climate scenarios from several models but also ensembles of hydrological models (HM) in such studies (e.g. Haddeland et al. 2014; Roudier et al. 2016; Gosling et al. 2017; Vetter et al. 2017).
Different types of hydrological models are applied for impact assessment depending on the scale of the study and data availability. The catchment-scale and regional models are usually calibrated and validated in advance, whereas the global- and continental-scale models are mostly applied using a multi-model ensemble without calibration or evaluation.
The importance of evaluation of global hydrological models (gHMs) in advance, prior to climate impact assessment, was underlined in several recent studies: Zhang et al. (2016), Beck et al. (2017), Hattermann et al. (2017) and Zaherpour et al. (2018), and a number of studies were devoted specifically to evaluation of gHMs and testing performance of model sets (Haddeland et al. 2011; Beck et al. 2016; Veldkamp et al. 2018; Zaherpour et al. 2018) or to cross-comparison of global- and regional-scale models (Zhang et al. 2016; Hattermann et al. 2017; Gosling et al. 2017).
Table 1 presents an overview of papers focused on evaluation of gHMs. They differ by the number of evaluated models, the number of catchments/gauge stations considered, the size of catchments, the temporal and spatial resolutions of indicators and the evaluation metrics applied. In papers published until 2015, mainly the temporally averaged indicators were analysed, like mean annual runoff and mean monthly runoff over a 30-year period, but in recent studies, also not aggregated indicators like annual runoff and monthly runoff get more attention, and different metrics are used for evaluation.
Usually, the results of model evaluation performed at the catchment scale are spatially aggregated for presentation of results in the papers, mostly to the global/continental scale or to climate zones or regime classes. The aggregated information could be useful, if there are distinct differences in evaluation metrics for climate zones; otherwise, the value of such assessments is restricted. Quite rarely, the results of model evaluation are shown for the catchment scale (Hattermann et al. 2017; Zaherpour et al. 2018).
Some studies include also the evaluation of indicators of hydrological extremes, focusing mostly on the high and low percentiles of runoff (Table 1). Regarding human-induced influences, most studies do not include them or consider naturalized discharge in small catchments. The global HMs started including human management in the early 2000s, e.g. irrigation in WaterGAP (Döll et al. 2003) and reservoirs in H08 (Hanasaki et al. 2006), and recent papers (Veldkamp et al. 2018; Zaherpour et al. 2018) include human influences parameterized using global databases.
In the papers by Gudmundsson et al. (2012a, 2012b), it was suggested that a mean or median of a multi-model ensemble should be presented as main output in climate impact studies, being the best predictors, as the variations in performance of individual models and in their projections are large. Since 2012, this approach was applied in numerous continental- and global-scale studies. However, recently, several authors questioned this statement and proved an opposite conclusion following from their assessments. For example, Zaherpour et al. (2018) observed that in some cases, the ensemble mean fails to perform better than any individual model from an ensemble, and this finding definitely challenges the commonly accepted perception about the best performance of the ensemble mean (EM). Interesting discussions on the ensemble mean approach can be found in Rougier (2016) and Beck et al. (2017).
Recently, a hypothesis that “good performance of hydrological models in the historical period increases confidence in projected climate impacts, and may decrease uncertainty of projections related to hydrological models” was tested (Krysanova et al. 2018), and it was proven based on examples from previous impact assessment studies and analysis of arguments “pro” and “contra” from literature. In this paper, guidelines for evaluation of catchment-scale and global-scale models (more simplified for gHMs), as well as criteria for exclusion of poorly performing models from an ensemble in impact studies, were suggested (see also Coron et al. 2011; Refsgaard et al. 2013; Roudier et al. 2016). It was also underlined that the application of models with weighting coefficients based on model performance could be reasonable (e.g. see Nohara et al. 2006; Yang et al. 2014) and may provide more credible results compared with the simple ensemble mean approach which disregards performance.
Zaherpour et al. (2018) evaluated simulations of a set of six global models participating in the Inter-Sectoral Impact Model Inter-comparison Project (ISIMIP, Warszawski et al. 2013, https://www.isimip.org/), for 40 large river basins. They applied a ratiometric integrated criterion, the ideal point error (IPE), which was standardized against a naïve benchmark model, where the observed discharge was shifted backwards by 1 month. This paper underlined the importance of understanding the strengths and deficiencies of global models in reproducing hydrological regime, extremes and interannual variability, influencing their preparedness for climate impact assessment.
Following recommendations in Krysanova et al. (2018) on model evaluation, and based on the model setup in Zaherpour et al. (2018), this study aims for an extended evaluation of gHMs for large river basins supplemented by an impact assessment using gHM simulations openly available in ISIMIP. The main objective is to extend the study by Zaherpour et al. (2018) applying another model evaluation approach based on simple and commonly used metrics to a larger set of river basins in the same eight hydrobelts (Meybeck et al. 2013) and provide a climate impact assessment taking into account the model evaluation results. Namely, the aims are:
-
a)
to evaluate six gHMs for 57 river basins in eight hydrobelts in the historical period applying four metrics for the monthly and long-term mean monthly (seasonal) dynamics and summarize them estimating an aggregated index (AI) of model performance
-
b)
to estimate weighting coefficients for all models in all basins based on AI, excluding cases where poor model performance does not allow estimation of meaningful weighting coefficients
-
c)
to do a climate impact assessment for a selection of river basins using the usual ensemble mean approach and the weighted mean approach based on model evaluation results, and compare outcomes of both.
2 Case study catchments
We have taken the same 40 large river basins as in Zaherpour et al. (2018) paper and added 17 more in order to improve their spatial distribution among eight hydrobelts and on six continents. The hydrobelts are strictly limited by catchment boundaries at a 30′ (0.5°) resolution. The classification of land area in hydrobelts takes into account more geo-hydrological factors compared with the Köppen classification in climate zones, including runoff, and thus, it could be more suitable for hydrological modelling. In the study of Zaherpour et al. (2018), two hydrobelts, boreal (BOR) and northern mid-latitude (NML), were covered by selected basins more densely, but there were only one or two basins in four other hydrobelts, which did not allow to perform a proper spatial analysis of results.
The aim to improve spatial distribution was reached by relaxing the size and observed data availability catchment selection criteria applied in Zaherpour et al. (2018) only partly. Due to poor availability of observed discharge data in some areas on the globe, some hydrobelts (e.g. northern dry, NDR) are still sparsely covered. Two hydrobelts, NDR and SML (southern mid-latitude), include only three basins each. Nevertheless, a larger number of basins in hydrobelts allows averaging of evaluation results and enables spatial analysis.
The following criteria were used for selections of the catchments:
-
They should be larger than 50,000 km2 to ensure that the catchments are of sufficient size to accommodate the output resolution of the models.
-
They should be independent (i.e. data from only one gauge was used for each catchment).
-
Observed monthly discharge should be available for 20 years or longer within the 1971–2010 period, which was assigned for the model evaluation and be without missing data.
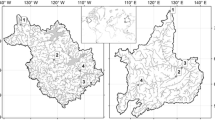
The selected 57 river basins and the corresponding gauge stations are listed in Table S1 (here and later “S” means that Table or Figure is in the Supplementary) and depicted in Fig. 1. Some characteristics of hydrobelts and catchments within them are shown in Table S2. It is obvious that most of these large basins do include significant human interventions, like reservoirs and water abstraction, which should be considered in the models.
Distribution of the 57 case study catchments (see Table S1) across eight hydrobelts. The hydrobelts are named: BOR, boreal; NML, northern mid-latitude; NDR, northern dry; NST, northern subtropical; EQT, equatorial; SML, southern mid-latitude; SDR, southern dry; SST, southern subtropical
3 Data and methods
3.1 Observed hydrological data
The observed monthly discharge data for 57 gauges were obtained from the Global Runoff Data Centre, GRDC (http://grdc.bafg.de), for 20 years or longer within the 1971–2010 period with no missing data, which was required for the model evaluation. Only in one case, for the Yangtze, hydrological data were obtained from the local authority.
3.2 Global hydrological models and model outputs
The ensemble of global models applied in this study includes DBH (Tang et al. 2007), H08 (Hanasaki et al. 2008), LPJmL (Rost et al. 2008), MATSIRO (Pokhrel et al. 2015), PCR-GLOBWB (Wada et al. 2014, a short name PCR will be used below) and WaterGAP2 (Müller Schmied et al. 2016). The LPJmL model is different from others being originally a dynamic global vegetation model (DGVM), but it has all features of a hydrological model, and can be classified as a combined DGVM/gHM model. The DBH and MATSIRO models belong to the class of land surface models (LSMs) and also have all variables and processes of a hydrological model. All models account for human water management related to water use, land use and operation of reservoirs and dams.
Only one model of six, WaterGAP2, was calibrated. It was calibrated for 1319 GRDC stations, covering ~ 54% of the global land area, by adjusting one effective parameter that determines runoff from soil in the dependence of soil saturation and up to two additional correction factors to match the long-term mean annual observed river discharge (see details in Hunger and Döll 2008; Müller Schmied et al. 2014, 2016; Müller Schmied 2017).
All models simulate surface and subsurface runoff, river discharge, snow cover, evapotranspiration and other hydrological variables across the land surface at 0.5° × 0.5° spatial resolution. A short description of processes considered in the models and model characteristics is available in the references above and in Hattermann et al. (2017).
Simulations for the historical period starting 1861 until 2005 and for the future period from 2006 until 2099 were previously done in the framework of ISIMIP and are openly available (ISIMIP 2a: historical period and ISIMIP 2b: projections for future at http://esgf-data.dkrz.de). Human water management interferences were included in all downloaded simulations.
The monthly observed and simulated discharge in cubic metres per second was converted to the catchment monthly discharge in millimetres per month by using the area upstream of the gauge according to the DDM30 (Döll and Lehner 2002) river network. As the global river network at 0.5 ° spatial resolution does not perfectly coincide with the GRDC river network, an area correction factor was applied to the GRDC discharge data to account for that (see Table S3).
3.3 Climate forcing data and climate scenarios
Two climate reanalysis data were used as forcing in the historical period 1971–2010: WATCH Forcing Data methodology applied to ERA-Interim reanalysis data (WFDEI, Weedon et al. 2014) and data from the Global Soil Wetness Project Phase 3 (GSWP3, Kim 2017). They have been also used in previous studies on model evaluation (Müller Schmied et al. 2016; Huang et al. 2017; Zaherpour et al. 2018).
The climate model data originate from the Coupled Model Intercomparison project (CMIP5, Taylor et al. 2012; https://pcmdi.llnl.gov/mips/cmip5/). Climate scenarios, which were used to run simulations, are available in ISIMIP from four models: GFDL-ESM2M, HadGEM2-ES, IPSL-CM5A-LR and MIROC5. All climate model outputs in ISIMIP have been bias-corrected using a trend-preserving method (Frieler et al. 2017).
3.4 Model evaluation approach
We used three common metrics, Nash and Sutcliffe efficiency (NSE; Nash and Sutcliffe 1970), percent bias (PBIAS, Moriasi et al. 2007) and bias in standard deviation (Δσ) (Gudmundsson et al. 2012b) (see formulas in Supplementary, Section S1), for the evaluation of models, taking into account the established in scientific literature thresholds for good and weak/satisfactory performance. For orientation on thresholds, we considered values suggested by Moriasi et al. (2007, 2015) for the catchment-scale models and relaxed (i.e. made less strict) these thresholds for the global-scale models. So, for the evaluation of monthly dynamics, we applied the following thresholds:
NSE | good: NSE ≥ 0.5 | satisfactory/weak: 0.3 ≤ NSE < 0.5, |
PBIAS (%) | good: − 25 ≤ PBIAS ≤ 25 | satisfactory/weak: − 35 ≤ PBIAS < − 25 or 25 < PBIAS ≤ 35, |
and performance with NSE < 0.3 or |PBIAS| exceeding 35% was evaluated as poor. The corresponding thresholds in Moriasi et al. (2015) for the monthly dynamics are for NSE: 0.7 and 0.55, and for PBIAS: 10% and 15%, correspondingly.
And for the evaluation of the long-term mean monthly (or seasonal) dynamics, we used the following:
NSE | good: NSE ≥ 0.7 | satisfactory/weak: 0.5 ≤ NSE < 0.7, |
Δσ (%) | good: − 25 ≤ Δσ ≤ 25 | satisfactory/weak: − 35 ≤ Δσ < − 25 or 25 < Δσ ≤ 35. |
If these criteria were not fulfilled for seasonal dynamics, i.e. NSE was < 0.5 or |Δσ| was larger than 35, the performance was assessed as poor.
After these performance metrics were estimated for every basin and model for both forcing datasets, the following scores were assigned to every criterion:
-
Good performance: score = 1
-
Satisfactory/weak performance: score = 0.5
-
Poor performance: score = 0
and finally summed. The total scores (minimum 0 and maximum 8 for 4 criteria with 2 forcings) were translated to an aggregated index (AI) dividing by 8, i.e. the maximum possible score. By that, the performance of each individual model over each catchment was evaluated with an AI ranging from 0 to 1. A similar model evaluation approach, considering river discharge and snow cover, was used in Gaedeke et al. (in review) for gHM evaluation in six Arctic basins.
3.5 Impact assessment approach
Only five of six models were used for impact assessment, because discharge projections from DBH were not available. For the historical period 1971–2000, we used the simulated “histsoc” (historically varying climate and socio-economic scenarios) time series driven by four GCMs, and for the future periods, 2041–2070 and 2071–2099, the “2005soc” time series (socio-economic scenarios fixed at 2005 level for future) for RCP2.6 and RCP6.0 driven by the same four GCMs. The subscript “soc” means that human influences such as reservoirs and irrigation were considered in the model simulations.
The climate impact assessment was performed for a selection of catchments applying two approaches, (1) the commonly used “ensemble mean” (EM) approach and (2) approach with the weighting coefficients (WCOs) based on models performance, and the results of both were compared. The basin selection procedure is described in Section 4.2.
The WCOs for impact assessment in river basins were assigned considering only models with AI ≥ 0.5 by dividing AI of this model by the sum of all AIs ≥ 0.5. We assumed that the WCO approach should be applied to basins with acceptable or good performance of at least one model having AI > 0.5. Therefore, if only one model has AI = 0.5 and all others have lower AIs for a certain basin, WCO cannot be assigned to this model, and impact assessment with WCOs cannot be done due to generally poor models performance in this basin.
4 Results
4.1 Model evaluation
The results of model evaluation in terms of scores from 0 to 8, aggregated indices from 0 to 1 and average AIs per basin and per model are presented in Table 2. The high scores ≥ 6 and AI ≥ 0.75 are marked as bold, and the basins with all AI < 0.5 (scores < 4) are shaded grey.
4.1.1 Performance per basin
There are 15 basins among 57 with a good or satisfactory model performance: eight basins with average AI > 0.5 (e.g. Mekong, Iguacu, Yangtze) and seven basins with average AI between 0.4 and 0.5 (e.g. Yenisei, Mississippi, Amur). These 15 basins include six large (> 1 M km2) and five rather small (50,000–150,000 km2). On the other hand, 11 basins shaded grey in Table 2 showed quite poor performance: all models have scores < 4 (AI < 0.5), and among them, 8 basins have all low scores ≤ 2 (AI ≤ 0.25) (e.g. Niger, Colorado, Darling).
In addition, the dependency of model performance on the size of drainage basins was checked. For that, all catchments were distributed into six classes by drainage area (A) size in thousands square kilometres: A ≤ 100, 100 < A ≤ 200, 200 < A ≤ 400, 400 < A ≤ 600, 600 < A ≤ 900 and A > 900. In all classes, one or several basins with poor performance (AI < 0.10) were found, and in all classes except one (200 < A ≤ 400), at least one basin with an acceptable or good performance (AI > 0.5) was found. The highest average AI in the 3rd class was 0.46 for Tapajos. So, we can conclude based on results in Table 2 that no dependency of model performance on the catchment size was found. However, this conclusion cannot be generalized, as the sample size was restricted (only five basins in the 4th class and six in the 5th).
Spatial analysis of evaluation results is presented in Section S2 and Table S4 (Supplementary).
4.1.2 Performance per model
The best performing model was WaterGAP2, with average AI = 0.67 over all basins, most probably resulting from calibration of this model. The MATSIRO and PCR models are following WaterGAP2 in this respect, but their average AIs are more than twice lower: 0.28 and 0.26 (Table 2). The lowest average performance was estimated for the DBH model. Table 3 presents a summary of models performance, listing in addition to average scores and average AI the numbers and percentages of basins with poor (AI = 0), acceptable and good (AI ≥ 0.5) and good (AI ≥ 0.75) performance.
In addition, the original metrics for the monthly and seasonal dynamics and two forcings for 57 catchments are presented as box plots in Figs. S1–S3 (Supplementary). The median NSE values are well below zero for DBH, LPJmL and H08, and their average NSE values are even lower. According to PBIAS and bias in SD, the same three models show significant overestimation of discharge (by 337%, 222% and 81%, on average) and amplitude of seasonal dynamics (by 424%, 314% and 176%, on average) in most of the basins, whereas MATSIRO moderately underestimates discharge, by 21% on average. According to Figs. S1–S3, WaterGAP2 has the best performance, followed by MATSIRO with a better performance than of the rest models. For some models, metrics for the average seasonal dynamics are worse than for the monthly dynamics.
4.1.3 Distribution of catchments in four groups
From the perspective of applying WCOs for use in climate impact assessment, the catchments can be divided into four groups, based upon their performance:
-
Group 1: impact assessment with WCOs is not possible. It includes 15 basins (26% of the total) with “poor” performance: 11 basins where all models have AI < 0.5, and 4 basins where only one model has AI = 0.5, and all others 0 or 0.13 (e.g. Yellow and Paraguai).
-
Group 2: impact assessment with WCOs is possible using only one model per basin. This comprises 16 basins (28%) where only one model has AI > 0.5; in 14 cases, it is WaterGAP2 and in two – PCR (Albany) or MATSIRO (Rhine).
-
Group 3: impact assessment is possible with two “satisfactory” or “good” performing models. There are 12 basins (21%) in this group, with two models having AI ≥ 0.5 (e.g. Volga, Fitzroy).
-
Group 4: three to five models with AI ≥ 0.5 can be applied for impact assessment with WCOs. This comprises 14 basins (25%). Among them is one basin, Mekong, where all six models have AI > 0.6.
4.2 Selection of basins for impact assessment
The climate impact assessment was done for 12 selected basins. Firstly, 12 basins were randomly selected from all hydrobelts (Table 4, upper part) before the model evaluation was done. However, after the model evaluation, we realized that in six basins (Table 4, shaded yellow), impact assessment with WCOs would be impossible due to poor model performance (see assumption in Section 3.5). Therefore, these basins were exchanged by six additional basins (Table 4, lower part), taking into account three additional criteria, drainage area size, AI values and number of models with AI ≥ 0.5, to have more or less even distribution of these factors among all selected basins.
The characteristics of the final 12 selected basins are shown in Table 5. They are located on all continents, and every hydrobelt is represented by one or two basins. Further, there are catchments of different sizes, from 98,000 km2 up to 4.6 M km2. Their aggregated indices vary from small (0.1) up to the highest (0.9), and the number of models which can be used for impact assessment with WCOs varies from one (Limpopo) up to five (Mekong). In that sense, it is a representative subset of the whole set of 57 catchments.
4.3 Impact assessment: comparison of results based on two methods
The aim of climate impact assessment was to compare projections for 12 selected river basins (Table 5) for the future periods 2041–2070 and 2071–2100 with simulations for the reference period 1971–2000 considering the long-term monthly means and annual means for RCPs 2.6 and 6.0. For the gHM ensemble averaging, two methods were applied: the usual ensemble mean approach and the weighted mean approach based on the model evaluation results (see WCOs in Table 4), and results of both were compared. The results of impact assessment are presented in Figs. 2, 3 and 4 and Fig. S4. Table 6 and Table S5 provide a summary of differences between impacts and uncertainties estimated using two methods for RCP 6.0 in the far future period.
Differences in impacts in terms of deviations of monthly means in the far future period 2071–2099 under RCP 6.0 from those in the reference period 1971–2000 for 12 river basins estimated using two approaches: (1) ensemble mean approach (red) and (2) mean based on weighting coefficients (blue). Note different Y scales used for 12 graphs
Estimated impacts of climate change on mean annual discharge as absolute differences in cubic metres per second between the future (mid and far) and reference periods for RCP 2.6 and RCP 6.0 using the ensemble mean approach (five models, red boxes) and mean with weighting coefficients (one to five models, blue boxes) for the Mackenzie, Mississippi, Santiago, Amazonas, Sao Francisco and Oranje basins
The same as Fig. 3 for the Volga, Lena, Limpopo, Mekong, Congo and Fitzroy basins
Figure 2 shows differences in impacts in terms of deviations of monthly means in the far future period under RCP 6.0 from those in the reference period estimated using the ensemble mean and the weighted mean approaches, both averaged over GCMs. This Figure allows to compare directions and magnitudes of changes and seasonal shifts based on two methods.
4.3.1 Directions of change
Regarding direction of change, results based on two methods can agree fully or partly or disagree (see Fig. 2). They agree fully for eight basins: on increase in discharge over all season for Lena, decrease in all months for Mississippi and Amazonas, decrease in the first half of a year and increase in the second one for Mekong, increase in cold season and decrease in summer for Mackenzie and Volga and increase in February–March (April) followed by decrease in other months for Fitzroy and Sao Francisco. They agree partly in two cases: increase from October to April/June and decrease in June/July to August for Santiago and increase in all months except November or October to November for Oranje. However, the directions of change differ between two approaches for Limpopo and Congo, where impacts based on EM are negative in most of the months, whereas they are mostly positive according to projections based on the WCO method.
4.3.2 Magnitude of change
We can also analyse how different are the deviations of monthly and annual means in the far future period under RCP 6.0 from those in the reference period based on two methods (Figs. 2, 3 and 4; Table 6).
As one can see in Fig. 2, impacts based on both methods are practically identical for Mekong and quite similar for Amazonas. This can be explained by a quite good performance of all five models for Mekong resulting in almost equal WCOs for all models and the application of two models with good and one with satisfactory performance for Amazonas. Note that these two catchments have the highest average AI values in the set of 12 basins.
There are only small monthly differences in impacts between two methods for Sao Francisco and Mississippi, not exceeding 5–7%, and mean annual differences are even lower: 1 and 3%, respectively.
For Congo and Fitzroy, impacts based on WCOs are higher than those based on EM: by 5–9% for Congo, and by 6–11% for Fitzroy in almost all months. The mean annual differences are smaller, counting to ca. 5.5% in both cases.
Projections for two Arctic basins, Mackenzie and Lena, show medium to large differences in both directions in 4 to 5 months, ranging from − 16 to + 18% for Mackenzie, and from − 7 to + 26% for Lena, but small annual differences due to “compensation” of negative and positive monthly deviances.
Impacts for Volga using two methods are different during winter and spring months, going up to 40% in March. Also, the mean annual impacts differ notably: by 10%.
And for Santiago, Oranje and Limpopo, differences are large in almost all months, reaching 91–95% for the first two and 205% for Limpopo. The mean annual differences for these basins are also large: 30, 36 and 51%, correspondingly (Table 6). These three basins have the lowest average AI values among all 12 catchments.
4.3.3 Spreads in projections
Figures 3 and 4 allow to compare mean annual impacts obtained with both methods as well as uncertainties represented by projection spreads. The full spreads in both methods are due to both driving GCMs and impact models, gHMs. In case of the EM approach, spreads in simulations are due to four GCMs and five gHMs, and in the WCO approach, they are due to four GCMs and one to five gHMs, and they differ depending on river basin and approach used. The differences in spreads between two methods are estimated in percent (Table S5) and shown as arrows in Table 6.
Comparing percentiles from 25 to 75% represented by boxes in Figs. 3 and 4, we can see that
-
in three cases, spreads are practically equal (Mekong, Mackenzie and Sao Francisco) and in one case slightly increased (Volga),
-
for five basins, spreads based on the WCO method are reduced by 15–31% (Amazonas, Fitzroy, Lena, Santiago and Oranje) compared with the EM approach,
-
in three cases (Mississippi, Congo and Limpopo), spreads of projections based on the WCO are reduced quite significantly, by 53–82% (Table S5).
And comparison of the full uncertainty ranges, from minimum to maximum in Figs. 3 and 4, shows that there are four possible options: either min/max ranges are practically the same for both methods (four cases), or they are decreased slightly (by < 20%, one case), moderately (by 21–50%, four cases) or significantly (by 51–82%, three cases), when the WCO method is applied (Table 6; Table S5).
In addition, Fig. S4 allows comparison of projections of mean monthly impacts and uncertainty ranges in cubic metres per second for RCP 6.0 in far future against the reference period based on two approaches for four basins. As one can see, projection spreads are moderately (Mississippi) or significantly (Mackenzie, Volga and Limpopo) smaller when the WCO method is applied. The projected peak of discharge in February and seasonal dynamics for Limpopo using the EM approach are about 4–5 times higher compared with peak and seasonal dynamics simulated with WCOs. When models with poor performance are excluded in the second approach, the peak and mean monthly dynamics become much lower, and dynamics in the reference period is much better comparable with the observed one (the latter not shown). So, the reduced uncertainty of projections based on WCO results not simply from the fact that less models are applied, but from using less models with better performance.
Of course, one explanation for the reduction of spreads when the WCO method is used is clear: the EM method is always based on five models, and in most cases, the WCO method is applied with less than five models (except for Mekong). However, we can also perceive that using the EM approach and including also poorly performing models in an ensemble, we “artificially” increase uncertainty of projections. This can be understood by considering an example of including in an impact study along with two-three well-performing models one else model with a significant overestimation of discharge by 200–300% (there are similar cases in our study) and looking how spreads would increase after adding this model.
5 Discussion
Weak and poor performance of gHMs: what to do?
When we see the weak and poor model evaluation results in many basins (Table 2, Table 3), three questions arise: (1) what are the reasons behind this, (2) what could be done to improve the models’ performance and (3) what should modellers do in basins where the performance of all models is bad: still use all models to estimate an ensemble mean with full uncertainty ranges?
One of the reasons of weak and poor performance is that gHMs are usually not calibrated at the basin scale. Grasping the general dynamics with a simple and robust structure and a few parameters has been considered more essential. Besides, there are differences in representation of processes in the models that could directly influence their performance. A further possible reason is a poor quality of input data, especially precipitation, in some regions.
What can be done? Since many gHMs have matured recently, it is perhaps time to pay more attention to model performance, appropriate parameter ranges, sensitivity analysis and calibration of discharge at the monthly time scale. Besides, checking the quality of input data, in particular precipitation, could be useful. The results of model evaluation in this study and differences in model performance suggest that the calibration of gHMs can improve their historical time performance and could lead to increasing credibility of projections for the future. The successful experience with WaterGAP2, as well as with H08 (Mateo et al. 2014) and Mac-PDM.09 (Gosling and Arnell 2011), is promising for other models. The calibration of gHMs is recommended, keeping all parameters within appropriate ranges and preserving the water balance. Of course, calibration only to the observed discharge is generally not sufficient, as there is no guarantee that a model that performs well in the historical climate will also perform well under changed climate conditions in future. Nevertheless, it is the first step to be done.
However, our model set includes two LSMs and one DGVM, with different concepts solving water balance linked to vegetation dynamics and carbon cycle, which makes calibration of such models challenging. This also suggests that the inclusion of other variables, like evapotranspiration, in addition to discharge in model evaluation and calibration could be fruitful (Schaphoff et al. 2018), not least to identify model-structural causes of simulation biases in addition to biases occurring due to the input data quality, in particular precipitation (Biemans et al. 2009). If a model significantly overestimates discharge (e.g. see Figs. S2, S3), this means that, most probably, it significantly underestimates evapotranspiration. Thus, bringing water balance closer to the observed one, modellers could improve representation of other important processes as well.
In the basins where performance of all models in the historical period is poor, the projections should be marked as being highly uncertain, for example, by shading in the maps (Krysanova et al. 2018).
Arguments for and against model calibration
There are no doubts that model calibration usually improves model’s performance in the historical period. Without calibration, the performance of gHMs is usually poor, often reaching several hundreds percent bias and large negative values of NSE (see Figs. S1–S3, Supplementary). Significant overestimation or underestimation of discharge in most cases means that other water flows are strongly underestimated/overestimated. Besides, we cannot state that gHMs are physically based models which do not need calibration of parameters.
The arguments for and against model calibration are directly connected with the arguments pro and contra model performance, which were discussed in detail in Krysanova et al. (2018, Table 3). Although not shown specifically in the present analysis, arguments in the Table referred to above, along with examples from this paper and other recent studies (Donnelly et al. 2016; Roudier et al. 2016; Hattermann et al. 2017), suggest that good performance of hydrological models in the historical period (after or without calibration) might increase confidence of projected climate impacts and decrease the spreads in projections related to hydrological models.
On the other hand, model calibration is of course not a panacea, and if models perform well without calibration (e.g. MATSIRO, PCR and LPJmL for the Mekong in our study), they could be applied for impact assessment without calibration.
Model robustness for future climate
Regarding calibration of a model in the historical period and its application under changed future climate conditions mentioned above, this problem was discussed in several recently published papers (Choi and Beven 2007; Refsgaard et al. 2013; Thirel et al. 2015; Krysanova et al. 2018). In the latter one, the new guidelines for model evaluation, including several additional tests to investigate robustness of hydrological models under changed climate condition, were proposed: (a) differential split-sample test for multiple gauges, (b) proxy climate test and (c) comparison of observed and simulated trends in discharge. However, such tests go far beyond the relatively simple and easy calibration to river discharge at the basin outlet, which we suggest for gHMs in this paper. Nevertheless, the further tests may follow.
Uncertainty and projection spread
The word “uncertainty” is used to denote the full uncertainty of hydrological models from several sources and also for uncertainty of deterministic models applied within the GCM-HM ensemble. If we treat the full uncertainty related to HMs as uncertainty of models applied in a probabilistic mode with sampling of model parameters, then of course it will be much larger compared with spreads of deterministic models applied with single parameter sets. Besides, the full uncertainty can also include variations due to diverse input data and changes in model structure. However, climate impact assessment is usually done applying hydrological models in a deterministic mode, with one set of parameters each (assigned or calibrated), within a multi-GCM-multi-HM ensemble, as was also done in our study. The shares of total variation or projection spread, often also called uncertainty (e.g. Haddeland et al. 2011; Dankers et al. 2014; Beck et al. 2017; Vetter et al. 2017), related to RCPs, GCMs and HMs could be quantified and compared. The quantification of uncertainty shares was not done in this study; the spreads were only compared visually and numerically (Figs. 3 and 4; Table 6; Table S5).
Not only model performance is important
However, not only satisfactory model performance in historical period is needed for improving impact assessment. The inclusion of processes that may play role under changing climate conditions (such as CO2 fertilization, glaciers, permafrost and groundwater) in the impact models is also of great value. For example, many gHMs do not consider CO2 fertilization effects (see Milly and Dunne 2016), thus tending to overestimate water scarcity. Therefore, models considering this aspect, like LPJmL and MATSIRO, would be better suited for climate impact assessments than other models, which do not include such effects (Döll et al. 2016). Another aspect could be groundwater representation which is still crude in many models. For example, the study of Pokhrel et al. (2014) demonstrated that water stress in Amazonas could be heavily overestimated due to lack of groundwater processes in a model.
Human impacts in the models
One important criterion for basin selection in this study was their size: they should be large enough to accommodate the output resolution of gHMs. This was an important reason to focus on large basins and not on smaller naturalized headwater parts of them. It is obvious that most of these large basins do include significant human interventions, like reservoirs and water abstraction, especially in dry areas, and ignoring them would lead to even weaker model results. For example, in the paper by Veldkamp et al. (2018), it was shown that the inclusion of human influences improved the gHM performance. Yes, parameterization of human management in the models added another layer of complexity, but it was possible using available global datasets, though not on the year-to-year basis but as average over the period. The modellers used state-of-the-art approaches and datasets for their integration. Nevertheless, there are of course limitations in the parameterizations (e.g. Döll et al. 2016), and a community effort is needed to handle them. In conclusion, due to three reasons, (i) there are hardly large natural basins with good observation data available, (ii) the models include currently the best available information on handling human impacts and (iii) the models show certain improvements when including human impact parameterizations, we decided to consider the simulation setup including human impacts.
Ensemble mean approach
As discussed by other authors before (Beck et al. 2016, 2017; Zaherpour et al. 2018) and as follows from our study, the EM approach is not the best and most reliable method for impact assessment using gHMs. It is suitable if all models perform well, or at least more than a half of them perform well or satisfactory, as the examples of Mekong and Amazonas show. Using the EM approach for impact assessment after the model evaluation is much better, because in such a case, the simulated impacts and uncertainties could be better interpreted. Besides, as follows from our analysis (Section 4.3.2; Table 6), the EM method is better suitable for analysis of mean annual than mean monthly projections.
There are also other problems above the improving model performance in basins with good data, for example poor quality and temporal-spatial deficits in observed river discharge data, parameter estimation for basins with considerable uncertainty in precipitation and parameter transfer to ungauged basins. The use of remote sensing and satellite observations may provide promising pathways to solve some of these problems.
6 Summary and conclusions
6.1 Summary of model evaluation
Comparing model evaluation results for six models, we can conclude that performance of WaterGAP2 was quite good, with acceptable AIs for 75% and good AIs for 51% of all catchments, and other five models showed a weak or poor performance in most of the basins. One obvious reason is the calibration of WaterGAP2. Other possible reasons and ways to solve the problem are discussed in Section 5.
Note that currently, research is ongoing for additional objective functions and calibration of WaterGAP2 to more than one variable, which will allow to exclude correction to the observed discharge applied now at some of the stations.
In 15 river basins of 57 (26% of all), all models showed low evaluation results, and in these basins, impact assessment with the WCO approach is not possible, and the application of the EM approach is questionable. In 16 basins (28%), only one model showed acceptable or good evaluation results (AI > 0.5), and, strictly speaking, the assessment of impacts is possible only with this one model. The third group includes 12 basins (21%), where impact studies could be done with two satisfactory or good performing models with AI ≥ 0.5. And in the rest 14 basins (25%), three to five models can be applied for impact assessment with WCOs.
6.2 Summary of comparison of impacts and uncertainties based on two methods
Comparison of climate change impacts using two methods leads to the following conclusions: from 18 selected river basins: (a) impact assessment with WCOs was not possible in six of them (~ 33%) due to poor performance of all models, (b) comparison of impacts in terms of mean monthly and mean annual discharge demonstrated negligible or small differences between impacts based on two methods in four basins (~ 22%), and differences in mean monthly discharge, mean annual discharge or both were moderate or large in eight cases (~ 44%), whereas the mean annual differences were lower compared with the mean monthly. However, these results cannot be generalized yet and require further checking.
Both methods of impact assessment, based on EM and WCOs, provided practically the same results for Mekong and similar results for Amazonas. Hence, the application of the EM approach could be justified in river basins, where all or more than a half of models perform well or satisfactorily.
The comparison of projection spreads derived from two methods and represented by 25–75% percentile boxes and the full ranges for mean annual changes in far future under RCP 6.0 for 12 investigated basins shows that they are equal or similar in four basins, notably decreased by 15–50% in five catchments and significantly decreased by 51–82% in three basins when the WCO method is used (Table 6; Table S5). We can conclude that the reduced uncertainty of projections based on the WCO method comes not simply from the fact that less models are applied, but from using less models with better performance.
6.3 Conclusions
The following conclusions can be made from the study.
-
Model evaluation is important. Our results suggest that prior to climate impact assessment, an evaluation of the global or regional hydrological models against observational time series should be done. Preferably, such evaluation has to be performed at the same (or finer) temporal scale at which the impacts are later presented and analysed. Also, the results of previous model evaluations at a suitable scale could be used for the interpretation of impact results.
-
The improvement of gHM performance, albeit challenging, is needed for making impact assessment studies more reliable and their results more credible. For that, model calibration using a few sensitive parameters would be meaningful to be applied for gHMs. Here, good quality of climate forcing data, which could influence performance of gHMs, is important.
-
The application of the WCO approach after model evaluation for climate impact assessment is a more reliable method compared with the EM approach, as this method can provide impact results that can be transmitted to end-users with higher credibility. The application of the WCO method could be especially recommended, if the mean monthly impacts and seasonal changes are of interest. And the EM method is better suitable for analysis of mean annual than of mean monthly changes. However, a good historical performance of a model does not solve all the problems, and the inclusion of hydrological processes which may play a role under warmer climate is indispensable as well.
As follows from our study, the way to improve credibility of projections under climate change could be outlined as follows:
-
Doing model evaluation before impact assessment, and then applying the WCO method if mean monthly projections are of interest, or the WCO or EM method if only average annual discharge should be projected. In case of projections for extremes, the models should be also evaluated for extremes in the historical period. The catchments with poor performance of all models and ungauged catchments should be indicated on the maps with projections as highly uncertain, e.g. by shading.
-
Including model calibration in gHMs could improve their performance in the historical period, increase credibility of projections and decrease uncertainty related to hydrological models in many catchments.
-
To go beyond that, the suggested model evaluation approach based on discharge should be extended to a more holistic assessment of several variables (discharge, evapotranspiration, snow cover) to calibrate and evaluate the models.
References
Beck HE et al (2015) Global maps of streamflow characteristics based on observations from several thousand catchments. J Hydrometeorol 16:1478–1501
Beck HE et al (2016) Global evaluation of runoff from ten state-of-the-art hydrological models. HESS Discuss 21:2889–2903
Beck HE et al (2017) Global evaluation of runoff from 10 state-of-the-art hydrological models. HESS 21:2881–2903. https://doi.org/10.5194/hess-21-2881-2017
Biemans H et al (2009) Impacts of precipitation uncertainty on discharge calculations for main river basins. J Hydrometeorol 10:1011–1025
Choi HT, Beven KJ (2007) Multi-period and multicriteria model conditioning to reduce prediction uncertainty in distributed rainfall-runoff modelling within GLUE framework. J Hydrol 332(3–4):316–336. https://doi.org/10.1016/j.jhydrol.2006.07.012
Coron L et al (2011) Pathologies of hydrological models used in changing climatic conditions: a review. Hydro-Climatology: Variability and Change, vol 344. IAHS Publ, pp 39–44
Dankers R et al (2014) First look at changes in flood hazard in the Inter-Sectoral Impact Model Intercomparison Project ensemble. Proc Natl Acad Sci U S A 111. https://doi.org/10.1073/pnas.1302078110
Döll P, Lehner B (2002) Validation of a new global 30-min drainage direction map. J Hydrol 258(1–4):214–231
Döll P et al (2003) A global hydrological model for deriving water availability indicators: model tuning and validation. J Hydrol 270(1–2):105–134
Döll P et al (2016) Modelling freshwater resources at the global scale: challenges and prospects. Surv Geophys 37(2):195–221. https://doi.org/10.1007/s10712-015-9343-1
Donnelly C et al (2016) Using flow signatures and catchment similarities to evaluate a multi-basin model (E-HYPE) across Europe. Hydrol Sci J 61(2):255–273. https://doi.org/10.1080/02626667.2015.1027710
Frieler et al (2017) Assessing the impacts of 1.5 °C global warming – simulation protocol of ISIMIP2b. Geosci Model Dev 10:4321–4345. https://doi.org/10.5194/gmd-10-4321-2017
Gaedeke et al (2020) Performance of global hydrological models for climate change projections in Pan-Arctic river basins. Clim Chang (in review)
Gosling SN, Arnell NW (2011) Simulating current global river runoff with a global hydrological model: model revisions, validation and sensitivity analysis. Hydrol Process 25:1129–1145. https://doi.org/10.1002/hyp.7727
Gosling SN et al (2017) A comparison of changes in river runoff from multiple global and catchment-scale hydrological models under global warming scenarios of 1 °C, 2 °C and 3 °C. Clim Chang 141(3):577–595. https://doi.org/10.1007/s10584-016-1773-3
Greuell W, Andersson JCM, Donnelly C, Feyen L, Gerten D, Ludwig F, Pisacane G, Roudier P, Schaphoff S (2015) Evaluation of five hydrological models across Europe and their suitability for making projections under climate change. Hydrol Earth Syst Sci Discuss 12(10):10289–10330
Gudmundsson L et al (2012a) Comparing large-scale hydrological model simulations to observed runoff percentiles in Europe. J Hydrometeorol 13:604–620
Gudmundsson L et al (2012b) Evaluation of nine large-scale hydrological models with respect to the seasonal runoff climatology in Europe. Water Resour Res 48:1–20
Haddeland I et al (2011) Multimodel estimate of the global terrestrial water balance: setup and first results J. Hydrometeorol. 12:869–884
Haddeland I et al (2014) Global water resources affected by human interventions and climate change. PNAS 111(9):3251–3256. https://doi.org/10.1073/pnas.1222475110
Hanasaki N et al (2006) A reservoir operation scheme for global river routing models. J Hydrol 327:2241
Hanasaki N et al (2008) An integrated model for the assessment of global water resources part 1: model description and input meteorological forcing. HESS 12:1007–1025
Hattermann FF et al (2017) Cross-scale intercomparison of climate change impacts simulated by regional and global hydrological models in eleven large river basins. Clim Chang 141:561–576
Huang S et al (2017) Evaluation of an ensemble of regional hydrological models in 12 large-scale river basins worldwide. Clim Chang 141(3):381–397. https://doi.org/10.1007/s10584-016-1841-8
Hunger M, Döll P (2008) Value of river discharge data for global-scale hydrological modeling. HESS 12:841–861. https://doi.org/10.5194/hess-12-841-2008
Kim H (2017) Global soil wetness project phase 3 atmospheric boundary conditions (experiment 1) [data set]. Data Integr Anal Syst. https://doi.org/10.20783/DIAS.501
Krysanova V et al (2018) How the performance of hydrological models relates to credibility of projections under climate change. Hydrol Sci J 63:696–720
Mateo CM et al (2014) Assessing the impacts of reservoir operation to floodplain inundation by combining hydrological, reservoir management, and hydrodynamic models. Water Resour Res 50:7245–7266. https://doi.org/10.1002/2013wr014845
Meybeck M et al (2013) Global hydrobelts and hydroregions: improved reporting scale for water-related issues? HESS 17:1093–1111
Milly P, Dunne K (2016) Potential evapotranspiration and continental drying. Nat Clim Chang 6:946–949. https://doi.org/10.1038/nclimate3046
Moriasi DN et al (2007) Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. ASABE 50:885–900
Moriasi DN et al (2015) Hydrologic and water quality models: performance measures and evaluation criteria. ASABE 58(6):1763–1785. https://doi.org/10.13031/trans.58.10715
Müller Schmied H (2017) Evaluation, modification and application of a global hydrological model, Phd-thesis, Goethe-University Frankfurt, http://publikationen.ub.uni-frankfurt.de/frontdoor/index/index/year/2017/docId/44073. Accessed 5 Sept 2020
Müller Schmied H et al (2014) Sensitivity of simulated global scale freshwater fluxes and storages to input data, hydrological model structure, human water use and calibration. HESS 18:3511–3538. https://doi.org/10.5194/hess-18-3511-2014
Müller Schmied H et al (2016) Variations of global and continental water balance components as impacted by climate forcing uncertainty and human water use. HESS 20(7):2877–2898. https://doi.org/10.5194/hess-20-2877-2016
Nash JE, Sutcliffe JV (1970) River flow forecasting through conceptual models part I-a discussion of principles. J Hydrol 10:282–290
Nohara D et al (2006) Impact of climate change on river discharge projected by multimodel ensemble. J Hydrometeorol 7:1076–1089
Pokhrel YN et al (2014) Potential hydrologic changes in the Amazon by the end of the 21st century and the groundwater buffer. Environ Res Lett 9:084004
Pokhrel YN et al (2015) Incorporation of groundwater pumping in a global land surface model with the representation of human impacts. Water Resour Res 51:78–96
Prudhomme C, Parry S, Hannaford J, Clark D.B, Hagemann S, Voss F (2011) How well do large-scale models reproduce regional hydrological extremes in Europe? J Hydrometeorol 12(6):1181–1204
Refsgaard JC et al (2013) A framework for testing the ability of models to project climate change and its impacts. Clim Chang 122(1–2):271–282. https://doi.org/10.1007/s10584-013-0990-2
Rost S et al (2008) Agricultural green and blue water consumption and its influence on the global water system. Water Resour Res 44:1–17
Roudier P et al (2016) Projections of future floods and hydrological droughts in Europe under a +2°C global warming. Clim Chang 135(2):341–355
Rougier J (2016) Ensemble averaging and mean squared error. J Clim 29(4):8865–8870. https://doi.org/10.1175/JCLI-D-16-0012.1
Schaphoff S et al (2018) LPJmL4 – a dynamic global vegetation model with managed land – part 2: model evaluation. Geosci Model Dev 11:1377–1403. https://doi.org/10.5194/gmd-11-1377-2018
Tang Q et al (2007) The influence of precipitation variability and partial irrigation within grid cells on a hydrological simulation. J Hydrometeorol 8:499–512
Taylor KE et al (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93:485–498
Thirel G et al (2015) On the need to test hydrological models under changing conditions. HSJ 60(7–8):1165–1173. https://doi.org/10.1080/02626667.2015.1050027
Veldkamp TIE et al (2018) Human impact parameterizations in global hydrological models improve estimates of monthly discharges and hydrological extremes: a multi-model validation study. Environ Res Lett 13:055008
Vetter T et al (2017) Evaluation of sources of uncertainty in projected hydrological changes under climate change in 12 large-scale river basins. Clim Chang 141:419–433. https://doi.org/10.1007/s10584-016-1794-y
Wada Y et al (2014) Global modeling of withdrawal, allocation and consumptive use of surface water and groundwater resources. Earth Sys Dyn 5:15–40
Warszawski L et al (2013) The Inter-Sectoral Impact Model Intercomparison Project (ISI-MIP): Project framework. PNAS 111(9):3228–3232
Weedon GP et al (2014) The WFDEI meteorological forcing data set: WATCH Forcing Data methodology applied to ERA-Interim reanalysis data. Water Resour Res 50:7505–7514. https://doi.org/10.1002/2014WR015638
Yang T et al (2014) Climate change and probabilistic scenario of streamflow extremes in an alpine region. J Geophys Res Atmos 119:8535–8551. https://doi.org/10.1002/2014JD021824
Zaherpour J et al (2018) Worldwide evaluation of mean and extreme runoff from six global-scale hydrological models that account for human impacts. Environ Res Lett 13:065015
Zhang YQ et al (2016) Evaluating regional and global hydrological models against streamflow and evapotranspiration measurements. J Hydrometeorol 17:995–1010
Acknowledgements
The authors are grateful to ISIMIP for providing gHM simulations for this study and to GRDC for providing discharge data.
Funding
Open Access funding provided by Projekt DEAL. Hannes Müller Schmied received partial support for this study by BMBF (grant no. 01LS1711F). Yusuke Satoh received support from JSPS KAKENHI (grant no. 17K12820). Qiuhong Tang received support from NSFC (41730645) and Newton Advanced Fellowship.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
ESM 1
(DOCX 4748 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Krysanova, V., Zaherpour, J., Didovets, I. et al. How evaluation of global hydrological models can help to improve credibility of river discharge projections under climate change. Climatic Change 163, 1353–1377 (2020). https://doi.org/10.1007/s10584-020-02840-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-020-02840-0