Abstract
Lake surface water temperatures (LSWTs) are sensitive to atmospheric warming and have previously been shown to respond to regional changes in the climate. Using a combination of in situ and simulated surface temperatures from 20 Central European lakes, with data spanning between 50 and ∼100 years, we investigate the long-term increase in annually averaged LSWT. We demonstrate that Central European lakes are warming most in spring and experience a seasonal variation in LSWT trends. We calculate significant LSWT warming during the past few decades and illustrate, using a sequential t test analysis of regime shifts, a substantial increase in annually averaged LSWT during the late 1980s, in response to an abrupt shift in the climate. Surface air temperature measurements from 122 meteorological stations situated throughout Central Europe demonstrate similar increases at this time. Climatic modification of LSWT has numerous consequences for water quality and lake ecosystems. Quantifying the response of LSWT increase to large-scale and abrupt climatic shifts is essential to understand how lakes will respond in the future.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Climate warming is occurring globally and is a first-order control that can affect lakes through a complex series of indirect and direct mechanisms, such as its influence on the catchment and on lake thermal and hydrological budgets (Adrian et al. 2009). An important primary response of a lake to climatic warming is change in lake surface water temperature (LSWT), with potential consequences for a broad range of physical, ecological and socioeconomic factors. For example, rising LSWT can influence lake evaporation leading to impacts on water level (Gronewold and Stow 2014) with consequences for commercial shipping, hydropower facilities and water security (Vörösmarty et al. 2000). Rising LSWTs can also result in the modification of the biochemical compositions of some algal species (Flaim et al. 2014), result in advanced zooplankton phenology and reduced phytoplankton biomass (Velthuis et al. 2017), promote the occurrence of toxic cyanobacterial blooms (Kosten et al. 2012) and threaten water quality (Huisman et al. 2005). Climatic modification of LSWT has, thus, important implications for local economies, which depend on lakes for drinking water, agricultural irrigation, recreation and tourism. A detailed understanding of LSWT warming, and the factors that control it, is therefore essential for climate change impact and water management studies.
Increases in LSWT have been documented in recent years at regional and global scales (Schneider and Hook 2010; Zhang et al. 2014; O’Reilly et al. 2015; Torbick et al. 2016; Woolway et al. 2016). However, much of our understanding of the physical impact of climatic warming on lakes has tended to focus on gradual long-term trends and specifically on a linear relationship through time. While a linear regression can be statistically significant and can be extremely useful to evaluate the direction of warming, it assumes that lakes undergo monotonic changes over time. This assumption can mask the occurrence of step changes (North et al. 2013; Van Cleave et al. 2014), and thus affect greatly the interpretations of the underlying mechanisms that are responsible for long-term change. Long-term changes in lake thermodynamic variables can be associated with a pronounced, nonlinear step change that indicates a rapid switch between stable states or regimes (Scheffer et al. 2001). Identifying this type of abrupt change in climate drivers and corresponding abrupt or gradual change in lake variables can improve understanding on the role of climate change on the ecosystem.
Abrupt changes in climate, termed climate regime shifts (CRS), are often distinguished by abrupt temporal changes in temperature. A well-documented example of a CRS is the late 1980s regime shift, triggered by anthropogenic and natural forcing (Reid et al. 2016). Its impact on the marine environment was particularly well documented, with examples of sea surface temperature increase throughout the Northern Hemisphere (Yasunaka and Hanawa 2003). It has also been observed in the atmosphere (Xiao et al. 2012), been shown to have had a substantial influence on groundwater (Figura et al. 2011), rivers and lakes (North et al. 2013). As yet though, the influence of the 1980s CRS on LSWT at a larger, macro-regional, spatial scale has not been investigated in detail. In this contribution, we aim to address this research gap by analysing LSWTs from 20 lakes in Central Europe with between 50 and ∼100 years of observational data. These lakes are exposed to similar climate forcing but are characterised by different morphometric features, thus are excellent study sites for investigating the response of LSWT to macro-regional scale changes in the climate. A numerical model is also used in this study to investigate if the response of LSWT to abrupt climatic shifts can be simulated from meteorological forcing data and assess if modelled LSWTs provide sufficiently reliable estimates of how LSWT responds to climate change, which will be critical for future decision making involving, among other things, water resource management policies.
2 Study sites
Our study sites were 20 Central European lakes situated in Austria (12), Switzerland (2) and Poland (6) (Fig. 1). The lakes vary in surface area between approximately 2.65 and 580 km2, in altitude between 56.9 m above sea level (a.s.l.) and 929.0 m a.s.l., in latitude between 46.44°N and 54.27°N, in mean depth between 1.0 and 154.4 m and in maximum depth between 1.80 and 310.0 m (Table 1).
3 Methods
In this section, we provide a detailed description of (i) the LSWT and surface air temperature (SAT) datasets used in this investigation, (ii) the statistical methods used to identify a regime shift and (iii) the one-dimensional thermodynamic model used to simulate LSWT, as well as the meteorological forcing data used to drive the model.
3.1 Lake temperature
We compiled in situ LSWT (defined as temperatures sampled between 0 and 1 m below the water surface) data from 20 lakes that have been sampled at least monthly during the past 100 years. LSWTs from 12 Austrian lakes were extracted from the yearbooks of the hydrographic service Austria (https://www.bmlfuw.gv.at/wasser/wasser-oesterreich/wasserkreislauf/hydrographische_daten/jahrbuecher.html), augmented by our own observations. All Austrian lakes included in this study had LSWT measurements from 1961 to 2010. Mondsee had LSWT measurements from 1909 to 2016 and Wörthersee had observations from 1910 to 2016. All Austrian lakes were sampled daily at a depth of ∼0.2 m. The samples were obtained from the lake level gauging station, and sampling was performed between 08:00 and 10:00 throughout the observational period. For lakes situated in Poland (6), LSWTs were measured at daily intervals at approximately 06:00 and a depth of ∼0.4 m. LSWTs used in this study were extracted from digitised historic daily records from the Institute of Meteorology and Water Management–National Research Institute, Poland. LSWTs in Lake Zurich were provided by the City of Zurich Water Supply and by the Amt für Abfall, Wasser, Energie, und Luft of the Canton of Zurich. LSWT was measured approximately monthly at the deepest point of the lake since 1936 at a depth of approximately 0.05–0.15 m until 2000 and approximately 0.1–0.3 m thereafter. LSWT was measured at approximately bi-monthly intervals in Lake Geneva at 09:00–11:30 from the middle of the lake at the deepest point since 1957. LSWT data from Lake Geneva was provided by the Commission International pour la Protection des Eaux du Leman (CIPEL).
Monthly averages for each lake with daily observational data were calculated as the average of all LSWTs measured for a given month. For lakes with bi-monthly or monthly measurements (Lakes Geneva and Zurich), we used linear interpolation to create a daily value for all dates between the beginning and end of the interpolation period (Sharma et al. 2015). Monthly averages for these lakes were then computed as the mean of all of LSWTs for a given month. The annual average for each lake was then calculated as the average of all monthly LSWTs for a given year. Throughout this manuscript, LSWTs are analysed as anomalies from the 1961 to 1991 average.
3.2 Surface air temperature
SAT observations were available from a number of sources and were collated for use in this study. All SAT data used were selected for periods that matched the available LSWT data. SAT observations from Poland were provided by the Institute of Meteorology and Water Management–National Research Institute in Poland and include observations from Chojnice (53.7°N, 17.6°E; Lake Charzykowskie), Suwalki (54.1°N, 22.9°E; Lake Hancza), Prabuty (53.8°N, 19.2°E; Lake Jeziorak), Gorzów Wielkopolski (52.7°N, 15.2°E; Lake Lubie), Mikolajki (53.8°N, 21.6°E; Lake Mikolajskie) and Zielona Góra (51.9°N, 15.5°E; Lake Slawskie). SAT observations in Austria include those measured at Klagenfurt airport (46.6°N, 14.3°E), data for which were available from the Historical Instrumental Climatological Surface Time Series Of The Greater Alpine Region (HISTALP) homogenised series (http://www.zamg.ac.at/histalp/dataset/station/csv.php). This data was used to represent SATs in Wörthersee and Ossiacher See, due to their relatively close proximity. SAT data for all other lakes included in this study were downloaded from the Goddard Institute for Space Studies (GISS) surface temperature analysis (GISTEMP) (GISTEMP Team 2016; Hansen et al. 2010) database (http://data.giss.nasa.gov/gistemp/). Stations were selected based on the minimum difference calculated between the lake centre coordinates and those of the meteorological stations. SATs from Salzburg airport (47.8°N, 13.0°E) were used to represent conditions in Attersee, Fuschlsee, Mondsee, Niedertrumer See, Wallersee and Wolfgangsee, and SATs from Sonnblick (47.1°N, 12.9°E) were used to represent conditions in Millstätter See, Weissensee and Zeller See. SATs for Neusiedler See were available from Graz airport (47.0°N, 15.4°E). For Lakes Geneva and Zurich, SATs were available from Geneva airport (46.2°N, 6.1°E) and Zurich Town (47.4°N, 8.6°E), respectively. Specific details of the individual lake data are provided in Table 1. To characterise trends in regional SAT, 122 meteorological stations from within a 300 km radius of any lake included in this study were also selected. These SAT observations were used to calculate the regional changes in SAT throughout the observational period.
3.3 Regime shift detection
Various methods have been implemented in biogeophysical sciences to detect regime shifts, the most common of which are designed to detect shifts in the mean. In this investigation, the sequential t test analysis of regime shifts (STARS) was used (Rodionov 2004). The STARS method is a parametric test to identify abrupt regime shifts and can be used to establish the difference between two subsequent regimes. Specifically, a shift occurs when a statistically significant difference exists between the mean value of a time series before and after a certain point, calculated via a t test analysis. In this investigation, LSWTs were tested using a threshold significance level of p = 0.05 and a Huber weight parameter of 1 (North et al. 2013; Magee et al. 2016).
3.4 Freshwater Lake model
To simulate LSWTs, we used the Freshwater Lake model, FLake (Mironov et al. 2010). FLake is a one-dimensional thermodynamic model developed for use as a lake parameterisation scheme in numerical weather prediction, climate modelling and other numerical prediction systems for environmental applications. For large-scale studies, FLake is an attractive lake model due to its computational efficiency and was used in this study to simulate the surface temperature of Central European lakes, as opposed to other models, due to lower computational cost. The meteorological variables required to drive FLake are SAT, U and V components of wind, surface solar and thermal radiation and specific humidity. A set of external parameters is also required to characterise the lakes to be simulated by FLake. These external parameters include fetch (m), latitude (°N), mean depth (m) and the light attenuation coefficient (Kd, m−1), which was estimated in this study as follows: Kd = 1.75/Secchi depth (Woolway et al. 2015).
3.4.1 Meteorological data
Meteorological forcing data used to drive FLake were from the European Centre for Medium-Range Weather Forecasts’ (ECMWF) twentieth Century reanalysis product (ERA-20C; European Centre for Medium-Range Weather Forecasts 2014) with each of the meteorological variables available at a spatial resolution of 1.125°. We selected data from the grid point situated closest to the lake centre coordinates. The meteorological forcing data were averaged to daily resolution. In addition to these surface meteorological data, we also analysed data for the surface geopotential and the temperature and geopotential height at 925 and 850 hPa levels (European Centre for Medium-Range Weather Forecasts 2014). The geopotential height was calculated as the geopotential (m2 s−2) divided by the gravitational constant (9.81 m s−2).
When the surface elevation, i.e. surface geopotential, of the ERA-20C data was not equivalent to the elevation of the lake, the SATs were corrected to over-lake values using appropriate lapse rates (Γ). The common method for correcting SAT to a specific elevation typically assumes a constant Γ of 5–6 °C km−1 (Hanna and Valdes 2001; Tabony 1985) or a Γ that varies seasonally as derived from published sources (Liston and Elder 2006). However, many studies have shown that fixed Γ may be problematic as they can vary substantially within short time periods (Rolland 2003), due to, among other things, synoptic circulations (Pagès and Miró 2010) and changing cloud cover (Minder et al. 2010). Therefore, in this study, we use an alternative method for determining site-specific Γ values. We followed the method of Gao et al. (2012), which calculates site-specific Γ by using model internal temperature profiles, i.e. temperatures at different pressure levels. Specifically, we calculated the difference between temperatures at 850 and 925 hPa and divided through the differences in the corresponding geopotential heights. These pressure levels were chosen following the suggestions of Gao et al. (2012) for locations under 1500 m a.s.l.
3.4.2 Initial conditions for FLake
The prognostic variables needed to initialise FLake include (i) mixed layer temperature, (ii) mixed layer depth, (iii) bottom temperature, (iv) mean temperature of the water column, (v) temperature at the ice upper surface and (vi) ice thickness. A straightforward solution would be to select physically reasonable fields and allow the model to run. However, FLake may be sensitive to initial conditions. Therefore, it is desirable to have a reasonably accurate representation of the lake conditions prior to running the model. In this study, we determined these initial conditions using a perpetual year solution (Kirillin et al. 2011). Specifically, initial conditions are determined by firstly running FLake with an arbitrary set of initial conditions for 1 year. The initial conditions, i.e. the prognostic variables, for the next year simulation are then specified using the lake model outputs from the end of the previous year. The procedure is repeated until the initial conditions are not altered from 1 year to the next. As we initialise FLake using a perpetual year solution, we ignore the first year of simulations in the regime shift detection approach. FLake was used to simulate LSWTs from 1960 (1961 after ignoring the first year, see above) to 2010, the years in which all lakes had available LSWT data.
3.5 Statistical methods
To evaluate FLake model performance, we used a number of statistical metrics. Specifically, we compared the annually averaged simulated and observed LSWTs using (i) mean absolute error (MAE); (ii) mean error (ME); (iii) root mean square error (RMSE); and (iv) the Nash Sutcliffe Efficiency index (NSE), which provides a normalised measure of model performance by evaluating the relative magnitude of the residual variance compared to the variance of the observations (Nash and Sutcliffe 1970).
4 Results
4.1 Rapid springtime warming of Central European lakes
On a month-by-month basis, all months for the 20 Central European lakes show warming from 1961 to 2010 and a clear seasonal pattern emerges with peak LSWT warming in late spring (Fig. 2a). In particular, May is the most rapidly warming month with temperature trends (0.62 °C decade−1) over 40% higher than the summer trends, on average. The average LSWT trend among all lakes is similar during spring (March to May; 0.47 °C decade−1) and summer (June to August; 0.46 °C decade−1). Conversely, in autumn, from September to November, LSWT trends (0.16 °C decade−1) are almost one-third of those calculated in spring and summer. Similar seasonal temperature trends are calculated for nearby SAT observations, which generally agree well with LSWT warming (Fig. 2b). In particular, averaged, i.e. among SAT stations situated near the lakes (n = 20), SAT trends peaked in May.
Comparisons of monthly averaged warming rates of surface air temperature (SAT) and lake surface water temperature (LSWT) in 20 Central European lakes from 1961 to 2010. a Grey lines illustrate the monthly LSWT warming rates for individual lakes and the black line shows the regional average warming rate for different months, with 95% confidence intervals. Different colours signify the seasons: winter (Dec, Jan, Feb; blue), spring (Mar, Apr, May; red), summer (Jun, Jul, Aug; orange) and autumn (Sep, Oct, Nov; light blue). b Points represent the relationship between LSWT and SAT warming rates for each month. Different colours signify different seasons, coloured similar to panel a. The black line demonstrates the least square fit to the monthly warming rates and the grey line is the 1:1 relationship. Error bars illustrate the 95% confidence intervals for the mean of the trends in each month for both SAT and LSWT
4.2 A century of lake temperature variability
For two Central European lakes with temperature observations spanning 107 years (1910–2016), we calculate substantial warming over the past century (Fig. 3). The majority of this warming has occurred in the last three decades. In particular, the annual averages, calculated from the monthly averaged data, demonstrate that LSWT warming accelerated during the last ∼30 years. While regression analysis of the annually averaged LSWT time series from Wörthersee and Mondsee yields a warming rate of 0.19 °C decade−1 and 0.18 °C decade−1, respectively, corresponding to an increase of about 2.03 and 1.93 °C over the 107 years, the actual warming (calculated as the difference between the 1910 to 1920 average compared to the 2006 to 2016 average) since 1910 is closer to 3.27 and 2.71 °C, respectively, due to the recent rapid increase in LSWT. The time series of LSWT anomalies demonstrate temperatures of up to 2 °C higher than the long-term average in 2016, observed in both lakes. Similar temperature anomalies are also observed at nearby Klagenfurt airport, being representative of SATs near Wörthersee. Specifically, we find that SAT anomalies in 2016 were 1.6 °C higher than the long-term average, but with similar long-term trends (0.16 °C decade−1). In addition, the regional average SAT (from 122 GISTEMP meteorological stations) in 2016 was over 2 °C higher than the long-term average.
In line with our previous findings of warming in all seasons, e.g. Fig. 2, we calculate a statistically significant increase in the annual minimum (0.24 °C decade−1; p < 0.001) and maximum (0.26 °C decade−1; p < 0.001) LSWT in Wörthersee over the past 107 years. Similar warming is observed in Mondsee, where we calculate a statistically significant increase in the annual minimum (0.13 °C decade−1; p < 0.001) and maximum (0.31 °C decade−1; p < 0.001) LSWT. Nearby monthly averaged SAT time series from Klagenfurt airport also displays an increase in the annual minimum (0.16 °C decade−1; p = 0.009) and maximum (0.18 °C decade−1; p < 0.001) temperature.
4.3 Macro-regional warming of air and water temperature in the 1980s
Each of the 20 studied lakes in Central Europe show a statistically significant rate of warming from 1961 to 2010 with a regional average warming rate of approximately 0.3 ± 0.05 °C decade−1 (p < 0.001). Similar warming rates were also calculated for the regional average SATs, i.e. from 122 GISTEMP stations, with a warming trend of 0.31 ± 0.06 °C decade−1. Despite the differences in morphometry and geographic setting, LSWTs fluctuated with a very high degree of coherence (R 2 = 0.97, p < 0.001 two-tail t test) across Central Europe, illustrating the influence of regional climate forcing.
The one-dimensional thermodynamic lake model FLake was used to simulate the surface temperature of 20 Central European lakes. FLake simulated LSWTs with success and reproduced the macro-regional scale patterns observed in the observational data. The performance of FLake in simulating LSWT is summarised via four metrics chosen in this study to evaluate model performance (see Sect. 3). In all cases, FLake provides satisfactory results with small values of RMSE, MAE and ME and high values of NSE using the annually averaged simulated and observed LSWT anomalies. Specifically, we calculate a mean, among all lakes, RMSE of 0.25 °C, MAE of 0.22 °C, ME of 0.07 °C and a NSE of 0.83 between observed and simulated annually averaged LSWT anomalies (Fig. 4).
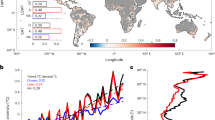
During the late 1980s, the time in which a noticeable increase in LSWT occurred, e.g. Fig. 3, Central Europe experienced a statistically significant shift in annually averaged SAT. Specifically, using a sequential t test analysis of regime shifts approach, we calculate a statistically significant step change in regionally averaged (n = 122) SAT centred on 1988 ± 3. In particular, the annual mean regional SAT in Central Europe underwent an abrupt increase of 1.0 °C, from prior to post 1988, dividing the period 1961–2010 into two regimes: regime I from 1961 to 1988 and regime II from 1989 to 2010. Similar shifts were calculated from individual meteorological station data situated throughout Central Europe (Fig. 5). Specifically, applying the same method to annually average SAT observations from meteorological stations in Poland, Austria and Switzerland, situated near each of the lakes, all demonstrated a statistically significant regime shift in the late 1980s and of similar magnitude to the regional average.
Statistically significant regime shifts in annually averaged surface temperature anomalies. Grey lines represent the annually averaged observed lake surface water temperature (LSWT) for each lake. Vertical lines signify regime shift years and horizontal lines demonstrate the longest period with a statistically significant result, both calculated from the observed LSWT. A white marker is used to show the modelled (FLake) step change year in LSWT for each lake, and a black marker is used to show the step change year calculated for nearby surface air temperature (SAT) observations
The abrupt increase in SAT in Central Europe was reflected in a corresponding abrupt increase in LSWT (Fig. 5). Analysis of the annual mean 20-lake time series confirmed the existence of an abrupt increase from Regime I to Regime II (centred on 1988 ± 2) with a magnitude of 0.97 °C, which ranged from a minimum of 0.54 °C in Wallersee to a maximum of 1.46 °C in Weissensee. In addition, 18 of the 20 lakes (not NiedertrumerSee and Attersee) experienced a post-1980 warming trend that exceeded the warming rate calculated prior to the 1980s.
Using the simulated LSWTs from FLake, we calculate a similar step change year to that estimated from the observed LSWT and SAT data (Fig. 5). In particular, FLake simulated a step change year in 1988 ± 1 closely matching those of the observational records. Analysis of the annual mean 20-lake simulated temperatures demonstrates a magnitude of warming in the region of 1.04 °C between the regimes, i.e. regime I to regime II, as described above.
5 Discussion
Based on long-term in situ LSWT data from 20 Central European lakes, we found a large-scale increase in LSWT during the past 50 to ∼100 years, consistent with other locations globally (Austin and Colman 2008; Magee et al. 2016). On a month-by-month basis, we found all seasons to display a warming trend, with potential consequences for a range of physical, chemical and biological processes in lakes. In 20 Central European lakes, spring was found to be the most rapidly warming season, consistent with previous findings (Schmid and Köster 2016). This is opposite to reports from other regions from around the world. For example, in Lake Superior, North America, LSWTs have been warming most rapidly in summer (Austin and Colman 2008). Also, in Britain and Ireland, lakes have been found to be warming most in winter (Woolway et al. 2016). In recent years, there has been a strong focus on investigating summer LSWT trends (Schneider and Hook 2010; O’Reilly et al. 2015; Torbick et al. 2016), with only a few investigations focussing on other seasons (Dokulil 2013; Schmid and Köster 2016; Woolway et al. 2016). While summer average LSWT measurements have undoubtedly been pivotal in our understanding and for evaluating the direction of warming globally, the existence of seasonal variations in LSWT warming rates raises the question of how representative are the prevailing quantitative understanding and causal attribution of LSWT warming at a global scale. A detailed understanding of the main drivers of LSWT warming among lakes should focus on all seasons.
While annually averaged LSWTs have experienced a statistically significant increase since the early 1960s, the majority of this warming has occurred in the last three decades, i.e. since the 1980s, a feature that was also reported by Austin and Colman (2008) for Lake Superior. Similar to Austin and Colman (2008), who investigated a ∼100-year time series of LSWT just downstream of Lake Superior, we also found similar increases in Lakes Mondsee and Wörthersee, which increased largely in line with SAT during the past ∼100 years. A similar warming rate of LSWT and SAT contradicts studies of lake surface heat budgets, which suggest that long-term rates of temperature change should be lower for water than air (Schmid et al. 2014). In particular, LSWTs are expected to increase at approximately 80% of SAT. Thus, at the macro-regional scale studied here, LSWTs are warming faster than expected from SAT trends alone. Similar patterns have also been observed in other regions globally, and in some lakes, LSWTs are warming faster than SAT (O’Reilly et al. 2015). Several causes could explain the differential in warming, including changes to internal lake processes such as the timing of lake stratification (Austin and Colman 2007) and in response to changes in large-scale climatic forcing such as solar radiation (Fink et al. 2014; Schmid and Köster 2016). Specifically, Schmid and Köster (2016) demonstrated that 60% of LSWT warming in Lower Lake Zurich was caused by SAT, and 40% by increased solar radiation.
At the global scale, ice-covered lakes have been described as warming the most rapidly (O’Reilly et al. 2015) where a decline in winter ice cover has been reported to result in an earlier onset of thermal stratification and, thus, increasing the period over which the lake warms. However, other studies have demonstrated that ice cover is not a prerequisite for rapid LSWT warming (Schneider et al. 2009; Schmid and Köster 2016), and modelling studies have shown no direct influence on summer LSWTs of the preceding winter ice cover (Zhong et al. 2016). In addition, recent studies have highlighted that excess LSWT warming may not solely be a result of an increase in the length of the warming period, but also important is the strength of stratification during the spring transition (Piccolroaz et al. 2015). Milder winter conditions together with increased SAT and solar radiation in spring, resulting in increased heat absorption by surface waters, is believed to be one of the main driving mechanisms of excess LSWT warming.
Our results demonstrate a coherent increase in LSWT during the late 1980s, captured by both in situ and modelled data and consistent with that observed by nearby and regionally averaged SAT measurements. In this study, we therefore demonstrate that lakes not only respond coherently to one another, as has been shown in previous studies (Magnuson et al. 1990; Livingstone et al. 2010), but can also respond coherently to step changes in external forcing. Moreover, our study shows that abrupt changes in large-scale climatic forcing can result in similarly abrupt regime shifts in LSWT and that a one-dimensional lake hydrodynamic model forced with climate reanalysis data can predict these changes. Specifically, we found that LSWTs simulated by climate reanalysis data was sufficient to capture the influence of the 1980s regime shift on LSWT in Central Europe, despite the exclusion of other processes known to influence LSWT, such as changing water clarity which can either amplify or suppress LSWT (Rose et al. 2016), and inflows which can be an important factor at high elevation, as melt water from glaciers could reduce warming trends of downstream lakes (Zhang et al. 2014). Similarly, local meteorological forcing data are not available for many lakes; therefore, it is encouraging that reanalysis data can be used to accurately predict LSWT changes. Some lakes in this study did not respond as expected to the CRS, e.g. Hancza (Fig. 5), suggesting that other processes play an important role in some lakes. However, given the usefulness of a hydrodynamic model for simulating regime shifts in LSWT at the macro-regional scale, future studies should aim to use such models to investigate further the influence of abrupt changes and aim to predict when future abrupt shifts will occur.
The close agreement between the timing of an abrupt shift in SAT and LSWT in 20 Central European lakes suggests that LSWT models which use SAT as a sole predictor may be suitable to estimate future abrupt shifts. The advantage of using a model that simulates LSWT from SAT alone is that future SAT projections based on general circulation models or regional climate models are commonly more reliable than those of other meteorological variables (Gleckler et al. 2008), and downscaling is typically associated with smaller uncertainties (Dettinger 2013). A number of regressive/statistical LSWT models (McCombie 1959; Webb 1974; Sharma et al. 2008) as well as a more sophisticated hybrid model (Piccolroaz et al. 2013; Toffolon et al. 2014; Piccolroaz et al. 2016) now exist. Given the usefulness of models for simulating gradual and abrupt shifts in LSWT, there are good prospects for better determinations of LSWT response to future gradual and abrupt climate change.
The impact of abrupt climatic shifts on aquatic ecosystems will likely differ from the impact of more gradual change. This has major implications for the ecosystem and requires a non-linear dynamic approach for evaluating long-term trends in lakes. Understanding, predicting and quantifying the thermal response of lakes to abrupt and gradual climate change are critical for future decision-making involving water resource management policies and to understand how ecosystems will respond in the future. If drastic changes in ecosystem functionality are to be avoided, aquatic ecosystems may have to adapt to not only gradual changes in water temperature as climate change progresses, but also to abrupt shifts.
References
Adrian R et al (2009) Lakes as sentinels of climate change. Limnol Oceanogr 54(6):2283–2297. doi:10.4319/lo.2009.54.6_part_2.2283
Austin JA, Colman SM (2007) Lake Superior summer water temperatures are increasing more rapidly than regional air temperatures: a positive ice-albedo feedback. Geophys Res Lett 34. doi:10.1029/2006GL029021
Austin JA, Colman SM (2008) A century of temperature variability in Lake Superior. Limnol Oceanogr 53:2724–2730. doi:10.4319/lo.2008.53.6.2724
Dettinger MD (2013) Projections and downscaling of 21st century temperatures, precipitation, radiative fluxes and winds for the southwestern US, with focus on Lake Tahoe. Clim Chang 116:17–33. doi:10.1007/s10584-012-0501-x
Dokulil MT (2013) Impact of climate warming on European inland waters. Inland Waters 4:27–40. doi:10.5268/IW-4.1.705
European Centre for Medium-Range Weather Forecasts (2014) ERA-20C Project (ECMWF Atmospheric Reanalysis of the 20th Century). Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory, Boulder, Colo. (Updated daily.) Accessed 25 Mar 2016. doi: 10.5065/D6VQ30QG
Figura S, Livingstone DM, Hoehn E, Kipfer R (2011) Regime shift in groundwater temperature triggered by the Arctic oscillation. Geophys Res Lett:38. doi:10.1029/2011GL049749
Fink G, Schmid M, Wahl B, Wolf T, Wüest A (2014) Heat flux modifications related to climate-induced warming of large European lakes. Water Resour Res 50:2072–2085. doi:10.1002/2013WR014448
Flaim G, Obertegger U, Anesi A, Guella G (2014) Temperature induced changes in lipid biomarkers and mycosporine-like amino acids in the psychrophilic dinoflagellate Peridinium aciculiferum. Freshw Biol 59:985–997. doi:10.1111/fwb.12321
Gao L, Bernhardt M, Schulz K (2012) Elevation correction of ERA-interim temperature data in complex terrain. Hydrol Earth Syst Sci 16:4661–4673. doi:10.5194/hess-16-4661-2012
GISTEMP Team (2016) GISS Surface Temperature Analysis (GISTEMP). NASA Goddard Institute for Space Studies. Dataset accessed 2016–02-25 at http://data.giss.nasa.gov/gistemp/
Gleckler PJ, Taylor KE, Doutriaux C (2008) Performance metrics for climate models. J Geophys Res 113:D06104. doi:10.1029/2007JD008972
Gronewold AD, Stow CA (2014) Water loss from the Great Lakes. Science 343(6175):1084–1085. doi:10.1126/science.1249978
Hanna E, Valdes P (2001) Validation of ECMWF (re)analysis surface climate data, 1979–1998, for Greenland and implications for mass balance modelling of the ice sheet. Int J Climatol 21:171–195. doi:10.1002/joc.609
Hansen J, Ruedy R, Sato M, Lo K (2010) Global surface temperature change. Rev Geophys 48:RG4004. doi:10.1029/2010RG000345
Huisman J, Matthijs HCP, Visser PM (2005) Harmful cyanobacteria. Springer, Berlin
Kirillin G et al (2011) FLake-global: online lake model with worldwide coverage. Environ Model Softw 26:683–684. doi:10.1016/j.envsoft.2010.12.004
Kosten S et al (2012) Warmer climates boost cyanobacterial dominance in shallow lakes. Glob Change Biol 18:118–126. doi:10.1111/j.1365-2486.2011.02488.x
Liston GE, Elder K (2006) A meteorological distribution system for high-resolution terrestrial modeling (MicroMet). J Hydrometeorol 7:217–234. doi:10.1175/JHM486.1
Livingstone DM, Adrian R, Arvola L, et al (2010) Regional and supra-regional coherence in limnological variables. In: George DG (ed) The impact of climate change on European lakes, Aquatic ecology series, vol 4. Springer, Dordrecht, pp 311–337. doi:10.1007/978-90-481-2945-4_17
Magee MR, Wu CH, Robertson DM, Lathrop RC, Hamilton DP (2016) Trends and abrupt changes in 104 years of ice cover and water temperature in a dimictic lake in response to air temperature, wind speed, and water clarity drivers. Hydrol Earth Syst Sci 20:1681–1702. doi:10.5194/hess-20-1681-2016
Magnuson JJ, Benson BJ, Kratz TK (1990) Temporal coherence in the limnology of a suite of lakes in Wisconsin, USA. Freshw Biol 23:145–149. doi:10.1111/j.1365-2427.1990.tb00259.x
McCombie AM (1959) Some relations between air temperatures and the surface water temperatures of lakes. Limnol Oceanogr 4:252–258. doi:10.4319/lo.1959.4.3.0252
Minder JR, Mote PW, Lundquist JD (2010) Surface temperature lapse rates over complex terrain: lessons from the Cascade Mountains. J Geophys Res-Atmos 115:D14122. doi:10.1029/2009jd013493
Mironov D et al (2010) Implementation of the lake parameterisation scheme FLake into the numerical weather prediction model COSMO. Boreal Environ Res 15:218–230
Nash JE, Sutcliffe JV (1970) River flow forecasting through conceptual models part I - a discussion of principles. J Hydrol 10:282–290. doi:10.1016/0022-1694(70)90255-6
North RP, Livingstone DM, Hari RE, Köster O, Niederhauser P, Kipfer R (2013) The physical impact of the late 1980s climate regime shift on Swiss rivers and lakes. Inland Waters 3:341–350. doi:10.5268/IW-3.3.560
O’Reilly C et al (2015) Rapid and highly variable warming of lake surface waters around the globe. Geophys Res Lett 42:10773–10781. doi:10.1002/2015GL066235
Pagès M, Miró JR (2010) Determining temperature lapse rates over mountain slopes using vertically weighted regression: a case study from the Pyrenees. Meteorol Appl 17:53–63. doi:10.1002/met.160
Piccolroaz S, Toffolon M, Majone B (2013) A simple lumped model to convert air temperature into surface water temperature in lakes. Hydrol Earth Syst Sci 17:3323–3338. doi:10.5194/hess-17-3323-2013
Piccolroaz S, Toffolon M, Majone B (2015) The role of stratification on lakes’ thermal response: the case of Lake Superior. Water Resour Res 51:7878–7894. doi:10.1002/2014WR016555
Piccolroaz S, Calamita E, Majone B, Gallice A, Siviglia A, Toffolon M (2016) Prediction of river water temperature: a comparison between a new family of hybrid models and statistical approaches. Hydrol Process 30(21):3901–3917. doi:10.1002/hyp.10913
Reid PC et al (2016) Global impacts of the 1980s regime shift. Glob Change Biol 22(2):682–703. doi:10.1111/gcb.13106
Rodionov SN (2004) A sequential algorithm for testing climate regime shifts. Geophys Res Lett 31:L09204. doi:10.1029/2004GL019448
Rolland C (2003) Spatial and seasonal variations of air temperature lapse rates in alpine regions. J Clim 16:1032–1046. doi:10.1175/1520-0442(2003)016<1032:SASVOA>2.0.CO;2
Rose KC, Winslow LA, Read JS, Hansen GJA (2016) Climate-induced warming of lakes can be either amplified or suppressed by trends in water clarity. Limnol Oceanogr Lett 1:44–53. doi:10.1002/lol2.10027
Scheffer M, Carpenter S, Foley JA, Folke C, Walker B (2001) Catastrophic shifts in ecosystems. Nature 413:591–596. doi:10.1038/35098000
Schmid M, Köster O (2016) Excess warming of a Central European lake by solar brightening. Water Resour Res 52:8103–8116. doi:10.1002/2016WR018651
Schmid M, Hunziker S, Wüest A (2014) Lake surface temperatures in a changing climate: a global sensitivity analysis. Clim Chang 124:301–315. doi:10.1007/s10584-014-1087-2
Schneider P, Hook SJ (2010) Space observations of inland water bodies show rapid surface warming since 1985. Geophys Res Lett 37:L22405. doi:10.1029/2010GL045059
Schneider P et al (2009) Satellite observations indicate rapid warming trend for lakes in California and Nevada. Geophys Res Lett 36:L22402. doi:10.1029/2009GL040846
Sharma S, Walker SC, Jackson DA (2008) Empirical modelling of lake water-temperature relationships: a comparison of approaches. Freshw Biol 53:897–911. doi:10.1111/j.1365-2427.2008.01943.x
Sharma S et al (2015) A global database of lake surface temperatures collected by in situ and satellite methods from 1985-2009. Sci Data 2. doi:10.1038/sdata.2015.8
Tabony RC (1985) The variation of surface-temperature with altitude. Meteorol Mag 114:37–48
Toffolon M et al (2014) Prediction of surface temperature in lakes with different morphology using air temperature. Limnol Oceanogr 59:2185–2202. doi:10.4319/lo.2014.59.6.2185
Torbick N, Ziniti B, Wu S, Linder E (2016) Spatiotemporal lake skin summer temperature trends in the northeast United States. Earth Interact 20:1–21. doi:10.1175/EI-D-16-0015.1
Van Cleave K, Lenters JD, Wang J, Verhamme EM (2014) A regime shift in Lake Superior ice cover, evaporation, and water temperature following the warm el Niño winter of 1997–1998. Limnol Oceanogr 59:1889–1898. doi:10.4319/lo.2014.59.6.1889
Velthuis M et al (2017) Warming advances top-down control and reduces producer biomass in a freshwater plankton community. Ecosphere 8(1):e01651. doi:10.1002/ecs2.1651
Vörösmarty CJ, Green P, Salisbury J, Lammers RB (2000) Global water resources: vulnerability from climate change and population growth. Science 289(5477):284–288. doi:10.1126/science.289.5477.284
Webb MS (1974) Surface temperatures of Lake Erie. Water Resour Res 10:199–210. doi:10.1029/WR010i002p00199
Woolway RI, Jones ID, Feuchtmayr H, Maberly SC (2015) A comparison of the diel variability in epilimnetic temperature for five lakes in the English Lake District. Inland Waters 5:139–154. doi:10.5268/IW-5.2.748
Woolway RI et al (2016) Lake surface temperatures [in “state of the climate in 2015”]. Bull Amer Meteor Soc 97(8):S17–S18
Xiao D, Li L, Zhao P (2012) Four-dimensional structures and physical process of the decadal abrupt changes of the northern extratropical ocean–atmosphere system in the 1980s. Int J Climatol 32:983–994. doi:10.1002/joc.2326
Yasunaka S, Hanawa K (2003) Regime shifts in the northern hemisphere SST field: revisited in relation to tropical variations. J Meteor Soc Japan 81:415–424. doi:10.2151/jmsj.81.415
Zhang G, Yao T, Xie H, Qin J, Ye Q, Dai Y, Guo R (2014) Estimating surface temperature changes of lakes in the Tibetan plateau using MODIS LST data. J Geophys Res Atmos 119:8552–8567. doi:10.1002/2014JD021615
Zhong Y, Notaro M, Vavrus SJ, Foster MJ (2016) Recent accelerated warming of the Laurentian Great Lakes: physical drivers. Limnol Oceanogr 61:1762–1786. doi:10.1002/lno.10331
Acknowledgements
RIW was funded by EUSTACE (EU Surface Temperature for All Corners of Earth) which received funding from the European Union’s Horizon 2020 Programme for Research and Innovation, under Grant Agreement no 640171. We would like to thank the numerous individuals who participated in many decades of measuring lake temperatures in each of the lakes included in this investigation. We thank Dr. Sebastiano Piccolroaz and an anonymous reviewer who provided a constructive review of a draft version of this work. Lake Geneva temperature data were provided by the Commission International pour la Protection des Eaux du Leman (CIPEL) and the Information System of the SOERE OLA (http://si-ola.inra.fr), INRA Thonon-les-Bains.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Woolway, R.I., Dokulil, M.T., Marszelewski, W. et al. Warming of Central European lakes and their response to the 1980s climate regime shift. Climatic Change 142, 505–520 (2017). https://doi.org/10.1007/s10584-017-1966-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-017-1966-4