Abstract
Many boreal waters are currently becoming browner with effects on biodiversity, fish production, biogeochemical processes and drinking water quality. The question arises whether and at which speed this browning will continue under future climate change. To answer the question we predicted the absorbance (a420) in 6347 lakes and streams of the boreal region under future climate change. For the prediction we modified a numerical model for a420 spatial variation which we tested on a temporal scale by simulating a420 inter-annual variation in 48 out of the 6347 Swedish waters. We observed that inter-annual a420 variation is strongly driven by precipitation that controls the water flushing through the landscape. Using the predicted worst case climate scenario for Sweden until 2030, i.e., a 32 % precipitation increase, and assuming a 10 % increase in imports of colored substances into headwaters but no change in land-cover, we predict that a420 in the 6347 lakes and streams will, in the worst case, increase by factors between 1.1 and 7.6 with a median of 1.3. This increase implies that a420 will rise from the present 0.1–86 m−1 (median: 7.3 m−1) in the 6347 waters to 0.1–154 m−1 (median: 10.1 m−1), which can cause problems for the preparation of drinking water in a variety of waters. Our model approach clearly demonstrates that a homogenous precipitation increase results in very heterogeneous a420 changes, where lakes with a long-term mean landscape water retention time between 1 and 3 years are particularly vulnerable to climate change induced browning. Since these lake types are quite often used as drinking water resources, preparedness is needed for such waters.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Clean water is a precious resource, and many expensive efforts are made globally to protect or create this commodity, in particular for drinking water (Richardson 2007). While particles can easily be removed from the water column by various filtration techniques, the removal of dissolved colored substances, commonly referred to as chromophoric dissolved organic matter, is far more complex and expensive (Eikebrokk et al. 2004; Volk et al. 2002). Chromophoric dissolved organic matter is usually dominated by brown-colored humic substances from terrestrial ecosystems (Thurman 1985), and frequently measured as absorbance of filtered water at a given wavelength, for example, 420 nm (a420) (Kirk 2003). In Swedish boreal surface waters, a420 is among the water chemical variables that showed fastest change during the past decades, implying that waters appear increasingly brownish (Weyhenmeyer 2008). Accelerated browning of freshwaters has been reported from most northern European countries as well as North America (reviewed by Monteith et al. 2007). Browning has frequently been associated with increasing concentrations of dissolved organic carbon (DOC) (Roulet and Moore 2006), and more recently also with increasing concentrations of iron (Kritzberg and Ekström 2012). For water quality managers, politicians and society there is now an urgent need to know in how far browning of freshwaters might continue in the near future, and if the browning process is equally fast in the millions of lakes and streams of the boreal region. To fill this knowledge gap, a water color model that can be applied to a large variety of inland waters is needed.
At present only rather few water color models are available of which none has been used to predict the future water color in freshwaters across a large geographical region. Many more models are available for the prediction of DOC. Considering the close relationship between DOC and a420 in waters (Pace and Cole 2002), DOC models might be applicable for the prediction of water color, provided that they are modified to account for the preferential loss of color to carbon during transport through the landscape (Molot and Dillon 1997). On the spatial scale, DOC has been found to be mainly influenced by land-cover, in particular the percentage of wetland and open water in the catchment and the type of vegetation (e.g., Canham et al. 2004; Kortelainen 1993; Larsen et al. 2011; Sobek et al. 2007; Xenopoulos et al. 2003). On the temporal scale, DOC variation has been attributed to variation in hydrology (Erlandsson et al. 2008), air temperature (Winterdahl et al. 2014) and the recovery from acid deposition (Evans et al. 2006; Monteith et al. 2007). From the numerous DOC studies it becomes clear that main drivers of DOC, and thereby most likely also of a420, are not necessarily coherent between the spatial and temporal scale. This is problematic when predictions for thousands of waters across a large geographical region need to be made, which is often requested by managers and politicians. In an ideal world, models that have been calibrated and validated on a temporal scale should be used for predictions but such models are not available for the majority of waters. If we want to know the fate of browning of freshwaters across a large geographical region we need to rely on spatial models that are transferable to the temporal scale. Such models are not yet available for a420. Our intention was therefore to test whether an existing numerical model for spatial a420 variation is transferable to the temporal scale. The existing a420 model accounts for the rapid a420 loss during transport through the landscape (Müller et al. 2013). We extended the model and predicted a420 spatial variation across 6347 Swedish boreal lakes and streams. As a next step we tested the model on the temporal scale by simulating a420 inter-annual variation in 48 out of the 6347 waters from 1988 to 2012. As a final step, we predicted a420 for the 6347 lakes and streams under future climate change. To simulate the maximum possible climate change induced change of a420 in Swedish inland waters which is important to know for managers and politicians we used the predicted worst case climate scenario for Sweden until 2030.
2 Methods
2.1 Lake and stream data
From the Swedish national freshwater inventory program we had water chemical and catchment data from 6035 lakes and 312 streams that are evenly distributed over Sweden (Fig. S1 in supplementary). All data can freely be downloaded at http://webstar.vatten.slu.se/db.html. The 6347 lakes and streams represent inland waters of the boreal and hemiboreal region. The lakes were small (median lake area: 0.4 km2) and shallow (median mean lake depth: 3.9 m). Both lakes and streams were generally nutrient-poor (median total phosphorus concentrations: 10 μg L−1) and humic (median total organic carbon concentrations: 9.1 mg L−1; median pH: 6.5). In this study, we used the absorbance of filtered (0.45 μm filter) water at 420 nm in a 5 cm cuvette as a measure of the color of water, which we further transferred to the Napierian absorption coefficient (a420) as recommended by Hu et al. (2002) (see supplementary). In addition, we used sulfate concentrations (SO4-S) in inland waters as a proxy for the influence of acid deposition. All samples were collected at a water depth of 0.5 m and analyzed by the certified water analyses laboratory at the Swedish University of Agricultural Sciences according to standard limnological methods during the past 40 years. A detailed method description including analytical precision and range is available at http://www.slu.se/en/departments/aquatic-sciences-assessment/laboratories/geochemical-laboratory/water-chemical-analyses/.
For the assessment of a420 spatial variation across the 6347 waters we used site-specific long-term median values during autumn when the water column is mixed (for a detailed description of sampling design and data selection see supplementary). Out of the 6347 waters we had 24 small boreal lakes and 24 small boreal streams with complete monthly time series (for lakes during the ice-free season May to October) during 1988 to 2012 (for location of the 48 waters see Fig. S1 in supplementary). The 48 waters were used to assess inter-annual a420 variation. Land-cover in the catchments of the 48 waters has not substantially changed during the time period 1988 to 2012.
2.2 Catchment and meteorological data
For each of the 6347 inland waters we had GIS-derived data on a variety of catchment variables (resolution: 100 m × 100 m; Table 1). For lakes, we also had data on mean depth and surface area. Using GIS we overlapped the lake and stream database with the database on meteorological variables from the Swedish Meteorological and Hydrological Institute at http://www.smhi.se and downloaded site-specific (i.e., interpolated data at the sampling point) long-term means of annual precipitation (P1961–1990), annual surface water runoff (R1961–1990), annual mean air temperature (MAT1961–1990), growing degree days (GDD1961–1990) and annual global radiation (RAD1961–1990) (for detailed description and units see Table 1). For the 48 waters with monthly data we also downloaded site-specific MAT and site-specific annual precipitation (P) during 1988 to 2012 from http://www.smhi.se according to the procedure described above. In addition, we downloaded annual mean precipitation for the whole of Sweden during 1988 to 2012, as well as the predicted worst case climate scenario for Sweden until 2030 (for a detailed description of the determination of Sweden’s climate scenarios see supplementary).
2.3 Modeling approach
2.3.1 Statistical evaluation of a420 variation
All statistical tests, including common statistical measures such as mean, median, and simple linear regressions as well as non-parametric tests, were run in JMP, version 11.0.0. A variety of variables were not normally distributed, tested by applying a Shapiro-Wilk test. We therefore used statistical tests that are insensitive to deviations from normality. These tests were: A) non-parametric Wilcoxon-test for group comparisons, B) non-parametric Kendall’s tau test for correlations between variables, C) partial least squares regression models (PLS) for the predictions of a420, and D) non-parametric Mann-Kendall trend tests to analyze changes over time. For the Mann-Kendall test we used annual mean values. From the test results we calculated changes over time in percentage by dividing the Theil slope by median values of 1988 to 2012 (for more detailed information on the statistical tests we refer to the supplementary).
2.3.2 Model for a420 spatial variation
Spatial variation in a420 has previously been modeled with the following approach (Müller et al. 2013):
where a420 corresponds to a420 at a sampling site (in m−1), a420,headwater is a420 in the headwaters of the site (in m−1), λ is the a420 decay rate in the landscape (in days−1) and WRT1961–1990 is the site-specific long-term mean (1961–1990) landscape water retention time by lakes upstream of the site (in days). We estimated WRT1961–1990 using GIS-derived climate and catchment data (see supplementary) and received the following model for a420 spatial variation:
(for abbreviations and variable/parameter explanations including units see Table 1). We used Eq. 2 to simulate a420 spatial variation across the 6347 waters. Since a420,headwater was not available for all sites we developed a a420,headwater model with available a420 data from headwaters. Out of the 6347 freshwaters we classified 291 waters as headwaters (249 lakes and 42 streams). We defined headwaters as waters that had zero percentage of upstream lake surface area in the catchment area. This classification implies that some higher-order streams are included in the category of headwaters. For the a420,headwater model we first identified major climate and catchment drivers for a420 variation in headwaters using PLS. We then developed an a420,headwater model with the main drivers as input variables and used it to predict a420,headwater for the 6347 sites. As a final step we modeled a420 spatial variation across the 6347 Swedish waters with Eq. 2 where the overall a420 decay rate in the landscape corresponded to 0.001 day−1 and Lakedepthmean to 4 m (for a detailed description how the parameter values were derived we refer to the supplementary).
2.3.3 Model transfer to the temporal scale
Since our final goal was to predict a420 in the 6347 lakes and streams under future climate change we needed to test whether the a420 spatial model is suitable for predictions on a temporal scale. We therefore transferred the a420 spatial model (Eq. 2) to the temporal scale according to:
(for abbreviations and variable/parameter explanations including units see Table 1). We tested the a420 model (Eq. 3) by simulating inter-annual a420 variation in 48 out of the 6347 waters from which we had data from 1988 to 2012. Because a420,headwater(t) was not available for the 48 waters we predicted a420,headwater(t) with the spatial a420,headwater model where we accounted for inter-annual variation in a420,headwater by using inter-annual variations of the main driving variables (see supplementary). To apply Eq. 3 to our 48 waters we also needed an estimate for site-specific inter-annual variation in R. For the estimation we multiplied site-specific R1961–1990 with the site-specific annual precipitation deviation from P1961–1990. This approach assumes that changes in runoff are directly related to precipitation changes in a 1:1 relationship. Such an assumption results in maximum runoff changes which we consider being acceptable as a worst case scenario. It is the most suitable assumption for our modeling purpose taking into account the large variation in precipitation-runoff relationships over time and space.
2.3.4 Model sensitivity analyses
To demonstrate the sensitivity of the a420 model (Eq. 3) to variations in input variables and parameters, i.e., to variations in headwater conditions, a420 decay rate, runoff and water flushing through the landscape, we performed model sensitivity analyses where we 1) increased a420,headwater by 50 %, 2) increased R by 50 % which in our model is equivalent to a 50 % decrease in the a420 decay rate in the landscape, and 3) decreased Lakedepthmean by 50 %, which reflects a runoff induced accelerated water flushing through the landscape.
3 Results
3.1 Spatial variation in a420: observation and modeling
The site-specific long-term median a420 of 6347 inland waters (6035 lakes and 312 streams) varied between 0.01 and 86 m−1 with a median of 7.2 m−1. Across the 291 headwaters (249 lakes and 42 streams out of the 6347 waters) the site-specific long-term median a420 ranged between 0.1 and 57 m−1, with no significant difference in a420,headwater between headwater streams and headwater lakes (non-parametric Wilcoxon test: P > 0.05). We found that a420,headwater spatial variation was best explained by variation in MAT1961–1990 when we used a PLS model with 16 catchment and climate variables as input variables (Table S1 in supplementary). SO4-S concentrations in the water were not important for the model performance (Table S1 in supplementary). MAT1961–1990 was highly significantly related to GDD1961–1990, RAD1961–1990 and variables describing the land-cover in the catchment of the headwaters, i.e., percentage of agricultural land, pasture, coniferous forest, deciduous forest, mixed forest, open wetland, and land without vegetation including urban land-cover (non-parametric Kendall’s tau test: P < 0.0001).
The relationship between MAT1961–1990 and a420,headwater spatial variation was hump-shaped with maximum a420,headwater at MAT1961–1990 between 4 and 6 °C (Fig. 1). Using MAT1961–1990 as input variable for a simple Gaussian Peak Shape model (eq. S3 in supplementary) we were able to predict 57 % (P < 0.0001) of a420,headwater variation across 291 headwaters. Comparing the predicted and empirical values, we received a slope of 1.03 and an insignificant intercept (P > 0.05). The residuals of the comparison between predicted and observed a420,headwater values were largest in the smallest catchments located in warmer geographical regions. Using the a420,headwater model (eq. S3 in supplementary) to predict a420,headwater for all 6347 sites we could, with Eq. 2, explain 54 % of the a420 variation across the 6347 waters (Fig. 2a). Comparing the predicted and empirical values of a420 in the 6347 waters, we received a slope of 1.01 and an insignificant intercept (P > 0.05).
Absorbance of filtered water at 420 nm (a420) in 291 Swedish headwaters (42 streams and 249 lakes) along a site-specific long-term mean (1961–1990) annual mean air temperature gradient (MAT1961–1990). Each dot represents a site-specific long-term median a420 autumn value. Shown are box plots for each degree MAT1961–1990. The curve represents predicted a420 values for each degree MAT1961–1990 according to Eq. S3 (see supplementary)
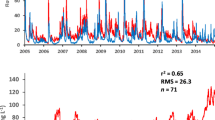
Relationship between predicted and observed absorbance of filtered water at 420 nm (a420). Panel a shows the prediction on a spatial scale (long-term median autumn values) for 6347 lakes and streams using Eq. 2 (see text) and panel b shows the prediction on a temporal scale (inter-annual variation, based on annual means) for 24 lakes and 24 streams during 1988 to 2012 using Eq. 3 (see text)
3.2 Inter-annual variation in a420: observation and modeling
Analyses of the data from the 48 waters (24 lakes and 24 streams) showed that the annual mean of a420 in the lakes and streams had changed between −43 and 139 % with a median of 50 % over the time period 1988 to 2012. Thus, during the past 25 years Swedish freshwaters have on average experienced an a420 increase by a factor of 1.5. During the same time period mean annual precipitation across Sweden has increased by 14 % from 650 to 740 mm yr−1. In 32 of the 48 waters the increase in a420 during 1988 to 2012 was significant (non-parametric Mann-Kendall-test: P < 0.05). The strongest a420 trend occurred in a small boreal lake. The a420 trends were significantly higher in lakes compared to streams (non-parametric Wilcoxon-test: P < 0.01). Changes over time in a420 (in % yr−1) were significantly increased with increasing site-specific landscape WRT1961–1990 (R 2 = 0.35, P < 0.05, n = 48).
When we simulated the observed inter-annual a420 variation in the 24 lakes and 24 streams with Eq. 3 where a420,headwater(t) was modeled using site-specific inter-annual variations in MAT (eq. S4 in supplementary) we received a poor model performance: R 2 = 0.10, P < 0.0001, n = 1200, slope 0.56, intercept: P < 0.01. The model performance became better when we ignored inter-annual variation in MAT and kept MAT1961–1990 from the spatial scale: R 2 = 0.36, P < 0.0001, n = 1200. However, the slope of the relationship between predicted and empirical a420 still deviated substantially from 1.0 (i.e., the slope corresponded to 0.89) and the intercept was still significant. To receive a regression slope close to 1.0 and an insignificant intercept we needed to recalibrate the model. In the recalibration process, a420,headwater was reduced to half and Lakedepthmean was reduced from 4 to 3 m. With the recalibrated model we were able to predict 39 % of the a420 variation in the 48 waters (24 lakes and 24 streams) during 1988 to 2012 (P < 0.0001, n = 1200, slope 1.02, intercept: P > 0.05; Fig. 2b). Analyzing inter-annual variation for each of the 24 lakes and 24 streams individually, using the same a420 decay rate in the landscape and Lakedepthmean for all waters we found significant relationships (P < 0.05) between predicted and observed a420 values in 35 waters with highly varying R 2 values.
3.3 Model sensitivity and future a420 development
The a420 model (Eq. 3) was most sensitive to variations in the water flushing through the landscape, i.e., Lakedepthmean. When we reduced Lakedepthmean by 50 % we received a420 changes in the 6347 inland waters by factors between 1.0 and 3.6 with a median of 1.1. Similar effects but less pronounced were found when we increased R by 50 %; here a420 changed by factors between 1.0 and 2.4 with a median of 1.1. The a420 response to changes in Lakedepthmean and R became increasingly pronounced along the WRT1961–1990 gradient (Fig. 3b and c). This is in contrast to the a420 response to changes in headwater conditions. When we increased a420,headwater by 50 % we received an a420 increase by a factor of 1.5 along the entire WRT1961–1990 gradient (Fig. 3b). Thus, according to the model an increase in a420 in headwaters results in similar a420 increases in all waters while changes in Lakedepthmean and R affect particularly waters with a longer WRT1961–1990.
Sensitivity of the absorbance of filtered water at 420 nm (a420) in 6347 Swedish inland waters to changes in surface water runoff (R), headwater conditions and mean lake depth in the catchment area through which water flushes (Lakedepthmean) along a site-specific long-term mean (1961–1990) landscape water retention time gradient (WRT1961–1990). Panel a shows observed long-term median a420 autumn values in 6347 inland waters. Panel b-e show model results. We ran our a420 model (nn) four times with varying values for variables and parameters and plotted the deviations from the present modeled a420 values for each of the 6347 inland waters. First we increased R by 50 % (panel b), second we increased a420 in headwaters by 50 %, third we decreased Lakedepthmean by 50 % (panel c), and finally we used the simulated worst case climate scenario for Sweden for 2030 with an increase in R by 32 %, a decrease in Lakedepthmean to 1 m and an increase in headwater a420 by 10 % (panel e). In panel e we plotted observed changes in a420 in 24 lakes and 24 streams over the time period 1988 to 2012
Considering the worst case climate scenario for Sweden until 2030 with a maximum R increase by 32 %, we predict that a420 will change by factors between 1.0 and 1.9 with a median of 1.1. Adding to the runoff increase also a 10 % a420 increase in headwaters, and considering a runoff induced accelerated water flushing through the landscape which we achieved by reducing Lakedepthmean to 1 m, we predict that a420 in Swedish lakes and streams will, at a maximum, increase by factors between 1.1 and 7.6 with a median of 1.3, provided that land-cover does not change (Fig. 3d). These changes are larger than the observed a420 changes in the 24 lakes and 24 streams during 1988 to 2012 (Fig. 3e).
4 Discussion
The modeling results show that many of the several hundred thousand freshwaters in Sweden will continue to become browner under the predicted worst case climate change scenarios for Sweden (Fig. 4). Most pronounced changes in a420 under the worst case scenario with a factor of more than 4 will occur in waters that have a WRT1961–1990 > 6 years (Fig. 3d). Waters with WRT1961–1990 > 6 years are not very common in the boreal region, and a420 in these waters is usually low (Fig. 3a). Thus, a strong relative change in a420 in the boreal region commonly results in only moderately high a420. Far more common in the boreal region are waters with WRT1961–1990 < 3 years (Müller et al. 2013). In these waters a420 is usually high (Fig. 3a), in particular in the warm and nutrient-rich southern part of Sweden (Fig. 4a). We predicted that maximum a420 under the worst case climate change scenario for Sweden will be reached in waters with WRT1961–1990 between 1 and 3 years located in the southern part of Sweden and to some extent at the east coast of Sweden where a420 at present is relatively high (Figs. 3a and 4a) and where it is going to increase by factors between 1.5 and 2.5 (Fig. 3d). In these waters preparedness for the preparation of drinking water is needed under the predicted future climate change. The Swedish Lake Mälaren with WRT1961–1990 of about 2.8 years is an example where recent trends in water color have caused problems for the preparation of drinking water (Köhler et al. 2013). Similar problems are known from other parts of the world (Roulet and Moore 2006).
Map of Sweden showing the present long-term median absorbance of filtered water at 420 nm (a420) in 6347 Swedish lakes and streams (panel a) and predicted a420 in the 6347 Swedish waters under the worst case climate scenario (see text, panel b). The red color represents waters with a420 > 20 m−1, the yellow color waters with a420 between 10 and 20 m−1 and blue waters with a420 < 10 m−1
Our worst case predictions considered a homogenous 10 % increase in a420 in headwaters but no change in land-cover. Land-cover was indirectly included as an input variable in the a420 model when we used MAT1961–1990 for the prediction of a420,headwater. MAT1961–1990 turned out to be the most important driver for a420,headwater spatial variation, most probably because MAT1961–1990 in Sweden is a suitable proxy for land-cover variation, runoff season length and RAD1961–1990, here shown by significant relationships between MAT1961–1990 and a variety of land-cover variables, between MAT1961–1990 and GDD1961–1990, and between MAT1961–1990 and RAD1961–1990. Land-cover as the main driver of colored dissolved organic matter, in this study measured as a420, is well known (Dillon and Molot 1997; Kortelainen et al. 2006). Also runoff season length and global radiation as important drivers for a420 variation are well documented (Vähätalo et al. 2000; Vodacek et al. 1997; Weyhenmeyer et al. 2014). Thus, MAT1961–199) in Sweden represents many catchment and climate variables which are known to drive a420 spatial variation. The relationship between MAT1961–1990 and a420,headwater was hump-shaped with maximum a420 at MAT1961–1990 between 4 and 6 °C (Fig. 1). A hump-shaped relationship to MAT1961–1990 has been found earlier, not for a420 but for DOC concentrations in streams (Laudon et al. 2012). To understand the underlying mechanism for such a hump-shaped relationship, i.e., to understand whether the relationship is caused by land-cover patterns, by a shift from transport to production limited systems as suggested by Laudon et al. (2012) or by other mechanisms, we would need far more data from various headwaters and over a longer time period which were not available to us. To model a420,headwater is a challenge but urgently needed to predict browning of freshwaters.
Land-cover remained similar during the past 25 years in the catchments of our 24 lakes and 24 streams. Consequently, MAT1961–1990 was still a suitable model input variable when we predicted a420 in the headwaters of the 48 waters. Although our simple numerical a420 model was not able to capture inter-annual variations in individual waters in all details, our observations and model simulations clearly showed that precipitation was one of the most important drivers for inter-annual variations in a420. Both trend analyses and model results further demonstrated that the observed increase in a420 in the 48 waters during the past 25 years was substantially faster than the concurrent precipitation increase. One obvious explanation for accelerated a420 increases is an increased soil export of colored dissolved organic matter. Increased soil export of colored dissolved organic matter has previously been related to decreasing sulfate deposition (Ekström et al. 2011; Evans et al. 2012; Monteith et al. 2007; Tipping and Hurley 1988). On a spatial scale we found no evidence that SO4-S concentrations have an influence on a420 variation, probably because of an overriding effect of land-cover. On a temporal scale, however, a420 could potentially have increased in headwaters as a result of decreased sulfate deposition during the past 25 years. We have no suitable data to confirm or deny this statement. Our sensitivity analyses showed however that a420 in waters with a long WRT1961–1990 are affected more by runoff changes than by changes in headwater conditions (Fig. 3b).
If accelerated a420 increases in downstream waters might not primarily be a result of an increased soil export of colored dissolved organic matter then other explanations are needed. Accelerated a420 increases in downstream waters can, for example, occur if runoff patterns through the landscape change. Runoff patterns are complex, and to model these in detail on large scales where also groundwater flows as well as precipitation intensity, duration and timing need to be considered goes beyond this study. However, we have indications that colored dissolved organic matter from soils is not equally diluted on the way downstream when precipitation increases. When we modeled a420 inter-annual variation over the past 25 years we needed to recalibrate our a420 model where the parameter Lakedepthmean was reduced from 4 to 3 m. Thus, it seems that not the entire lake volumes are flushed when precipitation increases, resulting in a rapid a420 increase in surface waters of downstream waters. Also the fact that the increase in a420 was significantly faster in lakes than in streams might give further evidence that an increase in precipitation focuses the flushing through lakes into a smaller fraction of the lake volume. In our worst case scenario we assumed that only the upper 1 m of the water bodies is flushed by the predicted strong precipitation increase. Although this might be unrealistic over a longer time period it might occur over a short time period under extreme precipitation events. These short pulse events are important to capture as they have far-reaching implications for the preparation of drinking water and other ecosystem services.
An accelerated a420 increase in waters with long WRT1961–1990 can also result from a decrease in the decay coefficient λ, corresponding to longer a420 half-lives. The a420 half-life which we calibrated in this study was shorter than previously found on a large scale (Algesten et al. 2004; Weyhenmeyer et al. 2012) and within a large lake basin (Köhler et al. 2013) but longer than on a small catchment scale (Moody et al. 2013). According to laboratory studies, λ is not constant but decreases the longer colored dissolved organic matter has been subjected to transformation processes (Koehler et al. 2012). Thus, it is possible that λ decreases but only if landscape WRT increases. Since we propose that landscape WRT has decreased over the past decades, it is highly unlikely that λ has decreased.
The numerical a420 model was kept very simple and required only very few input variables and parameters so that a420 in thousands of waters could be predicted. The weakest part of the model is the determination of a420,headwater which is highly variable. The model has also limitations when it comes to capture short-term a420 variations as a response to extreme runoff events, and a basic assumption of the model is that a420 transformations during transport from land to sea are mainly driven by hydrological processes. Despite these limitations the model is powerful in demonstrating differences in a420 responses to runoff changes depending on WRT1961–1990 of the waters. And although the model was calibrated for Swedish conditions, in particular a420,headwater the main result that lakes with a WRT1961–1990 between 1 and 3 years are particularly vulnerable to precipitation driven browning is valid for all waters that are hydrologically connected in the landscape.
5 Conclusions
Our study clearly demonstrates that both headwater conditions and a420 transformation during transport through the landscape need to be understood in order to predict future browning of freshwaters. Headwater conditions are highly variable. On the spatial scale headwater conditions are strongly driven by land-cover. We suggest that small changes in land-cover will most probably result in a420 changes that are substantially faster than the direct climate change induced a420 changes. Thus, priority in managing a420 should be put on managing land-cover. Direct climate change induced a420 changes become particularly apparent in downstream waters which we conclude from the observation that a homogenous precipitation increase caused an increasing a420 response along a landscape WRT1961–1990 gradient. Such large differences in a420 responses to the same climate change should be taken into account when water color risk assessments are done.
References
Algesten G, Sobek S, Bergström AK, Ågren A, Tranvik LJ, Jansson M (2004) Role of lakes for organic carbon cycling in the boreal zone. Glob Chang Biol 10:141–147
Canham CD, Pace ML, Papaik MJ, Primack AGB, Roy KM, Maranger RJ, Curran RP, Spada DM (2004) A spatially explicit watershed-scale analysis of dissolved organic carbon in Adirondack lakes. Ecol Appl 14:839–854
Dillon PJ, Molot LA (1997) Effect of landscape form on export of dissolved organic carbon, iron, and phosphorus from forested stream catchments. Water Resour Res 33:2591–2600
Eikebrokk B, Vogt RD, Liltved H (2004) NOM increase in Northern European source waters: discussion of possible causes and impacts on coagulation/contact filtration processes. In: Newcombe G, Ho L (eds) Natural Organic Material Research: Innovations and Applications for Drinking Water. Water Science and Technology: Water Supply, vol 4. IWA Publishing, London, p 47–54
Ekström SM, Kritzberg ES, Kleja DB, Larsson N, Nilsson PA, Graneli W, Bergkvist B (2011) Effect of acid deposition on quantity and quality of dissolved organic matter in soil-water. Environ Sci Technol 45:4733–4739
Erlandsson M, Buffam I, Folster J, Laudon H, Temnerud J, Weyhenmeyer GA, Bishop K (2008) Thirty-five years of synchrony in the organic matter concentrations of Swedish rivers explained by variation in flow and sulphate. Glob Chang Biol 14:1191–1198
Evans CD, Chapman PJ, Clark JM, Monteith DT, Cresser MS (2006) Alternative explanations for rising dissolved organic carbon export from organic soils. Glob Chang Biol 12:2044–2053
Evans CD, Jones TG, Burden A, Ostle N, Zielinski P, Cooper MDA, Peacock M, Clark JM, Oulehle F, Cooper D, Freeman C (2012) Acidity controls on dissolved organic carbon mobility in organic soils. Glob Chang Biol 18:3317–3331
Hu CM, Muller-Karger FE, Zepp RG (2002) Absorbance, absorption coefficient, and apparent quantum yield: a comment on common ambiguity in the use of these optical concepts. Limnol Oceanogr 47:1261–1267
Kirk JTO (2003) Light and photosynthesis in aquatic ecosystems. Cambridge University Press, Cambridge
Koehler B, von Wachenfeldt E, Kothawala D, Tranvik LJ (2012) Reactivity continuum of dissolved organic carbon decomposition in lake water. J Geophys Res Biogeosci 117. doi:10.1029/2011jg001793
Köhler SJ, Kothawala D, Futter MN, Liungman O, Tranvik L (2013) In-lake processes offset increased terrestrial inputs of dissolved organic carbon and color to lakes. Plos One 8. doi:10.1371/journal.pone.0070598
Kortelainen P (1993) Content of total organic-carbon in Finnish lakes and its relationship to catchment characteristics. Can J Fish Aquat Sci 50:1477–1483
Kortelainen P, Mattsson T, Finer L, Ahtiainen M, Saukkonen S, Sallantaus T (2006) Controls on the export of C, N, P and Fe from undisturbed boreal catchments, Finland. Aquat Sci 68:453–468
Kritzberg ES, Ekström SM (2012) Increasing iron concentrations in surface waters - a factor behind brownification? Biogeosciences 9:1465–1478
Larsen S, Andersen T, Hessen DO (2011) Predicting organic carbon in lakes from climate drivers and catchment properties. Glob Biogeochem Cycles 25. doi:10.1029/2010gb003908
Laudon H, Buttle J, Carey SK, McDonnell J, McGuire K, Seibert J, Shanley J, Soulsby C, Tetzlaff D (2012) Cross-regional prediction of long-term trajectory of stream water DOC response to climate change. Geophys Res Lett 39. doi:10.1029/2012gl053033
Livingstone DM, Lotter AF, Walker IR (1999) The decrease in summer surface water temperature with altitude in swiss alpine lakes: a comparison with air temperature lapse rates. Arct Antarct Alp Res 31:341–352
Molot LA, Dillon PJ (1997) Colour - mass balances and colour - dissolved organic carbon relationships in lakes and streams in central Ontario. Can J Fish Aquat Sci 54:2789–2795
Monteith DT, Stoddard JL, Evans CD, de Wit HA, Forsius M, Hogasen T, Wilander A, Skjelkvale BL, Jeffries DS, Vuorenmaa J, Keller B, Kopacek J, Vesely J (2007) Dissolved organic carbon trends resulting from changes in atmospheric deposition chemistry. Nature 450:537–540
Moody CS, Worrall F, Evans CD, Jones TG (2013) The rate of loss of dissolved organic carbon (DOC) through a catchment. J Hydrol 492:139–150
Müller RA, Futter MN, Sobek S, Nisell J, Bishop K, Weyhenmeyer GA (2013) Water renewal along the aquatic continuum offsets cumulative retention by lakes: implications for the character of organic carbon in boreal lakes. Aquat Sci 75:535–545
Pace ML, Cole JJ (2002) Synchronous variation of dissolved organic carbon and color in lakes. Limnol Oceanogr 47:333–342
Richardson SD (2007) Water analysis: emerging contaminants and current issues. Anal Chem 79:4295–4323
Roulet N, Moore TR (2006) Environmental chemistry - browning the waters. Nature 444:283–284
Sobek S, Tranvik LJ, Prairie YT, Kortelainen P, Cole JJ (2007) Patterns and regulation of dissolved organic carbon: an analysis of 7500 widely distributed lakes. Limnol Oceanogr 52:1208–1219
Thurman EM (1985) Organic geochemistry of natural waters. Nijhoff/Junk, Boston
Tipping E, Hurley MA (1988) A model of solid-solution interactions in acid organic soils, based on the complexation properties of humic substances. J Soil Sci 39:505–519
Vähätalo AV, Salkinoja-Salonen M, Taalas P, Salonen K (2000) Spectrum of the quantum yield for photochemical mineralization of dissolved organic carbon in a humic lake. Limnol Oceanogr 45:664–676
Vodacek A, Blough NV, DeGrandpre MD, Peltzer ET, Nelson RK (1997) Seasonal variation of CDOM and DOC in the Middle Atlantic Bight: terrestrial inputs and photooxidation. Limnol Oceanogr 42:674–686
Volk C, Wood L, Johnson B, Robinson J, Zhu HW, Kaplan L (2002) Monitoring dissolved organic carbon in surface and drinking waters. J Environ Monit 4:43–47
Weyhenmeyer GA (2008) Water chemical changes along a latitudinal gradient in relation to climate and atmospheric deposition. Clim Change 88:199–208
Weyhenmeyer GA, Fröberg M, Karltun E, Khalili M, Kothawala D, Temnerud J, Tranvik LJ (2012) Selective decay of terrestrial organic carbon during transport from land to sea. Glob Chang Biol 18:349–355
Weyhenmeyer GA, Prairie YT, Tranvik LJ (2014) Browning of boreal freshwaters coupled to carbon-iron interactions along the aquatic continuum. Plos One 9. doi:10.1371/journal.pone.0088104
Winterdahl M, Erlandsson M, Futter MN, Weyhenmeyer GA, Bishop K (2014) Intra-annual variability of organic carbon concentrations in running waters: drivers along a climatic gradient. Global Biogeochem Cycles 28:451–464
Xenopoulos MA, Lodge DM, Frentress J, Kreps TA, Bridgham SD, Grossman E, Jackson CJ (2003) Regional comparisons of watershed determinants of dissolved organic carbon in temperate lakes from the Upper Great Lakes region and selected regions globally. Limnol Oceanogr 48:2321–2334
Acknowledgments
Financial support was received from the Swedish Research Council (VR) and the Swedish Research Council for Environment, Agricultural Sciences and Spatial Planning (FORMAS). This work is part of and profited from the networks financed by NordForsk (CRAICC and DOMQUA) and the Norwegian Research Council (Norklima ECCO). Many thanks go to the Swedish Environmental Protection Agency and the staff of the laboratory of the Dept. of Aquatic Sciences and Assessment for financing, sampling and analyzing thousands of water samples, and to the Swedish Meteorological and Hydrological Institute for making meteorological data freely available. GIS data were kindly received from Jakob Nisell. Finally, we thank Nigel Roulet and two unknown reviewers for excellent reviews.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
ESM 1
(DOCX 253 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Weyhenmeyer, G.A., Müller, R.A., Norman, M. et al. Sensitivity of freshwaters to browning in response to future climate change. Climatic Change 134, 225–239 (2016). https://doi.org/10.1007/s10584-015-1514-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-015-1514-z