1 Introduction

Decision making would profit from reliable, high fidelity probability forecasts for climate variables on decadal to centennial timescales. Many forecast systems are available, but evaluations of their performance are not standardised, with many different scores being used to measure different aspects of performance. These are often not directly comparable across models or across different studies. EQUIP (the ‘End-to-end Quantification of Uncertainty for Impacts Prediction’ consortium project) aimed to provide guidance to users of information at the space and time scales of interest, and to develop approaches to enable evidence-based choice between alternate forecasting methods, based on reliable and informative measures of forecast skill. The intercomparison of simulation models is valuable in many ways; comparison of forecasts from simulation models with empirically-based reference forecasts provides additional information. In particular it aids in distinguishing the case when each forecast system does well, and so the best system cannot be identified (i.e. equifinality) from the case in which each forecast system performs very poorly (i.e. equidismality) (Beven 2006; Suckling and Smith 2013). Indeed some climate researchers have required the demonstration of skill against a more easily prepared reference forecast as a condition for accepting any complicated forecasting scheme as useful (von Storch and Zwiers 1999). This raises the question of how exactly to quantify skill.

Three measures of forecast system performance (hereafter, scores) are studied below and the desirability of their attributes is considered. It is critical to keep in mind that an entire forecast system is evaluated, not merely the model at its core. Each score in turn is then illustrated in the context of decadal forecasts of global mean temperature. Section 2 discusses several measures of forecast system performance, including the logarithmic score (Ignorance) (Good 1952; Roulston and Smith 2002), the Continuous Ranked Probability Score (CRPS) (Epstein 1969; Gneiting and Raftery 2007) and the Proper Linear score (PL) (Friedman 1983). General considerations for selecting a preferred score are discussed; CRPS is demonstrated capable of misleading behaviour. Section 3 then introduces the forecast targets and forecast systems to be considered in this paper. Both empirical and simulation models are identified and the primary target, global mean temperature (GMT), is discussed. Section 4 considers the performance of probability forecasts (both empirical and simulation-based) on decadal scales in the light of each of these scores.

2 Measuring forecast performance

Several scores are available for the evaluation of probabilistic forecasts (Bröcker and Smith 2007; Gneiting and Raftery 2007; Mason and Weigel 2009; Jolliffe and Stephenson 2012); each quantifies different attributes of the forecast. While the importance of using proper scores is well recognised (Bröcker and Smith 2007; Fricker et al. 2013), researchers often face requests to present results under a variety of scores. Indeed in the context of meteorological forecast evaluation there are several recommendations in the literature (Nurmi 2003; Randall et al. 2007; World Meteorological Organization 2008; Fricker et al. 2013; Goddard et al. 2013), although often with little discussion of which attributes different scores aim to quantify, or their strengths and weaknesses in a particular forecast setting. By convention, a lower score is taken to reflect a better forecast.

A score is a functional of both the forecast (whose pdfs are denoted by either p or q) and the observed outcome (X). It is useful to speak of the “True” distribution from which the outcome is drawn (hereafter, Q) without assuming that such a distribution exists in all cases of interest. Given a proper score, a forecast system providing Q will be preferred whenever it is included amongst those under consideration (Bröcker and Smith 2007; Fricker et al. 2013). When this is not the case, then even proper scores may rank two forecast systems differently, making it difficult to provide definitive statements about forecast quality. There are, however, desirable properties of the scores themselves that may help to narrow down the set of scores appropriate for a given task.

A score, S(p(x),X), is said to be ‘proper’ if inequality (1) holds for any pair of forecast pdfs, and ‘strictly proper’ when equality (1) is implies p = q:

$$ \int q(z) S(p(z), z) dz \geq \int q(z) S(q(z), z) dz. $$
(1)

For a given forecast p, a score is itself a random variable with values that depend on the observed outcome X. One can calculate the expected score of the forecast p when X is actually drawn from underlying distribution q. A proper score does not, in expectation, judge any other forecast p to score better than q as a forecast of q itself. The interpretation of proper does not, however, require one to believe that a “True” distribution Q exists. While use of a proper score might be motivated by concerns of hedging (Selten 1998), proper scores are preferred even when there is no human in the loop, as in parameter selection (Du and Smith 2012). For completeness, and without endorsement, the discussion below is not restricted to proper scores.

2.1 RMSE of the ensemble mean

The Root Mean Squared Error (RMSE) quantifies the distance between the ensemble mean, \(\bar x(i)\) of the ith forecast and the corresponding outcome, X(i), defined as,

$$ RMSE(\bar x,X)=\sqrt{\frac{1}{m} \sum\limits_{i=1}^{m}(\bar x(i) - X(i))^{2}}, $$
(2)

Note that rather than providing a score for a single forecast RMSE summarizes m forecasts. Any of the wide variety of forecast distributions with the same mean will achieve the same score. An alternative summary score resembling the RMSE can be defined via

$$ S_{RMSE}((p_{1},....p_{m}), (X_{1}, ...X_{m})) = \sqrt{\frac{1}{m} \sum\limits_{i=1}^{m}\left( {\int}^{\infty}_{-\infty} ({X_{i}} - z)^{2} p(i,z) dz.\right.} $$
(3)

The original RMSE re-emerges by setting the forecast p as a delta function at the ensemble mean. The integral term is sometimes referred to as the Mean Squared Error (MSE). This score is not proper, and the lowest score is attained when the standard deviation of the forecast is zero—an unfortunate incentive for an imperfect probabilistic forecast.

2.2 Naive linear and proper linear scores

The Naive Linear (NL) score is not proper. It is defined by:

$$ S_{NL}(p(x),X) = -p(X). $$
(4)

The NL score can be “made” strictly proper by the addition of an integral term over p to Eq. 4,

$$ S_{PL}(p(x),X) = -2p(X) + {\int}^{\infty}_{-\infty} p^{2}(z) dz, $$
(5)

resulting in the Proper Linear (PL) score (Friedman 1983). The PL score is related to the quadratic score, which is part of the power rule family that contains an infinite number of proper scores (Selten 1998). The popular Brier (1950) and Continuous Ranked Probability scores (Epstein 1969) are also special cases of the quadratic scoring rule family (Staël von Holstein 1978). The PL score itself rewards a forecast both for the probability placed on the outcome (the first term in Eq. 5) and for the shape of the distribution (the second term in Eq. 5). Narrower distributions are penalised regardless of the outcome. Arguably the second term clouds the interpretation of the score, unless one has some particular incentive to minimize this integral. This illustrates a case where an intuitive score, the probability of the outcome, can be made to be proper at the cost of some immediate intuitive appeal. Alternatively, in cases where it is meaningful to speak of the distribution from which the outcome is drawn (referred to as Q above), then PL is simply related to the integral of the squared difference between the forecast p(x) and Q(x). This point is revisited in Section 4.

2.3 Continuous ranked probability

The Continuous Ranked Probability Score (CRPS) is the integral of the square of the L 2 distance between the cumulative distribution function of the forecast p and a step function at the outcome (Epstein 1969),

$$ S_{CRPS}(p(x),X) = {\int}^{\infty}_{-\infty} \left( {\int}^{x}_{-\infty}p(z)dz - H(x-X) \right)^{2} dx, $$
(6)

where the Heaviside (step) function H is defined as follows:

$$ H(x) = \left\{\begin{array}{ll} 0 &~\text{if}~x < 0\\ 1 &~\text{if}~x \ge 0 \end{array}\right. $$
(7)

CRPS can be interpreted as the integral of the Brier score over all threshold values; for point forecasts CRPS reduces to the mean absolute error. The CRPS rewards a forecast for both its calibration and shape, but unlike the PL score they are assessed simultaneously. A decomposition into reliability and resolution components is possible (Hersbach 2000; Bröcker 2009). The CRPS is sometimes said to assign a value to a raw ensemble of point forecasts (Gneiting and Raftery 2007; Ferro et al. 2008; Bröcker 2012);Footnote 1 this claim is equivalent to interpreting the ensemble members as a probability forecast consisting of a collection of delta functions. Given that ensemble interpretation, any probability scoring rule can be applied, of course. CRPS is somewhat more tolerant of weaknesses of this delta function ensemble interpretation than the other scores discussed here.Footnote 2 The authors are unaware of an intuitive interpretation of the quantitative values of CRPS.

2.4 Ignorance

The Ignorance score (Good 1952; Roulston and Smith 2002) is a strictly proper score defined as,

$$ S(p(x),X) = -log_{2}(p(X)), $$
(8)

where p(X) is the density assigned to the outcome X. It is the only proper local score, rewarding a forecast solely for the probability density placed on the observed outcome, rather than for other features of the forecast distribution such as its shape. This makes computing the score significantly less computationally expensive. The Ignorance score corresponds to the expected wealth doubling (or halving) time of a Kelly investment strategy, and can be expressed as an effective interest rate (Hagedorn and Smith 2009). Kelly’s focus (Kelly 1956) was on information theory, specifically on providing a context for the mathematical results of Shannon (1948) while neither of them could define a “communication system” precisely. A gambling analogy was selected because it had the essential features of a communication system. Ignorance emerges as a natural measure of information content of probability forecasts in general.

Selten (1998) objects to the Ignorance score because it severely penalises forecasts that place very low probabilities on the observed outcome, and indeed Ignorance gives an infinitely bad score if an outcome occurs that the forecaster said was impossible. One of the present authors (TM) works in the insurance industry, however, and believes this to be a desirable property of a score—extreme model failure has been one of the key causes of distress in the financial services industry. Acknowledging unlikely possibilities as such and thereby avoiding the infinite penalty of having stated they were truly impossible might be seen as basic good practice (see, however, discussion by Borel (1962) regarding vanishingly small probabilities); adopting a minimum forecast probability to account for the imperfection of science is perhaps akin to adding a margin for safety in engineering terms. In the next section, CPRS is shown to be remarkably insensitive to outcomes in regions that are forecast to have vanishingly small or zero probability. No optimal balance regarding the appropriate level of sensitivity of scores has been generally agreed.

2.5 Comparing the behaviour of ignorance and CRPS

The Ignorance and CRPS scores corresponding to a variety of different outcomes given two bimodal forecast distributions are shown in Fig. 1. Figure 1a shows distributions with symmetric (thick blue) and asymmetric (thin red) shapes. Figure 1b compares the Ignorance (y) and CRPS (x) scores in the case of a symmetric bimodal distribution (the thick blue distribution in Fig. 1a) as the observed outcome moves across the forecast distribution from large negative values of x, through x = 0, to large positive values of x. The minimum (best) CRPS score is achieved by an outcome at the median of the underlying distribution, that is at x = 0 in the symmetric (thick blue) case, and near x = 0.7 in the asymmetric (thin red) case marked as a vertical line in Fig. 1a and as a black star in Fig. 1b. Ignorance is minimised when the outcome is at the mode of the forecast distribution (the green star in Fig. 1b). These two points do not correspond to the same outcome.

Fig. 1
figure 1

An example comparing the sensitivity of IGN (thick green) and CRPS (thin black) scores for outcomes in different regions of a forecast probability distribution. a Two bimodal forecast distributions, one symmetric (thick blue) and one asymmetric (thin red). b The Ignorance (y-axis) and CPRS (x-axis) scores given to each forecast distribution as the observed outcome moves across the range of each distribution. Note that minimal (best) scores occur for CRPS when the outcome falls at the median of the forecast distribution, while Ignorance is minimal when the outcome falls at a mode of the forecast distribution. Panels c and d show the Ignorance score (thick green) and CRPS score (thin black) as a function of the outcome given a symmetric bimodal forecast distribution. All forecast distributions consist of the sum of two Gaussian distributions, one centred at −1, the other at +1. Panels a, b and c reflect the results where each component has a standard deviation of 0.25. In panel d each component has a standard deviation of 0.125. In the symmetric forecasts, each component is equally weighted, while in the asymmetric forecast (reflected in the thin red curves of panel (a) and (b) the left component has weight 0.45 and the right 0.55

Full size image

This example shows that the CRPS score can rate an outcome from a structurally flawed forecast system highly even when both (a) the outcome is repeatedly observed where the forecast system has assigned a small probability and (b) the forecast repeatedly places significant probability mass in regions of vanishingly small (or zero) probability of occurring; Ignorance would penalise such forecast systems severely. Consider a bimodal forecast like the thick blue distribution in Fig. 1 (for example, strong winds forecast from either east or west but the direction is uncertain), and an underlying Q distribution which is unimodal with low variance centred at zero. The outcome is almost certainly close to zero, which is in a region where the forecast ascribes very low probability density—hence, the Ignorance score will heavily penalise the system producing the bimodal forecast. The CRPS however will give the forecast the best possible score when this outcome occurs. Figure 1c shows the IGN (thick green) and CRPS (thin black) as a function of the outcome corresponding to the asymmetric case in Fig. 1a above it. IGN(x) returns large (poor) values for outcomes far from one or the other mode. CRPS(x) returns large values for outcomes far from zero, but for values of x near zero low (good) scores are returned. Figure 1d reflects a case similar to 1c, where the width of each mode is halved: IGN returns low values on a more narrow range, while CRPS again returns a similar (low) score for points in the central low probability region. These two scores would give rather different impressions of forecast quality when evaluating this bimodal probability forecast when the outcome was generated, say, by a Gaussian distribution, with zero mean. The fact that both scores are proper restricts their behaviour to agree when given Q, but not when given an imperfect probability forecast.

Return to the symmetric (thick blue PDF) forecast in Fig. 1a and consider all possible forecasts with this bimodal shape but centered at some value of x = c, where c need not be zero as it is in Fig. 1a. Consider the case of an outcome at the origin, x = 0. Will IGN and CRPS rank members of this family of forecasts differently? Yes. IGN (and PL) will favour the forecasts that place higher probability on the outcome while CRPS will favour forecasts that have low probability on the outcome. In this case, IGN will favour (equally) the two forecasts with values of c such that a mode is at the origin, while CRPS will favour the forecast with c = 0 (shown), which has a local minimum of probability at the outcome. CRPS expresses a deliberate robust behaviour scoring this family of forecasts in a way that is unreasonable if not unacceptable.

Alternatively, one can view this effect in terms of the score as a function of the outcome. The thick blue curve in Fig. 1b plots the two curves in Fig. 1c against each other: the thick blue curve in Fig. 1b traces the trajectory of the point (CRPS(x), IGN(x)) as x goes from −10 to +10. Note that the minimum IGN occurs at a different point along this trajectory than the minimum CRPS. Specifically IGN is minimal at x = −1 and x = +1, CRPS is minimal at x = 0. The thin red curve traces the trajectory in the case when the modes are asymmetric, specifically when they have weights .45 (left) and .55 (right). In this case IGN(x) is a minimal at x = 1 (the unique mode) and CRPS is minimal near x = 0.667. Thus IGN scores the forecast as better when the outcome corresponds to large p(x) as might be deemed desirable; CRPS does not. While it might be possible to construct a situation where these behaviors of CPRS are desirable, these examples suggest CRPS be interpreted with great caution, if used at all, in normal forecast evaluation.

3 Contrasting the skill of decadal forecasts under different scores

In this section the behaviour and utility of different scores are contrasted by evaluating the performance of probabilistic decadal hindcasts of global mean temperature (GMT) from a simulation model (HadCM3) and from two simple empirical models (Static Climatology and Dynamic Climatology). Such evaluations allow comparisons of the relative skill of large simulation models against simple, computationally inexpensive, empirical models. The interpretation of that comparison, and its value, will vary with the score used.

3.1 Simulation-based hindcasts

The simulation based forecast system uses simulations from the UK Met Office HadCM3 model (Gordon et al. 2000), which formed part of the CMIP5 decadal hindcast experiment (Taylor et al. 2008). The forecast archive consists of a series of 10-member initial condition ensembles, launched annually between 1960–2009, and extended out to a lead time of 120 months. This HadCM3 forecast archive was from the CMIP5 library (last downloaded on 07-04-2014). Even so, the small forecast-outcome archive is a limiting factor in the analysis, especially since generating probabilistic forecasts from the ensemble members (Bröcker and Smith 2008; Suckling and Smith 2013) and the subsequent evaluation must be done in such a way as to avoid using the same information more than once (hereafter, information contamination) (Wilks 2005; Smith et al. 2014).

Figure 2 shows the 10-member ensembles of simulated GMT values for every tenth launch year over the full hindcast period; HadCRUT3 observations (Brohan et al. 2006) are shown for comparison. It is clear that the HadCM3 ensemble members are generally cooler than the observed temperatures from HadCRUT3 and would perform poorly if this systematic error were not accounted for. Unless otherwise noted, the ensemble interpretation applied below uses a lead-time dependent offset to account for this systematic error in HadCM3 simulations; the translation of model-values in the simulation into target quantities in the world is an important feature of the forecast system. Unless otherwise stated the ensemble is interpreted as a probability forecast, using the Ignorance score to determine the lead-time-dependent kernel offset and kernel width parameters under cross-validation. This procedure is described further in Bröcker and Smith (2008), Suckling and Smith (2013), Smith et al. (2014).

Fig. 2
figure 2

Individual HadCM3 ensemble members (thin grey) and HadCRUT3 observations (thick black) of global mean temperature (GMT) between 1960 and 2010. For clarity, only every tenth launch date of the HadCM3 simulations are shown

Full size image

3.2 The Dynamic Climatology empirical model

The Dynamic Climatology (DC) is an empirical model (Smith 1997; Suckling and Smith 2013) which uses the observed GMT record. At each launch time, the GMT value is initialised to its observed value from the HadCRUT3 record. An ℓ-step ahead ensemble forecast is generated by adding the set of observed ℓth differences (across the observed GMT record) to the initialised GMT value at launch, leaving out the period under consideration itself, (that is, adopting a cross-validation approach). For example a one year ahead forecast made in 1992 for the year 1993 is generated by adding each of the annually averaged consecutive year temperature differences between the years 1960–2012, except for the 1992–93 difference itself, to the observed annual average GMT value for the year 1992. Similarly, an n year ahead forecast is generated from the observed 1992 temperature and all the n year temperature differences over the hindcast period except for an intervalFootnote 3 about the point being forecast. This is a direct DC model. In general, one expects the dynamics of uncertainty to vary with initial condition (Smith 1994). This version of DC does not exploit that expectation: for a given lead time the same distribution of change in GMT is forecast each time. Note that if only non-overlapping intervals are considered, then these ensemble members are independent, as opposed to the HadCM3 ensembles which are ten internally consistent trajectories and are artificially enhanced by access to information from events during that period (volcanoes, for example). Generating trajectories from iterated DC models based on a sum of repeated draws from the distribution of one-year differences is also possible; doing so would require assumptions on temporal correlations, and the simpler direct DC scheme is adopted here as it already provides an interesting baseline for comparison with simulation models. A Static Climatology (SC) distribution is also generated as a reference forecast by direct kernel density estimation (Silverman 1998; Bröcker and Smith 2008) applied to the observed GMT values over the period 1960–2009.

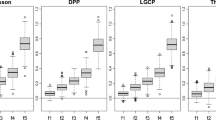
DC hindcasts are generated for every year in the period 1960–2009 for comparison with HadCM3. HadCM3 ensembles, each with 10 members, are available for every year from 1960 until 2009. Given that a ten year forecast evaluated with the target observed in year y shares 9 common years with the target in year y−1 and that in year y+1, information contamination is unavoidable if information involving these three years (y−1, y, and y+1) is treated as independent. For this reason,Footnote 4 the experiment was repeated independently starting in 1960, 1961, 1962, 1963, and 1964; for the HadCM3 forecast systems the scores shown in the Fig. 3 reflect the average of the result and the max-min range when the vertical bars have no caps. For the Static Climatology, bootstrap resampling bars are shown, with caps at the 10 % and 90 % range (as in Fig. 3a). Forecast systems under both approaches are shown from DC in Fig. 3; note the results are similar except for the expected increase due to smaller samples in the independent experiment case (with caps).

Fig. 3
figure 3

Performance of HadCM3 and DC forecast systems as a function of lead time under different skill scores: a PL score, b CRPS, c IGN relative to the Static Climatology and d IGN relative to DC. In panels a, b, and c the Static Climatology (SC) is shown for comparison; in panel c both HadCM3 and DC perform substantially better than SC on average; multiple-realization sample bars (vertical bars, no caps) show that this is the case in almost every realization. A unified DC forecast system (green dashed) is shown for comparison; traditional (10 %–90 %) bootstrap resample ranges (green dashed, with caps) reveal a similar result with somewhat improved sampling uncertainty. In Panel d the red dash-dotted line fluctuates between −0.25 bit to −0.75 bit indicating that on average the HadCM3 forecast system clearly outperforms the unified DC, placing between ∼20 % and 60 % more probability on the outcome than DC at various lead times. Some of the multiple-realization sample bars (no caps) reach zero in panel (d), indicating that in some realizations the DC outperforms HadCM3

Full size image

4 Interpreting probabilistic forecast skill scores

In this section, the evaluation of probabilistic hindcasts from the HadCM3 and DC models under different scores are interpreted and contrasted. The Static Climatology is taken as a reference forecast. Given the evident (physically expected and causally argued prior to 1960) upward drift in GMT, DC would be expected to provide a more relevant reference forecast (Suckling and Smith 2013).

The top three panels of Fig. 3 show skill according to the three different scores as a function of lead time. Sampling uncertainty in the skill score (due to the limited number of forecasts considered) is reflected in the bootstrap resampling range (plotted as vertical bars with caps) of the scores for each lead time, with the 10 %–90 % resampling intervals. The bootstrap resamples with replacement from the sample of forecast values; when the sample size is small these ranges can be large due merely to a few poor forecasts. This is a property of the size of the forecast-outcome archive, and may happen even when the outcome is drawn from the forecast distribution (that is, Q above), although this may be unlikely to happen. These resampling bars (with caps) are shown in Fig. 3 for the SC scores (black dotted) and the traditional unified DC scores (green dashed) (Suckling and Smith 2013); in these cases the sample size is relatively large. The outcomes of two ten year forecasts initiated in consecutive years are far from independent (as they have nine years in common). For this reason five evaluation experiments were considered, with consecutive initial conditions within each experiment separated by a period of five years (that is, 1960, 1965, 1970 ...). The vertical bars without caps in Fig. 3 reflect the results of repeating the entire forecast evaluation 5 times, one experiment initialized in each of 1960, 1961, 1962, 1963, and 1964. The vertical bars (without caps) show the range of these experiments, the solid line connects their mean.

It is clear that the different scores lead to different estimates of the relative skill provided by the alternate models. When the multiple-realization bars (no caps) overlap, then there is at least one set of experiments in which, at that lead time, the forecast system judged better on average performs less well than the forecast system which does less well when the results are averaged. Overlap between HadCM3 and DC is common under each score. Looking at the relative Ignorance directly (Fig. 3d) shows that HadCM3 outperforms DC in every individual case for lead times of 1, 2, 3 and 4 years. The extent to which the absolute values are meaningful varies with the score considered. In the case of the Ignorance score, the difference between two forecast systems reflects the number of additional “bits of information” in the better forecast: a difference of 2 bits corresponds to the better forecast system placing (on average, 22=) 4 times more probability on the outcome than the alternative forecast system, while a relative IGN of 4 bits would correspond to a factor of 16 and a difference of 0.5 a factor of roughly 1.41 (that is 21/2), in other words half a bit corresponds to a gain of about 41 %. For the other scores, the authors are not aware of any clear interpretation of the absolute value of the score. In some cases it makes sense to consider an integration over the “True” distribution (Q, above); in that case the expectation of the PL is the mean square difference between the forecast density p and the density from which the outcome is drawn Q. The interpretation of the expectation with respect to Q is cloudy in weather-like forecasting scenarios, where the same Q distribution is never seen twice over the lifetime of the system.Footnote 5 The Proper Linear score could be interpreted in cases where the second term in its definition (5) is motivated by the application (not merely for the sake of “making” the naive linear score proper).

Each score considered indicates that HadCM3 and DC consistently outperform the Static Climatology. The Ignorance score allows the simple interpretation of Fig. 3d that on average the HadCM3 ensemble decadal forecasts place about 70 % more probability on the outcome as DC in year one, then just over half a bit (∼41 % more) at longer lead times. Figure 3c shows that both the HadCM3 and DC models consistently place significantly more probability on the outcome than the Static Climatology.

Note that SC is roughly constant across lead times, which is to be expected as the same forecast distributions is issued (ignoring cross validation changes and the effect of the trend) for all lead times. Note also that this HadCM3 forecast system outperforms DC, while the HadGEM2 forecast system reported in Suckling and Smith (2013) did not outperform DC. Detailed reasons why this is the case are beyond the scope of this paper, nevertheless note (i) the HadCM3 system considered in this paper had ten ensemble members launched annually; whereas the HadGEM2 forecast system had only 3 members launched every 5 years. (ii) someFootnote 6 CMIP5 models are forced by major volcanoes, while the DC is not (the hindcasts for the GCMs include specific information on specific years, this version of DC does not), (iii) the multiple-realization bars (no caps) of HadCM3 and DC often overlap in CRPS and PL while the relative IGN in panel d shows a clear separation out to lead time five years or more; on average HadCM3 consistently scores just over half a bit better than DC.

One expects that as simulations, observations, models and ensemble experimental designs improve, the simulation forecast systems will outperform DC even more clearly. Future work will consider the design of better benchmark empirical models, accounting for (and quantifying) the false skill in forecast systems based upon CMIP simulations arising from their foreknowledge of events (volcano-like information), and relative skill in higher resolution targets (finer resolution in space and/or time).

Climate models are sometimes said to show more skill over longer temporal averages; the basis of this claim is unclear. Forecasts of five-year time averages of GMT from the HadCM3 and DC models (not shown) have similar levels of relative probabilistic skill to those of one-year averaged forecasts. The variance in “temperature” decreases when five year means are taken, and the apparent RMSE may appear “smaller”. Note, however, that the metric has changed as well, hence the scare quotes. The probability of the outcome in the two cases changes only slightly, indicating that in this case at least, the suggested gain in skill is a chimera.

5 Conclusions

Measures of skill play a critical role in the development, deployment and application of probability forecasts. The choice of score quite literally determines what can be seen in the forecasts, influencing not only forecast system design and model development, but also decisions on whether or not to purchase forecasts from that forecast system or invest in accordance with the probabilities from a forecast system.

The properties of some common skill scores have been discussed and illustrated. Even when the discussion is restricted to proper scores, there remains considerable variability between scores in terms of their sensitivity to outcomes in regions of low (or vanishing) probability; proper scores need not rank competing forecast systems in the same order when each forecast system is imperfect. In general, the Continuous Ranked Probability Score can define the best forecast system to be one which consistently assigns zero probability to the observed outcome, while the Ignorance score will assign an infinite penalty to an outcome which falls in a region the forecast states to be impossible; such issues should be considered when deciding which score is appropriate for a specific task. Ensemble interpretations (Bröcker and Smith 2008) which interpret a probability forecast as a single delta function (such as the ensemble mean) or as a collection of delta functions (reflecting, for example, the position of each ensemble member) rather than considering all the probabilistic information available may provide misleading estimates of skill in nonlinear systems. Scores can be used for a variety of different aims, of course. The properties desired of a score for parameter selection (Pisarenko and Sornette 2004; Du and Smith 2012) can be rather different from those desired in evaluating an operational forecast system.

A general methodology has been applied for probabilistic forecast evaluation, contrasting the properties of several proper scores when evaluating forecast systems of decadal ensemble hindcasts of global mean temperature from the HadCM3 model (part of the CMIP5 decadal archive). Each of the three proper scores in Section 2 were considered for evaluation of the results. The Ignorance score was shown to best discriminate between the performance of the different models. In addition, the Ignorance score can be interpreted directly, indicating, for example, that on average the HadCM3 forecast system places about 40 % more probability on the outcome (half a bit) than DC. Observations like these illustrate the advantages of scores which allow intuitive interpretation of relative forecast merits.

Enhanced use of empirical benchmark models in forecast evaluation and in deployment can motivate a deeper evaluation of simulation models. The use of empirical models as benchmarks allows the comparison of skill between forecast systems based upon state-of-the-art simulation models and those using simpler, inexpensive alternatives. As models evolve and improve, such benchmarks allow one to quantify this improvement: the HadCM3 forecast system in this paper out-performs DC, whereas a HadGEM2 forecast system (with its smaller ensemble size) did not (Suckling and Smith 2013). Such evaluations cannot be done purely through the intercomparison of an (evolving) set of state-of-the-art models. The use of task-appropriate scores can better convey the information available from near-term (decadal) forecasts to inform decision making. It can also be of use in judging limits on the likely fidelity of centennial forecasts. Ideally, identifying where the most reliable decadal information lies today, and communicating the limits in the fidelity expected from the best available probability forecasts, can both improve decision-making and strengthen the credibility of science in support of policy making.