Skip to main content

Advertisement

SpringerLink
Log in

Adaptive stochastic integrated assessment modeling of optimal greenhouse gas emission reductions

  • Published:
Climatic Change Aims and scope Submit manuscript

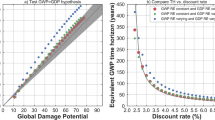
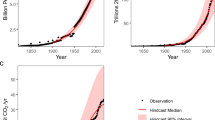
Abstract

We develop a method for finding optimal greenhouse gas reduction rates under ongoing uncertainty and re-evaluation of climate parameters over future decades. Uncertainty about climate change includes both overall climate sensitivity and the risk of extreme tipping point events. We incorporate both types of uncertainty into a stochastic model of climate and the economy that has the objective of reducing global greenhouse gas emissions at lowest overall cost over time. Solving this problem is computationally challenging; we introduce a two-step-ahead approximate dynamic programming algorithm to solve the finite time horizon stochastic problem. The uncertainty in climate sensitivity may narrow in the future as the behavior of the climate continues to be observed and as climate science progresses. To incorporate this future knowledge, we use a Bayesian framework to update the two correlated uncertainties over time. The method is illustrated with the DICE integrated assessment model, adding in current estimates of climate sensitivity uncertainty and tipping point risk with an endogenous updating of climate sensitivity based on the occurrence of tipping point events; the method could also be applied to other integrated assessment models with different characterizations of uncertainties and risks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Ackerman F, Stanton EA, Bueno R (2010) Fat tails, exponents, extreme uncertainty: Simulating catastrophe in dice. Ecol Econ 69(8):1657–1665

    Article  Google Scholar 

  • Cai Y, Judd K, Lontzek T (2012) Dsice: A dynamic stochastic integrated model of climate and economy. SSRN Scholarly Paper ID 1992674, Social Science Research Network

  • Cai Y, Judd K, Lontzek T (2013) The social cost of stochastic and irreversible climate change. Working Paper 18704, National Bureau of Economic Research

  • Costello CJ, Neubert MG, Polasky SA, Solow AR (2010) Bounded uncertainty and climate change economics. Proc Natl Acad Sci U S A 107(18):8108–10

    Article  Google Scholar 

  • Dowlatabadi H (1995) Integrated assessment models of climate-change - an incomplete overview. Energy Policy 23(4-5):289–296

    Article  Google Scholar 

  • Geist M, Pietquin O (2011) Parametric value function approximation: A unified view. In: 2011 IEEE Symposium on Adaptive Dynamic Programming And Reinforcement Learning (ADPRL), pp 9–16

  • Gerst MD, Howarth RB, Borsuk ME (2010) Accounting for the risk of extreme outcomes in an integrated assessment of climate change. Energy Policy 38(8):4540–4548

    Article  Google Scholar 

  • IPCC (2013) Climate change 2013: The physical science basis. Technical Report

  • Jones RN (2000) Managing uncertainty in climate change projections issues for impact assessment. Clim Chang 45(3/4):403–419

    Article  Google Scholar 

  • Kelly DL, Kolstad CD (1999) Bayesian learning, growth, and pollution. J Econ Dyn Control 23(4):491–518

    Article  Google Scholar 

  • Kriegler E, Hall JW, Held H, Dawson R, Schellnhuber HJ (2009) Imprecise probability assessment of tipping points in the climate system. Proc Natl Acad Sci U S A 106(13):5041–6

    Article  Google Scholar 

  • Lenton TM, Ciscar JC (2013) Integrating tipping points into climate impact assessments. Clim Chang 117(3):585–597

    Article  Google Scholar 

  • Mastrandrea MD, Schneider SH (2004) Probabilistic integrated assessment of “dangerous” climate change. Science 304(5670):571–5

    Article  Google Scholar 

  • Murphy JM, Sexton DM, Barnett DN, Jones GS, Webb MJ, Collins M, Stainforth DA (2004) Quantification of modelling uncertainties in a large ensemble of climate change simulations. Nature 430(7001):768–72

    Article  Google Scholar 

  • Murphy KP (2000) A survey of pomdp solution techniques. Technical report, UC Berkeley

    Google Scholar 

  • New M, Hulme M (2000) Representing uncertainty in climate change scenarios: a monte-carlo approach. Integr Assess 1(3):203–213

    Article  Google Scholar 

  • Newbold SC, Daigneault A (2009) Climate response uncertainty and the benefits of greenhouse gas emissions reductions. Environ Resour Econ 44(3):351–377

    Article  Google Scholar 

  • Nordhaus WD (1992) An optimal transition path for controlling greenhouse gases. Science 258(5086):1315–9

    Article  Google Scholar 

  • Nordhaus WD (2008) A Question of Balance: Weighing the Options on Global Warming Policies. illustrated edition edn. Yale University Press

  • Pindyck RS (2011) Fat tails, thin tails, and climate change policy. Rev Environ Econ Policy 5(2):258–274

    Article  Google Scholar 

  • Powell WB (2011) Approximate Dynamic Programming: Solving the Curses of Dimensionality, Wiley

  • Roe GH, Baker MB (2007) Why is climate sensitivity so unpredictable Science 318(5850):629–32

    Article  Google Scholar 

  • Rogelj J, Meinshausen M, Knutti R (2012) Global warming under old an new scenarios using ipcc climate sensitivity range estimates. Nat Clim Chang 2(4):248–253

    Article  Google Scholar 

  • Rumelhart DE, Hinton GE, Williams RJ (1986) Learning representations by back-propagating errors. Nature 323(6088):533–536

    Article  Google Scholar 

  • Russill C, Nyssa Z (2009) The tipping point trend in climate change communication. Glob Environ Chang-Hum Policy Dimens 19(3):336–344

    Article  Google Scholar 

  • Webster M, Santen N, Parpas P (2012) An approximate dynamic programming framework for modeling global climate policy under decision-dependent uncertainty. Comput Manag Sci 9(3):339–362

    Article  Google Scholar 

  • Weitzman ML (2009) On modeling and interpreting the economics of catastrophic climate change. Rev Econ Stat 91(1):1–19

    Article  Google Scholar 

  • Weitzman ML (2011) Fat-tailed uncertainty in the economics of catastrophic climate change. Rev Environ Econ Policy 5(2):275–292

    Article  Google Scholar 

  • Zickfeld K, Levermann A, Morgan MG, Kuhlbrodt T, Rahmstorf S, Keith DW (2007) Expert judgements on the response of the atlantic meridional overturning circulation to climate change. Clim Chang 82(3-4):235–265

    Article  Google Scholar 

  • Zickfeld K, Morgan MG, Frame DJ, Keith DW (2010) Expert judgments about transient climate response to alternative future trajectories of radiative forcing. Proc Natl Acad Sci U S A 107(28):12,451–6

    Article  Google Scholar 

Download references

Acknowledgments

The authors would like to extend their deepest appreciation to Dr. Hayriye Ayhan, Dr. Alexander Shapiro, and Dr. Roshan Joseph Vengazhiyil from the School of Industrial & Systems Engineering, as well as Dr. Athanasios Nenes from the School of Earth & Atmospheric Sciences at Georgia Institute of Technology for providing advice and intellectual insight into the research question.

Author information

Authors and Affiliations

  1. H. Milton Stewart School of Industrial and Systems Engineering, Georgia Institute of Technology, 765 Ferst Drive, Atlanta, GA, 30332-0205, USA

    Soheil Shayegh

  2. H. Milton Stewart School of Industrial and Systems Engineering and School of Public Policy, Georgia Institute of Technology, 765 Ferst Drive, Atlanta, GA, 30332-0205, USA

    Valerie M. Thomas

Authors
  1. Soheil Shayegh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Valerie M. Thomas
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Soheil Shayegh.

Electronic supplementary material

Below is the link to the electronic supplementary material.

(PDF 996 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shayegh, S., Thomas, V.M. Adaptive stochastic integrated assessment modeling of optimal greenhouse gas emission reductions. Climatic Change 128, 1–15 (2015). https://doi.org/10.1007/s10584-014-1300-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10584-014-1300-3

Keywords

Search

Navigation