Abstract
With record breaking heat waves, dryness, and floods in several parts of the world in recent years the question arises whether and to what extent the hazard of hydrometeorological extreme weather events has changed, and if changes can be attributed to specific causes. The methodology of probabilistic event attribution allows to evaluate such potential changes in the occurence probabilities of particular types of extreme events. We show that such a probabilistic assessment not only provides information on changing hazards in hydrometerological events but also permits statements about multivariate combinations of hydrometeorological variables. Hence attribution studies could be targeted specifically towards relevant impacts in particular sectors, if different suitable multivariate proxies are used. We demonstrate our methodology by using combinations of temperature, precipitation and humidity in the large ensemble of climate simulations within the weather@home project in order to derive impact-relevant quantities such as a seasonal water balance and heat stress imposed on the human body. Finally, we estimate the hazard probabilities of those events in South-East Europe, a region that has recently experienced severe summer dryness (2012) in combination with multiple heat waves.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Extreme weather and climate events have considerable and potentially highly destructive impacts on human societies and ecosystems, which include losses of human lives, economic and non-economic damages, and ecological responses (Meehl et al. 2000; Parmesan et al. 2000; Jentsch and Beierkuhnlein 2008; IPCC 2012; Reichstein et al. 2013). Meteorological extreme events in recent years (WMO 2011) have raised two major questions among scientists, decision-makers and the public (Coumou and Rahmstorf 2012):
-
whether and to what extent the magnitude and/or frequency of extreme events have increased,
-
and if such events are indeed linked to human-induced climate change.
Scientific studies have reported an increasing magnitude and frequency of some extreme events, such as heat waves and intense precipitation on different spatiotemporal scales, although reported changes are not evenly distributed (Allen and Ingram 2002; Benestad 2006; Alexander et al. 2006; Perkins et al. 2012; Coumou and Rahmstorf 2012; Hansen et al. 2012). Furthermore, it was pointed out that daily minimum temperatures are warming stronger than maximum temperatures and that the distributions of daily temperatures have shifted to higher temperatures, whereas changes in the variance are not as clearly pronounced (Donat and Alexander 2012; Donat et al. 2013). With respect to daily precipitation extremes, trends are generally more heterogenous, but nevertheless globally roughly two thirds of stations show increases, which lie mostly in the tropics and in higher latitudes (Westra et al. 2013).
Despite considerable natural climate variability, recent studies have highlighted the existence of a connection between human-induced global warming and changes in the odds of some meteorological extremes (Stott et al. 2004; Rahmstorf and Coumou 2011). This includes in particular threshold-exceeding heat extremes, which have been observed consistently with theoretical observations (Rahmstorf and Coumou 2011; Coumou et al. 2013) and are projected to further increase in frequency (Coumou and Robinson 2013). However, a causal attribution of any single extreme weather event to climate change in a deterministic sense is impossible (Allen et al. 2007), since any extreme event could occur ‘by chance’ in a natural climate. Hence approaches to attribute individual events deploy large climate model ensembles to derive probabilistic statements about rare extremes (Hegerl et al. 2006), which requires thorough model evaluation and bias adjustment (Massey et al. 2012). Such ‘Probabilistic Event Attribution’ has been demonstrated for several recent individual extreme weather events, such as heat waves in Western Europe and Russia (Stott et al. 2004; Otto et al. 2012), which mainly focus on one variable (e.g. 2m temperature) alone. Pall et al. (2011) extend this approach to study floods in England and Wales, using daily precipitation and combining a meteorological and hydrological model and analyses. However, many extreme events and their impacts on societies and ecosystems are characterised by a combination of extreme climate variables, and using joint quantities in order to evaluate more reliably present and future impacts of climatic changes has been suggested (Fischer and Knutti 2012).
An extraordinary dry summer season in combination with multiple heat waves reaching up to 40 °C has affected South-East Europe (SEE) in 2012 (Hydrometeorological Service of Serbia 2012b) and has been associated with losses in the order of billion euros (Gordana Simic, pers. comm.). This seems in line with studies that observed that heat wave intensity, length and frequency have increased in Europe over the last century (Della-Marta et al. 2007) and particularly in the last 50 years in South-East Europe (Kuglitsch et al. 2010). Those insights have been further substantiated by modelling studies that indicated that extreme temperatures are increasing more rapidly than mean temperatures in South-Central European regional climate simulations, indicating that heatwave frequency, amplitude, number and length will likely become more severe in this century (Fischer and Schär 2010).
However, changes in hydrometeorological phenomena that are not explicitly linked to temperatures - such as droughts -, are highly uncertain. Droughts are complex phenomena driven by human and hydrometeorological factors with impacts that differ greatly between locations. In this study, we focus on meteorological droughts or dryness, which is characterised by a precipitation deficit. Hence, we do not account for links between dryness and the socio-economic contexts of human water use. Projections of future conditions of dryness are highly non-trivial and uncertain, because land-atmosphere interactions and feedbacks can induce non-linear and self-enforcing events (Koster et al. 2004) and precipitation patterns are influenced by atmospheric components such as aerosols and large-scale atmospheric circulation patterns (Seneviratne et al. 2012). Furthermore, observational data of dryness and associated variables (e.g. soil moisture) is relatively rare (Seneviratne 2012). On a global scale, overall increases and decreases in meteorological droughts have been reported, highlighting the aforementioned uncertainties (Dai et al. 2004; Dai 2011; Sheffield and Wood 2008; Seneviratne 2012). Nevertheless, studies agree that drought indices in southern and southern-central Europe have recently increased (Alexander et al. 2006; Sheffield and Wood 2008). (Hoerling et al. 2012) assess and discuss the observed Mediterranean wintertime drying in detail and find that this drying signal is at least in part attributable to external anthropogenic forcing, and changing patterns in sea surface temperatures have likely played an important role. (Giorgi 2006) suggested the Mediterranean region and adjacent North-Eastern Europe as ‘climate hot spots’, mainly due to increasing summer precipitation deficits in the former region, and a pronounced regional warming combined with increasing interannual variability of precipitation in the latter.
In this study we explore the insights into inter-decadal changes to be gained from a probabilistic assessment targeted at the extreme summer of 2012 in South-East Europe. Hereby, we follow the definition of the World Meteorological Oranization’s Disaster Risk Reduction ProgrammeFootnote 1, in which the term ‘hydrometeorological hazard’ denotes a potentially damaging physical event, including extreme multivariate combinations of hydrometeorological variables. Accordingly, the broader notion of ‘risk’ implies a combination of hazard, exposure and vulnerability, which determines actual impacts. In this context, by utilizing ‘impact-relevant proxies’, we mean that the pertinent hydrometeorological variables or combinations thereof are likely to cause significant impacts in specific sectors with a strong connection to climate, particularly agriculture and human health.
First, we will derive indices of combinations of climate variables in order to obtain proxies for impact-relevant meteorological conditions. In particular, we deploy an index for seasonal/monthly precipitation deficits to estimate the hazard probability of summer dryness. Furthermore, we use the simplified wet bulb globe temperature as a proxy for heat stress imposed on the human body.
Second, we apply our methodology to asses changes in heat and dryness probabilities in South-East Europe using two decade-long climate ensembles similar to (Massey et al. 2012). A prerequisite to this approach is to obtain a large ensemble of simulations, which is evaluated and adjusted for relative biases with observational products. Hence, we first perform some basic tests and bias adjustment in order to ensure that past and present climatic conditions in South-East Europe are adequately represented.
2 Material and methods
2.1 Study Area
This study focuses on a recent hot and dry summer with exceptional multi-day heat waves in South-East Europe. The study region is bounded by 43.5-47 °N and 18.5-22 °E, spanning about 450 km in N-S and 300 km in W-E direction, and covers large parts of Northern Serbia and Southern Hungary, as well as smaller areas in Bosnia-Herzegovina, Croatia and Romania. The largest fraction of the region is part of the southern Pannonian Basin, whereas southeastern and southwestern stretches are covered by highlands. This region comprises relatively homogeneous topographical conditions which provides for better model performance. Although the region is geographically located at the crossroads between South-East and East-Central Europe, for both of which no universal geographical definition exists, the region will be henceforth referred to as ‘South-East Europe’, since its largest parts lie within states on the Balkan Peninsula.
The climate in the defined region is temperate to moderate continental and lies in a transitional zone between humid-continental climate to the north and east and humid-subtropical climate to the south and west (Peel et al. 2007). The average annual precipitation sums are in the range of 540 to 820 mm and precipitation falls throughout the year with a wetter season in summer (Hydrometeorological Service of Serbia 2012a). The average summer temperature in the E-OBS observational dataset for the study area has increased from 19.9°C in the 1960s to 21.4°C in the 2000s decade. Changes in mean precipitation seem less clear and are subject to large intra- and interannual variability. The E-OBS dataset points at a slight increase of summer rainfall since the 1960s.
2.2 Model simulations and observational data
A large number of climate simulations has been generated by volunteers through the climateprediction.net project (Allen 1999). In this project, members of the public donate idle computer time to compute large ensembles of climate model simulations. This study follows a similar methodological approach to (Massey et al. 2012), in which decade-long ensembles are assessed in order to determine meteorological risk of extreme weather. A large number of ensemble members (> 1500 for each decade) of possible weather in 1960-1970 are compared to simulations of 2000-2010 climate, with decade-long simulations being assumed to smooth the influence of natural climatic variability (Massey et al. 2012). The ensembles were generated by the HadAM3P general circulation model (GCM) and an embedded dynamical regional climate model (RCM) at a horizontal resolution of 1.25x 1.875° and 0.44x 0.44°, respectively. HadAM3P is based on a regular N96 Gaussian Grid with 19 vertical levels and a time step of 15 minutes. The model is based on the HadAM3 atmospheric GCM (Pope et al. 2000), with some improvements regarding the representation of clouds, radiative effects of convection, a more realistic sulphur cycle and changes to the land surface scheme (Massey 2013). The model is forced at the boundaries by observed sea-surface temperatures taken from the HadISST dataset (Rayner et al. 2003). For a detailed description of both models and the weather@home modelling setup, please see (Massey 2013) and Massey et al. (2014, submitted). The large number of simulations allows to assess climatic extremes, although a model evaluation is required to assess the model’s ability to reproduce observations of real climate variables and account for model bias (Massey et al. 2012). Importantly, the evaluation and bias adjustment procedure of the model ensemble on sub-monthly time scales does not include the extreme events in 2012, because otherwise occurrence of extremes would potentially be treated as evidence of its cause.
Observational data is crucial in order to assess potential biases in the model simulations. The high-resolution (0.22°×0.22°) land-only E-OBS dataset is used for model evaluation with daily mean temperatures (Haylock et al. 2008). Relative humidity is not available in the E-OBS data and was obtained from the NCEP reanalysis project (Kalnay et al. 1996). Furthermore, a simple plausibility check of the model’s simulations was conducted as a correlation analysis between 500 hPa geopotential heights and monthly temperatures using ERA-Interim reanalysis data (Dee et al. 2011).
Area-averaged 90-day time series of temperature and relative humidity were constructed for the summer season from the RCM ensemble. In addition, 30-day time series of daily temperatures and precipitation were constructed in order to analyse individual summer months. The applied bias adjustment procedure is outlined in the next subsection. We assess and discuss in this study only extremes in the summer season and hence, the return period estimates do not account for potentially similar conditions in other seasons. Return periods were derived by plotting each ensemble value against its rank in the entire sorted sample. A bootstrapping procedure similar to (Otto et al. 2013) was applied to derive 5 to 95% uncertainty intervals for return periods by resampling each ensemble 2500 times.
2.3 Model evaluation and bias adjustment
Basic tests are crucial in modelling studies in order to evaluate whether model output is in a plausible range. An initial large-scale check of the model’s ability to represent meteorologically plausible conditions is conducted as a correlation analysis of geopotential heights over Europe on temperatures and precipitation in the study region, similar to (Otto et al. 2012). This analysis is performed for monthly mean values in ensemble members in the 2000-2010 decade and 34 years of ERA-Interim data as a monthly correlation analysis and revealed that geopotential heights over southern and eastern Europe correlate well with SE European temperatures (Fig. 1). Precipitation shows an inverse pattern, in which dry Augusts in SE Europe are associated with high geopotential heights. Although some details are not well-represented in the model, which might also be due to the observations being noisier because of differences in the sample size (N Obs = 34 vs. N Model ≈ 1400), the model captures both patterns well. This might indicate relatively realistic large-scale meteorological conditions on monthly time scales and hence some confidence in the model. Despite a large warm bias that prevails in the global model (Fig. 1), geopotential heights in August 2012 are well within the scatter-plot of previously observed conditions, which might point at not fundamentally different meteorological conditions.
(Top) Pearson’s correlation coefficients between August temperatures in South-East Europe and geopotential heights in the ERA-Interim dataset (left) and the global model (right). (Center) Similar to above, correlation between SE European August precipitation and geopotential heights in the observations (left) and in HadAM3P (right). (Bottom) Scatter plots of August temperature (left) and precipitation (right) vs. ERA-Interim observations in SE Europe
Despite the good representation of large scale patterns and constant improvements in model formulation considerable biases in GCM and RCM simulations in many parts of the world persist. Hence statistical evaluation and an adjustment for relative biases with observational products is important for impact-relevant interpretations of model output (Massey et al. 2012), since ensemble simulations of the global and regional model have shown biases over European land regions (Otto et al. 2012; Massey 2013). For example, uncorrected averaged model ensembles underestimate summer warming between the 1960s and 2000s, and the slight increase of average summer precipitation in the E-OBS data of about 26mm is not reflected in resampled uncorrected model realizations (ΔP 2000s−1960s = −6 ± 46mm).
A simple mean and variance correction is applied to the area-averaged model output of temperatures and relative humidity for both decades to obtain a bias adjusted distribution MOD′:
Mean and standard deviation of the non-parametric modelled and observed distributions are specified by μ MOD , σ MOD and μ OBS , σ OBS , respectively. The model output is given by MOD. This simple correction procedure is used extensively to account for biased model output elsewhere (Massey et al. 2012). It can be considered as a sensible method, as it simply scales mean and variance of modelled data to match observations and thus does not qualitatively alter the distributions.
2.4 Assessment of impact-related variables
To ensure the usefulness of this study beyond scientific understanding alone we aim to address impact-related variables. However, it should be noted that a comprehensive assessment of disaster risk imposed by extreme weather is hardly possible with single meteorological variables alone, because vulnerability and exposure are likewise important (Huggel et al. 2013; IPCC 2012). Hence this study assesses multivariate proxies of hydrometeorological variables, which we assume to be in general more likely to be associated with significant societal impacts than ‘classical’ univariate meteorological variables (see also (Beniston 2009; Fischer and Knutti 2012)), although we emphasize that these indices are not ‘per se’ relevant for any particular impacts. More specifically, we have chosen two measures that are presumably a suitable proxy for evaluating monthly or seasonal dryness in ecosystems and the agricultural sector (a seasonal water balance), and for short-term (5-day) heat stress imposed on the human body.
With regard to summer 2012, most damages that were quantified in monetary terms were caused by dryness and wildfires, particularly affecting forest ecosystems and agriculture (Gordana Simic, pers. comm.), for which the former regional water balance might be a useful proxy. Multi-day heat waves had a considerable impact on human health, particularly on the elder population, which we assume to be reasonably approximated with the latter index. It should be further stressed that we are using spatially aggregated measures in a rectangular region in South-East Europe derived through uniform spatial weighting, which are bias adjusted with observational products. The estimated hazard probabilities are not uniform in a region that comprises greatly varying socio-economic and local meteorological conditions. Hence, absolute thresholds for specific impacts, e.g. for local agriculture in valleys, should not be confounded with spatially aggregated measures. Nevertheless, the assessment provides an estimate of how the probability of conditions similar to summer 2012, with large measurable effects on the ground in several countries, have changed between the 1960s and the present on a regional scale.
Water Balance
A comprehensive metric to assess meteorological droughts is very difficult to derive, as characteristics for dryness such as intensity, magnitude, duration and spatial extent are highly variable. Drought indices such as the Standardized Precipitation Index (SPI) are widely in use (Vicente-Serrano et al. 2010), in which a parametric distribution is fitted to data, and drought is defined as a relative deviation from the mean. This approach seems not very practical for decadal ensemble simulations such as in this study though, because dryness is not assumed to be stationary between both decades. Therefore, we define an absolute measure as the monthly and seasonal difference between precipitation (P) and potential evapotranspiration (PET), P−PET, similarly to the first step in the derivation of a PET-adjusted SPI (Vicente-Serrano et al. 2010). A combined consideration of these two quantities can hence be taken as a useful proxy for dryness (see also further discussion in (Sherwood and Fu 2014)), or a simple hypothetical water balance, as PET reflects environmental water demand. PET can be estimated with physical or empirical methods, where the former are likely to be more realistic, and the latter require less input data and emipirically estimate PET. The widely used (Thornthwaite 1948) method is applied in this study to compute PET from bias adjusted model output, so that
Herein, T is the monthly mean temperature (in °C), I is a location-specific heat index based on monthly-mean temperaturesFootnote 2 and m is a coefficientFootnote 3. K is a function of the number of days in a given month and the latitude, thus reflecting the average number of daytime hours in a given month. Although the empirical Thornthwaithe-method has been criticized as being oversimplistic and biased (Seneviratne 2012; Sheffield et al. 2012; Trenberth et al. 2014), the so-derived metric P−PET can be seen a simple proxy for dryness in any given month or season.
Heat Stress
Heat stress to the human body is not only a function of ambient temperatures, but depends also on other variables such as relative humidity. This is due to the body’s ability to release moisture more easily in dry air and hence enable cooling. Thus multivariate heat stress metrics are designed to reflect the fact that combinations of climate variables determine heat stress (Fischer and Knutti 2012). The simplified wet-bulb globe temperature (WBGT) is designed to reflect this concept and used by weather services to issue health warmings:
In the latter equation, T is air temperature and e denotes water vapour pressureFootnote 4 (Fischer and Knutti 2012).
3 Results
3.1 Model evaluation
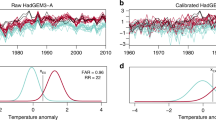
Despite large-scale plausible atmospheric regression patterns in the model, the evaluation of the model output with observations is crucial in order to assess and adjust potential model biases. A reasonable match of model output with observations is a prerequisite for assessing extreme events in the tails of the distribution. Five day rolling mean temperatures were individually adjusted for relative biases for the analysis of short term heat extremes (Fig. 2). Additionally, daily temperatures were bias adjusted and subsequently aggregated to derive monthly temperatures and PET (see Supplementary Online Material (SOM), Figure 1). The heat proxy WBGT was jointly biased-adjusted, i.e. using 5-day ‘observed’ and simulated WBGT values from the large ensemble (Fig. 2). The simple bias correction procedure was not applied to simulated precipitation though, because this could potentially introduce offsets or non-physical values in the dry tails of the distribution if for instance the variance in the ensemble differs to the observations. We also did not use more invasive or parametric bias correction techniques, because we are interested in the tails of the large ensemble, which could be highly sensitive if adjusted to ten years of observations. Nevertheless, since our study focuses on interdecadal changes of extremes, we argue that the considerable dry bias in the simulations (SOM, Figure 2) is consistent within the model between the two decades, and hence changes in the return periods of P−PET extremes can be evaluated.
Observed and modelled 5-day temperatures (top) for the summer season, with uncorrected (grey) and bias adjusted (black) simulated temperatures. The distribution of the ‘simplified wet bulb globe temperature’ as a proxy for 5-day heat stress (bottom) is shown for the ‘observations’ and the model. The red dots indicate a joint bias adjustment of WBGT, whereas the black dots show WBGT, when temperatures and relative humidities are accounted for individually (grey dots: uncorrected model)
Five day area-averaged uncorrected model ensembles show cold biases for both decades in lower quantiles in summer (Fig. 2) but relatively good agreement for the upper (hot) quantiles. Applying the simple bias adjustment procedure described above, temperatures match observations in the lower and upper quantiles, and considerable biases only remain in very few extreme values. This also holds for the correction of temperature biases for the individual summer months (SOM, Figure 1). A notable exception are June temperatures (SOM, Figure 1) in both decades, which seem to be not as well represented in the model.
For the five daily WBGT, we conducted both an individual (single variables) and joint bias adjustment (Fig. 2). We find that the uncorrected model ensemble is strongly biased towards too low relative humidity. However, both adjustment procedures are capable to remove this strong bias, particularly in the hot tail of the distribution. Since the joint correction w.r.t. observations shows slightly less biases, we use the so-derived ensemble for analyzing the odds of extreme conditions.
3.2 Changes in the odds of extreme weather
Summer 2012 was very hot and dry in SE Europe (Fig. 3). A high pressure zone prevailed throughout most of the summer, which made it the hottest and third-driest on record in Serbia (Hydrometeorological Service of Serbia 2012b). Seasonal temperature anomalies between 2°C and 5°C (relative to 1961-1990) and exceptionally low precipitation levels were recorded throughout southern Europe (Hydrometeorological Service of Serbia (2012b; Dong et al. (2012); Fig. 3). Several multi-day heat waves occurred in summer 2012 through high pressure ridges and anticyclones that caused advection of hot subtropical air into the SE European region. Maximum daily temperatures surpassed 40°C and minimum daily temperatures remained above 25°C in some locations for several days during two heat waves in August 2012 [Hydrometeorological Service of Serbia 2012b].
(Top) Summer 2012 seasonal temperature and precipitation anomalies with reference to 1960-1990. Black dots indicate the study region. (Center and Bottom) Time Series of summer 2012 observations, a climatological mean (1960-1990), observations of earlier summer weather in the 2000s and single ensemble members
A pronounced warming of mean summer temperatures of about 1.5°C was observed in the study region between the 1960s and 2000s. Changes in return periods of mean monthly temperatures reflect this pattern, as the frequency of very warm months has increased (horizontal difference between blue and red line in Figure 4). However, neither magnitude nor frequency of extreme warm months show uniform changes. The magnitude of a 10 year event in monthly or 5-day temperatures has increased by about 1.5°C to 2°C, which is relatively small compared to the anomaly itself (a 10-year heat event in 5-day temperatures is both in the 1960s and 2000s more than 6°C above the mean) but huge compared to global mean temperature increase. Observed magnitude increases are strongest in July mean temperatures, as a statistical ‘1-in-10 years’ warm July exceeded 22.7 °C in the 1960s and 24.8 °C in the 2000s. In addition, the frequency of very rare events in July with return periods of 100+ years in the 1960s shows a pronounced increase by about an order of magnitude. Similar, but slightly less pronounced changes are observed in June and August (Fig. 4). Interestingly, the changes in the tails of the temperature distribution in the ensemble in July and August, as well as for the 5-day temperatures in summer can be largely explained by the mean warming. This can be seen in Fig. 4, where the darkblue line represents the simulated ensemble of the 1960s with the added mean warming between the two decades.
Return periods of monthly mean temperatures in June, July, August and 5-day mean temperatures in summer (panel a) - d), respectively). Return periods of very warm 5-day mean temperatures model ensembles based on individual years in the 1960s and 2000s are shown in panel e) and f) for bias adjusted and non-corrected data, respectively
For some types of impacts, 5-day temperatures might be more relevant than monthly mean temperatures, for example as a proxy for short-term heat stress during a summer heat wave. The large model ensemble indicates a pronounced reduction in the return periods of those multi day heat wave events in the summer season. For instance an event similar to the highest 5-day average temperature in SEE 2012 returned in average only once or twice per century in the 1960s, whereas in the 2000s return periods of well below ten years are shown. Return periods were also calculated for single years in the large ensemble (Fig. 4, bottom two panels) and confirmed the overall picture of a pronounced increase in the frequency of heat extremes. Model ensembles for all years in the 2000s showed a distinctly higher frequency of warm extremes, both in bias adjusted and uncorrected simulations. This finding indicates that the interannual temperature variability between ensembles based only on individual years, which could be for example driven by different modes of the North Atlantic oscillation and associated different observed sea surface temperatures, is only of relatively minor importance in our study region compared to the interdecadal changes, which are mainly caused by other drivers such as greenhouse gases and aerosols. Since this holds both for the bias-corrected and non-corrected ensembles, this potentially confounding factor does not constrain our methodology, bias adjustment procedure and results.
However, with increasing temperatures evapotranspiration is elevated, which might induce a higher water demand for agricultural crops and in many ecosystems on monthly to seasonal time scales. Therefore it is conceivable that dryness has increased in the region, despite the absence of pronounced changes in the precipitation regime. The evaluation of the simple potential water balance as a measure for dryness shows a reduction in return periods of extreme monthly and seasonal water deficits (Fig. 5), albeit antecedent soil moisture and groundwater conditions were not accounted for. Furthermore, the precipitation ensemble shows a considerable dry bias, and hence statements should only be made with reference to interdecadal changes rather than absolute values of P−PET. Thus the measure is indicative of changes in the hazard of dryness but does not allow for a quantification of that risk.
On a seasonal scale (JJA), extreme summer dryness such as in summer 2012 now occurs much more frequently than in the 1960s (Fig. 5d). Nevertheless it should be noted that the frequency increase of dry summer events seems to be less pronounced than for temperature alone, which is due to effectively unchanged dry tails in the precipitation ensemble (SOM, Figure 3). In the individual months, a consistent change towards drier summer conditions can be seen in the large ensemble, albeit to a slightly varying degree. For example in June, slightly and non-significant drier extremes in the model ensemble might explain a little stronger increase in dryness compared to interdecadal changes in July and August.
Besides economic losses heat waves in summer have considerable effects on human health. Heat stress as expressed through a 5-day mean wet-bulb globe temperature is an indicator for these effects and was calculated for the summer months in SEE (Fig. 5). The observed average 5-day wet bulb globe temperature in summer has warmed from 23.4°C to 24.2°C in SE Europe between the two decades. Nevertheless, and despite the observed strong increase in 5-day temperature extremes, we find that the extreme hot tails of WBGT with return periods of more than 100 years have only marginally and not significantly increased. On the other hand, moderately warm events, with return periods between one and 20 years, show increased wet bulb globe temperatures and reduced return periods. For example, a 10-year event has warmed by about 0.3°C (from 28.4°C to about 28.7°C) in between the two decades. However, the observed changes in WBGT are clearly less pronounced than changes in 5-day temperatures alone. This could be explained by a decline in relative humidity in the 2000s, which partly counterbalances the effects of increasing 5-day temperatures. This finding is substantiated by calculating a counterfactual WBGT from the 1960s ensemble by adding the mean interdecadal warming (darkblue line in Fig. 5), which shows much higher wet bulb globe temperatures due to higher relative humidities.
In conclusion, it has been shown that the frequency of heat waves and other temperature-related quantities (WBGT; P−PET) has increased in South-Europe, but those increases are neither temporally nor with respect to the different metrics and variables uniform. This might indicate that impacts imposed on different sectors in the region might occur differently, with exposure and vulnerability being likewise major factors.
4 Discussion
This study has two key objectives:
(1) the derivation of suitable indices based on combinations of meteorological variables that might indicate impacts of extreme events and,
(2) the assessment of changes in extreme weather risk and impact-related variables from the model simulations.
The magnitude and frequency of monthly and 5-day warm temperature extremes in summer have increased considerably in SEE between the 1960s and the 2000s. These results agree with earlier studies on heat waves in Europe and Western Russia (Stott et al. 2004; Otto et al. 2012) but on a smaller spatial scale particularly in a region recently experiencing repeated heat waves. In addition to that indices combining temperature and precipitation to assess changes in dryness and heat stress risk have been analysed and also show an increase in return time. It should be noted that these model-based results are subject to uncertainties.
Firstly, decade-long observations are relatively short, which might limit the potential of bias correction methods. Hence, a follow-up study could explore the sensitivity of attribution results to different observational time periods and different observational data sets.
Secondly, the model output has to be interpreted within the methodological limitations of the climate model. In the context of this study, this includes particularly the ability of the climate model to reliably represent the frequency and magnitude of self-enforcing and complex extreme weather events such as heat waves and extreme dryness (Quesada et al. 2012). The large ensemble showed a considerable dry bias compared to observations, which highlights that the presented potential water balance proxy should be interpreted only in terms of the interdecadal changes, rather than absolute dryness.
Thirdly, the tails of the temperature and WBGT distributions are sensitive to the applied type of bias adjustment, which remains a fundamental methodological uncertainty. Our methodology is based on the assumption that the extreme tails are reasonably well simulated in the model, although largely unsampled in the observations. We applied a normalization based bias adjustment, which could successfully account for biases in the mean and variance of the simulated temperature and WBGT ensembles, without qualitatively altering the distribution.
Fourthly, the empirical Thornthwaithe method that was used to derive PET in the simple water balance model has been shown to be biased, because it is not based on physical principles (Seneviratne 2012; Sheffield et al. 2012; Sherwood and Fu 2014; Trenberth et al. 2014). Also, the applied water balance proxy P−PET does not account for several other factors that determine dryness, for example antecedent soil moisture deficits (Seneviratne 2012; Sheffield et al. 2012). Hence, a future study could address those caveats, for instance by calculating PET based on the Penman-Monteith methodology, and by accounting for time-dependent soil moisture deficits in European land regions.
However, despite these limitations our analysis allows to obtain robust results on the change in risk of extreme weather events characterised by the employed indices. In particular, this study has demonstrated firstly, that a hypothetical water balance (P−PET) points at more frequent extreme monthly and seasonal water deficits in summer in SE Europe despite the absence of clearly evident changes in the return times of summer precipitation. Secondly, we showed that a proxy for heat stress imposed on the human body (WBGT) indicates more frequent moderately warm 5-day periods in the summer season. We emphasize that such a multivariate assessment of meteorological variables is likely to be more relevant and a useful complement to a consideration of ‘meteorological’ variables alone in order to assess climate impacts (see also (Fischer and Knutti 2012)). Nevertheless, vulnerability and exposure are critically important and have to be considered if an assessment of disaster risk or climate impacts is to be carried out.
It should be noted further that extreme weather risk has not been attributed specifically to human drivers in this study, since changes in natural and anthropogenic forcing have both contributed to the probability of weather events (Peterson et al. 2012). Changes in natural forcings are known to have exerted influence on the global climate, although the bulk of global mean warming in the last 50 years has been due to anthropogenic forcing (Stott et al. 2000). A future study could corroborate the here derived results with a counterfactual experiment similar to Pall et al. (2011) or Otto et al. (2013), in which the model is run with pre-industrial climate forcings. This could be particularly meaningful, if it was combined with a model evaluation and observation-based accounting for biases over different time periods, as performed in this study.
Despite the above described limitations, however, we can show that with relatively easily obtained indices of dryness and heat stress quantitative insights into changes in extreme weather risk and impact-related joint variables can be revealed. We demonstrate in a follow up study (Sippel et al., in prep. ) that such results are indeed very valuable, within and beyond acadamia. For example, this kind of results could serve stakeholders to assist in adaptation planning in various sectors, such as health, water and agriculture in South-East Europe, which is highly vulnerable to climatic extreme events.
This example shows that even without detailed impact model simulations relevant quantitative information about potential changes of hazard in hydrometeorological extreme events can be inferred. These changes are, not unexpectedly, different depending on the selected proxy, with the heat stress index representing the health sector and the water deficit index being most relevant for the agricultural sector.
5 Conclusion
The main conclusion we can draw from this study is that hydrometeorological hazard has changed in South-East Europe including a distinct increase in the frequency of summer heat waves. Multivariate proxies for potential impacts show likewise pronounced changes and constitute a promising approach to link probabilistic attribution studies with more impact-relevant measures. These changes in hydrometeorological extremes can be attributed to changes in sea surface temperatures, which are subject to a mix of different natural and anthropogenic forcings, although a large fraction of the observed warming temperature between the 1960s and the 2000s are qualitatively attributable to human-induced climate changes (see e.g. (Stott et al. 2004)). The outlined findings have implications for regional adaptation planning as sector specific relevant variables are analysed in addition to purely meteorological variables. The obtained results are robust as regional model evaluation and bias adjustment with relatively fine-scaled observational data could largely remove biases in temperature distributions, although a considerable dry bias is prevalent in the precipitation ensemble.
This study is a promising example of how future research can extend attribution science towards more impact-relevant approaches. For this kind of research to be most useful an on-going dialogue between attribution scientists and stakeholders in the relevant sectors and regions is crucial in order to develop climate information tools that are relevant for adaptation planning.
Notes
\(I = {\sum }_{i=1}^{12} (\frac {T_{i}}{5})^{1.514}\)
m = 6.75 × 10−7 I 3 − 7.71 × 10−5 I 2 + 1.79 × 10−2 I + 0.492
Water vapour pressure is calculated from relative humidity in the model output by \(rH = \frac {e}{E} \times 100\%\). Herein, E reflects saturation vapour pressure, which can be approximated with the Magnus-Formula (Sonntag 1990): \(E (T) = 6.112 hPa \times e^{\frac {17.62 T}{243.12^{\circ } C +T}} \hbox {.}\)
References
Alexander L, Caesar J, Collins D, Gleason B, Haylock M, Klein Tank A, Trewin B, Rahimzadeh F, Trewin B, Zhang X et al (2006) Global observed changes in daily climate extremes of temperature and precipitation. J Geophys Res Atmos 111(D5)
Allen M (1999) Do-it-yourself climate prediction. Nat 401(6754):642–642
Allen M, Ingram W (2002) Constraints on future changes in climate and the hydrologic cycle. Nature 419(6903):224–232
Allen M, Frame D, Min S, Min S, Pall P, Stone D, Stott P, Yukimoto S (2007) Scientific challenges in the attribution of harm to human influence on climate. Univ Penn Law Rev:1353–1400
Benestad RE (2006) Can we expect more extreme precipitation on the monthly time scale? J Clim 19(4):630–637
Beniston M (2009) Trends in joint quantiles of temperature and precipitation in Europe since 1901 and projected for 2100. Geophys Res Lett 36(7)
Coumou D, Rahmstorf S (2012) A decade of weather extremes. Nature Clim Change 2(7):491–496
Coumou D, Robinson A (2013) Historic and future increase in the global land area affected by monthly heat extremes. Environ Res Lett 034(3):018
Coumou D, Robinson A, Rahmstorf S (2013) Global increase in record-breaking monthly-mean temperatures. Clim Change 118(3-4):771–782
Dai A (2011) Drought under global warming: a review. Wiley Interdiscip Rev Clim Change 2(1):45–65
Dai A, Trenberth K, Qian T (2004) A global dataset of palmer drought severity index for 1870-2002: Relationship with soil moisture and effects of surface warming. J Hydrometeorol 5(6):1117–1130
Dee D, Uppala S, Simmons A, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda M, Balsamo G, Bauer P, et al (2011) The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q J Roy Meteor Soc 137(656):553–597
Della-Marta P, Haylock M, Luterbacher J, Wanner H (2007) Doubled length of western European summer heat waves since 1880. J Geophys Res Atmos 112(D15)
Donat M, Alexander L (2012) The shifting probability distribution of global daytime and night-time temperatures. Geophys Res Lett 39(14)
Donat M, Alexander L, Yang H, Durre I, Vose R, Dunn R, Willett K, Aguilar E, Brunet M, Caesar J, et al (2013) Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The Hadex2 dataset. J Geophys Res Atmos 118(5):2098–2118
Dong B, Sutton R, Woollings T (2012) The extreme European summer of 2012. Bull Am Meteorol Soc 93(7):28–32
Fischer E, Knutti R (2012) Robust projections of combined humidity and temperature extremes. Nat Clim Change 3:126–130
Fischer E, Schär C (2010) Consistent geographical patterns of changes in high-impact European heatwaves. Nat Geosci 3(6):398–403
Giorgi F (2006) Climate change hot-spots. Geophys Res Lett L08(8):707
Hansen J, Sato M, Ruedy R (2012) Perception of climate change. Proc Natl Acad Sci USA 109(37):E2415—E2423
Haylock M, Hofstra N, Klein Tank A, Klok E, Jones P, New M (2008) A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006. J Geophys Res Atmos 113(D20)
Hegerl G, Karl T, Allen M, Bindoff N, Gillett N, Karoly D, Zhang X, Zwiers F (2006) Climate change detection and attribution: Beyond mean temperature signals. J Clim 19(20):5058–5077
Hoerling M, Eischeid J, Perlwitz J, Quan X, Zhang T, Pegion P (2012) On the increased frequency of Mediterranean drought. J Clim 25(6)
Huggel C, Stone D, Auffhammer M, Hansen G (2013) Loss and damage attribution. Nat Clim Change 3(8):694–696
Hydrometeorological Service of Serbia (2012a) Basic climate characteristics for the territory of serbia. http://www.hidmet.gov.rs/podaci/meteorologija/eng/
Hydrometeorological Service of Serbia (2012b) Climatological analysis of the year 2012 for the territory of the Republic of Serbia. Hydrometeorological Service of Serbia. http://www.hidmet.gov.rs
IPCC (2012) Managing the risks of extreme events and disasters to advance climate change adaptation Field CB, Barros V, Stocker T, Dahe Q, Dokken DJ, Ebi K, Mastrandrea MD, Mach KJ, Plattner GK, Allen SK, Tignor M, Midgley PM (eds), Cambridge University Press, Special Report of the Intergovernmental Panel on Climate Change
Jentsch A, Beierkuhnlein C (2008) Research frontiers in climate change: effects of extreme meteorological events on ecosystems. C R Geosci 340(9):621–628
Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J, et al (1996) The NCEP/NCAR 40-year reanalysis project. Bull Am Meteorol Soc 77(3):437–471
Koster R, Dirmeyer P, Guo Z, Bonan G, Chan E, Cox P, Gordon C, Kanae S, Kowalczyk E, Lawrence D, et al (2004) Regions of strong coupling between soil moisture and precipitation. Sci 305(5687):1138–1140
Kuglitsch F, Toreti A, Xoplaki E, Della-Marta P, Zerefos C, Türkeṡ M, Luterbacher J (2010) Heat wave changes in the eastern Mediterranean since 1960. Geophys Res Lett 37(4)
Massey N (2013) PhD-Thesis. UK, Oxford
Massey N, Aina T, Rye C, Otto F, Wilson S, Jones R, Allen M (2012) Have the odds of warm November temperatures and of cold December temperatures in Central England changed Bull Am Meteorol Soc 93:1057–1059
Meehl G, Karl T, Easterling D, Changnon S, Pielke R, Changnon D, Evans J, Groisman P, Knutson T, Kunkel K, et al (2000) An introduction to trends in extreme weather and climate events: Observations, socioeconomic impacts, terrestrial ecological impacts, and model projections. Bull Am Meteorol Soc 81(3):413–416
Otto F, Massey N, Oldenborgh G, Jones R, Allen M (2012) Reconciling two approaches to attribution of the2010 Russian heat wave. Geophys Res Lett 39(4)
Otto F, Jones R, Halladay K, Allen M (2013) Attribution of changes in precipitation patterns in African rainforests. Philos T Roy Soc B 368(1625)
Pall P, Aina T, Stone D, Stott P, Nozawa T, Hilberts A, Lohmann D, Allen M (2011) Anthropogenic greenhouse gas contribution to flood risk in England and Wales in autumn 2000. Nature 470(7334):382–385
Parmesan C, Root T, Willig M (2000) Impacts of extreme weather and climate on terrestrial biota. Bull Am Meteorol Soc 81(3):443–450
Peel M, Finlayson B, McMahon T (2007) Updated world map of the Koppen-Geiger climate classification̈. Hydrol Earth Syst Sci Discuss 4(2):439–473
Perkins S, Alexander L, Nairn J (2012) Increasing frequency, intensity and duration of observed global heatwaves and warm spells. Geophys Res Lett 39(20)
Peterson T, Stott P, Herring S (2012) Explaining extreme events of 2011 from a climate perspective. Bull Am Meteorol Soc 93(7):1041–1067
Pope V, Gallani M, Rowntree P, Stratton R (2000) The impact of new physical parametrizations in the Hadley Centre climate model: HadAM3. Clim Dyn 16(2-3):123–146
Quesada B, Vautard R, Yiou P, Hirschi M, Seneviratne S (2012) Asymmetric European summer heat predictability from wet and dry southern winters and springs. Nat Clim Change 2(10):736–741
Rahmstorf S, Coumou D (2011) Increase of extreme events in a warming world. Proc Natl Acad Sci USA 108(44):17,905–17,909
Rayner N, Parker D, Horton E, Folland C, Alexander L, Rowell D, Kent E, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res Atmos 108(D14)
Reichstein M, Bahn M, Ciais P, Frank D, Mahecha M, Seneviratne S, Zscheischler J, Beer C, Buchmann N, Frank D, et al (2013) Climate extremes and the carbon cycle. Nature 500(7462):287–295
Seneviratne S (2012) Climate science: Historical drought trends revisited. Nature 491(7424):338–339
Seneviratne S, Nicholls N, Easterling D, Goodess C, Kanae S, Kossin J, Luo Y, Marengo J, McInnes K, RahimiM, ReichsteinM, Sorteberg A, Vera C, Zhang X (2012). In: Field CB, Barros V, Stocker T, Dahe Q, Dokken DJ, Ebi K, Mastrandrea MD, Mach KJ, Plattner GK, Allen SK, Tignor M, Midgley PM (eds) Managing the risks of extreme events and disasters to advance climate change adaptation: special report of the intergovernmental panel on climate change. Cambridge University Press, Chapter 3, pp 109–230
Sheffield J, Wood E (2008) Projected changes in drought occurrence under future global warming from multi-model, multi-scenario, IPCC AR4 simulations. Clim Dyn 31(1):79–105
Sheffield J, Wood E, Roderick M (2012) Little change in global drought over the past 60 years. Nature 491(7424):435–438
Sherwood S, Fu Q (2014) A drier future Sci 343(6172):737–739
Sonntag D (1990) Important new values of the physical constants of 1986, vapour pressure formulations based on the its-90, and psychrometer formulae. Meteorol Z 70(5):340–344
Stott P, Stone D, Allen M (2004) Human contribution to the European heatwave of 2003. Nature 432(7017):610–614
Stott PA, Tett S, Jones G, Allen M, Mitchell J, Jenkins G (2000) External control of 20th century temperature by natural and anthropogenic forcings. Sci 290(5499):2133–2137
Thornthwaite C (1948) An approach toward a rational classification of climate. Geogr Rev 38(1):55–94
Trenberth K, Dai A, van der Schrier G, Jones P, Barichivich J, Briffa K, Sheffield J (2014) Global warming and changes in drought. Nat Clim Change 4(1):17–22
Vicente-Serrano S, Beguería S, López-Moreno J (2010) A multiscalar drought index sensitive to global warming: the standardized precipitation evapotranspiration index. J Clim 23(7):1696–1718
Westra S, Alexander L, Zwiers F (2013) Global increasing trends in annual maximum daily precipitation. J Clim 26(11)
WMO (2011) Weather extremes in a changing climate: hindsight on foresight. Geneva, Switzerland
Acknowledgments
We thank all participants of the climateprediction.net project, who donated their idle computer time for the purpose of generating the large ensemble of climate simulations. We appreciate the comments we received from Dáithí Stone and three anonymous reviewers on an earlier version of the manuscript. S. Sippel acknowledges funding provided by the German National Academic Foundation. We acknowledge the gridded E-OBS observational and the NCEP/ERA-Interim reanalysis datasets that were used in this study, which were provided from the EU-FP6 project ENSEMBLES (http://ensembles-eu.metoffice.com) and the data providers in the ECA&D project (http://www.ecad.eu), the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their Web site at http://www.esrl.noaa.gov/psd/ and from the ECMWF’s data portal (http://apps.ecmwf.int/datasets/data/interim_full_daily/), respectively.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sippel, S., Otto, F.E.L. Beyond climatological extremes - assessing how the odds of hydrometeorological extreme events in South-East Europe change in a warming climate. Climatic Change 125, 381–398 (2014). https://doi.org/10.1007/s10584-014-1153-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-014-1153-9