Solving the map overlay problem with a fuzzy approach

Abstract

The map overlay problem occurs when mismatched gridded data need to be combined, the problem consists of determining which portion of grid cells in one grid relates to the partly overlapping cells of the target grid. This problem contains inherent uncertainty, but it is an important and necessary first step in analysing and combining data; any improvement in achieving a more accurate relation between the grids will positively impact the subsequent analysis and conclusions. Here, a novel approach using techniques from fuzzy control and artificial intelligence is presented to provide a new methodology. The method uses a fuzzy inference system to decide how data represented in one grid can be distributed over another grid using any additionally available knowledge, thus mimicking the higher reasoning that we as humans would use to consider the problem.

1 Introduction

In order to compare different countries, the FCCC requires a single national value per country for e.g. CO2 emissions that stem from fossil-fuel burning. The authors in Boychuk and Bun (2014); Jonas and Nilsson (2007) explain that for countries with good emission statistics, the national fossil-fuel CO2 emissions are believed to exhibit a relative uncertainty of about ±5 % (95 % CI), but that a sub-national approach can differ considerably (i.e., the ±5 % for the 95 % CI does not hold any more). This is due to uncertainty at various levels, both uncertainty inherently present in the data, but also uncertainty introduced by processing and pre-processing the data. The International Workshop Series on Uncertainty in GHG Emission Inventories focuses on both the presence and on techniques on understanding, modelling and decreasing these uncertainties (Bun et al. 2007, 2010; Jonas et al. 2010). The sub-national data are usually obtained through the analysis of data coming from various sources, processed and combined into a national value, but the way the data are processed has a big impact on the introduced uncertainty and, consequently, on the results. To eliminate any inter-country uncertainty, a uniform and well-tested methodology should be used when building on sub-national emission approaches. However, even when using the same methodology, the uncertainty introduced by the processing of data is dependent on the source formats of the data, and how it behaves under subsequent processing. The solution to this is found by either obtaining data in a more similar way, to make all data compatible. But with most infrastructures in place, changes to this are unlikely to happen. The alternative is to pre-process the data so that the data exhibit a similar behaviour under the subsequent processing. The data are often represented in a gridded format, yet often different grids (e.g. CO₂ emissions and land use) are incompatible. By transforming them to compatible, matching grids, the processing should yield more consistent results.

This article presents a novel approach to pre-process data, to transform the data (e.g. emission data) so that it is better suited to be combined with other data (e.g. land use) while at the same time ensuring that the uncertainty and errors introduced by this transformation are kept to a minimum. As such, this methodology is at a very low level in the processing chain, but any decrease in uncertainty at such a low level should provide far more reliable results at the end of the processing and thus allow for more accurate analysis and comparison.

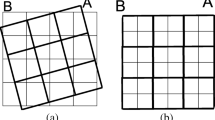
Commonly, data relating to different topics come from different sources: land use data can be provided by one source, emission data may come from another source, population data is again obtained elsewhere. Usually, the data are provided in a gridded format (Rigaux et al. 2002; Shekhar and Chawla 2003), which means that the map (or the region of interest) is overlayed with a grid dividing the map in different cells. In the case of a rectangular grid, each grid cell will be a rectangle or a square. With each cell, there is an association with a numerical value; which is deemed to be representative for the cell. The cell is however the smallest item for which there is data: the value associated with the cell can be the accumulation of data of 100 different points in the cell, can stem from one single point in the cell, can stem from several line sources, etc. There is no difference in appearance between these cells and no way of knowing this once the data is presented in the grid format. This is illustrated on Fig. 1a. There are, however, several problems with the data, particularly when the data need to be combined. As the data are obtained from different sources, the format in which they are provided can differ: the grids may not line up properly, the size of the grid cells may be different, or the grids might be rotated when compared to one another, etc.; as illustrated on Fig. 1b–e. This makes it difficult to relate data that is on different grids to one other and thus introduces uncertainty or errors. Additionally, not all data is complete, and cells of the grid may be without data.

Fig. 1

Different data distributions within a grid cell that result in the same value for the grid cell are shown in (a). The examples are: a single point source of value 100, two point sources of value 50, a line source of value 100 and an area source of value 100. Each of these are such that they are in one grid cell, which then has the value 100. When viewing the grid cell, it is not known what the underlying distribution is. Different incompatible grids are shown in b–e: a relative shift (b), a different grid size (c), a different orientation (d) and a combination (e)

This article does not contain any specific data analysis, nor are there any conclusions that directly relate to climate change, but it does introduce a novel solution method to transform a grid in order to match it to a different grid, a process that is used in many climate related studies. The proposed methodology makes use of data analysis, geometric matching and mathematical connections to solve format mismatches, it does not consider the higher concepts that relate to the meaning of the data (e.g. using ontologies to match differently labelled data, as in (Duckham and Worboys 2005)). The proposed methodology is still in a very early stage of development. As such, the examples shown are quite simple, but the prototype implementation and experiments on artificial datasets show promising results. The methodology is expected to be able to cope with any uncertainties and missing information, but the main focus for the time being is on developing the basic workings of the method. In Section 2, the map overlay problem along with current solution methods will be described. Reasoning about the problem and the possible use of any additional knowledge is also covered here. Section 3 considers how the intuitive approach can be simulated using techniques from artificial intelligence; it briefly introduces the necessary concepts (fuzzy set theory, fuzzy inference system) that will be used further along with giving a description of the new methodology. In Section 4, the methodology is applied to some examples and suggestions for future research are listed. Section 5 summarizes the article and contains conclusions.

2 The map overlay problem

2.1 Problem description

Spatially correlated numerical data are often represented by means of a data grid. This grid basically divides the map (or the region of interest) into a number of cells. For most grids, these cells are equal in size and shape (regular grid) and most commonly take the form of rectangles or squares. Each cell is considered to be atomic in the sense that it is not divided into smaller parts, and contains aggregated information for the area covered by the cell. With each cell, a numeric value is associated that is deemed representative for the cell. If we consider the example of the presence of a greenhouse gas, then the value associated with the cell indicates the amount of this particular gas in that particular cell. In reality, this amount may be evenly spread over the entire cell or it may be concentrated in a very small part of the cell; but as the cells are the smallest object considered, there is no way to confirm whether it is one or the other. This is illustrated in Fig. 1a.

Commonly, data from different sources need to be combined to draw conclusions: for instance, relating the measured concentrations of a particular gas in the atmosphere to the land use would require data from both concentrations and land use. While both data can be represented as gridded data, the grids used often don’t match: not only can there be a difference in cell sizes and shapes, but one grid can also be rotated when compared to another grid, translated, or a combination of these. This is a common problem with many data in literature, called the map overlay problem; the data are then said to be incompatible; some examples are shown on Fig. 1b–e.

To make these different datasets compatible, it is necessary to transform one of the grids to match the layout of the other grid: it needs to have the same number of grid cells, oriented in the same way, so that there is a 1:1 mapping of each cell in one grid to a cell in this other grid. The map overlay problem concerns the finding of such a mapping: it considers an input grid which contains data and a target grid that provides the new grid structure on which the input grid needs to be mapped. As mentioned before, nothing is known at a scale smaller than the cells; which makes the mapping of one grid to another extremely challenging. Consider the simple example on Fig. 2a.

Fig. 2

Examples to explain the problem: a Problem illustration: remapping grid A onto grid B, b Areal weighting: the value of each output cell is determined by the amount of overlap, c Areal smoothing: the value of each output cell is determined resampling a smooth surface that is fitted over the input data, d Intelligent reasoning using additional data: grid C supplies information on the distribution, which can be used to determine values in the output grid

Remapping the values of the grid cells of the input grid A to the output grid B is done by determining the values of x ^j _i in these formulas:

$$ \begin{array}{c}\hfill f\left({B}_1\right)={x}_1^1f\left({A}_1\right)\hfill \\ {}\hfill f\left({B}_2\right)={x}_2^1f\left({A}_1\right)\hfill \\ {}\hfill f\left({B}_3\right)={x}_3^1f\left({A}_1\right)+{x}_3^2f\left({A}_2\right)\hfill \\ {}\hfill =\left(1-{x}_1^1-{x}_2^1\right)f\left({A}_1\right)+\left(1-{x}_4^2-{x}_5^2\right)f\left({A}_2\right)\hfill \\ {}\hfill f\left({B}_4\right)={x}_4^2f\left({A}_2\right)\hfill \\ {}\hfill f\left({B}_5\right)={x}_5^2f\left({A}_2\right)\hfill \\ {}\hfill \cdots \hfill \end{array} $$

Where in x ^j _i , the index i refers to the cell number in the output grid, and j refers to the cell number in the input grid. This can be generalized as:

$$ f\left({B}_i\right)={\displaystyle \sum_j{x}_i^jf\left({A}_j\right)={\displaystyle \sum_{j\Big|{A}_j\cap {B}_i\ne \varnothing }{x}_i^jf\left({A}_j\right)}} $$

with constraints that

$$ \forall j,{\displaystyle \sum_i{x}_i^j=1} $$

While this looks straight forward, the problem is in finding the values of x ^j _i . In more complicated examples, it is obvious that more than two grid cells can make a contribution to the value of a new grid cell. From the example on Fig. 2a, it can also be seen that there is no single solution: there are different possible values for B ₁ and B ₂, providing their sum is constant.

The key to resampling the original grid to the new grid, is the ability to determine the true distribution of the data; thus going into further detail than that which the grid cells offer. Most current solution methods either assume a distribution of the data or aim to estimate the distribution of the data, and resample it in order to match the new grid. The output grid is specified by the user; the initial map overlay problem concerns transforming the input grid to this grid. The proposed method uses an additional grid, also specified by the user, to help transform the input grid, but the grid specification (cell size, orientation) does not have to match either the input or the output and does not change the output format. The additional grid should contain data that has a known and established correlation to the input data. The grid on which the data is provided does not have to match either input or output grids; however, the finer the grid, the better the results for transforming the input grid.

2.2 Current solution methods

Transforming one grid to another grid is comparable to determining what the first grid would be if it were represented by using the same grid cells as in the second grid. In literature, a number of solution methods exist. The grid cells as shown in Fig. 2a will be used to explain the most common method; for a more detailed overview we refer to (Gotway and Young 2002). In the example used, the input grid A contains three cells, the output grid B contains eight cells.

2.2.1 Areal weighting

The simplest and most commonly used method is areal weighting. It uses the portion of overlap of the grid cell to determine what portion of its associated numerical value will be considered in the new grid. This approach is considered to be relatively easy and straightforward. The result of areal weighting is illustrated on Fig. 2b. It will clear that the values of x ^j _i are determined by the surface area S:

$$ \begin{array}{c}\hfill f\left({B}_1\right)=S\left({B}_1\right)f\left({A}_1\right)\hfill \\ {}\hfill f\left({B}_2\right)=S\left({B}_2\right)f\left({A}_1\right)\hfill \\ {}\hfill f\left({B}_3\right)=S\left({B}_3\cap {A}_1\right)f\left({A}_1\right)+S\left({B}_3\cap {A}_2\right)f\left({A}_2\right)\hfill \\ {}\hfill f\left({B}_4\right)=S\left({B}_4\right)f\left({A}_2\right)\hfill \\ {}\hfill \cdots \hfill \end{array} $$

Basically, in this approach, it is assumed that the data in the cell are evenly distributed throughout the cell and that all cells are considered to be completely independent of one another. Resampling can be done over any grid without any difficulty. In some situations, the assumption combined with the simplicity may indeed be justification for its employment. The spread of a gas in the atmosphere in the absence of extreme sources is an example where use of the method is legitimate. However, when the associated numeric data is the result of a small number of extreme sources in the grid cell (e.g. a factory), then this approach may lead to either an over- or an underestimate in the new grid cell, depending on whether or not the factory is in the overlapping area.

2.2.2 Spatial smoothing

Spatial smoothing is a more complicated approach than areal weighting. Rather than assume that the data is evenly spread out over a cell, the distribution of the data within a cell is dependent on the neighbouring cells.

This is achieved by considering the grid in three dimensions, with the third dimension representing the associated data. In spatial smoothing methods, a smooth three-dimensional surface is fitted over the grid, as illustrated in Fig. 2c, after which the smooth surfaced is sampled using the target grid. Consequently, this method does not assume that the data modelled by the grid is evenly distributed over each cell, but rather assumes a smooth distribution over the region of interest: if the value of a cell is high, one expects higher values closer to it in the surrounding cells. In many situations, this method is more accurate than the previous method, but is still unable to cope with data that in reality is concentrated in a small area of the cell. This is, for instance, the case when modelling air pollution when a single factory is responsible for the value that will be associated with the grid cell in which it is contained (a point source): the presence of a point source in one cell does not imply sources close to it in neighbouring cells (in some urban planning schemes, it might even be the opposite, to avoid the placing of too many point sources in close proximity to one another).

2.2.3 Regression methods

In regression methods, the relation between both grids is examined, and patterns of overlap are established. Different methods exists, based on the way the patterns are established. (Flowerdew and Green 1994) determine zones, which are then used to establish the relation. This is then combined with an assumption of the distribution of the data (e.g. Poisson) in order to determine the values for the incompatible zones. Several underlying theoretical models can be used, but all the regression methods require key assumptions that normally are not part of the data and cannot be verified using the data. These assumptions mainly concern the distribution of the data, e.g. if the data is distributed in a Poisson or binomial distribution.

2.3 Using additional knowledge

2.3.1 Data fusion

The problem under consideration resembles to some extent the problem described in (Duckham and Worboys 2005). Both the problem and solution are, however, completely different: the authors in (Duckham and Worboys 2005) combine different datasets that relate to the same area of interest in order to create a new dataset that has the combined information of both source data sets. This combined information can be richer or have a higher accuracy. Their approach, however, is not intended for numerical data, but for labelled information. The different datasets can use a different schema (set of labels) to describe regions in the region of interest (the example uses land coverage and land use terms). As the labels are not always fully compatible, the authors propose a method of linking both schemas with a common ontology, and obtaining geometric intersections if the labelled regions do not match. The authors in (Fritz and See 2005) tackle the data fusion problem using a different approach. An expert supplies input regarding the assigned labels in different datasets; this knowledge is then modelled and matched using a fuzzy agreement. This allows the labels in different sets to be compared and combined correctly.

While both these approach are also using multiple datasets, the type of data processed and the goal of the processing is quite different from that which is presented in this article. In the aforementioned data fusion approaches, the goal is the combine annotations and labels added in different datasets by different people. This is not numerical information, but e.g. true land use information. The datasets are also not represented by grids but by vectorial maps.

2.3.2 Intuitive approach to grid remapping

The methods mentioned in Section 2.2 work on gridded data and transform the grid without any possibility to use additional data that might be available. Some key assumptions regarding data distribution are implied within the methods. While at first it seems that the only knowledge available is the input grid, it is very likely that there is additional knowledge available. Consider, for instance, an input grid that represents CO₂ concentrations on a course grid. From other research, the correlation between CO₂ levels and traffic is known. This means that we can use this known correlation to improve the CO₂ data set we have by using traffic information that is also available for the same region. Of course, the correlation between the input and additional datasets should be known beforehand, as this is a key assumption of the method. When this correlation is known, this information can be used to transform the grid that represents CO₂ emissions to a grid with a different cell size or with a different orientation.

The method that is presented allows for additional data to be taken into account when resampling the data to a new grid. Suppose additional data, which relates to the data in the input grid, is available in a grid containing five cells as shown on Fig. 2d.

Based on the values in the additional grid C, it is possible to guide the distribution of the values modelled on grid A to the new grid B. A low value in a cell of grid C suggests that the values in the overlapping cells of the output grid should also be lower.

By adopting a strict approach in the interpretation of this additional grid, it is possible to intuitively derive a simple distribution: proportional values for f(B ₁), f(B ₂), f(B ₄), f(B ₅). This interpretation means that the cells in the output grid B should have a value that is proportional to both the input grid A and the auxiliary grid C. In many situations, however, this cannot be achieved, as data in the grids can be slightly contradictory, a consequence of the fact that grids are approximations of the real situation. It is often not possible to derive a distribution when interpreting the related data grid with too strict an approach; but it is possible to derive a distribution that is still consistent with the input grid, and to some extent follows the related grid C. The related grid is thus only used to help determine the original, unknown distribution. Obviously, the grid used to help in transforming the data should contain a well established known relation to the input data. If the relationship between input grid and auxiliary grid are under investigation, any usage of the auxiliary grid in transforming the input grid may distort conclusions on the relationship between both grids.

To come to an intuitive solution consider cell B ₃ . To derive the f(B ₃), it is necessary to look at the grids A and C in the area around B ₃ . The cells that are of interest are A ₁ and A ₂ . Both have the same value, so they will not provide much information. On the other hand, the cell C ₂ that overlaps B ₃ has a very low value (f(C ₂) = 0), whereas its neighbouring cells have high values (f(C ₁) = f(C ₃) = 100). As the data in grid C are known to be related to the data in A, we can conclude that the data of grid A for this region should be spread more towards the neighbouring cells of B₃, so the value f(B ₃) should be low.

Consider B ₄ . Again, the values of the overlapping cells in A are the same, so this will not influence the result. But the overlapping cell of grid C, C ₃ has a high value. The neighbouring cells of C ₃ have a low value. This basically implies that the distribution of A over the cells in B should also be lower in the proximity of cell C ₃ .

Finally, consider B ₅ . Here, the values of the overlapping cells in A are different: f(A ₂) = 100, f(A ₃) = 0. The distribution of the data in grid C tell us that in B ₅ , the value should be lower: no contribution from A₃, and C₃ has a much higher value than C ₄ .

The use of additional information, in this example a single grid, can doubtless contribute to securing a distribution that is still consistent with the input grid, but at the same time it takes into account the added available knowledge. From the examples though, it can be seen that it is not always possible to find a unique solution, implying there is still some uncertainty on the accuracy of the newly obtained grid.

The above example only uses a proportional or inverse proportional relationship between cells. This relationship is, however, only considered at a local scale, meaning that high and low for both input grid and additional grid are defined for the location under consideration, independent of the definition of other locations. As such, the connection between the input grid and the additional grid is not quantitatively verified, but only relative values are considered, which makes the approach not dependent on linearity or non-linearity. By considering different rules, it is even possible to model different connections, e.g. : if a value is high or a value is low, then the output value should be high. The ultimate goal is to allow multiple additional data layers, and make allowance for different possible combinations (e.g. a high value in one and a low value in another can yield a result that might well be the same as a low value in one and a high value in the other). On the other hand, consideration of the more quantitative connection between the layers can also provide better results. Both of these aspects are an area of future research.

3 Using intelligent techniques

3.1 Introduction to fuzzy sets and fuzzy inference

3.1.1 Fuzzy sets

Fuzzy set theory was introduced by Zadeh in (Zadeh 1965) as an extension of classical set theory. In a classical set theory, an object either belongs or does not belong to a set. In fuzzy set theory, the objects are assigned a membership grade in the range [0,1] to express the relation of the object to the set. These membership grades can have different interpretations (Dubois and Prade 1999): a veristic interpretation means that all the objects belong to some extent to the set, with the membership grade indicating the extent; whereas a possibilistic interpretation means that doubt is expressed as to which elements belong; now the membership grade is expressing the possibility that an element belongs to the set. Lastly, it is also possible for the membership grades to represent degrees of truth. In (Dubois and Prade 1999) it was shown that all other interpretations can be traced back to one of these three. The formal definition of a fuzzy set $\tilde{A}$ in a universe U is given below

$$ \tilde{A}=\left\{\left(\left.x,{\mu}_{\tilde{A}}(x)\right|x\in U\right)\right\} $$

Its membership function ${\mu}_{\tilde{A}}(x)$ is

$$ \begin{array}{c}\hfill {\mu}_{\tilde{A}}:U\hfill \\ {}\hfill x\end{array}\begin{array}{c}\hfill \to \hfill \\ {}\hfill \mapsto \hfill \end{array}\begin{array}{c}\hfill \left[0,1\right]\hfill \\ {}\hfill {\mu}_{\tilde{A}}(x)\hfill \end{array} $$

Various operations on fuzzy sets are possible: intersection and union are defined by means of functions that work on the membership grades, called respectively t-norms and t-co-norms. Any function that satisfies the specific criteria is a t-norm, respectively t-conorm and can be used to calculate intersection or union (Klir and Yuan 1995; Zimmerman 1999). Commonly used t-norms and t-conorms are the Zadeh-min-max norms, which use the minimum as the intersection and the maximum as the union (other examples are limited sum and product, Lukasiewicz norm, …).

Fuzzy sets can be defined over any domain, but of particular interest here are fuzzy sets over the numerical domain, called fuzzy numbers: the membership function represents uncertainty about a numerical value. The fuzzy set must be convex and normalized (some authors also claim the support must be bounded, but this property is not strictly necessary) (Klir and Yuan 1995). Using Zadeh’s extension principle (Zadeh 1965), it is possible to define mathematical operators on such fuzzy numbers (addition, multiplication, etc.). Fuzzy sets can also be used to represent linguistic terms, such as “high” and “low”; this allows one to determine which numbers are considered high in a given context. Linguistic modifiers also exist and are usually a function that alters the membership function for the term it is associated with, allowing for an interpretation of the words like “very” and “somewhat”.

Finally, it is necessary to make a distinction between an inclusive and an exclusive interpretation: are values that match “very high” still considered to be “high”? In the real world, people could say about a person: “he is not tall, but he is very tall”, which is an exclusive interpretation: “very tall” does not imply “tall”. The main difficulty when using fuzzy sets is the definition of the membership functions: why are the fuzzy sets and membership grades chosen as they are, and on what information is this choice based?

3.1.2 Fuzzy inference system

A fuzzy inference system is a system that uses a rulebase and fuzzy set theory to arrive at solutions for given (numerical) problems (Mendel 2001; Klir and Yuan 1995). The rulebase consists of fuzzy premises and conclusions; it is comprised a set of rules that are of the form

$$ \mathrm{if}\;\underset{\mathrm{premise}}{\underbrace{x\;\mathrm{is}\;A}},\mathrm{then}\;\underset{\mathrm{conclusion}}{\underbrace{y\;\mathrm{is}\;B}} $$

Here “x is A” is the premise and “y is B” is the conclusion; x and y are values, with x the input value and y the output value. Both are commonly represented by fuzzy sets, even though x is usually a crisp value (crisp means not fuzzy). In the rule, A and B are labels, such as “high” or “low”, also represented by fuzzy sets as described above.

The “is” in the premise of the rules is a fuzzy match: this will return a value indicating how well the value x matches with label A. As all the rules are evaluated and the values are fuzzy, it is typical that more than one rule can match: a value x can be classified as “high” to some extent and at the same time as “low” to a much lesser extent. All the rules that match will play a part in determining the outcome, but of course the lower the extent to which a rule matches, the less important its contribution will be. It is possible to combine premises using logical operators (and, or, xor) to yield more complex rules. As multiple rules match, y should be assigned multiple values by different rules: all these values are aggregated using a fuzzy aggregator to yield one single fuzzy value. For each rule, the extent to which the premise matches impacts the value that is assigned to y.

The “is” in the conclusion is a basic assignment and will assign y with a fuzzy set that matches the label B. It is important to note that x and y can be from totally different domains, a classic example from fuzzy control is “if temperature is high, then the cooling fan speed is high”.

While the output of the inference system is a fuzzy set, in practise the output will be used to make a decision and as such it needs to be a crisp value. To derive a crisp value (defuzzification), different operators exist. The centroid calculation is the most commonly used; it is defined as the centre of the area under the membership function.

3.2 Defining the inference system

The parameters for the inference system used are derived from generated sample cases, for which an optimal solution is known. The relations between the parameters that are found and the optimal solution are then reflected in the rules. Due to the more technical nature of this explanation, and the strict page limitation, a detailed explanation of the procedure is available as supplementary material in (Online Resource 1).

4 Experiments

4.1 Description of the results

In this section, results of the methodology applied on the example in Fig. 2d for several inputs will be shown and discussed. The input grid A has three grid cells, the output grid B contains eight grid cells, but does not exactly overlap with A and the auxiliary grid C has five grid cells and overlaps fully with grid A. It is obvious that the grids are not aligned properly.

Table 1 holds the data for the input grid, the auxiliary grid; and the computed output grid. The first three cases have a distribution of the input data such that f(A ₁) = f(A ₂) = 100 and f(A ₃) = 0; the last three cases have the input distribution such that f(A ₁) = f(A ₃) = 100 and f(A ₂) = 0. In each of the cases, a different distribution of the auxiliary grid was considered, as shown in Table 1. Figure 3 offers a graphic view of each of the cases. For each case, the grid cells are shown; the surface area of the circles is representative of the values associated with the grid cells. Consequently, the sum of the areas of the circles in grid B equals the sum of the areas in grid A. There is no quantitative relation assumed between the auxiliary grid B and the grid A, it is just assumed that high values in B are an indication for high values in A.

Table 1 Overview of the cases used in the simulations

Fig. 3

Illustrations for the different cases from Table 1: A is the input grid, B is the output grid and C the auxiliary grid. The grid cells are drawn above each other for ease of visibility, but should cover each other as shown on Fig. 2d. The size of the circles reflects the relative value of the associated cell (a small circle is shown for 0 values, for purposes of illustration)

The behaviour of the methodology in different cases is clearly illustrated in Fig. 3.

Consider output cell B ₂ . From (Online Resource 1), the considered cells that play a part are: A ₁ (proportionally), C ₁ and C ₂ (proportionally), A ₂ (inverse proportionally). In all six cases, the value assigned to B ₂ is the same. The reason is that, while the values of the involved cells differ (C ₂ changes value), the locally computed definition for the fuzzy sets that defines low and high for the auxiliary grid is also changes. This is done in such a way, that the differing input is cancelled out. In the system, there is no difference between a value of, for example, 100 when low is defined as 0 and high is defined as 100, and a value of, for example, 200 when low is defined as 0 and high is defined as 200.

Cell B ₃ shows a much bigger variation. The cells involved in determining the output value are A ₁ and A ₂ (proportionally), C ₂ (proportionally), C ₁ and C ₃ (inverse proportionally). In case 1, the proportional and inverse proportional data is almost cancelled out, resulting in a value close to 50. In case 2, the value for C ₃ is much smaller than in case 1, which results in a larger value of 57 for B₃. In case 3, the value of C ₂ is decreased, and, as it is has a proportional relation to B ₃ , the value for B ₃ is again decreased. It is smaller than in case 1, as the higher value of C ₃ results in a higher value in B ₅ , which therefore compensates. The difference in cases 4 to 6 are explained by the change in the proportional and inverse proportional data from the auxiliary grid: in case 4 there is more inverse proportional than proportional (the value of C ₁ is greater than the value of C ₂ ), in case 5 they are equal, and in case 6 the proportional value is greater than the inverse proportional.

Cell B ₄ is influenced by A ₂ (proportional), C ₃ (proportional), C ₂ and C ₄ (inverse proportional). The first case has a greater value than cases 2 and 3, as C ₃ has a much higher value. The second and third cases result in the same value, as the change in the auxiliary grid also changes the definition for high, causing the change in values to be nullified. The value of 0 in the last three cases is due to the overlapping input field having 0 as an associated value.

Cell B ₅ is determined by A ₂ (proportional), C ₃ and C ₄ (proportional), A ₃ (inverse proportional) and C ₂ . The first two cases are the same, as the definitions for high for the auxiliary grid is also changed. Case 3 shows a higher value, as there is a greater proportional contribution from C ₄ .

The cells B ₆ , B ₇ and B ₈ can be considered together. They all are 0 in the first three cases, as the overlapping input field has a value of 0. In cases 4, 5 and 6, the latter two have higher values, which is the expected behaviour due to the values of C ₄ and C ₅ .

4.2 Observations of the methodology

From the cases in Fig. 3, it can be seen that the goal of using an auxiliary grid to guide the new distribution yields some interesting results. In general, the methodology does not yield contradictory effects: the output grid fully complies with the input grid. Compared to the traditional approaches (e.g. areal weighting, which would provide the same result for the first three cases), and the same result for the last three cases, it is clear that the additional data has an effect on the result.

The distribution in the output grid to some extent follows the auxiliary grid, but there are some exceptions. In the last three cases, the results appear to be consistent and as expected: larger values where the auxiliary grid overlaps, smaller values elsewhere. In the first two cases, the larger value of cell B ₅ stands out. This is mainly explained by the fact that B ₅ fully overlaps with A ₂ , and by the fact that the values of cells considered in the auxiliary grid cancel each other out, or the definition of high for the auxiliary values changes to yield this effect. Similarly, the value of B ₃ in case 3 stands out as counter intuitive, but with a value of 44 it is still considerably smaller than in cases 1 (52) and 2 (57), which is consistent with the desired result. A similar observation can be made for cell B ₆ in the last three cases: its value is perhaps higher than would be desired based on the auxiliary grid, but still the values for the cells that overlap with the cells of the auxiliary grid that have higher values also have higher values than B ₆ .

The results appear to achieve the desired goals, but still further testing and development of the methodology is required.

4.3 Future developments

The approach presented is a new concept and the first prototype implementation of a methodology that shows promising results, and as such justifies further research. The prototype allows us to experiment in order to see how the system behaves and derive reasons for its behaviour. The outcome of the fuzzy inference system is dependent on a large number of parameters.

Firstly, there are the parameters that concern the geometrical aspects of the problems, the definition of the cells that are considered to have an influence on a given output cell. This not only concerns choosing which cells will take part in determining the value for the output cell, but also determining the behaviour (proportional or inverse proportional) and adding weights to the cells to decrease their influence (e.g. if the distance becomes too great to be relevant). In the current implementation, no quantitative relationship between auxiliary and input grid is assumed, meaning that the quantitative relation between input grid and additional grid is only considered for the vicinity of a cell. A quantitative relation on a bigger scale can, however, be used to derive how big the impact of the auxiliary cell should be, and as such should provide better results. This is, however, not a trivial step, as too tight a relationship may cause overly narrow constraints and consequently prevent the system from reaching a satisfactory solution when data is contradictory or missing.

Secondly, there are the parameters that define the rule base: this is not only the number of rules, but also the definition of the rules themselves and the weights assigned to the rules. At present, the number of rules is derived from all the possible combinations of the values of the cells that play a part. It is, however, possible to limit the rules and, for instance, consider a fixed number of rules that are determined automatically by means of training data. The full impact of this is quite difficult to estimate for the time being, however. Each of the rules can also be assigned a weight, and at present, lower weights are assigned to contradicting rules. In the examples in this article, this yielded little impact, as the data used in the input was not really contradictory. This parameter may become more important when confronting the system with real world data or missing data.

Lastly, there are the parameters that relate to the fuzzy sets used and their definitions. This includes the definitions of the fuzzy sets that represent high and low; the definitions of minimal and maximal values that are used in these fuzzy sets and the number of sets that are considered for both input and output. Also, the definitions of minimum and maximum of the domain (explained in (Online Resource 1)) can be improved: the current definitions may impose to big limitations upon possible input sets.

5 Conclusion

In this article, a completely novel approach to the map overlay problem was presented. The described methodology is in a very early stage, but already shows interesting results. Rather than assuming a distribution of the data, knowledge from external data that are known to relate to the input data are used to find a more optimal distribution of the data after transformation to a new grid. The methodology uses concepts from fuzzy set theory and algorithms from artificial intelligence in order to mimic reasoning about the input data. A prototype implementation is under construction and can already process artificially generated data. The results show that in simple cases, the methodology achieves the pre-set goal, but additional testing and fine tuning is necessary in order to find the best possible solution for a given input. The current prototype already makes allowance for the processing of larger datasets. The next step is to generate artificial but large scale data, in order to fine tune the workings of the methodology using a fully controlled environment and to assess the performance; both in accuracy and processing speed. Experiments on real world data are expected to follow, in order to fully study the potential and outcome of the proposed methodology.