Tall tales and fat tails: the science and economics of extreme warming

Abstract

It has recently been highlighted that the economic value of climate change mitigation depends sensitively on the slim possibility of extreme warming. This insight has been obtained through a focus on the fat upper tail of the climate sensitivity probability distribution. However, while climate sensitivity is undoubtedly important, what ultimately matters is transient temperature change. A focus on transient temperature change stresses the interplay of climate sensitivity with other physical uncertainties, notably effective heat capacity. In this paper we present a conceptual analysis of the physical uncertainties in economic models of climate mitigation, leading to an empirical application of the DICE model, which investigates the interaction of uncertainty in climate sensitivity and the effective heat capacity. We expand on previous results exploring the sensitivity of economic evaluations to the tail of the climate sensitivity distribution alone, and demonstrate that uncertainty about the system’s effective heat capacity also plays a very important role. We go on to discuss complementary avenues of economic and scientific research that may help provide a better combined understanding of the physical and economic processes associated with a rapidly warming world.

Introduction

Recent studies have shown that economic analysis of climate change is sensitive to the slim possibility of extreme warming. According to Weitzman (2009) a sufficiently large (albeit still tiny) probability of extreme warming can make climate change mitigation policies appears infinitely valuable. The significance of this result has been debated but the implications for integrated assessment modeling are clear; that the possibility of extreme warming should be accounted for. A number of IAM studies have pursued this issue (Ackerman et al. 2010; Dietz 2011; Pycroft et al. 2011).

In these studies, a sufficiently high realization of the climate sensitivity (defined as the equilibrium surface warming that results from a doubling of atmospheric CO₂ concentration) gives rise to extreme warming, which, depending on assumptions about the damage function, can trigger substantial economic damages. If the probability of drawing such a high value is sufficiently large—or the climate sensitivity distribution has a ‘fat tail’ according to common usage—the possibility of extreme warming may come to dominate the economic calculus. It is unfortunate, then, that there are compelling reasons to describe our knowledge about the value of the climate sensitivity by a fat-tailed probability density function (pdf), at best (Frame et al. 2005; Allen et al. 2006; Weitzman 2009; Roe and Baker 2007; Baker and Roe 2009). Although there is some variability in the usage of the term, a fat-tailed distribution generally refers to one where the density in the upper tail approaches zero more slowly than the exponential distribution.

Beyond that it is fat, however, we do not actually know much about the shape of the tail (Frame et al. 2005; Allen et al. 2006; Roe and Baker 2007; Baker and Roe 2009). We must face up to this fact if the probability of extreme warming can overwhelm economic evaluation of climate policies. The existing IAM literature arguably fails to do this, tending to work with a single fat-tailed climate sensitivity distribution (Ackerman et al. 2010; Dietz 2011; Hope 2011). An alternative approach, suggested by Weitzman (2012), would be to stress-test IAMs by comparing multiple fat-tailed distributions. Weitzman did this very roughly with a toy model, although he considered uncertainty about the whole distribution at once, making it difficult to infer the importance of uncertainty about the tail. Pycroft etal. (2011) went further by varying the upper 50 % of the pdf while holding constant the lower half of the distribution. One of the ways we seek to advance the literature is to investigate the sensitivity of the economic value of a mitigation policy to the shape of the tail of the pdf, while fixing everything except the shape of the upper tail.

What matters, though, is not the probability that the climate sensitivity is high, but the probability of extreme warming (Allen et al. 2006; Marten 2011; Roe and Bauman 2012; Hof et al. 2012). Focusing solely on the climate sensitivity results in a failure to give the requisite importance to other physical parameters that greatly influence transient temperature change, notably the rate at which heat is taken up by the oceans, a process encapsulated in the concept of “effective heat capacity”. The effective heat capacity represents the amount of energy necessary to increase the Earth’s surface temperature by 1° C, so a lower value means the temperature will rise faster in response to a given energy input. The principal empirical contribution of this paper, therefore, is our exploration of joint uncertainty about the climate sensitivity and effective heat capacity. Low values of the heat capacity markedly increase the probability of extreme warming, and greatly amplify the sensitivity of economic analyses.

We begin in Section 2 by discussing the science of climate warming, and relating it to our empirical experiments with the DICE IAM in Section 3. We derive the fundamental equation of transient temperature change in DICE from basic physical principles, before discussing the role of climate sensitivity pdfs from the literature and asking what does uncertainty about the effective heat capacity imply for temperature forecasts? In Section 3 we consider the implications of these uncertainties for numerical evaluation of mitigation policy. Section 4 concludes with a discussion of complementary avenues of economic and physical science research that would most serve to improve future economic evaluation of climate change.

The science of extreme warming

In IAMs, the climate component tends to be very simple relative to most physical climate models. van Vuuren et al. (2011), Marten (2011) and others have evaluated the predictive performance of the simple climate modules in IAMs. In order to study the economic consequences of uncertainty about extreme warming in IAMs, it is helpful to first get a conceptual handle on the underlying physical uncertainties that drive the economic analysis. In this paper we employ the DICE model (Nordhaus 2008), so our discussion seeks to link its climate module to fundamental physical concepts, something that the bulk of the IAM literature neglects. DICE is one of the the most widely studied IAMs. In it economic damages from climate change depend exclusively on the global mean temperature change. In DICE, this quantity is calculated using Eq. 1.

$$ T_t = T_{t-1} + \xi_1 \left[ F_t - \frac{F_{2 \times CO_2}}{S}\left(T_{t-1}\right) - \xi_3\left(T_{t-1}-T^{LO}_{t-1}\right)\right] $$

(1)

T _t ::

Global mean surface temperature change at time t with respect to 1900

F _t ::

Radiative forcing at time t

$F_{2 \times CO_2}$::

Radiative forcing for a doubling of atmospheric CO ₂

S::

Climate sensitivity

$T^{LO}_t$::

Temperature of the lower oceans at time t with respect to 1900

ξ ₁::

‘speed of adjustment parameter’

ξ ₃::

‘coefficient of heat loss from the atmosphere to oceans’

To understand the physical basis of this equation, start by considering the planet’s surface, lower atmosphere and oceans as “the system”—a box into which energy flows in and out. In equilibrium the rate of energy input to the system (from the sun) equals the rate of energy lost (through radiation to space) so the energy content remains constant. Increasing atmospheric greenhouse gas concentrations represent a forcing which decreases the rate of energy loss, leading to an increase in energy content until feedbacks, including rising temperatures, increase the rate of energy loss again bringing the system back into balance. Since we are principally interested in changes from an assumed equilibrium state, the forcings, which decrease the rate of energy loss, can be thought of as increasing the rate of energy input; the feedbacks being a consequential increase in the rate of energy output. This is encapsulated by Eq. 2 (Andrews and Allen 2008; Senior and Mitchell 2000). The right hand side represents the overall rate of energy input to the system: radiative forcing F, reduced by the increase in the rate of energy output to space, the feedbacks, which are taken to be proportional to the surface temperature change T. The left hand side represents the rate of change of the system’s energy content, measured in terms of the change in surface temperature multiplied by an effective heat capacity for the system as a whole.

$$ C_{\rm eff}\frac{dT}{dt} = F - \lambda T $$

(2)

C _eff::

Effective heat capacity of the climate system

T::

Surface temperature change from some equilibrium state

F::

Radiative forcing

t::

time

λ::

a feedback parameter

Over short timeframes, decades not millennia, much of the excess energy input leads to warming of the upper oceans (Levitus et al. 2000; Lyman et al. 2010). More slowly the energy penetrates to the deep, or lower, oceans. An extension of the above model is therefore to consider that our system includes not the whole ocean but only the upper ocean, which is taken to be a well-mixed layer (and therefore warms uniformly), coupled to a second box which represents the deep ocean and into which heat diffuses. The deep ocean is usually not taken to be well-mixed but rather to have temperatures which decrease with depth (Hansen et al. 1985; Frame et al. 2005). A simpler form of this extension, though, would assume that the deep ocean too is well-mixed and can be represented by a single temperature, call it T ^LO. The flow of energy from the surface to the lower oceans is then taken to be proportional to their temperature difference. With this extension, we get Eq. 3. Note that T is still the surface temperature so the heat capacity now relates only to the upper box.

$$ \begin{array}{rll} C_{\rm up}\frac{dT}{dt} &=& F - \lambda T - \beta (T-T^{LO}) \label{Energy2box} \end{array}$$

(3)

C _up::

Effective heat capacity of the upper oceans, land surface and atmosphere

Equations 2 and 3 both represent energy conservation, but in one- and two-box systems respectively. Applying Euler’s method to discretize Eq. 3, and re-arranging we obtain Eq.4.

$$ \begin{array}{rll} T_t &=& T_{t-1} + \frac{\Delta t}{C_{\rm up}} \left[ F_{t-1} - \lambda T_{t-1} - \beta (T_{t-1}-T^{LO}_{t-1}) \right] \label{E2boxdiscT} \end{array} $$

(4)

t::

Now the number of the time-step not continuous time

Δt::

length of the time-step

Consideration of Eq. 2 for the equilibrium response to doubling the atmospheric CO ₂ concentrations shows that λ in Eq. 4 can be equated with $\frac{F_{2\times CO_2}}{S}$ in Eq. 1. We have thus arrived at a formulation that is almost identical to the temperature equation in the DICE model (Eq. 1).¹

The physical basis of Eq. 4 makes it easier to relate different sources of uncertainty in Eq. 1 to the various sources of uncertainty discussed in the physical science literature. We focus here on uncertainty about the climate sensitivity, S, and the heat capacities, C _eff and C _up.

Climate sensitivity

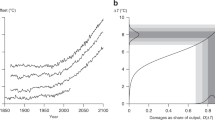
The value of S is not known with certainty. Instead, over the last two decades a large literature has emerged that seeks to quantify uncertainty about S via probability distributions. Many distributions have been published (see Fig. 2), along with a number of review and meta-analysis papers utilizing collections of distributions (Meinshausen et al. 2009). From this literature three stylized facts emerge. First, there are differences—at times large—between the various estimates. Second, all have a large positive skew and in most cases it satisfies the definition of a fat tail. Third, there are large differences between the various estimates of the upper tail.

The pdfs generated represent different assessments of epistemic uncertainty, each conditioned on a different set of assumptions (only some of which are usually made explicit) and founded on different underlying observational and/or model data. It is important to note, however, that S is being used as a proxy for λ which represents the feedbacks relevant at some point in time and is state-, and therefore time-dependent; as is S. The relevant distribution of S to use in an IAM will change over time within the simulation as the strength of different feedback processes vary. (Consider, for instance, the role of sea ice in the albedo feedback—this may be small for small increases in temperature, large for temperatures when the sea ice rapidly declines and smaller again when the area of remaining sea ice is small.) The foundation of some of the pdfs may make them them more relevant in the short term, others in the longer term and still others of limited relevance over the next 400 years or so; a time period typical of IAM simulations. On top of this, each of the methods has methodological advantages and disadvantages. Thus it is not possible to identify from the literature a single distribution which is most suitable for use in an IAM.

Setting aside the issue of time dependence, it is tempting to combine the various estimates, but this too is problematic. The distributions are not independent in terms of either methodology or data constraints, yet their degree of dependence is unclear. Thus neither naive combination nor more complicated weightings can be relied upon to give “the right” distribution. For the time being the upshot is to accept that the science has produced many different distributions and the economics must accept relatively large uncertainty, not just in the value of S, but in the uncertainty in the value of S—particularly in the tails of the distribution. There are opportunities to narrow our uncertainty for economic applications, but the first step must be to try to understand what uncertainty about the tail shape implies for the robustness of the economic analysis.

Effective heat capacity

Examination of Eq. 1 suggests that uncertainty in transient temperature change is dependent not just on climate sensitivity but also on uncertainty in the parameters ξ ₁ and ξ ₃ (and also in $F_{2\times CO_2}$, although $F_{2\times CO_2}$ is considered well known). Historically the majority of the heat has remained in the upper oceans (Levitus et al. 2000; Lyman et al. 2010), so we focus our attention on ξ ₁; ξ ₃ only being important for the transfer of heat to the deep oceans.

Comparing Eqs. 1 and 4 shows that $\xi_1 = \frac{\Delta t}{C_{\rm up}}$. The scientific literature does not provide constraints on C _up directly, but Frame et al. (2005) present uncertainty estimates for effective heat capacity, C _eff, giving 95 % confidence intervals of $(< 0.2~\textrm{GJm}^{-2}\textrm{K}^{-1}, > 1.7~\textrm{GJm}^{-2}\textrm{K}^{-1})$ for the latter half of the 20th century.² A first approximation of ξ ₁ from the observational data would simply be $\xi_1 = \frac{\Delta t}{C_{\rm eff}}$, but this can be refined using values from the first period of the DICE model to give the implied ratio of C _up to C _eff at the beginning of the 21st century; a value unlikely to be substantially different to that in the latter half of the 20th century and therefore comparable with observations. Equation 5, based on Eqs. 2 and 4, shows this relationship.

$$ \begin{array}{rll} \xi_1 &=& \frac{\Delta t}{C_{\rm up}} \approx \frac{\Delta t \left[ F_{1} - \frac{F_{2 \times CO_2}}{S} T_{1} \right]}{C_{\rm eff} \left[ F_{1} - \frac{F_{2 \times CO_2}}{S} T_{1} - \xi_3 (T_{1}-T^{LO}_{1}) \right]} \label{Auncert} \end{array} $$

(5)

The default DICE value for ξ ₁ is 0.208, which translates into a value for C _eff of $1.8~ \textrm{GJm}^{-2}\textrm{K}^{-1}$, on the high side of what the observations suggest is likely.³ A natural question to ask, then, is what the consequences would be of assuming a lower heat capacity.

With a lower heat capacity, a given energy input produces more rapid warming, while the equilibrium temperature of the system is not affected. The main consequence, then, is to ‘front-load’ warming. As Fig. 1 illustrates, this front-loading can more than compensate for a lower climate sensitivity in the short term, producing higher temperatures even with a lower climate sensitivity. For a given S, a lower effective heat capacity will tend to lead to faster warming, causing greater damages to occur in the nearer term, when the relieving effect of discounting is least felt. Uncertainty about the value of the effective heat capacity could therefore have important implications for the economic analysis of climate change.

Fig. 1

Time-series of global mean temperature from the DICE model for two combinations of climate sensitivity and effective heat capacity

The economics of extreme warming

In this section we empirically address the issues raised above. Our ultimate aim is to investigate how sensitive the economic value of a representative mitigation policy is to uncertainty about the shape of the tail of the climate sensitivity distribution and about the effective heat capacity of the system.

To evaluate the net economic benefits of mitigation, we conduct a typical comparison between a business-as-usual emissions scenario and a scenario in which there is intervention in the economy to abate emissions. The business-as-usual scenario is as standard in DICE-2009, while our mitigation scenario controls emissions so as to prevent the mean atmospheric concentration of CO ₂ from exceeding 500ppm in a stochastic set-up (see supplementary information for details).

We begin by investigating uncertainty about the upper tail of the climate sensitivity pdf. We take the standard deterministic version of DICE-2009 and replace the best guess for the climate sensitivity parameter with a pdf so that Monte Carlo simulations can be performed. We first fit a log-Normal pdf to the IPCC’s expert subjective confidence interval (a mode of 3° C with a density of 0.67 between 2° C and 4.5° C), plotted in both panels of Fig. 2. For convenience, and because this is the upper bound of the IPCC likely interval, we speak of everything above 4.5° C as the tail of the distribution. This pdf has 0.25 density in the tail.

Fig. 2

Distributions of the climate sensitivity. a Probability distributions of climate sensitivity produced by a number of recent studies (source: Meinshausen et al. (2009)). The solid black line is a log-normal fit to the IPCC AR4 expert subjective confidence interval - see text. b Black: as in a, Blue: as black line but with the probability mass in the tail (i.e. above 4.5) redistributed to reflect the Roe and Baker (2007) distribution, Green: as black line but with the probability mass in the tail) redistributed to reflect the frequency distribution presented in Stainforth et al. (2005)

We then perturb this log-Normal pdf to obtain two further fat-tailed distributions, by shifting probability mass around within the tail while keeping the distribution below 4.5° C fixed. In addition to the tail of the log-Normal itself, which is among the thinnest of fat-tailed distributions, we use the heavier tail of the distribution derived by Roe and Baker (2007). As an intermediate between these two cases, we use the tail of the log-logistic distribution fitted to simulation output from Stainforth et al. (2005).⁴ Note that, because the mass in the tail is fixed, these two distributions will have lower densities than the IPCC-distribution in the lower part of the tail, but higher densities in the upper part of the tail that is typically associated with extreme warming. The resulting pdfs are displayed in panel (b) of Fig. 2.

The Monte Carlo simulations run the DICE model out 400 years into the future for an ensemble of 100,000 climate sensitivities (see supplementary information). They reveal how the distribution of transient temperature trajectories change when we use a different pdf for the climate sensitivity (see Fig. 3). The lower quantiles and the mode are of course fixed by design, but there is a clear fanning out of the upper tail, which increases the mean of the distribution slightly. Comparable distributions can be plotted with and without the mitigation policy. This gives us what we need to conduct a standard, welfarist economic evaluation—i.e. we compute the expected discounted utility of the two emissions scenarios, and the difference between them is the economic value of mitigation. Technically, we measure the change in the stationary equivalent, defined as the difference in welfare between the two constant consumption paths that produce welfare equivalent to the expected values from each of the two emissions scenarios (see supplementary information for details). We use a standard constant relative risk aversion (CRRA) utility function with a coefficient of relative risk aversion of 1.5, and a pure rate of time preference of 1.5 %, both default values in DICE-2009. The results are reported in Table 1.

Fig. 3

Transient temperature change under varying climate sensitivity. Each blue line represents a run of DICE under the business-as-usual scenario, so more intense colouration can be loosely interpreted as a higher probability density. The solid white line traces the mean of the distribution. The vertical axis on the left-hand-side measures the transient temperature change, while the right-hand-axes measure the corresponding instantaneous climate damages, calculated using Nordhaus’ (N) and our high (H) damage functions respectively. Note that the trajectories of ΔT depicted here are obtained from runs of DICE with H. Due to the climate-economy feedback in DICE, using N will result in lower damages in early periods and consequently higher emissions and temperatures later on. Although the plot using N looks very similar (hence not reported here), one should be aware that when changing damage function one does not only read off a different number on the right-hand-axis but also obtain a different set of temperature trajectories

Table 1 Value of 500 ppm policy

Reading first the column entitled ‘Nordhaus damages’, which describes the results for the standard version of DICE-2009, notice that the shape of the tail does not appear to matter much for the value of the policy. Going from the thinnest (IPCC) to the fattest tail (Roe & Baker) increases the economic value of the policy by only 0.04 percentage points. But these results are for Nordhaus’ specification of the damage function, which has been criticized for being too sanguine about the economic impact of extreme warming (Weitzman 2012; Ackerman et al. 2010), the very scenario that interests us most. The damage function is an especially disputed and speculative element of any IAM because there are no data to constrain it at high temperatures. This makes it difficult to adjudicate between these positions on empirical grounds, though one might perhaps think it unreasonable that Nordhaus’ default function implies ‘only’ the equivalent of a 17 % loss of global GDP for a temperature increase of 10° C above the pre-industrial level, and less than a 50 % loss for a temperature increase of 20° C. One cannot help but wonder what tall tales need be imagined to account for such survival scenarios. Nordhaus’ damage function effectively assumes that catastrophic climate change is impossible.

It seems reasonable, then, for us to perform our experiments with an alternative damage function too. In Nordhaus’ specification, climate change damages increase as a quadratic function of temperature. To account for the potentially catastrophic consequences of extreme warming, others have suggested employing a more convex damage function (Weitzman 2012; Ackerman et al. 2010). We achieved this by adding a higher-order term, which returns very similar results to Nordhaus’ damage function for small temperature increases but much higher damages for large temperature changes. Our higher-order term corresponds to that used in equation 9 Dietz and Asheim (2012), with the coefficient on the higher-order term assuming the value 0.082 (the mean value in Dietz and Asheim 2012). Others have proposed even more convex damage functions (Weitzman 2012).

As the right-most column of Table 1 shows, with our ‘high’ damage function the precise shape of the tail matters hugely for the value of the policy. In going from the thinnest to the fattest tail, the economic value of the policy jumps from increasing consumption by a mere 0.47 %, to increasing it by fully 76.7 %. This clearly illustrates the role of the tail in economic analysis of climate change. Thus, provided we do not exclude the possibility of a climatic catastrophe, as Nordhaus’ damage function effectively does, economic assessments of climate policy are highly sensitive to what is assumed about the precise shape of the tail of the climate sensitivity distribution.

Until now, the discussion of uncertainty about extreme warming has focused exclusively on the climate sensitivity. This reflects the primary focus in the economics and physical climate science literatures. As we discussed in Section 2, however, transient temperature changes are also strongly influenced by the effective heat capacity of the system. In particular, uncertainty about the heat capacity has a strong impact on our ability to forecast nearer term transient temperatures. A lower heat capacity front-loads warming, and consequently alters the time profile of economic benefits associated with emissions abatement.

DICE implicitly assumes an effective heat capacity of $1.8~\textrm{GJm}^{-2}\textrm{K}^{-1}$ (see Section 2), which is on the high side of what is considered plausible (Frame et al. 2005), and a higher effective heat capacity suppresses large temperature increases in the short term. This is visible when we plot transient temperature change for heat capacities of approximately $1.2~\textrm{GJm}^{-2}\textrm{K}^{-1}$ and $0.6~\textrm{GJm}^{-2}\textrm{K}^{-1}$ (see Fig. 4), values closer to the median and lower end of the distribution in Frame et al. (2005).⁵

Fig. 4

Transient temperature change under varying climate sensitivity and effective heat capacity. Read as Fig. 3 but for three different values of the climate’s effective heat capacity

The implications for the economic value of the policy are stark. Table 2 reveals a dramatic change in the value of the policy when the heat capacity falls. Going from the IPCC to the Stainforth tail multiplies the value of the policy several thousand times, and as the tail gets fatter the value of the policy continues to snowball. Even a little uncertainty about the tail shape of the climate sensitivity pdf, which may seem relatively unimportant from a scientist’s perspective, becomes devastating for economic analysis. A lower effective heat capacity results in a more rapid warming response to emissions for a given climate sensitivity, which means not only that the mitigation policy is more valuable, but also that the value becomes much more sensitive to assumptions about the tail.

Table 2 Value of 500 ppm policy with varying effective heat capacity

The results in Tables 1 and 2 are best understood in the context of the temperature changes necessary to produce catastrophic economic damages. The economic criterion used to value future consumption assumes the willingness to pay is extremely high to avoid an outcome where consumption is extremely low. Any future periods with near-zero consumption will therefore completely dominate the calculation of the value of the policy, however far off in the future they are. A policy that can avert or even postpone such extreme warming will appear immensely valuable. With Nordhaus’ damage function, damages rise very slowly as temperatures rise. Because of thermal inertia, there is no value of the climate sensitivity (or reasonable combination of climate sensitivity and effective heat capacity) that can produce sufficient temperature change to drive economic output close to zero over the next 400 years. Consequently, uncertainty about the tail shape is not all that important (for completeness, Table 2 is replicated with Nordhaus’ damage function in the supplementary materials). With our high damage function, on the other hand, damages rise faster with temperatures. As a consequence, it is possible to reach sufficiently extreme temperatures under the business-as-usual scenario within the modeling horizon, but not with the 500ppm policy in place. With a sufficiently fat tail of the climate sensitivity pdf, therefore, our sample of climate sensitivities is likely to include some high values that result in catastrophic warming under business-as-usual. When there is the possibility of catastrophic warming, then, the value of the policy derives almost exclusively from its ability to compress down the upper tail of the distribution of transient temperature changes. The figures in Table 2 therefore closely correspond to the effects of the mitigation policy on the behaviour of the higher quantiles of the distribution, as shown in Fig. 5.

Fig. 5

Impacts of mitigation on the higher quantiles of transient temperature change. The three red lines in each panel trace the 95th, 99th, and 100th percentiles of the distribution of transient temperature changes (in ascending order) in the business-as-usual scenario. The three blue lines trace the corresponding quantiles in the mitigation policy scenario

The role of the heat capacity can also be understood in these terms. Firstly, as discussed earlier, a lower heat capacity front-loads warming, thus increasing the value of mitigation even in moderate warming scenarios. Secondly with a lower effective heat capacity, a lower climate sensitivity will be sufficient to produce extreme warming within the period of analysis. We are thus more likely to have extreme warming even with a thinner tail of the climate sensitivity distribution. This is why the red lines keep shifting higher and higher as we go from right to left in Fig. 5, and the value of mitigation derives primarily from averting these more and more catastrophic possibilities. This is also why the economic value of the policy increases so rapidly as we go from right to left in Table 2.

Discussion

Uncertainty about the shape of the fat upper tail of the climate sensitivity distribution can wreak havoc with economic analysis of climate policies. However, the climate sensitivity matters only indirectly. Economic analysis is sensitive to the probability of extreme warming, and high values of the climate sensitivity are only one of the factors that lead to rapid warming. As we have shown, uncertainty about the effective heat capacity also matters a great deal for economic analysis, and this uncertainty greatly amplifies the economic consequences of uncertainty about the shape of the tail of the climate sensitivity distribution.

With results like these, it is perhaps understandable that some have concluded the risk of a climate catastrophe should be the sole determinant of climate policy (Pindyck 2011). Whether one agrees with this assessment or not, it highlights the need to improve our understanding of the relevant risks. It would be valuable to place a greater emphasis on exploring uncertainty about the probability of very high transient temperature changes directly, which would entail a more inclusive discussion of the underlying physical uncertainties that accompany a rapidly warming world. A concrete example of this is carbon cycle feedbacks, which, studies suggest, are both influenced by and themselves influence the likelihood of higher or lower warming (Cox et al. 2000; Friedlingstein etal. 2006).

A secondary conclusion relates to the importance of the damage function in economic analysis. As we saw in Section 3, with one damage function the expected value of the policy was rather insensitive to the probability of extreme warming, while another damage function makes the economic analysis hypersensitive. This is because each damage function implicitly defines what level of warming is considered catastrophic, and uncertainty about extreme warming plays a profoundly different role in economic analysis depending on how we define ‘catastrophic’. For all of the focus on the economics of catastrophic climate change, surprisingly little attention has been paid to this issue. At a basic level, we must try to understand better the limits of human adaptation to climate change. A noteworthy example is provided by Sherwood and Huber (2010), who note that for wet-bulb temperatures above 35° C, dissipation of metabolic heat becomes impossible in humans and mammals, causing hyperthermia and death. They proceed to estimate that with an increase in global mean temperature of roughly 12° C, most of today’s population would be living in areas that would experience wet-bulb temperatures of more than 35° C for extended periods. Given how important the limits of adaptation appear to be for economic calculations, further exploration of such limitations may prove informative.

Our analysis indicates it would be especially valuable to gain a greater understanding of both the physical and social processes associated with a much warmer world. The proposed endeavour will necessarily be speculative in many respects. It will involve trying to understand which physical feedbacks will become significant in the next few centuries, and how much warming they can and cannot account for. It will require that we both imagine and take seriously the social and demographic processes that would accompany a quickly changing climate. The fat tail of the climate sensitivity distribution has perhaps been an effective vehicle for bringing attention to the issue of extreme warming, but it is time to move beyond this convenient metaphor and build a scientific view of society in a rapidly warming world.