Abstract
Direct Air Capture (DAC) of CO2 with chemicals, recently assessed in a dedicated study by the American Physical Society (APS), is further investigated with the aim of optimizing the design of the front-end section of its benchmark two-loop hydroxide-carbonate system. Two new correlations are developed that relate mass transfer and pressure drop to the air and liquid flow velocities in the countercurrent packed absorption column. These relationships enable an optimization to be performed over the parameters of the air contactor, specifically the velocities of air and liquid sorbent and the fraction of CO2 captured. Three structured Sulzer packings are considered: Mellapak-250Y, Mellapak-500Y, and Mellapak-CC. These differ in cost and pressure drop per unit length; Mellapak-CC is new and specifically designed for CO2 capture. Scaling laws are developed to estimate the costs of the alternative DAC systems relative to the APS benchmark, for plants capturing 1 Mt of CO2 per year from ambient air at 500 ppm CO2 concentration. The optimized avoided cost hardly differs across the three packing materials, ranging from $518/tCO2 for M-CC to $568/tCO2 for M-250Y. The $610/tCO2 avoided cost for the APS-DAC design used M-250 Y but was not optimized; thus, optimization with the same packing lowered the avoided cost of the APS system by 7 % and improved packing lowered the avoided cost by a further 9 % The overall optimization exercise confirms that capture from air with the APS benchmark system or systems with comparable avoided costs is not a competitive mitigation strategy as long as the energy system contains high-carbon power, since implementation of Carbon Capture and Storage, substitution with low-carbon power and end-use efficiency will offer lower avoided-cost strategies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In 2011, the American Physical Society (APS) published a report, Direct Air Capture of CO 2 with Chemicals. “Direct air capture” (DAC) involves a system with an “air contactor” where ambient air flows over a chemical sorbent that selectively removes the CO2. The CO2 is then released as a concentrated stream for disposal or reuse, while the sorbent is regenerated and the CO2-depleted air is returned to the atmosphere. DAC is one of a small number of strategies that might allow the world someday to lower the atmospheric concentration of CO2.
This article augments the APS report, which we will call “APS-DAC” here. We focus primarily on the economic analysis of a specific system (Chapter 2 of APS-DAC), whose design was drawn from a previous paper (Baciocchi et al. 2006), called BSM here.Footnote 1 APS-DAC was based solely on the design of the absorber section developed in BSM, with component costs provided independently. Here we provide detailed and updated results, as well as, for the first time, an economic optimization for that system. The optimization conveys considerable insight into the kinds of tradeoffs that come into play in any design of a gas separation system.
Section 2 briefly summarizes some qualitative conclusions from APS-DAC. Section 3 develops the economic optimization. Section 4 discusses generic issues of DAC. Section 5 presents conclusions.
2 Summary of the american physical society’s technology assessment
This section summarizes a few of the quantitative and qualitative conclusions of APS-DAC, under three headings: physical scale of the air contactor, net-carbon considerations, and costs.
2.1 Physical scale of the air contactor
A contactor will capture about 20 t of CO2 per year for each square meter of area through which the air flows, if the average flow velocity is 2 m/s and half of the CO2 is removed (we will see below that 2 m/s and 50 % capture are typical values). Since a 1,000-megawatt coal power plant emits about six million metric tons of CO2 per year, the corresponding DAC system consisting of structures 10-meters high that remove CO2 from the atmosphere as fast as this coal plant emits CO2 would require structures whose total length would be about 30 km.
2.2 Net-carbon considerations
It is obvious that any air capture strategy must remove more CO2 from the atmosphere than is emitted to the atmosphere during the capture and storage process: the net flow of CO2 out of the atmosphere must be positive. In DAC two of the largest energy demands are expected to be the energy to move the air through the contactor and the energy to regenerate the sorbent. Either of them can defeat the CO2 removal objective if it is sufficiently carbon-intensive.
The impact of moving the air with fans can be substantial. Assume 50 % removal of CO2 from ambient air (assumed having a CO2 concentration of 400 ppm), 80 % fan-system efficiency (power delivered to the air divided by electric power used), and a pressure drop of 1,000 Pa. If coal-based power (with a typical carbon intensity of 1,000 kgCO2/MWh) runs the fans, almost exactly one carbon atom enters the atmosphere at coal plants for each atom captured at the DAC plant, thus resulting in a perfectly useless system with an infinite cost per net ton of CO2 removed. Pressure drop, therefore, becomes a critical design variable, and low-carbon power is dictated.
A second major requirement is the energy to undo the bonding of the CO2 and regenerate the sorbent. For capture processes that use a solid adsorbent and a thermal swing, thermal energy will also be required to heat and evaporate water vapor co-adsorbed with the CO2. Water vapor will condense in the micropores of hydrophilic microporous solids, such as ion-exchange resins or functionalized silicas, and the thermal treatment that releases CO2 will also release water. An anion exchange resin in its ambient state at room temperature can contain more than 50 % water by weight (Dowex™ Ion Exchange Resins, Product Information Catalog), and metal oxides with high surface area, when used to create functionalized CO2 adsorbents, can contain similar amounts of moisture (Saint Gobain 2006). For example, an adsorbent that can capture 50 g of CO2 per kilogram, if it contains 20 % moisture, will release up to 200 g of water during regeneration. If the heat of vaporization of this water is provided by natural gas, approximately 470 kg of CO2 could be generated per ton of CO2 released, not including the energy to heat up the adsorbent and the adsorbed water and CO2. Once again, low-carbon energy sources are dictated.
Low-carbon power could be some form of renewable energy (e.g., wind, hydro, solar), or nuclear power, or fossil-fuel power accompanied by CO2 capture and storage (CCS). Of these options, fossil fuel power produced at the facility and co-capture and co-storage of air-CO2 and fossil-fuel-CO2 is particularly interesting.
However, using low-carbon energy for DAC, no matter what its source, carries an opportunity cost as long as DAC facilities are located within a regional electric power system where high-carbon power is still being produced. Instead of powering the DAC system, the same low-carbon energy source could instead be used to displace some of that high-carbon power.
2.3 Costs and cost implications
A cost estimate is developed in APS-DAC “for a benchmark system that could conceivably be built today, using a simplified costing methodology applied in industry to early-stage projects” (APS-DAC, p. ii). With many specified additional assumptions, retained throughout this paper, the estimated avoided cost (the cost when net carbon is taken into account) is $610/tCO2. To normalize this result, APS-DAC also estimates $80/tCO2 to be the avoided cost for a specific system that captures CO2 from the flue gas at a coal power plant. The CO2 concentration in the flue gas, at 12 %, is 300 times larger than it is in air. Neither case considers costs incurred after the CO2 has been separated in concentrated form, such as the costs of transport to and injection into an underground storage facility. It is worth noting that a different cost estimate, of about $1,000/tCO2, has been published recently, based on a top-down approach (House et al. 2011).
New approaches that lower the cost of the CO2 sorption-desorption system may well be applicable to both air capture and flue-gas capture. For this reason, APS-DAC considers the order-of-magnitude ratio of costs for air-capture versus flue-gas capture to be a more robust estimate than either cost. From this perspective, the prospect that one would simultaneously emit CO2 from a traditional coal power plant and remove it from the atmosphere is bizarre. Quoting APS-DAC again: “[E]ven if costs fall significantly, coherent CO2 mitigation would result in the deployment of DAC only after nearly all significant point sources of fossil CO2 emissions are eliminated, either by substitution of non-fossil alternatives or by capture of nearly all of their CO2 emissions.”
2.4 Constraints on scale-up
This article is appearing in a special issue on carbon dioxide removal (CDR) that presents the perspectives of modelers of the future global economy on the one hand and engineers and natural scientists on the other hand. Ideally, this paper, which comes from the engineering side, would address all the micro and macro questions of interest to modelers. In reality, both APS-DAC and this paper address only micro questions, i.e., the physical characteristics, costs, and barriers to deployment of a single DAC system. We learn that the system is likely to be modular and to be highly constrained by net-carbon considerations, for example. However, a modeler will also ask macro questions, notably about the ultimate scale of global deployment and the constraints on the pace of getting there. These important issues are not treated here.
Indeed, every approach to climate change mitigation involves a huge deployment sustained over decades (thousand of gigawatts of some form of electric power, hundreds of millions of hectares of some use of land). No full answers about pace and ultimate scale exist for any approach, but some constraints can be identified. In the case of DAC, the most important constraints on pace of deployment probably take the form of upper limits on global industrial capacity – the number of projects the world might be able to build in parallel; careful study of this topic, to the best of our knowledge, has not yet been done.
Constraints on ultimate scale are probably less severe than constraints on pace. Land constraints, which dominate biological forms of CDR, are far less constraining for DAC. Moreover, one should not expect constraints on DAC to arise from the need not to overwhelm watersheds or airsheds with hazardous air and water emissions, since there is ample room to design environmental safety into air capture facilities. There are also no obvious scale constraints arising from the scarcity of materials. One constraint on ultimate scale may come from CO2 storage capacity, a constraint that is not particular to DAC and indeed is treated in several papers in this issue dealing with biological CO2 capture and storage (BECCS).
One may ask why this paper further explores the APS-DAC benchmark system, given its estimated avoided cost of $600/tCO2, a cost so high that the system is highly unlikely ever to be deployed. Our answer is that the benchmark system serves well as a model system, yielding generalizable insights. In particular, alternative parameter choices for the benchmark system, explored in the following section, illuminate trade-offs broadly relevant to any system design.
3 A benchmark two-loop hydroxide-carbonate DAC system and its optimization
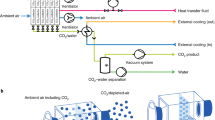
The APS-DAC system (see Fig. 1 identical to 2.B5.1b in APS-DAC) absorbs CO2 by passing ambient air over a solution of sodium hydroxide in a closed counter-current absorber. The solution containing sodium carbonate is then contacted with calcium hydroxide to exchange metals and form calcium carbonate that precipitates. The solid calcium carbonate is decomposed in a natural-gas-fueled, oxygen-fired kiln, with capture of the released CO2. The benchmark system, discussed in BSM, Stolaroff et al. (2008) and Zeman (2008), is conservative relative to the alternative systems discussed in Section 4: it uses only durable, well-tested materials.
The air contactor (CO2 absorber) and the precipitator where sodium and calcium ions are exchanged are the only components of the APS-DAC system that we revisit in this paper for optimization; the design and the cost of the remaining part of the DAC plant depends only on the total amount of CO2 captured that does not change from APS-DAC. The physical parameters for these components were developed in BSM; costs and financial assumptions were added in APS-DAC. Here, we augment those analyses with new parameterizations and data that concern the choice of the packing material and the process operating conditions, which affect the cost of the absorber and its energy requirements, and thus the cost of the total system. Accordingly, in this section, we examine tradeoffs and optimization opportunities in two steps. In Section 3.1 we develop a full parameterization of the absorber. In Section 3.2, we present scaling rules for the costs of the components and then develop the full-system cost and its sensitivity to changes in the absorber’s parameters, holding all other APS-DAC assumptions constant. In Section 3.3 we report the results of optimizations of capture cost and avoided cost for the three packings. The analysis is in the spirit of APS-DAC, where the emphasis has been on completeness and transparency.
3.1 Design elements
The APS-DAC plant design assumes a plant capturing 1 Mt/yr of CO2 from ambient air at a molar CO2 inlet concentration, y in = 0.0005 (500 ppm, a CO2 concentration about 25 % higher than today). We vary the absorbing solution’s sodium hydroxide concentration, [NaOH] in mol/L (or molarity, M); the air velocity through the absorber, w G [m/s]; the solution velocity, w L [m/h]; and the CO2 capture fraction, r [−], which is defined in terms of incoming and outgoing molar concentrations, y in and y out, r = (y in- y out)/ y in.
3.1.1 Packing options
We consider three Sulzer Mellapak structured packing materials: Mellapak 250.Y (M-250Y), Mellapak 500.Y (M-500Y), and Mellapak CC (M-CC). M-250Y and M-500Y were considered in the APS-DAC study and in BSM. M-CC is a new packing that Sulzer Chemtech has commercialized recently, optimized for post-combustion CO2 capture and similar applications (Menon and Duss 2011); because literature data on M-CC are incomplete, some of its properties have been assumed.
Moving beyond APS-DAC, we will introduce below a new relationship for the effective specific surface area of the packing. Instead of literature data, we use the latest version of the software package, Sulcol 3.0, provided by Sulzer Chemtech, to calculate the specific pressure drop for each packing. At the same time, we correct an unfortunate unit conversion error in BSM, which entailed interpreting literature data on M-250Y and M-500Y at a pressure drop of 10 mbar/m (1,000 Pa/m) as if at 100 Pa/m, and thus resulted in an underestimation of pressure drops.
3.1.2 Number of units, air velocity, and fraction captured
At 500 ppm of CO2 by volume, one cubic meter of air contains 0.92 g CO2. Therefore, the 1 Mt CO2 captured in 1 year in the DAC plant is contained in 1.09 · 1012 m3 of air. At a capture fraction, r, the rate at which air must be processed is 1.09 · 1012/r m3/yr, or equivalently 38,000/r m3/s, when we consider 8,000 operating hours per year. We assume that the air contactor contains a number of (identical) absorbers, N, through each of which the air flows at a rate, Sw G, where S is the absorbers’ cross-section and w G is the air velocity through the absorber. Then the air flow rate through the contactor can be expressed as the product, NSw G . As in APS-DAC, we assume S = 113 m2, corresponding to an absorption diameter of 12 m. This design specification leads to the following constraint on the DAC operating and design variables:
For example, the air contactor contains 335 absorbers when w G = 2 m/s, and r = 0.5, as in APS-DAC. Each absorber captures 3,000 tCO2/yr, or about 9 tCO2/day.
Note that a 10 % increase of the atmospheric CO2 concentration leads to a value of 300 m/s on the right hand side of Eq. (1) and a corresponding 10 % decrease in the number of absorbers if the capture fraction and air velocity are unchanged.
3.1.3 Effective packing specific surface, column height and solution velocity
The absorber column height, H [m], can be calculated based on inlet and outlet CO2 concentration by solving the following differential material balance equation:
where y is the CO2 mole fraction along the column; y * is the CO2 mole fraction in equilibrium with the bulk liquid phase at position z along the column, hence in principle a function of [NaOH]; K G is the overall mass transfer coefficient in terms of gas phase mole fractions; and a e is the packing effective specific surface [m−1], i.e. the specific interface area between gas and liquid through which CO2 is absorbed into the scrubbing solution.
The parameters K G and a e thus determine the column efficiency, i.e. the larger the product of their values, the shorter the column for the same separation task and the same air velocity – provided that these parameters fall within the range of operating conditions defined as “loading.” Loading conditions require the packing to operate well and the column not to reach the state, called “flooding,” where mass transfer resistances and pressure drop diverge and the column cannot be operated any more. Loading requires air velocities between about 0.2 and 2 m/s with M-500Y, between about 0.5 and 2.5 m/s with M-250Y, and between about 0.7 and 3 m/s with M-CC (the M-CC range is still uncertain because of a lack of precise data for this newer packing material).
The overall mass transfer coefficient K G [m/s], sometimes called the piston velocity, accounts for mass transfer through the gas and the liquid phases. It is calculated through the following equation:
where H cp [kmol/(m3 atm)] is the Henry’s constant, defined as the ratio between the CO2 molar concentration in solution and its equilibrium partial pressure in atm; k G [m/s] is the gas-phase mass transfer coefficient; k L [m/s] is the liquid phase mass transfer coefficient; R = 0.082 atm m3/(kmol K) is the gas constant; and T [K] is the temperature (293 K in our case). The parameter K G is in principle a function of the gas and liquid velocities. However, in the case at hand the liquid phase is controlling (Pohorecki and Moniuk 1988) and the mass transfer coefficient is independent of the liquid velocity and only weakly dependent on [NaOH] (Pohorecki and Moniuk 1988). In this paper, we use K G = 0.003 m/s throughout the operating range of interest, notably for [NaOH] between 2 and 4 mol/L (BSM).Footnote 2
As for the packing effective specific surface, a e, it is the product of the nominal specific surface area of the packing, a p, and an efficiency factor that describes how effectively the packing is being used. The values of a p are 250 m−1 for M-250Y and M-CC and 500 m−1 for M-500Y. In the situations of interest here, the effectiveness increases as a weak power of the velocity of the solution and is independent of the velocity of the air. Many experimental data have been correlated, with an uncertainty of about ±15 %, by the following simple power law (Tsai et al. 2009):
where w p is the velocity where the efficiency factor is 1, namely 38 m/h for M-250Y and M-CC, and 81 m/h for M-500Y. Alternatively, in the second relationship of Eq. (4), a r is a reference effective specific surface, i.e. its value at w L = w L,r ; if the reference velocity w L,r = 10 m/h, then the reference effective specific surface is 200 m−1 for M-250Y and M-CC and 360 m−1 for M-500Y. This “wetting equation” expresses the fact that, at slow solution flow rates, the packing surface does not become adequately wetted. However, because of the weak power dependence, a e is typically not much below the geometric surface, even though our liquid flow rates are far below w p . At the same solution velocity, M-500Y is less wetted than M-250Y or M-CC, and the effective specific surface of M-500Y is only about 1.8 times larger than that of M-250Y and M-CC, rather than twice as large. Note that the parameters used in the APS-DAC system, which assumes 250Y packing, the values a e = 165 m−1 and wL = 7.7 m/h, do not satisfy Eq. 4. Assuming Eq. 4 and a 7.7 m/h liquid velocity leads to an effective specific surface area around 190 m−1.
In solving the mass balance equation (Eq. 2), it is a good assumption that the gas phase equilibrium concentration, y*, is zero everywhere, as a consequence of the NaOH solution being a very strong absorber. Therefore integrating Eq. 2 yields:
As in the chemical engineering literature, here H OG = w G/(K G a e) [m] is the height of a transfer unit, which decreases with increasing absorption efficiency (the product of mass transfer coefficient and effective specific surface) and increases with gas velocity. Also, N OG = ln((1/(1-r)) is the number of transfer units, which depends only on the capture rate in this case. Assuming r = 0.5, as in APS-DAC, N OG would be 0.69, and less than one transfer unit of height H OG would be sufficient. In the chemical industry typical separations involve values of r much closer to 1.0 and therefore require more than one transfer unit.
Using the wetting equation, the height of a transfer unit can be expressed as:
where H OG,r = w G,r/(K G a r) [m] is the height of a transfer unit in a column operated at reference gas and liquid velocities; when these values are given by 1 m/s and 10 m/h, respectively, then H OG,r is 1.65 m for M-250Y and M-CC and 0.93 m for M-500Y. Thus, in this case, an absorber using the packings M-250Y and M-CC is 1.8 times taller than one using M-500Y, a factor almost exactly compensated by a unit price for M-500Y about 1.7 times higher than for the other two packings.
Finally, the volume of each absorber, V a , is V a = HS, and the total packing volume of the DAC plant, V, can be written as:
The total packing volume does not depend on the air velocity in the range of “loading” conditions of the column considered here.
3.1.4 The total pressure drop
If the specific pressure drop (pressure drop per unit length) through the absorber, dp/dz, is constant, then the total pressure drop through the absorber, Δp tot , is:
Moving beyond APS-DAC, we assume that dp/dz depends only on the two countercurrent velocities, w G and w L , and that these velocities are constant through the absorber. Using Sulcol 3.0 software and data from Sulzer Chemtech (the packing manufacturer), we find that under dry conditions, the specific pressure drop, (dp/dz) dry , depends on the air velocity, w G , according to Ergun equation:
where k 1 and k 2 are parameters characteristic of the packing material. The pressure drop is augmented in the presence of a countercurrent liquid flow, w L , by a term proportional to w L :
where Δwet is an exponential function of the air velocity, and k 3 and k 4 are two additional parameters characteristic of the packing material. Values of the four parameters (k 1 , k 2 , k 3 , and k 4 ) for the three packing materials are reported in Table 1.
Note that the parameters used in the APS-DAC system, which assumes 250-Y packing, w G = 2.0 m/s, w L = 7.7 m/h and dp/dz = 100 Pa/m, do not satisfy Eq. 10. Rather, a larger pressure drop is obtained for these flow velocities. Under dry conditions the specific pressure drop for M-250Y and assuming w G = 2.0 m/s, (dp/dz) dry is 1.46 mbar/m or 146 Pa/m. Adding the third term in Eq. 10 to take into account the pressure drop created by liquid flow and assuming w L = 7.7 m/h produces an additional 20 Pa/m, for a total pressure drop of 166 Pa/m. Table 1 also reports ratios of packing costs per unit volume; the reference cost, from APS-DAC, is $1,700/m3 for M-250Y.
The total pressure drop, Δp tot , has a minimum with respect to w L , when all other parameters are held constant, because the column height, H, decreases as w L increases (since wetting of the packing becomes more effective) and the specific pressure drop increases as w L increases. The minimum value, w L,min , is
the specific pressure drop at w L,min is
and the minimum is rather shallow. Using the equations and the parameters above, for air velocities between 0.5 m/s and 2.5 m/s the ratio of the specific pressure drops in M-500Y packing and M-250Y packing is between 2 and 1.7, with an average value of about 1.8, and the specific pressure drop in the M-CC packing is about 40 % of that in the M-250Y packing.
3.1.5 The fan power demand
We assume that air is driven through the absorber by fans. The power needed, P fan [W], is the product of the air flow rate through the column, NSw G , and the total pressure drop, divided by the system efficiency (neglected here). Then:
which can be recast as follows using Eq. (7) for V and Eqs. (8) and (10) for Δp tot :
where B and H OG,r were introduced earlier. The only terms that are different for the different packings are the reference height of a transfer unit, H OG,r , and the expression between brackets that gives the specific pressure drop. For the same velocities and capture rates, the power demands for the M-250Y and M-500Y packings turn out to be roughly equal and two and a half times larger than the power demand for the M-CC packing.
3.2 The effect of design variables on costs
In discussing costs, we use APS-DAC as a reference for the costing methodology, and we introduce scaling rules to enable comparison of alternative designs. The capture cost, i.e. the total cost for capturing one ton of CO2, C cap , is the sum of capital cost recovery (C capex ) and operating cost (C opex ):
3.2.1 Capital cost
C capex is calculated from the “fully built up” capital costs, an annual capital charge rate, and an annual throughput. In conformity with the costing methodology, “fully built up” capital costs are obtained from the bare equipment costs (BEC) of components by multiplying by 4.5 (see APS-DAC, Appendix 2A). To turn fully built-up capital costs into C capex , we assume a cost recovery from the fully built up capital cost of 5 %/yr for depreciation and 7 %/yr for return on investment. Thus:
where CR is the CO2 capture rate, i.e. 1 million tons/year in the APS-DAC design.
The total bare equipment cost presented in APS-DAC can be viewed as the sum of four terms:
Here, the first and second terms refer to the absorber: C P is the bare cost of column packing, and C S is bare cost of the shell and internals. The third and fourth terms refer to the back end: C x is the bare cost of the precipitator and C reg is the bare cost of all other back-end components.
We assume that C P scales with the total volume of the absorbers, V = NHS, to the power 0.9 (nearly linearly, because packing is a bulk commodity). That is:
where the subscript r throughout this section refers to values in APS-DAC (see the first column of data in Table 2 for these values). C P,r is $160 million, and V r is 106,000 m3.
We assume that the cost of shell and internals, C S, scales with the number of absorbers, N, to the 0.85 power (an approximation to reflect efficiency impacts that occur as production volumes increase or decrease), and that the cost of an individual absorber scales with its surface area to the 0.7 power. Our absorber is a 12 m diameter cylinder with a variable center section filled with packing and two caps with flat ends, each 2 m long. The caps house the liquid and gas distributors. The reference length of the center section for the APS-DAC (H r ) absorber is the 2.8 m, so its central section accounts for 20 % of the surface area and the caps account for 80 %. Then:
The value of C S,r is $130 million; thus, in APS-DAC, the costs of packing and of shell and internals are approximately equal, and each accounts for roughly half of the total absorber capital cost.
As for the regeneration section (the “back end”), we assume that only the precipitator (where sodium carbonate is exchanged with calcium carbonate) depends on the absorber parameters. Its capital cost, C x , is assumed to be proportional to the flow rate of solution circulated through the absorbers, i.e. Nw L S. Hence:
where C x,r is $25 million; the liquid velocity, w L,ref , is 7.7 m/h; and N r is 335 in the APS-DAC design. The remainder of the regeneration – the calciner, the air separation unit (ASU) and the CO2 compressor – depends only on the amount of CO2 captured, which we hold constant. Its cost, therefore, is:
where C reg,r is $165 million ($120 million for the calciner, $15 million for the ASU and $31 million for the compressor).
Combining Eqs. (18)–(21) yields:
For the reference case, BEC r is $480 million, the fully built up cost is $2,200 million, and C capex,r is $260/tCO2 (the sum of $87/tCO2 for the packing, $70/tCO2 for the shell and internals, $14/tCO2 for the precipitator and $89/tCO2 for the other components of the back end).
The APS-DAC reference bare equipment costs and reference system parameters assume a system with a 90 % capacity factor, characteristic of a “baseload” system. Assuming a baseload system is optimistic: realistic systems may exhibit sub-optimal capture efficiency under some environmental conditions (low air temperature, high humidity, high wind speed, high air pollution).
3.2.2 Operating cost
The operating cost per ton CO2 captured, C opex , is given by:
where C ml is the cost of maintenance and labor, C fan is the cost of fan power, C be is the cost for back-end electricity (regeneration section), and C other is the sum of the cost of natural gas for firing the kiln and the cost of chemicals.
In agreement with the APS-DAC costing methodology, labor and maintenance costs sum to 3.9 %/yr of the fully built-up capital costs (3.0 %/yr and 0.9 %/yr for labor and maintenance, respectively), so that
As for the operating cost for fan power, we assume here that the electricity cost is fixed at its value in APS-DAC, $71/MWh, in which case the fan power cost scales linearly with fan power consumption:
The fan power consumption for the APS-DAC reference system, P fan , is 0.19 MWh/tCO2, and C fan,r is $14/ton CO2. (A 10 % contribution of pumps to power consumption is included in P fan here.)
We assume that all other operating costs are unchanged, relative to APS-DAC. The cost for electricity in the regeneration section, C be, r is $21/ton CO2 ($11/ton CO2 for the ASU, $8/ton CO2 for the compressor, and $2/ton CO2 for the precipitator). C other,r is $50/ton CO2 (the sum of $46/ton CO2 for the natural gas at $6 per million Btu firing the kiln and $4/ton CO2 to chemicals). Thus:
For the APS-DAC reference system C opex,r is $170/tCO2 (the sum of $86/tCO2 for maintenance and labor, $14/tCO2 for fan power, $21/tCO2 for back-end electricity, and $50/tCO2 for natural gas and chemicals).
Finally, for the APS-DAC reference system, the total capture cost is $430/tCO2. A total of $160/tCO2 is not varied in the optimization presented in Section 3.3 ($89/tCO2 for fixed back-end CAPEX and $71/tCO2 for fixed back-end OPEX). The remaining $270/tCO2, or 63 % of the total capture cost, is affected by the optimization.
3.2.3 Avoided cost
As discussed extensively in APS-DAC and in Section 2 above, carbon dioxide emissions associated with the energy to run the absorber figure prominently in the cost analysis. Associated with the “capture” cost, C cap , there is an “avoided” cost of CO2 removal from the atmosphere, C avo :
There are three energy terms in the denominator: Q reg is the heat required for regeneration, P fan is the electricity required to power the fans (which includes also the negligible power demand for liquid pumping), and P reg is the electricity required for regeneration. The two carbon intensities in the denominator, c Q , and c W , are, respectively, for heat and electricity. Thus, the product c W P fan gives the tons of CO2 emitted by the external power plant that provides electricity for the fans, per ton of CO2 captured by the DAC plant, etc. Following APS-DAC, we assume that the carbon intensity of heat for regeneration, c Q , is zero, since the CO2 produced is internal to the process and captured at the DAC plant. We assume that the electricity for the entire system is provided from a grid with a carbon intensity of 610 kgCO2/MWh, which corresponds to c W = 0.0048 MW−1.
3.3 Optimization
We treat the gas velocity, w G , the liquid velocity, w L , and the capture rate, r, as the variables that can be manipulated to optimize the DAC plant performance. We constrain the gas and liquid velocities not to come close to the “flooding” regime of the absorbers. For these conditions, the design relationships and scaling rules developed above are accurate enough to compare alternative absorber designs with the design chosen in APS-DAC. We specify the amount of CO2 to be captured in the DAC plant, i.e. one million ton per year. We explore the optimization of both the “capture” cost, C cap , and the “avoided” cost, C avo.
The optimization has been carried using commercial software for constrained optimization, namely the Matlab routine “fmincon”. We have run the optimization from different initial conditions, thus making sure that the optimum is not local but global. The results of such optimizations are reported in Table 2, where the seven columns report operating conditions, DAC plant size, and costs for the APS-DAC plant and three pairs of other plants, each pair corresponding to a different packing material. Within each pair are the design parameters that minimize “capture” cost and “avoided” cost.
3.3.1 Optimal design
The data in Table 2 show that the designs that optimize “capture” cost and “avoided” cost for the same packing material are quite different, reflecting the CO2 emissions associated with external power, which impact avoided cost. For M-250Y, where the difference is largest, the optimal pressure drop through the column, Δp tot (and the cost of fan power, P fan ) is about four times smaller for the avoided-cost optimization. This is achieved by slower air and liquid velocities and a larger number of shorter columns; in addition, the capture fraction is larger. Similar, though smaller effects are seen for M-500Y and M-CC.
The optimized avoided cost hardly differs across the three packing materials, which ranges from $518/tCO2 for M-CC to $568/tCO2 for M-250Y. This range is considerably narrower than the likely uncertainty in each cost estimate. M-500Y exhibits shorter columns because of the higher specific pressure drop and higher mass transfer efficiency than the other two packings, but the number of absorbers is similar for all packings. For systems with optimized avoided cost, the pressure drop, Δp tot , is only slightly less for M-CC than for M-250Y, even though the M-CC packing has a much lower pressure drop per unit length, dP/dz, than M-250Y. The optimized M-CC system compensates by having a higher air speed and a taller column than the optimized M-250Y system—a result that is tentative, considering the incompleteness of the M-CC data in Table 2.
As for the APS-DAC design, which used M-250Y but was not optimized and did not impose the constraints expressed in Eqs. 4 and 10, its velocities, column height, pressure drop, and number of absorbers are not far from the corresponding values obtained for the six optimized designs. The APS-DAC packing effective specific surface, a e , is about 20 % smaller than its value for the optimized designs for M-250Y and M-CC, and accordingly the overall packing volume for the APS-DAC system is somewhat larger. The APS-DAC “capture” cost of $430/tCO2 is about ten percent higher than the three optimized “capture” costs. The APS-DAC “avoided” cost of $610/tCO2 is between 10 % and 20 % higher than the three optimized “avoided”: $568/tCO2, $556/tCO2, and $518/tCO2 for M-250Y, M-500Y, and M-CC, respectively.
4 Generic issues around DAC
The benchmark DAC system is one of a number of potential approaches. Other proposed routes involve systems with novel contactor designs using chemical cycles (Mahmoudkhani and Keith 2009; Holmes and Keith 2012) and novel solid adsorption systems using physical cycles (Wang et al. 2011; Jones 2011). This section reviews some of the constraints that will need to be satisfied in order for any DAC system to be considered practical and economic.
4.1 Health, safety and environment requirements
Primary containment is a concern when air capture systems involve corrosive and/or toxic chemicals. If a caustic solution is used to capture CO2 and the contactor is unenclosed, then the treated air at a large air-capture complex can entrain a mist that releases tonnes of caustic solution per day into the environment. While such losses may be managed during normal operations, in the case of high wind they may be considerable. The costs to control these mists may be significant, and in some locations permitting may not even be possible.
Water loss associated with evaporation from an aqueous solvent into the air flowing over it can be significant, especially if large quantities of process water are required (see Box 2.6 in APS-DAC for a quantitative analysis).
Prevention of the degradation of water quality is yet another source of costs. Any waste water generated in an air capture process may need to be controlled for pH, nitrogen content, and salt concentrations before being released to the environment.
4.2 Polluted intake air
Pollutants in the intake air can make it difficult to achieve a high on-line capacity factor for the air capture system. Trace strong-acid components in the air, such as SOx and NOx, may irreversibly poison hydroxide solutions or functionalized solid adsorbents. Suppose the intake air has concentrations of NOx and SOx equal to the 2009 US average annual allowable values. The combined concentration is then 80 ppb (US EPA 2011), and a sorption material with 400 ppm of CO2 may lose 0.02 % of its capacity per cycle. For a solid adsorbent with no mechanism to remove the nitrate and sulfate salts that form, 50 % of its capacity will be lost after 2,500 cycles. If the adsorbent is cycled once an hour, it will lose 50 % capacity in four months, and in case it is an engineered specialty material, its replacement will add significant cost to the DAC process.
Moreover, inorganic and organic particulate matter must be filtered out of the intake air, because any foreign matter that breaks through could react with the caustic solution or clog the pores of a solid sorbent, causing either formation of precipitates or gels, or adsorbent degradation, respectively.
4.3 Sorbent stability
A DAC sorbent must withstand a very large number of CO2 uptake and recovery cycles without losing performance. The captured CO2 can be removed from caustic scrubbing solutions by precipitating the CO2 with a species whose carbonate has low solubility, thus regenerating the absorbent. This operation needs to be carefully controlled to avoid carryover of this species into the absorber, where CO2 from the air could result in precipitation of carbonates in the absorber and scaling. For example, while calcium carbonate is nearly insoluble in water (solubility less than 0.01 g/L), calcium hydroxide, that might be used to precipitate the carbonate from a sodium-hydroxide-based solution, has a water solubility of 1.8 g/L. As a result, if a material quantity of calcium hydroxide is present in the regenerated sodium hydroxide solution, calcium carbonate will precipitate in the absorber section upon contact with air, causing fouling and reduced absorber efficiency.
The cycling of solid polymeric sorbents functionalized with amine or alkyl ammonium ions may have a different challenge as a result of limited chemical stability, especially if regeneration involves heating the sorbent. Examples of such phenomena suggest an in-service life of 1 to 2 years before replacement is necessary.
5 Conclusions
The APS report on air capture provides a benchmark system, with specific physical parameters and costs, and shows the intermediate steps that lead to an estimate of about $600/tCO2 for the avoided cost of capture. Lacking in that report, but provided here, is an optimization over the parameters of the air contactor, specifically an optimization over the velocities of the air and the liquid sorbent and over the fraction of CO2 captured. With the help of scaling laws that were not imposed in APS-DAC, optimized CO2 capture costs are calculated for three choices of packing material. The packings differ substantially from one another in either cost or pressure drop per unit length, yet the optimized systems have similar costs, as a result of compensating values of the column height and the flow velocities. The optimized avoided costs are from 10 % to 20 % lower for the three packings.
Relative to APS-DAC, financial assumptions are not varied, notably including the assumption that the system performs at 90 % capacity independent of environmental conditions. Capital costs for the back-end (except the precipitator) are kept fixed; these are about one third of the total capital costs. The cost of packing of each kind is also fixed, as is the total size of the system (1 MtCO2 captured per year) and the diameter of every absorber (12 m).
The energy strategy in APS-DAC is also retained here: electricity is purchased from the grid, but the thermal energy required for regeneration in the calciner is produced from natural gas on site. The CO2 from the natural gas combustion is assumed to be captured with no associated emissions and co-compressed with the CO2 captured from air. Emissions associated with grid power strongly affect the difference between a system optimized for lowest capture cost versus lowest avoided cost; fan power is three to four times less in the systems optimized for avoided cost.
Further work could attempt to parameterize capture rate as a function of air temperature and other environmental variables and to explore how design parameters are affected by variations in packing and energy costs and by designs with on-site electricity generation. The spatial distribution of the array of several hundred absorbers could be studied for sites with specific meteorology.
All such suggestions for further work need to be tempered with realism, however. The point most emphasized in APS-DAC and here is that capture of CO2 from air is likely to be much more expensive than capture of CO2 from large concentrated sources – notably, coal and natural gas power plants. An air capture system with an avoided cost above $500/tCO2 will almost surely not be a competitive climate mitigation strategy until nearly all power plants venting CO2 into the atmosphere have been either modified to capture their emissions, or replaced by low-carbon alternatives, or made redundant by energy efficiency measures.
Notes
MM, MD, and RS were co-authors of APS-DAC; MM and RB were co-authors of BSM.
Two limiting situations prove the weak dependence of K G on operating conditions: (a) at a gas velocity of 1 m/s and a 2 M NaOH concentration, one finds H cp = 0.018 kmol/(m3 atm), k G = 0.011 m/s and k L = 0.0086 m/s, thus leading to K G = 0.0028 m/s; (b) if w G = 2.5 m/s and [NaOH] = 4 M, then H cp = 0.0094 kmol/(m3 atm), k G = 0.023 m/s and k L = 0.016 m/s, leading to K G = 0.0032 m/s.
References
American Physical Society (2011) Direct air capture of CO2 with chemicals – a technology assessment for the APS panel on public affairs
Baciocchi R, Storti G, Mazzotti M (2006) Process design and energy requirements for the capture of carbon dioxide from air. Chem Eng Process 45:1047–1058
Holmes G, Keith DW (2012) An air–liquid contactor for large-scale capture of CO2 from air. Phil Trans R Soc A 370:4380–4403
House KZ, Baclig AC, Ranjan M, van Nierop EA, Wilcox J, Herzog HJ (2011) Economic and energetic analysis of capturing CO2 from ambient air. Proc Natl Acad Sci USA 108:20428–20433
Jones CW (2011) CO2 capture from dilute gases as a component of modern global carbon management. Annu Rev Chem Biomol Eng 2:31–52
Mahmoudkhani M, Keith DW (2009) Low-energy sodium hydroxide recovery for CO2 capture from atmospheric air—thermodynamic analysis. Int J Greenhouse Gas Contr 3:376–384
Menon A, Duss M (2011) The new Sulzer Mellapak M-CC and AY Plus DC structured packings for post-combustion capture. IEAGHG 1st post-combustion capture conference
Pohorecki R, Moniuk W (1988) Kinetics of reaction between carbon dioxide and hydroxyl ions in aqueous electrolyte solutions. Chem Eng Sci 43:1677–1684
Saint Gobain (2006) NorPro catalyst carriers – typical properties. http://www.norpro.saintgobain.com/uploadedFiles/SGnorpro/Documents/CatalystCarriers-TypicalProperties-pf.pdf
Stolaroff JK, Keith DW, Lowry GV (2008) Carbon dioxide capture from atmospheric air using sodium hydroxide spray. Environ Sci Technol 42:2728–2735
Tsai RE, Seibert AF, Eldridge RB, Rochelle GT (2009) Influence of viscosity and surface tension on the effective mass transfer area of structured packing. Energy Procedia 1:1197–1204
US EPA (2011) National ambient air quality standards http://www.epa.gov/air/criteria.html
Wang T, Lackner KS, Wright A (2011) Moisture swing sorbent for carbon dioxide capture from ambient air. Environ Sci Technol 45:6670–6675
Zeman F (2008) Experimental results for capturing CO2 from the atmosphere. AICHE J 54:1396–1399
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is part of a Special Issue on “Carbon Dioxide Removal from the Atmosphere: Complementary Insights from Science and Modeling” edited by Massimo Tavoni, Robert Socolow, and Carlo Carraro.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mazzotti, M., Baciocchi, R., Desmond, M.J. et al. Direct air capture of CO2 with chemicals: optimization of a two-loop hydroxide carbonate system using a countercurrent air-liquid contactor. Climatic Change 118, 119–135 (2013). https://doi.org/10.1007/s10584-012-0679-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-012-0679-y