1 Introduction

Aviation affects the climate in several ways. The burning of jet fuel results in CO2 emissions, NOx emissions, the formation of contrails and emissions of water vapor, sulfur and soot.

NOx emissions enhance troposheric O3 concentrations (which warms the surface) and lead to the depletion of CH4 (this depletion has a cooling effect) which in turn leads to a reduction of tropospheric O3 concentrations, so called primary mode ozone (see Wild et al. 2001; Stevenson et al. 2004).Footnote 1 The impact on ozone following NOx emissions also depends on where (geographical location and altitude) and when (season) the emissions take place. NOx emitted at high altitudes has a stronger impact on ozone formation. These changes in the atmospheric concentration of trace gases imply both a positive and negative forcing of the climate, the global average net effect of which depends on both the time scale and the atmospheric chemistry model.

Furthermore, aviation leads to the formation of contrails (Schumann 1996). Contrails affect the earth’s radiation balance by reflecting incoming solar radiation and by absorbing and re-emitting long wave heat radiation. The global average net effect is a heating of the climate system (Penner et al. 1999; Sausen et al. 2005; Lee et al. 2010). For a specific contrail, the net effect depends on where and when it is formed. Nighttime or wintertime, for instance, there is less or no incoming shortwave radiation so the cooling effect of contrails drops (wintertime) or disappears altogether (nighttime). In addition to night/day and winter/summer variations, the climatic impact of contrails also depends on the temperature and the albedo of the underlying surface as well as the optical depth of the contrail (with in turn depends on its physical thickness, its particle density, and the size and shape of the particles). In addition, contrails may spread and induce the formation of cirrus clouds that also influence the heat budget of the planet (see e.g., Lee et al. 2010).

A thorough review of the chemistry and physics of the climate impact of aviation is beyond the scope of this paper, and the reader is referred to e.g., Penner et al. (1999), Lee et al. (2010).

The aim of this study is to estimate CO2-equivalent emission weighting factors, i.e., the factor by which CO2 emissions should be multiplied in order to get a CO2-equivalent emission weighting factor (EWF) for aviation. These forcers have different time scales, from hours to centuries, which makes it non-trivial to compare the climate effects from the different forcers on a single scale. There is no unique and objectively correct way to do that since all attempts to weigh different gases against each other will depend on subjective choices, such as the time horizon and the question of what to value (e.g., the change in global annual average surface temperature, integrated radiative forcing, discounted economic damages or costs to meet a climate stabilization target).

For that reasons, we use in this paper five different approaches (so called metrics) to compare the impacts from the different climate forcers from aviation over time.

Three of them are physically based:

  • The Global Warming Potential (GWP) metric is a measure of the integrated radiative forcing from the emission of 1 kg of a gas, say CH4, compared to the integrated radiative forcing of 1 kg of CO2 (Forster et al. 2007a).

  • The Global Temperature change Potential (GTP) is a measure of the temperature response at time H from a kg of gas X emitted at present, divided by the temperature response at time H from a kg of emission of CO2 at present (Shine et al. 2005). It should be noted that whereas GWP is an integrated measure (the contribution each year is taken into account with equal weight), GTP only looks at the temperature response in the end-year. The 100-year GTP value for CH4 is thus significantly lower than its corresponding GWP value (since the perturbation life time of methane is around 12 years).

  • The Sustained GTP (SGTP) metric is defined as the temperature response at time H following the sustained (constant) emission of 1 kg of gas X per year, divided by the temperature response at time H from constant emissions of 1 kg CO2 per year.

The time horizon for all these three metrics is critical but rather arbitrary.

In addition, we consider two economics-based metrics:

  • Relative Damage Cost (RDC). RDC is defined as the ratio of the climate damage in economic terms from emission of 1 kg of greenhouse gas X compared to the climate damage in economic terms of the emission of 1 kg of CO2.

  • Cost-Effective Trade-Off (CETO). CETO is defined as the ratio of the shadow prices of the emission of 1 kg of greenhouse gas X to the shadow price of 1 kg of CO2, under the assumption that a specific climate target should be met at the lowest possible cost.

The primary focus is to estimate the emissions weighting factors (EWFs) from aviation using the two economics-based metrics (which will be defined more carefully in Section 3). These two metrics have received support by several analysts (see for example, Schmalensee 1993, Hammitt et al. 1996, and Manne and Richels 2001). We also compare these economic based EWFs with our own and others estimates of EWFs using the physically based metrics (Forster et al. 2007b; Lee et al. 2010). Dorbian et al. (2011) estimated (independently of our paper) EWFs using RDC. Our results are compared with theirs. Finally, we perform a sensitivity analysis for all five metrics.

Estimating CO2-equivalent emissions weighting factors (in physical and economic metrics) is useful when assessing to what extent various measures to reduce contrails and NOx may be cost effective. For instance, the probability of contrail formation is reduced when flying at lower altitudes, but this increases fuel consumption and CO2 emissions. Insights into how this reduction in radiative forcing from contrails should be weighed against the increase in radiative forcing from the higher CO2 emissions can be gained by using the metrics.

Finally, the IPCC special report on aviation (Penner et al. 1999) estimated the radiative forcing (RF) from aviation for the year 1992. The total RF from past aviation until 1992 was estimated to be 48.5 mW/m2–a factor 2.7 higher than the contribution from carbon dioxide from aviation alone. This factor of total RF, from aviation, to CO2 only, from aviation, is usually referred to as the Radiative Forcing Index (RFI). However, uncertainties in this IPCC estimate of RFI are large, and it does not include aviation-induced cirrus clouds (which on their own could be as high as all other forcers combined). These estimates were updated by Sausen et al. (2005) for 2000, who reported a factor of 1.9 higher for all forcers (once again excluding aviation-induced cirrus clouds) compared to the radiative forcing from aviation-related CO2, only, and Lee et al. (2010) who reported a factor of 2 for the year 2005.

The RFI has been misunderstood by many including policy makers and others. The index has been interpreted as the “CO2-equivalent” EWF from aviation. The index has been used in this way by many carbon offset initiatives and carbon footprint calculators. For example, the Swedish government offsets its aviation related emissions by assuming that CO2 emissions from aviation should be multiplied by a factor of 2.5.

However, this interpretation is erroneous since the RFI gives the radiative forcing ratio in a particular year caused by all historic emissions from aviation up until that year (see Forster et al. 2006; Fuglestvedt et al. 2010). RFI is a backward looking perspective depending on past and current emissions, whereas calculating the CO2-equivalent emissions from aviation requires a forward looking perspective, taking into account the current and future impact of current aviation on the climate.

The paper is structured as follows. Section 2 presents the model and its parameter values. In Section 3 we present the economic based metrics for comparing impacts over time. In Section 4 we present our results and compare them with the physically-based metrics. Section 5 contains the sensitivity analysis, and Section 6 presents our conclusions.

2 Model and parameterization

In order to estimate climate metrics for emissions/forcers from the global average aviation sector we use a climate economy model MiMiC (Johansson et al. 2006; Johansson 2010).

MiMiC consists of two parts. There is a physical description of the climate system, which contains an energy balance model, greenhouse gas cycles and estimates of the radiative forcing from CO2, N2O, CH4, other long lived greenhouses gases and aerosols. For the purpose of this paper, we also included a linear representation of NOx-O3-CH4 chemistry, and contrails. MiMiC also contains an economic sub-module with representations of the cost to reduce CO2, N2O and CH4 as well as assumptions about future global GDP levels and reference emission scenarios for greenhouse gases and aerosols (for details on marginal abatement cost functions, GDP and reference scenarios, see Johansson et al. 2006, and Johansson 2010) as well as the cost of climate damages (represented as a function of the temperature change).

MiMiC is an optimization model and can be run in a cost-benefit mode, where the model weighs the cost of reductions to the cost of future climate damage in order to find the “optimal” level of reductions, or a cost-effectiveness mode where the modeler sets a predefined climate target and the model finds the least cost emissions trajectory towards that target. In this paper, the cost-benefit mode is not applied.

When estimating CETO, the full scale version of MiMiC is used in the cost-effectiveness mode (the model simultaneously calculates the shadow prices on CO2, NOx and contrails, and the least-cost emission and concentration pathways towards the predefined temperature target). We optimize towards a 2 K temperature ceiling. The discount rate, which is used when calculating the net present value of abatement cost, is 3% per year. The model runs between the years 1880 and 2200 with yearly time-steps.

However, when estimating the three physical indicators and the relative damage cost indicator, the optimization framework is not needed. Rather, it is sufficient to calculate (1) the time dynamics of the forcers from aviation, (2) the radiative forcing over time and (3) the temperature response over time. If the aim is to calculate global warming potentials, integration takes place over the radiative forcing over time, if the aim is to calculate the relative damage cost, integration takes place over the temperature response. We assume a constant background atmosphere when estimating GWP, GTP, SGTP and RDC. The assumption is standard when calculating GWPs (see e.g., Forster et al. 2007a). The different subcomponents of the model required to perform these calculations are described in some more detail below.

2.1 Radiative forcing from aviation

In Lee et al. (2010), the radiative forcing in 2005 from all aviation up until that year from CO2 was 28 mW/m2, from O3 26.3 mW/m2, from methane −12.5 mW/m2, from linear contrails 11.8 mW/m2. From H2O, direct sulphate and direct soot the combined forcing is 1.4 mW/m2. The forcing from aviation induced clouds (including linear contrails) is estimated to be 33 mW/m2. There are large uncertainties in all these forcing contributions from aviation (with the exception of CO2). However, the total uncertainty is dominated by aviation induced clouds (including linear contrails); the radiative forcing from aviation induced clouds lies in the range 11–87 mW/m2.

Since the combined radiative forcing of water vapor, direct sulfate and soot from aviation is small in comparison to the forcing of NOx induced methane and ozone, as well as contrails and CO2, we only focus on these forcers in this paper. In our model, the radiative forcing from pulse emissions of CO2 and NOx are calculated explicitly (see sections 2.2 and 2.3). For contrails and aviation induced cirrus, we use the estimates provided by Lee et al. (2010).

2.2 Greenhouse gas mass balances and radiative forcing

CO2 concentrations are modeled by a linear pulse representation of the Bern carbon cycle model used in Forster et al. (2007a). To calculate the radiative forcing from CO2 we apply the equation for radiative forcing given in Ramaswamy et al. (2001). When estimating GWP, SGTP, GTP and RDC, we have assumed a constant atmospheric CO2 concentration equal to 375 ppmv, which gives a forcing of 1.8·10−15 W/m2/kg CO2.

CH4 and N2O concentrations are modeled using the global mean mass-balance equations given in Prather et al. (2001), taking the feedback effect CH4 has on its own atmospheric lifetime into account (leading to a perturbation lifetime of about 12 years, see Table 1). The equations for radiative forcing are the expressions given in Ramaswamy et al. (2001). We also include the indirect effect of methane concentration on tropospheric ozone and stratospheric water vapor concentrations by adding 40% to the direct radiative forcing from methane, in line with Forster et al. (2007a).

Table 1 Derived steady state radiative forcing (RF) for sustained emissions of 1 kg NOx (N) per year
Full size table

When estimating CETO, the atmospheric concentration of greenhouses gases varies over time. The radiative forcing varies logarithmically with the atmospheric concentration of CO2, and with the square root of the atmospheric concentration of CH4 and N2O. The concentrations of the greenhouse gases are determined by the temperature constraint which should be met at the lowest possible net present value cost. For instance, if the climate sensitivity is high, it means that the concentration required to meet the temperature target has to be rather low, and vice versa. Further, the marginal abatement costs of the different gases will determine how much CO2 is abated versus the other gases.

2.3 Radiative forcing from NOx induced methane and ozone

The life time of NOx in the upper troposphere is on the order of a few days, but NOx emissions trigger a pulse increase in the concentration of tropospheric O3 (that will last for about a month) and a pulse decrease in the concentration of CH4 (with an e-folding time of a decade). Since CH4 is an important precursor to tropospheric O3 the concentration of O3 will drop if the CH4 concentration drops. This drop in O3 levels will follow the same time profile as that of CH4. Thus, following a pulse emission of NOx, we will first see higher ozone concentrations for the first couple of months, followed by a prolonged period of lower ozone levels (see Stevenson et al. 2004).

We have used two different studies to estimate the ozone/methane impact of NOx emissions from aviation, Stevenson et al. (2004), and Wild et al. (2001) as they were reported in Fuglestvedt et al. (2010). In our main case we use the model by Wild et al. (2001).

There is still a lot of uncertainty surrounding their results (see Table 1). However, the increase in O3 and the drop of CH4 are coupled, since the O3 response leads to OH which in turn depletes CH4. Thus, it would be erroneous to assume a very strong ozone response and a very weak methane response.

Data for the steady state radiative forcing response to sustained emissions of 1 kg of NOx per year are given in Table 1. The differences between the two models do not only depend on differences in atmospheric chemistry models but may also depend on, for instance, differences when it comes to how radiative forcing is modeled and assumptions about background concentration of the trace gases.

For ground-based constant emissions of NOx the net steady state radiative forcing from the NOx induced O3 and CH4 tends to cancel or become slightly negative (Derwent et al. 2001; Derwent et al. 2008, Wild et al. 2001; Forster et al. 2007a), i.e., the combined impact of NOx emissions on O3 and CH4 tend to cool the climate. For high altitude NOx, the picture is mixed, where some models suggest a positive contribution and others a negative for a sustained emission pulse (see Table 1).

2.4 Climate efficacies

In modeling studies the global average surface temperature response to inhomogeneous forcings such as contrails or ozone is different from an equally large change in radiative forcing from CO2 alone (Hansen et al. 2005 and Forster et al. 2007a). The ratio between the temperature response from a radiative forcing of 1 W/m2 from a greenhouse gas X to that of 1 W/m2 of CO2 is called the climate efficacy. Forster et al. (2007a) report that the climate efficacy for ozone has been estimated to lie in the range 0.6–1.1. For contrails, Ponater et al. (2005) estimated the efficacy to 0.59, and, more recently, Rap et al. (2010) estimated it to 0.31.

Uncertainties about the climate efficacies are, however, large, and since very few studies have been performed and since it is even unclear whether the climate efficacy of ozone is larger or lower than unity, we have in our temperature model assumed that all climate efficacies are equal to unity. In the sensitivity analysis, we discuss what a change in these parameters could imply.

2.5 Temperature calculations

The energy balance model used to calculate the temperature response from changes in radiative forcing is a globally averaged box model with three layers. This three-box model consists of a mixed ocean-atmosphere layer, an intermediate ocean layer, and a deep ocean layer. The climate sensitivity is set to 0.8 K/W/m2 (in the base case)

This energy balance model is calibrated to emulate a linear Upwelling Diffusion Energy Balance Model (UDEBM) with polar overturning (see Johansson 2010, in particular appendix 1–2 for details). The assumptions for the UDEBM include a heat diffusivity of 2 cm2/s, upwelling rate of 4 m/year, and a ratio of polar water warming to average ocean warming of 0.2, in line with standard assumptions for UDEBMs, as in for example Hoffert et al. (1980), Shine et al. (2005).

3 Metrics and emissions weighting factors

In this section, we define the two economics based metrics in more detail. The first is based on cost-benefit analysis (where the focus is on the net present value of future climate damages) and the second is based on cost-effectiveness analysis (where the least-cost emission and concentration pathways to reach a predefined temperature target is estimated).

3.1 Metric 1: Relative Damage Cost (RDC)

The Relative Damage Cost metric is defined as the net present value of the economic damage from the global average surface temperature change following a unit pulse emission of gas X in relation to the net present value of the economic damage from the temperature change from a unit pulse emission of CO2. This approach has been used, in other contexts, by several authors, e.g., Schmalensee (1993), Reilly and Richards (1993), Hammitt et al. (1996) and Kandlikar (1996), and very recently, in the context of aviation, by Dorbian et al. (2011).

We calculate the relative damage cost of 1 Tg NOx in relation to 1 Tg CO2 assuming that damages are linear in the temperature change (in section 5, where sensitivity analysis is performed, a quadratic damage function is used) and proportional to global GDP (e.g., Nordhaus 1994 and Azar and Sterner 1996):

$$ RD{C_{{N{O_x}}}} = \frac{{\int_0^H {k\Delta {T_{{N{O_x}}}}(t)Y(t){e^{{ - rt}}}dt} }}{{\int_0^H {k\Delta {T_{{C{O_2}}}}(t)Y(t){e^{{ - rt}}}dt} }} $$
(1)

Here, ΔT is the temperature change of a pulse emission of CO2 or NOx, H is the time horizon, r is the discount rate and global GDP is denoted by Y(t). The parameter k is the proportionality constant, typically a few percent of GDP for an increase in the global annual mean surface temperature of 3 K above the preindustrial level (since we are only interested in relative damages, the value for this parameter does not matter, as can easily be seen in equation 1). We assume that Y(t) grows exponentially with the growth rate g, thus equation (1) can be simplified to

$$ RD{C_{{N{O_x}}}} = \frac{{\int_0^H {\Delta {T_{{N{O_x}}}}(t){e^{{\left( {g - r} \right)t}}}dt} }}{{\int_0^H {\Delta {T_{{C{O_2}}}}(t){e^{{\left( {g - r} \right)t}}}dt} }} $$
(2)

The relative damage cost from contrails is estimated in a similar manner. We estimate the average temperature response from contrails per Tg CO2 emitted when calculating the relative damage metric for contrails. The global annual average radiative forcing is set to be 0.0184 mW/m2/Tg CO2. This way of scaling contrails to CO2 is also done for all the other metrics.

When estimating this metric, we assume that GDP growth is 2% per year (slightly below the growth rate during this century in the SRES A2 scenarioFootnote 2) and damages are integrated over 300 years with a discount rate of 3%/year (in the base case). A discount rate of 3%/year and a growth rate of 2%/year implies an “effective” discounting of 1%/year, or to be more specific that the temperature response is discounted by 1%/year.

Comparison with GWP and SGTP values with a 100 year time horizon is made with the RDC indicator using a discount rate of 3%/year and a growth rate of 2%/year, since an “effective discount rate” of 1%/year roughly corresponds to a time horizon of 100 years.

For a discount rate equal to the growth rate, the indicator becomes equal to the integral over future temperature changes from the forcer divided by the integral over future temperature changes from a pulse of CO2 and the choice of time horizon is critical to the result. (Azar and Johansson (2011) show that this integrated temperature response metric is equal to SGTP under linearised conditions).

3.2 Metric 2: Cost-Effective Trade-Off ratio (CETO)

In the construction of CETO, one takes a cost-effectiveness approach. CETO is defined as the ratio of the shadow price of the non-CO2 forcer to the shadow price of carbon dioxide (this ratio will change over time since the shadow prices change over time).

Shadow prices are obtained in optimization frameworks. In this case, they represent the additional cost to meet the target if the emission of a particular gas a particular year is increased by one unit. It can be seen as the willingness to pay for emitting one additional unit of gas X for a given temperature target. It can also be interpreted as the optimal tax on the gas required to meet the climate target at the lowest possible cost. The CETO then becomes the ratio of the optimal tax per unit of gas X compared to the optimal tax per unit of CO2.

This approach has been used to compare CO2, methane, and nitrous oxide in previous studies, e.g., Michaelis (1992), Kandlikar (1996), Manne and Richels (2001), O’Neill (2003), Johansson et al. (2006, 2008), and Shine et al. (2007), but so far it has not been applied to aviation. For a formalized derivation of this metric, see Johansson (2011). This metric is sometimes called Global Cost Potential (GCP) but we choose here to use a term that more accurately describes the way the metric is defined.

The difference between RDC and CETO is that RDC is based on a cost-benefit approach whereas CETO is based on a cost-effectiveness approach. More specifically, using the RDC metric, the focus is on the net present value of all costs caused by emitting one unit of gas X, whereas in CETO, the focus is on the cost-effective tax on the emission of gas X required to reach the temperature target at the lowest possible cost.

Interestingly, in the limit that the damages from climate change become infinite for temperature changes above 2 K, and zero for temperature changes below 2 K, we have a damage cost function that would generate the same solution that one would obtain if a ceiling on the temperature change is set at 2 K in an optimizing climate economy model.

3.3 Emission weighting factors (EWFs) and normalized pulse emissions

Emissions weighting factors (the “CO2-equivalent emissions” of aviation per kg of CO2 emissions) are estimated by

$$ EWF = \frac{{\sum\nolimits_i {{M_i}{E_i}} }}{{{E_{{C{O_2}}}}}} $$
(3)

where M i is the metric value for gas (or forcer) i, and E i is the emission of gas/forcer i where i = (CO2, NOx and contrails).

3.4 Normalised pulse emission

The emission weighting factor is expressed per Tg of CO2. Thus, ECO2 is set at 1 Tg. Based on the estimates of annual emissions from aviation reported in Lee et al. (2010), we set the average NOx emissions to be 0.00137 Tg N per Tg CO2. For contrails, M is estimated per Tg of CO2, and thus Econtrails/ECO2 = 1. It is assumed that the pulse last 1 year.

GWP, GTP, SGTP and RDC are estimated for the year 2005, while CETO is estimated over time. We assume the same normalization holds over the entire period. This assumption of a constant relation between CO2, NOx and contrails is broadly in line with the existing literature on scenarios for aviation emissions.Footnote 3

4 Results

In this section, we first calculate the temperature response for a pulse emission from aviation (an average flight in 2005). This gives insight into the dynamics of the temperature response to the different forcers, which is useful for the understanding of the different metrics. We then estimate the EWFs for the two economics based metrics. We also calculate the EWFs for the physically based metrics and compare the results towards the end of this section. Since physically based metrics have been estimated before, we pay less attention to these results.

4.1 Temperature response from a pulse emission

In Fig. 1 the temperature response from the normalized emission pulse described in Section 3.3 is shown.Footnote 4 The dynamics of the temperature response from CO2 is governed by two opposing factors: the inertia of the oceans and the decline of the CO2 perturbation in the atmosphere. The combined effect is that the temperature response to a CO2 pulse is fairly constant over time, after the initial warming (Matthews and Caldeira 2008).

Fig. 1
figure 1

The temperature response from 1 Tg CO2 and associated NOx and contrails from aviation

Full size image

The temperature response from contrails is initially strong but once the forcing is removed (the atmospheric life time is in the order of hours), the temperature increase drops so that only a very weak signal is left after 100 years.

The dynamics of the temperature response for the NOx pulse are more complicated. Initially, the increased ozone concentration gives a strong temperature increase, but the life time of ozone is less than a few months, and the depletion of methane, which causes reduction in forcing has an e-folding time (perturbation time) of roughly 12 years. The radiative forcing from a NOx pulse becomes negative shortly after the pulse is ended and the temperature response becomes negative after 6–7 years and remains negative for most of the century (see Fig. 1).Footnote 5

GTP values for NOx can be obtained by dividing the NOx temperature response in the graph with 0.00137 (i.e. the NOx emissions aviation (in Tg N) per Tg of CO2, see section 3.3). Using the NOx model by Stevenson et al., we get a NOx GTP value (50 year time horizon) equal to −48. Our values are similar to those of Fuglestvedt et al. and Lee et al., but not exactly the same since different energy balance models have been used. Fuglestvedt et al., for instance, estimate the corresponding GTP value at −59. For contrails we get GTP(20) = 0.21 and GTP(100) = 0.029. Fuglestvedt et al. get the same value for GTP (20) and 0.030 for GTP (100).

4.2 Emissions weighting factors using the Relative Damage Cost (RDC) metric

We present the EWFs for the relative damage cost metric in Fig. 2. For a discount rate of 3%/year we get an EWF equal to 1.4 when using the NOx model given by Wild et al. (2001). Since contrails are short-lived, their contribution to EWFs become positively dependent on the discount rate. The higher the discount rate, the larger weight will be put on the short term impacts, and the relative contribution from contrails (and other short term forcers) will increase. This also holds for NOx, but the mechanism is a bit more complicated since there is also a cooling component (reductions in the methane concentrations) associated with NOx (see Fig. 1 from which it is clear that a higher discount rate will give a higher integrated warming effect, since more weight is given to the temperature response early on that is positive).

Fig. 2
figure 2

Emissions weighting factor as a function of the discount rate obtained with the forcing impact of NOX presented in Wild et al. (2001)

Full size image

Dorbian et al. (2011) present EFWs using the RDC metric, and find, using a discount rate of 3%/year, a value of 1.3 (their mid-lens case). The value corresponds well with our estimate of 1.4. However, the reason for this similarity is rather complex, and is a result of a number of counteracting factors. For instance, we have used constant background concentrations, whereas they have used growing background concentrations of CO2. This means that the marginal radiative forcing of a pulse emissions of CO2 drops over time in their runs, which implies that their estimate of the GWP of the contrail contribution becomes almost twice as a large as our estimate (as well as the estimates by Forster et al. (2007b) and Lee et al. (2010) who assumed constant background concentrations). On the other hand, Dorbian et al. use non-linear damage functions which imply that the relative contribution from contrails drops (which we also find, see the sensitivity section 5 on non-linear damage functions). They end up at a similar contribution from linear contrails as we do (0.25 versus 0.24), despite different modeling assumptions.

4.3 Emissions weighting factors using the cost-effective trade-off

The EWF based on CETO is shown in Fig. 3 (the impact of NOx and contrails are shown both individually and in combination). The time dynamics is rather complex but can be understood in the following way: The contrail contribution grows slowly over time as the temperature ceiling is approached. The reason why it is lower early on is that a forcing several decades ahead of the ceiling has a lower temperature impact when the target is met than a forcing that takes place closer in time (as can be seen from Fig. 1). The NOx contribution to CETO based EWF is negative for time horizons longer than 5–6 years ahead of stabilisation i.e., the effect is a cooling (see Fig. 1). This causes the cost-effective tax on NOx to be negative. This is equivalent to saying that the optimal tax to meet a 2°C target includes a (temporary) subsidy on aviation NOx emissions since these emissions temporarily keep down the temperature increase. This results in a negative contribution to EWF (see Fig. 3). As the time approaches the date of stabilization (2088, in this model) the tax grows more negative before it very rapidly turns positive a few years before the stabilization date. This last effect is due to the enhanced short-term ozone warming that follows from the NOx emissions. After a short peak in the tax at the date of stabilization, the optimal NOx tax stabilizes.

Fig. 3
figure 3

EWF based on the Cost-Effective Trade-Off metric (CETO). The upper (green) line shows the EWF for CO2, contrails, and NOx (Wild et al.), whereas the lower lines show the contribution of contrails and NOx on their own, as shares of the contribution from CO2

Full size image

Combining the contribution from NOx and contrails with the contribution of CO2 gives the CETO based EWF that is roughly equal to 1 until half a decade before temperature stabilization occurs (until then the negative and growing impact of NOx and positive and growing contrails tend to cancel). Then half a decade before temperature stabilization, it suddenly jumps to about 2 at the date of stabilization and remains at that level. The reason for the large jump is that the CETO for NOx turns positive a few years before stabilization (due to the heating generated by tropospheric ozone) and as a result the EWF using CETO quickly doubles.

4.4 Comparison with physically based metrics

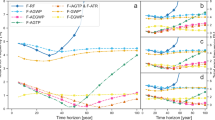
In Fig. 4 we compare our results in one graph that shows the emissions weighting factor (EWFs) for different metrics given a time horizon of 100 (for the applicable cases). It is clear that the choice of metric has a strong influence on the estimated EWF value.

Fig. 4
figure 4

Emissions weighting factors using different metrics (aviation induced cirrus are not included)

Full size image

Our results for GWP based EWFs are similar to those of Forster et al. (2007b) and Lee et al. (2010). Forster et al. (2007b) find that the CO2-equivalent emissions from aviation (including CO2, NOx and contrails) using a 100-year GWP approach would be 20% higher than if only the aviation-related CO2 emissions are considered. Lee et al. (2010) find slightly higher values (30–40% depending on the NOx model). GTP 100 values were found to be close to unity (i.e., the non-CO2 impact is very small compared to CO2) in their study (as well as in ours).

Although some estimates of EWF are very different depending on the metric used, e.g., the EWF-based GTP and GWP, strong similarities can be seen between the EWFs based on GWP-100, SGTP-100, and RDC-3%/yr. GWP and SGTP are closely related, so the similarity of their results is not surprising (Shine et al. 2005; Azar and Johansson 2011).

The CETO and the GTP results resemble each other (See Shine et al. (2007), Tol et al. (2008), Johansson (2011)), when there is long time until temperature stabilization occurs. Once stabilization has occurred, GTP is no longer applicable whereas CETO more resembles RDC, see Johansson (2011).

In Fig. 4, we report the CETO value for 2010. The reason both CETO and GTP give EWFs close to 1 is that the impact of a contrail or a NOx emission now on atmospheric temperatures 50–100 years into the future is very low (see Fig. 1), basically negilible.

In Figs. 5 and 6, we show, for the sake of illustration, the resemblance between the CETO and the GTP values for NOx (Fig. 5) and contrails (Fig. 6). GTP values are shown in reversed order so that GTP 50 is given at 2038 and GTP 20 at 2068, i.e., 50 and 20 years before the peak the 2°C target is met in the model. It can be seen that the difference between CETO and GTP grows over time.

Fig. 5
figure 5

The blue line shows the CETO value for NOx (the shadow price on NOx per kg N divided by the shadow price on CO2 per kg over time). For comparison we also show the GTP value for NOx (the red dashed line). The calculations are based on the parameterization obtained from Wild et al. (2001). The GTP value is not applicable beyond the year when stabilization occurs (year 2088 in this case), and reaches by that year the value 13300

Full size image
Fig. 6
figure 6

The blue line shows the CETO value for contrails (the shadow price on the contrails formed associated with fuel burning leading to 1 kg of CO2, on average over the global aviation fleet divided by the shadow price on CO2 per kg over time). For comparison we also show the GTP value for contrails (the red dashed line). The GTP value is not applicable beyond the year when stabilization occurs (year 2088 in this case), and reaches by that year the value 8

Full size image

Finally, it may be of interest to compare the radiative forcing index (RFI) based estimate of the NOx contribution with that obtained using our metrics. In 2005, the RF from aviation NOx (the combined impact of ozone and methane) is 13.8 mW/m2 (as reported in Lee et al. 2010). The contribution from CO2 (historic aviation until the year 2005) is 28 mW/m2. Thus, the role of NOx is more important (roughly half of that corresponding to CO2) when using RFI than when using GWP, SGTP and RDC (where the impact is around 10% of the total when using a 100 year time horizon). The reason is partly that the RF from O3 corresponds to the current emissions, whereas the RF from methane corresponds to a weighted average of the emissions during the past decade (or so), i.e., reflecting the emission level that prevailed several years ago. For that reason, the positive forcing from the ozone response corresponds to the current aviation level, whereas the negative forcing from methane depletion corresponds to a lower aviation level. This is the reason why the RFI index give a rather large positive value for ozone and methane combined. If NOx emissions from aviation were to stabilize, the NOx contribution to RFI would drop significantly.

5 Sensitivity analysis

In this section, we investigate how uncertainties about aviation induced cirrus, climate efficacies, the time horizon for the analysis, the choice of NOx model, the climate sensitivity and the choice of damage function affect our results for the EWFs.

5.1 Including aviation induced cirrus

So far, we have not included aviation induced cirrus in our analysis. Uncertainties about its radiative forcing are very large. Here we use data from Lee et al., assuming a best guess value of 33 mW/m2, and an uncertainty range of 11–87 mW/m2. These values include the contribution from persistent linear contrails. The result can be seen in Fig. 7. For an AIC forcing at the upper possible range, the AIC contribution to the EWFs when based on GWP, SGTP or RDC tends to be larger than those based on CO2 and NOx combined. For the CETO (and GTP-100) based metric the contribution from non-CO2 forcers remain small.

Fig. 7
figure 7

EWFs with aviation-induced cirrus (AIC) included. Uncertainty bars refer to uncertainties in aviation-induced cirrus only

Full size image

5.2 Climate efficacies

The climate efficacy for methane is believed to be slightly higher than 1; the ozone efficacy is assessed to be somewhere in the range 0.6–1.1 by Forster et al. (2007a), whereas Ponater et al. (2005) report a value of 1.37. The efficacy for contrails (and cirrus) is estimated to be 0.31–0.59 (Forster et al. 2007a; Ponater et al. 2005, Rap et al. 2010). If we had used these values instead, the contribution of contrails and cirrus to the different metrics would be scaled linearly by a factor 0.31–0.59, which would imply a significant drop for the importance of this forcer.Footnote 6 More research into estimating efficacies for ozone and contrails is warranted.

5.3 Shorter time horizon

So far we have estimated the emissions weighting factor for a 100-year time horizon (for GWP, GTP, and SGTP), and RDC (with a discount rate of 3%/year, 1% above the assumed growth rate in the economy). For CETO we had a time perspective of 78 years (in Fig. 4) since the temperature reaches the 2°C ceiling by the year 2088 in our base case.

If, on the other hand, we use a 20 year time horizon, larger weight is given to near-term impacts of aviation (the discount rate is set at 7%/year for RDC, 5% above the growth in the economy, so the “effective discount rate” roughly corresponds to a 20 year time horizon). In Fig. 8, we display the emissions weighting factors for these shorter time horizons.

Fig. 8
figure 8

Emissions weighting factors using a short time horizon (20 years for GWP, GTP, SGTP and CETO) and a higher discount rate for the economic indicator

Full size image

The RDC (as well as GWP and SGTP) metrics become significantly higher for both NOx and contrails. The RDC based EWF is approximately 2.5. However, the CETO (and GTP) based emissions weighting factor remains roughly equal to one; the higher value for contrails is cancelled by the equally large negative value for the NOx temperature response (the CETO metric is estimated 20 years ahead of the time when the temperature constraint is met).

5.4 Climate sensitivity

The GWP-based value does not depend on the climate sensitivity in our analysis (in reality there may be feedback effects on the carbon cycle and methane decay from changes in the climate and this may affect the GWP values somewhat, see e.g., Reisinger et al. 2011). Since SGTP asymptotically approaches GWP (Shine et al. 2005; Azar and Johansson 2011), and the RDC metric is closely related to SGTP (at least for low discount rates, Azar and Johansson 2011), it follows that the sensitivity for these metrics with respect to the climate sensitivity is very low.

However, the GTP metric is more sensitive. The 100-year GTP value for contrails roughly doubles if the climate sensitivity increases by 50%. The climate inertia increases with increasing climate sensitivity; as a consequence, the temperature response from contrails lingers for a longer period of time. However, since the contrail contribution to a 100-year GTP-based emissions weighting factor is only 3% of the contribution from CO2, the impact of a change in the climate sensitivity will nevertheless be relatively small.

Changes in the climate sensitivity affect CETO-based emissions weighting factors more significantly. If the climate sensitivity increases by 50% (from 0.8 K/W/m2 to 1.2 K/W/m2), the emissions weighting factor stabilizes at approximately 1.6 (instead of 2 in the base case, see Fig. 3). The reason for this is that a higher climate sensitivity implies that atmospheric CO2 is stabilized at a lower value, which implies a higher radiative forcing per kg of CO2 added to the atmosphere at this concentration level. This implies that the denominator is greater, and thus that the metric value becomes smaller. During the transition phase toward the time when the temperature stabilizes, the CETO-based EWF values change only very marginally as a result of changes in the climate sensitivity.

5.5 Choice of NOx model

In our base case we have used the NOX model by Wild et al. (2001). This model gives a stronger warming for aviation NOx than the model by Stevenson et al. (2004) (whose steady state radiative forcing response to a sustained emissions change is in fact negative, see Table 1). When using Stevenson et al., we get close to zero impact for NOx in the EWF for all metrics when using a 100 year time horizon (or a 3%/year discount rate). For instance, using this NOx model, and the GWP metric, the EWF becomes equal to 1.2.

5.6 Choice of damage function when estimating the RDC

When estimating the EWF using the relative damage cost metric, we assumed that economic damages from climate changes are linear in the global annual average surface temperature change. Some studies have suggested that damages are non-linear in the temperature response, e.g., Nordhaus (1994) who assumed a damage function quadratic in the temperature change. Under such conditions, the RDC for NOx is given by

$$ RD{C_{{N{O_x}}}} = \frac{{\int_0^H {\left[ {{{\left( {{T_B}(t) + \Delta {T_{{N{O_x}}}}(t)} \right)}^2} - T_B^2(t)} \right]{e^{{\left( {g - r} \right)t}}}dt} }}{{\int_0^H {\left[ {{{\left( {{T_B}(t) + \Delta {T_{{C{O_2}}}}(t)} \right)}^2} - T_B^2(t)} \right]{e^{{\left( {g - r} \right)t}}}dt} }} \approx \frac{{\int_0^H {{T_B}(t) \cdot \Delta {T_{{N{O_x}}}}(t){e^{{\left( {g - r} \right)t}}}dt} }}{{\int_0^H {{T_B}(t) \cdot \Delta {T_{{C{O_2}}}}(t){e^{{\left( {g - r} \right)t}}}dt} }} $$
(4)

where T B is the temperature change in the background scenario, and ΔT is the change in temperature following a pulse emission of CO2 or NOx (on top of the background scenario). The approximation holds only for small pulses. For contrails, the RDC is estimated in a similar manner (see section 3.1). In the case with a quadratic damage function, the change in temperature from the emission pulse is multiplied with the change in the background temperature which is not the case when using linear damage functions (compare equation (4) with equation (2)).

Assuming a discount rate equal to 3%/year, a time horizon of 300 years, an economic growth rate of 2%/year, and a “background” temperature scenario reaching a stabilization target of 2 K by 2088 (based on the runs with MiMiC in this paper), we get that RDCNOx = 0.071 (which can be compared to 0.14 when using a linear damage function) and RDCcontrails = 0.16 (which can be compared to 0.24 when using a linear damage function). The main reason why a quadratic damage function yields a lower RDC for contrails is that the temperature response from CO2 is multiplied by the background temperature, and since it increases over time the integral in the denominator increases compared to a case with linear damages. (This calculation also takes into fact that CO2 concentrations increase and peak at 460 ppm when estimating the background temperature scenario. This leads to lower marginal radiative forcing from CO2 and thus a lower temperature response from the pulse emission of CO2 as compared to the case with constant background concentrations of CO2 as shown in Fig. 1). The multiplication with the background temperature also takes place in the nominator, but the temperature response of contrails is more short-lived, so the value of the integral in the nominator does not increase as much. Thus, for that reason, RDC for contrails using a quadratic damage functions becomes lower than when using a linear damage function.

The short lived temperature response also partly explains why RDC for NOx is lower (for a quadratic damage function), but in this case there is the added complication that the temperature response after only a few years is negative (see Fig. 1). Thus, the temperature response that is magnified by the background temperature scenario is negative and, hence, reduces the expected damage from NOx emission. This explains why the RDCNOX value drops more in relative terms than the RDCcontrail value.

6 Conclusion

In this paper we have used five different metrics to estimate an emissions weighting factor (EWF) that gives the CO2 equivalent emissions per kg of CO2 emissions from aviation. The metrics used are: GWP, GTP, SGTP, and two economic metrics, relative damage cost (RDC) and a cost-effective trade-off (CETO). The relative damage cost metric compares the estimated net present value cost of the temperature response from contrails and NOX in comparison with CO2. The cost-effective trade-off metric compares the cost-effective taxes on emissions of NOx and contrails in relation to the cost-effective tax on CO2. RDC based EWFs for aviation have recently been estimated by Dorbian et al. (2011) while CETO based EWFs have not been estimated before.

Our contribution to the literature is an estimate of the economically based metrics, comparisons with physically based metrics and a detailed sensitivity analysis.

Our results can be summarized as follows:

  • GWP (100), SGTP (100) and RDC (3%/year) give rather similar results. If aviation induced cirrus is not included, the EWFs are estimated to lie in the range 1.3–1.4.

  • If aviation induced cirrus is included, uncertainties increase and the EWF for these three metrics ends up in the range 1.3–2.9, with a “best estimate” of 1.7 (using the GWP metric) and 1.8 using SGTP and RDC.

  • Assuming a shorter time horizon for the analysis, the EWF is higher: GWP (20), SGTP (20) and RDC (7%/year) end up in the range 2.2–2.7 (not including aviation induced cirrus).

  • GTP and CETO measures give values very close to unity (both GTP-20 and GTP-100, and CETO values at present and at 20 years prior the date of stabilization). CETO values at and beyond the year the global average surface temperature stabilizes at the two degree target are approximately equal to 2 using a climate sensitivity of 0.8 K/W/m2 (excluding aviation induced cirrus).

The choice of metric depends on the aim of the policy. If the aim of the climate policy is to stabilize the global average surface temperature at 2 K above the pre-industrial level at lowest possible cost, then the CETO metric provides by definition the most cost-effective way. This approach gives very little weight to short lived non-CO2 forcers from aviation at present, but doubles the EWF when the temperature has increased to 2°C above pre-industrial levels. If on the other hand it is argued it is the integrated net present value cost of the temperature response that matters, RDC may be used. If so, EWF is estimated at 1.4 at present.

There are strong similarities between the different metrics. RDC values are similar to GWP and SGTP values, and CETO values are similar to GTP far in time from the year in which the temperature stabilizes at the target while CETO is similar to the RDC after stabilization has occurred.Footnote 7

6.1 Applicability of the emission weighting factors

The estimated emissions weighting factor pertains to a global average flight, and cannot be applied to individual flights. Applying the factor to individual flights in a policy situation would result in a too blunt policy instrument since when and where the flights occur has a significant impact on both NOx-O3-CH4 chemistry as well as the formation of contrails, and, consequently, the resulting climate impact. For example, one particular flight may not contribute to contrails, whereas another flight may lead to very strong contrail formations and may induce cirrus if it flies in a region supersaturated with ice (Haywood et al. 2009); night flights have a stronger warming effect than daytime flights; winter flights may warm the surface more than summer flights; etc.

Applying the same EWFs on all flights would not create incentives to minimize climate impact of aviation in an efficient manner. For instance, if a plane flies at lower altitudes, it may cause less contrails at the expense of higher CO2 emissions (due to higher air resistance at lower altitudes). In order to reduce the climate impact of aviation, it might be preferable for this flight to fly at lower altitudes if it thereby avoids forming contrails. However, if all flights are credited with the same EWF regardless of actual contrail formation, there would be no incentives to reduce flight altitude. On the contrary, the flight would be made responsible for larger CO2-equivalent emissions (since the actual CO2 emissions would be higher and multiplied by a constant EWF). If the aim is to reduce the climate impact of aviation, policy instruments that take into account this heterogeneity and thereby create incentives to reduce contrails should be developed (see Gierens et al. 2008 for different ways to reduce contrail impact).

Further, there is much uncertainty about the radiative forcing (relevant for all metrics) and the climate response (e.g., the efficacy of the different gases/contrails), in particular for contrails and aviation induced cirrus. In addition, the time horizon (or the discount rate used) over which not only GWP but all these measures are calculated are critical and (rather) arbitrary.

Forster et al. (2006, 2007b) argue that the uncertainties and heterogeneity of the climate impacts of aviation are so large that the climate impact of contrails and NOx should not be included in policy schemes such as the EU emissions trading scheme.

Rather, the EWFs can still be useful for overall assessments of aviation CO2, NOx and contrails. When trade-offs between these forcers should be carried out, economic metrics may be useful. However, uncertainties associated with the economic metrics are even larger than the physical ones. The uncertainties that exist with the physical-based metrics remain, and the problem of the arbitrary time horizon using the physical indicators is replaced by the question of which discount rate is most appropriate, and which damage function that should be used (in the RDC case) and by the choice of temperature target (in the CETO case). This paper does not propose that these economic metrics are necessarily better equipped to estimate the CO2-equivalent emissions from aviation. The aim is, rather, to estimate the emissions weighting factors for different metrics, to contribute with some new insights and provide a basis for further discussions on how to deal with the non-CO2 climate impact of aviation.