Harmonization of land-use scenarios for the period 1500–2100: 600 years of global gridded annual land-use transitions, wood harvest, and resulting secondary lands

Abstract

In preparation for the fifth Assessment Report (AR5) of the Intergovernmental Panel on Climate Change (IPCC), the international community is developing new advanced Earth System Models (ESMs) to assess the combined effects of human activities (e.g. land use and fossil fuel emissions) on the carbon-climate system. In addition, four Representative Concentration Pathway (RCP) scenarios of the future (2005–2100) are being provided by four Integrated Assessment Model (IAM) teams to be used as input to the ESMs for future carbon-climate projections (Moss et al. 2010). The diversity of approaches and requirements among IAMs and ESMs for tracking land-use change, along with the dependence of model projections on land-use history, presents a challenge for effectively passing data between these communities and for smoothly transitioning from the historical estimates to future projections. Here, a harmonized set of land-use scenarios are presented that smoothly connects historical reconstructions of land use with future projections, in the format required by ESMs. The land-use harmonization strategy estimates fractional land-use patterns and underlying land-use transitions annually for the time period 1500–2100 at 0.5° × 0.5° resolution. Inputs include new gridded historical maps of crop and pasture data from HYDE 3.1 for 1500–2005, updated estimates of historical national wood harvest and of shifting cultivation, and future information on crop, pasture, and wood harvest from the IAM implementations of the RCPs for the period 2005–2100. The computational method integrates these multiple data sources, while minimizing differences at the transition between the historical reconstruction ending conditions and IAM initial conditions, and working to preserve the future changes depicted by the IAMs at the grid cell level. This study for the first time harmonizes land-use history data together with future scenario information from multiple IAMs into a single consistent, spatially gridded, set of land-use change scenarios for studies of human impacts on the past, present, and future Earth system.

1 Introduction

The evidence is now overwhelming that human activity has significantly altered basic element cycles (e.g. of carbon and nitrogen), the water cycle, and the land surface (e.g. vegetation cover, albedo) at regional, continental, and planetary scales, and that these alterations are influencing the regional and global environment, including the Earth’s climate system. During the last 300 years, >50% of the land surface has been affected by land-use activities, >25% of forests have been permanently cleared, agriculture occupies >30% of the land surface, and globally there are 10–44 10⁶ km² of land that are recovering from previous human land-use activities (Turner et al. 1990; Vitousek et al. 1997; Warring and Running 1998; Hurtt et al. 2006). Cumulatively, land-use emissions of carbon to date are comparable to fossil fuel emissions (Houghton 1999). Land-use changes have altered the surface albedo, surface aerodynamic roughness, and rooting depth and terrestrial carbon balance, with resulting effects on regional-global weather, hydrology and climate (Pielke et al. 2002; Roy et al. 2003; Brovkin et al. 2004; D’Almeida et al. 2007; Piao et al. 2007; Piao et al. 2009; Pitman et al. 2009; Shevliakova et al. 2009; Pongratz et al. 2010; Betts et al. 2007). Habitat loss is the primary cause of species extinctions (UNEP 2002; Mace et al. 2005). Looking ahead, population and the demand for energy, food, fiber, and water are all expected to increase, placing even greater pressure on the Earth system (Steffen et al. 2003). Future loss of the Amazon forest, logging of boreal forests, and other land-use changes could exacerbate the extinction crisis and lead to additional regional–global climate changes (Bonan et al. 1992; Cox et al. 2000; DeFries et al. 2002; D’Almeida et al. 2006; 2007; Wise et al. 2009a,b).

Quantification of the effects of past and future land-use changes on climate is important for explaining historical changes in climate, partitioning human and natural influences on climate, and improving future projections (Betts 2007; Feddema et al. 2005; McCarthy et al. 2010). New advanced Earth System Models (ESMs) are now able to explore the combined biogeochemical and biogeophysical effects of land-use changes and greenhouse gas emissions on the Earth’s climate system. Some of these models have previously used scenarios of past and future land-use changes (for example, in the ensemble of 23 climate models used for projections in the IPCC 4th Assessment Report (Meehl et al. 2007), land-use change was included in the Hadley Centre model HadGEM1 (Johns et al. 2006) and the GISS-EH and GISS-ER models). However, most models have not previously included gridded land use, and in those that have, treatment of land use was inconsistent and incomplete and there were particular difficulties with reconciling the interface of past land-use reconstructions and future projections.

Here we present the development of a new “harmonized” set of global gridded land-use change scenarios designed for use in ESMs. Each harmonized case smoothly connects new spatially gridded historical reconstructions of land-use changes, with new future projections from Integrated Assessment Models (IAMs) of four Representative Concentration Pathways (RCPs) (Moss et al. 2010), in a format required by ESMs. The diversity of approaches among historical reconstructions, IAMs, and ESMs for tracking land-use changes is large, making the need to treat land-use consistently and comprehensively between approaches and across time periods an important challenge.

Previously, the Global Land-use Model (GLM) produced historical global estimates of 1° × 1° fractional land-use patterns (e.g. crop, pasture, secondary and primary) and underlying land-use transitions annually 1700–2000 (Hurtt et al. 2006). “Secondary” refers to land previously disturbed by human activities and recovering, while “primary” refers to land previously undisturbed by human activities in GLM, both since the beginning of the historical simulation. Land-use transitions describe the annual changes in land use, such as harvesting trees and establishing or abandoning agricultural land, that often directly alter land-surface characteristics that, in turn, affect energy, water, and carbon exchanges between the land surface and the atmosphere. Resulting land-use products have been successfully used as input to both regional models (e.g. ED) and global dynamic land models (e.g. LM3V) able to track the consequences of these changes for both the carbon cycle and climate (Hurtt et al. 2002; Roy et al. 2003; Shevliakova et al. 2009). These studies have made use of the detailed land-use transition information to quantify land conversion events and track the resulting demographic effects of land disturbance and recovery, ultimately helping to close regional and global carbon budgets.

In this study, the GLM framework was extended to produce new estimates of global land-use patterns and underlying annual land-use transitions, including urbanization, at 0.5° × 0.5° resolution beginning in 1500, and connecting smoothly in 2005 to the future projections provided by IAMs to 2100. Because of the large scope of the project, this work included the production and analysis of >1600 complete global harmonized land-use cases developed to quantify the sensitivity of results to key model inputs, attributes, and assumptions.

2 Methods

The Global Land-use Model (GLM) (Hurtt et al. 2006) was adapted and extended to generate a harmonized set of global gridded land-use change scenarios for the period 1500–2100. GLM computes land-use patterns and sub-grid cell land-use transitions using an accounting-based method that tracks the state of the land surface in each half-degree grid cell, annually, as a function of the land surface at the previous time-step. This can be represented using the following matrix equation:

$$ \begin{gathered} l\left( {x,\,t + 1} \right) = A\left( {x,\,t} \right)\,l\left( {x,\,t} \right) \hfill \\ x = \left( {1,\, \ldots, N} \right),\,t = \left( {{t_0}, \ldots, \,{t_f}\,} \right) \hfill \\ \end{gathered} $$

(1)

where l(x, t) is a vector giving the fractions of grid cell area in each land-use category (i.e. crop, pasture, urban, primary, secondary) in grid cell x and year t, and A(x, t) is a matrix giving the land-use transition rates between N land-use categories in grid cell x and year t. Each element, a _ij (x, t), of the matrix A(x, t) gives the rate at which land-use type j was converted to land-use type i between the years t and t+Δt.

$$ A\left( {x,t} \right) = {\left[ {\begin{array}{*{20}{c}} {{a_{{11}}}\left( {x,t} \right)} & \cdots & {{a_{{1n}}}\left( {x,t} \right)} \\ \vdots & {{a_{{ij}}}\left( {x,t} \right)} & \vdots \\ {{a_{{n1}}}\left( {x,t} \right)} & \cdots & {{a_{{nn}}}\left( {x,t} \right)} \\ \end{array} } \right] {{\left( {i,j = 1 \ldots N} \right)}}} $$

(2)

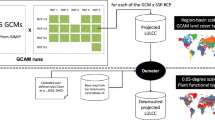
GLM solves Eq. 1 annually for every 0.5° × 0.5° terrestrial grid cell globally for 1500–2100, determining on the order 10⁹ unknowns. Since Eq. 1 is a large, under-determined system, the goal was to solve for the matrix A (the land-use transitions in Eq. 2) for every grid cell at each time step by constraining the system with inputs including historical reconstructions and future projections of: i) land use (crop, pasture, urban), ii) wood harvest, and iii) potential biomass and recovery rate. Because these inputs do not fully constrain the problem, additional assumptions were made including: iv) the priority of primary or secondary land for wood harvesting and agricultural conversion, v) the inclusiveness in wood harvest statistics of wood cut in conversion of forest to agricultural land use, vi) the spatial pattern of wood harvest, and vii) the residence time of land in agricultural use. These model factors i–vii are described in more detail below. Furthermore, since the model factors are not uniquely known, a sensitivity analysis was performed. Model input-output is illustrated in Fig. 1.

Fig. 1

Schematic diagram of model inputs, outputs, and decisions. Land-use categories tracked are Primary, Secondary, Crop, Pasture, and Urban (see text). “F” denotes sub-grid scale fractional coverage

2.1 Historical maps of land use

For the years 1500–2005, land-use (cropland, pasture, urban, and ice/water) was based on the HYDE model. The HYDE database v3.1 (Klein Goldewijk et al. 2010; Klein Goldewijk et al. 2011) contained gridded time series of historical population and land-use data for the Holocene. The aim and purpose of the database was to sketch a plausible scenario of the historical development of human population growth and corresponding agricultural activities across the world since about 12,000 years ago, such as the conversion of natural ecosystems into cropland and pasture (ecosystems used for livestock grazing). The main input sources used were national data from the U.N. Food and Agricultural Organization (FAO 2008), supplemented with numerous historical statistics and census data, and a combination of satellite-derived current land cover from the DISCover version 2 data using the IGBP classification map (Loveland et al. 2000) and Global Land Cover (GLC) based on the Global Land Cover 2000 VEGA2000 data (Bartholome et al. 2002). These statistics were combined with different allocation algorithms and time-dependent weighting maps, in order to create spatially gridded maps for cropland and pasture at 5′ × 5′ resolution. Weighting maps were defined for the present day by satellite maps, and for the past by combining several factors such as population density, soil suitability, distance to rivers or lakes, slopes, and specific biomes.

A subset of HYDE 3.1 was used to provide global gridded crop, pasture, ice/water, and urban land area at 5′ × 5′ resolution every 10 years from 1500 to 2000, and in 2005. These data were aggregated to 0.5° × 0.5° resolution, and converted from absolute area of each grid cell to grid cell fractional area. They were then linearly interpolated in time to produce annual maps of crop, pasture, and urban fractions for each 0.5° grid cell. The ice and water fractions of each grid cell were assumed constant over time. By subtracting the land-use and ice and water fractions from each grid cell, the fractions of each grid cell occupied by natural vegetation (either primary or secondary) were also determined. The HYDE 3.1 dataset also included a global map that assigned a country code to each terrestrial grid cell, at 5′ resolution. This map served as a basis to generate a similar map at 0.5° resolution that was consistent with the 0.5° maps of land-use data where every grid cell with ice/water fraction less than 1 was assigned a country code. This resulted in a global map containing 192 countries.

To evaluate the sensitivity to this land-use history information, an alternative ‘No-data’ land-use history was developed in which the crop and pasture fraction of each grid cell increased linearly from zero in 1500 to the HYDE values in 2005, using the same ice/water fraction map as above.

2.2 Historical national statistics on wood harvest

For 1961–2005, FAO national wood harvest volume data were used for both coniferous and non-coniferous round wood, along with wood harvest density values of 0.225 Mg C m⁻³ for coniferous wood and 0.325 Mg C m⁻³ for non-coniferous wood (Houghton and Hackler 2000) to convert these statistics to weight of carbon harvested. National wood harvest totals were aggregated to the 1990 country list. Data for the U.S. were disaggregated into coterminous (99%) and Alaska (1%) after 1960 (Smith et al. 2001).

For years prior to 1961, annual national wood harvest statistics were estimated by multiplying the national per capita wood harvest rate by the national population. National population was derived from the HYDE population data. National per capita wood harvest rates in 1920 were taken from those published by Zon and Sparhawk (1923). Between 1920 and 1961, data were interpolated between the 1920 per capita wood harvest rates from Zon and Sparhawk and the 1961 per capita wood harvest rates computed from the 1961 FAO wood harvest data and the 1961 national population data from HYDE 3.1. Prior to 1920, the per capita wood harvest rates were assumed constant at the 1920 rates published by Zon and Sparhawk. The reconstructed national wood harvest data were increased by a slash fraction of 30% to account for non-harvested losses from forests that occur during the wood harvesting process (Hurtt et al. 2006).

From 1500–2005, the global cumulative total wood harvest was 136 Pg C including slash (Fig. 2). Annual wood harvest was less than 0.1 Pg C y⁻¹ until ~1800, first exceeded 1 Pg C y⁻¹ in 1976, and increased to 1.3 Pg C y⁻¹ in 2005 (all including slash). These estimates were similar (within ~1%) to the previous wood harvest reconstruction of Hurtt et al. (2006). This study used a newer FAO dataset, 192 countries (on a 0.5° resolution map), and replaced previously-used USA and China wood harvest data (Houghton and Hackler 2000 and Houghton and Hackler 2003 respectively) with FAO data for those countries, but these changes largely compensated for each other.

Fig. 2

Annual national wood harvest (in PgC/year) for 1500–2005. (FSU = Former Soviet Union.) Integrated total is 136 PgC (including slash)

To evaluate the sensitivity of wood harvest information, simulations with zero wood harvest, and “No data” simulations that assumed national wood harvest statistics increased linearly from zero at the beginning of the historical period up to the FAO values in 2005, were also included.

2.3 Biomass density

To convert quantities of harvested wood into areas of impacted land, and to discriminate forested land from non-forested land for wood harvest activities, information was needed on the historical distribution of above-ground C stocks and forest extent, and on their recovery following wood harvest and land-use abandonment. As no global, gridded, historical record of this is available, a simple global terrestrial model was used to provide a consistent set of estimates of both global land cover and carbon stocks (Hurtt et al. 2006). Estimates of ecosystem properties were based on a global extension of the Miami-LU ecosystem model (Hurtt et al. 2002). Miami-LU is driven by the empirically based Miami Model of net primary production (Leith 1975), and has associated simple submodels of natural plant mortality, disturbance from fire, and organic matter decomposition. The model tracks subgrid-scale heterogeneity resulting from land-use changes in a manner similar to the more advanced Ecosystem Demography (ED) model (Hurtt et al. 1998; Moorcroft et al. 2001; Hurtt et al. 2002).

Miami-LU was run globally at 0.5° × 0.5° resolution for a spin-up period of 1000 years using average climate data from the ISLSCP-I data set (Meeson et al. 1995; Sellers et al. 1995). It resulted in an estimated global stock of potential plant carbon of 695 Pg C (Fig. 3). For comparison, estimates of preindustrial carbon stocks, which should be somewhat lower due to pre-1850 land-use effects, are 610 Pg C (Siegenthaler and Sarmiento 1993) and 620 Pg C (Houghton 1999). Estimates of contemporary carbon stocks, which should be substantially lower due to land-use activities, are 466–654 Pg C (Prentice et al. 2001). To differentiate forest from non-forest areas, a definition based on the aboveground standing stock of natural cover of at least 2 kg C m⁻² was used (Hurtt et al. 2006). Each grid cell was thus identified as potential forest or non-forest based on potential biomass. Using this definition, 58.6 × 10⁶ km² (42%) of the land surface was potential forest. For comparison, forest area based on the BIOME model was estimated at 60 × 10⁶ km² (Klein Goldewijk 2001). Finally, Miami-LU was also used to estimate the recovery of carbon stocks on secondary lands, in order to determine the amount of secondary forest carbon available for wood harvest each year. The application used here tracked the mean age of secondary land, and did not account explicitly for the complete age distribution within secondary lands, or the potential effects of land degradation, climate variability, forest management, fire management, or pollution that may have occurred.

Fig. 3

Potential vegetation biomass density (kg C m⁻²) from Miami-LU. Land is considered to be forest if the potential biomass density is >2 kg C m⁻² (after Hurtt et al. 2006)

2.4 Future land-use and wood harvest data from Integrated Assessment Models

For 2005–2100, land-use and wood harvest information were based on four different Representative Concentration Pathways derived from four different Integrated Assessment Models. These datasets are also to be used to drive the CMIP5 climate model simulations and are described in detail elsewhere (Moss et al. 2010; Thomson et al. 2010; Masui et al. 2011; Riahi et al. 2011; van Vuuren et al. 2011a,b) and summarized below and in Table 1.

Table 1 Properties of RCPs used in this analysis

2.4.1 RCP8.5-MESSAGE

RCP8.5 was a emissions pathway which reaches a radiative forcing of 8.5 W/m⁻² and rising in 2100. RCP8.5 was simulated in a structure of interlinked disciplinary and sectorial models referred to as the IIASA Integrated Assessment (IA) Modeling Framework (Riahi et al. 2007). Within the framework, consistency of land-cover changes (urban areas, cropland, and forest areas) was achieved through the exchange of spatially explicit information between the world food system model (AEZ–WFS) and the forest management model (DIMA), which were linked to the MESSAGE energy system model. The AEZ–WFS (Agro-Ecological Zoning – World Food System) model framework projected alternative development paths of the agriculture sector (Fischer et al. 2002a, 2002b; Fischer 2009; Riahi et al. 2011). The DIMA model (Dynamic Integrated Model of Forestry and Alternative Land Use) was a spatial model simulating forestry processes to meet specific regional timber and bioenergy demand (Riahi et al. 2011; Rokityanskiy et al. 2007). An important feature of the RCP8.5 was the increase in cultivated land by about 185 million ha from 2000 to 2050 and another 120 million ha from 2050 to 2100. While aggregate arable land use in developed countries slightly decreased, all of the net increases occured in developing countries. This strong increase in agricultural resource use was driven by the increasing population, which rose to 12 billion people by 2100. Yield improvements and intensification were assumed to account for most of the needed production increases: while global agricultural output in the scenario increased by 135% by 2080, cultivated land expanded by only 16% above 2005 levels. While agricultural land was expanding, forest cover declined over the century by 300 million ha from 2000 to 2050 and another 150 million ha from 2050 to 2100.

2.4.2 RCP6-AIM

RCP6 was a med-high emission pathway with mitigation actions taken late in the century to stabilize radiative forcing at 6 W m⁻² after 2100 without ever exceeding that level. RCP6 was simulated using the AIM (Asia-Pacific Integrated Model) and other models developed at the National Institute for Environmental Studies (NIES) in Japan. The trajectory of RCP6 was based on a SRES B2 scenario (IPCC 2000), with population updated to the UN medium variant (UN 2007) up to 2050 and UN (2004) for beyond 2050. The global emission pathway for RCP6 was calculated using the AIM/Impact[Policy], which combines the global economy model with a simple climate model. Then, the AIM/CGE[Global], a global computable general equilibrium model, was used to represent the consistent GHG emissions and land-use scenario up to 2100 for 24 regions. Finally, the emission and land-use scenario was downscaled into 0.5° × 0.5° grids. In the AIM/CGE[Global], land was treated as a production factor for agriculture, livestock, forestry and biomass energy production. The land productivity was assumed to be extended from historical trends but does not exceed the regional potential. Urban land-use increased due to population and economic growth, while cropland area expanded due to increasing food demand. Grassland area declined while total forested area extent remained constant throughout the century.

2.4.3 RCP4.5-GCAM

RCP4.5 was a low stabilization scenario that stabilized radiative forcing at 4.5 W m⁻² (~650 ppm CO₂-equivalent) before 2100 without ever exceeding that value. RCP4.5 was simulated with the Global Change Assessment Model (GCAM; formerly MiniCAM), a dynamic recursive economic model driven by population and labor productivity assumptions that determine potential GDP in each of 14 regions at 15-year time steps (Kim et al. 2006; Clarke et al. 2007; Brenkert et al. 2003). The RCP4.5 scenario was based on scenarios in Clarke et al. (2007). Land use was modeled fully endogenously in the GCAM for 14 global regions and the RCP4.5 incorporates updated land-use modeling and terrestrial emissions pricing assumptions as reported in Wise et al. (2009a,b). As a stabilization scenario, RCP4.5 assumed that global GHG emissions prices are invoked to limit emissions and therefore radiative forcing. The emissions pricing assumed that all carbon emissions are charged an equal penalty price; thus, reductions in land-use change carbon emissions constituted an available mitigation strategy and as a result GCAM simulated the preservation of large stocks of terrestrial carbon in forests and an overall expansion in forested area throughout the 21^st century. Agricultural land declined slightly due to this afforestation, yet food demand was still met through crop yield improvements, dietary shifts, production efficiency and international trade.

2.4.4 RCP2.6-IMAGE

RCP2.6 (also referred to as RCP3PD) represented a very low emission scenario and explores the feasibility of limiting climate change to less than 2°C by limiting radiative forcing to a peak of 3 Wm⁻² in mid-century, declining to 2.6 W m⁻² in 2100. The underlying scenario was simulated with the IMAGE model (van Vuuren et al. 2011b). The RCP2.6 scenario was based on the Adapting Mosaic scenario of the Millennium Ecosystem Assessment. The overall trends in land use and land cover were mainly determined by demand, trade and production of agricultural products and bio-energy modeled at the level of 24 world regions. Land use was downscaled to the grid level by a set of allocation rules. These rules allocated land use on the basis of: 1) agricultural productivity, 2) proximity to existing agricultural areas, 3) proximity to current water bodies and cities, and 4) a random factor (MNP 2006). Land-use change in the RCP2.6 followed a trend of agricultural land relocating from high income to low income regions, and a clear increase in bio-energy production was evident with new area for bioenergy crops occurring near current agricultural areas.

2.5 Harmonization of inputs

Harmonization of inputs involved minimizing the difference between the end of the historical reconstruction and beginning of future projections, and preserving as much information on the future from IAMs as possible. Representatives from the IAM and ESM communities were first engaged in discussions to reach general agreement on 2005 global land-use definitions and values. Prior to harmonization, inconsistencies in definitions of cropland, pasture, and wood harvest resulted in significant discrepancies (up to as much as 100%) between IAM values for their initial year (2005), and the HYDE 3.1 or FAO final year values (also 2005). Afterwards, these inconsistencies were reduced to <12%, except for RCP8.5-MESSAGE pasture, which used a very different definition based on grazing intensity.

Although agreement on 2005 land-use values was generally good at the global scale, there were still significant differences spatially (Fig. 4). To address this issue, IAM decadal changes in land use were aggregated over a 2° × 2° grid, and these changes were applied sequentially to the 2005 land-use distribution of HYDE3.1. In rare cases in which these changes could not occur in these sub-regions (e.g., an increase in crop area greater than the land area available), changes were applied in neighboring sub-regions by radiating outward. The resulting 2° × 2° grids were then disaggregated into 0.5° × 0.5° grids, weighted by available land for crop and pasture increases, and applied proportionally for cropland or pasture decreases, and interpolated temporally to get annual grids. Figure 5 illustrates the resulting retention of the spatial patterns of cumulative land-use changes as a function of spatial scale, which increases markedly with decreased resolution. Since GCAM did not generate gridded land-use output for RCP4.5, decadal regional changes were gridded by applying agricultural land-use changes as close as possible to existing historical land-use patterns (in a similar way to the harmonization of the other RCPs), and with a preference for locating agricultural land abandonment in potentially forested areas and agricultural land expansion in potentially unforested areas (for consistency with the RCP4.5 value of biomass carbon). For the future, wood harvest values from IAM’s were retained in order to preserve the carbon fluxes associated with these values, while the spatial pattern of wood harvesting was determined using the algorithms described below.

Fig. 4

Grid cell comparison of 2005 crop fractional area (after reaching near global agreement, and prior to harmonization): HYDE (x-axis) and IAM (y-axis) for: (a) RCP8.5-MESSAGE, (b) RCP6-AIM, and (c) RCP2.6-IMAGE. Note that RCP4.5-GCAM produced regional cropland areas, and could not be compared to HYDE on a grid cell by grid cell basis

Fig. 5

Projected changes 2005–2100 at multiple spatial scales: Original IAM changes (x-axis), harmonized changes (y-axis) for cropland (upper row) and pasture (lower row). Gray dots are changes at the half-degree grid cell scale, black dots are changes at the 2-degree grid cell scale, and red circles are changes at the regional scale (see Table 1 for IAM details). (a,d) RCP8.5-MESSAGE, (b,e) RCP6-AIM, (c,f) RCP2.6-IMAGE. Note that RCP4.5-GCAM produced regional land use areas, and so 0.5° and 2° grid cell comparisons could not be made

2.6 Additional major factors

2.6.1 Shifting cultivation and agricultural residence time

Although much agricultural land is relatively permanent, in some regions of the world shifting cultivation or swidden agriculture occurs, in which land is cleared, farmed for a number of years until no longer sufficiently productive, and then abandoned and allowed to re-grow (i.e., fallowed) while other nearby land is cleared (or re-cleared) and farmed. Over the past millennium, shifting cultivation has gradually been restricted to the tropics (Olofsson and Hickler 2008). Precise spatial patterns and rates of shifting cultivation are not well known. Here, the spatial domain of shifting cultivation was specified using the global map from Butler (1980), shown in Fig. 6. Following Hurtt et al. (2006), within each grid cell in the domain of shifting cultivation, an average land abandonment rate of 6.7% yr⁻¹ was applied to all agricultural land. In addition to the simulations that include shifting cultivation, simulations were performed that did not include shifting cultivation.

Fig. 6

Map of regions where land use includes shifting cultivation (after Butler 1980)

2.6.2 Inclusiveness of wood harvest data

Generally, it is unclear whether or not the wood cut on land cleared for agriculture is counted towards national wood harvest statistics, or whether national wood harvest statistics represent solely dedicated wood harvest operations. Clearly, the inclusion of cleared land will reduce the area of land needing to be logged to fulfill the national wood harvest estimates. To evaluate the sensitivity of this decision, two cases were evaluated. In the first case, all wood on land cleared for agriculture was counted towards meeting the national wood harvest estimates. Additional wood harvest was only conducted when the land cleared for agriculture did not provide enough wood to meet the estimates. In the second case, none of the wood cleared in agriculture was counted towards meeting the wood harvest numbers, and wood harvest demand was met only through explicit wood harvesting activities.

2.6.3 Priority of land for conversion

Land being converted for agriculture or used for wood harvest will be either primary vegetation or secondary vegetation. The decision of whether to prioritize primary or secondary land for conversion and logging will influence the resulting secondary land area, age, and biomass. Because the decision of which natural vegetation type to prioritize is undoubtedly variable in space and time, due to a complex array of socio-economic and productivity factors, the range of possibilities was bracketed by performing simulations that prioritized primary land for land-use activity, as well as simulations that prioritized secondary land. In each case, after the area “preferred” land type has been used, further land-use demand (if any) was met on the non-preferred land type.

2.6.4 Spatial pattern of wood harvesting

The spatial pattern of wood harvest directly affects the resulting patterns and structure of secondary forests. However, the spatial patterns of wood harvesting within countries are more detailed and generally less well known than aggregated national harvests estimated above. Some sub-national temporal reconstructions or spatial snapshots exist (e.g., Zon and Sparhawk 1923; Haden-Guest et al. 1956; Richards and Tucker 1988), but other than Hurtt et al. (2006), no global gridded historical database has been published. One factor that clearly constrains the potential patterns for wood harvesting is the presence of forests. This factor was used in all of the analyses, and was a necessary but not sufficient condition to uniquely specify patterns of wood harvesting. Previously, two additional factors were assessed, one in which wood harvesting preferentially occurred close to existing land use, and a second in which it was applied equally across all forested land within a country (Hurtt et al. 2006). Here, only the former is considered and assumed to be more realistic due to proximity to transportation infrastructure (accessibility) or local markets (FAO 2001). In this case, wood harvest activities occurred first in those grid cells that contained other land-use activities (i.e. crop, pasture, urban, or secondary), and then radiated outward from these grid cells until wood harvest demand was met.

2.6.5 Inclusion of urban land use

The HYDE 3.1 land-use dataset included urban land area. Here, cases were considered both with and without urban land. In the simulations that did not include any urban land, the urban land area reported by HYDE was reassigned to natural vegetation. Although global urban area is small in these estimates, and associated transitions into and out-of urban are also small, urban land use may still be included in some ESMs due to its high applied relevance, unique biogeophysical properties, significance as a source of human-related emissions, or other reasons.

2.6.6 Historical start date

Different historical time points are interesting for different applications. Some models and applications are interested in long historical periods starting in 1500 or earlier, while others focus on the beginning of the industrial revolution, or future only. The starting year for the historical simulations plays an important role in determining the area, age, and biomass of the secondary lands resulting from agriculture and wood harvesting. To test the sensitivity of results to the simulation start date, simulations were run that began in 1500, 1700, 1850, and also 2005. Simulations were all initialized with corresponding HYDE maps of crop, pasture, and urban area, but were assumed not have any secondary land area at that time, i.e., all natural vegetation was assumed to be in a “primary” state.

2.7 Methodology for calculating land-use transitions

2.7.1 Determining agricultural land-use transitions

Following Hurtt et al. (2006), a book-keeping approach was used to calculate annual land-use transition rates between five possible land-use types—cropland, pasture, urban (if included), primary, and secondary—given the data inputs and additional factors discussed above. To determine these, the change in urban area in each grid cell was first computed and applied proportionally to the cropland, pasture, and secondary land-use categories within the grid cell. If there was not enough land available between cropland, pasture and secondary for a given urban land-use increase, the remaining area needed was from the primary land within the grid cell. Next, minimum transition rates were calculated between the remaining three land-use types (cropland, pasture, and other; where other was defined as the sum of primary and secondary), based on the gridded annual input data on land-use patterns (adjusted for the transitions into and out of those types associated with urban land-use change and computed on the previous step). With only three land-use types, unique minimum transitions (i.e. solutions to Eq. 1) could be easily determined. Additional transitions associated with shifting cultivation and wood harvest were then determined. In cases of shifting cultivation, land-use transitions from crop to other, other to crop, pasture to other, and other to pasture were all increased by the abandonment rate of agricultural land. Transitions from other were then partitioned into transitions from primary and secondary based on the prioritization chosen and availability. All transitions from crop or pasture to other were defined as transitions to secondary. The amount of wood cut in converting land to agriculture was determined by overlaying these transitions with estimates of biomass density.

2.7.2 Determining area cleared by wood harvest

For each country or region, the amount of annual wood harvest that was met by land conversion to agriculture depended on the assumed inclusiveness of wood harvest and other factors described above. Any remaining unmet wood harvest following land conversions was met through additional explicit wood harvesting. Wood harvesting of primary land was represented by the transition “primary to secondary”. Harvesting of secondary land was represented by the age- (and biomass-) resetting transition “secondary to secondary”. To calculate these transitions in area units, wood harvest was converted to area units using the carbon density of land affected (Hurtt et al. 2006).

For the period 1500–2005, the selection of specific grid cells to be logged within a country depended on the presence of forest, the priority of land for conversion/wood harvesting (primary or secondary), and the assumed spatial pattern of wood harvesting (Hurtt et al. 2006). In cases where primary land was prioritized, transitions from primary to secondary were calculated proportionally for each grid cell that met the spatial pattern of wood harvesting criteria described above. If primary forest in a country could not meet the demand, or if secondary forests were prioritized, secondary forests were logged based on maturity. Logging of secondary forests was implemented assuming an average probability of harvest vs. biomass function parameterized from detailed age-specific harvesting algorithms previously developed and applied in the U.S. (Hurtt et al. 2002, 2006). If mature secondary forests could not satisfy the wood harvest demand for a country, primary forests were cut to meet the remaining demand. In cases when both primary forest and mature secondary forest could not meet national wood harvest demand, remaining (non-mature) secondary forests were cut proportionally from all grid cells. Finally, in rare cases when the combination of available primary and secondary forest within a country could not meet national wood harvest demand, non-forest grid cells were harvested proportionally to meet remaining demand. (Note that a non-forested 0.5° × 0.5° grid cell with mean potential aboveground biomass density <2 kg C m² could have scattered woody vegetation.)

For the period 2005–2100, the wood harvesting method depended on whether the IAM provided regional or gridded future wood harvest projections. For IAMs that provided regional wood harvest projections (IMAGE and GCAM), the ratio of each country’s wood harvest to the regional wood harvest in 2005 was first calculated. Then, for 2005–2100 each region’s wood harvest was divided into national wood harvest amounts by multiplying the regional wood harvest by the 2005 national wood harvest ratios. Within countries, the spatial pattern of wood harvesting used the algorithms developed for the land-use history reconstruction described above. For IAMs that provided gridded wood harvest projections, these were used whenever possible. Any wood harvest that could not be met within the specified grid cell was tracked and the unmet amount from all grid cells within each region was applied elsewhere in the region using an approach analogous to that used in the historical period.

3 Results

In total, 1664 complete global harmonized land-use cases were constructed using all combinations of input data and factors described above (Table 2), and including additional sensitivity studies around four focal cases. The aggregate results from these cases are summarized in statistics showing the range of potential values for gross and net transitions, resulting secondary land area and age, and implied above-ground carbon fluxes (Fig. 7). To evaluate sensitivity, cases were paired in which only a single factor was changed, and the differences between them were calculated for six output metrics: total gross land-use transitions from the starting year to 2100, total net land-use transitions to 2100, global area of secondary land in 2100, global mean age of secondary land in 2100, cumulative loss of above-ground biomass carbon to 2100, and cumulative net loss in above-ground biomass carbon to 2100 (Fig. 8). Generally, the sensitivity of each factor varied by output metric, and depended strongly on other model assumptions. These sensitivity results are followed by a more detailed description of the results for four focal scenarios (one for each RCP) that are based on the best information available.

Table 2 Model factors

Fig. 7

Simulated range in (a) total global gross transitions (10⁷ km² y^-1), and (b) total global net transitions into use (10⁵ km² y⁻¹), (c) total global secondary land area (10⁷ km²), (d) global mean age of secondary land (y), (e) global cumulative loss of above-ground biomass (Pg C), (f) global cumulative net loss in above-ground biomass (Pg C). All runs (light gray region; n = 1536) and data-based runs (dark gray region; n = 256), and ‘focal case’ simulations (heavy solid lines) are depicted. “All” includes cases with and without historical data and wood harvest used as inputs. “Data-based” runs use reconstructed wood harvest, and HYDE land-use history (see Table 2)

Fig. 8

Model sensitivity to factors for (a) total gross land-use transitions from the start of the simulation to 2100 (10⁹ km²), (b) total net land-use transitions from the start of the simulation to 2100 (10⁷ km²), (c) total secondary land area in 2100 (10⁷ km²), (d) global mean age of secondary land in 2100 (Years), (e) cumulative global loss of above-ground biomass carbon from the start of the simulation to 2100 (Pg C), and (f) cumulative net loss in above-ground biomass carbon from the start of the simulation to 2100 (Pg C). Each symbol represents the difference in simulated values for a pair of simulations that differ in only the factor identified on the horizontal axis. Red symbols represent paired data-based simulations (i.e., that do not use H0, L0, or L4 in Table 2) while black symbols represent simulations that do use H0, L0, or L4

3.1 Aggregate results and model sensitivity

Gross transitions

Gross transitions are a measure of all land-use change activity; specifically, they are the sum of the absolute value of all land-use transitions. In most cases, total gross transitions (the sum of gross transitions across the domain) increased through time, from 0 in 1500 to nearly 20 × 10⁶ km² y⁻¹ by 2100 (Fig. 7a). High values were generated in cases with shifting cultivation and maximum wood harvest. Low values were generated by cases with no shifting cultivation, and no wood harvest. In paired comparisons, factors that had a large impact on total gross land-use transitions included the residency time of agricultural land, the inclusion of wood harvest, and the priority of primary vs. secondary land for conversion and wood harvest (Fig. 8). Cases with shifting cultivation generated 80–800 × 10⁶ km² more gross transitions than the minimum transition assumption.

Net transitions

Net transitions measure only net changes in land use (i.e., net transitions exclude wood harvest on secondary forests, and agricultural land abandonment that is offset by land conversions to agriculture—net transitions specifically exclude shifting cultivation, but also other historical redistribution of agriculture across a region). As expected, net land-use transitions were smaller than gross. Total net land-use transitions generally peaked in the mid-1900s at 0.1–0.9 × 10⁶ km² y⁻¹, and fell to −0.08–0.3 × 10⁶ km² y⁻¹ by 2100 (Fig. 7b). High values were due to cases with primary land priority and late start date; low values occurred with secondary land priority, inclusion of agricultural clearing in wood harvest, and early start date, and negative values reflected net abandonment of agricultural land. In paired comparisons, net land-use transitions depended most strongly on wood harvest history and choice of simulation start date (Fig. 8).

Secondary area

Patterns of gross and net transitions have implications for estimates of secondary land. For secondary land area, the results from all simulations ranged from no increase to an increase of 63 × 10⁶ km² from 1500 to 2100, about half of which was forested (Fig. 7c). The full range was bounded on the bottom by cases that excluded wood harvest and shifting cultivation, had a late start date, and used secondary land priority, and on the top by cases that maximized wood harvest, included shifting cultivation, prioritized primary land for land-use changes, and had an early start date (Table 2). Data-based cases had an intermediate range of secondary land of 0–36 × 10⁶ km² by 2005 and 16–60 × 10⁶ km² by 2100. Secondary area was most sensitive to the priority of land for land use, inclusion of wood harvest, the simulation start date, and the choice of land-use history product used (Fig. 8). This sensitivity varied strongly as a function of the values for the other factors. For example, land priority had a relatively large impact on secondary land in cases with shifting cultivation because of the large amount of secondary land generated in these cases. Similarly, the abandonment of agricultural land generated more net secondary land when primary land was a priority for land-use change. Wood harvesting was most important when wood from clearing for agriculture was excluded from harvest.

Secondary age

The mean age of secondary land was calculated each year for each grid cell and aggregated to a global mean age. The global mean age was defined as zero in the start year. By 2005, the range across all simulations was 0–133 years (Fig. 7d). For data-based cases, the range was 0–83 years. By 2100 the range across all cases was 0–208 years, and 3–91 years for data-based cases. Low mean-age values resulted from cases with secondary land priority, shifting cultivation, and in which wood from agricultural clearing counted toward harvest. High values resulted from cases with minimum transitions and primary land priority. The mean age of secondary land in 2100 was most sensitive to land-use history, wood harvesting, and simulation start date (since although simulations that started later had less secondary land overall, they also had less time for that secondary to regrow) (Fig. 8). Perhaps surprisingly, almost all simulations with wood harvesting had older secondary land than the corresponding simulations without it. Wood harvesting generally added more secondary land, and this land typically had longer periods of recovery and regrowth before re-harvest than fallow agricultural land (Hurtt et al. 2006).

Cumulative loss of above-ground biomass carbon

The cumulative loss of above ground biomass resulting from land-use transitions (i.e., the sum of all losses) is an important metric of the gross effects of land use on the terrestrial carbon cycle. Over all runs, this metric started near zero in 1500 and increased to 160–940 Pg C by 2005, and as high as 1300 Pg C by 2100 (Fig. 7e). As expected, the range from data-based cases was smaller, between 160–600 Pg C by 2005, and 340–990 Pg C by 2100. High values resulted from simulations with early start date, primary priority, maximum wood harvest, and shifting cultivation, while low values resulted from simulations with late start date, secondary priority, and minimum transitions only. The inclusion of shifting cultivation, wood harvesting, primary land priority, and start date all strongly affected the cumulative loss of above-ground biomass, each responsible for up to 500 Pg C of gross clearing by 2100 in paired simulation comparisons (Fig. 8).

Cumulative net loss in above-ground biomass carbon

The cumulative net loss in above-ground biomass is the difference between the estimated above-ground biomass including land use, and the estimated biomass of potential vegetation (695 Pg C). The metric includes both the losses of above-ground biomass due to land-use and the gains due to regrowth. Net losses in above-ground biomass ranged from zero in 1500, to 110–325 Pg C by 2100 (Fig. 7f). Historically, net losses were estimated to be relatively modest to the middle of the 19th century, accelerating rapidly through the 20th century as the rate of regrowth of biomass was not able to keep up with land-use change related emissions, and divergent estimates over the 21st century. High values typically resulted from simulations that included shifting cultivation and wood harvest while low values resulted from simulations that did not include these factors. Several factors strongly affected net losses in above ground biomass, including: inclusion of historical land-use data, shifting cultivation, wood harvest, and future scenario (Fig. 8). Each of these factors was responsible for up to 100 Pg C net in paired simulation comparisons.

3.2 Focal cases

Four focal cases, one corresponding to each RCP, were chosen for detailed analyses based on three criteria: quality of data inputs, the reasonableness of model assumptions, and comparisons to previous estimates. All four cases shared the same historical reconstruction and set of model factors, and differed only by RCP input data for 2005–2100. All cases applied minimum transitions outside the tropics, and included shifting cultivation in the tropics as described above. Primary land was used as a priority for land conversion and wood harvest on all continents, except Eurasia, where secondary land was prioritized. In addition, wood harvesting from land conversion was not counted towards fulfilling national wood harvest demand, except in Eurasia. These decisions were made following Hurtt et al. (2006) for best agreement with FAO estimates of secondary land area in 1990.

Historically, the area of cropland increased at an accelerating rate from 2.34 × 10⁶ km² in 1500, to 5.64 × 10⁶ km² in 1850, and 15.6 × 10⁶ km² by 2005 (Fig. 9). Pasture increased faster from 2.61 × 10⁶ km² in 1500, to 7.74 × 10⁶ km² in 1850, and to 33.4 × 10⁶ km² by 2005. Urban went from near 0 in 1500 to 0.59 × 10⁶ km² by 2005. During this same period, primary land area decreased from 125 × 10⁶ km² to 50.7 × 10⁶ km², while secondary land increased from 0 to 29.7 × 10⁶ km², about half of which was forested. Focal cases were generally well within the range of all simulations in terms of gross transitions, net transitions, secondary land area, secondary land age, and estimates of carbon flux (Fig. 7, Tables 3 and 4).

Fig. 9

Time series of fraction of global land surface area (excluding ice and open water) occupied by urban land (brown), cropland (blue), pasture (yellow), secondary non-forest (light pink), secondary forest (dark pink), primary non-forest (light green), primary forest (dark green) for 1500–2100 (a) RCP8.5-MESSAGE, (b) RCP6-AIM, (c) RCP4.5-GCAM, (d) RCP2.6-IMAGE. The total global ice-free land area was 129,930,555 km²

Table 3 Mean gross and net land-use transitions by continent and century

Table 4 Secondary land area and mean age of secondary land by continent and century

The new land-use history reconstruction derived here compared favorably to prior reconstructions by Hurtt et al. (2006) and other references across a range of important diagnostics, albeit now at higher spatial resolution. The percent of the land surface impacted by human activity was 60% (previous range 42–68%). The total increase in secondary land in 2000 was 28.9 × 10⁶ km² (previously 10–44 × 10⁶ km²). The percent of secondary land increase that’s forested was 47% (previously 50%). The percent of secondary land generated by shifting cultivation and wood harvest was 86% (previously 70–90%). Total wood harvest including slash 1850–1990 was 84 Pg C (previously 85 Pg C). Total wood clearing for agriculture 1850–1990 was 170 Pg C (previously 105–158 Pg C; Houghton (1999) 149 Pg C). The area of forested land in shifting cultivation fallow in the year 2000 was 3.9 × 10⁶ km² (previously 4.6–6.2 × 10⁶ km², Lanly (1985) 4 × 10⁶ km²). Rates of land clearing for shifting cultivation at that date were 0.58 × 10⁶ km² y⁻¹ (previously 0.48–0.65 × 10⁶ km² y⁻¹, Rojstaczer et al. (2001) 0.6–0.9 × 10⁶ km² y⁻¹). Total gross transitions in 2000 were 2.9 × 10⁶ km² y⁻¹ (previously 0.55–4.2 × 10⁶ km² y⁻¹), and total net transitions in 2000 were 0.17 × 10⁶ km² y⁻¹ (previously 0–0.17 × 10⁶ km² y⁻¹). Both contemporary global cropland and pasture area were somewhat higher than previously estimated, (1990 cropland 15.1 × 10⁶ km² vs. 12.1 × 10⁶ km², and 1990 pasture 33.1 × 10⁶ km² vs. 25.8 × 10⁶ km²), differences attributable directly to the new land-use input (HYDE 3).

For the future, three cases projected cropland increases (RCP2.6-IMAGE, RCP6-AIM, RCP8.5-MESSAGE), three projected pasture decreases (RCP2.6-IMAGE, RCP4.5-GCAM, RCP6-AIM). Only one case projected increases in both cropland and pasture (RCP8.5-MESSAGE). However, all four cases projected large increases in wood harvesting, which contributed to large increases in secondary area and corresponding reductions in primary area by 2100. In 2100, RCP8.5-MESSAGE had 18.4 × 10⁶ km² cropland, 37.1 × 10⁶ km² pasture, and 41.8 × 10⁶ km² secondary; RCP6-AIM had 19.3 × 10⁶ km² cropland, 17.9 × 10⁶ km² pasture, and 52.3 × 10⁶ km² secondary; RCP4.5-GCAM had 11.3 × 10⁶ km² cropland, 28.7 × 10⁶ km² pasture, and 51.1 × 10⁶ km² secondary; RCP2.6-IMAGE had 21.0 × 10⁶ km² cropland, 32.7 × 10⁶ km² pasture, and 40.6 × 10⁶ km² secondary. In all cases, approximately half of all secondary land was forested, and the estimated mean age of secondary forest ranged from 66 y (RCP8.5-MESSAGE) to 84 y (RCP4.5-GCAM).

3.2.1 Spatio-temporal patterns of land-use transitions, secondary area, and secondary age

Historically, most of the world was estimated to still be in primary condition (not used since 1500) as of 1850. Crop and pasture and secondary were generally widespread, at low density (low fractional coverage), and the Amazon Basin was largely still in primary condition. Gross transitions were generally highest in Africa with an average of 312 × 10³ km² y⁻¹ over 1800–1900, compared with 549 × 10³ km²y⁻¹ globally (Table 3), and net transitions highest in the Eastern U.S. corresponding to a period of net clearing for agriculture and wood harvest at that time (Fig. 10). Across North America, net transitions were 44 × 10³ km² y⁻¹ over 1800–1900 and across Eurasia they were as high as 74 × 10³ km² y⁻¹ over that same period (Table 3). By 2005, patterns of crop, pasture, and secondary intensified (areas of high fractional coverage). Major areas of cropland in North America, Europe and Asia were readily identifiable, as were areas of pasture in the Western U.S., southern South America, parts of Africa, Eurasia, and Australia. Important areas of secondary land were distributed in the Eastern U.S., Europe, and Africa, along with South America. Over the period 1900–2000, average secondary land area was highest in Africa where it was 10.4 × 10⁶ km² while the secondary land with lowest mean age was in North America where it had an average age of 77.4 years (Table 4). Gross transitions were highest in Africa, and net transitions highest in South America, Africa, and Southeast Asia (Fig. 11) with high values of 968 × 10³ km² y⁻¹ (mean gross transitions 1900–2000 for Africa), 159 × 10³ km² y⁻¹ (mean net transitions 1900–2000 for Eurasia) (Table 3).

Fig. 10

Focal case simulations 1850: a. fraction of each grid cell occupied by cropland in 1850, b. fraction of each grid cell occupied by pasture, c. fraction of each grid cell occupied by urban land, d. fraction of each grid cell occupied by primary vegetation, e. fraction of each grid cell occupied by secondary vegetation, f. mean age (in years) of secondary lands in each half degree grid cell, g. mean gross transitions (km² year^-1) over 20 year interval for each grid cell, h. mean net transitions (km² year⁻¹) over 20 year interval for each grid cell

Fig. 11

As in Fig. 10, but for 2005

For the future, the four different RCPs produced different spatial-temporal patterns of future land-use area and land-use transitions. By 2100, RCP8.5-MESSAGE had areas of high-density cropland in U.S., Europe, and S.E. Asia. High-density pasture areas were evident in Western U.S., Eurasia, South Africa, and Australia (Fig. 12). Primary forest was most concentrated in northern high latitudes and parts of Amazonia, while secondary vegetation was common in the U.S., Africa, South America, and Eurasia. Gross transitions were highest in parts of Africa and S.E. Asia and South America, with mean values during 2000–2100 of 1935 × 10³ km² y⁻¹ in Eurasia and 1590 × 10³ km² y⁻¹ in Africa. Net transitions were highest in S.E. Asia, with mean values during 2000–2100 of 113 × 10³ km² y⁻¹ in Eurasia (Table 5). Patterns from RCP6-AIM were broadly similar, with less pasture generally and especially in the U.S., Africa, Eurasia, and Australia (Fig. 13). RCP4.5-GCAM had less cropland overall than either of the previous RCPs, more land with no fractional cropland, and had high-density areas of secondary in U.S., Africa, and Eurasia (Fig. 14). Mean secondary land areas during 2000–2100 were 16.3 × 10⁶ km² in Eurasia, 14.3 × 10⁶ km² in Africa, and 5.33 × 10³ km² in North America (Table 6), with gross transitions highest in Africa, and net transitions highest in Eurasia and Northern North America (Table 5, Fig. 14). RCP2.6-IMAGE had the most cropland, second most pasture, and least secondary. Key spatial patterns from harmonized RCP2.6-IMAGE are illustrated in Fig. 15.

Fig. 12

Focal case simulation 2100, RCP8.5-MESSAGE: a. fraction of each grid cell occupied by cropland, b. fraction of each grid cell occupied by pasture, c. fraction of each grid cell occupied by urban land, d. fraction of each grid cell occupied by primary vegetation, e. fraction of each grid cell occupied by secondary vegetation, f. age (in years) of secondary lands in each grid cell, g. mean gross transitions (km² year⁻¹) over 20 year interval for each grid cell, h. mean net transitions (km² year⁻¹) over 20 year interval for each grid cell

Table 5 Mean gross and net land-use transitions 2000–2100 by RCP

Fig. 13

As in Fig. 12, but for RCP6-AIM

Fig. 14

As in Fig. 12, but for RCP4.5-GCAM

Table 6 Mean Secondary land area and mean age of secondary land 2000–2100 by RCP

Fig. 15

As in Fig. 12, but for RCP2.6-IMAGE

4 Discussion

Land use is essential for production of food, feed, fiber, and fuel, and affects the biogeochemistry, biogeophysics, biodiversity, and climate of the Earth. Quantitatively understanding the effects of land-use activities on the Earth system requires that the best technical expertise and data on land use be incorporated into the best Earth system models. Ultimately, models must treat changing land-use patterns, transitions, management practices, and the resulting effects on vegetation, biogeochemistry, and biogeophysics consistently in the past, present, and future. The strategy described here is a nascent approach for harmonizing land-use patterns and transitions across multiple models, model types, history, and future scenarios. As such, it is designed to facilitate fuller and more consistent treatments of how land-use changes influence the Earth system, particularly gridded effects on biogeochemistry, biogeophysics, and biodiversity.

Previous studies have demonstrated the utility of historical gridded land-use-transition estimates for use in regional-global carbon/climate modeling studies (Pacala et al. 2001; Hurtt et al. 2002; Roy et al. 2003; Shevliakova et al. 2009). Land-use transitions not only create important changes to ecosystems (e.g. cutting of forests, planting of crops, etc.), but also leave behind a legacy of secondary land in various stages of recovery from prior use. One potentially encouraging point is that despite the increased pressure for resources embodied in all four future scenarios, future increases in agricultural land and decreases in forest area may not be inevitable. From these RCPs, total agricultural land (crop + pasture) is projected to add 6.56 × 10⁶ km² (+13%), or lose 11.8 × 10⁶ km² (−24%) by 2100, depending on RCP. Because additional agricultural land use could reduce carbon storage and reduce forest habitat for biodiversity and have other negative impacts on ecosystem services (Sala et al. 2000), potential reductions in agricultural land and gains in forest could do the opposite (Pereira et al. 2010). However, all RCPs project large increases in wood harvest and resulting secondary lands, with wood harvest projected to increase 51–200%, and secondary area projected to increase by 10.6–22.4 × 10⁶ km² (35–75%). Thus, while forested land area may actually increase under some scenarios, remaining forested land may be more impacted overall. Taken together these results suggest that additional metrics beyond land-use areas, that capture forest condition as well as area, will be needed for both carbon/climate modeling and future impact assessments. Wood harvesting and secondary re-growth, not generally included in most global models to date, are likely to play an increasing role in Earth system dynamics and applications in the future.

Sensitivity analyses were a key feature of this study, and were designed to quantify the importance of model inputs, attributes, and assumptions on results. Key findings from these analyses indicated that shifting cultivation, wood harvesting, and simulation start date all strongly affect estimated secondary land area, secondary land age, and carbon fluxes. This was also true in the focal cases and in the future. For example, averaged across all RCPs, omitting shifting cultivation reduced mean secondary area in 2100 by an average of 13%, omitting wood harvest reduced secondary area by an average of 57%. Excluding both processes and starting the simulation in 2005 reduced secondary area in 2100 by 84%. Not surprisingly, omitting these factors also translated into large estimated carbon flux differences: 36–78% (300–660 Pg C) cumulative, and 8–34% (20–88 Pg C) net. For most metrics, the choice of RCP, while important, had a smaller impact than the inclusion of wood harvest, shifting cultivation and choice of start date. The main exception to this was in the cumulative net losses from above ground biomass, in which the policies that valued carbon from biomass in RCP4.5-GCAM resulted in losses from wood harvest etc. being largely offset by carbon gains on other lands.

The need for global data on annual global gridded land-use transitions past-to-future presents a large and underdetermined problem. While the approach taken to solving this problem here relied on using an ambitious combination of multiple model inputs and other model factors, these results must be considered uncertain and highly dependent on the inputs and assumptions used, as the sensitivity analyses illustrated. Overall, uncertainty is expected to be highest in the distant past and future, and at high spatial resolutions. In the future, these uncertainties could be addressed using additional inputs. For example, data on high spatial resolution land-conversion events observed with Land-Sat (e.g., Masek et al. 2008; Hansen et al. 2008), together with data on the spatial pattern of vegetation height (Lefsky 2010), could in principle be used to better constrain the spatial-temporal patterns of land-use transitions in the past and future.

As a global harmonization activity spanning multiple groups and approaches, the empirically-based carbon model (MIAMI-LU) used in this study was necessarily simple and transparent. Since the core data products from this study are annual maps of land-use transitions (in area units), it is possible and even expected that other carbon models and/or ESMs using these products may produce different carbon results from these same land-use changes. However, previous studies using earlier products did not produce substantially different results under similar conditions (Hurtt et al. 2006; Shevliakova et al. 2009), and in fact used the close correspondence of estimated wood harvest based on area, to that reported in carbon units, as partial validation of their model.

Use of these products in various ESMs may require additional model-dependent challenges. Full implementation will require that these models develop a subgrid-scale parameterization for tracking different land-use fractions and the land-conversion events between them. In addition, models that focus on land cover will need to develop methods for predicting how these land-use changes translate into land-cover changes, if it is not already inherent in their prognostic design. Additional challenges include the effects of land-use changes on vegetation and on soil and below-ground biomass carbon, the fate of harvested material and wood products, and the diversity of management practices that occur on agricultural lands (Ramankutty et al. 2007; van Minnen et al. 2009).

Looking ahead, one particular challenge is biofuels. Biofuels are an important component of RCP climate mitigation strategies, and are handled differently among the RCPs: three included biofuels in their cropland category (RCP6-AIM, RCP4.5-GCAM, RCP2.6-IMAGE), and one in its wood harvest results (RCP8-MESSAGE). All three mitigation cases (RCP6-AIM, RCP4.5-GCAM, and RCP2.6-IMAGE) also use carbon capture and storage of biofuel as a means of producing a carbon sink. Accurately representing biofuel production, harvest, and fate in ESMs will be necessary if they are to accurately reproduce the RCPs intended by IAMs.

Finally, while harmonizing land-use information across IAMs and ESMs and between historical and future time periods is a major advance, future studies are needed to build on past work and include human activity into fully-coupled ESMs (Voldoire et al. 2007). Doing so will eliminate remaining potential inconsistencies between future land-use patterns and crop yields and forest biomass production, and underlying predictions of climate and ecosystem functions.