Abstract
A more sustainable future calls for bio-based alternatives to replace plastic foams for various applications, such as packaging, insulation and cushioning. Some bio-based foams emerging in scientific publications are fabricated using liquid foam templating and methyl cellulose as well as fibers as main constituents. Scaling up of the production, however, requires a comprehensive understanding of the rheology of the foam during the shaping and drying processes. In this article, we report rheological studies of cellulose based systems in the context of thermal gelation. In more precise terms, we study how the presence of cellulose fibers and other additive materials influences the thermal gelation properties of methyl cellulose. We observe that the rheological properties, while heavily dependent on the material composition, are reasonably adjustable by appropriate material choices. The fibers are seen to decrease the temperature required for methyl cellulose to undergo a viscoelastic transition which is useful in the solid foam fabrication process. We anticipate that in the present application, the fibers increase the stability of the desired structure during the drying stage of the foam.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Increasing consciousness of problems with plastic waste (Rochman et al. 2013) and production (Cabernard et al. 2022) demands alternative solutions, especially for single-use plastics. Prominent alternatives are cellulose polymers and derivatives. Cellulose is a bio-based polymer abundant in nature. The main sources of cellulose are wood pulps (Klemm et al. 2005), however, cellulose can be harvested from many other more sustainable sources such as agricultural wastes (Ee and Li 2021).
Over the last century, plastics have been the dominant material in polymer foams with applications ranging from cushioning, packaging and insulation (Khemani 1997). However, recently more foams and aerogels have appeared with fully bio-based ingredients and relevant functionalities. Such composite materials can be prepared from various fiber sizes ranging from macroscopic cellulose fibers (Reichler et al. 2021) to nanocellulose fibers (Hu et al. 2016; Lavoine and Bergström 2017; Kontturi et al. 2018; Voisin et al. 2018; Ee and Li 2021) and the applications are abundant. Depending on their properties they may find applications in packaging, electronics, medical scaffolds and ultra lightweight aerogels (Hjelt et al. 2020). A few typical examples of fabrication methods are 3D printing (Voisin et al. 2018), freeze drying (Guo et al. , 2018) and drying from a stabilized emulsion or foam (Studart et al. 2007). The present study focuses on the latter method.
Production of solid foam from liquid foam by drying requires a surfactant that sustains the stability of the foam under sufficient heat. The possible challenges with stability during the fabrication process of solid foams originate from the dynamic properties characteristic of foams such as coarsening, coalescence and drainage (Andrieux et al. 2018), all highly dependent on temperature. Methyl cellulose (MC) provides the required properties as, when dissolved in water, exhibits a thermoreversible sol–gel transition on temperatures around 45–70 \(^\circ\)C (Kobayashi et al. 1999). Upon heating, MC systems turn into hydrogels with a relaxation time increasing several decades, depending on the polymer concentration (Desbrieres et al. 2000). The former allows a methyl cellulose stabilized foam to hold the structure during a rapid drying process. However, at a temperature below the gelation transition, MC forms a viscous polymer suspension which can be easily shaped during the fabrication process, but still maintains the wet state foam stability required in the process. The fabrication of the designed foam relies on balancing the time scales of wet forming and viscoelastic transition (Andrieux et al. 2018). After the foam reaches the desired shape, it should be rapidly heated to form the gel that will hold its shape during drying. This property was utilized in our previous studies (Reichler et al. 2021; Miranda-Valdez et al. 2023) where a nozzle extrudes parallel rods of liquid foam on a conveyor belt to dry under infrared lamps. The present article was prepared simultaneously with another research where the setup produces sheets of foam with a moving blade and the sheets then dry under hot air flow (manuscript under preparation by Ketoja et. al). Both methods utilize the rheological properties of methyl cellulose solution. The bubbles of foam elongate at the wet state, and the solid foam inherits the property as anisotropy in the bubble shape and fiber orientation (Reichler et al. 2021) and Ketoja et al. (manuscript in preparation).
The gelation of MC has been widely studied recently (Coughlin et al. 2021), and transmission electron microscopy revealed that MC forms a load-bearing fibril network upon heating (Lott et al. 2013). However, the effect of added fibers on MC gelation still requires further studies as that represents a condition in the fabrication process of composite materials. Previously the gelation of suspensions containing mixtures of MC and other materials has been studied with added kappa carragen (Almeida et al. 2018), cellulose nano crystals (Hynninen et al. 2018) and macroscopic fibers (Miranda-Valdez et al. 2022). These demonstrate systematic studies about the effect of additives on the rheology of methyl cellulose sol–gel transition and similar research was conducted here. To gain a more comprehensive picture of the rheological effects, Gaussian processes could be applied to the experimental data of the present study in a similar way as Miranda-Valdez et al. (2022) describe. The Gaussian processes can fit a surface to the existing measurement data. The fit enables interpolating rheology curves or quantities, such as viscoelastic transition temperature, for concentrations between the actual measurements. Here we use fibers produced with high-consistency enzymatic fibrillation (HefCel) process which results in rigid micro fibers with a heterogeneous size distribution described e.g. in (Lehmonen et al. 2017). Producing composite foams from a suspension of methyl cellulose and HefCel fibers requires understanding of the thermal gel transition of the suspension with different solid contents and fiber concentrations.
Materials and methods
To prepare the cellulose-based suspensions, we used a commercial methyl cellulose, labeled Methocel (Special Ingredients Ltd, United Kingdom) and HefCel cellulose fibers, which were kindly provided by the VTT Technical Research Centre of Finland Ltd. Methocel polymer follows the European standard for food additives E461, having a content of methoxyl groups (−OCH\(_{3}\)) between 25 and 33% and a hydroxypropyl content no larger than 5%, according to the manufacturer (JECFA 2006). The typical viscosity of the Methocel polymer (2% aqueous solution at 20 \(^{\circ }\)C) is reported by the manufacturer to be between 3000 and 5600 mPa s. Regarding HefCel fibers, their manufacture and physical properties have been disclosed elsewhere (Hiltunen et al. 2013; Jaiswal et al. 2021; Pere et al. 2020). In summary, HefCel technology produces highly fibrillated cellulose fibers with a wide fiber length distribution and an average arithmetic fiber length (l) of 20 \({\mu }\)m. Figure S1 in the Supplementary Material provides a microscopy image of aqueous HefCel suspension showing the varying size distribution of the fibers.
We formulated suspensions based on cellulose as listed in Table 1. The preparation process consisted of dispersing MC in hot water (70\(^{\circ }\)C); hot water corresponded to one third of the total water content. Then, we added water at room temperature and HefCel fibers to adjust the solid content of the suspensions. The HefCel does not dissolve into water which limits the maximum amount of HefCel in our experiments: without the increase in the viscosity of the sample facilitated by the methyl cellulose, the HefCel would sediment on the bottom of the mixture within an hour. For all the samples, we used tap water. According to our local provider (HSY, Finland), the water has a pH = 8.5 at 23 \(^{\circ }\)C, conductivity of 160 \(\mu\)S/cm, permanent hardness of 3\(^{\circ }\)dH, and 0.71 mmol/L of HCO\(_{3}\) (alkalinity). To avoid any effects from changes in the water quality, most of the measurements were conducted within one week (measurements 1, 4 and 8 in Table 1 were measured two weeks after the others). The suspensions were stirred for 1 h at 700 rpm (at 25 \(^{\circ }\)C) and chilled overnight at 5 \(^{\circ }\)C before assessing their rheological properties.
Before rheological testing, we heated and observed a selected suspension under cross-polarized light. This experiment required using an Olympus BX53M optical microscope (Japan) with a DP74 camera attachment (Olympus, Japan). A gamma filter (530 nm) helped create a contrast between fibers and MC. The method consisted of heating the sample above the transition temperature and cooling it to room temperature, whilst the camera captured different frames of the process.
Rheometer experiments
a Top view of the serrated Couette geometry. The wall on the left side corresponds to the fixed cup, and the one on the right side is the measuring bob geometry. b Method to identify the transition from a viscoelastic liquid to a viscoelastic solid in a cellulose-based system loaded with fibers. The methodology consists of fitting slope 1 before the exponential decay of \(\tan {\delta }\), and slope 2 after it. The transition temperature is therefore estimated from the intersection between slope 1 and slope 2
We evaluated the rheology of methyl cellulose suspensions with different fiber content using the serrated Couette geometry (also called “concentric cylinder" or “cup and bob") depicted in Fig. 1a. The measuring tool for the MCR 302 rheometer (Anton Paar, Austria) was a CC17/P6 bob (Anton Paar, Austria), and the lower geometry was a custom stainless steel cup with a radius = 27.1 mm. The cup teeth in Fig. 1a have a height of 0.50 mm, a width of 1.50 mm, and a spacing of 1.50 mm. For each suspension, we identified its viscoelastic transition temperature (\(T_{v}\)) from a viscoelastic liquid to a viscoelastic solid based on the exponential decay of the loss factor \(\tan {\delta }\). Figure 1b explains the methodology for estimating \(T_{v}\) from an isochronous curve of \(\tan {\delta }\) as a function of temperature. The same method has been previously tested in Miranda-Valdez et al. (2022) and there it was noted that \(T_{v}\) value differs up to 2\(^{\circ }\)C from the gelation temperature of the material defined as the crossover of loss and storage moduli curves.
To identify \(T_{v}\), we performed dynamic thermomechanical analyzes (DMTA). DMTA tests required deforming the samples in the linear viscoelastic region by applying an oscillatory strain (\(\gamma\)) of 1% with an angular frequency (\(\omega\)) of 6.28 rad/s. These parameters were chosen to match the conditions in production processes used in Ref. Reichler et al. (2021) and Ketoja et al. (manuscript in preparation) where the foam is laid on a conveyor belt as rods or flattened to a sheet with a blade. During the experiments, the storage modulus (\(G^{\prime }\)) and the loss modulus (\(G^{\prime \prime }\)) were recorded while a temperature profile was programmed to heat the samples from 25 to 70 \(^{\circ }\)C at 1 \(^{\circ }\)C/min. The heating conditions were matched with foam solidifcation process described in Ref. Reichler et al. (2021). Supplementary Figure S2 verifies that the measurements with the chosen parameters remain in the linear viscoelastic region. The heating control used a Peltier temperature device C-PTD 180/Air (Anton Paar, Austria). From the experimental results, we computed \(\tan {\delta }\) as the ratio of \(G^{\prime \prime }/G^{\prime }\). The loss factor, \(\tan {\delta }\), is a measure of the heat dissipated through the internal frictions in a viscoelastic material (Ghanbari et al. 2020). Additionally, we calculated the magnitude of \(\tan {\delta }\) at \(T_{v}\) to assess the effect of the fibers on the energy dissipation of the systems.
Results and discussion
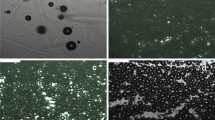
The studied systems transitioned from viscoelastic liquids to viscoelastic solids upon heating and under constant dynamic shear strain. This “viscoelastic transition temperature" (\(T_{v}\)) derives from the lower critical solution temperature (LCST) of MC, resulting from multiple non-covalent interactions between the hydrophobic sites and hydroxyl groups in the polymer (Arvidson et al. 2013; Coughlin et al. 2021; Fairclough et al. 2012). From a microscopic perspective, Fig. 2 presents via polarized microscopy the viscoelastic transition that occurs in an MC-fiber system, where the MC matrix is depicted by the purple field, and the randomly oriented fibers are the slender particles with optical contrast. The polarization images show that, when heating MC above the viscoelastic transition temperature, the polymer forms an isotropic structured matrix similar to the one observed in isotropic nanocellulose gels (Haywood and Davis 2017; Fairclough et al. 2012). Figure 2a shows the material at high temperature (i.e., T > \(T_{v}\)), during which the MC matrix decreases the visible birefringence intensity of the fibers. The former occurs when the connectivity in the MC volume increases and a volume-spanning cluster appears in a process referred to as percolation and the phenomenon might be correlated to the fibril network formation process of MC (Arvidson et al. 2013; Hatakeyama et al. 2007; Kobayashi et al. 1999; Ebini and Sorensen 2019; Coughlin et al. 2021). Figure 2b shows an intermediate behavior between a viscoelastic solid and a viscoelastic liquid, and Fig. 2c shows the material when it behaves as a viscoelastic liquid. In Fig. 2c, as the MC matrix is in the sol state, the light intensity is higher than the observed at higher temperatures. In the gel state, the MC matrix brings aggregates close to each other, which scatters the light, as observed in Fig. 2a, b.
DMTA experiments
Figure 3 displays \(G'\) and \(G''\) curves with respect to the increasing temperature for two different HefCel contents at solid content 3%. The curves both show the general trends during the transition to gel (Supplementary Figures S3 and S4 show similar curves from all the experiments with solid content 3 % and 4 % respectively). Figure S3 also shows loss and storage moduli for suspension only containing HefCel. Due to the sedimentation of fibers, we used a standard CC27 (Anton Paar, Austria) bob-and-cup geometry instead of the serrated geometry to measure these results. The resulting curves show no evidence of crosslinking as the moduli remain independent of the temperature. The rheological curves show a decay in the moduli as the temperature increases before abruptly increasing when the material starts transitioning to a viscoelastic solid. However, in the systems without fiber, we observed that before the moduli increase exponentially, there is an abrupt decay that is typically observed in hydroxypropyl methycellulose Fairclough et al. (2012). We attribute the latter to the presence of a small number of hydroxypropyl moieties in the polymer. It is worth mentioning that the experiments were performed at a single heating rate and angular frequency. There is evidence that the gel transition of MC is dependent on the experimental conditions (Arvidson et al. 2013). Given the results shown in Fig. 3, the addition of fibers to aqueous MC systems affects their viscoelastic properties. \(G^{\prime }\) and \(G^{\prime \prime }\) decrease proportionally to HefCel content. This is not surprising as on such small solid contents HefCel does not form a load bearing fiber network but instead the fibers float on the suspension freely. The phenomenon is better illustrated in the isothermal plots in Fig. 4. However, the drop in \(G^{\prime }\) and \(G^{\prime \prime }\) as a function of HefCel concentration is more notable in the system with a solid content of 4% (see Fig. 4). On higher temperatures, on the other hand, the fibers entangle with the methyl cellulose matrix enhancing the elastic and viscous responses and decreasing the transition temperature. Similar effects on high temperatures were also observed in the study of the gelation of methyl cellulose with CNC fibers (Hynninen et al. 2018).
The loss (solid symbols) and storage (open symbols) moduli of MC-HefCel suspension at (a) 25 \(^\circ\)C and (b) 50 \(^\circ\)C with different HefCel fractions. The images show decreasing trends on both G’ and G” for both solid contents. A small peak in moduli is observed with solid content 3 % when approximately 15 % of the solid consists of HefCel. This point is verified with two separate measurements at 15 % and 16 % HefCel fraction
Figure 4 further reveals a local maximum in both loss and storage moduli at solid content 3 %. Both the panels (a) at 25 \(^\circ\)C and (b) at 50 \(^\circ\)C in Fig. 4 exhibit the maximum at HefCel percentage close to 15 %. To check the reliability of the observation of local maximum in the moduli two measurements were performed close to 15 % HefCel fraction. Suspension loses the property at higher solid content of 4 %, however,there the measurements become noisy possibly due to air bubbles trapped in the suspension due to extremely high viscosity. Few air bubbles were noticed in two of the solid content 4 % experiments (size 2-3 % of the suspension volume). The bubbles collapse to small bubbles during the mixing. The origin of the maximum observed at s.c. 3 % is beyond the scope of the present manuscript. However, knowledge of a local maximum in moduli can be utilized in the production processes making for example MC-fiber based foams.
Viscoelastic transition
Figure 5 shows that, at the time of heating, the suspensions dissipate energy as \(\tan {\delta }\) increases. Three additional curves for s.c. 3 % and the loss factor curves for s.c. 4 % are added in Supplementary Figures S5 and S6. Energy dissipation derives from molecular frictions between polymer chains. Subsequently, \(\tan {\delta }\) decreases significantly in response to the reduced mobility induced by the LCST behavior of MC (Miranda-Valdez et al. 2022). The drop in \(\tan {\delta }\) is inversely proportional to \(G^{\prime }\), which symbolizes a gradual increase in elastic forces in the material and restricted molecular mobility (Arvidson et al. 2013; Coughlin et al. 2021; Li 2002; Schmidt et al. 2018). Furthermore, we observed that the magnitudes of \(G^{\prime }\) and \(\tan {\delta }\) are sensible to fiber and MC content. In particular, Fig. 5 shows how energy dissipation in the \(T_{v}\) region decreases when the fiber content is higher. Such smoothing seen during the curve decay may be correlated with the MC concentration in the suspensions. MC, as the continuous matrix, is the constituent reflecting its viscous nature. Thus, reducing the MC content (i.e., increasing the fiber content) entails lower damping via molecular relaxations.
Regarding the viscoelastic transition of each suspension, the fiber content clearly affects the \(T_{v}\). From the temperatures estimated in Fig. 6, an increase in fiber content tends to lower \(T_{v}\). Korhonen and Budtova (2019) reported a similar trend in other cellulose-based suspensions, for which a higher fiber concentration led to an acceleration of the transition kinetics. In our case, there is evidence of interactions between the MC matrix and the fibers. As we increased the fiber content, the MC concentration in the suspensions decreased proportionally to the fixed solid content. Typically, lowering the concentration of MC means exceeding the reference transition temperature, as molecular mobility is reduced and the polymer requires higher temperatures to percolate in the suspension (Arvidson et al. 2013; Lott et al. 2013, 2013). However, as Fig. 6 shows, adding fibers yields an opposite trend despite the MC content being reduced at the same time.
To describe the phenomenon observed in Fig. 6, we calculated the magnitude of the loss factor at \(T_{v}\). A \(\tan {\delta }\) greater than 1 typically defines a compliant system that dissipates energy via molecular frictions. As the fiber content increases in the cellulose systems, the elastic forces influence more on the rheological behavior of the suspensions, reducing the viscous and compliant nature of the systems. The correlation in Fig. 7 shows that \(\tan {\delta }\) tends to decrease with fiber concentration. This decrease in \(\tan {\delta }\) is strictly related to the fibers, as they represent a large part of the elastic forces in the suspensions. Hence, from Figs. 6 and 7, we infer that increasing the fiber content helps to develop the elastic hydrogel matrix of MC at lower temperatures because there is less free space in the system to be filled by the cellulose derivative network. However, the mechanism of how the former occurs is a topic of further research. Previous research suggests that the presence of cellulose fibers increases the probability of forming physical cross-links in cellulose-based suspensions (Korhonen and Budtova 2019).
Conclusions
We tested the effect of enzymatically fibrillated micro- or nano-cellulose fibers on the thermal sol–gel transition of aqueous methyl cellulose mixture. The focus was on properties relevant to the fabrication process of cellular composite materials based on fibers and methyl cellulose. Using the extrapolation method on the loss factor, we determined the transition temperatures. The temperature for methyl cellulose solution only is around 66 \(^\circ\)C independent of the solid content. The addition of fibers decreases the transition temperature modestly which can be viewed as a positive effect considering the energy consumption of manufacturing solid composite foams. In addition, we observed a local maximum in viscoelastic moduli around fiber fraction of 15% when the fraction of methyl cellulose and fibers was varied. Such maximum may be utilized in e.g. production process of fiber-based foams, and the mechanism causing it also provides an interesting topic for further research.
A further investigation of mechanical properties near transition reveals smoothing of the viscoelastic transition with increasing fiber content. Such smoothing was expected since a similar effect has been reported in the gelation of methyl cellulose solution with added CNC fibers (Hynninen et al. 2018). The dependence of the loss factor on the temperature demonstrates the smoothing since without the fibers change to exponential decrease with viscoelasticity occurs abruptly while with fibers a clear transition interval emerges. As a consequence, the loss factor (i.e., energy dissipation of the systems) measured at the transition temperature decreases with fiber concentration. These indicate a higher ratio of elastic to viscous response. In fabricating polymer foams, the desired morphology prepared on wet state becomes less stable since the material will attempt to restore its original shape. In the processes of References (Reichler et al. 2021) and Ketoja et al. (manuscript in preparation), the aimed structure has elongated bubbles which also lead to oriented fibers. The increased elasticity before the viscoelastic transition then increases the relaxation speed of the bubbles. However, earlier studies have shown that in fiber laden foams the main elastic behavior originates from the liquid–gas interfaces rather than from the continuous medium (Viitanen et al. 2019). As a consequence, added fibers may actually even slow down the relaxation leading to improved preservation of the desired structure through the gelation and drying process.
References
Almeida N, Rakesh L, Zhao J (2018) The effect of kappa carrageenan and salt on thermoreversible gelation of methylcellulose. Polym Bull 75(9):4227–4243
Andrieux S, Quell A, Stubenrauch C et al (2018) Liquid foam templating-a route to tailor-made polymer foams. Adv Colloid Interface Sci 256:276–290
Arvidson SA, Lott JR, Mcallister JW et al (2013) Interplay of phase separation and thermoreversible gelation in aqueous methylcellulose solutions. Macromolecules 46(1):300–309. https://doi.org/10.1021/ma3019359
Cabernard L, Pfister S, Oberschelp C et al (2022) Growing environmental footprint of plastics driven by coal combustion. Nat Sustain 5(2):139–148
Coughlin ML, Liberman L, Ertem SP et al (2021) Methyl cellulose solutions and gels: fibril formation and gelation properties. Prog Polym Sci 112(101):324. https://doi.org/10.1016/j.progpolymsci.2020.101324
Desbrieres J, Hirrien M, Ross-Murphy S (2000) Thermogelation of methylcellulose: rheological considerations. Polymer 41(7):2451–2461
Ebini RH, Sorensen CM (2019) Light scattering studies of the sol-to-gel transition in particulate systems. J Colloid Interface Sci 556:577–583. https://doi.org/10.1016/j.jcis.2019.08.075
Ee LY, Li SFY (2021) Recent advances in 3d printing of nanocellulose: structure, preparation, and application prospects. Nanoscale Adv 3(5):1167–1208
Fairclough JPA, Yu H, Kelly O et al (2012) Interplay between gelation and phase separation in aqueous solutions of methylcellulose and hydroxypropylmethylcellulose. Langmuir 28(28):10551–10557. https://doi.org/10.1021/la300971r
Ghanbari A, Mousavi Z, Heuzey M et al (2020) Experimental methods in chemical engineering: Rheometry. Can J Chem Eng 98(7):1456–1470. https://doi.org/10.1002/cjce.23749
Guo W, Wang X, Zhang P et al (2018) Nano-fibrillated cellulose-hydroxyapatite based composite foams with excellent fire resistance. Carbohydr Polym 195:71–78
Hatakeyama H, Onishi T, Endo T et al (2007) Gelation of chemically cross-linked methylcellulose studied by DSC and AFM. Carbohydr Polym 69(4):792–798. https://doi.org/10.1016/j.carbpol.2007.02.022
Haywood AD, Davis VA (2017) Effects of liquid crystalline and shear alignment on the optical properties of cellulose nanocrystal films. Cellulose 24(2):705–716. https://doi.org/10.1007/s10570-016-1150-4
Hiltunen J, Kemppainen K, Pere J (2013) Process for producing fibrillated cellulose material
Hjelt T, Ketoja JA, Kiiskinen H et al (2020) Foam forming of fiber products: a review. J Dispers Sci Technol 43(10):1462–1497
Hu Z, Xu R, Cranston ED et al (2016) Stable aqueous foams from cellulose nanocrystals and methyl cellulose. Biomacromol 17(12):4095–4099
Hynninen V, Hietala S, McKee JR et al (2018) Inverse thermoreversible mechanical stiffening and birefringence in a methylcellulose/cellulose nanocrystal hydrogel. Biomacromol 19(7):2795–2804. https://doi.org/10.1021/acs.biomac.8b00392
Jaiswal AK, Kumar V, Khakalo A et al (2021) Rheological behavior of high consistency enzymatically fibrillated cellulose suspensions. Cellulose 28(4):2087–2104. https://doi.org/10.1007/s10570-021-03688-y
JECFA (2006) Monograph 1. combined compendium of food additive specifications
Khemani KC (1997) Polymeric foams: an overview. In: Khemani KC (ed) Polymeric foams Science and Technology. ACS Publications, Washington, DC
Klemm D, Heublein B, Fink HP et al (2005) Cellulose: fascinating biopolymer and sustainable raw material. Angew Chem Int Ed Engl 44(22):3358–3393
Kobayashi K, Ci H, Lodge TP (1999) Thermoreversible gelation of aqueous methylcellulose solutions. Macromolecules 32(21):7070–7077
Kontturi E, Laaksonen P, Linder MB et al (2018) Advanced materials through assembly of nanocelluloses. Adv Mater 30(24):1703779
Korhonen O, Budtova T (2019) Gelation of cellulose-NAOH solutions in the presence of cellulose fibers. Carbohydr Polym 224(115):152. https://doi.org/10.1016/j.carbpol.2019.115152
Lavoine N, Bergström L (2017) Nanocellulose-based foams and aerogels: processing, properties, and applications. J Mater Chem A 5(31):16105–16117
Lehmonen J, Pere J, Hytönen E et al (2017) Effect of cellulose microfibril (CMF) addition on strength properties of middle ply of board. Cellulose 24(2):1041–1055
Li L (2002) Thermal gelation of methylcellulose in water: scaling and thermoreversibility. Macromolecules 35(15):5990–5998. https://doi.org/10.1021/ma0201781
Lott JR, Mcallister JW, Arvidson SA et al (2013) Fibrillar structure of methylcellulose hydrogels. Biomacromol 14(8):2484–2488. https://doi.org/10.1021/bm400694r
Lott JR, Mcallister JW, Wasbrough M et al (2013) Fibrillar structure in aqueous methylcellulose solutions and gels. Macromolecules 46(24):9760–9771. https://doi.org/10.1021/ma4021642
Miranda-Valdez IY, Viitanen L, Mac Intyre J et al (2022) Predicting effect of fibers on thermal gelation of methylcellulose using bayesian optimization. Carbohydr Polym 298:119921
Miranda-Valdez IY, Coffeng S, Zhou Y et al (2023) Foam-formed biocomposites based on cellulose products and lignin. Cellulose. https://doi.org/10.1007/s10570-022-05041-3
Pere J, Tammelin T, Niemi P et al (2020) Production of high solid nanocellulose by enzyme-aided fibrillation coupled with mild mechanical treatment. ACS Sustain Chem Eng 8(51):18853–18863. https://doi.org/10.1021/acssuschemeng.0c05202
Reichler M, Rabensteiner S, Törnblom L et al (2021) Scalable method for bio-based solid foams that mimic wood. Sci Rep 11(1):1–11
Rochman CM, Browne MA, Halpern BS et al (2013) Classify plastic waste as hazardous. Nature 494(7436):169–171
Schmidt PW, Morozova S, Owens PM et al (2018) Molecular weight dependence of methylcellulose fibrillar networks. Macromolecules 51(19):7767–7775. https://doi.org/10.1021/acs.macromol.8b01292
Studart AR, Gonzenbach UT, Akartuna I et al (2007) Materials from foams and emulsions stabilized by colloidal particles. J Mater Chem 17(31):3283–3289
Viitanen L, Halonen A, Friström E et al (2019) Constriction flow of cellulose laden air-aqueous foam. BioResources 14(3):5716–5728
Voisin HP, Gordeyeva K, Siqueira G et al (2018) 3d printing of strong lightweight cellular structures using polysaccharide-based composite foams. ACS Sustain Chem Eng 6(12):17160–17167
Acknowledgments
We acknowledge Jukka Ketoja, Elina Pääkkönen and Tuomo Hjelt from VTT for providing the fibers and useful discussions during the research project.
Funding
Open Access funding provided by Aalto University. J. K. acknowledges funding from Academy of Finland (308235). M. J. A., A. P. and J. K. acknowledge support from FinnCERES flagship (151830423), Business Finland (211835) and Future Makers (Älyä Vaahtoihin) programs.
Author information
Authors and Affiliations
Contributions
LV, JK, AP and MA planned the work. IYM performed the microscopy experiments. LV performed the rheology experiments. LV and IYM. did the data analysis. LV and IYM wrote the main manuscript text. JK, AP and MA supervised the work. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Viitanen, L., Miranda-Valdez, I.Y., Koivisto, J. et al. Thermal gelation of cellulose based suspensions. Cellulose 30, 4215–4223 (2023). https://doi.org/10.1007/s10570-023-05150-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10570-023-05150-7