Introduction

Ionic liquids (ILs) are organic salts composed mainly of anions and cations with melting temperatures below 100 °C. They are characterized by unique properties, including non-volatility, non-inflammability, wide electrochemical windows, high thermal stability, and good electrical conductivity (Wagner et al. 2020). The properties of ILs can be tuned by selecting the appropriate combination of cation and anion, which gives excellent possibilities for synthesizing many ionic liquids and allows their various applications (Kaur et al. 2022; Ornaghi et al. 2022; Pei et al. 2022; Mecerreyes 2015). About two decades ago, ionic liquids (ILs) have been noted as powerful solvents for polysaccharides since (Swatloski et al. 2002) reported the dissolution of cellulose with IL, 1-butyl-3-methylimidazolium chloride (BMIMCl), in relatively high concentrations. Further research revealed the mechanism of cellulose dissolution by ionic liquids (Feng and Chen 2008; Wei et al. 2018; Li et al. 2018). This involves breaking some of the hydrogen bonds of the hydroxyl (–OH) groups in the cellulose structure. It happens mainly by the anions which strongly bind to the most external hydroxyl groups in cellulose chains and form negatively charged complexes. This weakens the intermolecular hydrogen bonds between the cellulose chains, reducing their stiffness. The role of cations is not completely clear, but it is assumed that they are interspersed between the cellulose chains because of the charge imbalances. This causes the separation between cellulose chains and disrupts its layered structure leading to the dissolution of cellulose (Takada and Kadokawa 2015; Uto et al. 2018). The distribution of the molar mass of cellulose decreases with increasing dissolution time. During dissolution time, the broadness of the minimum phase on the vGP plot (van Gurp-Palmen) also indicates an increase in cellulose polydispersity (Ahn et al. 2016).

Ionic liquids are still considered an alternative green solvent in chemical processes, but the ability to design their properties allows them to be used to obtain also advanced energy materials, artificial intelligence materials, smart sensors, advanced materials for batteries and electrolytes, biomedicine, and drug delivery (Kaur et al. 2022; Ornaghi et al. 2022; Pei et al. 2022). In applications where ILs are used as device components (for example, in an electronic area), they must be immobilized into a solid matrix as they are fluid by definition. Hence the great interest in ionogels. Gels can simply be defined as materials composed of a liquid phase dispersed in a solid phase. When IL forms the liquid phase, the gel material is named ionogel (Hopson et al. 2021) but also ionic liquid gel (Marr and Marr 2016) or ion gel (Kaszynska et al. 2017; Zhu et al. 2019). We can classify the ionogels according to different criteria. Considering the gelation mechanism, physical and chemical ionogels can be distinguished. In physical ionogels, the formation of the 3D internal network is formed by non-covalent, weak, reversible interactions (hydrogen bonds, van der Waals, hydrophobic) (Winter 2001; Le Bideau et al. 2011). Covalent bonds form the matrix in chemical ionogels (Marr and Marr 2016). According to the nature of the solid matrix, the ionogels can be classified as synthetic polymer ionogels and biopolymers-based ionogels (Takada and Kadokawa 2015; Liu et al. 2020). The advantage of ionogels based on biopolymers over those based on synthetic polymers results from the properties of biopolymers, such as biodegradability, biocompatibility, renewability, and low cost. Biopolymers can be an alternative to petroleum-based polymers. Their increasing use may slow down the destruction of our planet. Among the biopolymers, cellulose is the most attractive because it's the world's most abundant naturally occurring polymer. Besides the properties of all other biopolymers, cellulose is characterized by high specific strength and modulus and has a great possibility of surface modifications (Pascual and Eugenio Martin 2019).

Cellulose ionogels, known since 2008, combine the properties of cellulose acting as a matrix and an ionic liquid (Hopson et al. 2021; Takada and Kadokawa 2015; Kaszynska et al. 2017; Zhu et al. 2019). In addition, various types of cellulose (micro and non-crystalline, micro and non-fibrous, bacterial and cellulose derivatives such as methylcellulose) offer the possibility of creating ionogels for multiple applications. Cellulose ionogels are considered the most promising solid electrolytes of the future (Zhu et al. 2019) due to their high conductivity (10−2 S/m to about 8 S/m) and wide electrochemical potential window (Song et al. 2013; Zhang et al. 2017). For example, methyl cellulose-based ionogel exhibited thermal stability up to 200 °C and ionic conductivity order of 10–2 S/m at room temperature (Chereddy et al. 2020). The advances in the field of cellulose-based gel and solid electrolytes for lithium-ion and sodium-ion batteries have been discussed by Zhang (Zhang et al. 2022, 2018). Cellulose ionogels are also used in medicine and pharmacology (Mallik et al. 2019; Villar-Chavero et al. 2020).

The gelation process for physical cellulose ionogels is still not well recognized. It strongly depends on the type of cellulose, its concentration, and the ionic liquid (Swatloski et al. 2002; Kadokawa et al. 2008; Le Bideau et al. 2011; Marr and Marr 2016; Smith et al. 2017; Chereddy et al. 2020). The effects of cellulose nanocrystals (CNC) and microcrystalline cellulose (CMC) on the dissolution and gel or films properties and microstructure is well recognized in the literature (Jin et al. 2022; Popescu et al. 2020; Monshizadeh 2015; Qi et al. 2008). Cellulose ionogels are physical gels thus, the gelification process is reversible and occurs through non-covalent interactions. It seems that water absorbed from the environment during the gelation process plays a crucial role in the gelification of ILs. Since cellulose is insoluble in water, it forms aggregates that can act as cross-linking points to form a gel. These aggregates cause the entanglement of cellulose chains, which leads to breaking some ionic liquid-cellulose bonds (initial cellulose dissolution process), restoring cellulose-cellulose hydrogen bonds, and initiating the gelling process (Kadokawa et al. 2008; Kaszynska et al. 2017; Lee et al. 2017; Zhao et al. 2020).

The properties of the ionogel are closely related to the properties of the IL used for its synthesis. Generally, for electrochemical applications, ionic liquids based on imidazolium cation such as [BMIM]+ and [EMIM]+ are most suited due to their high electrical conductivity and ability to dissolve cellulose, and gel formation (Swatloski et al. 2002; Uto et al. 2018).

In our laboratory, we focus on the study of solid ion conductors, which is why we chose an ionic liquid, BMIMCl, composed of the 1-butyl-3-methylimidazolium cation—[BMIM]+ with chloride anion [Cl]− as a small hydrogen bond acceptor for the synthesis of ionogel with cellulose (Kadokawa et al. 2008). Different types of cellulose can be used to form ionogel with ionic liquid. We are searching for ionogel materials for the electrochemical application. This is associated with the high conductivity of IL. Ionogel should retain the main properties of the ionic liquid (apart from its outflow). However, immobilization of IL in the matrix usually decreases the translational motions of ions directly responsible for ionic conductivity. Fast translational diffusion of ions implies fast conductivity and vice-versa. Nuclear Magnetic Resonance (NMR) is an effective technique for studying ions' rotational and translational diffusion. Since NMR is sensitive to the studied nuclei, it is possible to measure the diffusion separately for cations and anions. For example, IL is composed of 1H-containing cations and 19F-containing ions. The translational diffusion can be measured by the NMR gradient method (NMR diffusometry) (Price 2008) but also (under some conditions) by Fast Field Cycling NMR relaxometry (Kimmich and Anoardo 2004). Both methods allowed us to determine the translational diffusion coefficient that describes the self-diffusion of the ions.

This article presents the research results on the influence of microcrystalline (CMC) and nanocrystalline (CNC) cellulose matrices on the dynamics of 1-butyl-3-methylimidazole chloride ionic liquid and its electrical conductivity in ionogels formed by these types of cellulose and BMIMCl. The article's ionogels are CNC/BMIMCl and CMC/BMIMCl, respectively. The formation of ionogels was described and confirmed by 1H MAS NMR spectroscopy. The 2D heteronuclear correlation spectroscopy (1H − 13C CPMAS HETCOR) experiment was performed to disclose what type of hydrogen bonds dominate the interactions between cellulose and ionic liquid. The translational diffusion of cations was measured by Fast Field Cycling NMR relaxometry method. The analysis of the relaxometry data allows the determination of the translation self-diffusion coefficient of cations. The electric conductivity of BMIMCl ionogels was measured by the thermal scanning conductometry method (Bielejewski 2015). All measurements were performed for 10 wt.% CNC/BMIMCl and 10 wt.% CMC/BMIMCl ionogels and bulk BMIMCl, for comparison.

Experimental

Materials and ionogel preparation

The ionic liquid 1-butyl-3-methylimidazolium chloride (BMIMCl) of high purity (CAS No. 79917-90-1, ≥ 98% (HPLC)) was purchased from Sigma-Aldrich and used without further purification. The nanocrystalline cellulose CNC (with diameter: 10–20 nm and length of cellulose chains: 300–900 nm) and microcrystalline cellulose CMC (CAS No. 9004-34-6), type 50 (with a length of cellulose chains: 50 μm) were purchased from PowderNano and Warchem, respectively. The cellulose materials were used without any modification. The ionogels were obtained by dissolving a proper amount of CNC and CMC in BMIMCl to prepare a 10 wt.% mixture that was then heated at 90 °C for 120 h. The solutions were cooled to room temperature and left for 7 days to form stable and color-stable ionogels over time. To convert the gels again to their liquid form, it needs only to be heated at 90 °C to start a flow; afterward, they can be again transferred to the gels form upon cooling. The melting temperature of neat BMIMCl is equal to 65 °C. After the ionogel preparation procedure involving heating and cooling, the final water content in the samples was estimated to be at the level of 5% based on the total weight of the sample and individual components used to prepare the sample.

Methods

1 H and 13 C NMR solid-state spectroscopy

The NMR 1H and 13C spectra were recorded on a Bruker Avance III HD spectrometer coupled to 11.7 T wide bore superconducting magnet operating at 500 MHz 1H Larmor frequency and 125.76 MHz 13C Larmor frequency. All spectra were recorded at 298 K stabilized temperature using the magic-angle spinning technique for high-resolution NMR spectroscopy in solid-state using 4 mm rotors. To check whether the experimental conditions do not disturb the internal structure of investigated samples (the measurements were performed in the gel phase for CMC and CNC samples and very viscous liquid state for pure ionic liquid sample), the stress tests were performed to determine the spinning frequency that will not affect the internal structure of samples. The safe spinning frequency was set to 2 kHz for all samples and nuclei. With a higher spin frequency, the spectrum changed over time, indicating changes in the sample's internal structure. A direct polarization pulse sequence was used to measure the 1H spectra with an excitation pulse length of 3 μs, the recycling delay was 3 s, and the number of scans was 512.

The 13C spectra were recorded with a 1H-13C cross-polarization sequence with two contact times, a long one (3 ms) and a shorter one (0.75 ms), to exclude any coupling to remote protons. The extended contact time causes no significant change in the spectra except for better signal-to-noise (S/N) ratio. Proton decoupling was obtained by using TPPM at an 83 kHz radiofrequency field. At the same time, the recycle time was set to 3 s, and 4096 scans were added, leading to almost 4 h of data accumulation per spectrum.

The 2D 1H-13C heteronuclear correlation (HETCOR) measurements were performed with the use of the frequency-switched Lee-Goldburg decoupling (FSLG) sequence (Bielecki et al. 1989) and MAS spinning rate of 2 kHz. The FSLG pulse sequence with a transverse 1H field strength of 83 kHz was used for homonuclear 1H decoupling (Taylor 2004). The total number of scans was equal to 16384 what allowed to obtain well resolved correlation spectra with high S/N ratio. The spectra were referenced to adamantine (1.76 ppm, 1H, and 37.85 ppm, 13C).

FFC spin–lattice relaxation

The spin–lattice relaxation times T1 (R1 = 1/T1) of bulk ionic liquid BMIMCl and confined in the matrix of 10 wt.% of CNC and CMC were measured using a Stelar FFC NMR relaxometer covering 1H Larmor frequencies from 10 to 40 MHz in the temperature range of 298–368 K.

Electrical conductivity measurements

The ionic conductivity σ was measured by thermal scanning conductometry (TSC) in the temperature range 299–362 K, using a self-assembled conductometer consisting of a Mettler Toledo S230 unit equipped with an InLab 710 conductivity sensor (Bielejewski et al. 2015).

Results and discussions

NMR spectra

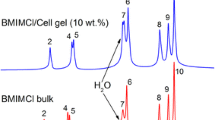
The 1H NMR spectra recorded with the MAS technique for studied samples provide information on the structural features of the self-assembled ionic liquid-containing systems based on the chemical shift effect experienced by a particular nucleus. The three main factors that affect the shielding of the nucleus are electronegativity, the magnetic anisotropy of systems, and hydrogen bonding. Due to the investigated materials' specific composition, all three can influence recorded spectra. Figure 1 shows the 1H spectra recorded at room temperature for a pure ionic liquid sample and CNC/BMIMCl and CMC/BMIMCl ionogels with the chemical shift for given functional groups as inserts.

Fig. 1
figure 1

1H MAS NMR spectra of pure ionic liquid (black line), CNC/BMIMCl (red line), and CMC/BMIMCl (blue line), ionogels at room temperature with the chemical shift for given functional groups

Full size image

The high molecular dynamics of investigated samples, even in the gel state, allowed us to obtain very well-resolved proton spectra, which allowed us to assign the peaks to particular functional groups in the structure of the IL. The analysis of the chemical shifts at a specific nucleus showed changes in the shielding of protons, based on which we can conclude how the [BMIM]+ cation is involved in interactions affecting the electric charge distributions in the molecule. A distinct difference can be seen between ionogel samples and pure IL. In the spectral range from 11 to 8 ppm, the signals come from the protons in the imidazole ring. In the range from 5.5 to 4 ppm, we can observe the protons attached to the carbons chemically bonded next to the aromatic ring and a signal from residual water molecules. In the range from 2.5 to 0.5 ppm, the signals from the protons in the alkane chain are observed. The spectra from both ionogel samples have minor changes in the chemical shift range from 5.5 to 4 ppm and 2.5 to 0.5 ppm. In the range from 11 to 8 ppm, the spectra look identically for both ionogels. However, they differ substantially from the spectra of pure IL. The main change in the chemical shift range from 5.5 to 4 ppm is observed for the peak of residual water content.

Analyzing the character of the observed chemical shifts indicates the deshielding effect of protons in the alkane chain. Considering the main possible mechanisms of the shielding/deshielding effect for protons, we can presume that the methyl group at the end of the alkane chain is involved in interaction which change the distribution of the electric charge on the molecule. Such change can be cause by additional intermolecular interactions. Considering the composition of investigated system this interaction can be caused by creation of hydrogen bond between methyl group and hydroxyl groups in cellulose matrix. Due to inductive effect this interaction is also felt by protons further down the chain. This assumption will be discussed later during an analysis of the 2D HETCOR experiment. The two peaks from protons bonded to carbons next to the aromatic ring show no change in the position, irrespective of whether they are in the gel phase or not, and are insensitive to the presence of the cellulose matrix. However, the residual peak of water shows an upfield shift of its resonance frequency, meaning that the water molecules present in the system from the natural moisture of BMIMCl become more shielded. To explain this effect, it is worth considering how water molecules can interact with BMIMCl. In the paper by Jonathan M. Voss et al. (Voss et al. 2016) from theoretical and experimental FT-IR studies, it has been shown that water molecules (of enough content) form clusters of water ring isomers that preferentially interact with the delocalized electric charge by situating on the top of the imidazolium ring. This is what we expect for the neat IL sample. Moreover, this indicates that any change in the interaction between water molecules and [BMIM]+ cation should be reflected by the peaks from the imidazole ring protons, as the interaction will modify the magnetic anisotropy of the π electrons. The signal from imidazole ring protons (Fig. 1. the range from 11 to 8 ppm) can be seen for neat ionic liquid and both ionogels. A strong shielding effect is observed upon transforming neat IL to the gel phase. The change of the chemical shift towards lower fields indicates that the π electrons more efficiently screen the protons. Thus, any disturbing interactions are reduced. Therefore, it can be concluded that the interaction of the water clusters with the imidazole ring of the [BMIM]+ cation is reduced upon gelation of the IL. Does the question arise, what is the reason for such change? To answer this, we need information on what happens to the second component of the studied ionogels, meaning the cellulosic material. Unfortunately, the 1H did not allow the record of the signals from cellulose at 10 wt.% due to the small signal and overlapping with the signals from IL in the range from 5.5 to 4 ppm. To get a signal from the cellulosic matrix, the 13C spectra of investigated systems have been measured and are presented in Fig. 2.

Fig. 2
figure 2

The 1H-13C CP MAS spectra for bulk BMIMCl, CNC, and CMC recorded at a spinning frequency of 2 kHz, and additionally a static spectrum for neat IL

Full size image

The reason for recording a static 13C spectrum for a neat IL sample is a too strong reduction of the dipole–dipole coupling upon spinning the sample already at 2 kHz, which results in a very weak S/N ratio for the recorded spectrum. Moreover, the drastic drop of the S/N ratio upon spinning in the case of neat IL, which is not observed for ionogels, indicates how strongly the gelation influenced the molecular dynamics of the IL molecules. The 13C spectra of ionogels gave evidence for the presence of the ionic liquid and the cellulose. The analysis of the chemical shift of the 13C nucleus leads to the conclusion that no shift of the peaks has been observed for all studied samples. This can be understood as the interactions causing changes in the chemical shifts of protons are of weak strength and influence much smaller than the chemical shift of carbons. Therefore, to explain what happens in the studied systems upon gelation, the 2D heteronuclear 1H-13C correlation spectra were measured. Figure 3a and b show 1H-13C HETCOR spectra for CMC/BMIMCl. and CNC/BMIMCl.

Fig. 3
figure 3

1H-13C HETCOR spectra for (a) CMC/BMIMCl (b) CNC/BMIMCl ionogels

Full size image

From the HETCOR experiment, the dipolar interaction between protons and carbons can be seen as cross-peaks, allowing us to assign a given interaction between which parts of the molecule occur. On the main diagonal, we can see the cross-peaks from the protons directly bonded to carbons in the ionic liquid molecule. Moreover, a correlation between the most intense signals from protons and carbons of cellulose is observed. For CMC/BMIMCl, no other cross-peaks were observed. Still, for the CNC/BMIMCl, an additional cross-peak appeared in the upper section of Fig. 3b which correspond to the interaction between the methyl group of the [BMIM]+ cation located in the alkyl chain and the carbons from the glucose ring in the cellulose molecule. This additional peak is probably due to the hydrogen bond created between the cation and the OH groups in the glucose ring. The absence of a corresponding signal in the CMC/BMIMCl sample, considering the results from 1H spectra, indicates only that the number of related hydrogen bonds in this system is much smaller than in CNC/BMIMCl, thus making this signal impossible to be detected in 2D HETCOR experiment. This assumption is confirmed by the 1H spectrum, where an additional deshielding effect was observed, which can be explained by creating a hydrogen bond between [BMIM]+ cation and cellulose matrix. Moreover, the broadening of the cross-peak of the cellulose (on the protons chemical shift scale) can be explained by additional H-bonding of the water molecules to the cellulose, which correlates well with the shielding effect observed in the 1H spectra for the imidazole and water protons. Based on the obtained data, it can be concluded that the residual water molecules present in neat ionic liquid upon gelation with cellulosic material have created hydrogen bonds with the glucose ring of the cellulose molecules and thus reduce its interactions with the imidazole ring of the [BMIM]+ cation.

Cation dynamics

The FFC experiment can be performed in a broad range of magnetic fields, corresponding to the range of about 10 to 40 MHz (referring to 1H resonance frequency). This allows probing, in one single experiment, the molecular motions on the time scale from ms to ns. The conventional NMR relaxation experiment performed at a single, high magnetic field (resonance frequency) gives access to faster dynamics, rotational motion, and sometimes fast, short-range translational diffusion. However, the fast motions do not lead to high conductivity because of their local character. The slow, long-range translational diffusion is responsible for the conductivity, and this type of diffusion can be probed by the FFC method. In this method, the information about the dynamics is encoded in the parameter known as relaxation time, mostly the spin–lattice relaxation time, T1 (R1 = 1/T1 is called spin–lattice relaxation rate). The T1 in FFC is measured as a function of the magnetic field strength, but the data are usually presented in a plot as R1 vs. resonance frequency. This plot is named the relaxation dispersion profile and reflects the shape of the spectral density functions, which are Fourier transforms of the corresponding time correlation functions, characterizing the molecular (ion) motions modulating the spin interactions that cause the relaxation process. These interactions, for 1H nuclei, are dominated by intra-molecular (intra-ionic) and inter-molecular (inter-ionic) dipole–dipole interactions. The intra-molecular interactions fluctuate in time due to the rotational dynamics within the molecule (ions) containing the studied species. In contrast, the inter-molecular ones are modulated by translation diffusion of the whole molecules (ions). The relaxation rate is determined by the strengths of the dipole–dipole interactions, the time scale of the motion, and its mechanism. From the spin relaxation theory (Abragam 1961; Kowalewski and Maler 2006), it is known that the molecular (ionic) motion occurring on a time scale being of the order of the reciprocal resonance frequency is most efficient as the source of the relaxation process. This means that at a low magnetic field (low resonance frequency), one probes slow dynamics, while faster dynamics processes come into play at the increasing resonance frequency. That is why the FFC experiment is as important as it allows you to simultaneously study translational and rotational dynamics.

Figure 4 presents the 1H relaxation dispersion profiles for pure BMIMCl, CNC/BMIMCl, and CMC/BMIMCl ionogels as a function of temperature. Each of the NMRD profiles was measured three times independently, and the presented data are the mean average values with less than 4% uncertainty at the lowest magnetic fields. The error was calculated as standard deviation and fell in the size of the data points on the figures.

Fig. 4
figure 4

The 1H relaxation dispersion profiles for CNC/BMIMCl and CMC/BMIMCl ionogels and pure BMIMCl, for comparison

Full size image

The profiles show general trends, a decrease in R1 with increasing temperature. This is a consequence of the change of the IL viscosity, which in bulk changes from 10.6 Pas at 298 K to 0.1 Pas at 368 K. A higher viscosity value results in slower cation dynamics, stronger dipole–dipole interactions and consequently leads to a shorter T1 (or longer R1). Observed slight differences in R1 values between IL and ionogels for a given temperature and resonance frequency, indicating an increase in viscosity after adding CNC or CMC to IL. The dispersion profiles in Fig. 4 are a linear combination of inter—and intra- molecular contributions, as presented in our paper (Kaszynska et al. 2017). The contribution to the total spin–lattice relaxation predominantly due to the rotational motion of cations is well pronounced at 298 K as a decrease of R1. Increasing the temperature shifts this contribution toward a higher frequency (above 1 MHz). The intermolecular (translational) contribution to the relaxation dominates in the low-frequency range when almost linear dependence on the frequency is seen in Fig. 4. For this work, the dispersion data presented in Fig. 4 were used to calculate the self-diffusion coefficients of ionic liquid cations using the method described in the literature (Kruk et al. 2012; Kaszynska et al. 2017).

It is known from relaxation theory that translational spectral densities show universal behavior at low frequencies: the linearity of the square root with frequency. At low frequencies, the translational contribution ∝\(\sqrt \omega\) is dominant to R1 and can be described by Eq. 1:

$$R_{1} (\omega ) = R_{1} (0) - 0.31N_{H} \left( {\frac{{\mu_{0} }}{4\pi }\gamma_{H} \hbar } \right)^{2} \left( {\frac{\pi }{D}} \right)^{3/2} \sqrt \omega$$
(1)

Here R1 (0) is a constant at low frequencies representing the relaxation contribution from rotational dynamics (intramolecular contribution). NH is the proton density, μo is the permeability of free space, γH is the gyromagnetic ratio of 1H, and D is the self-diffusion coefficient.

The dispersion data in Fig. 4 has been redrawn in the representation of R1 vs \(\sqrt \omega\) as shown in Fig. 5 for the selected temperatures. The low-field (frequency) region where Eq. 1 can be applied is taken as the region where R1 vs \(\sqrt \omega\) could be represented with a linear fit. With increasing temperature, the linear region is expanded to a higher frequency. The solid lines in Fig. 5 present the best fit of Eq. 1 to the experimental data.

Fig. 5
figure 5

1H spin–lattice relaxation rate for [BMIM]+ cations versus the square root of the resonance frequency. The solid lines are the linear fit to Eq. 1

Full size image

The fitting procedure to the data in Fig. 5 allows the determination of the self-diffusion coefficients of the IL cation in the bulk and ionogels. The obtained self-diffusion coefficients D are presented in Table 1 and Fig. 6, plotted as a function of inverse temperature. The observed linear dependencies of the diffusion coefficients are well described by the Arrhenius law:

$$D = D_{0 } exp\left( { - E_{a}^{diff} /RT} \right)$$
(2)

where Eadiff is the activation energy for diffusion, R is the gas constant, and D0 denotes the pre-exponential factor. The values of D and the activation energies of translational diffusion for the [BMIM]+ cations in cellulose ionogels slightly differ from the values for the cations in the pure ionic liquid. This is a result of cation dynamics constraints by the cellulose matrix. Moreover, the cations experience these limitations to a greater extent in the matrix formed by the CMC.

Table 1 Self-diffusion coefficients D obtained from fitting Eq. 1 to experimental points in Fig. 5 and activation energies for diffusion Eadiff in studied systems obtained from fitting Eq. 2 to data in Fig. 6
Full size table
Fig. 6
figure 6

The translational diffusion coefficients and activation energies of [BMIM]+ cations in CNC/BMIMCl, CMC/BMIMCl ionogels, and bulk IL

Full size image

Figure 7 shows the activation energies calculated from FFC data (Fig. 4) as a function of frequency. Values decreased with increasing field (frequency), but those in the low field range reasonable matches the values of activation energies obtained from temperature dependencies of self-diffusion coefficients of the IL cation in the bulk and ionogels (Fig. 6). This support the assignment of intermolecular motions (translational diffusions) to the low field region.

Fig. 7
figure 7

1H spin–lattice relaxation energies presented as a function of resonance frequency calculated from FFC NMR (data in Fig. 4)

Full size image

Most likely, the activation energies calculated in the higher frequency ranges of the FFCs are associated with fast, reorienting cation motions, which are characterized by lower energy than translational motion.

Ionogels conductivity

The ionic liquid 1-butyl-3-methylimidazolium chloride (BMIMCl) was used in the tests. The [BMIM]+ is a positive electric charge cation, and the electrically negative anion is chlorine [Cl]−. Optimizing the molecular structure of BMIMCl by the DFT method (with BVP86/TZVP/ DGA1 model and Gaussian09 calculations) revealed many conformations of cation–anion pair with a narrow energy range. Depending on the localization of the chlorine anion to the cation, these energies vary from hundredths part to several dozen kJ/mol (del Olmo et al. 2014). These energies constitute the total energy of the BMIMCl macromolecule of the most probable conformation. Electric conductivity is the phenomenon of directed transfer of electric charges through positive or negative carriers (electrons, ions) occurring in a material medium under the influence of an applied external electric field and depends on the concentration of current carriers and their mobility according to the formula σ = qnμ, were q, n and μ are the charges, concentration, and mobility of the current carriers, respectively. The main factor influencing the conductivity of all bodies is temperature, which changes the system's dynamics. The varying temperature may change the concentration and mobility of electric charge carriers. The least energetically demanding process of increasing conductivity at temperature is ion dissociation (connected with EaVFT activation energy), then mobility associated with increasing cations and anions diffusion (connected with Eadiff activation energy).

The temperature-dependent ion mobilities (like conductivities) are described by fitting conductivity experimental data to the Vogel−Fulcher−Tamman Equation (Fulcher 1925):

$$\sigma \left( T \right) = \sigma_{0} {\text{exp}}\left[ { - \frac{B}{{\left( {T - T_{0} } \right)}}} \right]$$
(3)

As a result, we obtain physical parameters (B, T0, and σ0), all dependent on the contents of the sample. The B parameter has a temperature unit and relates to the activation energy of the charge carrier’s motion and can be replaced by DAT0, where DA is Angell’s strength parameter. The stronger liquid has a larger DA (Angell 1991, 1995). This parameter is inversely related to the fragility of polymer dynamics (Rhoades et al. 2016). Angell's parameter characterizes the class of materials. The lower value of DA indicates less temperature resistance. The parameter generally describes material classes and is similar for similar systems. The higher value of DA (> 30) is characteristic of less fragile or Arrhenius-like behavior samples, the lower (< 30) is typical of fragile systems and soft matter, and σ0 is the intrinsic conductivity at a very high temperature (Lin and Colby 2015). The so-called “Vogel temperature”, T0, defines the low-temperature limit of the conductivity curves and is the temperature where ion mobility approaches zero and polymer relaxation time extrapolates to infinity (Ye and Elabd 2011; Dudowicz et al. 2015). Although the relationship between T0 and Tg (glass transition temperature) has been repeatedly confirmed as T0 = Tg—50 K, it is very often invalid due to the “decoupling” of polymer chain motion (Mudraboyina et al. 2014). The σ0 is the highest conductivity at infinite temperature. The pseudo-activation energy for ionic conductivity, EaVFT, can be calculated from B = EaVFT/kB, where kB is the Boltzmann constant, equal to 1,380,649 × 10−23 J/K (Pei et al. 2022). The pseudo-activation EaVFT energies vary from a few to several kJ/mol for this family of ionic liquids (Bandrés et al. 2010; Arkhipova et al. 2019). The diffusion activation energies of Eadiff are typically ten times higher than EaVFT (Liu et al. 2012; Pilar et al. 2017; D’Agostino et al. 2018). The correlation between ion diffusion and ionic conductivity is described by the Nernst-Einstein relation σ = [ne2/kT]/[D+ + D-], where n is the number of ions per specific volume and e is the electron charge, k is the Boltzmann's constant, T is temperature and D+ and D− are the diffusion coefficient of the cation and anion, respectively (Hayamizu et al. 2004). For the BMIMCl ionic liquid, the simulated diffusion coefficients for cation and anion are comparable and equal to 6.8 × 10−12 m2/s and 6.7 × 10−12 m2/s, respectively. (Kowsari et al. 2008). D’Agostino and co-workers showed in their work the diffusion coefficients for cations and anions in ionic liquids composed of the same cations [EMIM]+ and anions with significantly different volumes: [OAc]− and [TSFI] −. Due to the Coulombic interactions, the smaller anion diffuses slower than, the larger one because of stronger interaction with the cation. The electric charge density of the anion determines the strength of the interaction with the cation (D’Agostino et al. 2018).

The main goal of our study of the ionic conductivity of an ionic liquid confined in a cellulose matrix was to find out whether cellulose's molecular weight influences the conductivity's value. The ionic conductivity σ was measured for the pure ionic liquid, and the liquid gelled into nano and micro cellulose matrix (CNC, CMC) in the range of temperature 299–362 K. The polymer matrix CNC or CMC limits the dynamics of the bulk ionic liquid trapped inside. So, a difference in the ionic conductivity values for all samples was expected. The temperature dependencies of ionic conductivity of the polymer electrolytes based on cellulose (CNC, CMC) and pure ionic liquid are shown in Fig. 8. The presented data are the mean average values from four out of five subsequent measurements. The first measurement was always omitted to eliminate the influence of poor electric contact with electrodes after inserting them into samples. The uncertainty calculated as standard deviation was less than 5%. In the range of measured temperatures, the highest ionic conductivity values were measured for the pure ionic liquid BMIMCl, the lower for the ionic liquid trapped in the CNC, and the lowest for the ionic liquid trapped in the CMC matrix.

Fig. 8
figure 8

The temperature dependencies of ionic conductivity for Bulk BMIMCl and that confined in CNC and CMC ionogels. The solid lines are the best fit of Eq. 3 to experimental points with fitting parameters given in Table 2

Full size image

The best Eq. 3 fitting parameters to experimental points are shown in Table 2. The DA parameters were calculated by DA = B/T0 relation, and ionic conductivity pseudo-activation energy EaVFT were obtained by EaVFT = BkB as 2.44 and 4,75 kJ/mol, 3.36 and 5.77 kJ/mol, 3.39 and 6.72 kJ/mol for bulk BMIMCl, IL confined in CNC and CMC, respectively. Angell's strength parameters DA are similar for both gels (3.36, 3.39) and differ for bulk BMIMCl (2.44) as expected as a material parameter'. The ionic liquids with a DA parameter between 3.1 and 5.8 (and less) could be classified as extremely weak and fragile liquids with weaker, nondirectional intermolecular interactions by which the molecules form an unorganized dense packing in the fluid, which leads to greater susceptibility to structural chance with increasing of temperature (Schreiner et al. 2010). The activation barrier B for ion conduction is greater in ionogels (771–778 K) than in pure BMIMCl (586 K) and increases the activation energy of ionic conductivity in gels. This indicates that cellulose dynamics more likely rule gels' ionic conductivity than pure ionic liquid's intrinsic conductivity behavior. A similar relationship was found in Aquivion membranes swelled in a 1-ethyl-3-methylimidazolium trifluoromethanesulfonate ionic liquid—[EMIM]+[Tf]− (Lin and Colby 2015).

Table 2 Fitting parameters of Eq. 3 to experimental data in Fig. 8
Full size table

The obtained results very well correspond with literature data for ionic liquids containing the same cation [BMIM]+ (1-butyl-3-methylimidazolium). For pure 1-butyl-3-methylimidazolium tetrafluoroborate [BMIM]+[BF4]− the B and T0 parameters are 806 K and 167 K, respectively. The DA parameter was calculated as 4.8, and ionic conductivity pseudo-activation energy EaVFT can be calculated as 6.7 kJ/mol (Stoppa et al. 2010). The [BMIM]+ [TFSI]− ionic liquid (1-butyl-3-methylimidazolium bis(trifluoromethyl sulfonyl)imide) gives the B and T0 parameters as 692 K and 164 K, respectively. The EaVFT pseudo-activation energy and DA parameter can be easily calculated as 5.8 kJ/mol and 4.2, respectively (D’Agostino et al. 2018). Xiaojing Wang (Wang et al. 2014) and Vila (Vila et al. 2006) and co-workers reported similar parameters for [BMIM]+ and [EMIM]−—based ionic liquids calculated by conductivity.

The pseudo-activation energy EaVFT is in the range of the Hartree’s energy of the selected ion pair conformers (the lowest Hartree’s energy for H-Cl in BMIMCl is equal to 0.001 Hartree = 2.62 kJ/mol) (del Olmo et al. 2014). In the case of BMIMCl ionic liquid (because of stable and induced cation and anion dipole moment, respectively), the van der Waals interactions (0.5–4 kJ/mol) play a major and predominant role in the maintenance of ion pairs (hydrogen and chemical bonds energy are 4–40 kJ/mol and 40–500 kJ/mol, respectively). The calculated center of mass and residual dipole moment of [BMIM]+ cation equals 4.9 D and 6.6 D, respectively (Jin et al. 2008). Therefore, we can assume that the main factor influencing the conductivity in BMIMCl are the electrostatic, van der Waals forces, or weak hydrogen bonds connected with the ion pair dissociation mechanism, and then, as the energy of the system increases, the diffusion mechanism will contribute. The presence of water molecules (due to BMIMCl and cellulose hydrophilicity) also weakened the cation–anion interaction in ionic liquid (Kotov et al. 2016). So, we expect the lowest BMIMCl anion-cation separated energy to lie in the several kJ/mol range. The diffusion activation energy Eadiff is at least several times higher than the conductivity pseudo activation energy EaVFT and increases with increasing interaction between cation and anion in ionic liquid (D’Agostino et al. 2018). Figure 2 at (Bystrov et al. 2019) shows the cation [BMIM]+ diffusion coefficient measured by the diffusometry method at NMR 500 MHz for ionic liquids with different anions. We can see in this figure that the slope of the diffusion relations as a function of temperature (and hence the activation energy Eadiff) is greater for monatomic anions than for larger molecules. In our investigation, we obtain diffusion activation energy for cation [BMIM]+ (with anion [Cl]−) as 47.51 ± 1.09 kJ/mol, surrounded by a larger anion, [BF4]− this energy decreases to 42.1 ± 0.8 kJ/mol (Cascão et al. 2018). The self-diffusion coefficient measurements of ionic liquids on graphite surface gives the activation barrier 38.0 kJ/mol, 20.6 kJ/mol and 16.6 kJ/mol for [Cl]−, [PF6]− and [TF2N]− anions in [BMIM]+ -based ionic liquids, respectively (Dou et al. 2010). The electric charge density decreases (lower interaction with cation) with increasing anionic volumes. The anionic volumes for [Cl]−, [PF6]− and [TF2N]− are equal 0.047 nm3, 0.111 nm3 and 0.230 nm3, respectively (Marcus 2015).

Conclusion

Electricity consumption increases year by year, which requires the search for advanced electrolytes and contributed to the continuous increase in interest in ionic liquids. To prevent them from leaking from electronic devices, they should be solid. To meet this requirement, ILs should be immobilized in solid matrices such as cellulose. In the ionogel formed in this way, the solid part of the gel phase consists of a cellulose matrix with large free spaces (pores) that can slow down the dynamics of ionic liquid molecules (cations, anions, clusters, or ion aggregates), forming the ionogel liquid part. From the point of view of technological applications of such ionogels, it is crucial to determine to what extent the entrapment of BMIMCl in the cellulose matrix affects the ion dynamics and electrical conductivity.

The results obtained show that the dynamics of conducting species [BMIM]+ cations (and most probably [Cl]− anions) in the cellulose matrix are reduced to a small extent. For example, at the 369 K, the value of the self-diffusion coefficient of [BMIM]+ cations is equal to 6.42 × 10−12 m2/s (Fig. 6) for bulk IL, 3.79 × 10−12 m2/s for that confined in CNC/BMIMCL, and 3.01 × 10−12 m2/s for IL confined in CMC/BMIMCl ionogels. Also, the influence of the cellulose matrix on the electrical conductivity of the ionic liquid in ionogels is insignificant. At 350 K, the electrical conductivity of bulk BMIMCl is equal to 1.15 S/m and 0.86 S/m, and 0.78 S/m (Fig. 8) for CNC/BMIMCl and CMC/BMIMCl ionogels, respectively. To be useful in electrochemical applications, the material containing IL should have a conductivity of S/m. The studied ionogels fulfill this condition above 300 K. This makes them promising electrolytes for electrical appliances. The effect of CMC and CNC cellulose matrices on the dynamics of 1-butyl-3-methylimidazole chloride ionic liquid and its electrical conductivity in ionogels formed by these types of cellulose and BMIMCl slightly differ. The CNC/BMIMCl ionogel is characterized by higher conductivity values in the measured temperature range than CMC/BMIMCl ionogel. The question is, why? We find the answer to this question in NMR spectra. The 1H MAS spectra (Fig. 1) show, through the observed chemical shift compared to the chemical shift of the protons in the bulk IL, the interaction of the IL imidazole ring protons with cellulose, which is the same for both ionogels. However, the HETCOR experiment (Fig. 3) revealed in CNC/BMIMCl ionogel additional interactions between the methyl group of the [BMIM]+ located in the alkyl chain and the carbons of the glucose ring in the cellulose molecule. Therefore, it can be concluded that IL cations interact more strongly with the CNC matrix during gelation than with the CMC matrix. As a result, more cations (and possibly anions) bind to cellulose in the CNC/BMIMCl than in CMC/BMIMCl, leading to a lower number of "electrochemically" active ions in CNC/BMIMCl. Assuming that the structure of the cellulose matrix in both ionogels is similar, the smaller number of conductive ions closed in similar cavities is characterized by greater mobility (translational diffusion), which ultimately results in higher conductivity observed for the CNC/BMIMCl ionogel.