Introduction

Low-density gels exhibiting yield stress and time - dependent elasto-viscous features are ubiquitous in practical applications such as food, biomedicine, and energy industries (Li et al. 2021). Therefore, developing environmentally friendly, sustainable, and renewable alternatives for applications in these fields is crucial. To this end, highly refined cellulose materials, including cellulose nanofibers (CNFs), cellulose microfibers (CMFs), TEMPO-oxidized cellulose nanofibers (TEMPO-CNFs), and cellulose nanocrystals (CNCs), could be utilized further. From a rheological perspective, these materials possess fascinating properties. In general, they are shear-thinning, but their accurate characterization is sensitive to concentration, morphology, the size distribution of fibers, temperature, and manufacturing processes (Li et al. 2021; Liao 2021). For instance, CNF suspensions display yielding behavior where the yielding point is a function of shear history and solid content (Poling-Skutvik et al. 2020; Iotti et al. 2011). Similar to the behavior of other low-density suspensions, their shear rheology exhibits hysteresis typically at shear rates below \(100~\mathrm {s^{-1}}\). This hysteresis is specifically characteristic of thixotropic fluids (Divoux et al. 2013; Barnes 1997). At higher temperatures beyond \(60~\mathrm {^{\circ }C}\), the hysteresis vanishes. This is accompanied by a decrease in viscosity in some CMF samples (Iotti et al. 2011). Such hysteresis is dependent on the solid concentration: no thixotropic or hysteretic behavior has been reported for TEMPO-CNFs at low concentrations (Liao 2021; Iotti et al. 2011; Sanandiya et al. 2019). Moreover, rheological studies of these materials using oscillatory shear have sometimes identified linear viscoelastic regions and gel-like behavior depending on the morphology and concentration of the sample (Nechyporchuk et al. 2016; Lasseuguette et al. 2008; Liao et al. 2021).

CNF suspensions possess a wide particle size distribution ranging from 1 to \(50~\mathrm {nm}\) (diameter) and 1 to \(100~\mathrm {\mu m}\) (length), resulting in an aspect ratio from 100 to 2000 (Liao 2021; Hubbe et al. 2017). In contrast, TEMPO-CNFs contain fibers of the size range of \(3-5~\mathrm {nm}\) diameter, \(0.5-10~\mathrm {\mu m}\) length, and \(300-1000\) aspect ratio (Liao et al. 2021; Isogai et al. 2011; Levanic et al. 2020; Nechyporchuk et al. 2014; Šebenik et al. 2019). The diffusion time scales associated with such particle size distribution imply spatially non - homogeneous thixotropic evolution, particularly when an imperfect mixing of the material occurs (Mohtaschemi et al. 2014).

In TEMPO-CNFs, the combination of such complex rheology becomes further complicated by the fiber’s internal structure and water swelling resulting in peculiar flow behavior in shear flow (Liao et al. 2021; Fneich et al. 2019; Pääkkönen et al. 2016; Dimic-Misic et al. 2013). Against this background, we present an experimental analysis specifically on the non-trivial time-dependent rheological behavior of TEMPO-CNFs, which has not been sufficiently examined. Our study aims to yield new information on the aging and rejuvenation processes of TEMPO-CNFs (Šebenik et al. 2019). We approach the problem by rheological characterization and analysis of the dynamics of a free-falling solid object through the aged samples.

Among the well-known low-density gels, Laponite exhibits comparable rheology to TEMPO-CNFs. Therefore, creating a mixture of these two substances may satisfy the required gel property for some biomedical applications (Šebenik et al. 2020). Laponite gels were the subject of several studies involving Stokes’ experiment. For the first time in 2004, steel spheres with a diameter of \(3~\mathrm {mm}\) were submerged into Laponite RD® suspensions (\(3~\mathrm {wt\%}\)), that had aged for around \(40~\mathrm {min}\). The experiment displayed a continuously decreasing velocity with time and verified that in the presence of thixotropy, the disturbed area surrounding the sphere dominates the settling behavior (Ferroir et al. 2004). Later, characterization based on examining the flow field in Laponite (\(2.5~\mathrm {wt\%}\)) with a range of aging times between \(30-220~\mathrm {min}\), conducted the breaking of the flow field fore-aft symmetry dependent on both the aging time and the stress exerted by the solid object (Gueslin et al. 2006). In addition, the observed fluidized layer around the solid object becomes thinner with aging (Tabuteau et al. 2007; Gueslin et al. 2006). Further investigations discovered that viscoelasticity has a significant impact on the fore-aft symmetry breaking that is characterized by a negative wake behind the sphere (Gueslin et al. 2009). This is reminiscent of the viscoelastic overshoot familiar from non-thixotropic complex fluids, such as foams (Arigo and McKinley 1998; Dollet and Graner 2007; Viitanen et al. 2019). Further research in the field has reported an irregular quasi-periodic speed regime for a \(3~\mathrm {mm}\) steel sphere in Laponite B® (\(1.5~\mathrm {wt\%}\)) and it concluded to be the result of shear banding (Fazilati et al. 2017). Furthermore, inserting \(2-6~\mathrm {mm}\) spherical steel objects in Laponite XLG® (\(2.8~\mathrm {wt\%}\)), aged for \(1-3~\mathrm {h}\), displayed regimes of either decreasing or increasing velocity. These regimes may or may not reach a steady state where the microstructure breakage rate governs the motion (Biswas et al. 2021).

Generally, the complex shear flow and the associated settling regimes are dependent on the concentration, the Laponite variant, as well as aging and solid-phase characteristics. This behavior is also in stark contrast to a simple yield stress microgel such as Carbopol, that beyond the critical stress, a terminal settling velocity is expected (Tabuteau et al. 2007; Putz et al. 2008; Sgreva et al. 2020). Similar settling behavior as in Laponite was also observed in other non-Newtonian fluids. For instance, in a Xanthan suspension, which is thixotropic, viscoelastic, and shear-thinning, the time dependence of the viscosity was shown to dictate the velocity of the solid sphere (Moseley et al. 2019). Going beyond thixotropic fluids, in a dense cornstarch suspension, a typical rheopectic fluid, the formation, and relaxation of a jammed layer under the object were demonstrated to produce an oscillatory settling velocity ending in a stop-go cycle (Von Kann et al. 2011).

The literature reports cooperative rheological models extended to explain solid-fluid interactions (Ferroir et al. 2004; Fazilati et al. 2017; Biswas et al. 2021; Moseley et al. 2019; Von Kann et al. 2011). However, finding an accurate link between the Stoke’s experiment and rheological data has proven to be difficult, since the two experiments typically probe the sample properties at different scales (Gueslin et al. 2009). Besides considering the essential influence of rheology, the local particles configuration and their morphology may significantly alter interactions (Sgreva et al. 2020).

In this study, we first characterize the TEMPO-CNFs following the protocols of rheological measurements proposed in Divoux et al. (2011, 2013). Then, we proceed to the settling experiments where we vary the aging time of the fluid and the size of the sphere. As far as we know, this is the first study of its kind for TEMPO-CNFs. We characterize the yield properties of the fluid by finding the smallest particle able to penetrate the sample. Observation of different irregularities in the motion of the solid sphere shows that the size distribution of the fibers induces variations in the local rheological properties, which tend to be magnified by the aging time. The experimental observations are reflected based on a modeling approach that involves thixotropy.

The article is organized as follows. First, we explain our material and methodology. Next, the rheological characterization and settling behavior are discussed. Finally, we present our conclusions.

Materials and methods

Materials

We used TEMPO-CNFs with a concentration of \(1.16~\mathrm {wt\%}\) produced from softwood Kraft pulp by VTT (Finland)  (Pöhler et al. 2020; Leppiniemi et al. 2017; Skogberg et al. 2017). Since the gel-like suspension was highly dense for our settling experiments, we diluted the suspension with high purity Finnish tap water down to a \(0.58~\mathrm {wt\%}\) fibril concentration. The density of the final solution was \(\rho _f = 1057~\mathrm {kg \cdot m}^{-3}\). To form a homogenized sample, it was gently mixed using a mechanical stirrer at low speed for \(3~\mathrm {h}\). Then, it was deposited in a rectangular glass container and mixed again for an extra \(30~\mathrm {min}\). During the mixing process, small air bubbles were created in the suspension. Therefore, the suspension was left to rest at a low temperature (6 \(^{\circ }\)C) for one week, during which the bubbles would coarsen and rise to the top of the container.

Rheological measurements

The suspension was characterized by utilizing Antor-Paar MCR302 rheometer with a special serrated bob and cup geometry. A grooved geometry was used to reduce the effects of wall slip (gap width 5.22 mm). Each time, the suspension was mixed for 2 min before filling the cup and then left to rest for one hour at room temperature. A pre-shear of \(10^{3}\) s\(^{-1}\) for 300 s was applied before each rheological test to reset the shear history.

We run two different protocols of measurement. The first was a flow curve with the shear rate between \({\dot{\gamma }}_{min} = 10^{-3}\) s\(^{-1}\) to \({\dot{\gamma }}_{max} = 10^{3}\) s\(^{-1}\) through N successive logarithmically spaced steps of duration \(\delta t\) (Divoux et al. 2013). The flow curves are measured first with decreasing shear rate ramp, then immediately followed by an increasing shear rate ramp. The second measurement was a Small Amplitude Oscillatory Shear (SAOS) test using an oscillatory frequency \(f = 1\) Hz and a strain of \(\gamma = 0.01\) followed by a shear start-up. Time-dependent SAOS test and stress variation of shear start-up were carried out at several steps N and shear rates \({\dot{\gamma }}\).

Settling of spheres

Figure 1 shows the experimental setup. The TEMPO-CNF \(0.58~\mathrm {wt\%}\) was placed in a rectangular glass container of dimensions \(0.15 \times 0.15 \times 0.5~\mathrm {m}\) and a piston plate with several holes of diameter \(0.4~\mathrm {mm}\) was used to mix the suspension before each measurement (Fig. 1b) and reset the shear history. Next, we left the suspension to rest at 6 \(^{\circ }\)C to introduce an aging time \(t_{a}\) (0 s to 16 days). The imaging is implemented using a Canon M3 camera, which takes compressed video at \(1920 \times 1080\) pixels using the h.264 encoding. The camera was positioned perpendicular and at a fixed distance of \(1.75~\mathrm {m}\) to the container. The videos were analyzed using a custom-made MATLAB script that tracks the object using standard procedures.

For each experiment, one sphere was released without initial velocity and placed at least \(0.05~\mathrm {m}\) away from the container’s walls to avoid any wall-particle interaction (Fig. 1c). We used solid steel spheres of density equal to \(\rho _s = 7800~\mathrm {kg \cdot m}^{-3}\) and a diameter \(d_s\) that ranges between \(3.5 - 8~\mathrm {mm}\) (Fig. 1d). At each stage, care was taken to avoid any evaporation by sealing the container appropriately.

Fig. 1
figure 1

a Schematic of the experiment setup. The rectangular tank containing the fluid is \(50~\mathrm {cm}\) high and \(15~\mathrm {cm}\) wide. b-d Photograph of the settling process inside the container: The suspension was mixed using a piston (b) for \(4~\mathrm {min}\). The solid steel sphere was placed in the initial position (c) and left to settling (d)

Full size image

Rheological characterization

Figure 2a shows the flow curve obtained by first decreasing the shear rate (arrow down) in \(N = 90\) logarithmically spaced steps with a duration time of \(\delta t = 5, 10, 50, 100\) s per point, and then increasing the shear rate (arrow up). For the smallest duration time, we observed a slight hysteresis between decreasing and increasing shear-rate sweeps for \({\dot{\gamma }} \le 1~\mathrm {s}^{-1}\). Furthermore, the size of the hysteresis cycle increases as the duration time \(\delta t\) is increased from 5 to \(100~\mathrm {s}\). In line with other studies across the whole range of cellulose-based suspensions, at low shear rates, the flow curve of up-sweep lies under the down-sweep. According to the present understanding this is related to wall slip (Iotti et al. 2011; Koponen 2020; Saarinen et al. 2014; Nechyporchuk et al. 2014; Martoïa et at. 2015).

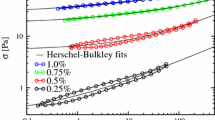
The rheology of yield stress fluids is often modeled using the Herschel-Bulkley model:

$$\begin{aligned} \sigma = \left\{ \begin{array}{ll} \sigma _T + K {\dot{\gamma }}^n &{} \sigma > \sigma _T \\ 0 &{} \sigma \le \sigma _T \end{array} \right. \end{aligned}$$
(1)

Figure 2b shows that the flow curve, neglecting the aging effects, may be fitted by such a simple model. Here, the fitting parameters are \(\sigma _T = 20.65~\mathrm {Pa}\), \(K = 11.18~\mathrm {Pa\cdot s}^n\) and \(n = 0.358\). While n is constant for different measurement times, \(\sigma _T\) and K decrease when \(\delta t\) increases. Note that given the thixotropic nature of the suspension, we do not expect that the Herschel-Bulkley model is capable to fit the hysteresis loop (Iotti et al. 2011).

Fig. 2
figure 2

a Flow curves \(\sigma \) versus \(\dot{\gamma }\) obtained by first decreasing the shear rate from \(10^3\) to \(10^{-3}\) s\(^{-1}\) in \(N = 90\) logarithmically spaced steps of duration \(\delta t\) each, and then increasing \(\dot{\gamma }\) over the same range. Each curve corresponds to a different time interval per step. b The experimental data can be fitted with a Herschel-Bulkley model (dashed black line). The exponent is \(n = 0.358\)

Full size image

Next, to probe the dynamics of the structure aging and rejuvenation, we carry out a SAOS test followed by a shear start-up, and the results of both tests are shown in Fig. 3. First, we performed the SAOS using an oscillation frequency \(f = 1\) Hz and strain amplitude \(\gamma = 0.01\) at \(22~^{\circ }\)C after a pre-shear of \(1000~\mathrm {s}^{-1}\) for \(300~\mathrm {s}\) . Here, the structure of the sample is first broken, and then SAOS is used to monitor the structure build-up for different waiting times, t. The storage modulus is considered as an appropriate measure reflecting the state of the structure. Figure 3a shows how the \(G'\) increases with time as the sample relax after pre-shearing. We observed that the storage modulus \(G^{\prime }\) grows logarithmically with time as seen in Fig. 3a (the fitting parameters are presented in Table 1).

Table 1 Fitting parameters for the storage modulus \(G^{\prime }\) shown in Fig. 3a
Full size table

At the end of the SAOS measurement, we applied a shear start-up where a constant shear rate \({\dot{\gamma }} = 0.25~\mathrm {s}^{-1}\) is imposed at \(t = 0\) s. The shear stress \(\sigma \) is monitored as shown in Fig. 3b. It follows a well-known viscoelastic response: the stress initially increases linearly with time before passing through a maximum and finally decreases to a steady-state value. However, in this case, one must note the small drift in the shear stress even after \(\gamma = 35\), which is the manifestation of thixotropy. Another observation is the increase of the stress overshoot with aging time t that is associated with the increase of \(G'\) (Fig. 3b inset).

Fig. 3
figure 3

a Storage modulus \(G^{\prime }\) in SAOS test increases logarithmically with the waiting time between initial applied pre-shear of \(1000~\mathrm {s}^{-1}\) (for 300 s) and the following shear start-up test. The oscillation frequency is \(f = 1\) Hz, the strain amplitude is \(\gamma =0.01\) and the temperature is \(T =22~{^\circ }\)C. b Shear stress \(\sigma \) versus shear strain \(\gamma \) in the shear start-up test. A shear rate \({\dot{\gamma }} = 0.25~\mathrm {s}^{-1}\) was imposed at \(t = 0\) s after the SAOS test, Fig. 3a). The overshoot increases with the aging time t (inset)

Full size image

Now, we turn our attention to the shear start-up response of the TEMPO-CNFs under different shear rates. When following the previously introduced protocol of imposing the initial pre-shear of \(1000~\mathrm {s}^{-1}\) to reset the microstructure, and then applying a SAOS test at a constant waiting time of \(t = 15~\mathrm {min}\), this time the storage modulus \(G'\) appears approximately the same for all cases. The consequent shear start-up result at different imposed shear rates is shown in Fig. 4. Effectively, both the stress overshoot \(\sigma \) (Fig. 4 inset) and its corresponding strain value increase with the shear rate \({\dot{\gamma }}\). Note the dependence of the stress on shear rate, which roughly aligns with the data in Fig. 2. For a simple yield stress fluid, the maximum stress overshoot occurs at relatively the same values of strain (Benzi et al. 2021). In the TEMPO-CNFs, this is not the case, but the maximum slightly shifts towards higher values of strain, visible even at such a modest shear rate range.

Fig. 4
figure 4

Shear stress \(\sigma \) versus shear strain \(\gamma \) in a shear start-up test. Before the measurement, first a pre-shear of \(1000~\mathrm {s}^{-1}\) for 300 s was imposed, and then a SAOS test with an oscillatory frequency \(f = 1\) Hz and strain \(\gamma = 0.01\) was applied for \(t = 15\) min where as a result, the storage modulus \(G^{\prime }\) increases from around 72 Pa to around 114 Pa. In shear start up test, both the stress overshoot and the corresponding strain increase with the shear rate \({\dot{\gamma }}\) (\(0.05~\mathrm {s}^{-1}\) to \(0.5~\mathrm {s}^{-1}\)). Inset shows the stress overshoot values versus shear rate

Full size image

Sphere settling

We carried out a total of 67 experiments to observe the different behaviors of sphere settling with aging. According to our observations, the motion of the sphere along the x- and y-axis is negligible. Thus, the analysis focuses along the z-axis. Then, we sort the sphere behaviors based on the \(\ell _z\) displacement. Examples of the different trajectories are shown in Fig. 5. These regimes, which are observable depending on the diameter of the sphere \(d_s\) and the aging time \(t_a\) of the sample, are the following:

  1. 1.

    No-motion regime: the sphere remains jammed at its initial position for extended periods of time;

  2. 2.

    Linear regime: the sphere falls rapidly through the sample with a specific velocity;

  3. 3.

    Logarithmic regime: the sphere velocity progressively decreases and never reaches a steady value within the observation window;

  4. 4.

    Irregular regime: the sphere moves irregularly in a sequence of alternating linear and no-motion regimes.

Fig. 5
figure 5

Sphere behavior along its path \(\ell _z\) in TEMPO-CNF \(0.58~\mathrm {wt\%}\). Quantitatively different regimes of motion are observed for different sphere diameters \(d_s\) and aging time \(t_a\) of the sample. They are further classified to four categories

Full size image

We classify trajectories according to a criterion similar to Sgreva et al. (2020). For each regime, the total displacement of the sphere can be characterized as follows: In the no-motion regime, the stress field imposed by the weight of the sphere is not sufficient to break down the cellulose fibers structure. As a result, the sphere either fails to move or moves less than \(5~\mathrm {cm}\) after a long time. In the logarithmic regime, the sphere may end stationary in the middle of the container or reach the container bottom. On the contrary in linear and irregular regimes, the sphere always travels through the entire material.

We first notice that there is a halting time \(\varDelta t\) in which the sphere is required to overcome the yield stress associated with the local fibril network. When this halting time tends to zero, the sphere does not stop at any intermediate point. This behavior is associated with either a linear or logarithmic regime (Fig. 5). We next study these two regimes, so that the motion is described with a linear or semi-logarithmic fit. The goodness of the fit is determined by the root-mean-square error (RMSE) and both values, \(\mathrm {RMSE}_{lin}\) and \(\mathrm {RMSE}_{log}\), are compared to determine the regime (Fig. 6a). The results illustrate the validity of the linear and logarithmic regimes. The ratio \(\mathrm {RMSE}_{lin}/\mathrm {RMSE}_{log}\) determines the logarithmic regime: if the ratio is larger than unity the sedimentation is better represented by a logarithmic fit.

Finally, the intermittent regime is defined when the sphere locally halts for some time of \(\varDelta t~\mathrm {s}\) to overcome the yield stress. For this stop-and-go behavior, the sphere trajectory is irregular (Fig. 5), possibly mixed with a linear or logarithmic regime. Then to differentiate it from other regimes, we fit a linear curve and evaluate the goodness of the fit. To do this, we compute the mean velocity \({\bar{v}}_z\) of data and its standard deviation \(\mathrm {std}(v_z)\). Then, the linear regime is defined by two conditions: \(\mathrm {RMSE}_{lin} < \mathrm {RMSE}_{log}\) and \(\mathrm {std}(v_z)/{\bar{v}}_z < {\mathcal {T}}\) for some threshold \({\mathcal {T}}\). Based on the measurement error, we estimate the threshold \({\mathcal {T}} = 0.25\), below which all linear cases are located as Fig. 6b shows. Thresholding reveals in a total of 15 experiments that exhibit irregular motion (the blue triangles in Fig. 6b) independent of the sphere diameters \(d_s\).

Fig. 6
figure 6

a Comparison of root-mean-square error (RMSE) for linear \(\mathrm {RMSE}_{lin}\) and logarithmic regimes \(\mathrm {RMSE}_{log}\). Red circles indicate a better linear fit whereas blue triangles a better semilog fit. b Ratio \(\mathrm {std}(v_z)/{\bar{v}}_z\) for those falling profiles that have been linearly fitted. The threshold \({\mathcal {T}}\) (black dashed line) is set to 0.25, below (above) which linear (irregular) regime is found, respectively. Linear regime: red circles; irregular regime: blue triangles

Full size image

Structural model

The wide variety of regimes is a consequence of the material internal structure, where above a specific concentration, the fluid behavior changes (Bonn et al. 2017). Coussot et al. (2002) proposed a simple \(\lambda \)-model, in which the time evolution of the structural parameter is governed by the aging (restructuring) and shear rejuvenation (destructuring) terms:

$$\begin{aligned} \frac{d\lambda }{dt} = \frac{1}{\theta } - \alpha \lambda {\dot{\gamma }} \; \end{aligned}$$
(2)

Here, \(\lambda \) assumed to increase with a constant rate of \(1/\theta \), where \(\theta \) is the characteristic restructuring time scale. Destructuring time scale considered proportional to both the shear rate \({{\dot{\gamma }}}\) and the state degree of the structure \(\lambda \), in which \(\alpha \) is a material-dependent parameter. The competition between these two terms controls the settling behavior, and therefore, the characteristic of each settling regime.

This model suffices to discuss many of the features we observe in experiments. In rheology measurements, the hysteresis loop is governed by the ratio between the restructuring and destructuring rates (Iotti et al. 2011). When the destructuring rate, proportional to the rate of shear, tends to zero, the material becomes aged and displays more elastic solid features (Fig. 3). In Stokes’ experiments, the model adequately explains different settling behaviors, as we will explain later on. On the contrary, the \(\lambda \)-model involves a single time scale insufficient to explain the full complexity present in TEMPO-CNFs (Koponen 2020). Thus, describing the material quantitatively requires a more precise and detailed model to be developed (Puisto et al. 2012; Mohtaschemi et al. 2014; Mwasame et al. 2019).

No-motion regime

In this regime, since the weight of the sphere is not enough to overcome the yield stress \(\sigma _T\), the internal structure remains unbroken (\(1/\theta \gg \alpha \lambda {\dot{\gamma }}\)). Therefore, we can estimate the yield stress based on the normal force generated by the sphere as \(\sigma _T = g d_s^{min} \varDelta \rho / 21\), being \(\varDelta \rho = \rho _s - \rho _f\) (as we show in the following section, Eq. 4). Table 2 shows the threshold stress imposed on the fluid by the smallest sphere of diameter \(d_s\) that is incapable of penetrating the fluid at all. This value certainly grows as the aging time increases.

Table 2 Smallest sphere of diameter \(d_s^{min}\) that does not penetrate the material with the aging time \(t_a\)
Full size table

Linear regime

The linear regime is the classic behavior that a sphere adopts in a Newtonian fluid, and it was also reported in simple and thixotropic yield stress fluids (Ferroir et al. 2004; Tabuteau et al. 2007; Fazilati et al. 2017). The regime can be described using two dimensionless numbers: the Bingham \(\mathrm {Bi} = \sigma _T / ( K(v/d_s)^n )\) and yield \(\mathrm {Y} = 3\sigma _T / (g d_s \varDelta \rho )\). Earlier studies for Carbopol gel (Tabuteau et al. 2007) and aqueous dispersions of superabsorbent polymers (Sgreva et al. 2020) have shown that the relationship between those numbers is given by:

$$\begin{aligned} \frac{1}{\mathrm {Y}} = 7 + \frac{8.52}{\mathrm {Bi}} \; \end{aligned}$$
(3)

This equation may be rewritten into a Herschel-Bulkley type of relation (see Eq. 1):

$$\begin{aligned} \frac{g d_s \varDelta \rho }{3} = 7\sigma _T + 8.52 K \Big ( \frac{v_z}{d_s} \Big )^n \; \end{aligned}$$
(4)

We then proceed to determine the traveling velocity \(v_z\) of the sphere. Figure 7 shows the experimental data (dots) together with the linear relation of Eq. 4 (solid lines), which is still valid for TEMPO-CNFs. Interestingly, for the unaged case, we find that the exponent is \(n = 0.35\), as we showed for the flow curve (see Fig. 2b). Similarly, the effective yield stress and consistency are \(\sigma _T = 10.15\) Pa and \(K = 9.64\) \(\mathrm {Pa}\cdot \mathrm {s}^n\), respectively, which are comparable with values obtained in the rheology measurement.

Fig. 7
figure 7

Stress induced by the sphere to the fluid as a function of the \((v_z / d_s)^n\). The data is fitted with a Herschel-Bulkley model (Sgreva et al. 2020), with exponent \(n = 0.35\) and \(n = 0.44\) for the material with no-aging and aging history, respectively. ’Aging’ case includes all experiments with initial aging time larger than zero, resulting in linear sphere motion

Full size image

According to Eq. 2, when the aging time increases, the internal structure of the sample is reinforced, and thus a higher equivalent induced shear rate \((v_z / d_s)\) is required. Therefore, the exponent increases to \(n = 0.44\) as can be seen in Fig. 7. In addition, the effective yield stress and consistency increase to \(\sigma _T = 10.85~\mathrm {Pa}\) and \(K = 18.02\) \(\mathrm {Pa}\cdot \mathrm {s}^n\), respectively.

Irregular regime

Figure 8 displays the settling velocity of four typical irregular cases. In some short aged gels, traveling time into the material can be longer than the aging time, such as for \(d_s = 5~\mathrm {mm}\) at \(t_a = 221~\mathrm {min}\). Thus away from the sphere, the restructuring of the cellulose fibers continuously occurs during the experiment. This leads to a situation where the sphere enters a different material state than at the beginning of the experiment. Oftentimes for several days aged samples, chaotic stop-go cycles can be witnessed such as for \(d_s = 5.5~\mathrm {mm}\) at \(t_a = 5~\mathrm {d}\) or \(d_s = 7~\mathrm {mm}\) at \(t_a = 16~\mathrm {mm}\). It implies that the stress field around the sphere is affected by the local configuration of the fiber network even though the gravitational-induced stress remains constant. As a result, the sphere-gel interaction suggests a local halting time \(\varDelta t\), depending on the size of the sphere \(d_s\) and the aging time \(t_a\). The irregular settling for appropriately short \(\varDelta t\) can be addressed as a semi-oscillatory motion such as in a case of \(d_s = 7~\mathrm {mm}\) at \(t_a = 300~\mathrm {min}\).

Fig. 8
figure 8

Settling velocity in vertical direction (z-axis) for four typical cases of irregular regime

Full size image

Previously it has been shown that the irregular motion in a polymer gel is a consequence of the size of the sphere being comparable with the size distribution of grain particles of the gel where the non-homogeneity of the gel arises and influences the sphere-gel interaction Sgreva et al. (2020). We expect a similar phenomenon drives the occurrence of the irregular regime in TEMPO-CNFs. The difference, however, is that here the sphere deals with fibril flocs (Koponen 2020; Saarinen et al. 2014) the size and configuration of which evolves due to aging and rejuvenating processes that do not develop at the same rates in the whole sample, judging from fig. 8. This leads to different yield stress, viscosity, and elastic modulus at each moment in front of the sphere, which changes the halting time \(\varDelta t\) of penetrating the sphere.

Irregular regime can be obtained from the equation of motion of the settling sphere (Arigo and McKinley 1997; Von Kann et al. 2013), which is described by:

$$\begin{aligned} m \ddot{z} - m^* g = D(z,{\dot{z}},t) \; \end{aligned}$$
(5)

where \(m^*\) is the sphere’s mass with the buoyancy correction and D is the drag force. To solve this equation, the functional shape of the stress considering both viscoelastic and thixotropic components and the yield stress is required. In general term, the stress is given by \(\sigma = \sigma (\eta ,{\dot{\gamma }},t,{\dot{\sigma }})\) that for instance, considering the Maxwell viscoelastic model, it can read (Lehtinen et al. 2013; Armstrong et al. 2016):

$$\begin{aligned} \sigma = \eta (\lambda ) {\dot{\gamma }} - \frac{\eta (\lambda )}{G_0(\lambda )} \frac{\partial \sigma }{\partial t} \end{aligned}$$
(6)

where \(G_0(\lambda )\) is the shear modulus. Then, depending on the drag force on the surface of the sphere, D, a function of \(\sigma (\eta ,{\dot{\gamma }},t,{\dot{\sigma }})\), the velocity of the sphere, \({\dot{z}}\), follows:

$$\begin{aligned} -{\dot{z}} = \frac{{\dot{D}}}{G^*} + \frac{D}{\eta ^*} \; \end{aligned}$$
(7)

A particular solution to the set of equations was shown by Von Kann et al. (2013), where the frequency of oscillation depends on \(\eta \) and \(G_0\). For a thixotropic gel, however, \(G^*\) and \(\eta ^*\) couple to the micro-structure and a solution of the structural constitutive model (Eq. 2) in time and space are involved. Utilizing the rheological tests, we have shown that for TEMPO-CNFs, \(G^*\) and \(\eta ^*\), are shear history-dependent, which results in the occurrence of multiple frequencies of oscillation and manifests itself by a complete irregular motion (see Fig. 5). However, future numerical simulations will help to more thoroughly formulate this complex settling.

In addition, to better understand this regime, we compute the drag correction factor of time-dependent elasto-viscous fluids (Mrokowska and Krztoń-Maziopa 2019):

$$\begin{aligned} \mathrm {K_D} = \frac{v_s}{v_z} \; \end{aligned}$$
(8)

where \(v_z\) and \(v_s\) are respectively denoting average traveling velocity of the sphere in TEMPO-CNFs and the terminal settling velocity in an equivalent Stokes’ flow:

$$\begin{aligned} v_s = \frac{g (\rho _s -\rho _f)d_s^2}{18\eta _0} \; \end{aligned}$$
(9)

where based on the the flow curve data at \({{\dot{\gamma }}} = 1000~\mathrm {s}^{-1}\), the viscosity \(\eta _0 = 0.17\) \(\mathrm {Pa}\cdot \mathrm {s}\).

Moreover, the Deborah number \(\mathrm {De} = \tau / \tau _z\) is defined as the ratio of the fluid elastic relaxation time, \(\tau \), to the average traveling time \(\tau _z\) of the sphere into the fluid. According to the SAOS experimental data, the elastic relaxation time follows a logarithmic growth with aging time (Shaukat et al. 2009):

$$\begin{aligned} \tau = \frac{G^{\prime }}{2 \pi f G^{\prime \prime }} = \tau _0 + a \log (t_a) \; \end{aligned}$$
(10)

where \(\tau _0 = 0.493\) s and \(a = 0.124\). Figure 9 indicates a decreasing trend for \(\mathrm {K_D}\) with \(\mathrm {De}\), similar to other viscoelastic fluids. Moreover, the data implies that settling in TEMPO-CNFs is particularly slower than in a simple Stokes fluid.

Fig. 9
figure 9

Drag correction factor \(\mathrm {K_D}\) as a function of the Deborah number \(\mathrm {De}\). Green square stands for the irregular regime and blue circle indicates data for the linear regime in rejuvenated (no-aging) samples

Full size image

Conclusion

The time-dependent flow behavior of TEMPO nanofibrillated cellulose gels (\(0.58~\mathrm {wt\%}\)) was investigated utilizing two different methods: a rheological characterization and settling of a solid spherical object.

A hysteresis loop was observed by sweeping down and up the shear rate in the flow curve measurement, which increased with point time \(\delta t\). Consequently, the flow behavior for the present material batch was indeed dependent on the shear history. When the hysteresis is relatively small, the Herschel-Bulkley model with an exponent \(n = 0.358\) could be applied to adequately capture the flow curve. The model could also imply that the yield stress slightly decreases with increasing \(\delta t\). However, it cannot explain the hysteresis in the flow curve. Additionally, monitoring the structure build-up by applying the SAOS experiment revealed that the storage modulus \(G^{\prime }\) follows a logarithmic behavior with time, where a longer waiting time in the SAOS test resulted in more development of a stress overshoot in the subsequent shear start-up test. Increasing the imposed shear rate in the shear start-up measurement also indicated an increase in the stress overshoot, which relaxed at higher strain values towards the values measured in the flow curve experiment. In conclusion, the rheological data suggested age-dependent moduli, and this manifests in age-dependent yield properties, which can be observed e.g. as the stress overshoot during the shear start-up experiment.

In line with other simple and thixotropic yield stress fluids (Ferroir et al. 2004; Fazilati et al. 2017; Sgreva et al. 2020), the settling motion of the sphere exhibited a variety of regimes as seen in Fig. 10.

Fig. 10
figure 10

Regions for the four different behaviors of the settling sphere. The plot displays zones as a function of the sphere diameter \(d_s\) (x-axis) and the aging time \(t_a\) (y-axis). The transitions between different regions are not exact and should be viewed as qualitative rather than quantitative

Full size image

The existence of these regimes can be justified as follows. Judging by Figure 7 and Table 2, a specific threshold yield stress value is associated with each aging time. Small spheres cannot overcome this stress leading to the no-motion regime. In contrast, large spheres which impose a stress above the threshold value fall with a constant velocity leading to the linear settling regime. Between these two sizes, two separate regimes appear, the logarithmic and an irregular one. The logarithmic regime is mostly apparent in rejuvenated samples (no-aging). The irregular regime highlights our proposition that aging is also a local phenomenon, and the same material will have regions of different yield stresses despite the same shear history.

From a modeling perspective, a linear relationship between the effective settling velocity and the weight of the sphere can be defined for the linear regime where the sphere descends without significant perturbations. Thus, a Herschel-Bulkley type model was fitted to the settling data in this regime where the exponent and the yield stress perfectly conform to the rheological measurements, \(n = 0.35\) and \(\sigma _T = 10.15~\mathrm {Pa}\) (rejuvenated samples). For aged samples, the exponent n and the yield stress increase to \(n = 0.44\) and \(\sigma _T = 10.85~\mathrm {Pa}\).

In the irregular regime, as the transit time of the sphere decreases, the CNF response time is important (Eq. 2), and for longer aging time, the sphere velocity data displayed a scatter around the linear motion. Therefore, a mean velocity based on the data was computed. The drag correction factor \(\mathrm {K_D}\) for this material, calculated from the mean velocity, decreases as the Deborah number \(\mathrm {De}\) increases. In the irregular and logarithmic regimes, our model comparisons would need to be extended to a more realistic geometry involving a joint simulation of the material (aging) response and the sphere settling dynamics.

Contrary to other low-density gels and Laponite in particular, our TEMPO-CNF samples required a longer aging time to recreate the structure and even rejuvenated samples seemed to possess a considerable yield stress. With aging, the yield stress increased as anticipated for a thixotropic-viscoelastic yield stress gel. Under specific conditions involving an appropriate mass for the solid sphere, an irregular settling can be observed. Moreover, depending on the local halting time \(\varDelta t\) stoppage periods appear in the irregular regime which this feature distinguishes it from a semi-oscillatory settling in Laponite B® (\(1.5~\mathrm {wt\%}\)) (Fazilati et al. 2017), for instance. Long traveling time in certain irregular cases indicates that the restructuring time scale is more dominant in the present system compared to for instance Laponite XLG® (\(2.8~\mathrm {wt\%}\)) (Biswas et al. 2021). These dissimilarities most likely relate to the completely different internal particle structures between the present system and the ones studied before.