Cellulose aerogel particles: control of particle and textural properties in jet cutting process

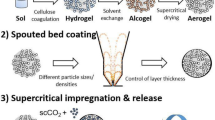
Abstract

Reported approach aims for the synthesis of spherical cellulose beads with high production rates (0.7–4.1 kg/h of hydrogel) via the so-called jet cutting method. To form particles, jets of aqueous cellulose/sodium hydroxide solutions were cut into pieces and collected in a gelation bath (30 wt% aqueous H₂SO₄, 20 °C). After solvent exchange with ethanol and subsequent supercritical drying, cellulose aerogel particles were obtained. The particles showed high specific surface areas (ca. 400 m²/g) and low bulk (untapped) densities (0.06–0.10 g/cm³). Variation of cellulose content (4–7 wt%) and jet cutting process parameters (cutting frequency, nozzle diameter, jet velocity) turned to be useful parameters for controlling the particles size and shape. Highly spherical particles with sphericity SPH ≥ 0.92 were obtained in a broad range of achievable particle sizes (0.4–1.0 mm), with an optimum of SPH at 6 wt% cellulose content.

Introduction

Aerogels being known as the lightest solid materials have a tremendous potential in a wide range of applications, where high pore volume and high surface area play major roles. Aerogels low densities (< 0.2 g/cm³), high porosities (> 90% v/v), high specific internal surfaces (up to 1200 m²/g) are extraordinary properties, which make them useful materials in many different areas. With the depletion of fossil fuel and increasing environmental concerns, there is an increased need for the use of sustainable and eco-friendly educts, bringing biopolymer based aerogels more in the focus over the last decades (Smirnova and Gurikov 2018). Cellulose based aerogels are promising materials in this context, because they are made from an abundant and cheap source while offering a wide range of potential applications e.g. in adsorption, thermal insulation, separation, drug delivery, medical and food sectors and in electro-chemistry after pyrolysis (Fu et al. 2016; Hayase et al. 2014; Deuber et al. 2018; Druel et al. 2018; Mikkonen et al. 2013, 2014; Jack et al. 2017; Cao and Mezzenga 2020; Shen et al. 2015). Despite the wide range of possible applications, the transition from feasibility studies to industrial scale has been realized only in a few cases (Huang 2012). The preparation of aerogels heavily relies on supercritical fluid technology and thus cannot be thought as purely chemical synthesis: it necessarily requires profound engineering knowledge. The overall scheme of biopolymer aerogel production involves three steps: (I) formation of a hydrogel through different mechanisms; (II) solvent exchange; (III) supercritical drying with carbon dioxide at high pressure (~ 120 bar) (Ganesan et al. 2018; García-Gonzáles et al. 2011). During the gel formation (I) an in situ shaping is possible. This first step significantly determines the physicochemical and mechanical properties of the resulting aerogel. Fast gel formation (i.e. fast reaction kinetics) allows the production of small aerogel particles with well-defined sizes, while slow gel formation is advantageous for the production of homogeneous and larger aerogel structures, e.g. monoliths and slabs. The production of aerogels in particulate form offers advantages such as application in controlled drug release or good sorption performance (García-Gonzáles et al. 2011; Wu and Liu 2017; Krishna Rao et al. 2006).The particles sphericity may have decisive effects on their mechanical stability and applicability, since non-spherical shapes may reduce gel bead strength, leading to cracking in tear shape and non-spherical beads, e.g. resulting in the release of encapsulants (Jin-Wook Woo et al. 2007; Al-Hajry et al. 1999). In addition, high sphericity also improves the aesthetics, which may be desirable for food and pharma applications and is beneficial for controlled mass- and heat transfer, as well as for flowability and compaction (Lee et al. 2013).

Hydrogel particles are classically produced by dripping and spraying methods or emulsion gelation, whereas dripping methods are feasible for the production of particles with diameters > 300 µm (Menshutina et al. 2017; Gonçalves et al. 2016; Druel et al. 2020). In the context of aerogel production, particle sizes above 100 µm are most suitable for batch supercritical drying as they demonstrate neither agglomeration, nor caking behavior, while the mass transfer can be influenced by the flow rate of CO₂ (Selmer et al. 2018, 2019). Furthermore, small aerogel particles can be dried with sc-CO₂ with a continuous process, as we recently demonstrated (Mißfeldt et al. 2020).

However, only moderate production rates can be achieved in classical dripping methods or variations thereof. Furthermore, these methods are often limited by high viscosity of the processed polymeric solutions. In the field of high throughput processes, jet cutting of biopolymer solutions has been shown to be a promising and scalable method for production of hydrogel particles with particle diameters in the range from ~ 0.3 up to 1.5 mm (Preibisch et al. 2018; López-Iglesias et al. 2020). The basic principle of jet cutting is the generation of droplets by splitting a liquid jet into segments with a rotating cutting disc. In first works on the jet cutting process, the influence of some process parameters on size and shape of the resulting hydrogel particles were investigated, but no systematical studies including quantification of influences on particles sphericity were carried out (Preibisch et al. 2018; Prüsse et al. 2000, 2008; Paulo et al. 2017).

The cited publications have in common that alginate was used as material system. Due to its fast gelation, alginate acts as an ideal model system for description and characterization of the jet cutting process, as shown by (Prüsse et al. 2008). Preibisch et al. demonstrated that slower gelation leads to more deformed particles for the same material system (Preibisch et al. 2018). If the results obtained with alginate are compared to the production of cellulose particles via jet cutting, the challenge to determine suitable (and therefore fast) gelation conditions for cellulose solutions arises. Cellulose solutions are generally not easy-gelling agents, with the exception of aqueous cellulose/sodium hydroxide (NaOH) (Budtova 2019). In addition, ionic liquids, which are powerful solvents for cellulose, can be used for dissolution of cellulose and subsequent production of hydrogel beads (Budtova 2019). In order to form a hydrogel from dissolved cellulose, gelation or coagulation has to be initiated, whereas the choice of the right conditions depends on the targeted macroscopic shape and application as well as on the applied cellulose solution. Gelation of cellulose solutions is induced by heat, whilephysical coagulation by phase separationoccurs in cellulose non-solvents like acids or ethanol in case of aqueous cellulose/NaOH solutions (Budtova 2019; Gericke et al. 2013).

Druel et al. (2018) successfully produced cellulose aerogel beads with specific surface areas in the range from 240 to 300 m²/g via jet cutting by dissolving cellulose (2–3 wt%) in an ionic liquid (5-diazabicyclo[4.3.0]non-5- enium propionate) and coagulate the solutions in different cellulose non-solvents (water, isopropanol, ethanol). In this case, cellulose concentration was identified as the main influence factor for size and shape of the particles, achieving larger particles at higher cellulose concentrations. While the documented work demonstrates principal applicability of the jet cutting process for production of porous cellulose particles, the sphericity of the produced particles was not quantified, and the process parameters of the jet cutting process were not in the focus. Besides a basic, empirical geometrical approach (Eq. 1, Prüsse et al. 2002), no models are documented in literature for prediction of particles size produced by jet cutting,

$$ d_{particle} = \sqrt[3]{{\frac{3}{2} \cdot d_{nozzle}^{2} \cdot \left[ {\frac{{v_{jet} }}{{f_{cut} }}} \right] - d_{wire} }} $$

(1)

where d_particle is the particle diameter [mm], d_nozzle is the nozzle diameter [mm], ν_jet is the jet velocity [mm/s], f_cut is the cutting frequency (Hz) and d_wire is the diameter of the cutting wire [mm].

Although Eq. 1 includes some process parameters, it is unclear whether it is generally applicable to the production of hydro- and aerogels, since the physicochemical properties of the solutions are not explicitly considered. When it comes to the production of hydro- and aerogels, shrinkage during gel formation and later processing steps has also to be taken into account: for example, a volume shrinkage up to 40% has been documented for gel formation from aqueous cellulose/NaOH solutions (5 wt% cellulose content) coagulated in 0.1 mol/L acetic acid solutions (Sescousse and Budtova 2009).

This work aims at addressing the above points and determines process conditions for the production of cellulose-based, highly spherical hydro- and aerogel particles with the jet cutting method, using only cheap and biocompatible educts. Our strategy is divided into the following sub-steps: (1) Identification of a green synthesis route for the production of spherical cellulose hydrogel particles; (2) Application of the reaction conditions identified in the step one to the jet cutting process; (3) Quantification and modelling of jet the cutting process and (4) Processing of the jet-cut hydrogels to aerogels. Since for the application of aerogel particles the macroscopic characteristics as well as the microstructure play decisive roles, we aim in our work for a holistic approach, which includes the influence of jet cutting process parameters and biopolymer content on both: particle and textural properties.

Materials and methods

Materials and experimentation

Preparation of aqueous stock solutions

A quantity of 20–35 g microcrystalline cellulose type II (JRS Pharma GmbH & Co. KG, Vivapure®, 101 was dispersed in 200 g demineralized water and left for swelling at 5 °C for at least for 30 min. 38 g of NaOH (Merck KGaA) were dissolved in 227–242 g demineralized water and cooled to − 9 °C. The swollen cellulose/water dispersion was added to the NaOH solution and stirred (500 rpm) at − 9 °C for two hours in a double jacket glass reactor with a volume of 500 mL to achieve a homogeneous cellulose solution with a cellulose content of 4–7 wt% (Table 1).

Table 1 Recipes for the preparation of cellulose solutions

The solutions were stored at 5 °C for a maximum of 24 h and used for further processing.

Preparation of coagulation bath solutions

Different coagulation bath solutions consisting of diluted (5.0–33 wt%) aqueous sulfuric acid (H₂SO₄, Merck Millipore, Emsure®), and ethanol 99.9% (EtOH, Carl Roth GmbH & Co. KG) were used to induce the coagulation of the cellulose solutions. Temperature of the coagulation bath solutions was varied from 20 to 50 °C.

Hydrogel particle production via dripping method

Cellulose solutions were extruded from syringes (needle diameter = 0.4 mm) into the coagulation bath resulting in an initial droplet volume of 6.88 mm³. Two coagulation baths were employed: with aqueous sulfuric acid and with anhydrous ethanol. The distance between the syringe tip and the coagulation bath was kept small (3 cm) in order to minimize the impact force originating when droplets hit the surface of the coagulation bath. Precooled cellulose solutions (5 °C) were used in order to avoid thermal gelation of cellulose during the runs before getting in contact with the coagulation bath. During all experiments, the pH of acidic coagulation baths was controlled before experiments and after extruding 100 hydrogel particles. The pH change was ≤ 0.1 in case of coagulation induced by sulfuric acid due to a high excess of the acid compared to the amount of NaOH introduced with the cellulose solution. Hydrogel particles were collected with a mesh and washed with demineralized water until a pH value of 2 (for acid induced coagulation) or respectively 9 (EtOH induced coagulation) was reached. Washed particles were transferred to the solvent exchange step.

Hydrogel particle production via jet cutting method

A jet cutter (geniaLab BioTechnologie GmbH, type S: S1702A) was used for the continuous production of spherical hydrogels. The mode of operation is shown schematically in Fig. 1: precooled cellulose solution (5 °C) was filled into a storage tank and extruded by compressed air through the nozzle (1) passing the rotating cutting disc (2) which cut the liquid jet into small segments.

Fig. 1

Scheme of the jet cutting process

The initially cylindrical segments form spherical droplets while falling directly into a constantly stirred coagulation bath (3). Based on the results presented in "Determination of coagulation conditions for production of spherical cellulose particles" section, 30 wt% aqueous H₂SO₄ (pH 0.1) was used as coagulation solution in jet cutting experiments. Four process parameters were varied in 64 runs: the cutting frequency (f_cut), the nozzle diameter (d_nozzle), the jet velocity (v_jet) and the cellulose content (c_cell), all other parameters were fixed (see "Materials and Experimentation"Sect. 0). An overview of the varied process parameters is summarized in Table 2, while the settings for the individual experiments are presented in the supplementary information (Online Resource 1, Table S1–S4).

Table 2 Ranges for variable process parameters of jet cutting experiments

A maximum of 1 L cellulose solution was processed during each run, corresponding to a maximum change of the pH value of + 0.15 in the coagulation bath. The distance between the nozzle outlet and the surface of the coagulation bath was kept constant at 130 cm. Further constant parameters for all experiments were: the employed cutting disc (24 wires with a thickness of 0.15 mm), the angle between the nozzle and cutting disc (10°) and the temperatures of the cellulose solution and the coagulation solution, 5 and 20 °C, respectively. The hydrogel particles were collected in a mesh and washed with demineralized water till a pH of 2 was reached in the water phase. After washing, the particles were transferred to the solvent exchange.

Solvent exchange

Solvent exchange was carried out by immersion of the resulting hydrogel particles in 99.9 wt% ethanol until a minimum final concentration of 98 wt% ethanol inside the hydrogel particles was reached (controlled by density measurements, Anton Paar, DMA 4500 M). Approximately 7 L EtOH per liter hydrogel were used.

Supercritical drying

After the solvent exchange, the particles were sealed into a filter paper bag and placed into a high pressure autoclave with an overall volume of 3.9 L for supercritical drying with CO₂. The supercritical drying was performed at a temperature of 60 °C and pressure of 120 bar. A continuous flow of CO₂ (flow rate = 80–110 g/min) was set through the autoclave until complete extraction of ethanol was achieved after 4 h. The dried particles were collected after slow depressurization (1 bar/min) of the autoclave. Dried particles were stored in sealed tubes (25 mL, Sarstedt) in a desiccator prior to analysis.

Specific surface area and pore size distribution

Low temperature N₂ adsorption–desorption analysis was used to investigate microstructural properties of the aerogels (Nova 3000e Surface Area Analyzer, Quantachrome Instruments, Boynton Beach, USA). Single determination was carried out for particles produced via dripping method. Particles produced via jet cutting were measured in triplicate (three measurements of individual batches at each cellulose concentration). An overall sample mass of 20–30 mg was used for each analysis. The specific surface area was determined using the BET (Brunauer–Emmett–Teller) method. The pore volume and mean pore diameter were estimated by the BJH (Barrett–Joyner–Halendia) method. All samples were degassed under vacuum at 60 °C for 6 h prior to analysis.

Bulk density

Bulk (untapped density) of aerogel particles was measured using a graduated cylinder. Dry aerogel particles (0.3 g) were filled in the cylinder up to a certain volume without tapping. The bulk density was calculated as a ratio of the particles weight and the occupied volume.

Viscosity

Shear depend viscosity of aqueous cellulose/NaOH solutions with a temperature of 5 °C was determined with a rheometer (Kinexus Pro, Malvern Insturments), covering shear rates in the range 10–10,000 s⁻¹.

Coagulation kinetics and shrinkage during coagulation

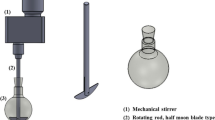
Determination of coagulation kinetics and shrinkage was carried out according to the same protocol as for the dripping method, with the following modifications: only one drop was produced during each run, which was collected in a polystyrene cell (Sarstedt, 10 · 10 · 45 mm), filled with 3 mL of coagulation solution. The cell was placed between a high speed camera (IMAC-CCD S30 video camera module connected to a Leica MZ 125 stereomicroscope) and a light source. The opacity and shape of the droplet during coagulation was monitored with a rate of twenty frames per second. All measurements were carried out in triplicate, evaluation of the results was done by image analysis (Software ImageJ). Shrinkage was determined by evaluation of the maximum particle diameter of the hydrogel droplet d_hydro. Coagulation kinetics was evaluated based on the opacity of the droplet, which was represented by grayscale from 0 to 255, with 255 corresponding as reference (complete transparent droplet). Values of grayscale represented the average along the droplets main axis.

Scanning electron microscope

The surface properties and the inner structure of the aerogels were characterized via scanning electron microscopy (SEM, Zeiss Supra VP55, Jena, Germany). The intact and cut particles were sputtered with a thin layer of gold (Sputter Coater SCD 050, BAL-TEC) before analysis was started. The measurements were carried out under high vacuum at an accelerating voltage of 2–5 kV and a working distance of 5.8–9.0 mm.

Image analysis of hydrogel and alcogel Particles

The size and shape of wet gels was determined based on pictures taken by an optical microscope (particles with diameter < 1 mm, VisiScope TL384H, VWR International GmbH Darmstadt, Germany) or camera (Particles with diameter > 1 mm, Canon E0S). 50 particles per experiment were evaluated for determination of the mean particle diameter d_mean. Image analysis method (Software ImageJ) was used to determine d_mean. In case of irregular shaped particles, the average of the maximum and minimum diameter was used for calculation of d_mean.

Image analysis aerogel particles

Size and shape of dry aerogel particles were determined with a Camsizer XT system (Retsch Technology) in free fall mode. All characterizations were carried out according to DIN 66,141. Particle size d_particle was calculated from the longest feret-diameter and the shortest chord-diameter of each particle projection as follows:

$$ d_{particle} = \sqrt {x_{Fe max}^{2} - x_{c min}^{2} } $$

(2)

with x_{Fe max} being the longest feret-diameter and x_{c min} being the shortest chord-diameter of each particle projection. The particle diameter d_particle of aerogels is given as cumulative distribution [50% passing, Q₃(50)], based on volume. Particles sphericity SPH is given according to ISO 9276-6 as:

$$ SPH = \frac{4\pi A}{{P^{2} }} $$

(3)

where P is the measured perimeter/circumference of a particle projection and A is the measured area covered by a particle projection. For an ideal sphere SPH is equal to 1 and for real samples is lower than 1. The polydispersity of the samples is given as the Span value based on volume:

$$Span= \frac{x{Q}_{3}\left(90\right)- x{Q}_{3}\left(10\right) }{x{Q}_{3}\left(50\right)}$$

(4)

with xQ₃ = Q₃ values, where a given particle diameter x is reached, based on volume.

Results and discussion

Determination of coagulation conditions for production of spherical cellulose particles

In order to focus on the influence of coagulation conditions on particles properties while excluding the complex process variables introduced by cutting process, a simple syringe dripping method was used for particle production at first. The choice of the material system was motivated by cost- and application aspects: dissolution of aqueous cellulose/NaOH solutions was chosen as cheap, bio- and food compatible way for preparation of cellulose stock solutions. It has been shown, that coagulation of cellulose solutions in aqueous HNO₃ results in highly spherical aerogel particles with shape supporting skin on the surface (Trygg et al. 2013). In this work we aimed for a similar approach, replacing HNO₃ with non-toxic and food grade coagulation media. Two coagulation systems were investigated: acidic coagulation in aqueous solutions of H₂SO₄ and coagulation in ethanol (EtOH).

The effects of acid content c_H2SO4 (5–33 wt%) and temperature of the coagulation solution T_gel (20 and 50 °C) were investigated. Different shapes of cellulose hydrogels were obtained in dependence of the acids content and choice of coagulation solution (Fig. 2).

Fig. 2

Cellulose hydrogel particles produced via dripping method under different coagulation conditions: a EtOH, flakes b c_H2SO4 = 5 wt%, hollow structures c c_H2SO4 = 15 wt%, elongated and round particles d c_H2SO4 = 33 wt%, highly spherical particles_. All pictures are from experiments carried out at T_gel = 20 °C

Particles coagulated in EtOH showed flat and flake-like appearance with mean diameter larger than the thickness. Acid induced coagulation lead by contrast to hollow, donut like structures with mean diameter larger than the thickness at the lowest acid concentration (5 wt%). Particles for which the thickness was comparable to the mean diameter were obtained at c_H2SO4 ≥ 15 wt%, whereas slightly elongated species were produced at c_H2SO4 = 15–20 wt% and highly spherical hydrogel particles at c_H2SO4 ≥ 25 wt%. The mean particle diameter d_mean was not affected by the coagulation baths temperature and acid concentration (average d_mean = 2.36 ± 0.02 mm) (Fig. 3). The results for the acid induced coagulation show that acid concentration has a significant influence on macroscopic shape, indicating that droplets are faster stabilized at higher acid concentrations. The phase separation processes for coagulation in EtOH seemed not to be fast enough, leading to strong deformation of the droplet.

Fig. 3

Mean diameter of hydrogels and BET surface area of aerogels in dependence of c_H2SO4 in dripping method. All values are given as the average of the experiments at T_Gel = 20 °C and 50 °C, the error bars corresponding to the standard deviation of the averaged. Dashed lines represent the average of all values

As changes of macroscopic shape are also documented in comparable works of, their results are discussed in relation to our work in the following (Trygg et al. 2013; Sescousse et al. 2011). In the latter publication, pure water was used as coagulation medium and the changes of particles shape could be attributed to different process parameters such falling length (0.5–10 cm) of the droplet and water temperature (20–40 °C). Spherical particles were obtained at higher coagulation bath temperatures (40 °C) and with cellulose solutions which were thermally pre-gelled for 60 min. The pre-gelation step changes the viscosity of the cellulose solution and has a beneficial effect on the stabilization of droplets and maximization of coagulation rate. From the process optimization point of view the pre-gelling can be considered as an undesired extra-step. Furthermore, an increased viscosity of the pre-gelled solution may cause nozzle blockage (Preibisch et al. 2018). In this work, no pregalation took place, thus, the changes of the macroscopic shape can only be attributed to the changes of c_H2SO4 without any need of pre-gelation and higher temperatures for the production of round particles. While the BET surface area of aerogels was 115 ± 6.5 m²/g for gels coagulated in EtOH, higher surface areas were obtained by acidic coagulation, with no specific trend in dependence of acids concentration and temperature (average = 357 ± 30 m²/g) (Fig. 3). Achieved surface areas are in the general higher range and are in good agreement with values reported for cellulose II aerogels coagulated from NaOH/urea/H₂O, LiOH/urea/H₂O (Budtova 2019).

Examination of SEM pictures of cellulose aerogels revealed, that the macroscopic shape adopted at the coagulation step was retained during solvent exchange and supercritical drying (Fig. 4a, b). Particles gelled in presence of H₂SO₄ possess a thin skin with a thickness less than 1 µm, which encloses the inner open porous structure and has a smooth surface (Fig. 4c–e, g–i). The fast formation of a skin may be decisive for the production of round particles, as it can help to fix the particle shape at the beginning of the coagulation process. Even though it was not possible to clearly detect open pores on the skin surface, the results from nitrogen adsorption/desorption analysis prove the permeability (and therefore porosity) of the skin as N₂ is able to enter the inner part of the aerogel particles. An open macroporous network is clearly seen on SEM pictures, being not significantly affected by acid concentration (Fig. 4f). Since combined results from BET analysis as well as SEM pictures of the inner structure both support the assumption, that variation of c_H2SO4 does not affect the porous network, we can conclude that the acid concentration only influences the skin formation kinetics, and therefore the macroscopic shape of the particles. Once the skin is formed, further coagulation of cellulose (and therefore formation of the inner porous structure) should be diffusion-controlled. Thus, the coagulation rate should mainly depend on the thickness of the skin, but the latter was observed not to be significantly affected under conditions studied (Fig. 4d–e, g–i). Formation of a dense layer below the skin would affect the inner microstructure and would have been detected by N₂ porosimetry (Trygg et al. 2013). Therefore, the data suggest that cellulose coagulation in the inner of gel particles occurred homogeneously in acidic solutions under all investigated conditions. Hence, variation of acid content is suitable to control the particles shape, without influencing the microporous structure and properties dependent thereon.

Fig. 4

SEM pictures of cellulose aerogels produced via dripping method. a–f, i T_gel = 20 °C, g, h T_gel = 50 °C a whole particle, coagulated in ethanol b whole particle, coagulated in acid c_H2SO4 = 33 wt% c Surface of particle, c_H2SO4 = 33 wt% (left) and c_H2SO4 = 5 wt% (right) d skin and inner porous structure of particle, c_H2SO4 = 33 wt% e skin and inner porous structure of particle, c_H2SO4 = 5 wt% f inner porous structure of particle, c_H2SO4 = 33 wt% (left) and c_H2SO4 = 5 wt% (right), g skin and inner porous structure of particle, c_H2SO4 = 15 wt%, h skin and inner porous structure of particle, c_H2SO4 = 5 wt%, i skin and inner porous structure of particle, c_H2SO4 = 15 wt%

Summarizing, we can say that the neutralization with sulfuric acid suggested in this work is a simple, economical and green approach towards spherical cellulose gel particles. However the coagulation mechanisms are not yet fully understood. Since several processes take place at once (e.g. diffusion of H₃O⁺ and OH⁻, neutralization reactions which may also cause temperature rise, phase separation and coagulation of dissolved cellulose), kinetic studies of coagulation at high acids concentrations are of great importance to get insights into the overall reaction order and time as well as the factors influencing skin formation. This is a part of our ongoing work.

Particle production via jet cutting

Cellulose hydrogel particles were produced via jet cutting and processed to aerogels particles, which were characterized with respect to the particle diameters (d_particle), sphericity (SPH) and particle size distribution (quantified as Span). Based on the results, a process window for production of particles with high SPH and narrow particle size distributions (target product) could be identified. The given points are discussed in detail in the following.

Particle diameter

Values of d_particle for aerogels were in the range from 0.4 to 1.0 mm, and highly dependent on d_nozzle while only slightly influenced by f_cut and v_jet in the investigated range of parameters. v_jet (3.18–8.91 m/s) was chosen within the boundaries of the process: Too high jet velocities lead to destruction of droplets when hitting the coagulation baths surface, while too low velocities result in high cutting losses or complete deflection of the jet when contacting the cutting disc. Within these limits, production rates of 0.7–4.1 kg hydrogel per hour could be achieved. The particle size increased linearly with d_nozzle, which is consistent with the predictions from the geometrical model for the jet cutting process (Eq. 1, Fig. 5). Values calculated with Eq. 1 reproduce experimental trends, but are significantly and systematically higher than the experimental results (with an average deviation from experimental results of 38%).

Fig. 5

Dependence of aerogel particles diameter d_particle on the nozzle diameter d_nozzle at different cellulose concentrations in comparison with values predicted with Eq. 1. Each data point represents all settings with a fixed nozzle diameter, but variating f_cut and v_jet (4 data sets each). The error bars correspond to the standard deviation of the averaged values, straight lines are the linear fits, and dashed lines represent the 95% confidence interval

This deviation is to be discussed in relation to shrinkage of the particles, which is not taken into account in Eq. 1 and may occur in all steps of cellulose aerogel production: 1. coagulation, 2. solvent exchange, 3. supercritical drying³⁵. The degree of shrinkage may vary significantly in dependence of many parameters, e.g. type and concentration of cellulose, dissolution medium, type of non-solvent, solvent exchange strategy, macroscopic shape/size of the material and supercritical drying conditions. Therefore, a direct comparison with the results reported in literature is difficult (Budtova 2019; Sescousse and Budtova 2009; Long et al. 2018; Picher et al. 2014; Schestakow et al. 2016; Heath and Thielemans 2010; Innerlohinger et al. 2006). A high variability of the shrinkage degree during solvent exchange (step 2) is reported for biopolymers in general. As we recently demonstrated analyzing of a large dataset of biopolymer gels, the following empirical exponential relation can be used to quantify the degree of shrinkage of a hydrogel with the biopolymer concentration ${c}_{bp}$ (in wt%):

$$ Y = 1 - 0.728e^{{\left( { - 0.301c_{bp} } \right)}} $$

(5)

with $Y$ is the volumetric yield after the solvent exchange (ratio of the final volume to the initial volume) (Gurikov et al. 2019; Subrahmanyam et al. 2015).

Following Eq. 5, a volumetric shrinkage of approximately 9–22% (corresponding to 3–8% linear shrinkage) could be expected during solvent exchange step for the range of c_cell = 4–7 wt%. The experimentally measured total volumetric shrinkage of ~ 14% (corresponding to a linear shrinkage of ~ 5%) from hydrogel to aerogel (steps 2 and 3) is in the same range compared to these values as well as to the wide range (6.5–75%) reported for cellulose-based materials (Budtova 2019; Heath and Thielemans 2010) and was independent of c_cell. This result may be attributed to the skin effect, which can provide mechanical stabilization during solvent exchange and supercritical drying, hence protecting the inner porous structure. Since the shrinkage in steps 2 and 3 is not sufficient to explain the differences between calculated (Eq. 1) and the experimental values of d_particle, main shrinkage during the coagulation (step 1), where the gel structure still undergoes dynamic formation and possesses a higher flexibility, should be considered. Shrinkage during coagulation was therefore studied in a separate setup, where size and opacity of single droplets (average initial droplet diameter d₀ = 3.0 ± 0.1 mm) were monitored by a high speed camera over time (Fig. 6).

Fig. 6

Changes of size and opacity (normalized) of cellulose (c_cell = 5 wt%) hydrogel droplets over time in 30 wt% aqueous H₂SO₄ at T_gel = 20 °C, averaged values of triple determinations. The error corresponds to the standard deviation. O/O₀ is the opacity at time t relative to the initial opacity, d_hydrogel corresponds to the maximum particle diameter at time t

After a short contact of ~ 1 s with aqueous H₂SO₄ solution, transparent (and therefore non-detectable by the camera) droplets became increasingly opaque. Since change of opacity corresponds to the formation of a cellulose 3D-network from dissolved cellulose, the measured changes are indicative for the coagulation progress. Degrees of coagulation and shrinkage were found to be directly related, no further changes were detected after a short reaction time (< 1 min). The coagulation progress followed strictly first order kinetics profile, showing that one factor is dominating the complex coagulation mechanism, which is assumed to be diffusion of H₃O⁺ into the inner part of the particle. Expressed as reaction rate, a first order rate constant k_gel = (9.2 ± 0.3) 10^–2 s⁻¹ for coagulation can be calculated from linear fitting (R² > 0.991) of ln o/o₀ vs t. Taking into account the overall linear shrinkage during the hydrogel formation (10%) and additional linear shrinkage during further processing (5%), Eq. 1. can simply be supplemented by a shrinkage factor $s$ [%] (equivalent to the total linear shrinkage), which increases the average accuracy of the predicted particle diameter by 21–83%:

$$ \frac{{d_{particle} }}{s} = \sqrt[3]{{\frac{3}{2} \cdot d_{nozzle}^{2} \cdot \left[ {\frac{{v_{jet} }}{{f_{cut} }}} \right] - d_{wire} }} $$

(6)

Remaining deviations may be explained by following factors: (1) small fraction of the solution in the jet cutting forms smaller particles (so called cutting and spray losses) which eventually also fall into the coagulation bath; (2) initial shrinkage in the first second of the reaction right after contact of the droplet with the coagulation medium (which was not taken into account). Thus, Eq. 1 and refined Eq. 6 are generally suitable for the description of cellulose aerogel particles production via jet cutting and allows an approximate estimation of the final aerogel particle size as a function of jet cutting parameters. A more precise, but purely empirical interpolative prediction for this system is provided by statistical modelling which was made based on our experimental results (Eq. 7):

$$ d_{particle} = 2.5 \cdot 10^{ - 2} + 1.4 \cdot d_{nozzle} - 7.0 \cdot 10^{ - 5} \cdot f_{cut} + 3.6 \cdot 10^{ - 2} \cdot v_{jet} $$

(7)

This simple linear process model proved to be sufficient for a highly accurate (average accuracy of 93%, R²_model = 0.90) description. The statistical relevance of the model terms was verified by analysis of variances (ANOVA), documenting adequate precision and signal-to-noise ratio as well as the significance of the individual influence factors (Online Resource 1, Table S5–S6). In accordance with the experimental results, all jet cutting parameters were significant with the largest influence of d_nozzle on d_particle. Since c_cell was a non-significant term, cellulose concentration is not included in the model Eq. 7.

Sphericity

Despite the relevance for many applications, no systematic quantitative descriptions of the influences of jet cutting process parameters on SPH of hydro- and aerogels have so far been published, to the best of authors’ knowledge. Qualitative descriptions can be found in the works of Preibisch et al. (2018). and Prüsse et al. (2000, 2002 and 2008), quantitative SPH values in the range of 0.71–0.92 have been given by López-Iglesias et al. (2020) for some selected jet cutting parameters. Thus, the goal of this work is to produce highly spherical aerogel particles and to establish quantitative relations between the sphericity and jet cutter settings and c_cell.

A rough categorization of particles quality in terms of SPH is carried out by definition of three particle categories (Fig. 7): SPH < 0.88 “poor” (particle irregularly shaped surface, partially deformed), SPH = 0.88–0.91 “medium” (slightly deformed surface, partially elongated particles) and SPH ≥ 0.92 “good” (intact surface, from slightly elongated to perfectly round particles). SPH correlates linearly (R² = 0.999) with cellulose concentration in the range c_cell = 4–6 wt% (Fig. 8, Eq. 8):

$$ SPH = \left( {0.767 \pm 0.004} \right) + \left( {2.95 \pm 0.07} \right) \cdot 10^{ - 2} \cdot c_{cell} $$

(8)

Fig. 7

Pictures of cellulose hydrogels in water. The sphericity SPH values of the corresponding aerogels are: a 0.86, b 0.92, c 0.96

Fig. 8

Sphericity SPH in dependence of cellulose concentration c_cel and corresponding viscosity (see inset). Each data point represents the averaged results from all experiments at the corresponding cellulose concentration with different settings of jet cutting parameters (16 runs each). The errors bars correspond to the standard deviation of the averaged values, therefore representing the influence of jet cutting parameters on SPH at a given c_cell. The straight lines represent linear fitting, and the dashed lines are the 95% confidence intervals. Double headed arrows represent the ranges of qualitative particle quality

Increasing c_cell leads to a higher viscosity of aqueous cellulose/NaOH solutions, which has a beneficial effect on formation of round hydrogel beads in dripping processes, since elastic properties are dominating over viscous ones, helping the droplets to resist impact forces when hitting the coagulation baths surface (Sescousse et al. 2011).

It is notable that with decreasing c_cell jet cutting process parameters gain higher influence as represented by the error bars in Fig. 8. It can be assumed that deformation of the liquid droplets def_droplet during the impact on the surface of the coagulation bath is the decisive event for the resulting SPH, with high deformations during impact resulting in low sphericities of the products. Therefore this trend can be explained by the relation of the droplet sizes d_droplet and viscoelastic properties of the solutions: According to description of droplet deformation via Ohnesorge number, the deformation of the droplets during impact can be considered being a function of the viscosity of the solutions and the droplet diameter:

$$ \frac{{\sqrt {d_{droplet} } }}{{\upeta }} \to { }def_{droplet} $$

(9)

With η = kinematic viscosity of cellulose solutions [Pa s].

Since d_droplet depends on jet cutting process parameters, higher varieties of deformation during impact and broader ranges of SPH of resulting aerogels particles are obtained at low cellulose concentration with lower viscosities (Fig S1). This is reflected in detail by comparison of SPH with d_particle at different cellulose concentrations (Fig. 9). A threshold of d_particle = 0.6 mm can be identified: particles with d_particle ≤ 0.6 mm have a high and constant sphericity (0.92–0.96): for small particles the viscoelastic properties of the cellulose/NaOH solutions are therefore sufficient to allow the droplets to reshape during impact. Above the threshold, SPH decreases drastically at c_cell = 4–5 wt%, while particles with good quality could be obtained up to d_particle = 0.95 mm at higher cellulose concentrations, which have sufficient viscosity to withstand increased deformation forces.

Fig. 9

Sphericity of aerogel particles in dependence of particle diameter at different cellulose concentrations (measured data left, contour plot of SPH predicted by model Eq .10 right). Left: Each point represents an experimental run solid lines are exponential fits. Dotted lines highlight the area of high sphericity (horizontal) and the threshold of d_particle for production of highly sphereous particles at low cellulose concentrations (vertical)

In the range of d_particle < 0.6 mm SPH increases slightly with increasing cellulose content up to 6 wt%, while further increase to 7 wt% leads to a slight decrease of SPH (Figs. 8, 9), showing that other effects, e.g. changes of skin formation or coagulation kinetics, counteract the viscoelastic stabilization in this case.

An adequate quantitative description of SPH requires therefore the integration of the complex interactions between d_particle and c_cell. This is carried out by statistical evaluation of the individual fits for each cellulose concentration (Fig. 9). A full quadratic description proved applicability of this approach, providing a suitable prediction of SPH in dependence of model terms (R²_model = 0.96, p values of all terms < 1.0 · 10^–3, variance inflation factors of all terms < 2.3):

$$ \begin{aligned} \sqrt {SPH} = & 0.75 + \left( {5.7 \cdot 10^{ - 1} \cdot d_{particle} } \right) + \left( { 4.9 \cdot 10^{ - 2} \cdot c_{cell} } \right) - \left( { 6.6 \cdot 10^{ - 2} \cdot c_{cell} \cdot d_{particle} } \right) \\ & - \left( {6.6 \cdot 10^{ - 1} \cdot d_{particle}^{2} } \right) - \left( {3.0 \cdot 10^{ - 3} \cdot c_{cell}^{2} } \right) + \left( {8.1 \cdot 10^{ - 2} \cdot d_{particle}^{2} \cdot c_{cell} } \right) \\ \end{aligned} $$

(10)

The corresponding contour plot reflects the interpolated experimental results, with high SPH at each cellulose concentration for d_particle < 0.6 mm and higher influence on SPH at d_particle > 0.6 mm (Fig. 9, right). The plot shows that a maximum of SPH lies at d_particle ≈ 0.5 mm and c_cell ≈ 6 wt%.

Particle size distribution

Besides SPH, particle size distribution as characterized by Span, is another important characteristics of the particles quality. Span of aerogel particles produced by jet cutting was in the range of ~ 0.2–0.9. A large value of span points to a broad and/or multimodal particle size distribution. To our knowledge, there are no strict recommendations what ranges of Span values are attributed to the qualitative terms “monomodal” and “multimodal” size distributions. In this work a categorization is carried out based on the particle size distributions (Online Resource 1, Fig S2–S5) and from optical microscopy pictures of corresponding hydrogels. We classified a distribution as “monomodal/narrow” at Span ≤ 0.45 and “multimodal/broad” distributions at Span > 0.45 (Fig. 10, left). It is to note that such categorization may significantly depend on the evaluated system: for instance, Chebil et al. (2018) defined a monomodal distribution for Span values less than 1.2. We observed that Span values are highly related to SPH (Fig. 10, right), which is rooted in the evaluation method: because size and shape is evaluated based on the projected area, different orientation, for instance, slightly elongated or flattened species, leads to broadening of detected distributions.

Fig. 10

Exemplary particle size distributions (left), Span in dependence of SPH and c_cell (right). The solid line corresponds to global fitting of all data points with a power function, the dashed lines to the 95% confidence interval

Narrow distributions are observed at SPH > 0.92. Some relatively high Span values at c_cell = 7 wt% at SPH = 0.90–0.94 can be explained by the entrapment of air bubbles inside the particles at these conditions. From a practical standpoint, our results show that narrow and monomodal size distributions are achievable via jet cutting at all cellulose concentrations studied in this work.

Jet cutting process

Based on all presented results, a process window of jet cutting parameters can be suggested for the production of particles with high sphericity (Online Resource 1, Table S9). Besides the product properties, issues regarding the process such as bubble formation and nozzle blockage are also taken into account.

Blockage or runaway of the jets angle occurred sometimes at higher cellulose content (6–7 wt%) and for nozzles with small diameter (200–300 µm). Since aqueous NaOH/cellulose solutions are gelling over time (also in the feeding vessel of the jet cutting device) and the gel point depends on c_cell and temperature, thermal gelation of cellulose solution leftovers near the nozzle outlet may result in partial or full blockage of the liquid jet (Gavillon and Budtova 2008; Cedric Roy and Budtova 2003). It is important to note that the process window could be enlarged by: (1) feeding from a cooled chamber to minimize the gelation of the stock solution; (2) degassing of the coagulation solution in order to exclude bubble entrapment effects in large particles at high cellulose content.

At the current state, an optimum for particles with maximized SPH, narrow particle size distribution and good processability can be identified in the range of d_particle ≈ 500–600 µm at c_cell = 6 wt%, working with a nozzle diameter of 400 µm.

Influence of cellulose content on porous structure

Cellulose aerogels from the jet cutting process were analyzed for textural properties after drying and the relations of jet cutting process parameters and cellulose content were determined. Textural properties were only dependent on cellulose content and not related to particle size and sphericity. Interestingly, cellulose content had no specific effect on the BET specific surface area. The latter was found to be on average equal to 376 ± 37 m²/g (Fig. 11). As we discussed above, a ~ 10% decrease in the droplet diameter during coagulation was observed. A further ~ 5% linear decrease in the droplet diameter was observed during the solvent exchange and drying processes (Fig. 11).

Fig. 11

Linear shrinkage of hydrogel particles and specific surface area of resulting cellulose aerogels particles from the jet cutting process as a function of the cellulose concentration. Dashed lines represent the average values

These size reductions translate into a linear decrease of $\left( {1{ }{-}{ }0.10} \right)\cdot\left( {1{ }{-}{ }0.05} \right) = 0.855$ for the entire transformation from cellulose solution to the final aerogel. This linear decrease corresponds to the total volumetric change of ${0.855}^{3}=0.625$, i.e. around 63% volume of the cellulose solution is preserved in the gelation, solvent exchange and supercritical drying steps. The volume reduction allows a simple estimation of the envelope densities of the resulting aerogels, as they are difficult to measure experimentally (Gurikov et al. 2019, see supporting information for details).The envelope densities $\left.{\rho }_{e}({c}_{cell}\right)$ can be estimated to be 0.07, 0.09, 0.11 and 0.13 g/cm³ for 4, 5, 6 and 7 wt% cellulose solutions, respectively.

The shape of pores in cellulose aerogels is still under discussion, and has been reported to be non-cylindrical, e.g. net-like aerogel structures were obtained for gels derived from water/NaOH cellulose solutions (Budtova 2019; Rege et al. 2016). Despite of well-known limitations for all types of cellulose aerogels, the average pore width ${d}_{pore}\left({c}_{cell}\right)$ can formally be calculated from the cylindrical pores model using the envelope densities ${\rho }_{e}$ as follows (Rege et al. 2016):

$$ d_{pore} \left( {c_{cell} } \right) = \frac{4}{{\left. {S(c_{cell} } \right)}}\left( {\frac{1}{{\left. {\rho_{e} (c_{cell} } \right)}} - \frac{1}{{\rho_{s} }}} \right) $$

(11)

where S(c_cell) is the specific surface area [m²/g] at the corresponding cellulose concentration, ${\rho }_{s}$ is the skeletal density of cellulose (1.53 g/cm³).

Because the specific surface area does not depend on ${c}_{cell}$, the pore width is a reciprocal function of the envelope density. Figure 12a demonstrated this relation for the BJH pore diameters calculated from corresponding pore size distributions (Fig. 12b). A linear relation (R² = 0.998) can indeed be seen between ${d}_{pore}$ and ${\rho }_{e}^{-1}$, with the slope of 1.04 ± 0.06. The slope would formally correspond to a value of the surface area ten times larger than what was measured by nitrogen adsorption. This implies that a large contribution to the total pore volume given by the term $1/{\rho }_{e}-1/{\rho }_{s}$ in Eq. (11) comes from macropores. Similar observations were reported for other biopolymer aerogels (Gurikov et. al 2015), but only seldom articulated in the literature. The BJH pore volume was measured to be constant within experimental errors (3.1–3.8 g/cm³) across the cellulose concentrations studied. Therefore, the BJH pore volume amounts to 23–45% of the total pore volume.

Fig. 12

a Relation between pore diameter and reciprocal envelope density according to the cylindrical pore model, Eq. (10), straight line represents the linear fit, dashed lines the 95% confidence interval; b experimental BJH pore size distributions

Figure 13a demonstrates a linear increase in bulk (untapped) densities with increasing cellulose concentration. It is interesting to compare envelope and bulk densities, because the former are difficult to measure experimentally, whereas the latter is easily accessible: In our case a linear relation was obtained between them (R² = 0.94), (Fig. 13b). As expected for non-monosized particles, the slope of the line is larger than that expected for random packing of hard spheres ($\sim$ 0.5–0.6). Therefore, when performed in a controlled manner, the bulk density may be used for a rough estimation of the envelope density.

Fig. 13

a bulk density of aerogel particles; b relation between envelope and bulk density. Straight lines represent linear fits, dashed lines the 95% confidence interval

Conclusions

Highly spherical cellulose aerogel particles were successfully produced via the jet cutting process. Preliminary tests via dripping method showed, that coagulation of aqueous NaOH/solutions in aqueous solutions of H₂SO₄ (ca. 30 wt%) led to the formation of round particles, with a thin skin on the particles surface. The influence of the jet cutting process parameters such as jet velocity, nozzle diameter and cutting frequency as well as cellulose content on particle size, shape and particle size distribution was determined, enabling a full quantitative description of the relations between the process parameters. It was found that in the investigated range of parameters the particle size is mainly determined by the nozzle diameter, whereas sphericity is related to the particle diameter and cellulose content. Interpolative models allowed the prediction of macroscopic properties and the identification of optimal process settings for achieving maximum sphericity. The porous structure of cellulose aerogels particles can be controlled by variation of the cellulose content: larger total pore volumes and sizes (for mesopores) were obtained at lower cellulose content. The specific surface area was shown to remain constant at all process conditions. Determination of the shrinkage behavior showed that the coagulation process contributes the most to the overall shrinkage. Shrinkage during the solvent exchange and supercritical drying was demonstrated to be independent of cellulose concentration, which is most likely due to the stabilizing effect of the skin formation. The complex processes during coagulation are still to be understood, in particular the coagulation kinetics and shrinkage during coagulation should have significant impact on micro- and macroscopic properties of the materials, and will be therefore in the focal point of our future works. From the perspective of production on an industrial scale, this work demonstrates a biocompatible and economical way for the production of round cellulose aerogel particles at throughput rates of several kg hydrogel per hour. The possibility of scale up is given by numbering up: e.g. multi-nozzle approaches allow for simple increase of the production rates, while keeping the influences of jet cutting parameters constant. While the results regarding jet cutting process parameters should be principally transferable to other fast-gelling systems, physicochemical parameters of the reaction system like reaction mechanism and kinetics play also an important role for particle shaping and have therefore to be taken into account individually.