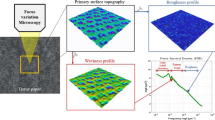
Abstract
Tissue paper softness relies on two major factors, the bulk softness, which can be indicated by the elasticity of the sheet, and surface softness. Measurement of surface softness is complicated and often requires a multi-step process. A key parameter defining surface softness is the topography of the surface, particularly the crepe structure and its periodicity. Herein, we present a novel approach to measure and quantify the tissue paper surface crepe structure and periodicity based on the detection of waviness along the sample using laser scanning confocal microscopy (LSM) and X-ray tomography (XRT). In addition, field emission scanning electron microscope (FESEM) was used to characterize the tissue paper surface. We demonstrate that surface topography is directly correlated to the erosion of the doctor blade, which is used to remove the dry tissue paper from the Yankee cylinder. Because of its accuracy and simplicity, the laser confocal microscopy method has the potential to be used directly on the production line to monitor the production process of the tissue paper. XRT revealed more structural details of the tissue paper structure in 3D, and it allowed for the reconstruction of the surface and the internal structure of the tissue paper.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Tissue paper consists of a mixture of pulp fibers, which determines the structure of the paper and its properties together with the fiber characteristics and the production process (Raunio 2014; Skedung et al. 2010). The properties of the fibers and the production process can influence the softness, dry strength, wet strength, and absorption of tissue paper. These paper properties are tailored according to end-application needs. For instance, users want toilet paper to be softer and have a high dry strength rather than an optimized appearance. These features are achieved by using a blend of recycled fibers and chemical pulp. On the other hand, kitchen towel requires high wet strength, absorption capacity, and a decorative appearance, which is attained by using a blend of virgin chemical and mechanical pulp.
Tissue paper is commonly produced through a dry-crepe process. Dry-crepe machines are one-press roll machines in which paper is dewatered by heating. The machine’s main component is a press roll—the Yankee cylinder—which is steam heated to dry the tissue paper web; i.e. the purpose of Yankee cylinder is to dry the tissue paper web.(Ramasubramanian et al. 2011). The paper web adheres to the Yankee cylinder (Fig. 1). The adhesion, controlled by different additives such as modifiers and release agents (Oliver 1980; Rose 2004), helps transport the paper web and enables the creation of crepe folds in the final product.
A schematic diagram depicting the dry-crepe tissue machine. The brown color depicts the path of the paper (redrawn from Hermans and Hada 2004)
Researchers have studied the creping mechanism in the machine direction, and they have shown the crepe folding mechanism in detail (McConnel 2004; Ramasubramanian et al. 2011; Sun 2000). As the doctor blade comes into contact with the tissue sheet, the sheet begins to warp (create crepe folds) (Fig. 2). The creping process generates a wavy microstructure in the tissue paper, breaking up the tissue structure into micro and macro folds (Hollmark 1972). The crepe fold structure is affected by different factors, including the adhesion force between the tissue paper and the dryer and the impact angle of the doctor blade. Low adhesion typically yields wide crepe folds and vice versa (Stitt 2002). The doctor blade scrapes the paper off from the Yankee cylinder and is responsible for creating the crepe structure. As the blade wears off, the creping structure is modified and believed to affect the perceived softness. In addition, the creping process affects the free fiber ends and holes in the tissue network. Indeed, stable creping conditions produce more periodic fiber ends and fewer holes in the tissue network structure (Allen 1994; Raunio and Ritala 2013). The crepe structure is adjusted by the cutting—or the impact angle—of the doctor blade at the Yankee cylinder. For example, a larger impact angle creates fewer and wider crepe folds (Boudreau and Barbier 2014).
Propagation of the creping pattern as the sheet contacts the doctor blade in an ideal steady state: a the sheet and its adhesive layer on the Yankee cylinder are propagating to the cutting blade; b as they reach the blade, delamination occurs and the sheet is freed from the adhesive layer; c the delamination propagates and buckling starts as it is the most energetically favorable reaction; d the sheet collapses completely, the crepe fold is formed, and then the whole cycle is repeated
Preferences, such as softness, vary between individuals, markets, and cultures, so they are difficult to quantify even though softness can be measured by modern hand mimicking equipment. However, certain properties that influence the perception of softness—such as crepe count, crepe-to-stretch ratio, sheet density, strength, stiffness, and creping geometry—can be measured and controlled (Ramasubramanian and Shmagin 2000). Several methods—both internal techniques used by the tissue paper companies and external processes like scanning electron microscopy (Chinga and Helle 2003) and atomic force microscopy (Chinga et al. 2003; Haunschild et al. 1998)—have been used to understand the softness of tissue paper.
In this work, we used laser scanning confocal microscopy (LSM) to analyze several parameters of crepes, such as crepe count, waviness, and the average height of the crepes, and we determined the connection between these parameters and the softness of the end-product during an operational cycle of the doctor blade. LSM is mainly used in biomedical science (Hovis and Heuer 2010), and in analyzing the surface roughness of different printed paper grades (Chinga et al. 2003). In those cases, LSM proved to be robust and accurate in providing topographical data with high resolution without destroying the sample (Chinga et al. 2003). Even though confocal microscopy was invented in 1955 by Minsky (1988), its potential was increased immensely with laser light sources and high computing power (Amos and White 2003; Hamilton and Wilson 1982; Xiao et al. 1988). In addition, we used X-ray tomography (XRT) to visualize and quantify the hierarchical design of tissue samples. XRT is a nondestructive method that repeatedly acquires images (i.e., projections) resulting from the sample’s absorption of X-rays (Kak et al. 2002). Finally, the novel application of microtomography was supplemented with more traditional methods of analysis, such as field emission scanning electron microscopy (FESEM) which was used to image the planar structure of the tissue paper in high resolution. This work is an attempt to create a systematic approach to measure the surface a single ply tissue paper using an easy, approachable and a simple method that can be used both by companies, and academics.
Materials and methods
Materials
Commercial tissue paper, consisting of a blend of kraft softwood, hardwood, and bleached chemi-thermomechanical pulps with a ratio of 20:73:7 wt%, was used in this study. The grammage of paper was an average of 17.8 g/m2. Tissue paper samples were collected as a function of production time during the doctoral blade cycle immediately before exchanging the old doctor blade (T-38) for a new blade and then after using a new doctor blade for a whole cycle until the blade wore down again (T674). All the samples were single ply samples (see Table 1).
Laser scanning confocal microscopy (LSM)
A Keyence VK-X250K LSM (Osaka, Japan) was used to determine the surface structural features of the tissue paper. The microscope was equipped with laser confocal optics to measure the depth of field across the specimen. LSM uses two light sources, a laser light source with a wavelength of 408 nm and a white light source, to provide image and height information (shape and roughness).
Detection of light intensity and surface height profile
The Gaussian shaped laser beam of LSM had a full width of half maximum of 130 nm at the focus point on the sample surface, defining the spatial resolution. The resulting scanned imaged was divided by a constant number of pixels (2048 × 1536) for all measurements. The depth profile was obtained by driving the objective lens in the Z axis repeatedly. The device read the intensity of each Z position for each pixel, determined the Z axis position of the maximum intensity, and recorded the intensity and color information for that position. The highest intensity was obtained at the focal point in the Z direction, which provided the height profile of the specimen. Based on this information, three types of images were constructed: a deep field color image, a laser intensity image, and a height image (Fig. 3).
Determination of surface waviness
LSM was used to provide local alterations in the surface height profile (i.e., surface roughness), and periodical changes in height at longer intervals (i.e., waviness) (Fig. 4). This information can describe the crepe structure and further the surface topography of the tissue paper.
The waviness profile was analyzed using VK analyzer software (Keyence, Japan) and calculated using “line waviness.” Nine lines were drawn perpendicular to the crepe structure in different locations over the scanned area of the samples. From the line, a primary profile curve graph was recorded, and a phase compensation filter with cut-offs λf = 0.08 mm and λc = 0.8 mm was applied to obtain a waviness profile. The average waviness of the profile (Wc) and arithmetic mean height (Wa) were determined from the waviness profile. They are defined as:
and
where m is the number of periods, Rti is the peak-to-peak amplitude of one full period i, and lr is the sampling length (Fig. 5). Wc is the average of the height of the profile curve elements (peaks and neighboring valleys) along the sampling length. The arithmetic mean waviness (Wa) is the average of the absolute values along the sampling length. Wp/cm is the crepe count per centimeter as measured by the LSM.
Surface waviness was calculated based on the lines using parameters defined in the ISO 4287:1997 (Institution 1997). From the line, a profile curve graph was created, and the average values were then calculated. A phase compensation filter cut-off was applied to the primary curve signal with λf and λc values of 0.08 mm and 0.8 mm, respectively.
Field emission scanning electron microscopy (FESEM)
A field emission scanning electron microscope (FESEM; Zeiss Ultra Plus, Carl Zeiss SMT AG, Germany) was used to study the morphology of the tissue papers in the planar direction. The tissue paper samples were coated with Platinum (Pt), and 3–5 kV acceleration voltage was used during imaging.
X-ray microtomography (XRT)
XRT was performed using a Zeiss Xradia XRM 520 X-ray tomograph (Carl Zeiss, USA). Details about the measuring process and conditions are found in the supplement (S1). The 3D rendering video can be found as supplementary (V1).
MATLAB code
The crepe structure and wave count were analyzed from the XRT image data (S1) using a custom-written script in MATLAB® (MATLAB version 2019a, The MathWorks, Inc., Natick, Massachusetts). Each slice from the tomography volume images was reduced to a single average wave in the x–y plane after removing all small objects in the image. The crepe count was then calculated per measured length.
The MATLAB code first binarized the image stack and then removed all single voxels that are separated from the main structure in the image, producing a “cleaner” image stack (The stack refers to the thickness of the tissue paper as shown in Fig. 6a). Next, individual objects were mapped out in the volume, removing all but the largest objects (i.e., the tissue fibers). The code then reduced the binarized image into a single average wave (line) to the middle of the stack. This procedure was done for all images in the stack (Fig. 6c). From the resulting figure (Fig. 6c), the number of peaks can be calculated (crepe count) which allows quantitative analysis.
Measurement of tissue paper thickness
The paper thickness was measured using a Hanatek FT3 precision thickness gauge (UK) at three different points on the specimen (middle point and the two ends), and the average thickness was calculated.
Results and discussion
Structural characteristics of the tissue paper
As the doctor blade wears down, it affects the crepe structure of the tissue paper, which changes the properties (e.g., softness) of the paper (Ramasubramanian and Shmagin 2000). The crepe count per centimeter and bulk thickness of paper samples—as measured by the paper manufacturer using optical microscope imaging—are shown in Fig. 7. The samples were set perpendicular to the optical field, and the creping wave amount was determined from nine different positions with a sampling length of 5.5 mm. The crepe count varied from 68 to 52 cm−1. With the new blade, the crepe count was around 63 crepes/cm. The crepe count decreased as the blade wore down, reaching 53 crepes/cm at 597 min (~ 18% decrease). The bulk thickness, in turn, decreased from 119 to 88 µm with the new blade (~ 30% decrease). Bulk thickness then increased reaching 108 µm, with a reduction in thickness at the end of the blade operating cycle.
As the blade wore down, the homogeneity of the paper structure decreased, and the crepe waves were more random and had no clear shape. This, in turn, increased the bulk thickness of the single ply. The paper roughness increased, and the peaks became more scattered across the tissue surface.
Analyzing surface topography of tissue paper by FESEM
FESEM images showed significant differences in the surface topography of tissue paper as a function of production time (as the blade wore down) (Fig. 8). By the end of the usage time for the doctor blade, the tissue paper structure was less uniform, with low crepe count per centimeter, incoherent peaks, and poor network structure (sample T-38, Fig. 8a–c). The structure of crepes was also broad, and several defects (e.g., holes and voids) were observed in the network, those surface defects and voids could be also attributed not only to the condition of the doctor blade but also to the network distribution at this given time of the production. These changes likely affect the softness properties of the end-product. After a new doctor blade was installed, a more periodic and homogeneous structure with fewer holes was noted (sample T0, Fig. 8d–f). LSM has the advantage of being a nondestructive method, so it does not affect the wave structure and height of the sample, while FESEM samples need to be treated (using sputtering) for conductivity. This treatment may change the height of the sample and affect the qualitative parameters. However, the clear resolution of the FESEM enabled observation of the fiber structure in detail.
FESEM images of tissue paper samples obtained with the old doctor blade (T-38) showing nonuniform crepe structure (a–c) and immediately after changing to a new blade (T0) showing a more uniform crepe structure (d–f) with different magnifications (90×, 200× and 500× consecutively). The circled areas are to indicate the holes in the surface with bigger holes in the T-38 samples
Analysis of tissue papers by laser scanning confocal microscopy
Both sides of the tissue paper samples were imaged using LSM. The crepe side (top side) (Fig. 9a, b) was clearly visible and distinguishable from the bottom side (the Yankee cylinder side, Fig. 9c, d) of the tissue paper for samples T0 and T-38. When the doctor blade was changed, an immediate enhancement was visible in the creping pattern, as observed with the FESEM analysis. Comparison of the old doctor blade (T-38, Fig. 9a) with a new blade (T0, Fig. 9b) showed that the new crepe pattern was more homogeneous and visible, and it had fewer holes (Fig. 9b).
LSM images of the top (crepe) side of a a T-38 sample and b a T0 sample, and the bottom side of c a T-38 sample and d a T0 sample. The top side of the T0 sample b has uniform crepes while the top side of the T-38 sample a has nonuniform crepe structure. The bottom side is where the paper network is attached to the Yankee cylinder, showing no clear crepe patterns
Waviness determination and surface parameters
The crepe count (Wp/cm) obtained at the end of the working life of the old doctor blade was low (~ 33 crepes). However, the crepe count increased (about 19% or ~ 40 crepes/cm) when a new doctor blade was installed, with a continuous decrease as the blade wore down reaching the value of ~ 25 crepes/cm. The absolute values for the crepes were measured with the LSM (Fig. 10). LSM detected the waviness using a combination of a confocal laser and an optical microscope, which detected the crepe structure more accurately at the given field of view. The LSM counted one wave period, including two zero crossings—the minima and maxima—as one wave. By contrast, in the manufacturer’s method, the crepes are counted manually using an optical microscope, resulting in less accurate counts. In addition, when the cut off values were applied to the waviness structure, all small rough areas that can be mistaken as a full crepe were excluded, increasing the accuracy of the result acquired by the LSM.
The mean waviness (Wa) showed a different behavior than the wave count. That is, the Wa started with a high value (~ 12 µm) with the old doctor blade and decreased when the new blade was installed. However, contrary to crepe count, Wa then increased slightly over time as a function of time, dropping from ~ 13 µm at (0 min) to ~ 9 µm at the end of operation time of the blade (700 min). Thus, when the doctor blade wears down and the length of one period (minima to maxima) becomes long and irregular, increasing the value of Wa.
In contrast to crepe count, the average waviness (Wc) decreased by 18% (from 44 to 37 µm) when a new doctor blade was inserted. Rt values might be high if the waves are not homogenous or if random peaks and valleys are present. The crepes were more periodic and homogenous after the blade was changed, thereby decreasing the Wc. For the same sampling length for all the samples, a lower crepe count resulted in larger amplitudes (with the old blade). When a new blade was in use, crepes were more periodic. This resulted in smaller amplitudes and a decrease in the Wc. The Wc remained between 36 and 40 µm until the processing time reached 400 min, after which it increased until it reached the maximum value of 55 µm at around 700 min. This likely indicated the wearing of the blade as the structure of the crepes became less homogeneous and Wc increased (Ramasubramanian et al. 2011; Ramasubramanian and Shmagin 2000). The decrease in crepe count and the height and structure of the crepes affected the overall end-product quality, and they can indicate the softness of the tissue paper. In addition, as a blade wears down, the integrity of the tissue is altered, which also affects the softness of the end-product.
Distance between the crepes
The distance between crepes was measured from LSM images using a plane measurement tool with the VK analyzer software. In the plane measurement, the width of each crepe was measured first to determine the center. Straight lines were specified from the center of one crepe to the center of the other (3 lines/crepe) and their distance was measured. An illustration of the process is shown in Fig. 11.
The distance between the crepes increased as the blade wore down (Fig. 12). This trend was similar to Wc (Fig. 10c). The increase of the average distance between crepes was fast and almost linear as a function of the operational time of the blade. That distance increased from approximately 160 µm to 390 µm (~ 80% increase). This was also associated with a decrease in the crepe count/area (Fig. 10a). It is likely that the worn blade formed fewer sharp crepes, resulting in wider valleys between the crepes. The increase in the crepe distance affects the perception of the softness of the final product.
Perceptional softness correlation
The hand feel and surface smoothness are factors that distinguish the perceptual softness of the tissue papers (Skedung et al. 2011, 2013). These values—measured by the paper manufacturer—are presented together with the Wp/cm, Wa, and Wc from LSM in Fig. 13. The hand feel follows the same trend as the crepe count, where the Wp/cm is low at T-38, The measured hand feel value is also low at T-38 (corresponding to a higher surface smoothness). For the T0 sample (new doctor blade), the hand-feel peaks and then decreases as a function of the production time. There is a second peak in the hand feel values around T500–T600. This behavior is presumably due to the randomness of the crepe structure that can still be considered as “soft.” When the crepe folds are inhomogeneous, nonperiodic, and long, the surface is perceived as “soft”: because the hand feel cannot differentiate in the micro scale between proper crepe waves and inhomogeneous peaks if they are less than 760 nm in height (Skedung et al. 2011).
The surface smoothness showed the same trend as the mean waviness (Wa). The smoothness is high at T-38, similar to the Wa curve, followed by a decrease and plateau behavior in both the surface smoothness and the Wa data. The waves became periodic and homogenous when a new doctor blade was inserted, which drops the arithmetic mean waviness across the whole width of the paper. As the blade wears down, the waves become less homogeneous (e.g., one crepe can have a low Rt and then the next can have a high Rt, which is shown in the slight increase in the Wa behavior). Surface smoothness slightly increased towards the end of the production time, showing the same trend as the Wa. This increase is due to the fact that more of the inhomogeneous and broad crepes are considered “soft” (Skedung et al. 2013).
3D rendering of the tissue paper structure
The VK analyzer software allows images to be 3D rendered through the z-stack. LSM focus variation captures multiple optical images while the lens moves up and down (Fig. 3). These images were used to construct a 3D shape according to the height of the focus position.
The images in Figs. 14 and 15 depict the crepe pattern and height variation of the tissue paper structure from the analysis of LSM data. The T0 sample (Fig. 14a) illustrates a homogenous crepe pattern with a relatively uniform peak and valley structure, compared to the T-38 sample (Fig. 14b) in which the crepes are randomly located. Moreover, the T0 sample showed a lower maximum height of crepes (140 µm) compared to the T-38 sample (200 µm) (Fig. 15). These features are presumably behind the better hand feel of the T0 sample. Thus, surface roughness and surface height inhomogeneity increased as the blade wore down. Contrary to the popular assumption that only homogenous surface patterns are smooth, micro-scale inhomogeneity can improve the appearance of the tissue surface (Skedung et al. 2013, 2011). As the tissue structure became less homogeneous (e.g., around T500-T600), the average perceptual softness remained and surface smoothness slightly increased. This result likely occurred due to the irregular peaks stacking together to form larger crepes creating a soft surface topography feel (Fig. 15). Indeed, it is reported that the finger cannot differentiate roughness below 270 nm in height (Skedung et al. 2013).
Structural analysis using XRT
XRT allows the visualization of the tissue paper structure in both 2D and 3D images (Fig. 6). The visualization is important in illustrating crepe structure, fiber ends, and thickness of the tissue paper.
Crepe count was calculated from the XRT images using the MATLAB code. The results and comparison between the crepe count from the different methods used in this paper are presented in the supplementary data (S1).
Conclusions
We studied the characteristics of tissue paper using multi-technique characterization methods. The macroscopic and microscopic structural characteristics of tissue paper were measured using FESEM, LSM, and XRT, and they were linked to the production cycle of the tissue paper. FESEM showed the detailed surface topography of the tissue paper, while LSM estimated the topographical structure of the tissue paper. The creping pattern/cm, Wc, and Wa were quantified and compared to the values measured internally by the tissue paper manufacturer, who used optical microscopy. The periodicity and homogeneity of crepe waves were observed to decrease over time as the doctoral blade wore down. However, the Wa, Wc, and Wp/cm showed weak to no correlation with the surface smoothness and hand feel. The XRT data were used to depict the structure of tissue paper in 3D. Using MATLAB, we showed that the crepe count resulting from the XRT image analysis could be close to the crepe count calculated from LSM after taking all measurement and calculation conditions into account (such as small peak counts).
References
Allen DB (1994) Development of a mechanical stylus based surface analysis system for soft paper products Tappi. In: Nonwovens Conference on ProcOrlando FL 133–8
Amos WB, White JG (2003) How the confocal laser scanning microscope entered biological research. Biol Cell 95:335–342. https://doi.org/10.1016/S0248-4900(03)00078-9
Boudreau J, Barbier C (2014) Laboratory creping equipment. J Adhes Sci Technol 28:561–572. https://doi.org/10.1080/01694243.2013.849843
Chinga G, Helle T (2003) Staining with OsO4 in the study of coated paper structure. Pap Ja Puu 85:44–48
Chinga G, Gregersen Ø, Dougherty B (2003) Paper surface characterisation by laser profilometry and image analysis. Microsc Anal 96:21–24
Hamilton DK, Wilson T (1982) Three-dimensional surface measurement using the confocal scanning microscope. Appl Phys B Photophys Laser Chem 27:211–213. https://doi.org/10.1007/BF00697444
Haunschild A, Pfau A, Schmidt-Thümmes J, Graf K, Lawrenz D, Gispert N (1998) Surface of coated papers studied by AFM-Influence of plastic pigments on microstructure and gloss. In: Coating papermakers conference. Tappi Press, pp 301–310
Hermans M, Hada S (2004) Modified conventional wet pressed tissue machine. US6921460B2
Hollmark H (1972) Study of the creping process on an experimental paper machine. STFI-Medd. Ser. B
Hovis DB, Heuer AH (2010) The use of laser scanning confocal microscopy (LSCM) in materials science: use of LSCM in materials science. J Microsc 240:173–180. https://doi.org/10.1111/j.1365-2818.2010.03399.x
Institution BS (1997) BSI standards catalogue. The Institution
Kak AC, Slaney M, Wang G (2002) Principles of computerized tomographic imaging. Med Phys 29:107. https://doi.org/10.1118/1.1455742
McConnel W (2004) The science of creping. Tissue World Am. Miami Beach FL
Minsky M (1988) Memoir on inventing the confocal scanning microscope. Scanning 10:128–138. https://doi.org/10.1002/sca.4950100403
Oliver JF (1980) Dry-creping of tissue paper-a review of basic factors. Tappi 63:91–95
Ramasubramanian MK, Shmagin DL (2000) An experimental investigation of the creping process in low-density paper manufacturing. J Manuf Sci Eng 122:576–581. https://doi.org/10.1115/1.1285908
Ramasubramanian MK, Sun Z, Gupta S (2011) Modeling and simulation of the creping process 7
Raunio J-P (2014) Quality characterization of tissue and newsprint paper based on image measurements; possibilities of on-line imaging. Tampereen Tek Yliop Julk-Tamp Univ Technol Publ 1270
Raunio J-P, Ritala R (2013) Method for detecting free fiber ends in tissue paper. Meas Sci Technol 24:125206. https://doi.org/10.1088/0957-0233/24/12/125206
Rose G (2004) Crepe adhesive modifiers improve tissue runnability. Prod Qual 120:22–26
Skedung L, Danerlöv K, Olofsson U, Aikala M, Niemi K, Kettle J, Rutland MW (2010) Finger friction measurements on coated and uncoated printing papers. Tribol Lett 37:389–399. https://doi.org/10.1007/s11249-009-9538-z
Skedung L, Danerlöv K, Olofsson U, Michael Johannesson C, Aikala M, Kettle J, Arvidsson M, Berglund B, Rutland MW (2011) Tactile perception: finger friction, surface roughness and perceived coarseness. Tribol Int 44:505–512. https://doi.org/10.1016/j.triboint.2010.04.010
Skedung L, Arvidsson M, Chung JY, Stafford CM, Berglund B, Rutland MW (2013) Feeling small: exploring the tactile perception limits. Sci Rep 3:2617. https://doi.org/10.1038/srep02617
Stitt J (2002) Better bond quality between sheet and Yankee dryer coating creates softer tissue. Pulp Pap 76:54–59
Sun Z (2000) Debonding and buckling of a thin short-fiber nonwoven bonded to a rigid surface and its application to the creeping process
Xiao GQ, Corle TR, Kino GS (1988) Real-time confocal scanning optical microscope. Appl Phys Lett 53:716–718. https://doi.org/10.1063/1.99814
Acknowledgments
This work was supported by the I4Future doctoral program, which is part of the European Union’s Horizon 2020 research and innovation program under Marie Skłodowska-Curie Grant Agreement No. 713606. M.Y. Ismail would like to thank UPM-Kymmene Oyj for their constant help providing samples and data. The authors acknowledge the assistance of Mr. Tun Tun Nyo in introducing the working principles of the laser confocal microscopy. The SEM analysis part of the work was carried out with the support of the Centre for Material Analysis, University of Oulu, Finland. In addition, we are deeply grateful for Dr. Sakari Karhula and our colleagues at the Biocentre at the University of Oulu for their assistance with the MATLAB code. Finally, M.Y.I. would like to thank Dr. Amr Hamada for his insightful help with the MATLAB code.
Funding
Open access funding provided by University of Oulu including Oulu University Hospital.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there are no competing financial interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary material 2 (MPG 72326 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ismail, M.Y., Patanen, M., Kauppinen, S. et al. Surface analysis of tissue paper using laser scanning confocal microscopy and micro-computed topography. Cellulose 27, 8989–9003 (2020). https://doi.org/10.1007/s10570-020-03399-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10570-020-03399-w