Angular segregation of fibres in pipe flow: floc formation and utilization for length-based fibre separation

Abstract

Cellulose fibres are prone to flocculate and form aggregates that are deformable by the hydrodynamic stress. In this work I document for coiled pipe flow, known to have secondary motion in the pipe cross-sectional plane, an accumulation of fibre flocs and fibre aggregates at the outer bend. That is the segregation into a section in the pipe cross-section and hence presents a case of angular segregation. The segregation was studied for non-coherent crowded fibre flocs. For that, segregation benefited from fibre concentration and suffered from increased hydrodynamic stress expressed by increasing Reynolds number. Based on the observed segregation of fibres a flow splitter was designed that separated the flow at 1/3 of the tube diameter measured from the inner bend. The outer bend suspension length-weighted fibre length was found to increase. For the best case in this work, the difference between outer and inner bend relative to the feed fibre length was 22%. As for radial and axial segregation, which are known, also angular segregation is fibre-length sensitive. As such it can be exploited for length fractionation of networking and aggregating elongated particles, for example fibres.

Introduction

Highly elongated particles, for example, cellulose fibres, flocculate and form a porous network from elastic interlocking (Kerekes et al. 1985; Soszynski 1987; Soszynski and Kerekes 1988a, b): cohesion from fibre–fibre friction exceeds dispersion, for example from hydrodynamic stress. Whilst the network of flocculated fibres can withstand dispersion at moderate stress, it can undergo deformation (Meyer 1964). The fibre network in suspension flow through straight pipes was found consolidating towards the centre what yields a near-wall annulus free of fibres. Steenberg and Wahren (Steenberg and Wahren 1960) found that this annulus contains small particles, i.e. fibre-fines, that are not coherently incorporated in the fibre network. This describes the case of radial fibre segregation by the fibre length. An illustration is given in Fig. 1 first row, with long fibres consolidated to a radius r_Fibre smaller than the pipe radius R_Pipe. Fibre-fines (i.e. particles smaller than 200 µm (ISO 16,065–2)) are suspended in the pipe cross-section. Redlinger-Pohn et al. (2017a,b) successfully utilized the flow situation for fibre-length fractionation. In a process termed hydrodynamic fractionation, they removed the near-wall suspension essentially free of long fibres by side-channels and hence separated fibre-fines exclusively.

Fig. 1

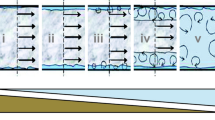
Illustration of fibre segregation in pipe flow as seen from the top and front view. First row: radial fibre segregation in annular plug flow. Fibres are confined to a consolidated network smaller than the tube radius, i.e. r_Fibre < R_Pipe. Fibre-fines are present in the firbes free area, i.e. > r_Fibre. Second row: axial fibre segregation. Fibres and fibre-fines appear in alternating compartments in flow direction z. Third row: angular fibre segregation. Fibres segregate to a segment in the tube cross-section denoted by an angle φ_Fibre < 2π

Axial segregation, illustrated in Fig. 1 second row, is another example of length-based fibre segregation from fibre crowding and network deformation. In principle, it describes the flow of long and short fibres (or fibre-fines) in consecutive compartments, documented by Johansson and Kubát (1956) for fibre suspension slug flow. Within the liquid slug, a secondary motion, that is parallel to the flow direction, arises. The secondary motion is in flow direction at the pipe centre and counter flow direction at the pipe wall. Suspended material is transported to the slug front, i.e. after the bubble, where fibres flocculate and form a plug. Fibre-fines are mixed in the liquid slug and hence tail the long fibres in the transport direction. The principle was utilized commercially for industrial length-based fibre fractionation, for example in the Johnson fractionator (Olgard 1970; Olgard and Axenfalk 1972).

Following the nomenclature of cylindrical coordinates, the question arises on the existence of angular segregation, i.e. segregation and preferential accumulation of fibres in a circular segment of the tube cross-section, i.e. φ_Fibre < 2π, illustrated in Fig. 1 third row. In fact, angular segregation of long fibres was hinted on by Redlinger-Pohn et al. (2016a; b) being the leading mechanism in tube flow fraction. Tube flow fractionation is a commercial preparation technique of cellulose pulp for analytics from Metso (Metso Automation Oy, Finland, (Niinimäki et al. 2007)). The fractionator was introduced by Silvy and Pascal as an auxiliary unit for sample preparation as a “tube of a few hundred meters long which may be rolled up to avoid bulkiness” (Silvy and Pascal 1990). A fibre pulp sample injected into a flow through the coiled tube separated the fibres by their length: long fibres exit the tube first, followed by short fibres and fibre-fines (Laitinen et al. 2006, 2011). That separation result is comparable to axial segregation (compare to Fig. 1 second row Johansson and Kubát (1956)) which led to confusion on the separation mechanism in the literature (Krogerus et al. 2003). The argument based on the outflow results ignores a fundamental difference between slug flow and coiled pipe flow: the secondary motion is parallel to the flow direction in slug flow (Talimi et al. 2012) and normal to the flow direction in coiled-pipe flow (Dean 1927; Vashisth et al. 2008). The cross-sectional mixing flow or secondary motion arises from a pressure imbalance between the outer and inner bend of the coiled pipe resulting from centrifugal forces. In addition, the velocity maximum is deflected from the pipe centre to the coiled-pipe outer bend. The secondary motion is known to (i) re-suspend non-flocculating particles (Koutsky and Adler 1964; Palazoglu and Sandeep 2004) (ii) enhance mixing (Naphon and Wongwises 2006) and (iii) promote colloidal flocculation of polymers (Carissimi et al. 2018). Redlinger-Pohn et al. (2016a; b) compared numerical results of individual fibres transported in the coiled pipe flow to experiments with cellulose fibre samples and argued from differences, that long fibres in coiled pipe flow flocculate. The observed length-separation at the outflow was addressed to differences in the networking capabilities of long and short fibres. The separation quality of 0.3 mm and 4 mm fibres was tested for concentrations yielding non-coherent and coherent flocs. The separation was unsatisfactory for a fibre sample yielding coherent flocs. Further, they documented a decreasing residence time of fibre length fractions with a increasing fibre concentration C (cohesion) and an decreasing Reynolds number Re (dispersion). That agrees with a recommendation in Krogerus et al. (2003) to operate the tube flow fractionator with concentrations below the threshold for coherent flocs. An indication of angular segregation was found by Jagiello et al. (2016) who split the coiled tube outflow in an inner and outer bend flow. The outer bend flow mean fibre length l₁ was larger compared to the inner bend flow with a negative dependence of the length difference on the Reynolds number Re. But doubt remained on the segregation mechanism for two reasons: (i) an opaque tube prevented visual observation, and (ii) the earlier mentioned confusion in literature.

With hindsight on the increased demand for separated fibre and fibre-fines streams for the production of paper and board with dedicatedly set and tuned properties (Odabas et al. 2016; Mayr et al. 2017; Fischer et al. 2017; Bossu et al. 2019), angular segregation and its potential for length-based fibre separation should be re-addressed. Commonly applied pressure screening relies on the individual treatment of each particle, i.e. fibre or fibre-fines, and invests energy to disperse the networked fibres (an overview on pressure screening is for example given by Jokinen (2007)). Processes that can utilize fibre flocculation and fibre networking avoid the need for this extra energy (Olgard and Axenfalk 1972; Redlinger-Pohn et al. 2017a, b; Schmid et al. 2019).

In this paper I will provide visual evidence of angular segregation from coiled suspension flow. This insight and understanding are then transferred into a prototypical separation process. The results are promising and present a simple and straight-forward way of separating fibre pulp by the fibre length.

The paper is organized as follows. In Section 2 I describe the setting for the visual observation and fibre pulp separation. In Section 3 I present the results from both studies. In Section 4 I elucidate the fibre segregation in coiled suspension flow. In Section 5 I conclude the study. The Appendix adds further comments on the observed fibre segregation and contains scaling analysis mentioned in the discussion. The Supplement Material shows the high-speed recordings of flocculating fibres in coiled tube flow.

Materials and methods

The choice of fibre was taken with hindsight on the optical investigation. Dyed fibres have a larger contrast and are less transparent. For simplicity and from availability, mono-coloured napkin tissue paper (Aro Napkins, Metro whole-seller shop brand) was re- slushed after soaking in water for a minimum of 24 h. Availability (in the institute's social room) led to the use of two types of coloured napkins: blue and red. Blue was used for video observation and red for the length-based fibre separation. The properties of the fibre pulp from re-slushed napkins were determined with a L&W Fibre Tester Plus (ABB, Sweden). The mean properties are listed in Table 1. l₁ is the length-weighted and l₃ is the volume-weighted mean fibre-length.

Table 1 Length-weighted (l₁) and volume-weighted (l₃) mean fibre length and average fibre coarseness cs as measured with the L&W Fibre Tester Plus (ABB, Sweden)

The fibre interaction is characterized by the crowding number N_CW (Kerekes and Schell 1992):

$$N_{CW} = 5\,\,\left[ {\frac{kg}{{m^{3} }}} \right]\frac{{C\,l_{1}^{2} }}{cs}$$

(1)

cs is the average line density of the fibre (coarseness in pulp and paper nomenclature) and C the mass-based fibre concentration in [%]. Kerekes and Schell (1992) have shown, that coherent networks form for N_CW ≥ 60 (for a length to diameter aspect ratio AR > 20). Between 16 < N_CW < 60, fibres aggregate and form flocs that are more easily dispersible (Kerekes 2006). For N_CW < 16, fibres interact without flocculation. The concentration in the experiments corresponded to N_CW ranging from 4 to 20. That is within the optimum of N_CW < 60 (Krogerus et al. 2003) and non-coherent flocculation can be assumed.

The experimental setup, sketched in Fig. 2, followed work of Redlinger-Pohn et al. (2016a) and Jagiello et al. (2016) and consisted of a transparent tube, D_Tube = 16 mm, coiled at a diameter of D_Coil = 400 mm. The curvature, $\kappa = {{D_{Tube} } \mathord{\left/ {\vphantom {{D_{Tube} } {D_{Coil} }}} \right. \kern-\nulldelimiterspace} {D_{Coil} }}$, calculates to 0.04. The coordinate h runs along the coil radius R_Coil from the tube inner bend to the tube outer bend.

Fig. 2

Experimental set-up: a transparent tube D_Tube = 16 mm coiled at a diameter D_Coil = 400 mm (R_Coil = 200 mm). The curvature κ = 0.04. The light transmission through the fibre suspension is recorded 1.5 coils from the inlet. The sample is split into an inner bend and outer bend flow after 1.75 coil. h is a coordinate in the direction of the coil radius from the tube inner to the tube outer bend

Greyscale images of the suspension flow were recorded after 1.5 coils from the inlet (0.25 coils from the outlet) at a frequency of 500 Hz. Low transmission and higher grey value correspond to higher fibre concentration. The light absorption is expressed as time-averaged relative light absorption RLA and calculated as the grey image compliment compared to the maximum of 255. The RLA was calculated as mean over 200 recorded images along h. The recorded high-speed videos are presented in the Supplement Material.

The suspension flow was split into an inner and outer bend flow after 1.75 coils from the inlet. The prototypical flow splitter was 3D printed in-house. The design was guided by results from the optical investigation. Details are hence presented in the results section.

A typical metrics to report the condition of a coiled flow is the Dean number Da (see for example (Dean 1927; Itō 1959; Naphon and Wongwises 2006; Vashisth et al. 2008)):

$$Da = {\text{Re}} \sqrt \kappa ,{\text{with}}$$

(2)

$${\text{Re}} = \frac{{U_{Bulk} D_{Tube} }}{\nu }$$

(3)

which characterizes the effect of inertial, viscous, and centrifugal forces on the flow. Re is the Reynolds number, ν the kinematic viscosity, and U_Bulk the average stream-wise velocity. Canton et al. (2017) however showed in a recent and dedicated work that different flow conditions exist for the same Da but different combinations of Re and κ. The experimental settings in this work are hence reported with their Reynolds number Re and curvature κ.

Results

Observation of fibre crowding in coiled suspension flow

Figure 3 provides a visual of the fibre suspension motion in coiled suspension flow observed from a top view. The case fibre concentration C, corresponding crowding number N_CW, and Reynolds number Re (based on the mean flow rate, D_Tube, and the viscosity of water as a reference, ν = 10^–6 m²/s) are stated for each case. N_CW is calculated according to Eq. 1 with values for Blue (Table 1).

Fig. 3

First frame of each case recorded video (full video in the Supplement Material). The images state the case label letter (a–f). The flow direction is from the left to the right of the image. The light absorbance, i.e. higher grey value, corresponds to the local fibre concentration C. The exposure time, fibre concentration C, crowding number N_CW and Reynolds number Re is stated for each case. Local fibre crowds or aggregates are indicated by a white frame. b evaluation position for the time-averaged light absorption shown in Fig. 4. e and f the inner pipe bend area is bright from over-exposure. The exposure time was adjusted to the higher concentration at the outer bend

Recordings in Fig. 3 capture fibre segregation to the outer tube bend and the formation of flocs already at a low crowding number of N_CW = 8. The fibre crowding benefits from the fibre concentration C and suffers from increased hydrodynamic stress, i.e. higher Reynolds number Re. The time-averaged RLA profile along h (from the inner to outer tube bend) is shown in Fig. 4, at a position, indicated in Fig. 3B. The error bar is 5 times the standard deviation of the RLA in time and hence an indicator of the local fibre crowding. RLA standard deviation is high for large temporal (or in stream-wise direction) differences in the local fibre concentration.

Fig. 4

Relative light absorbance along h for cases presented in Fig. 3. Re = 9000 in grey and Re = 19,000 in black. a C = 0.04%, N_CW = 4. b C = 0.07%, N_CW = 8. c C = 0.18%, N_CW = 18. The error bar is 5 times the standard deviation in RLA and presents a fluctuation of the local fibre concentration with time

At N_CW = 4 (Fig. 4a) RLA was nearly constant with a slim increase towards the outer bend for Re = 9000. The fibres were well distributed in the tube. At N_CW = 8 (Fig. 4b) RLA increases between h = 0.2 to h = 0.7 from the inner bend to the outer bend at Re = 9000. Fibres were segregated to the outer bend. The difference between outer and inner bend was significantly lower at Re = 19,000. That documents a dispersion of fibre aggregates at increased hydrodynamic stress in the coiled tube flow. At N_CW = 18 (Fig. 4c) RLA was significantly higher at the outer bend for both Re cases. The inner bend area was however over-exposed, and a small concentration of fibres may have been concealed by the bright background. Noteworthy is a subtle difference from increased Re at N_CW = 18 (Fig. 4c): RLA at the outer bend was slightly decreased. Also in Fig. 3f bright spots that indicate fibre depletion can be identified what differs from the situation at lower Re (Fig. 3e). This difference will be addressed in the discussion. The RLA standard deviation is low for N_CW = 4 (Fig. 4a). The fibres were well-dispersed also in stream-wise direction and no flocculation of significance was observed (Fig. 3a, b). The RLA standard deviation is also low for N_CW = 18 (Fig. 4c). Fibres were observed flocculated and segregated to the outer bend. The local fibre concentration with time (or in stream-wise direction) was low. An exception is the outer bend area at Re = 19,000: RLA is not only decreased but also varying in time. The RLA standard deviation is comparatively high for N_CW = 8 (Fig. 4b). At Re = 9000, fibres were observed aggregating into distinguishable flocs (Fig. 3c) with an increasing RLA towards the outer bend (Fig. 4b, grey line). The RLA standard deviation is large at the inner bend which suggests dynamic local fibre flocculation and dispersion. Figure 3c documents some of the fibre aggregates segregated to the outer bend appearing stretched towards the inner bend. That will be addressed in the discussion.

Table 2 Separation results from splitting the coiled pipe flow. Δl_1,rel is the difference of the outer bend to inner bend l₁ relative to the feed l_{1, Feed}

The fibre suspension flow through the coiled tube from observation (videos are included in the Supplementary Material) is described in detail in the Appendix, Table 3.

Length-based separation of fibre pulp

Observations of the suspension flow showed segregation of flocculated fibres to the outer bend, i.e. h > 0.3. The flow splitter was designed accordingly and separated the inner from the outer bend flow at h = D_Tube/3. The prototypical flow splitter as realized by 3D printing is presented in Fig. 5. Two areas are highlighted: the splitter blade in red and an area of observed flow recirculation in orange.

Fig. 5

CAD model cut for 3D printing of the flow splitter. The inner bend suspension flow was split from the outer bend suspension flow at h = D_Tube/3. The yellow area marks a zone of lower pressure and observed fluid recirculation. The red area marks the flow splitter which is prone to fibre stapling

A splitter blade, i.e. a sharp edge in flow direction, is known to accumulate fibres by stapling. Kerekes et al. (1985) for example used it as floc generator, and Eßl (2017) showed that even openings larger than the fibre length can clog from stapling at low flow speed. The area of the inner bend section is smaller than the outer bend section, and the velocity is higher at the outer bend (high velocity counters stapling. See for example (Eßl 2017)). Speculative, stapled fibres could impact the ratio of flow split and change the separation quality by being re-entrained at the outer bend or inner bend flow. The impact of the splitter blade on the fibre separation quality was not attained in this proof-of-concept. For the inner bend outflow, the expansion led to a region of lower pressure and a recirculation which impacted the upstream flow. The test settings and average results for the separation proof-of-concept study are listed in Table 2. The first two settings correspond to case D (Fig. 3d) and case F (Fig. 3f).

The results of the separation study (Table 2) agree well with the visually observed fibre segregation (Fig. 3). Separation 1, N_CW = 11 and Re = 19,436 was characterized by a homogenous fibre distribution. The inner bend suspension and the outer bend suspension mean fibre length l₁ was comparable and the difference Δl_1,rel was only 4% of the feed l_1,Feed. Separation 2, N_CW = 21 and Re = 19,206 was characterized by fibre segregation to the outer bend. The difference in the mean fibre length from the outer bend suspension to the inner bend suspension Δl₁ was 0.335 mm and Δl_1,rel = 22% of the feed fibre length l_1,Feed. RLA (Fig. 4c) was found increased from h > 0.3. The third case, N_CW = 20 and Re = 25,356 has no corresponding case in the visual observation study. Higher Re from increased fluid motion can deform or disperse a fibre network. Here I found Δl₁ = 0.262 mm, what is Δl_1,rel = 22% of the feed fibre length l_1,Feed. A reduction in the separation quality Δl_1,rel compared to case 2 of 20% for an increase in the treated suspension flow rate of 24%.

Despite the flow splitter design faults, measured differences in the inner bend and outer bend fibre-length distribution (Table 2) agree well with the observation of the fibre aggregation shown in Fig. 3. Further, it is proof, that the observed segregation is preferent for longer fibres and hence full-fills the case of angular length-based fibre segregation as described in the introduction (compare Fig. 1 third row).

Discussion

The argument of length-based fibre segregation stems from the observed fibre aggregation at the outer bend and a measured increase of l₁ in the corresponding case. The fibre suspension motion in the cross-section was inaccessible in this study. The nature of the flocculation phenomena will be elucidated based on a comparative literature discussion. Surprisingly, the cross-sectional flow field in coiled pipe flow (Fig. 6: fluid only, corresponding to cases in Redlinger-Pohn et al. (2016a), Re = 3316, κ = 0.043) and the flow field in a semi-filled horizontal rotating cylinder, i.e. Jacqueline floc generator (Fig. 7, adapted from Soszynski (Soszynski 1987)) show similarities. Both are characterized by a larger mixing vortex which stretches the half-pipe cross-section with respect to the equatorial/horizontal centre plane.

Fig. 6

Secondary motion of coiled pipe flow at Re = 3316 and κ = 0.043 presented in Redlinger-Pohn et al. (2016a). White arrows present the flow direction and the secondary velocity U_Sec magnitude is given by the contour colour. The upper half indicates deacceleration (solid ellipse) and acceleration (dashed ellipse) zones in the cross-section. The upper half is overlaid with the position of fibre segregation h (Fig. 4) and corresponding segment φ. Indices relate to cases in Fig. 3

Fig. 7

Secondary motion of a flocculating fibre suspension, in a semi-filled horizontal cylinder, rotating at ϖ = 2π rad/s. The flow field is presented by the arrows. The solid ellipse presents the deacceleration zone with observed flocculation. Figure adapted from Soszynski (Soszynski 1987)

Soszynski (Soszynski 1987) reported for fibre suspension flow in the Jacqueline floc generator:

• (i) temporal aggregation of fibres for a concentration below the rigidity threshold (N_CW < 60),

• (ii) the formation of coherent flocs for higher concentration in the deacceleration zone (marked by a solid ellipse in Fig. 7 at r/R = 0.6 and angles of 50° to 90°),

• (iii) which is characterized by a sharp velocity gradient, i.e. change from upwards-outwards flow to inwards flow.

• (iv) The flocs withstood dispersion from hydrodynamic stress when moving through the cylinder cross-section and compacted when re-entering the flocculation zone.

Soszynski (1987) suggested, that a cyclic flow through acceleration and deacceleration zones is required for flocculation. Both zones are present in the secondary motion of the coiled pipe flow (Fig. 6). Focusing on the secondary motion, fibres move through (i) a deacceleration zone at the inner bend centre, and (ii) an acceleration zone at the outer bend wall. Both areas are indicated in Fig. 6, cross-section upper half as full and dashed ellipse, respectively. The position h of changes in RLA (Fig. 4) is drawn on-top of the flow field. h = 0.5 corresponds to the location of the secondary velocity maximum and h = 0.3 corresponds to the location of a vortex at the inner bend which directs the suspension towards the tube centre. A clear crowding and floc formation event was not observable from the tube top-view recordings (Fig. 3 and Supplementary Material). But for Case C (Fig. 3c), N_CW = 8, a deformation of flocs at the outer bend and thinning of the fibre flocs at h≈0.5 was noted. And a high standard deviation in RLA was recorded (Fig. 4b, grey line). The results suggest, that the formed fibre aggregates did not withstand dispersion by the secondary motion fully. Instead, fibres did undergo a dynamic dispersion and aggregation process in the cross-section. For a higher fibre concentration, case E (Fig. 3e) with a bulk crowding number N_CW of 18, no comparable dispersion event was noticed. Additionally, the deformation of the aggregates at the outer bend observed for case C was not observed for case E.

The mixing flow in a coiled pipe differs from the mixing flow in the Jacqueline floc generator by centrifugal forces acting in direction of the coil radius R_Coil (or h) and the contribution of an axial (stream-wise) flow. Centrifugal forces may lead to sedimentation of the fibres and/or fibre aggregates towards the outer bend in addition to their transportation by the secondary motion. An estimation of scales is provided in the Appendix. The contribution of centrifugal forces increases with the curvature κ (which was constant in this study) and the Reynolds number Re. For the highest value, i.e. Re = 25,356, the ratio of the sedimentation velocity from centrifugal forces and the secondary motion at the equatorial centre plane is 0.09. Hence, centrifugal forces can be neglected and the fibre motion and segregation documented in this study can be attributed to the flow secondary motion. The mixing flow in the coiled pipe is imposed on a stream-wise flow. The maximum velocity of the stream-wise flow is shifted to the outer bend, i.e. h = 0.92 for the case of Re = 3316 and κ = 0.043 (Redlinger-Pohn et al. 2016a), and Appendix Fig. 8). Fibre flocs and aggregates moving from the inner bend to the outer bend hence move through an additional acceleration zone into an area of local high shear at the outer bend. Fibre aggregates in case C (shown in Fig. 3c) were accordingly deformed in flow direction. The RLA for case F is lower than for case E at the other bend (Fig. 4c) what agrees with a local dispersion of fibres aggregates in the high shear zone at the outer bend.

Fig. 8

Coiled pipe velocity profile at Re = 3316 and increasing curvature κ. Corresponding to Redlinger-Pohn et al. (2016a). a the stream-wise velocity component U_stream relative to the mean velocity U_mean at the horizontal mid-plane is plotted form the inner bend to the outer bend along h. The velocity maximum is deflected to the outer bend for curvature κ = 0.04 and 0.1 and is found at h = 0.92. b 3D visualization of the coiled pipe flow profile. The stream-wise velocity maximum at the outer bend and mixing vortex at the inner bend is highlighted

For straight pipe flow it was shown that for formed fibre networks, the fluid moves at the same speed as the network what results in a plug flow velocity profile (Jäsberg and Kataja 2009; Nikbakht et al. 2014; MacKenzie et al. 2018). Likewise, Soszynski (1987) documented that the flow profile for the case of temporal fibre aggregation and the case of coherent floc formation differed slightly. It is conceivable, that fibre aggregates in the flocculating coiled fibre suspension flow modified the flow field locally. The state of fibre flocculation in straight pipe flow was correlated to the pressure loss curve (see for example (Duffy et al. 1976; Hemström et al. 1976)). Similar measurements can be envisioned to characterize the fibre flocculation in coiled pipe flow and map the flocculation in the Re-κ space in future work (see for inspiration the work of Itō (1959) on the friction factor in coiled suspension flow and Canton et al. (2017) for a recent discussion).

The angular segregation was studied below the rigidity threshold N_CW < 60 where non-coherent fibre aggregation is expected. In the regime, the angular segregation benefited from a higher fibre concentration C, i.e. increased fibre floc strength and a lower Reynolds number Re, i.e. increased dispersion from hydrodynamic stress. That is unique for flocculation from elastic interlocking and different from colloidal flocculation of polymers which also benefits from higher Re (Carissimi et al. 2018). It raises the question if dispersion, respectively re-suspension, is needed for angular segregation for what it may be limited to the regime of non-coherent flocs, i.e. N_CW < 60. That limit was reported for the treatment of fibre samples injected into coiled pipe flow (Krogerus et al. 2003) and should be addressed for continuous fibre suspension flow in future studies. A second limitation not discussed here is the tube size of D_Tube < 50 mm (Krogerus et al. 2003). It is conceivable, that the velocity gradient for larger tube diameter as seen by the fibre simply becomes too small to promote flocculation (for example for l₁ = 1 mm, the ratio D_Tube/l₁ = 50). Soszynski noted steeper velocity gradients for flocculation in the Jacqueline floc generator as compared to the non-flocculating case (Soszynski 1987). The flow field for flocculation in coiled pipe flow can be addressed in future studies experimentally, for example by magnetic resonance velocimetry (MacKenzie et al. 2018) or numerically as the motion of interacting flexible elongated particles (Tozzi et al. 2005; Schmid et al. 2000; Lindström and Uesaka 2007).

Length-based fibre separation by flow splitting was documented in this study for a fibre suspension propagating 1.75 coil through a tube with D_Tube = 16 mm at κ = 0.04 what equals a tube length of 2.2 m. That is by two orders of magnitude shorter than the tube of, for example, 100 m length, used by Silvy and Pascal (1990) and work thereafter. That difference comes from two different attributes of the coiled flow causing angular segregation and axial separation. A scaling analysis is provided in the Appendix. Angular segregation results from mixing in the cross-section and consequent segregation of networked fibres towards the outer bend. The minimum tube length for this study setup was estimated from the Dean vortex turn-over time (i.e. a particle is mixed in the cross-section once) to 1 m. Axial separation results from the stream-wise velocity difference and the fact that fibres aggregated at the outer bend are entrained in the faser flow (see Fig. 9 in the Appendix). The aggregate mean velocity at the outer bend was measured from the recorded images (Fig. 10 in Appendix) to 1.1 times the average velocity. To achieve a good enough separation resolution in the axial direction, i.e. time interval of two consecutive samples of at least 5 s, a 100 m long tube is needed.

Fig. 9

Relevant velocities and forces on a particle suspended in a coiled flow. F_C is the centrifugal force in coil radius direction R_Coil. U_S,L is the average velocity at the outer 2/3rd of the pipe. U_E and U_C are components of the secondary motion at the equatorial centre plane and along the circumference, respectively. U_sed,a is the sedimentation velocity in the centrifugal acceleration field

Fig. 10

Propagation speed of a flock, here for case C (Re≈9000, κ = 0.04, compare to Fig. 3). The tube segment length was measured to 5.73D_Tube. The traced fibre flock is pictured after 20, 40, and 72 frames and remained for total 76 frames in the segment

A separation effect in direction of h was recently also documented for rectangular coiled channels. Wang et al. (2020) separated ca. 1 µm long (l₁) cellulose-fibrils from smaller fibrils. The longer 1 µm fibril was found accumulating at the outer bend of a 45 µm high (H_Channel) and 300 µm wide channel. For micro-particles, a separation from the complex interplay of lift-force and drag force from the secondary motion (Ookawara et al. 2006; Di Carlo 2009; Redlinger-Pohn and Radl 2017) is known. Redlinger-Pohn and Radl (Redlinger-Pohn and Radl 2017) have shown that the accumulation at the outer bend appears only for confinements H_Channel/l₁ < 13. In Wang et al. (2020) the confinement was H_Channel/l₁ = 45 and the fibres were highly elongated. As in previous studies on fibre tube flow fractionation, only the resulting suspension properties are known but the process itself is a black box. Cross-sectional mixing may also promote aggregation of highly elongated particles in the nm and µm size range. Certainly, that should be addressed in future studies.

Summary and conclusions

In this work I documented the fibre flocculation and fibre aggregation in coiled suspension flow at comparable low crowding number, i.e. N_CW = 8 for Re = 9000. The formed aggregates segregated towards the outer bend of the coiled pipe, which presents angular segregation in pipe flow, i.e. fibre accumulation in a circular segment of the tube cross-section. The angular segregation was studied for cases below the rigidity threshold N_CW < 60, hence non-coherent fibre flocs, and a tube diameter of D_Tube = 16 mm (D_Tube/l_1,Fibre = 8 to 10). Literature notes upper limitation for the pipe diameter (D_Tube < 50 mm) and fibre concentration. Those should be addressed in future studies. The quality of the angular segregation was probed by flow splitting after 1.75 tube coil (ca. 2 m tube length). The flow splitter design was based on the observation results. The flow was separated in an inner bend flow and an outer bend flow at 0.3D_Tube in the coil radius R_Coil direction. The spread in mean fibre length l₁ between outer and inner bend suspension flow was 22% maximum.

For the studied cases, I found the fibre segregation benefiting from an increased fibre concentration and suffering from increased hydrodynamic stress, i.e. higher flow velocity expressed by a higher Reynolds number. The segregation of fibre aggregates to the outer bend was documented after 1.5 coils, ca. 2 m but may already be found after 1 coil, i.e. 1 loop, based on an estimated secondary motion turn over time. That raises an interesting question of whether fibre pulp suspensions transported through pipes are mixed or segregated in pipe bents and turns. In this study, I document angular fibre segregation as a promising route for pulp fibre separation by the length. This observation may also explain the documented separation of cellulose nano-fibrils in coiled channel flow (Wang et al. 2020). But some key work for future utilization of coiled pipe flow for the length-based fibre separation remains to be done. The understanding of the fibre flocculation in the Reynolds number Re and curvature κ space should be refined. A comparison of the coiled fibre suspension pressure drop to the pressure drop of coiled water flow (Itō 1959) may allow a quantification of the state of flocculation. Phase-contrast magnetic resonance velocimetry (MacKenzie et al. 2018) may allow the direct measurement of the cross-sectional flow profile what allows a detail discussion of the fibre aggregation and dispersion process. The design of the axial flow splitter should be rethought, or replaced by other flow-splitting strategies, for example side-channel splitting as used in hydrodynamic fractionation (Redlinger-Pohn et al. 2017b).

Appendices

Appendix

See Figs. 8, 9, 10.

Notes on the fibre motion

Table 3 summarizes the fibre motion observation from the video recordings (Supplement Material) for the studied combinations of Reynolds number Re and fibre concentration C. The case labeling corresponds to the case labeling in Fig. 3.

Table 3 Description of the suspension motion from flow observation. Case labeling corresponds to the labeling in Fig. 3

Fluid motion in coiled pipe flow

The curved flow induces centrifugal forces in direction of the coil radius and causes a pressure difference between the inner bend I and the outer bend O. The pressure difference gives rise to a secondary motion in a plane normal to the flow direction, i.e. the pipe cross-section. The velocity maximum is shifted from the tube centre toward the outer bend O, i.e. h = 0.92. The change of the streamwise velocity profile along h with the curvature κ is presented in Fig. 8a. Figure 8b shows the profile of a coiled pipe flow: secondary motion imposed on the stream-wise flow. Simulation results correspond to cases discussed in Redlinger-Pohn et al. (2016a): Re = 3316 and κ = 0.00 (pipe), κ = 0.04 (this work), κ = 0.10.

Centrifugal sedimentation of fibres in pipe flow

The centrifugal force in R_Coil or h direction differs with the density and leads to sedimentation of heavier particles, for example fibres with a density ratio to water of 1.3 (Redlinger-Pohn et al., 2016a), to the outer bend. The significance of sedimentation in the centrifugal field is estimated from a comparison of the sedimentation velocity in the centrifugal field U_sed,a to the secondary motion at the equatorial centre plane U_E (from the inner bend to the outer bend) and along the circumference U_C (from the outer bend to the inner bend). The quantities are described in Fig. 9. The magnitude of the secondary motion was estimated from Redlinger-Pohn et al. (2016a) to be U_C = 0.15U_Bulk and U_E = 0.02U_Bulk (see Fig. 6).

The fibre sedimentation velocity can be calculated from the force balance on the fibre,

$$0 = F_{C} - F_{A} - F_{H} = \left( {\rho_{F} - \rho_{W} } \right)V_{F} a_{z} - F_{H}$$

(4)

where F_A is the buoyancy force opposite to the centrifugal force F_C and F_H is the hydrodynamic drag force. ρ_F and ρ_W are the fibre and water density, respectively. The drag force coefficient c_d for a fibre scales with its aspect ratio AR (i.e. the ratio of the fibre length l to the fibre diameter d) and depends on fibre orientation with respect to the direction of acceleration (see for example (Fan and Ahmadi 1995)). The drag force coefficient for a fibre orientated parallel (c_d,p) and normal (c_d,n) to the direction of acceleration is:

$$c_{d,p} = \frac{{8\left( {AR^{2} - 1} \right)}}{{\left[ {{{\left( {2AR^{2} - 1} \right)\ln \left( {AR + \left( {AR^{2} - 1} \right)^{0.5} } \right)} \mathord{\left/ {\vphantom {{\left( {2AR^{2} - 1} \right)\ln \left( {AR + \left( {AR^{2} - 1} \right)^{0.5} } \right)} {\left( {AR^{2} - 1} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {AR^{2} - 1} \right)}}} \right] - AR}}$$

(5)

$$c_{d,n} = \frac{{16\left( {AR^{2} - 1} \right)}}{{\left[ {{{\left( {2AR^{2} - 3} \right)\ln \left( {AR + \left( {AR^{2} - 1} \right)^{0.5} } \right)} \mathord{\left/ {\vphantom {{\left( {2AR^{2} - 3} \right)\ln \left( {AR + \left( {AR^{2} - 1} \right)^{0.5} } \right)} {\left( {AR^{2} - 1} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {AR^{2} - 1} \right)}}} \right] - AR}}$$

(6)

The hydrodynamic drag force is formulated as:

$$F_{H} = \eta \pi \frac{l}{2AR}c_{d} U_{sed,a}$$

(7)

η is the fluid dynamic viscosity. The orientation of individual fibres in coiled suspension flow was reported by Redlinger-Pohn et al. (2016a) to be in stream-wise direction and hence normal to the direction of sedimentation. Combining Eq. 7 with Eq. 4 and Eq. 6 allows solving for U_sed,a. The centrifugal acceleration, $a_{z} = 2{{U_{Bulk}^{2} } \mathord{\left/ {\vphantom {{U_{Bulk}^{2} } {D_{Coil} }}} \right. \kern-\nulldelimiterspace} {D_{Coil} }}$, is 1.57 m/s² and 7.08 m/s² for Re = 9000 and Re = 19,000, respectively. Estimations (Table 4) are attained for a fibre with length l = 5 mm and an aspect ratio AR = 100 in water with η = 1 mPa^.s and ρ_W = 1000 kg/m³.

The relative magnitude of sedimentation in the centrifugal field increased with the Reynolds number Re and curvature κ as D_Coil decreases. The latter was constant in this study. The impact of sedimentation from centrifugal acceleration at settings in this study is small.

Table 4 Estimation of the fibre sedimentation velocity in the centrifugal field of a coiled suspension flow in comparison to the secondary motion

Further, fibres at the studied concentration interact and are not individually suspended. A fibre network or fibre aggregates can be viewed as large porous particles. The aggregate density is close to the density of water. Networks withstanding dispersion can deform (for example consolidation towards the outer bend). The deformation from the centrifugal acceleration needs to be regarded again in relation to the impact of the secondary motion. Fibres locked in the network may have a lower, close to 0, velocity in h or R_Coil direction. For that, hydrodyamic drag forces from the secondary motion would deform the network. From the estimation in Table 4 can be argued that network deformation form the secondary motion drag force is larger than deformation from the centrifugal force. Hence, fibre motion, aggregation, and dispersion for cases discussed in this paper can be attributed to the secondary motion.

Scaling angular segregation and axial separation in coiled tube flow

Angular segregation was observed in this study after 1.5 coils what equals a tube length L_Tube of 1.9 m ($L_{Tube} = 1.5D_{Tube} \pi \kappa^{ - 1}$, with D_Tube = 16 mm). That is much shorter than a 100 m tube used in tube flow fractionation to attain axial separation of a pulp sample (Silvy and Pascal 1990; Laitinen et al. 2011; Jagiello et al. 2016; Redlinger-Pohn et al. 2016a).

Cause for angular segregation is the mixing in the pipe or tube cross-section by the secondary motion. A mixing time t_Mix can be estimated for a particle entrained in a Dean vortex, spanning the half cross-section (Dean vortex turn-over time). The particle moves in the cross-section from the outer bend to the inner bend along the tube half-circumference at a speed U_C and along the equatorial/horizontal centre plane at a speed of U_E (see Fig. 9).

$$t_{Mix} = \frac{{D_{Tube} \pi }}{2}\frac{1}{{U_{C} }} + D_{Tube} \frac{1}{{U_{E} }}$$

(8)

The propagation in stream-wise direction L_P can be estimated as the product of the mixing time t_Mix and the mean stream-wise velocity U_Bulk:

$$L_{P} = t_{Mix} U_{Bulk} = \frac{{D_{Tube} \pi }}{2}\frac{{U_{Bulk} }}{{U_{C} }} + D_{Tube} \frac{{U_{Bulk} }}{{U_{E} }}$$

(9)

The propagation per tube coil L_P,Coil for one turn-over is attained form comparing L_P to the coil length, i.e. the circumference of the coil with D_Coil = k⁻¹D_Tube.

$$L_{P,Coil} = \frac{{L_{P} }}{{L_{Coil} }} = \frac{{L_{P} \kappa }}{{D_{Tube} \pi }} = \kappa \left( {\frac{1}{2}\frac{{U_{Bulk} }}{{U_{C} }} + \frac{1}{\pi }\frac{{U_{Bulk} }}{{U_{E} }}} \right)$$

(10)

With U_C = 0.15U_Bulk and U_E = 0.02U_Bulk propagation length calculates to L_P = 1 m and L_P,Coil of 0.77 (with D_Tube = 16 mm and k = 0.04). Observations of angular segregation and length-based separation in this paper were attained at approx. twice this value, hence, two theoretical turn-over in the tube cross-section from the secondary mixing motion.

Fibre aggregates segregated to the outer tube bend are entrained in a faster stream-wise flow (see Fig. 8). Hence, the mean stream-wise velocity of longer fibres U_S,L is higher than the mean stream-wise velocity of non-aggregated or non-flocculated and in the cross-section mixed shorter fibres or fibre-fines U_S,F. The separation time t_TF between fractions scales with the difference in mean stream-wise velocity and the tube length L_TF:

$$t_{TF} = L_{TF} \left| {\frac{1}{{U_{S,F} }} - \frac{1}{{U_{S,L} }}} \right|$$

(11)

The fibre aggregates velocity at the outer bend was estimated by tracing fibre flocks in the imaged tube segment (an example is given for case C in Fig. 10. The corresponding video is in the Supplement Material). The tube segment was measured to 5.73D_Tube length and the fibre flock is tracked for 76 frames, taken at a frame rate of 500 Hz.

The propagation velocity calculated to 0.603 m/s. The bulk velocity at Re = 9000 is U_Bulk = 0.56 m/s (Table 4). The relative fibre velocity calculates to U_S,L≈1.1U_Bulk. That agrees with the average streamwise velocity along the equatorial centre line from h = 0.33 to h = 1 of ca. 1.13U_Bulk from fluid simulations (Fig. 8). Fibre-fines and small particles can be assumed well mixed in the cross-section and their mean velocity U_S,F≈1U_Bulk. The tube flow fractionation sampling interval t_TF in previous work was adjusted to the flow rate being a minimum 5 s (Jagiello et al. 2016; Redlinger-Pohn et al. 2016a). For a case of Re = 9000 and D_Tube = 16 mm, the minimum tube length to attain measurable axial separation calculates to 31 m. That is an order of magnitude larger than the propagation length for angular segregation. Further, the axial separation attained by tube flow fractionation is not ideal in long fibres and fibre-fines but in consecutive compartments of decreasing fibre length. Hence, the tube length needs to be appropriate long to achieve attainable axial separation. That may explain the “tube of a few hundred meters” used by Silvy and Pascal (1990) and in succeeding work (Laitinen et al. 2011; Jagiello et al. 2016; Redlinger-Pohn et al. 2016a). Redlinger-Pohn et al. (2016a) reported the relative residence time per fibre fraction τ_L from separation in a 100 m tube with D_Tube = 16 mm coiled at κ = 0.043. The Reynolds number was Re = 6926. The residence time is inversely correlated to the fraction specific mean propagation speed U_S,L (${U}_{Bulk}/{U}_{S,L}={\tau }_{L}$). Table 5 lists U_S,L calculated from the fraction residence time in Redlinger-Pohn et al. (2016a) for sulfite pulp, 0.25 wt% (Redlinger-Pohn et al. 2016a), and t_TF as difference from the longest fibre fraction. t_TF for fibre-fines after 100 m separation was measured by them to 21.6 s.

Above, I estimated a tube length of 31 m for t_TF = 5 s (and U_S,F = 1.1U_Bulk). Scaling the separation time t_TF to a 100 m tube and accounting for the different flow rates (scaled by the Reynolds number ratio 9000/6926 as the same viscosity of water and tube diameter D_Tube are used as reference) results to 21.0 s. The axial separation measured from tube flow fractionation (Redlinger-Pohn et al. 2016a) and estimated from angular segregation agree well.

Table 5 Fibre length fraction, stream-wise propagation velocity per fraction U_S,Fraction and fraction separation time t_TF. Values from Redlinger-Pohn et al. (2016a)

The aggregation of fibres and their angular segregation is quick. The difference in the mean stream-wise velocity of the fibre aggregates at the outer bend to the mean bulk velocity is small, and separation in axial direction hence needs residence time within the tube. The tube length for tube flow fractionation, i.e. 100 m, is hence longer than the tube length for flow-splitting after angular segregation, i.e. 1 m. This analysis also suggests that the choice of tube length can tune the separation achieved by tube flow fractionation.