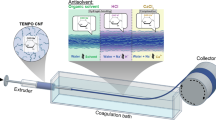
Abstract
In this paper, we report new results related to the development of a novel regenerated cellulose fiber process of the Lyocell type, denoted Ioncell™, and characterized by the use of a powerful direct cellulose solvent, 1,5-diaza- bicyclo[4.3.0]non-5-enium acetate ([DBNH][OAc]) a superbase-based ionic liquid (IL). The focus of this work is on the effects of air gap conditioning (AGC) during the dry-jet wet spinning operation. The installation of an AGC system on the spinning line led to significant improvements of the fiber properties. The fiber titer variation decreased significantly, and the fiber toughness increased by approximately 50% when controlling the temperature and the relative humidity in the airgap using a convective air flow. The presence of water vapor in the air stream was a determinant factor for the improvement of the fiber elongation. The interaction of water vapor with the spinning dope was investigated using dynamic vapor sorption. The diffusion coefficient of water vapor inside the dope could be identified from those experiments and used in a numerical simulation model of the heat and water vapor transfer in the air gap between the spinning dope and the surrounding air. The experimental and simulation results suggest that dope convective cooling and surface hydration lead to a higher fiber toughness.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Ioncell® is a new Lyocell-type process to produce man-made cellulosic fibers (MMCFs). It is based on the direct dissolution of a cellulose substrate, preferably a dissolving pulp, in an ionic liquid (IL), air gap (AG) spinning of the solution (spinning dope) in a water bath, and a subsequent solvent recovery step in which the IL, H2O and impurities generated are separated. The entire process is operated in a closed loop (Michud et al. 2016b, c).
The AG is the vertical distance separating the exit of the spinneret and the coagulation bath surface. It is an important part of Lyocell-type dry-jet wet spinning processes and allows the simultaneous use of a spinneret at 70–90 °C and a coagulation bath at 10–20 °C. More importantly, the incipient filament can be stretched in the AG. This so-called draw creates a uniaxial stress tensor in the filament and results in pronounced polymer orientation. The resulting fibers have good mechanical properties and linear density values suitable for both textile and technical applications.
Several phenomena happen in the AG:
The filament temperature decreases by heat transfer from the filament to the surrounding atmosphere.
The IL components can evaporate from the dope, and water vapor can diffuse from the surroundings into the filament.
Due to the draw, the incipient filament accelerates towards the bath and its diameter decreases.
The cellulose chains are oriented in the axial direction due to the draw.
The incipient filament viscosity shows a gradient along the AG due to the temperature variation in the filament, changes in moisture content, and strain hardening of the stretched filament.
Air gap conditioning (AGC) has been studied extensively for the Lyocell process based on N-methyl morpholine N-oxide (NMMO) monohydrate as a cellulose solvent. Sold by Lenzing AG under the tradename Tencel™, it had a market volume of ca. 220,000 annual tones in 2018, with another 100,000 tons plant being built currently (The fiber year 2019). It is thus the most important man-made cellulosic fiber alternative to the viscose process (currently 5.6 Mio. annual tons).
The discovery of the significance of the AGC was critical for the successful Lyocell process scale-up. Several patents followed its discovery (White et al. 1994; Schwanninger et al. 1995; Jürgen 1996), and since then, understanding the mechanism to enable design optimization has been a high research priority.
For instance, Mortimer et al. (1996) studied the influence of AGC on the formation of a filament spun from a solution of cellulose in NMMO/H2O. They investigated the air-gap length (LAG), air temperature (Tair) and relative humidity (RH), and the water content in the polymer solution. The study showed that all these parameters have a strong influence on the spinnability and structure formation process and cause significant changes to the resulting fiber properties.
The authors observed that the die swell is reduced by conditioning the AG, with warm and humid air (30 °C, RH = 100%), but especially with cold and dry air (0 °C, RH = 0%).
Concerning the fibers properties, they found that the general effect of the air-gap conditions on fiber tenacity showed certain interactions; the strongest fibers were spun with a long, dry air gap (0 °C, RH = 0%) or a short, humid air gap (30 °C, RH = 100%). Surprisingly, they observed that none of the tested conditions had a significant effect on the structure of the fibers as measured by birefringence or wide angle X-ray diffraction (WAXD), despite having a strong influence on the fiber properties.
AGC optimization in Tencel® fiber production (formerly Courtaulds Ltd) was investigated through empirical pilot scale practical/iterative studies, in-depth investigations of model systems (often single filament) and development of computer simulations (Hayhurst and Banks 2005). In parallel, other researchers brought additional insights on the Lyocell NMMO-based process, such as Shao et al. who measured online the tensile force as well as the filament diameter and temperature across the AG and developed a numerical simulation tool for of the Lyocell fiber spinning process. However, their experimental and numerical work did not included the case of humid air in the AG (Shao et al. 2003).
A recent state-of-the-art review article describing IL-based cellulose dissolution and spinning processes evidenced the rapid development of the IL-based Lyocell processes towards a pre-industrialization level (Hermanutz et al. 2019). Nevertheless, among the numerous studies on the this topic, only few refer to the AG, but without a real focus on the conditioning and its effects on the process stability or fiber properties (Xia et al. 2015, 2016; Michud et al. 2016a).
To the authors’ best knowledge, only Zhang et al. (2017) paper explicitly deals with the effects of AGC on the dope spinnability and fibers properties (Zhang et al. 2017). Zhang et al. (2017) used 1-butyl-3-methylimidazolium chloride ([BMIM]Cl) as IL, and observed that the spinnability of cellulose–IL solutions greatly varied with the ambient temperature and humidity in the AG. They found that low Tair and RH in the AG were important to obtain fibers with a high tensile strength at a high draw ratio. The authors also reported that at low RH, the fluctuation in the measured fibers properties was greatly reduced compared to the case with high RH.
Although the work of Zhang et al. (2017) is novel and good, it can be questioned at different levels:
The investigated Tair and RH ranges could have been wider in order to cover a wider range of the possible conditions. We understand however that the authors could have had some limitations since the experiments were performed in a temperature and humidity-controlled room, which does not confer a high flexibility.
The experiments made by the authors could have been better designed since they varied only one variable at a time, respectively at one fixed Tair and RH levels (see Fig. 3 in their paper). They could therefore have missed an optimum in the Tair-RH experimental space they defined (Leardi 2009; Mäkelä 2017).
In addition, the moisture and heat transfer between the filament and the surroundings may be under-optimized due to the absence of a directed convective airflow. A directed convective airflow on the filament could have enhanced the transport of mass and heat at the filament-air interface and therefore accentuated the effect of AGC on the dope spinnability as well as on the fiber properties.
Overall, it seems that except the study of Zhang et al. (2017) the AGC in the IL-based Lyocell type processes has not yet fully captured the attention of the researchers.
In this article, we would like to present new insights into the effects of the AGC in the IL-based cellulose dissolution and spinning processes, taking the Ioncell™ process as a case example.
We will discuss the effects of AGC on the spinnability and fibers properties. We will present some elements of discussion on the fate of the IL, as well as on the dope-moisture interactions in the AG. With the help of numerical simulation, we will finally postulate the phenomena which lead to improved fibers when using the AGC.
Material and methods
Raw materials
Ionic liquid
1,5-Diazabicyclo[4.3.0]non-5-enium acetate ([DBNH][OAc]) was synthesized by protonation of 1,5-diazabicyclo[4.3.0]non-5-ene (DBN) (99%, Fluorochem, UK) with acetic acid (99.8%).[DBNH][OAc] was prepared by the slow and controlled addition of an equimolar amount of acetic acid (HOAc) to DBN. The mixture was stirred and cooled in the beginning at 25 °C to divert the exothermic reaction enthalpy. When approaching equimolar amounts in the mixture, the system was heated at 70 °C to avoid the crystallization of the IL. The system was kept for another hour at this temperature under mixing to ensure the reaction runs until completion. The water content of the synthesized IL is lower than 0.5 wt.%. The stoichiometry of the IL was checked with proton NMR analysis.
The cellulose pulp
Prehydrolysis-kraft birch dissolving pulp (91.3% cellulose I, mass-average molecular weight, Mw = 263 kg mol−1, number-average molecular weight, Mn = 73 kg mol−1 and polydispersity 3.6) was received as air-dried sheets from Stora Enso Enocell mill (Finland), cut into powder form in a Wiley mill (1 mm sieve) and used for the dope preparation.
Spinning dope preparation
About 0.5 kg of spinning dope (13% cellulose in the ionic liquid) was prepared with a vertical kneader system. Air-dried pulp was added to the molten IL while pre-mixing manually with a Teflon spatula. The mixture was then kneaded for 1.5 h at 10 rpm and 80 °C in 30–50 mbar vacuum to avoid inclusion of air bubbles. The solution was then press-filtered with a hydraulic press at 2 MPa and 90 °C through layered filter mesh (GKD Ymax2, 5 µm nominal, Gebr. Kufferath AG, Germany) to remove the residual undissolved particles.
The spinning dope was then shaped into small 10 g cylindrical pieces (about 10 cm length and 1 cm diameter). Each of the small dope pieces was protected with a plastic film and stored in a closed plastic container inside a cold room (6 °C) until the respective spinning experiments were conducted.
To determine the rheological properties of the dope, its viscoelastic behavior was studied using an Anton Paar MCR 302 rheometer with plate-plate geometry (25 mm plate diameter, 1 mm gap size). Dynamic frequency sweep tests were performed at constant strain of 1% within an angular frequency range of 0.1–100 s−1. The tests were performed at five temperatures between 60 and 100 °C with a 10 °C step. Complex viscosity, storage, and loss moduli were measured, and the frequency and modulus at the crossover point (COP) were calculated. Assuming that the Cox–Merz rule was valid (Cox and Merz 1958), we determined the zero shear viscosity by fitting the complex viscosity data with the three parameters Cross viscosity model. From the rheological data, and prior observation on the spinning stability zone of similar dopes, we could determine the target spinning temperature window (73–79 °C), corresponding to a zero shear viscosity around 30,000 Pa.s and an angular frequency at the COP of 1 Hz (Ma et al. 2018). The rheological data are shown in the first ESI section.
Spinning experiments
Experimental set-up
The spinning experiments were performed with a newly developed single-filament spinning unit. The cellulose dope is extruded through a single-hole spinneret (capillary Length L = 200 µm, capillary Diameter, D = 100 µm) into the AG zone. The filament leaves the spinneret with a velocity vext and accelerates towards the water surface due to the take-up force exerted by a rotating take-up device allowing for controlled take-up velocities vtup. The ratio between the take-up and extrusion velocities is the draw ratio (\(D_{R}\)).
An air humidifier (Cellkraft AB, Sweden) was used to direct a controlled flow of air at a specific Tair (± 0.1 °C) and RH (± 0.6% in 0–40% RH range and ± 1.0% 40–97% RH range). The conditioned air was blown from a 6 mm diameter circular nozzle and directed toward the filament. An external humidity probe (Vaisala Oyj) is placed just before the nozzle for the control of Tair and RH. A schematic representation of the incipient filament in the AG during the AGC spinning experiments is shown in Fig. 1.
Design of experiments (DOE)
The effects of AGC during the spinning were first assessed through preliminary screening experiments to better define the experimental ranges in term of admissible airflow rate (Fair), Tair and vext. Through all the spinning experiments, the DR is maintained at six, the coagulation water is maintained at 10 °C and the LAG at 1.2 cm. The parameters investigated were Fair, Tair, vext and RH. The screening experiments are summarized in Table 1.
Based on the results of the screening experiments, the effects of AGC were investigated according to a two factors central composite design (CCD) for optimization purposes (Brereton 2003). The two design factors are Tair and RH, varied respectively in the ranges of 30–60 °C and 0–70%. The experimental design is shown in Table 2. It includes eleven experiments, four axial points, four star points, and three replicates at the center point.
The extrusion velocity was fixed at 1.9 m/min, the DR at 6, the LAG at 12 mm, and the Fair rate at 10 l/min, as a result of the screening tests.
A quadratic regression equation is used to approximate the response \({\varvec{y}}\), which stands for any of the fiber properties. Individual models for each of the desired response can be obtained through solving the general linear regression equation (Eq. 1), by minimizing the sum of squares of model residuals through the least-squares estimate (Eq. 2).
where \(\user2{ y}\) denoted a vector of response values, \({\mathbf{X}}\) the mean-centered and coded design matrix, including interaction and second-order terms, \({\mathbf{b}}\) a vector of model coefficients, and \({\varvec{\varepsilon}}\) the model residuals. Statistically insignificant model terms were excluded based on a Student t-test. The performance of the models was expressed through the R2 value, which indicated the proportion of data variation explained by each model. All the mathematical calculations were done using Matlab® according to Brereton (2003).
Fibers characterization
After washing, the fibers were first dried at ambient laboratory atmosphere and then kept in a conditioned room (temperature of 20 ± 2 °C and relative humidity of 65 ± 2%) at least 48 h in order to reach the equilibrium state with the surrounding atmosphere. Up to now, we found that the washing behavior of IL is similar to that of NMMO, so that similar IL residual values of about 50–500 ppm can be expected. A final figure cannot be given at present but will be hopefully published soon when we will have the complete set of washing results.
Fiber mechanical properties
The fiber mechanical properties, elongation (El), tenacity (Ten) and titer (Tit) were measured using a Favigraph tensile tester (Textechno H. Stein GmbH & Co, Germany), with at least 0.6 cN/tex pretension in the conditioned state according to the ISO 5079 standard (temperature of 20 ± 2 °C and relative humidity of 65 ± 2%). The values were averages from 20 individual fibers. The gauge length was 20 mm and the testing speed was 20 mm/min. The pretension weights were 100–500 mg and maximum force of the cell load was 20 cN or 100 cN.
Fiber orientation
The average total orientation of cellulose in the spun fibers was determined using a polarized light microscope (Zeiss Axio Scope) equipped with a 5λ Berek compensator. The birefringence Δn of the specimen was obtain by dividing the retardation of the polarized light by the thickness of the fiber which was calculated from the linear density (titer) using a cellulose density value of 1.5 g/cm3 (Männer et al. 2011). The total orientation factor fOR was then derived by dividing Δn by the maximum birefringence of cellulose 0.062 (Lenz et al. 1994; Adusumalli et al. 2009).
Dynamic vapor sorption
The water vapor-cellulose solution interaction was investigated using a dynamic vapor sorption (DVS) apparatus (DVS advantage, Surface Measurement Systems, London, UK) at controlled temperature and RH. In the DVS device, the temperature is controlled by electrical heating, and the RH by controlling the proportions of a dry N2 gas and a water vapor-saturated N2 gas using mass flow controllers. The total flow rate around the sample is 100 cm3/min. Data acquisition was done every 20 s.
In order to have a defined sample geometry, the dope was shaped into discs with a defined thickness of 595 ± 22 µm and a diameter of 6 ± 0.1 mm using a metallic mold (see Figure S4 in the DVS section of the ESI).
Two types of sorption–desorption experiments were performed:
The so-called step-tests after the completion of a drying stage under pure N2, the RH was increased from zero to a target value (sorption), and then decreased back to zero (desorption). At each step, constant RH was maintained until the change in the sample mass over time \(\left( {\frac{dm}{{dt}}} \right)\) was 0.002%/min or lower over a 10-min period. The \(\frac{dm}{{dt}}\) was calculated using the slope in a 10-min window. If this criterion is not met after 3600 min, the next step starts.
The characteristic DVS parameters extracted from those tests are:
\(\Delta m{ }_{Dry}\) change in mass during the “drying stage” under pure N2.
\(\Delta m{ }_{Sor}\) change in mass during the “sorption stage” under the target RH.
\(\Delta m{ }_{Des}\) change in mass during the “desorption stage” under pure N2.
\(\frac{dm}{{dt}}{ }_{max Sor}\) maximum rate of mass change during the “desorption stage” under the target RH.
\(\frac{dm}{{dt}}{ }_{max Des}\) maximum rate of mass change during the “desorption stage” under pure N2.
Sorption–desorption isotherm tests the RH is increased from 0 to 90% by steps of 5% (sorption) and then decreased back to zero by step of 5% (desorption). The RH is changed when the \(\frac{dm}{{dt}}\) is equal or lower than 0.002%/min, or when the time exceeds 1500 min without meeting the \(\frac{dm}{{dt}}\) criterion.
The DVS experiments are summarized in Table 3.
Thermo-gravimetric analysis coupled to mass spectrometry (TGA-MS)
Investigating the dope thermal stability is relevant when studying the AGC as the IL constituents may leave to the gas phase upon heating. Thermo-Gravimetric Analysis coupled to Mass Spectrometry (TGA-MS) was used in order to investigate the thermal stability of the dope.
TGA-MS analysis was performed using a NETZSCH STA 449 F3 Jupiter device coupled to quadrupole mass spectrometer QMS 403 Quadro Aëolos. A shaped dope disc (≈25 mg) was inserted into an alumina crucible and heated from 40 to 900 °C under a flow of He (70 mL/min).
Part of the evolved gases were directed to the QMS through a quartz capillary tube heated electrically at 250 °C. The evolved gases were ionized with an electron impact ion source at 70 eV.
Data acquisition was done in a Linear Histogram Scanning (HIS) mode in the 0–150 amu range. This method allows direct comparison between the rate of weight loss and the mass spectra signal. Identification of the components evolved at a specific temperature was made by comparing the spectrum recorded with the NIST (National Institute of Standards and Technology, Gaithersburg, Maryland) MS database. The focus was on the MS spectra of HOAc and DBN which are the main dope components, and the most likely to evolve to the gas phase at moderate temperatures (< 100 °C).
A Matlab routine was created for the treatment of the TGA-MS data and extract the TGA indicators listed below:
\(T_{onset}\) temperature at a weight loss of 1%;
\(T_{peak}\) temperature at the maximum mass loss rate;
\(DTG_{peak}\) maximum mass loss rate;
\(T_{off set}\) temperature at a weight loss of 99%;
\(Y_{residue}\) final solid residue percentage.
Results and discussion
Effects of the AGC on the dope spinnability and fibers properties
Screening experiments
Upon the installation of AGC system, a first set of experiments at a constant DR of six was performed for parameter screening purposes. The experimental conditions and fibers properties derived are presented in Table 4.
Experiments P1 and P2 were performed with two different extrusion velocities of 1.9 and 3.8 m/min, and without AGC. They represent the reference experiments. During those reference experiments, the temperature and RH humidity in the laboratory were respectively in the range of 20–23 °C and 60–65%. The reader can notice that the elongation decreased when increasing the extrusion velocity. A longer residence time in the AG in Exp P1 would have allowed a higher fiber stretching compared to Exp P2. Experiments P3 and P4 were performed with a volumetric airflow (Fair) of 10 l/min at 40 °C and 90% RH. The fibers obtained in those experiments showed higher elongation and tenacity compared to the reference experiments P1 and P2. Convective cooling and humidification in the AG seem to have positive effects on the fibers properties.
Increasing the temperature to 50ºC and keeping RH at 90% (Exp P5) leads to an increase in elongation up to 15.2% compared to 12.0% obtained without AGC in Exp P1. However, when increasing the extrusion velocity to 3.8 m/min (Exp P6), the elongation decreased to 12.2%. This might be related to the shorter residence time in the AG leading to a lower filament cooling and humidification.
The importance of the air humidity is demonstrated in Exp P7 (dry air) for which the elongation dropped to 9.3%, compared to the 12.2% obtained in Exp S6 in which a nearly saturated air was used in the AG. Finally, Exp P8 and P9 show that increasing the airflow rate does not affect the fiber properties when comparing them with Exp P6. It seems that there are no external mass or heat transfer limitations in the investigated airflow range. Increasing the Fair to 40 l/min (Exp P10) induced high turbulences on the water surface and a high drag on the filament, inhibiting consequently the spinning process.
Optimization experiments
After the first set of screening experiments, vext and Fair were kept constant, respectively at 1.9 m/min and 10 l/min. Only the effects of the Tair and RH were investigated according to a central composite DOE. The experimental conditions and fiber mechanical properties are shown in Table 5. The reader can notice that the highest elongation of 16.0 ± 1.3%, was obtained in Exp D3, with a conditioned air at 30 °C and 70% RH (0.021 kg H2O/m3 of dry air). When compared to the reference case without AGC, for which the elongation was 12.0 ± 2.2%, the increase in the elongation appears to be quite substantial (+ 34%) and statistically significant. The tenacity was equally improved by decreasing the Tair and increasing the RH compared to the reference case without AGC.
To illustrate further the effects of AGC, Fig. 2a shows the average tenacity-elongation curves for the fibers obtained with the AGC (Exp D3: 30ºC and 70% RH) and without AGC. The fiber modulus of toughness (J/g) is proportional to the integral area below each curve. Using simple numerical integration based on the trapezoidal rule, the fiber modulus of toughness is estimated respectively at 50.4 J/g with the AGC (Exp D3), and 33.7 J/g without AGC, which represents the highest value observed for the experiments and a modulus of toughness increase of almost 50%compared to the reference case without AGC. All the value of the modulus of toughness are given in Table 5.
a Tenacity-elongation curves for fibers obtained with the AGC (30 °C and 70% RH) and without AGC (DR = 6, \(v_{ext}\) = 1.9 m/min, Tbath = 10 °C). The colored area below the curves are proportional to the fiber toughness. b Titer variation coefficient (VC) for the different spinning experiments with and without AGC
The titer was almost constant for all the experiments except for those performed at 60 °C with humid air, for which the titer was almost double. We could not yet find an explanation for this observation.
The fiber titer homogeneity improved when used AGC as shown in Fig. 2b. The fiber titer is indeed more homogeneous (VC≈14%) when using the AGC, regardless of the air temperature and RH, than when operating without AGC (VC≈24%). This result is relevant for subsequent yarn spinning operations, in which fluctuations of the fiber titer must be minimized.
The effect of AGC on the fiber titer homogeneity is in line with the observations reported by Zhang et al. (2017) despite they used a multifilament spinneret, with larger hole diameter of 0.27 mm. However, the results presented here are not completely in line with theirs, as they suggested to operate with a low RH in order to optimize the spinning conditions and fiber properties. The difference in the used ILs and hence the cellulose solutions properties, might be behind the different observations and conclusions.
Using the design matrix and the experimental results, the regression model coefficients for the tenacity and elongation were calculated and their significance were assessed using a Student t-test. Only the significant coefficients, for which the 95% level standard error does not cross the zero line, were retained in the final models (see Figure S2 in the ESI). Both models show the significance of the interaction effect (through the coefficient b12) of the air temperature and RH, indicating that the air should be cooled down while keeping its RH high. The models for the elongation and tenacity explain respectively 76% and 79% of the variance. Although those values are not high, the models could still give an idea about the direction of highest variance in elongation and tenacity (see Figure S3 in the ESI). The contour plots of the elongation and tenacity are given in Fig. 3. Both contour plots show clearly that in order to increase the fiber elongation and tenacity, Tair should be lowered and the RH should be increased.
Overall, and in the light of the actual results, we can confidently state that the AGC has noticeable effects on the IL-based dry-jet wet spinning of cellulose solutions in [DBNH][OAc], as it leads to more homogeneous fibers with improved mechanical properties.
The AGC experiments suggest that in order to impart the fiber a high toughness, the incipient filament must be cooled and humidified in the AG.
A possible explanation is that at high RH the filament absorbs water at the outer surface areas. The outer cellulose layers start then to (pre)coagulate and the aggregate dimensions increase (radius of gyration), creating lateral interactions which is a prerequisite for increased elongation. At the same time, the low temperature ensures a higher extensional viscosity which could lead to a higher tenacity.
Curiously, despite the variation in the fiber mechanical properties, the total orientation did not showed significant variation for the different conditions in the air gap, and mostly the best case orientation (T = 30ºC, RH = 70%), is very similar to the orientation obtained without AGC. This finding is in line with that of Morortimer and Peguy (1996) who observed that none of the tested conditions in the AG had a significant effect on the structure of the fibers as measured by birefringence or wide angle X-ray diffraction (WAXD), despite having a strong influence on the fiber properties. This result is even more surprising regarding the major differences between the IL and NMMO dopes.
Insights into the interactions between water vapor and the spinning dope
So far, we showed the importance of the AGC during the spinning operation in order to enhance the fiber properties. Along with the cooling effect provided by the convective airflow, the presence of moisture is a determinant factor to improve the fiber mechanical properties. In order to shed more light on the role of moisture, the dope-moisture interaction was investigated using DVS measurements.
DVS experiments
The step tests
An example of a DVS step test performed at 25 °C and 90% RH is shown in Fig. 4. The changes in mass and RH over time are shown on the top, and the rate of mass change is shown on the bottom. The different stages of drying, sorption and desorption, as well as the characteristic DVS parameters are indicated for the purpose of clarity. Similar figures for the three other DVS step test experiments are given in Figure S5 in the ESI section on DVS.
The characteristic DVS indicators derived from the step test experiments are summarized in Table 6. The results show that there is a significant mass loss during the drying stage, which increases with the temperature, from an average of 8.22% at 25 °C to an average of 15.47% at 50 °C. At 25 °C, the base line is almost flat after the drying or desorption stages, while at 50 °C, it shows a visible slope denoting a continuous mass loss. The mass loss could be due to the presence of water in the dope, which could have been introduced during the preparation and handling of the cellulose-IL solution and dope discs. It is a plausible explanation since the IL and the dope are very hygroscopic material (Huddleston et al. 2001; Seddon et al. 2000; Di Francesco et al. 2011). Nonetheless, some of the acid or base molecules, which are not ionized, or interacting with the cellulose chains could also evaporate and contribute to the observed mass loss. An evolved gas analysis as a function of the temperature is needed to fully elucidate this issue.
During the sorption stage, the mass uptake was systematically higher at 25 °C than at 50 °C at equivalent RH. It tremendously increased from 11.90 to 161.05% (more than 13 folds) when increasing the RH from 10 to 90% at 25 °C. Similarly, it increased from 8.9 to 105.3% (close to 12 folds) in the same RH range at 50 °C.
As shown in Table 6, the mass uptake during the sorption stage shows an abrupt increase when the absolute humidity increases in the range of 0.01 to 0.02 kg/m3.
The maximum sorption rate shows a linear relationship (R2 > 0.98) with the absolute humidity as depicted in Fig. 5. The increase in the maximum sorption rate is due to an increase of the water vapor flux towards the dope surface, which is directly proportional to the water vapor concentration gradient between the surroundings and the dope surface. At the dope surface, the water vapor flux \({\mathbf{N}}_{{{\varvec{H}}_{2} {\varvec{O}}}}\), can be written according to the Fick’s first law of diffusion (Eq. 3) as the product of a diffusion coefficient \({\text{ D}}_{{{\text{ H}}_{2} {\text{ O}}}}\), and a concentration gradient \(\frac{{dC_{{{\text{ H}}_{2} {\text{ O}}}} }}{dx}\):
During the desorption stage, the final mass loss was always higher than the mass uptake regardless of the experimental conditions. The difference is much more accentuated at 50 °C compared to 25 °C due to the continuous mass loss well depicted by the base line drift. In addition, the spinning dope state after the step test at 50 °C and 10% RH changed markedly compared to the initial state. The cross-polarized microscopy images showed greater amount of undissolved cellulose in comparison to the initial dope, which suggests a neat change in the solution composition (see Figure S9 in the ESI). The change in the solution state maybe due to composition change by evaporation and /or hydrolysis and condensation reactions of the IL components (Ahmad et al. 2016). More details about those reactions are given in the Figure S10 in the ESI.
The desorption rate follows the same trend as the sorption rate and increased as expected with the concentration gradient in the surrounding air. However, the reader could notice that the maximum sorption and desorption rates were quite close at low RH but differed substantially at high RH. The desorption rate was much higher than the sorption rate at 90% RH.
The very high sorption capacity and substantial differences of the maximum sorption and desorption rates at high RH were quite intriguing and unexpected. We performed consequently the same experiment at 25 °C and 90% RH in a humidity cell (GenRH – Humidity Generator, DVS advantage, Surface Measurement Systems, London, UK)) were the dope disc could be visually monitored under the flow of humid air. The dope disc was first dried overnight under a pure nitrogen flow and then put under a flow of humid air (25 °C and 90% RH). After ≈100 min, water condensation was clearly visible on the dope surface (see Figure S11 in the ESI). This result implies that at first, water can diffuse inside the dope, but beyond a certain limit, diffusion is no more possible, and condensation starts to occur. A water shell forms consequently around the dope disc. It must be noted that no condensation or water layer formation were noticed when performing the same experiments at 25 °C with 10% RH. The limit is not reached in this case.
In the light of those observations, the DVS experiments could be better interpreted:
The high sorption capacity observed at high RH of 90% results from both diffusion inside the dope, cellulose coagulation at the surface of the disc, with the cellulose skin growing slowly, followed by a water layer formation on the dope surface by condensation. In contrast, at a low RH of 10%, the much lower mass uptake would result solely from the diffusion of water vapor inside the dope without the formation of a water layer on the dope disc surface.
The higher desorption rates relatively to the sorption rates, observed at 90% RH are due to the initial evaporation of the condensed water from the outer water layer surrounding the dope. There, the water molecules would have fewer interactions with the IL or cellulose molecules compared to the water molecules that diffused inside the dope disc and could hence leave to the gas phase at a faster rate.
Overall, those results show a high interaction between the cellulose-IL dope and moisture. This is a direct consequence of the high IL hygroscopic nature. ILs were shown to absorb water to varying extents either from wet surfaces or from the air; even the hydrophobic ILs absorb traces of water rapidly (Huddleston et al. 2001; Seddon et al. 2000; Di Francesco et al. 2011). To confirm the IL hygroscopic character, we performed the DVS experiment with the IL at 25 °C and 10% RH. We observed a higher mass uptake of 15.3% for the pure IL compared to 11.9% obtained with the Cellulose-IL dope. The durations to reach the sorption equilibrium were quite close for the IL and for the cellulose-solution. Both the IL and the dope showed similar kinetics of water uptake at 25 °C and 10% RH, which suggest that the presence of cellulose does not affect too much the water uptake in those conditions. Regarding the water mass uptake at the equilibrium, the [DBNH][OAc] IL can be regarded as highly hydrophilic according to Cao et al. (2012, 2013). The results are detailed in the ESI, Sect. 3.
The spinning experiments highlighted the importance of the AGC when using a directed airflow on the filament at low temperature and high RH in order to improve the fibers properties. The optimal conditions observed during the spinning experiments were better explained by the DVS experiments, which showed that decreasing the temperature and increasing the RH resulted in the highest water mass uptake as well as into high sorption rate. Estimating the moisture diffusivity in the incipient filament and the filament residence time in the AG should give a better understanding of the observed results and state if it has to do with a surface hydration or a coagulation. This will be discussed in the next sections.
Estimation of the water vapor diffusion coefficient in the spinning dope
The moisture diffusion coefficient in the dope could be identified from the sorption stage during the DVS step tests performed with 10% RH at 25 ºC and 50ºC, which did not show any water layer formation on the dope. The details of the modelling procedure are given in the ESI Sect. 3.d related to the DVS experiments. The experimental and modeled DVS data are shown in Fig. 6 and the identified diffusion coefficient are given in Table 7.
The reader can notice that there is a good agreement between the experimental DVS data and the diffusion models. The estimated diffusion coefficient are 1.5E−11 and 6.4E−11 m2/s, respectively at 25 °C and 50 °C. The same order of magnitude of the diffusion coefficient of water vapor in several ILs is reported in the work of Rocha and Shiflett (2019).
Assuming that the diffusion coefficient depends on the temperature following an Arrhenius law given in Eq. 4, The diffusion coefficient at infinite temperature \(D_{0}\) and the activation energy \(E_{a}\) can be determined accordingly.
\(D_{0}\) and \(E_{a}\) are estimated respectively to 1.6 × 10–3 m2/s and 45.7 kJ/mol. This expression could be used as a good estimate of the diffusivity in simulation studies like the one we will discuss in the section dedicated to the numerical simulation.
DVS Sorption/Desorption isotherms experiments
The sorption–desorption isotherms at 25 °C and 50 °C are shown in Fig. 7. The isotherms show a nearly reversible process of sorption–desorption in the investigated temperatures and RH range.
A deviation in the final desorption stage is observed at 50 °C with a noticeable lower mass compared than the initial one. A similar mass loss was observed during the step-test when increasing the temperature to 50 °C.
One can also notice that the water uptake increases as the RH increases during the successive steps, though the equilibrium is not achieved at high RH values.
Similar data on DVS of cellulose solution in ILs are unfortunately lacking in the literature, which makes the discussion difficult. Nonetheless, since the Cellulose-IL solution is largely composed of IL, a comparison with similar DVS experiments made on pure ILs can be made.
For instance, Hummel et al. (2011) performed DVS experiments on various ILs, and also observed that gradually absorbed water accelerates further moisture uptake at higher humidity levels (Hummel et al. 2011). They also noticed the existence of a small hysteresis in the sorption isotherms and indicated the difficulty of achieving the equilibrium at high RH levels.
Their results should be however contrasted with those of Vitz et al. (2009) who observed equal sorption and desorption behavior for various ILs, suggesting that the sorption and desorption of water is a completely reversible process (Vitz et al. 2009).
Figure 8 illustrates part of the sorption isotherm experiment at 80 °C. It shows that the mass increases when increasing the RH, but start quickly to decrease again when the sorption rate decreases towards the equilibrium. This strange mass variation pattern is likely to be the superposition of a mass uptake due to the water vapor sorption and a mass loss from the IL components in the dope mathematically expressed in Eq. 5:
When the sorption rate is high enough in the beginning of the sorption process, the overall mass change is positive, but when it decreases towards the equilibrium, the overall mass change becomes negative due the higher mass loss rate from the IL components.
Increasing further the temperature to 80 °C induced a higher mass loss to the gas phase compared to the experiments done at 50 °C. The experiment was aborted at 60% RH since no reasonable sorption isotherm could be obtained under these conditions. TGA-MS analysis showed that the \(T_{onset}\) is around 65 °C, meaning that the dope has already lost 1% of its mass when reaching this temperature. The mass loss rate at the onset temperature \(\frac{dm}{{dt}}_{onset}\) is estimated at ca. 0.3%/min. However, this thermal behavior would not have impacts on the spinning process as the residence time of the dope in the air gap would be lower than 0.1 s. A detailed discussion on the TGA-MS analysis and thermal stability is given in the Sect. 5 of the ESI.
Simulation of the heat and mass transfer between a single filament and the surrounding air during the conditioned AG spinning.
In steady state conditions during filament spinning, the filament segment in the air gap must be in equilibrium with its surrounding. Hence, we will model the water content and temperature distributions in the filament as static with regard to the position between spinneret and regeneration bath, in spite of the fact that the filament is in vertical motion with material entering at the spinneret and exiting to the regeneration bath.
The interaction between the filament shape on one hand and the temperature and moisture distributions on the other goes in both directions. It is obvious that the shape and velocity of the filament affects the rate of heat and moisture exchange with the surrounding air, but the temperatures and water concentrations in the filament also regulate the viscosity of the dope and thereby the filament shape. Unfortunately, our knowledge of the extensional viscosity as function of temperature, water content and shear rate is still insufficient. We also lack the empirical observations of the velocity or diameter of the filament in the air gap. Therefore, this study will restrict itself to a simple model where the filament undergoes a uniform acceleration in the air gap and estimate the water content and temperature distributions in steady state conditions.
From mass conservation, it follows that:
Here ρ is the density of the dope whereas (z) and d(z) are the velocity and diameter respectively at the vertical position z in the air gap. From Eq. 6 we then obtain an expression for the diameter at an arbitrary point as a function of the velocity at the same point and the corresponding values at the spinneret.
In addition, assuming uniform acceleration, the laws of kinematics render:
Here z is the distance from the spinneret and LAG the length of the air gap.
Inserting Eqs. 8 into Eq. 7 then leads to an expression of the filament diameter as a direct function of the distance from the spinneret.
Due to the simplifications, the filament diameter described by Eq. 9 is probably not very precise, but because our objective is merely to obtain a qualitative estimation of the temperature and moisture distributions in the filament, the description suffices for our needs. Hence, we employed the COMSOL Multhiphysics® simulation software to calculate the stationary distributions of temperature and water for a filament, the diameter of which follows Eq. 9 for a DR of 6 and LAG of 12 mm. Furthermore, the other conditions of the filament and its environment are the same as in the experiment D3 for which the filament elongation and tenacity were the highest. Accordingly, the filament enters the air gap through a capillary of diameter 100 μm with a speed of 1.9 m/min, and at a temperature of 80 °C. Air at a temperature of 30 °C, and with relative humidity 0.7 moves transversally to the filament at a flow rate of 10 l/min.
The convection–diffusion equation together with the appropriate boundary conditions describes the underlying dynamics of both the temperature and water concentration distributions in the filament.
The conservation of mass for the water vapor reads:
\({\mathbf{v}}\) is the velocity vector which has the only component depending on the z direction according to Eq. 8.
The conservation of energy reads:
\(k\) is the dope thermal conductivity taken as the weightd sum of the thermal conductivity of the cellulose and the IL.
\(C_{p }\) is the heat capacity of the dope taken as the weighted sum of the heat capacity of the cellulose and the IL.
Because the distributions of both water content and temperature in the air gap are stationary, the left hand side of Eqs. 10 and 11 is zero.
The boundary conditions are as follows:
Dope air interface:
$${\mathbf{N}}_{{{\mathbf{H}}_{2} {\mathbf{O}}}}^{{\partial {{\varvec{\Omega}}}}} \cdot {\mathbf{n}} = \gamma_{m} \left( {C_{{{\text{H}}_{2} {\text{O}}}}^{\infty } - C_{{{\text{H}}_{2} {\text{O}}}}^{\partial \Omega } } \right){.}$$(12)$${\mathbf{q}}^{{\partial {{\varvec{\Omega}}}}} \cdot {\mathbf{n}} = \gamma_{h} \left( {{\text{T}}^{{\partial {\Omega }}} - {\text{T}}^{\infty } } \right)$$(13)Spinneret surface:
$$C_{{{\text{H}}_{2} {\text{O}}}}^{\partial \Omega } = 0$$(14)$${\text{T}}^{{\partial {\Omega }}} = {\text{T}}^{{{\text{spinneret}}}}$$(15)Water surface
$$C_{{{\text{H}}_{2} {\text{O}}}}^{\partial \Omega } = 0$$(16)$${\text{T}}^{{\partial {\Omega }}} = {\text{T}}^{{{\text{bath}}}}$$(17)
\(\gamma_{m}\) and \(\gamma_{h}\) are respectively the moisture and heat transfer coefficient at the dope-air interface. The superscripts \({\Omega }\) and \(\infty\) designate respectively the dope surface and the surrounding air.
Furthermore, we estimate the two transfer coefficients employing the Nusselt and Sherwood numbers of which the former gives the ratio of convective to conductive heat transfer and the latter the ratio of convective to diffusive mass transfer.
In Eq. 18, Nu, and \(k_{air}\) are the Nusselt number for flow past a cylinder and the thermal conductivity of air. Correspondingly, in Eq. 19, γm is the mass transfer coefficient while Sh and Dwa are the Sherwood number for flow past a cylinder and diffusivity of water molecules in air. In both the equations, λ is the characteristic length.
Equations 20 and 21 render the Nusselt and Sherwood numbers respectively for the flow past a cylinder (Bergman et al. 2011).
Here Re, Pr, and Sc denote the Reynolds, Prandtl and Schmidt numbers respectively.
In the three definitions above, ρ, ν, λ and μ are the fluid density, fluid speed, characteristic linear dimension and dynamic viscosity. Furthermore, cp and k denote the specific heat and thermal conductivity respectively. Finally, D is the mass diffusivity.
COMSOL Multiphysics is a Finite Element software. In other words, it numerically solves differential equations by dividing the domain of the problem into several sub domains and extracting the solution by means of the calculus of variation. For our filament problem, the boundary region with transfer of water molecules and heat through the surface is numerically very challenging. For the simulation to converge, we increase the mesh density towards the boundary, as Fig. 9 shows. Because of the cylindrical symmetry of the filament, we need to work only in two dimensions, height and radius.
Figure 10 shows the simulated temperature and water concentration distributions. We observe that whereas the temperature in the filament depends almost entirely on the distance from the spinneret, with almost constant temperature in the radial direction, the water has time to enter only the outer layers of the filament. In particular, the water content of the filament is very low, only 44 μg water/ 1 kg dope.
The simulation results suggest that the improved toughness results from the combined convective cooling and outermost surface hydration of the filament in the AG.
Conclusion and perspectives
Dry-jet spinning using [DBNH][OAc] ionic liquid is influenced by the conditions in the air gap. Cooling and humidification lead to better fibers properties in terms of titer homogeneity and modulus of toughness. Experimental diffusivity measurements and numerical simulation suggest that the moisture affects the dope in the air-gap through an outer surface hydration.
The installation of an AGC system in the spinning line is therefore highly recommended. Future studies will include the installation and optimization of the AGC on a bigger scale using a multi-hole spinneret in batch mode, and ultimately in a continuous pilot plant. The effect of cooling and humidification will be also further investigated through additional experimental and modelling research work. We will also tackle some challenging experimental measurements related to the dope elongational viscosity and inline filament temperature and diameter.
References
Adusumalli RB, Keckes J, Martinschitz KJ et al (2009) Comparison of molecular orientation and mechanical properties of lyocell fibre tow and staple fibres. Cellulose 16:765–772. https://doi.org/10.1007/s10570-009-9292-2
Ahmad W, Ostonen A, Jakobsson K et al (2016) Feasibility of thermal separation in recycling of the distillable ionic liquid [DBNH][OAc] in cellulose fiber production. Chem Eng Res Des 114:287–298. https://doi.org/10.1016/j.cherd.2016.08.032
Bergman T, Lavine A, Incropera F, Dewitt D (2011) Fundamentals of heat and mass transfer, 7th edn. Wiley, New York
Brereton RG (2003) Chemometrics: data analysis for the laboratory and chemical plant. Wiley, New York
Cao Y, Chen Y, Lu L et al (2013) Water sorption in functionalized ionic liquids: Kinetics and intermolecular interactions. Ind Eng Chem Res 52:2073–2083. https://doi.org/10.1021/ie302850z
Cao Y, Chen Y, Sun X et al (2012) Water sorption in ionic liquids: kinetics, mechanisms and hydrophilicity. Phys Chem Chem Phys 14:12252–12262. https://doi.org/10.1039/c2cp41798g
Cox W, Merz E (1958) Correlation of dynamic and steady flow properties. J Polym Sci 28:619–622
Di Francesco F, Calisi N, Creatini M et al (2011) Water sorption by anhydrous ionic liquids. Green Chem 13:1712–1717. https://doi.org/10.1039/c1gc15080d
Hayhurst MJ, Banks AJ (2005) Observations on lyocell fibre formation. Lenzinger Berichte 84:103–109
Hermanutz F, Vocht MP, Panzier N, Buchmeiser MR (2019) Processing of cellulose using ionic liquids. Macromol Mater Eng 304:1–8. https://doi.org/10.1002/mame.201800450
Huddleston JG, Visser AE, Reichert WM et al (2001) Characterization and comparison of hydrophilic and hydrophobic room temperature ionic liquids incorporating the imidazolium cation. Green Chem 3:156–164. https://doi.org/10.1039/b103275p
Hummel M, Froschauer C, Laus G et al (2011) Dimethyl phosphorothioate and phosphoroselenoate ionic liquids as solvent media for cellulosic materials. Green Chem 13:2507–2517. https://doi.org/10.1039/c1gc15407a
Jürgen P (1996) Method of producing shaped cellulose bodies, and yarn made of cellulose filaments, vol 13
Leardi R (2009) Experimental design in chemistry: a tutorial. Anal Chim Acta 652:161–172. https://doi.org/10.1016/j.aca.2009.06.015
Lenz J, Schurz J, Wrentschur E (1994) On the elongation mechanism of regenerated cellulose fibres. Holzforschung 48:72–76. https://doi.org/10.1515/hfsg.1994.48.s1.72
Ma Y, Stubb J, Kontro I et al (2018) Filament spinning of unbleached birch kraft pulps: effect of pulping intensity on the processability and the fiber properties. Carbohydr Polym 179:145–151. https://doi.org/10.1016/j.carbpol.2017.09.079
Mäkelä M (2017) Experimental design and response surface methodology in energy applications: a tutorial review. Energy Convers Manag 151:630–640. https://doi.org/10.1016/j.enconman.2017.09.021
Männer J, Ivanoff D, Morley RJ, Jary S (2011) TENCEL new cellulose fibers for carpets. Lenzinger Ber 89:60–71. https://doi.org/10.1017/CBO9781107415324.004
Michud A, Hummel M, Sixta H (2016a) Influence of process parameters on the structure formation of man-made cellulosic fibers from ionic liquid solution. J Appl Polym Sci 133:1–9. https://doi.org/10.1002/app.43718
Michud A, King A, Parviainen A et al (2016b) Process for the production of shaped cellulose articles
Michud A, Tanttu M, Asaadi S et al (2016) Ioncell-F: ionic liquid-based cellulosic textile fibers as an alternative to viscose and Lyocell. Text Res J 86:543–552. https://doi.org/10.1177/0040517515591774
Mortimer SA, Peguy AA (1996) The influence of air-gap conditions on the structure formation of lyocell fibers. J Appl Polym Sci 60:1747–1756. https://doi.org/10.1002/(SICI)1097-4628(19960606)60:10%3c1747:AID-APP28%3e3.0.CO;2-#
Rocha MA, Shiflett MB (2019) Water Sorption and Diffusivity in [C 2 C 1 im][BF 4 ], [C 4 C 1 im][OAc], and [C 4 C 1 im][Cl]. Ind Eng Chem Res 58:1743–1753. https://doi.org/10.1021/acs.iecr.8b05689
Schwanninger F, Ecker F, Feilmair W, Schrempf C (1995) Spinning device, vol 18
Seddon KR, Stark A, Torres MJ (2000) Influence of chloride, water, and organic solvents on the physical properties of ionic liquids. Pure Appl Chem 72:2275–2287. https://doi.org/10.1351/pac200072122275
Shao H, Liu R, Hu X (2003) Computer modelling of the Lyocell fibre spinning process. Autex Res J 3:16–22
The Fiber Year (2019)
Vitz J, Erdmenger T, Haensch C, Schubert US (2009) Extended dissolution studies of cellulose in imidazolium based ionic liquids. Green Chem 11:417–424. https://doi.org/10.1039/b818061j
White AP, Hayhurst MJ, Owens A, et al (1994) Spinning cell, vol 23
Xia X, Gong M, Wang C et al (2015) Dynamic modeling of dry-jet wet spinning of cellulose/[BMIM]Cl solution: complete deformation in the air-gap region. Cellulose 22:1963–1976. https://doi.org/10.1007/s10570-015-0613-3
Xia X, Wang J, Wang H, Zhang Y (2016) Numerical investigation of spinneret geometric effect on spinning dynamics of dry-jet wet-spinning of cellulose/[BMIM]Cl solution. J Appl Polym Sci 133:1–11. https://doi.org/10.1002/app.43962
Zhang J, Yamagishi N, Tominaga K, Gotoh Y (2017) High-strength regenerated cellulose fibers spun from 1-butyl-3-methylimidazolium chloride solutions. J Appl Polym Sci 134:1–9. https://doi.org/10.1002/app.45551
Acknowledgments
Open access funding provided by Aalto University. This project has received funding from the Business Finland’s new knowledge and business from research ideas program (Tutkimuksesta uutta tietoa ja liiketoimintaa, TUTL). The authors would like to thank Michael Altgen for the training and support during the dynamic vapor sorption experiments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Guizani, C., Nieminen, K., Rissanen, M. et al. New insights into the air gap conditioning effects during the dry-jet wet spinning of an ionic liquid-cellulose solution. Cellulose 27, 4931–4948 (2020). https://doi.org/10.1007/s10570-020-03115-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10570-020-03115-8