Abstract
We investigate the potential of Brillouin Light Scattering (BLS) Microspectroscopy for fast non-invasive all-optical assessment of the mechanical properties of viscose fibers and bleached softwood pulp. Using an optimized Brillouin spectrometer, we demonstrate fast spatial mapping of the complex longitudinal modulus over extended areas (> 100 µm). Our results reveal that while the softwood pulp has a relatively uniform moduli, the viscous fibers have significant spatial heterogeneous in the moduli. Specifically, the viscose fibers exhibited a regular pattern of increasing and decreasing modulus normal to the fiber axis. The potential influence of a locally changing refractive index is investigated by holographic phase microscopy and ruled out. We discuss our results in light of the anisotropic mechanical properties of the fibers and are able to estimate the relative difference between the modulus along the fiber axis and that perpendicular to it. Results are presented alongside reference measurements of the quasi-static mechanical properties transverse to the fiber axes obtained using AFM-nanoindentation which reveal a similar trend, hinting at the potential usefulness of BLS for mechanical characterization applications. However, more detailed investigations are called for to uncover all the factors influencing the measured high-frequency BLS modulus and its significance in relation to physical properties of the fiber that may be of practical interest.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The mechanical properties of pulp fibers have been investigated using numerous different approaches. Longitudinal (i.e. along the fiber axis) measurements of fiber properties like the E-modulus and the breaking strength are usually studied using fiber tensile testing (Kompella and Lambros 2002; Burgert et al. 2005; Fischer et al. 2012; Jajcinovic et al. 2018) [see also Fischer (2013) and Jajcinovic (2017) for extensive reviews]. In contrast the transverse properties of fibers (i.e. perpendicular to the fiber axis) were initially investigated via compressive measurements on wet fibers (Hartler and Nyren 1970; Dunford and Wild 2002; Wild et al. 2005). Bergander et al. carried out tests on radial double-wall cut wood strips in an environmental scanning electron microscope (Bergander and Salmen 2000). Atomic Force Microscopy (AFM) based methods have also been used to investigate fiber properties such as flexibility and conformability (Nilsson et al. 2000; Pettersson et al. 2017) as well as transverse mechanical properties (Ganser et al. 2013; Ganser and Teichert 2017). A comprehensive list of literature on the topic can be found in Czibula et al. (2019).
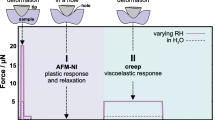
While the viscoelastic nature of cellulosic fibers has been known for a long time, earlier studies focused predominantly on the creep behaviour of fibers in the longitudinal direction (Stanzl-Tschegg and Navi 2008; Cisse et al. 2015). The viscoelastic behaviour of wood has been characterized for pine specimens along the grain direction (Penneru et al. 2006) and for green wood in the transverse direction (Bardet and Gril 2002). However, only recently has fiber viscoelasticity in the transverse direction been addressed using an AFM-Nano-Indentation (NI) based method (Ganser et al. 2018) at varying levels of relative humidity (RH) (Czibula et al. 2019).
In this work spontaneous Brillouin Light Scattering (BLS) Microspectroscopy is applied to probe the mechanical properties of cellulosic fibers. Spontaneous BLS is based on the inelastic scattering of light from acoustic phonons that are inherently present in the probed material. Acoustic phonons are collective molecular excitations, which unlike optical phonons, have a significantly lower energy (in the GHz range) and will extend over many molecules. BLS measures the effective velocity of these excitations, by measuring the frequency shift of the so-called BLS peaks relative to the probing laser. In a typical BLS microspectroscopy experiment when one couples to a single acoustic phonon mode, one observes two Brillouin scattering peaks on either side of the probing laser frequency, which correspond to the “creation” and “annihilation” of a phonon. The shift of these peaks relative to the elastic scattering peak (i.e. frequency of the probing laser) is directly proportional to the hypersonic velocity of the phonons via Eq. (1). The velocity can in turn be used to calculate the elastic storage modulus at the corresponding frequency via the Christoffel equation [Eq. (2)].
Key advantages of BLS microscopy are that it is a completely non-invasive, non-contact method that can measure mechanical properties in short acquisition times (~ 100 ms or less per position). This is particularly useful for investigation of pulp fibers, as their small size (length 0.6–3 mm, width 15–40 µm) require elaborate sample preparation and intricate micromachinery for mechanical testing. Another potentially promising aspect of BLS microscopy is that it can be used to evaluate the full elastic tensor of anisotropic materials. Due to the fibril orientation in the S2 wall and the misalignment between the fibril orientation angle and the fiber axis, the fiber should be described by an orthotropic material model of the fiber wall, explicitly taking into account also the fibril orientation angle (Magnusson and Östlund 2013). As thus the fibers can be characterized by either performing mechanical measurements in the longitudinal and the transverse direction—i.e. two tensile plus two shear moduli—together with the fibril angle, or, by performing direct orthogonal measurements of the three tensile moduli plus the three shear moduli. Measurement of pulp fiber shear moduli is even more complicated than tensile moduli, and to the best of our knowledge has not been done. BLS has routinely been used to measure mechanical properties and even the complete elastic tensor of biological fibers such as for spider silk (Koski et al. 2013), proteins (Randall et al. 1979; Speziale et al. 2003), collagens (Harley et al. 1977; Cusack and Miller 1979; Edginton et al. 2016), muscle fibers (Berovic et al. 1989), or recently bamboo wood splinters (Williams et al. 2019). Being a non-contact method able to measure the full elastic tensor (i.e. the elastic moduli and shear moduli in all three spatial directions) BLS has the potential to provide substantial progress for mechanical testing of cellulosic fibers and, at the same time, resolve the laborious and complicated issues in fiber handling during mechanical testing.
In this work we demonstrate the applicability of the method for cellulosic fibers by analyzing the BLS-measured mechanical properties of pulp- and viscose fibers. Specifically, the elastic modulus (storage modulus) representing the elastic behavior and the loss modulus (dampening coefficient) representing the viscous behavior are evaluated. By adjusting the effective solid angle over which we are probing and detecting (via the effective numerical aperture of the objective lens) we are able to transition between coupling to predominantly acoustic phonon modes perpendicular to the fiber axis and acoustic phonon modes both perpendicular and parallel to the fiber axis. We note that because of the employed back-scattering geometry and polarization of detection we are exclusively measuring longitudinal acoustic phonons, which in turn yield the so-called longitudinal moduli. In this brief communication we also for the first time to our knowledge demonstrate the feasibility of using a Virtual Imaged Phase Array (VIPA)-based imaging spectrometer for studying such fibers. While having a lower spectral resolution and finesse than the traditionally employed multi-pass Fabry–Perot spectrometers (Sandercock 1970), it also has some advantages in regard to required acquisition time and illumination intensity, as well as affordability, which would be important for wider research and potentially also industrial applications.
Materials and methods
Fibers
The two different fibers investigated were hand ribbon shaped viscose fibers (Leonardo fiber from Kelheim Fibers) and fully bleached softwood kraft pulp fiber from industrial production (Sappi). For the BLS measurements two viscose fibers and two softwood fibers were investigated. Reference measurements, by AFM-NI, were carried out on fully bleached Canadian softwood kraft pulp (Canfor) at about 50% RH. AFM-NI data of round shaped viscose fibers from Kelheim were used as the second reference.
Calculation of elastic modulus from BLS measurements
The measured BLS frequency shift \(\nu_{B}\) (GHz) is in general related to the speed of the probed acoustic phonons \({\text{V}}_{{\hat{\varvec{q}}}}\) for a given scattering wavevector \(\hat{\varvec{q}}\) via:
where n is the refractive index (written here as a tensor for the general anisotropic case), \(\nu_{0}\) is the frequency of the probing laser, and c is the vacuum speed of light. (In the backscattering geometry this reduces to \(\nu_{B} = \pm 2 {\text{n}} c^{ - 1} \nu_{0} V\)). The propagation of phonons in the \(\hat{x}_{i}\) direction is described by (Berne and Pecora 2000):
where ρ is the mass density and \(c_{ijkl}\) is the stiffness tensor. It follows that the components of the latter can be calculated from the measured acoustic velocity (Eq. 1) via (Berne and Pecora 2000):
For the case of an isotropic material in the back-scattering geometry one would probe the first three diagonal components (\(c_{1111} = c_{2222} = c_{3333}\)), such that the position of the BLS peaks directly yield the longitudinal storage modulus M′:
The corresponding loss modulus (M″) can be obtained from the lifetime of the phonons—which is manifested in the homogeneous broadening of the BLS peak \(\varGamma_{B}\)-via (Carroll and Patterson 1984; Floudas et al. 1991)
The case of anisotropic samples—as is the case with the studied fibers—is more subtle, given the distinct elastic moduli in different directions. For the studied fibers we may assume a transverse anisotropic symmetry such that measurements will yield a linear combination of the modulus parallel and perpendicular to the fiber axis (\(M_{||}\) and \(M_{ \bot }\). respectively). The respective contribution of these can be calculated from Eqs. 1 and 3 by considering the projection of the scattering wavevector on the stiffness tensor.
Finite numerical aperture
In order to achieve a high lateral spatial resolution, one needs to probe with a correspondingly large numerical aperture (NA). Finite NA measurements will in the studied case result in two modifications to the measured spectrum. Firstly, one would observe an inherent effective broadening and slight shift in the peak position of the BLS signal resulting from the frequency dependence of the scattering wavevector (Eq. 1) (Antonacci et al. 2013). This can readily be calculated by integrating Eq. 1 over the probed solid angles. Secondly, one may observe an effective broadening due to the anisotropy of the sample, namely that the phonon speed is dependent on direction. To illustrate the latter for the samples studied here, let us assume the fibers are orientated in the \(\hat{x}_{1}\) direction and we probe along the perpendicular \(\hat{x}_{3}\)-axis, such that \(c_{1111} \left( { = M_{||} } \right) \ne c_{2222} = c_{3333} ( = M_{ \bot }\)). By increasing the effective probing NA from ≈ 0 one will thus transition from probing exclusively \(M_{ \bot }\) to probing a linear combination of \(M_{ \bot }\) and \(M_{||}\). Given that \(M_{||} \ne M_{ \bot }\) this will result in an effective broadening with increasing NA and a shift in the measured \(\nu_{B}\) to lower (higher) frequencies if \(M_{||} < M_{ \bot }\) (\(M_{||} > M_{ \bot }\)). The exact dependence can again be obtained by integrating Eq. 1 over the probed solid angles, this time taking these symmetry conditions into account and noting that there will also likely be an associated anisotropy in the refractive index (i.e. \(n_{||} \ne n_{ \bot }\)). Since we do not have access to the latter, in this study we calculate an effective elastic modulus (\(\bar{M}\)). This is obtained by calculating a single effective acoustic velocity (\(V_{{\hat{\varvec{q}} }} = V\)) from Eq. 1 assuming the back-scattering geometry and an effective refractive index (\({\mathbf{n}} \cdot \hat{\varvec{q}} = n\)), and subsequently calculating the complex modulus from Eqs.’s 4 and 5. Prior to fitting the BLS spectra to obtain \(\nu_{B}\) and \(\varGamma_{B}\) the results are deconvolved with the elastic scattering peak and corrected for broadening exclusively due to the finite NA as described below. The effective refractive index (1.3–1.4) was taken from holographic phase microscopy measurements (see below) on the same samples, and a density of 1500 kg/m3 was assumed throughout.
Measurements on the same samples using a very small NA (< 0.01) were used to estimate the contribution of \(M_{ \bot }\) to the total high-NA measured Modulus, since the former can be assumed to exclusively probe in the direction transverse to the fiber axis. The ratio of the elastic modulus along the fiber axis to that perpendicular to the fiber axis was also estimated via:
where \(\nu_{B}\) is measured BLS-shift with NA = 1, and \(\nu_{B}^{ \bot }\) is that measured for NA < 0.01.
An effective loss tangent is also calculated from the measured effective storage and loss moduli as \(\tan \left( \delta \right) = \bar{M}^{\prime \prime } /\bar{M}^{\prime }\) for each of the measured samples.
BLS setup
The employed setup consists of a self-built confocal sample scanning Brillouin microscope as described in e.g. Elsayad et al. (2016). In particular this consisted of an inverted microscope frame (iX73 by Olympus, Japan) with the laser and spectrometer coupled to the lower right port. Samples were mounted on standard microscopy slides and imaged through standard 170 µm glass coverslips. An objective (numerical aperture (NA) = 1.3, 60×, Si-immersion oil, Olympus, Japan) was employed for all BLSM measurements. The aperture of which was only partially filled yielded an effective NA ~ 1.0. The measured (optical) lateral and axial resolution (corresponding to the probing volume) were 290 nm and 650–700 nm as determined from the Full Width Half Maximum of the Point Spread Function. To assure optimum confocality the physical pinhole was fixed at 100 µm, corresponding to just over one Airy unit with the employed tube lens. Excitation was performed via a solid state single-mode 532 nm laser (Torus by Quantum Laser, Germany), passed through an optical isolator, expanded, and coupled into the optical path via a 90:10 non-polarizing beam splitter. The sample was scanned using a long travel range 3-axis piezo stage (Physik Instrumente, Germany) and for each position one spectrum was acquired. Average laser power at the sample was kept low and measured to be below 3 mW. The dwell time per scanned point was fixed at 100 ms. After the pinhole the beam passed through a polarizer and 2 nm narrow band pass filter centered at 532 nm.
The Brillouin spectrometer consisted of a cross dispersion Virtual Imaged Phased Array (VIPA) spectrometer similar to the one described in Scarcelli et al. (2015) with the elastic scattering peaks blocked by masks at intermediate imaging planes. The employed VIPAs (Light Machinery, Canada) each had a free spectral range of 30 GHz. Also employed were self-fabricated gradient apodization filters prior to each VIPA. The resulting spectral projection was subsequently Fourier filtered using a Lyot stop (Edrei et al. 2017) and magnified. Finally, the Brillouin spectra consisting of only the Brillouin peaks, was imaged on a cooled EM-CCD camera (ImageEM II, Hamamatsu, Japan) which was read out for each scan point. Measurements on distilled water and spectroscopic grade ethanol before and after each scan where used for scaling the dispersion axis of the spectral projection. All spectra were fitted with Lorentzian functions with a quadratic background correction term, using a standard least-squares fitting algorithm in Matlab as described in Elsayad et al. (2016).
To account for the instrumental spectral response as well as the contribution from multiple-scattering in the sample, the spectra was deconvolved with a measurement of the elastic Rayleigh scattering peak measured in each respective sample. This was performed by optically attenuating the laser and opening the slits of the spatial masks in the spectrometer. Since our laser line has a line-width (kHz–MHz) that is orders of magnitude smaller than the spectral resolution, a straight forward deconvolution can be assumed to accurately capture the spectral response of our setup. This however will not account for the spectral broadening induced by the finite NA (see below).
To account for this, measurements were performed at different effective NAs by placing a ring-actuated iris diaphragm (Thorlabs, Germany) immediately behind the objective lens. By closing the iris (which could be done with an accuracy of several hundred microns) we could tune the effective NA from < 0.01 up to the maximum of the objective lens. We note that this would equally affect the probing and detection NA. The effective NA (\(NA_{\text{eff}}\)) was calculated from the radius (R) of the iris aperture via: \(NA_{\text{eff}} = nR\left( {w^{2} + R^{2} } \right)^{ - 1/2}\), where \(w\) is the working distance of the objective lens. The results on distilled water showed an increase in the line width by a factor of \(1.9\left( { \pm 0.1} \right)\) from NA ~ 0 to NA = 1.0, with a small shift in the peak position to lower frequencies of 310 MHz (~ 4%).
The effect of changing the effective NA from ~ 0 to 1.0 was also measured on each of the samples using the same approach. To determine the contribution from the anisotropy to the observed broadening, the measured frequency shift and line width at each NA was corrected in the sample measurements by a multiplicative factor corresponding to the effective modification in the peak position and linewidth (see above) measured in distilled water for the same corresponding NA relative to the low-NA limit.
BLS measurement time
The total time consumed by the sample preparation and the BLSM measurements amounted to approx. 3–4 h. During this time calibration measurements were performed and multiple areas of approx. 100 × 100 µm were measured, each of which were divided into 21 × 5 measurement spots.
Testing conditions
It is important to note that BLSM measurements are very sensitive to the level of hydration (Wu et al. 2018) as well as temperature. Also, cellulose fiber mechanical properties are strongly affected by relative humidity under ambient conditions (Jajcinovic et al. 2018). Special care was thus taken that these were kept at the same level (25 °C, 30–50% RH) for all measured samples.
Holographic phase microscopy
Refractive index tomograms were acquired on a commercial holographic phase microscope with rotating scanner (3D Cell Explorer, Nanolive SA, Lausanne, Switzerland) with a Nikon BE Plan 60 × NA 0.8 objective lens. The size of acquired tomogram was 93.1 × 93.1 × 35.7 μm (XYZ). Water was used as the reference refractive index (1.330) in all measurements. The software “Steve 1.6.3496” (Nanolive SA) was used for image acquisition and reconstruction, and maximum intensity projections were plotted using FIJI/ImageJ.
AFM nanoindentation
All AFM measurements were performed with an Asylum Research MFP-3D AFM. The instrument is equipped with a closed-loop planar x–y-scanner with a scanning range of 85 × 85 µm2 and a z-range of about 15 µm. For the experiments, four-sided pyramidal, full diamond probes (ND-DYIRS, Advanced Diamond Technology) with a tip apex radius of about 50 nm have been used. The spring constant of the cantilever was about 60 N/m and calibration of the cantilever was performed according to Hutter and Bechhoefer (1993). In AFM-NI, the sample surface is plastically deformed and according to the Oliver–Pharr method (Oliver and Pharr 1992) the reduced modulus Er and the hardness H can be obtained. The method has been successfully established for pulp and viscose fibers before and is thoroughly described in Ganser et al. (2013) and Ganser and Teichert (2017).
Results and discussion
Figure 1 shows spatial maps of the measured BLS frequency shift \(\nu_{B}\) of the viscose and bleached softwood Kraft fibers and the calculated effective transversal storage modulus (\(\bar{M}\)) and widefield transmitted light pictures of each fiber. While the pulp fibers seem to have a quite uniform elastic modulus the viscose fibers exhibit a regular longitudinal stripe pattern. Along the fiber axis there are elongated regions with lower (low region, 4.2 GPa) and higher (high region, 5.4 GPa) effective transversal moduli.
a, b Transmitted light widefield microscopy images of the viscose and bleached softwood Kraft fibers respectively. c, d confocal spatial maps of the BLS-frequency shift. e, f the calculated effective transversal storage modulus (see main text) from a, b. Note The widefield pictures in a, b were taken through a different microscope port and with a different magnification, and are thus not spatially aligned with the confocal BLS-maps in c–f
Figure 2 shows the effect of increasing the effective numerical aperture (NA = 0.01–1) for the viscose (high region and low region separately) and bleached softwood Kraft fibers. The plotted storage and loss modulus have in each case been corrected for the effect of finite NA excitation/detection by a linear coefficient determined from measuring distilled water with the corresponding NA (see above). As such the observed changes with NA can be attributed to the anisotropy of the sample. In all cases one sees an increase in both the loss modulus (line width) and the storage modulus (frequency shift) with increasing NA. The latter suggests that the component of the storage modulus along the fiber axis is larger than that perpendicular to the fiber axis. This corresponds to the anisotropic nature of both, viscose (strong orientation of cellulose due to stretching during the spinning process) and wood fibers (strong orientation of fibrils in S2 wall). The loss modulus as well as the loss tangent also show an increasing trend with increasing NA, however the errors on the measurements are quite high.
Measurements of the properties over a changing NA. The storage modulus a shows a consistent trend to higher moduli at higher NA. These results show that, as expected, the storage modulus along the fiber axis is higher than perpendicular to it. The loss modulus (b) and the loss tangent (c) also appear to show a similar trend but the associated uncertainties are too large to draw any definitive conclusions
As the BLS frequency shift scales linearly with the refractive index (Eq. 1) we used holographic phase microscopy to investigate whether there are any significant differences in n (between and within samples) which could account for any observed variations in the frequency shift. Maximum intensity projections of the reconstructed refractive index holograms are shown for two different representative sample types in Fig. 3. The local variation of the refractive index is in each case rather low and therefore cannot in itself explain the differences in the calculated longitudinal modulus (see above). Interestingly similar longitudinal patterns in the viscose fiber can be observed for the refractive index maps (Fig. 3a) as for the storage modulus (Fig. 2c, e), which might be the result of the drawing of the filaments during the spinning process.
Table 1 summarizes the results for the refractive index n, BLS frequency shift \(\nu_{B}\), the measured effective longitudinal storage and loss moduli (\(\bar{M}^{\prime }\) and \(\bar{M}^{\prime \prime }\)) and the loss tangent for the two fiber types. Also shown is the derived ratio of the storage modulus perpendicular and along the fiber axis (\(M_{ \bot }^{\prime } /M_{||}^{\prime }\)), calculated from the point measurements at different NA’s (see above). We note that for this calculation an isotropic refractive index is assumed for each of the sample regions (as referenced in table), which is likely not the case. The calculations for all NA’s can be found in the ESI.
As also evident from the spatial maps (Fig. 1) the low region of the viscose fibers and the softwood pulp have comparable values for \(\bar{M}^{\prime }\) while the (longitudinal) “stripes” in the viscose fiber (high region) have a significantly larger \(\bar{M}^{\prime }\). We suspect the differences may be related to either a local densification of the material or a local hardening of the structure.
Table 1 also shows reference data for the reduced modulus in the transverse fiber direction obtained from AFM-NI of viscose and bleached softwood pulp fibers. In comparison the measurements from AFM-NI are higher for the viscose and lower for softwood pulp. While these show a similar trend to the average effective longitudinal storage moduli measured with BLS, the percentage difference is significantly larger between the two types of fiber. It is often the case when attempting to perform correlative AFM and BLS studies that relatively large changes in the AFM measured (Young’s) moduli will correspond to only subtle changes in the BLS-measured (longitudinal) moduli—in many cases scaling in a roughly semi-logarithmic fashion (e.g. Scarcelli et al. 2015). It should be noted though that currently such relations are empirical and lacking theoretical foundation, given the different boundary conditions of the measured moduli and the vastly different frequency regimes probed (quasi-static vs. GHz) which will be sensitive to distinct mechanical relaxation processes. It is also understood that under high hydration levels (> 90%) the solvent can dominate the contribution to the modulus measured with BLS and such an apparent correlation breaks down (Wu et al. 2018).
In the context of the current study it is also necessary to emphasize that the references were not measured on the same fibers. The counterintuitive result that the quasi-static AFM measurements yield an effectively lower modulus may possibly be due to the effective length scales probed with BLS. Since the probed phonons have a wavelength of approximately 100–200 nm with decay lengths on the order of 1 µm, they probe an effective collective response. Aside from more detailed knowledge of molecular level interactions, interpretation of the BLS spectra would for the case of heterogeneous media also require (ultra-)structural considerations on these scales especially for the viscous fibers.
The loss tangent (tan(δ)) relates the storage and the loss modulus and is a measure of how well energy is dissipated in the material. A tan(δ) = 0 would mean that the material is fully elastic while a number > 1 means that more energy is dissipated than stored. Importantly in the case of BLS measurements the loss tangent will be independent of the density and refractive index (which cancel out—Eqs. 4 and 5) which means that a change in loss modulus indicates a “true” change in the moduli of the structure. Within experimental uncertainties the loss tangent was similar between the two fiber types, with the values being in the same range than quasi-static measurements (Zhou et al. 2001; Csóka et al. 2012).
Given the frequency of the probed phonons in BLS, the most relevant mechanical relaxation times probed will be on the scale of picoseconds. It is possible to extract effective mechanical relaxation times (\(\tau\)) from BLS measurements by driving the sample across a thermodynamic phase transition (at which \(\nu_{B} \tau \sim \,1\)), e.g. Carroll and Patterson (1984). It is however in general challenging to obtain the relaxation times from the BLS measurements, as they will also depend to a large degree on the distribution (model) of relaxation times (Floudas et al. 1991). A detailed investigation of this would also benefit from complementary lower frequency broader-bandwidth techniques (such as photon correlation spectroscopy), which is beyond the scope of the current study.
Conclusions
We have demonstrated spatial mapping of the high-frequency effective transversal storage and loss modulus for viscose and softwood pulp fibers using a VIPA based Brillouin Microscope. Reference measurements with AFM-NI revealed a similar trend—namely a larger elastic modulus for viscous than softwood pulp fibers, although a direct comparison between the two moduli is at this point unjustified given the different mechanical relaxation processes probed.
Our results suggest that Brillouin microscopy can serve as a fast and reliable technique to investigate the high-frequency mechanical properties of cellulosic fibers. One demonstrated advantage is the ability to map the properties in different directions (longitudinal and transverse to the fiber axis). In addition it has the ability to rapidly and all-optically map properties over larger areas using a VIPA based spectrometer such as was employed here. In this regard we see much potential for BLS microscopy for understanding and testing the mechanical properties of cellulose fibers as it is also less cumbersome and a lot faster than direct mechanical testing. Extensions of the technique to e.g. consecutively probing at different angles (scattering wavevectors) can also be used to investigate the full elastic (stiffness) tensor of the fiber material, i.e. tension stiffness and shear stiffness in all three spatial directions, as has been demonstrated for other natural fiber materials (Koski et al. 2013; Edginton et al. 2016). It is however important to note that the measured properties with BLS are by construction different than those probed with most other mechanical testing techniques. This will be due to the high-frequency regime probed (where coupling of constituents/solutes to liquids will be much stronger and the latter will have a high modulus) and the different boundary conditions associated with deriving the elastic modulus from the speed of acoustic phonons. While there is ongoing active research in the direction of both empirically and theoretically relating the BLS measured moduli to more familiar structural and physical parameters and shedding light on their relevance in assessing otherwise relevant chemical/physical properties, the current study demonstrates the practical feasibility and potential of Brillouin microscopy for studying the anisotropic mechanical properties of cellulosic fibers.
References
Antonacci G, Foreman MR, Paterson C, Török P (2013) Spectral broadening in Brillouin imaging. Appl Phys Lett 103:221105. https://doi.org/10.1063/1.4836477
Bardet S, Gril J (2002) Modelling the transverse viscoelasticity of green wood using a combination of two parabolic elements. Comptes Rendus Mécanique 330:549–556. https://doi.org/10.1016/S1631-0721(02)01503-6
Bergander A, Salmen L (2000) The transverse elastic modulus of the native wood fibre wall. J Pulp Pap Sci 26:234
Berne BJ, Pecora R (2000) Dynamic light scattering: with applications to chemistry, biology, and physics. Courier Corporation, North Chelmsford
Berovic N, Thomas N, Thornhill RA, Vaughan JM (1989) Observation of Brillouin scattering from single muscle fibres. Eur Biophys J 17:69–74. https://doi.org/10.1007/BF00257104
Burgert I, Frühmann K, Keckes J et al (2005) Microtensile testing of wood fibers combined with video extensometry for efficient strain detection. Holzforschung 57:661–664. https://doi.org/10.1515/HF.2003.099
Carroll PJ, Patterson GD (1984) Rayleigh–Brillouin spectroscopy of simple viscoelastic liquids. J Chem Phys 81:1666–1675. https://doi.org/10.1063/1.447892
Cisse O, Placet V, Guicheret-Retel V et al (2015) Creep behaviour of single hemp fibres. Part I: viscoelastic properties and their scattering under constant climate. J Mater Sci 50:1996–2006. https://doi.org/10.1007/s10853-014-8767-1
Csóka L, Božanić DK, Nagy V et al (2012) Viscoelastic properties and antimicrobial activity of cellulose fiber sheets impregnated with Ag nanoparticles. Carbohydr Polym 90:1139–1146. https://doi.org/10.1016/j.carbpol.2012.06.065
Cusack S, Miller A (1979) Determination of the elastic constants of collagen by Brillouin light scattering. J Mol Biol 135:39–51. https://doi.org/10.1016/0022-2836(79)90339-5
Czibula C, Ganser C, Seidlhofer T et al (2019) Transverse viscoelastic properties of pulp fibers investigated with an atomic force microscopy method. J Mater Sci 54:11448. https://doi.org/10.1007/s10853-019-03707-1
Dunford J, Wild P (2002) Cyclic transverse compression of single wood-pulp fibres. J Pulp Pap Sci 28:136–141
Edginton RS, Mattana S, Caponi S et al (2016) Preparation of extracellular matrix protein fibers for Brillouin spectroscopy. J Vis Exp. https://doi.org/10.3791/54648
Edrei E, Gather MC, Scarcelli G (2017) Integration of spectral coronagraphy within VIPA-based spectrometers for high extinction Brillouin imaging. Opt Express 25:6895–6903. https://doi.org/10.1364/OE.25.006895
Elsayad K, Werner S, Gallemí M et al (2016) Mapping the subcellular mechanical properties of live cells in tissues with fluorescence emission–Brillouin imaging. Sci Signal 9:rs5. https://doi.org/10.1126/scisignal.aaf6326
Fischer WJ (2013) A novel direct method for mechanical testing of individual fibers and fiber to fiber joints. Technische Universität Graz, Graz
Fischer WJ, Hirn U, Bauer W, Schennach R (2012) Testing of individual fiber–fiber joints under biaxial load and simultaneous analysis of deformation. Nord Pulp Pap Res J 27:237–244. https://doi.org/10.3183/npprj-2012-27-02-p237-244
Floudas G, Fytas G, Alig I (1991) Brillouin scattering from bulk polybutadiene: distribution of relaxation times versus single relaxation time approach. Polymer 32:2307–2311. https://doi.org/10.1016/0032-3861(91)90065-Q
Ganser C (2014) Influence of water on mechanical properties of cellulosic materials studied by AFM based methods. University of Leoben, Leoben
Ganser C, Teichert C (2017) AFM-based Nanoindentation of cellulosic fibers. In: Tiwari A, Natarajan S (eds) Applied nanoindentation in advanced materials. Wiley, New York, pp 247–267
Ganser C, Hirn U, Rohm S et al (2013) AFM nanoindentation of pulp fibers and thin cellulose films at varying relative humidity. Holzforschung 68:53–60. https://doi.org/10.1515/hf-2013-0014
Ganser C, Czibula C, Tscharnuter D et al (2018) Combining adhesive contact mechanics with a viscoelastic material model to probe local material properties by AFM. Soft Matter 14:140–150. https://doi.org/10.1039/C7SM02057K
Harley R, James D, Miller A, White JW (1977) Phonons and the elastic moduli of collagen and muscle. Nature 267:285–287. https://doi.org/10.1038/267285a0
Hartler N, Nyren J (1970) Transverse compressibility of pulp fibers. 2. Influence of cooking method, yield, beating, and drying. Tappi 53:820
Hutter JL, Bechhoefer J (1993) Calibration of atomic-force microscope tips. Rev Sci Instrum 64:1868–1873. https://doi.org/10.1063/1.1143970
Jajcinovic M (2017) Strength of individual fibres and fibre to fibre joints—influence of the pulp type, environmental conditions and the degree of refining. Technische Universität Graz, Graz
Jajcinovic M, Fischer WJ, Mautner A et al (2018) Influence of relative humidity on the strength of hardwood and softwood pulp fibres and fibre to fibre joints. Cellulose 25:2681–2690. https://doi.org/10.1007/s10570-018-1720-8
Kompella MK, Lambros J (2002) Micromechanical characterization of cellulose fibers. Polym Test 21:523–530. https://doi.org/10.1016/S0142-9418(01)00119-2
Koski KJ, Akhenblit P, McKiernan K, Yarger JL (2013) Non-invasive determination of the complete elastic moduli of spider silks. Nat Mater 12:262–267. https://doi.org/10.1038/nmat3549
Magnusson MS, Östlund S (2013) Numerical evaluation of interfibre joint strength measurements in terms of three-dimensional resultant forces and moments. Cellulose 20:1691–1710. https://doi.org/10.1007/s10570-013-9939-x
Nilsson B, Wågberg L, Gray D (2000) Conformability of wet pulp fibres at small length scales. FSCN, Mitthögskolan, Sundsvall
Oliver WC, Pharr GM (1992) An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J Mater Res 7:1564–1583. https://doi.org/10.1557/JMR.1992.1564
Penneru AP, Jayaraman K, Bhattacharyya D (2006) Viscoelastic behaviour of solid wood under compressive loading. Holzforschung 60:294–298. https://doi.org/10.1515/HF.2006.047
Pettersson T, Hellwig J, Gustafsson P-J, Stenström S (2017) Measurement of the flexibility of wet cellulose fibres using atomic force microscopy. Cellulose 24:4139–4149. https://doi.org/10.1007/s10570-017-1407-6
Randall JT, Vaughan JM, Buckingham AD et al (1979) Brillouin scattering in systems of biological significance. Philos Trans R Soc Lond Ser A Math Phys Sci 293:341–348. https://doi.org/10.1098/rsta.1979.0101
Sandercock JR (1970) Brillouin scattering study of SbSI using a double-passed, stabilised scanning interferometer. Opt Commun 2:73–76. https://doi.org/10.1016/0030-4018(70)90047-7
Scarcelli G, Polacheck WJ, Nia HT et al (2015) Noncontact three-dimensional mapping of intracellular hydro-mechanical properties by Brillouin microscopy. Nat Methods 12:1132–1134. https://doi.org/10.1038/nmeth.3616
Speziale S, Jiang F, Caylor CL et al (2003) Sound velocity and elasticity of tetragonal lysozyme crystals by Brillouin spectroscopy. Biophys J 85:3202–3213. https://doi.org/10.1016/S0006-3495(03)74738-9
Stanzl-Tschegg SE, Navi P (2008) Fracture behaviour of wood and its composites. A review COST action E35 2004–2008: wood machining—micromechanics and fracture. Holzforschung 63:139–149. https://doi.org/10.1515/HF.2009.012
Wild P, Omholt I, Steinke D, Schuetze A (2005) Experimental characterization of the behaviour of wet single wood-pulp fibres under transverse compression. J Pulp Pap Sci 31:116–120
Williams DR, Nurco DJ, Rahbar N, Koski KJ (2019) Elasticity of bamboo fiber variants from Brillouin spectroscopy. Materialia 5:100240. https://doi.org/10.1016/j.mtla.2019.100240
Wu P-J, Kabakova IV, Ruberti JW et al (2018) Water content, not stiffness, dominates Brillouin spectroscopy measurements in hydrated materials. Nat Methods 15:561–562. https://doi.org/10.1038/s41592-018-0076-1
Zhou Tashiro K, Hongo T et al (2001) Influence of water on structure and mechanical properties of regenerated cellulose studied by an organized combination of infrared spectra, X-ray diffraction, and dynamic viscoelastic data measured as functions of temperature and humidity. Macromolecules 34:1274–1280. https://doi.org/10.1021/ma001507x
Acknowledgments
Open access funding provided by Graz University of Technology. The financial support by the Austrian Federal Ministry for Digital and Economic Affairs and the National Foundation for Research Technology and Development is gratefully acknowledged. Furthermore, the authors want to thank Canon Production Printing, Mondi, Kelheim Fibres and SIG Combibloc for their financial support. The authors thank Lisa-Marie Weniger for assistance with the AFM-NI measurements. KE acknowledges support from the Austrian Ministry of Science and the City of Vienna (Vision 2020). Georg Urstöger and Kareem Elsayad contributed equally to the publication and share first authorship.
Funding
Funding was provided by Christian Doppler Forschungsgesellschaft (Grant: CD Laboratory for Fiber Swelling and Paper Performance).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Elsayad, K., Urstöger, G., Czibula, C. et al. Mechanical Properties of cellulose fibers measured by Brillouin spectroscopy. Cellulose 27, 4209–4220 (2020). https://doi.org/10.1007/s10570-020-03075-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10570-020-03075-z