Abstract
Organization of nanoparticles is essential in order to control their light-matter interactions. We present cellulose nanocrystal suspension organization in flow towards a unidirectional state. Visualization of evolving polarization patterns of the cellulose nanocrystal suspensions is combined with steady and oscillatory shear rheology. Elucidation of the chiral nematic mesophase in a continuous process towards unidirectional order enables control of alignment in a suspension precursor for structural films and reveals thus far in situ unrevealed transition states that were not detectable by rheology alone. The coupled analytics enabled the suspensions of interest to be divided into rheological gels and rheological liquid crystal fluids with detailed information on the microtransition phases. Both populations experienced submicron organization and reached macro-scale homogeneity with unidirectional ordering in continued shear. We quantify the time, shear rate, and recovery time after shear to design an optimizing formation process for controlled wet structures as precursors for dry products.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Cellulose is synthetized in the wood cell wall in fibrils exhibiting periodicity in molecular ordering. Less ordered regions are susceptible to hydrolysis, and this enables extraction of the ordered regions as particles. The resulting cellulose nanocrystals (CNC) have lengths in hundreds of nanometers and widths in the 3–5 nm range (Rånby 1951; Marchessault et al. 1959; Habibi et al. 2010). The molecular and particular chirality has been identified as a source for self-assembly of the CNC in suspensions in liquid crystal phases that induce color in visible range but also via birefringence (Gray 2016).
The anisotropic CNCs display periodicity in suspensions (Lagerwall et al. 2014) and the formation of liquid crystalline states and chiral nematic mesophases has been proven by polarized light microscopy and circular dichroism, and takes place above a critical concentration that depends on the CNC properties (Dumanli et al. 2014). CNC suspensions and films that are placed between a polarizer and analyzer exhibit a colorful pattern given that periodicity is present in observable length scales. The exhibited colors are referred to as the polarization or birefringence pattern and reveal organization in the suspension.
Existence of the chiral periodicity in CNC suspensions is proven by a so-called fingerprint pattern in which lines indicate the pitch of the chiral order. The structure acts as a layered pattern where the pitch of the chiral defines the periodicity of the layers (Dong et al. 1996; Pan et al. 2010). The suspensions and films also exhibit birefringence without showing the fingerprint pattern (Dumanli et al. 2014). An increase in the concentration of the CNC suspension is reported to result in a transition to a gel state in which the chiral ordering is no longer detected but instead only birefringence appears (Shafiei-Sabet et al. 2012). Birefringence can additionally arise from any repeating pattern in a structure, nematic ordering being one of them. The characteristics of nematic ordering are less often described than the characteristics of chiral ordering within the literature on CNC suspensions. Kondo et al. (2001) have introduced nematic cellulose structures from dissolved cellulose grades. Recent efforts in the research of CNC suspensions have been applied into the mechanisms of transition from nematic to chiral states. Gray suggested a twist-bend state to be an intermediate in the transition (Gray 2017). Evaporation of liquids arrests the non-equilibrium states into the solid hierarchies. Hence, control of the suspension organization prior to drying is a prerequisite for building controllably hierarchical, crystalline, cellulose structures from CNCs (Mu and Gray 2014).
Controlling the flow conditions of CNC suspensions appears to be a simple way to exert structural change. This would involve both flow-induced organization into nematogenic structures as well as their orientation dynamics. Furthermore, flow-controlled ordering could have potential for scalability to continuous production, e.g. of films. However, the dynamics of nematogenic structures in even simple flow conditions, i.e. simple shear flow, is anything but trivial, as revealed by experimental, theoretical, and numerical studies (Mewis et al. 1997; Grosso et al. 2001). The nematic domain directors exhibit complex spatio-temporal dynamics in the transition from random orientation to flow-induced alignment. Namely, tumbling, wagging, kayaking, log-rolling, and combinations thereof, as well as chaotic motion, have been observed prior to stationary in-plane flow alignment (Forest et al. 2004; Tao et al. 2006). It should be noted, however, that most of the observations cited have been performed on liquid crystalline polymers. Alignment using shear (Ebeling et al. 1999; Diaz et al. 2013; Chowdhury et al. 2017) of crystalline cellulose domains has indicated that alignment is induced by increasing the shear rate in a CNC suspension. In addition, Lagerwall et al. (2014) have shown that shearing of CNC suspensions aligns the domains and improves the film optical isotropy. The organization also affects mechanical performance in the direction of the orientation (Reising et al. 2012). Shear-assisted organization has been shown to promote piezoelectric properties in thin films (Csoka et al. 2011, 2012) and affect thermal expansion in thick films (Diaz et al. 2013).
There are strong indications that the CNC microstructure influences the macroscopic flow behavior of suspensions and rheological measurements can be employed to explore this correlation (Dong and Gray 1997; Beck-Candanedo et al. 2005). For instance, by increasing the concentration of CNC suspension, the microstructural transitions take place and have been tracked by rheo-microscopy and rheoSANS (rheology and small angle neutron scattering) (Mykhaylyk 2010; Mykhaylyk et al. 2012; Shafiei-Sabet et al. 2012; Shafeiei-Sabet et al. 2013; Shafiei-Sabet et al. 2014; Haywood and Davis 2017; Haywood et al. 2017). The microstructure shifts from isotropic (disoriented) at low concentration to anisotropic (oriented) at higher concentration. The transition depends on aspect ratio, concentration, surface charge, and ionic strength (Dong et al. 1996; Bercea and Navard 2000; Boluk et al. 2011; Urena-Benavides et al. 2011; Wu et al. 2014; Li et al. 2015;Hubbe et al. 2017). Shafiei-Sabet et al. (2012, 2013, 2014) used polarized optical microscopy attached to a rheometer to characterize the CNC suspension: ultrasound energy, temperature, degree of surface sulphation, and ionic strength were parameters able to change the microstructure, and therefore the rheological behavior of CNC suspensions. Haywood et al. (2017) used RheoSANS to recognize the effects of CNC concentration on microstructure alignment and viscosity. Three distinct rheological responses over specific concentrations were observed due to varying shear responses of the isotropic and liquid crystals domains in the biphasic CNC suspension.
We apply shear to disrupt the intrinsic organization in CNC suspensions. The goal is to resolve the interplay between shear flow and CNC concentration for controlled organization and induced alignment CNC suspensions. The transition from a static hierarchy to an induced one is monitored by rheological characterization and alteration in birefringence patterns and is recorded in situ. The optical observations are performed at flow-domain scale in order to connect the findings to flow-assisted shaping, e.g. coating, additive manufacturing. A detailed description of the orientation dynamics and influence of shear rate is provided. The results demonstrate that birefringence patterns are much more sensitive to structural changes compared to bulk rheological material properties and that the coupled analytics enables to resolve the organization as well as transition states. Furthermore, an unexpected microphase transition is shown; this transition is characterized by radially periodic birefringence patterns at intermediate shear rates.
Experimental
Cellulose nanocrystals were purchased from CelluForce (NCC® Montreal, Canada). They were suspended in MilliQ-water (Millipore) in 5–8 wt% concentrations. The suspensions were mixed in a bench shaker for 24 h and treated in an ultrasound bath prior to analysis. We note that the suspension rheology is greatly affected by the sample preparation procedure and the concentration regimes cannot be considered universal. We avoided extensive ultrasonication as it has been reported to promote multidomain formation (Liu et al. 2014).
All rheological measurements were performed on an Anton Paar MCR 702 Twin Drive rheometer (Graz, Austria). The tests were performed in single motor-transducer configuration using a custom rheo-optical visualization setup based on the P-PTD200/GL accessory. A schematic overview of the custom setup is shown in Fig. 1a. It comprises a parallel plate geometry of (2R =) 43 mm diameter, with a measurement gap of 1 mm. The lower plate and the outer area of the upper geometry (L approx. 7.5 mm) were transparent (glass). Two linear polarizers (spectral range 400–700 nm) were placed above the upper geometry and below the lower plate at a 45° relative orientation (0, 45)°. A light source was placed above the geometry and an optical camera below. Thus, video recordings of the shear tests were performed at 60 fps in HD format (1280 × 720 pi) using a 100 mm macro lens combined with a 25 mm extension tube (Canon, Tokyo, Japan). The observation area consists of a circular sector (IIIrd quadrant) as highlighted in Fig. 1a, the view from below. An optical visualization (video recording frame) of the observation area in the absence of any measurement sample is shown in Fig. 1b, and a corresponding visualization with a CNC suspension loaded in the measurement gap is exemplified in Fig. 1c. The white areas in Fig. 1c represent isotropic organization. We have translated the visualization into space-time diagrams to emphasize the time and deformation/deformation rate dependence of the plate–plate flow: The reference pixel line A–A in Fig. 1c was extracted from each video frame and added to a newly constructed image, Fig. 1d. The temperature of the measurement cell was maintained via a Peltier system in contact with the lower plate. All experiments were performed at 23 °C. Both steady shear and oscillatory measurements were performed. A custom transient procedure was applied to ensure a steady state at each shear rate. Thereafter, the steady state parameters were computed by post-processing the transient data. To emphasize the influence of shear-induced structural orientation, each steady shear test was repeated, with a relaxation time of 600 s in-between tests. The relaxation time was chosen such that no visible changes in the birefringence patterns occurred. Suspensions with 5 wt% and 6 wt% CNC could be repeated two times while those containing 7 wt% and 8 wt% CNC could be repeated three times before rim drying effects could be observed.
a Schematic overview of the custom rheo-optical setup. b Optical visualization in the absence of a measurement sample. c Optical visualization of a CNC suspension in the absence of deformation. d Space-time visualization of the sample in (c) subjected to a step shear rate (100 s−1) input followed by relaxation
Results and discussion
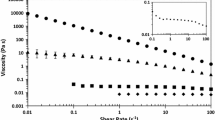
The increasing CNC concentration in the suspensions was reflected in increasing steady shear viscosity (Fig. 2) with the 5 wt% suspension standing out as having the lowest viscosity. This suspension also exhibited irregularities in the viscosity function (non-monotonic behavior) that can be divided into three regimes. This tendency in polymer solutions has been described as liquid crystal phase transition when the system transitions from a piled polydomain system to a dispersed polydomain system and finally into a monodomain continuous phase (Onogi and Asada 1980). The suspensions with 6–8 wt% exhibited a steady shear thinning region. Consequently, the 5–8 wt% suspensions were grouped into two categories: rheological liquid crystals (5 wt%) and other rheological shear thinning fluids (6–8 wt%).
Evolution of CNC suspension flow was recorded simultaneously with the steady shear tests (Fig. 2) and converted into the space-time representation in which development of birefringence patterning of one line (L in Fig. 1) in the observation region is depicted (Fig. 3). Because the time required to achieve a steady state at low shear rates is significantly higher compared to high shear rates, the time intervals for each shear rate were adjusted to be equidistant for a clearer representation. Based on the findings, the following critical shear rates can be distinguished: \( \dot{\gamma }_{0} \)—the shear rate limit for linear behavior, i.e. below which no significant distortions in the birefringence patterns were observed; \( \dot{\gamma }_{2} \)—critical shear rate for the onset of the uniform birefringence pattern detected starting from the highest local shear rate inside the gap, \( \dot{\gamma }_{\hbox{max} } |_{{\varOmega = {\text{Ct}}.}} = {\text{R}}\varOmega /{\text{h}} \) (and consequently highest shear stress); \( \dot{\gamma }_{3} \)—shear rate after which ‘Maltese-cross’-type birefringence patterns are observed (relative to the observation area).
Space-time optical visualizations of the birefringence pattern development in steady shear measurements for a 8 wt% CNC, b 7 wt% CNC, c 6 wt% CNC, and d 5 wt% CNC. The representations correspond to the data in Fig. 2. The height of each space-time plot is equal to distance L = 7.5 mm (section A–A) in Fig. 1. Time intervals for each shear rate were manually adjusted to be equidistant
At low shear rates \( (\dot{\gamma } < \dot{\gamma }_{0} ) \), no significant distortions were observed in the (initial) birefringence structure. This is evidenced in the space-time visualizations as a preservation of the color structure across shear rates. This can be assumed to be an apparent linear viscoelastic regime, where induced shear stresses are comparable to Brownian stresses across the self-assembled CNC structures (Larson 1999). The critical shear rate for the onset of significant structural distortions (\( \dot{\gamma }_{0} \)) appeared to be increasing with increasing CNC concentration. We note that within the limit of the listed shear rates, the birefringence color spectrum did not alter but the initial (t = 0) color aggregates were distorted. Changes in patterns were observed above the stated shear rates, signifying a shear-induced structural organization (nonlinear viscoelastic regime). The onset of a uniformly distributed optical pattern, i.e. a Maltese cross, could be observed starting from the outer region of the geometry where the shear stresses are highest (see Supporting Information Figure S1) and growing towards the inside of the flow domain. A summary of the critical shear rates can be found in Table 1 and these rates are labeled in Fig. 3.
For all suspension concentrations, a range of colors within the observation region was observed before the shear was initiated (Fig. 4, “still” frames on the left): Larger isochromatic areas appear with increasing CNC content. The frames in Fig. 4 indicated with “A” and “B” correspond to the notations in Fig. 3 and present the evolution of birefringence patterns within the observation region. At state A, that is between \( \dot{\gamma }_{0} \) and \( \dot{\gamma }_{2} \), the 6–8 wt% suspensions differ from one another with respect to pattern configuration, but the theme of the pattern is similar.
Still frames right after setting the measurement gap (t = 0) and at selected shear rates, i.e. 0.5 s−1 and 100 s−1, respectively: a 8 wt% CNC, b 7 wt% CNC, c 6 wt% CNC and d 5 wt% CNC. Frames marked with (A) and (B) correspond to the markers in Fig. 3
In the case of the 5 wt% CNC suspension, a distinct radially periodic birefringence pattern was observed with its onset at approximately 0.1 s−1, (\( \dot{\gamma }_{1} \) in Fig. 3d), see 0.5 s−1 in Fig. 4d and Supporting Information Movie 1. The pattern consists of regularly spaced darker concentric stripes separated by lighter concentric stripes. The radial patterns do not appear to be affected by azimuthal positioning with respect to the linear polarizer/analyzer setup. However, the visualizations highlight background coloring, emphasizing the polydomain texture of the birefringence patterns. Therefore, the patterns can signify that the 5 wt% CNC suspension is biphasic and that the microstructure consists of either nematic and isotropic, or several, mesophases (e.g. nematic and chiral nematic). The patterns are maintained until \( \dot{\gamma }_{2} \), although the background birefringence coloring may change. This type of birefringence pattern was unique to the 5 wt% CNC concentration and was limited to the [\( \dot{\gamma }_{1} \), \( \dot{\gamma }_{2} \)] shear rate range. The low shear rate range could suggest that in-plane as well as out-of-plane motions of the directors in the region are possible (Grosso et al. 2001; Forest et al. 2004). This could facilitate the self-organization of the isotropic case into stripes for increased flowability. Furthermore, the inclusion of a chaotic region before \( \dot{\gamma }_{2} \) could help in erasing the isotropic (darker coloration) patterns, resulting in uniform flow-induced oriented nematic flow fields. Above \( \dot{\gamma }_{3} \), a Maltese-cross pattern was found, meaning that either of the principal stress directions of the crystalline regions coincides with the plane of polarization of the polarizer.
We note that for all the suspensions with the present setup, the Maltese-cross color pattern is predominantly pink/light green (see state B in Fig. 4a–d column on right). The onset of uniform flow-induced orientation was found to vary with CNC concentration, with the lowest values being recorded for 5 wt% and 8 wt% CNC. However, the respective local shear stresses corresponding to c were approximately 50 Pa for 8 wt%, 45 Pa for 7 wt%, 24 Pa for 6 wt%, and 1.2 Pa for 5 wt% CNC, i.e. the maximal shear stresses are proportional to the CNC concentration.
We highlight that there is no particular feature in the viscosity functions in Fig. 2 that corresponds to the phase transitions detected via the imaging setup for most CNC concentrations above 5 wt%. This makes the coupling to the visualization a prerequisite for detailed analysis and consequent understanding of the intrinsic flow characteristics.
The critical shear rates are translated into a phase diagram (Fig. 5). For liquid crystalline polymers there is typically a critical concentration below which the system is isotropic and above which it becomes anisotropic (Hermans Jr 1962; Onogi and Asada 1980). Within the current series of observations we note that the case represented by the 5 wt% system is likely to occur for a range of concentrations as the transformation between the two populations, rheological gels and rheological liquid crystal fluid, resides between the concentrations 5 and 6 wt%. We see this behavior in the development of the \( \dot{\gamma }_{2} \) (and \( \dot{\gamma }_{3} \)) that indicates the alignment in the suspensions.
“Phase diagram” showing the critical shear rates in Table 1 as function of CNC concentration
We further investigated the influence of shear history and relaxation on the rheological behavior of the suspensions by repeating the shear tests after a waiting period (Run 1: start → stop—Pause 600 s—Run 2: start → stop—Pause 600 s—Run 3: start → stop, Fig. 6). Differences in shear material response are recorded at low shear rates, with the viscosity underestimated compared to the initial shear test (Run 1). However, at higher shear rates, i.e. above 1 s−1, the differences between tests are negligible. An additional effect of the shear history is observable for 5 wt% CNC as the viscosity function of the second shear test contains fewer irregularities. Visualization of the procedure on the birefringence pattern development is presented in Fig. 6e (space-time plot) for the 7 wt% suspension and corresponding video (still) frame visualizations are shown in Fig. 7. Similar behavior was valid for all concentrations. The similarity between the birefringence patterns in the repeated tests confirms that most of the shear-induced orientation is preserved throughout the repeat tests, especially when the birefringence field color homogeneity is being considered and the original (t = 0 in Fig. 4) birefringence patterns are no longer recovered. However, a new, pre-oriented, equilibrium configuration is reached during each pause period that does not equal the one immediately after the shear event. Two examples of relaxation time between tests are presented in Figure S2 (Supplementary Information).
Still frames corresponding to 7 wt% CNC third run after setting the gap (t = 0) and at selected shear rates, i.e. 0.5 s−1 and 100 s−1. Frames marked with (A) and (B) correspond to the markers in Fig. 6e
Dynamic strain sweep measurements where the frequency is fixed, and in which the deformation or strain amplitude is progressively increased in an oscillatory experiment, were performed to determine the elastic (storage, G′) and viscous (loss, G″) moduli of the suspensions (Fig. 8). The 5 wt% suspension exhibited rheological liquid crystal fluid behavior (G″ > G′) complying with the categorization within Fig. 2. The suspensions with 6–8 wt% showed a cross-over after which we found G′ > G″ and confirmed them as rheological gels. Corresponding space-time visualizations for Fig. 8 are presented in Figure S3, and selected individual measurement cycles as well as corresponding still frames are presented in Figure S4.
Samples with CNC concentration above 6 wt% exhibit weak strain overshoot (Wyss et al. 2007) (inset in Fig. 8). The behavior has been associated with the destruction of microstructural networks (Derakhshandeh et al. 2013). Similar transition sequences comparable to the findings of the steady shear tests described earlier were observed (see Figure S4). However, the Maltese-cross orientation patterns were not recorded within the limit of the nonlinear region of the strain sweep tests. We highlight that, in the case of the 5 wt% sample, the same special birefringence pattern was recorded for strain amplitudes of \( \dot{\gamma }_{0} > 150\% \). This corresponds to shear rate amplitude of \( \dot{\gamma }_{0} > 0.5\,{\text{s}}^{ - 1} \), which is comparable to the shear rates for the special pattern observed in steady shear tests. Interestingly, in contrast to all other birefringence patterns, the patterns appear independent of the direction of shear in terms of birefringence imaging, whereas for all other structures including the background coloring during the special pattern flow changes with the change in direction indicating a differentiating network behavior, see also Supplementary Information—Movie 2. The crowding numbers (Celzard et al. 2009) for the suspensions are between 26 and 41 and indicate a network formation in all of the cases. Hence, we hypothesize the behavior is due to the co-existence of distinct periodic phases in the 5 wt% suspension.
Liquid crystalline polymer solutions have been characterized by the appearance of phases with increasing shear rates thus producing anomalous viscosity functions (Onogi and Asada 1980). We report that behavior in Fig. 2 for the 5 wt% suspension, and it has also been reported for sulfated CNC suspensions with increasing ultrasonication treatment (Shafiei-Sabet et al. 2012). Its appearance for CNC suspensions is related to the degree of freedom that the particles experience to self-assemble towards the chiral nematic mesophase state to shearing. A review by Onogi and Asada (1980) considered the liquid crystalline polymer literature and brought it into a presentation of phase transitions in flow. They presented a schematic that the domain development in shear takes place via a piled polydomain system, that becomes a dispersed polydomain system, and finally into a monodomain continuous phase. In the case of CNC, the initial state of the suspension is a matter of concentration (Figure S5) and sample history. The 5 wt% suspension contains piled systems, CNC tactoids with isotropic or nematic ordering in between the ordered regions.
For example, Marrucci and Ciferri (1977) suggested that the nematic phase and organization can be used for creating aligned structures. They extended the Flory theory about organization of rod-like particles (Flory 1956) into an application of the extensional flow field and the possibility of achieving a steady state in the shear. Here, the shear of the dilute systems is likely to transfer to the nematic alignment via an intermediate state where the piled systems are dispersed into less organized media (also containing CNCs). A special feature is displayed as the flow-induced special pattern presented in Fig. 4. The development of the phases is reflected in the rheology data and the first region (region I) appears at low shear rates, which represents a constant decrease of viscosity and corresponds to the shear thinning, where the chiral and nematic domains start to align. The second region (region II) appears at intermediate shear rates and is characterized by a plateau where almost all the chiral and nematic domains are aligned. The third region (region III) appears at higher shear rates, which represents again a shear thinning, in this case a high shear rate causes alignment and the CNCs exhibit unidirectional ordering, presumably nematic ordering parallel to the flow direction.
Starting with 6 wt%, the suspensions contain piled systems with periodic ordering, but they are closely located and packed to form a crowded suspension. We have not been able to identify the fingerprint area that typically denotes the chiral nematic domains (aligned to the observation direction) in the concentrated systems. However, in the case of the gel state these domains can be misaligned with respect to one another due to the packing and can make detection challenging. The concentrated systems are likely to experience lateral organization rather than an apparent vertical organization when shear is applied. Indeed, Marrucci and Ciferri (1977) concluded that the largest contribution to orientation is obtained from an increase in (polymer) concentration. Observing the alignment perpendicular to plane, a direct transition from the initial state to the unidirectional nematic phase is seen. We assume that the transition includes several stages that are not identifiable in the macro–micro visualization, but this will need a complementary technique in order to be elucidated. The motion can include tumbling, wagging, kayaking, log-rolling, and combinations thereof, as well as chaotic motion.
Conclusions
In this work, a detailed account of microphase transition sequences of CNC suspensions in shear flow through combined rheology and polarized light optical visualizations was provided. Rheology is an essential tool for the characterization of suspension flow properties; however, birefringence patterns proved to be more sensitive to flow-induced structural changes than rheology alone. Thus, critical shear rate conditions for linear (no visible birefringence pattern distortions), nonlinear (pattern distortions), and the onset and development of a uniformly oriented flow field (Maltese-cross pattern) were determined from birefringence pattern dynamics and proved difficult to detect in the corresponding shear viscosity functions. Furthermore, a novel transition state was revealed consisting of radially periodic birefringence patterns at intermediate shear rates prior to the onset of a uniform orientation in the flow direction (Maltese-cross pattern). The radially periodic birefringence patterns correspond to the organization of biphasic CNC suspensions in flow as an intermediate state as they move towards unidirectional alignment. The results could be significant for understanding how to design flow conditions that control the ordering in CNC suspensions, including subtle recovery phenomena. In addition, the unexpected microphase transition sequence detected for the biphasic concentration within a limited shear rate range could suggest the existence of novel flow-induced structural states that could be explored for, for example, CNC film performance.
Associated Content
The following files are available free of charge. A PDF file including figures on space-time optical visualizations of the local shear stress, space-time visualizations showing examples of relaxation in-between runs, space-time visualization of the strain sweep experiments, examples of space-time visualization of oscillation cycles and still frames of the birefringence patterns, and a schematic presentation of steady state viscosity development. Two movies about the evolution of the polarization patterns of the suspensions in flow are available separately.
References
Beck-Candanedo S, Roman M, Gray DG (2005) Effect of reaction conditions on the properties and behavior of wood cellulose nanocrystal suspensions. Biomacromolecules 6(2):1048–1054
Bercea M, Navard P (2000) Shear dynamics of aqueous suspensions of cellulose whiskers. Macromolecules 33(16):6011–6016
Boluk Y, Lahiji R, Zhao L, McDermott MT (2011) Suspension viscosities and shape parameter of cellulose nanocrystals (CNC). J Colloids Surf A 377(1–3):297–303
Celzard A, Fierro V, Kerekes R (2009) Flocculation of cellulose fibres: new comparison of crowding factor with percolation and effective-medium theories. Cellulose 16(6):983–987
Chowdhury RA, Peng SX, Youngblood J (2017) Improved order parameter (alignment) determination in cellulose nanocrystal (CNC) films by a simple optical birefringence method. Cellulose 24(5):1957–1970
Csoka L, Hoeger IC, Peralta P, Peszlen I, Rojas OJ (2011) Dielectrophoresis of cellulose nanocrystals and alignment in ultrathin films by electric field-assisted shear assembly. J Colloid Interface Sci 363(1):206–212
Csoka L, Hoeger IC, Rojas OJ, Peszlen I, Pawlak JJ, Peralta PN (2012) Piezoelectric effect of cellulose nanocrystals thin films. ACS Macro Lett 1(7):867–870
Derakhshandeh B, Petekidis G, Shafiei Sabet S, Hamad WY, Hatzikiriakos SG (2013) Ageing, yielding, and rheology of nanocrystalline cellulose suspensions. J Rheol 57(1):131–148
Diaz JA, Wu X, Martini A, Youngblood JP, Moon RJ (2013) Thermal expansion of self-organized and shear-oriented cellulose nanocrystal films. Biomacromolecules 14(8):2900–2908
Dong XM, Gray DG (1997) Effect of counterions on ordered phase formation in suspensions of charged rod-like cellulose crystallites. Langmuir 13(8):2404–2409
Dong XM, Kimura T, Revol J-F, Gray DG (1996) Effects of ionic strength on the isotropic-chiral nematic phase transition of suspensions of cellulose crystallites. Langmuir 12(8):2076–2082
Dumanli AG, van der Kooij HM, Kamita G, Reisner E, Baumberg JJ, Steiner U, Vignolini S (2014) Digital color in cellulose nanocrystal films. ACS Appl Mater Interface 6(15):12302–12306
Ebeling T, Paillet M, Borsali R, Diat O, Dufresne A, Cavaille JY, Chanzy H (1999) Shear-induced orientation phenomena in suspensions of cellulose microcrystals, revealed by small angle X-ray scattering. Langmuir 15(19):6123–6126
Flory PJ (1956) Phase equilibria in solutions of rod-like particles. Proc R Soc Lond Ser A 234(1196):73–89
Forest M, Wang Q, Zhou RH (2004) The flow-phase diagram of Doi–Hess theory for sheared nematic polymers II: finite shear rates. Rheol Acta 44(1):80–93
Gray DG (2016) Recent advances in chiral nematic structure and iridescent color of cellulose nanocrystal films. Nanomaterials 6(11):213
Gray DG (2017) Order and gelation of cellulose nanocrystal suspensions: an overview of some issues. Philos Trans R Soc A 376(2112):20170038
Grosso M, Keunings R, Crescitelli S, Maffettone PL (2001) Prediction of chaotic dynamics in sheared liquid crystalline polymers. Phys Rev Lett 86(14):3184–3187
Habibi Y, Lucia LA, Rojas OJ (2010) Cellulose nanocrystals: chemistry, self-assembly, and applications. Chem Rev 110(6):3479–3500
Haywood AD, Davis VA (2017) Effects of liquid crystalline and shear alignment on the optical properties of cellulose nanocrystal films. Cellulose 24(2):705–716
Haywood AD, Weigandt KM, Saha P, Noor M, Green MJ, Davis VA (2017) New insights into the flow and microstructural relaxation behavior of biphasic cellulose nanocrystal dispersions from RheoSANS. Soft Matter 13(45):8451–8462
Hermans J Jr (1962) The viscosity of concentrated solutions of rigid rodlike molecules (poly-γ-benzyl-l-glutamate in m-cresol). J Colloid Sci 17(7):638–648
Hubbe MA, Tayeb P, Joyce M, Tyagi P, Kehoe M, Dimic-Misic K, Pal L (2017) Rheology of nanocellulose-rich aqueous suspensions: a review. BioResources 12(4):9556–9661
Kondo T, Togawa E, Brown RM (2001) “Nematic ordered cellulose”: a concept of glucan chain association. Biomacromolecules 2(4):1324–1330
Lagerwall JPF, Schutz C, Salajkova M, Noh J, Park JH, Scalia G, Bergstrom L (2014) Cellulose nanocrystal-based materials: from liquid crystal self-assembly and glass formation to multifunctional thin films. NPG Asia Mater 6(1):e80
Larson RG (1999) The structure and rheology of complex fluids. Oxford University Press, New York, p 86
Li M-C, Wu Q, Song K, Lee S, Qing Y, Wu Y (2015) Cellulose nanoparticles: structure–morphology–rheology relationships. ACS Sustain Chem Eng 3(5):821–832
Liu D, Wang S, Ma Z, Tian D, Gu M, Lin F (2014) Structure–color mechanism of iridescent cellulose nanocrystal films. RSC Adv 4(74):39322–39331
Marchessault RH, Morehead FF, Walter NM (1959) Liquid crystal systems from fibrillar polysaccharides. Nature 184(4686):632–633
Marrucci G, Ciferri A (1977) Phase equilibria of rod-like molecules in an extensional flow field. J Polym Sci Polym Lett Ed 15(11):643–648
Mewis J, Mortier M, Vermant J, Moldenaers P (1997) Experimental evidence for the existence of a wagging regime in polymeric liquid crystals. Macromolecules 30(5):1323–1328
Mu X, Gray DG (2014) Formation of chiral nematic films from cellulose nanocrystal suspensions is a two-stage process. Langmuir 30(31):9256–9260
Mykhaylyk OO (2010) Time-resolved polarized light imaging of sheared materials: application to polymer crystallization. Soft Matter 6(18):4430–4440
Mykhaylyk OO, Parnell AJ, Pryke A, Fairclough JPA (2012) Direct imaging of the orientational dynamics of block copolymer lamellar phase subjected to shear flow. Macromolecules 45(12):5260–5272
Onogi S, Asada T (1980) Rheology and rheo-optics of polymer liquid crystals. Springer, Rheology, pp 127–147
Pan J, Hamad W, Straus SK (2010) Parameters affecting the chiral nematic phase of nanocrystalline cellulose films. Macromolecules 43(8):3851–3858
Rånby BG (1951) Fibrous macromolecular systems. Cellulose and muscle. The colloidal properties of cellulose micelles. Discuss Faraday Soc 11:158–164
Reising AB, Moon RJ, Youngblood JP (2012) Effect of particle alignment on mechanical properties of neat cellulose nanocrystal films. J Sci Technol For Prod Process 2(6):32–41
Shafeiei-Sabet S, Hamad WY, Hatzikiriakos SG (2013) Influence of degree of sulfation on the rheology of cellulose nanocrystal suspensions. Rheol Acta 52(8–9):741–751
Shafiei-Sabet S, Hamad WY, Hatzikiriakos SG (2012) Rheology of nanocrystalline cellulose aqueous suspensions. Langmuir 28(49):17124–17133
Shafiei-Sabet S, Hamad W, Hatzikiriakos S (2014) Ionic strength effects on the microstructure and shear rheology of cellulose nanocrystal suspensions. Cellulose 21(5):3347–3359
Tao YG, den Otter WK, Briels WJ (2006) Periodic orientational motions of rigid liquid-crystalline polymers in shear flow. J Chem Phys 124(20):204902
Urena-Benavides EE, Ao GY, Davis VA, Kitchens CL (2011) Rheology and phase behavior of lyotropic cellulose nanocrystal suspensions. Macromolecules 44(22):8990–8998
Wu Q, Meng YJ, Wang SQ, Li YJ, Fu SY, Ma LF, Harper D (2014) Rheological behavior of cellulose nanocrystal suspension: influence of concentration and aspect ratio. J Appl Polym Sci 131(15):40525
Wyss HM, Miyazaki K, Mattsson J, Hu Z, Reichman DR, Weitz DA (2007) Strain-rate frequency superposition: a rheological probe of structural relaxation in soft materials. Phys Rev Lett 98(23):238303
Acknowledgments
Open access funding provided by Chalmers University of Technology.
Funding
The authors acknowledge the Area of Advance Materials at Chalmers University of Technology for funding All-Wood Composite Platform and this work. RK and TN are grateful for the financial support of the Wallenberg Wood Science Center (WWSC).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary material 1 (MOV 6643 kb)
Supplementary material 2 (MOV 13192 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kádár, R., Fazilati, M. & Nypelö, T. Unexpected microphase transitions in flow towards nematic order of cellulose nanocrystals. Cellulose 27, 2003–2014 (2020). https://doi.org/10.1007/s10570-019-02888-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10570-019-02888-x