Abstract
Energy minimizations for unstretched and stretched cellulose models using an all-atom empirical force field (molecular mechanics) have been performed to investigate the mechanism for auxetic (negative Poisson’s ratio) response in crystalline cellulose Iβ from kraft cooked Norway spruce. An initial investigation to identify an appropriate force field led to a study of the structure and elastic constants from models employing the CVFF force field. Negative values of on-axis Poisson’s ratios ν 31 and ν 13 in the x 1–x 3 plane containing the chain direction (x 3) were realized in energy minimizations employing a stress perpendicular to the hydrogen-bonded cellobiose sheets to simulate swelling in this direction due to the kraft cooking process. Energy minimizations of structural evolution due to stretching along the x 3 chain direction of the ‘swollen’ (kraft cooked) model identified chain rotation about the chain axis combined with inextensible secondary bonds as the most likely mechanism for auxetic response.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Interest in determining the structure and properties of crystalline cellulose is due to the wide-ranging applications for cellulose and also for the potential to develop synthetic derivatives. Cellulose is a linear polymer formed by β-1,4-linked D-glucopyranose residues with high crystallinity, and has two main crystalline forms (cellulose I and cellulose II). Cellulose I has two crystalline allomorphs, designated cellulose Iα and Iβ (Atalla and Van der Hart 1984; Van der Hart and Atalla 1984).
Interestingly, experimental measurements of a negative value of Poisson’s ratio have been reported in crystalline cellulose II (Nakamura et al. 2004) and also in kraft cooked Norway spruce (Peura et al. 2006), which comprises crystalline cellulose Iβ. A negative value of Poisson’s ratio corresponds to auxetic behavior (Evans et al. 1991) and is characterized by a transverse expansion upon axial stretching of the material. Negative Poisson’s ratios have also been reported in a Raman spectroscopy study of the deformation of fibrous networks of bacterial cellulose and microcrystalline cellulose filaments (Tanpichai et al. 2012) and in a variety of paper and paperboard grades (fibrous materials consisting of self-binding cellulose fibers) (Stenberg and Fellers 2002; Verma et al. 2014). The origin of the auxetic nature of the fibrous networks has been attributed to the fiber network structure containing bent fibers forming re-entrant structures, facilitated by strong hydrogen bonds at the junctions where fibers overlap (Tanpichai et al. 2012; Verma et al. 2014). In the case of the kraft cooked Norway spruce study, the negative Poisson’s ratio in crystalline cellulose Iβ was identified as ν 31, corresponding to an increase in the inter-planar separation (along the x 1 direction) of planar sheets (in the x 2–x 3 plane) of parallel cellobiose chains for a tensile load applied along the cellobiose chain axis (x 3) direction. Peura et al. (2006) suggested the auxetic effect may be attributed to non-alignment of microfibrils leading to a component of the stretching force acting perpendicular to the hydrogen-bonded sheets, and shearing effects between individual cells and cell wall layers.
Auxetic materials are attracting interest for their apparently anomalous behavior, and also because the ability to tailor materials to display negative Poisson’s ratio response can open up routes to extreme values of other properties not available for non-auxetic materials (Evans 1990; Greaves et al. 2011). Examples of enhanced properties as a consequence of the auxetic effect include fracture toughness (Lakes 1987), double (synclastic) curvature under pure bending (Lakes 1987; Evans 1991), indentation resistance (Alderson et al. 1994), shear rigidity, (Choi and Lakes 1992) and ultrasonic (Alderson et al. 1997) and vibration (Howell et al. 1991; Scarpa et al. 2005) damping.
Auxetic metals, polymers, composites and ceramics are known, from the macroscale to the nanoscale, and include natural as well as man-made materials (Greaves et al. 2011; Alderson and Alderson 2007; Evans and Alderson 2000). In terms of auxetic polymers, macroporous thermoplastic (Lakes 1987) and thermoset (Friis et al. 1988) foams have been developed, as have microporous polymers in the form of tape or ribbon (Caddock and Evans 1989), monolithic cylinders and plaques (Alderson and Evans 1992), and also in monofilament (Alderson et al. 2002) and film (Ravirala et al. 2005) form. Locally auxetic behavior has also been reported at the sub-micron scale in elastomeric polypropylene (Franke and Magerle 2011). At the molecular scale, early proposed auxetic polymers comprised covalently-bonded molecular honeycomb structures based on the macroscale re-entrant hexagonal honeycomb geometry known to realize auxetic response (Evans et al. 1991). Molecular modeling has shown that such molecular honeycombs would indeed be auxetic, but their heavily cross-linked structure renders them largely intractable from a synthesis point of view. Other theoretical molecular-level auxetic polymers have included 2D molecular honeycombs based on alternative known macroscale auxetic mechanisms (e.g. cooperatively rotating triangles) (Grima et al. 2005), 3D ‘twisted chain’ auxetics having a coupled polydiacetylene chain network (Baughman and Galvão 1993) and site-connectivity driven main-chain liquid crystalline polymers (He et al. 1998). In this latter example, the auxetic effect is achieved through chain separation driven by stress-induced rotation of laterally attached rods in main chains comprising rigid rod units connected by flexible spacer units. However, a fully developed synthetic molecular-level auxetic polymer remains elusive.
The reports of auxetic behavior in crystalline cellulose, therefore, provide natural systems to investigate in the drive to identify structures and mechanisms leading to auxetic response in crystalline polymers at the molecular scale. Conversely, the aforementioned reports in the literature of single-crystal mechanisms for auxetic response in polymers, and indeed other crystalline systems such as some silicates (Yeganeh-Haeri et al. 1992; Keskar and Chelikowsky 1992; Alderson and Evans 2002) and zeolites (Grima et al. 2000), suggest an investigation into a possible single-crystal explanation for the auxetic response in cellulose Iβ is required.
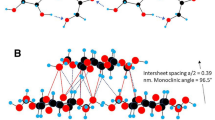
In terms of crystal structure, cellulose Iβ has a monoclinic unit cell within which there are two cellobiose chains aligned parallel to the crystallographic c axis (Nishiyama et al. 2002; French 2014). Matthews et al. (2006) note that Nishiyama’s structure is in good agreement with the structure derived earlier by Finkenstadt and Millane (1998). The cellobiose repeat units are bonded by covalent bonds along each chain. One chain (the origin or corner chain) passes through atomic coordinates (0, 0) and the other chain (the center chain) passes through (1/2, 1/2) in the a–b plane (see Fig. 1a). The center chain is translated along c by ~c/4 with respect to the corner chain. Each neighboring chain is bonded by hydrogen bonding to form stable planar sheets in the b–c plane, and neighboring sheets are held together by weak van der Waals-type interactions and weak C–H···O bonds to form a stacked sheet structure along the a axis (Simon et al. 1988). The precise nature of the packing of the chains in cellulose allomorphs has been the subject of much investigation over many years. Alternative packing arrangements of the chains are present in the literature and distinct chains can rotate about the c axis. A host of packing conformations are, then, possible and a number of these were identified in stable form in Molecular Dynamics simulations (Kroon-Batenburg et al. 1996). The chains pack in the ‘parallel up’ configuration in cellulose Iβ (Nishiyama et al. 2002).
In kraft cooked Norway spruce, the kraft cooking process removes the lignin-hemicellulose matrix leading to a swelling of the crystallographic a lattice parameter (Peura et al. 2006). Swelling of the lattice parameter a is also known to occur during dehydration of crystalline cellulose (Zabler et al. 2010).
A number of studies have been undertaken on the mechanical properties of cellulose. A Mori–Tanaka approach and self-consistent scheme have been employed to model the elastic properties of a distribution of cellulose Iβ crystallites in an amorphous matrix (nanofibrillated cellulose), predicting a ~56 % loss of stiffness compared to that of cellulose crystals along the main axis (Josefsson et al. 2013). Considering purely crystalline cellulose Iβ, commercial bleached ramie fibre (Nakamura et al. 2004), and early- and late-wood and juvenile and mature wood of Norway spruce (Peura et al. 2006) possess positive crystalline cellulose Iβ Poisson’s ratios. These are consistent with ab initio density functional theory (DFT) calculations of crystalline cellulose Iβ where the Poisson’s ratio is calculated to vary between +0.003 and +0.715, depending on direction (Dri et al. 2013). The dramatic modification of the ν 31 Poisson’s ratio from positive to negative value as a result of the kraft cooking process suggests a possible mechanistic link with the swelling of the a lattice parameter upon removal of the lignin-hemicellulose matrix.
Numerous values for the Young’s modulus along the chain axis of crystalline cellulose have been reported, showing wide variation typically in the range 134–220 GPa (Sakurada et al. 1962; Tashiro and Kobayashi 1991; Salmén 2004; Diddens et al. 2008), and theoretical upper limits as high as 246 and 319 GPa (Gillis 1969). Transverse Young’s modulus values of 15 and 27.2 GPa have also been reported (Salmén 2004; Diddens et al. 2008). The variability in reported Young’s moduli values has been attributed in the DFT calculations of crystalline cellulose Iβ by Dri et al. (2013) to misalignment of crystals displaying highly anisotropic elastic response.
Molecular modeling can provide insight not achievable experimentally, but for crystalline cellulose structure and properties is challenging due in part to the presence of strongly polar bonds in close proximity, and the large range of configurations and conformations that can be formed (Foley et al. 2012). This is complicated by the variability of experimental data for validation, which may be related to microfibril history, size and aspect ratio (Matthews et al. 2012). Consequently, numerous carbohydrate-specific (Foley et al. 2012) and non-carbohydrate force fields have been used to model cellulose and related carbohydrate molecules. Carbohydrate force fields include the modified AMBER (Homans 1990), GLYCAM06 (Kirschner et al. 2008), CHARMM (Guvench et al. 2008) and GROMOS 45a4 (Lins and Hünenberger 2005) force fields. The CHARMM and AMBER-related GLYCAM06 force fields have, for example, recently been employed in Molecular Dynamics simulations and found to be reasonably accurate in predicting the crystal structures of a range of small molecule cellulose analogues (Miyamoto et al. 2016). CHARMM has also been used in Molecular Dynamics simulations of small microcrystallites of cellulose Iβ in aqueous solution (Matthews et al. 2006). Unit-cell swelling (in particular the a lattice parameter), tilting of the molecular chains about the chain axis and inter-layer hydrogen bonds were predicted. Similar effects were predicted in hydrated cellulose Iβ microfibrils with the GLYCAM06 force field, but not the Gromos 45a4 force field (Matthews et al. 2012). The unit-cell expansion and structures predicted by the CHARMM and GLYCAM06 force fields are similar to structures in simulations at elevated temperature (Matthews et al. 2011) and are consistent with experimental observation of anisotropic thermal expansion (Wada et al. 2010).
The CVFF (Consistent Valence Force Field) force field (Hagler et al. 1979a) is an example of one that is not recognized specifically for study of carbohydrates, but has been used to model the conformation of oligosaccharides (Hardy and Sarko 1993; Hagler et al. 1979b; Siebert et al. 1992). In a combined molecular mechanics and molecular dynamics study of the conformation of carbohydrate molecules, the CVFF force field was found to predict the conformation reasonably well in comparison to experimental nmr data (Asensio et al. 1995). A modified AMBER force field (Homans 1990), parameterized specifically for saccharides, was in qualitative agreement in the same investigation.
This paper reports a modeling investigation into the origins of the auxetic response in crystalline cellulose Iβ. We aim to investigate qualitatively if there is a single-crystal mechanism that can explain the experimental negative values of ν 31 following the kraft cooking process. Given the evident need for further experimental characterization to provide improved comparison with force field predictions, unresolved issues relating to the effects of microfibril size and shape on mechanical properties, and the sensitivity of predicted properties on carbohydrate force field parametrization, the intention here is not to achieve high quantitative accuracy in Poisson’s ratio. Rather, we aim to probe the effects of unit-cell swelling, also observed following the kraft cooking process, on the structure and elastic properties of an infinite crystal of cellulose Iβ. We undertake molecular mechanics energy minimizations using a range of force fields to identify a suitable one for the prediction of the structure of undeformed cellulose Iβ. A more detailed analysis using the identified force field is then undertaken to identify the structure and elastic properties in the unloaded form and also with a stress condition applied to simulate the swelling along the a lattice parameter observed following the kraft cooking process.
Experimental section
Computational details
Molecular mechanics energy minimizations were carried out using the Cerius2 (version 4.6) and Materials Studio (version 4.1) molecular modeling packages (Accelrys). The following force fields, which have been parameterized to simulate the properties of organic networks, were assessed for their ability to accurately predict the structure of crystalline cellulose Iβ: Compass (Sun 1998; Sun et al. 1998; Rigby et al. 1997), Dreiding (Mayo et al. 1990), Universal (Rappé et al. 1992), CVFF (Hagler et al. 1979a) and PCFF (polymer consistent force field) (Sun et al. 1994). These force fields have all been previously used to model cellulose, see for example Eichhorn and Davies (2006), Bazooyar et al. (2012), Dri et al. (2015), Asensio et al. (1995), and Mazeau and Heux (2003). The force field which gave the best overall prediction of lattice parameters and bond parameters (lengths and angles) was then selected for a more detailed investigation into the prediction of the elastic constants of single-crystal cellulose Iβ before and after unit-cell swelling.
The model of cellulose Iβ was built using the Visualiser module within Materials Studio. The monoclinic unit cell was constructed with cell parameters determined previously (Nishiyama et al. 2002) from X-ray and neutron diffraction: a = 7.784 Å, b = 8.201 Å, c = 10.380 Å and γ = 96.55°. Space group P21 was assigned to the crystal. The carbon, hydrogen and oxygen atoms were then built into the cell according to the published fractional coordinates (Nishiyama et al. 2002). The refined crystal structure of cellulose Iβ displays some hydrogen bond disorder (Nishiyama et al. 2002). In this work the hydrogens not included in the refined structure were assigned using the adjust hydrogen function in the materials visualizer module, which considers several factors such as common oxidation state, hydridization, formal charge, and number and order of bonds. A hydrogen bond cut-off of A–H = 3 Å was employed, close to the value of 2.8 Å used by Nishiyama et al. (2002) and Miyamoto et al. (2016). Periodic boundary conditions were applied to simulate an infinite cellulose Iβ framework. Ewald summation was carried out to calculate the non-bond interactions (van der Waals and electrostatic). A convergence study showed the van der Waals energy varied significantly as the repulsive cut-off radius increased from 4 to 5 Å (−33.77 to −25.32 kcal mol−1, respectively), but did not change significantly as the cut-off radius was increased further (−25.16 kcal mol−1 at 10 Å). Equally, the van der Waals energy varied between −16.10 and −25.21 kcal mol−1 as the attractive cut-off radius increased from 6 to 12 Å and then remained virtually unchanged for further increases (−25.24 kcal mol−1 at 18 Å). Accordingly, a cut-off radius of 15.5 Å was employed for the non-bond interactions, corresponding to the Fine quality setting in Materials Studio. For comparison, Miyamoto et al. (2016) employed switching functions from 12.0 to 14.0 Å for van der Waals interactions, and a 12 Å cut off for electrostatic interactions in simulations of the crystal structures of a range of small molecule cellulose analogues. Matthews et al. (2006) employed a non-bond interaction cut-off of 15 Å, and Matthews et al. (2012) applied a non-bonded cut-off distance of 10 Å for simulations using the CHARMM35 and GLYCAM06 force fields, whereas they used a long-range electrostatic interactions cutoff of 8 Å and a twin-range cut-off (inner cut-off of 8 Å and outer cut-off of 14 Å) for van der Waals interactions for the Gromos 45a4 force field.
The potential energy of the undeformed structure was minimized using the smart minimizer option, combining the steepest descent, ABNR (adjusted basis set Newton–Raphson) and quasi-Newton methods. The quality of the geometry optimization calculation was set to Fine within Materials Studio 4.1, corresponding to an energy convergence criterion of less than 0.0001 kcal mol−1. During minimization, the P21 space group symmetry was converted to P1 and all cell parameters were set as variables. Convergence was achieved within the maximum number of minimization steps which was set at 5000 iterations.
The second derivative of the energy expression was used to compute the stiffness matrix C, and the on-axis elastic constants were obtained directly from the compliance matrix. The on-axis Poisson’s ratios (ν ij) and Young’s moduli (E i) were calculated from the compliance coefficients (s ij) using:
where the subscripts i and j refer to directions x i and x j parallel and perpendicular to the loading direction, respectively. The mutually orthogonal principal axes x 2 and x 3 used for the description of mechanical properties in Cerius 2 and Materials Studio coincide with the b and c lattice parameter crystallographic directions, respectively, and the a lattice parameter crystallographic direction lies in the plane of the x 1 and x 2 principal axes but at an angle γ to the x 2 axis—see Fig. 1b.
Results
Force field selection
To assess the variation between predicted and experimental values for each force field, a discrepancy factor was defined by:
where x = a, b, c, γ, bond angle, volume, etc. and the subscripts exp and mod represent experimental and predicted model values, respectively.
Unit-cell parameters
The predicted lattice parameters and unit-cell volume (V) of cellulose Iβ for all force fields employed are compared with published experimental data (Nishiyama et al. 2002) in the Supporting Information (Online Resource Table 1) and the calculated discrepancy factors are shown in Fig. 2.
Discrepancy factors for the force field predictions (Materials Studio) of unit-cell parameters compared with the experimental data of Nishiyama et al. (2002)
The CVFF force field gives the closest agreement with the experimental data, generally agreeing to within approximately 2 % or better for the lattice parameters and volume. The Universal force field fares the worst of the five force fields studied in this respect, typically being an order of magnitude worse in agreement than the CVFF force field. The CVFF force field has been parameterized using peptide and protein structures and has been extended to handle more general systems having similar functional groups, whereas the Universal force field is a general purpose force field with full coverage of the periodic table. The Universal force field is known to have only moderate accuracy for the prediction of geometries and conformational energy differences of organic molecules.
Bond parameters
All force fields reproduced the experimental covalent bond lengths to within better than 3 % discrepancy, with the exception of the C4–C5 bond length in the corner chain where the discrepancy was ≤4.5 % (Fig. 3 and Supporting Information Online Resource Table 2). The discrepancies between the force field model predictions and the experimental data (Nishiyama et al. 2002) for selected torsion angles are shown in Fig. 4. With the notable exception of the hydroxymethyl group torsion angle χ′ (C4–C5–C6–O6) for the center chain, the force fields generally predict the torsion angles for the center and corner chains to better than 10 % discrepancy. The force fields predict χ and χ′ values tending towards those for an ideal tg conformation (180°, −60°) whereas the experimental values for the center chain in particular deviate from ideality (χ = 158° and χ′ = −83°)—Supporting Information Online Resource Table 3. The CVFF force field appears to reproduce the torsion angles of the corner chain better than any of the other force fields. There is no clear cut best force field for the prediction of the torsion angles of the center chain.
Discrepancy factors for the force field bond length predictions compared with the experimental data of Nishiyama et al. (2002)
Discrepancy factors for the force field bond angle predictions compared with the experimental data of Nishiyama et al. (2002)
Based on the above modeling of the structural parameters of cellulose Iβ, the CVFF force field was selected for a more detailed investigation into the structure and mechanical properties of cellulose Iβ.
Detailed undeformed structure investigation
Three models employing the CVFF force field have been employed in this part of the investigation. CVFF1 is the model developed above. CVFF2 incorporated a triaxial stress condition in order to reproduce the undeformed experimental lattice parameters for cellulose Iβ. Finally, CVFF3 incorporated a stress in the x 1 direction to simulate the swelling along this axis observed during processing in the experimental measurement of negative Poisson’s ratio response in kraft cooked Norway spruce (Peura et al. 2006). The triaxial stress applied in the CVFF2 model was determined from:
where:
and c ij are elastic stiffness constants (i, j = 1, 2, 3) predicted from CVFF1. ε c is the strain in the c lattice parameter required to convert the lattice parameter from CVFF1 to the experimental value. The subscripts exp and CVFF1 represent experimental and CVFF1 model predicted values, respectively. Similar expressions were used for ε a and ε b . The stresses calculated in this way and employed in the CVFF2 model were: σ 1 = 0.38 GPa, σ 2 = 0.32 GPa and σ 3 = −3.98 GPa.
For the CVFF3 model, a preliminary assessment of the effect of a (swelling) stress in the x 1 direction showed the appearance of negative on-axis Poisson’s ratios in the x 1–x 3 plane occurred when σ 1 > 0.76 GPa (Fig. 5). Hence a tensile stress along the x 1 direction of σ 1 = 0.8 GPa was applied to the CVFF1 model to simulate both the swelling of lattice parameter a and the appearance of auxetic behavior observed after processing by Peura et al. (2006).
The unit-cell parameters and bond torsion angles for the CVFF1, CVFF2 and CVFF3 models are presented in Table 1. As expected, the CVFF2 model is in very close agreement with experimental unit-cell parameters (better than 0.3 % discrepancy for all parameters). The CVFF3 model displays the intended swelling in lattice parameter a, showing an increase of 7 % over the CVFF1 value. This is accompanied by a decrease in b by almost 3 % relative to CVFF1. Lattice parameter c remains largely unchanged between CVFF1 and CVFF3. There is little significant variation between the 3 models in the prediction of the torsion angles.
The hydrogen bond disorder reported experimentally for cellulose Iβ (Nishiyama et al. 2002) makes an accurate prediction of the hydrogen bond network very difficult for force field-based energy minimizations of the type reported in this paper. Nevertheless, we report the hydrogen bonding predicted from the CVFF1 model in Table 2 and Online Resource Fig. 1.
The hydrogen bonding network is predicted to comprise of O2–H···O6, O3–H···O5 and O6–H···O3 in the b–c plane for both the corner and center sheets. An additional O2–H···O1 hydrogen bond is predicted for the corner sheet. No hydrogen bonding is predicted between neighboring sheets by the CVFF1 model. Given the complexity of the multiple hydrogen bond network in cellulose Iβ, the level of agreement between the predicted CVFF1 model hydrogen bond parameters and the values proposed from X-ray and neutron scattering studies (Nishiyama et al. 2002; Table 2) is considered acceptable. With the exception of additional C4–H···O2 bonds between adjacent sheets predicted by the CVFF3 model there are no significant additional or different features predicted from the CVFF2 and CVFF3 models.
Projections of the unit cell in the x 1–x 2 plane, i.e. normal to the chain axes, are shown in Fig. 6 for the experimental and minimized CVFF1 and CVFF3 structures. The experimental atomic coordinates produce corner and center chains having similar rotations (tilt angles δ1 and δ2, respectively) about the c axis. In the CVFF1 model the corner and center chains undergo anticlockwise and clockwise rotation, respectively, relative to the experimental chain orientation. The opposing rotations about the c axis of the two distinct chains in the model structures are exaggerated further in the CVFF3 model, and are accompanied by the presence of the aforementioned C4–H···O2 bonds between adjacent sheets and the intended swelling of the unit-cell along the x1 direction.
Detailed elastic constants investigation
The compliance coefficients predicted from the CVFF1, CVFF2 and CVFF3 models, calculated from the 2nd derivative of the energy expression, are presented in the Online Resource Table 4. Table 3 contains the values of ν ij , and E i calculated from the compliance coefficients using Eqs. (1) and (2).
The Young’s modulus along the chain length (E 3) is higher for CVFF2 than for CVFF1, whilst the two transverse Young’s moduli are lower. However, the CVFF1 and CVFF2 models return very similar positive Poisson’s ratios to each other, generally agreeing to two decimal places for each Poisson’s ratio, implying the triaxial stress applied in CVFF2 to correct for deviation of the CVFF1 lattice parameters from the known experimental values has little effect on the predicted Poisson’s ratio response.
The CVFF3 model predicts a slightly lower E 3 and order of magnitude lower E 1 and E 2 values than the CVFF1 and CVFF2 models. Higher positive on-axis Poisson’s ratios in the x 1–x 2 plane are predicted by the CVFF3 model. Positive on-axis Poisson’s ratios are also predicted in the x 2–x 3 plane, with ν 23 and ν 32 being, respectively, lower and higher than predicted by the CVFF1 and CVFF2 models. As noted above, negative on-axis Poisson’s ratios are predicted by the CVFF3 model in the x 1–x 3 plane, reaching as low as ν 31 = −0.406.
To check the auxetic response in the x 1–x 3 plane for the CVFF3 model, energy minimizations were performed for 0.5 GPa increments of stress along the x 3 axis, maintaining σ 1 = 0.8 GPa and σ 2 = 0 GPa in all cases. The choice of stress increment along x 3 is similar to that used in previous molecular mechanics studies on the response of crystalline polymers to an applied stress (Evans et al. 1995; Nkansah et al. 1994; Alderson et al. 2005). Figure 7 shows the calculated true strains in the transverse x 1 and x 2 directions as a function of strain in the loading x 3 direction. The true strains were calculated from the lattice parameters as follows:
where the subscript ‘0’ indicates the parameter value at σ 3 = 0 GPa. The strains along x 1 and x 2 increase and decrease, respectively, with increasing strain along x 3 , consistent with the negative and positive signs of ν 31 and ν 32 calculated from the 2nd derivative of the energy expression (Table 3). The Poisson’s ratios in the undeformed CVFF3 model are determined from the negative of the slope of the 2nd order polynomial fit curve in Fig. 7 at ε3 = 0 for each case, giving ν 31 = −0.559 and ν 32 = +0.718. These compare to values calculated from the 2nd derivative of the energy expression (Table 3) of ν 31 = −0.406 and ν 32 = +0.623.
Figure 8 shows the CVFF3 model Poisson’s ratios (2nd derivative method) as a function of applied true strain for loading along the chain (x 3 ) direction. The negative and positive Poisson’s ratios ν 31 and ν 32 , respectively, are both predicted to vary with strain, with magnitude increasing with increasing strain. Poisson’s ratios ν 12 , ν 21 , ν 13 and ν 23 are predicted to be almost independent of strain by comparison. Preliminary energy minimizations (data not shown) for the CVFF1 and CVFF2 models showed these two models to display identical trends to each other with all Poisson’s ratios remaining constant (and positive) over the strain range covered in Fig. 8.
Structural evolution with stress along the x 3 direction
Given that the CVFF3 model predicts the on-axis auxetic behavior of cellulose Iβ, this model was selected to perform a detailed investigation of the variation in the structure of cellulose Iβ under loading in the x 3 direction, in an attempt to identify the mechanism for auxetic response.
Chain unfolding in the x 2–x 3 plane
Figure 9a shows a repeat cellobiose unit with best-fit plane ABDE created by Materials Studio shown as a semi-transparent surface with an arrow normal to the plane indicating its orientation. The best fit plane is defined as a plane where the (mass weighted) root mean square distances from the plane to the selected atoms are minimized. The selected atoms used to generate the best-fit plane ABDE were O1, C1, C2, C3, C4, C5, C6, O2, O3, O5, O6 and O1(O4). For clarity, only atoms related to the torsion angles ϕ and ψ, and the bridging angle τ (=C1–O1–C4) are labelled in Fig. 9a. Plane ABDE is almost parallel to the x 2–x 3 plane, indicated by the arrow normal to the plane being aligned nearly parallel to the x 1 axis. Atom O1 lies above the plane ABDE and O4 below the plane ABDE (i.e. bonds C1–O1 and O4–C4 are over and below the plane ABDE, respectively). The glycosidic torsion angles ψ and ϕ are defined as the angle between plane C5–C4–O4(O1) and plane C4–O4(O1)–C1 and the angle between planes O5–C1–O1 and C1–O1–C4, respectively.
a Projection in the x 2–x 3 plane of a repeat cellobiose unit with best-fit plane ABDE created by Materials Studio. ϕ and ψ are the torsion angles defined by (C4–O1–C1–O5) and (C1–O4(O1)–C4–C5), respectively. τ is angle C1–O1–C4. b Predicted change in bridging angle τ and torsion angles ϕ and ψ (i = τ, ϕ or ψ) as a function of strain in the loading (x 3) direction. c Predicted change in O1···O4(O1) distance in cellobiose unit as a function of strain in the loading (x 3) direction
The glycosidic bridging angle τ is predicted to increase with increasing tensile strain in the loading (x 3) direction (Fig. 9b), indicating an unfolding of the backbone chain along the x 3 axis in the x 2–x 3 plane. The chain unfolding in the x 2–x 3 plane is accompanied by a predicted increase with loading strain in the O1···O4(O1) distance (Fig. 9c) which implies some stretching of the cellobiose unit along the axis connecting O1 and O4(O1) also occurs.
Chain rotation in the x 1–x 2 plane
Figure 9b also shows the predicted variations of the helical parameters ϕ (C4–O1–C1–O5) and ψ (C1–O4(O1)–C4–C5). ϕ is predicted to increase and ψ is predicted to decrease with increasing tensile strain in the loading (x 3 ) direction. This corresponds to the plane ABDE rotating about the O1–O4(O1) axis. Since the O1–O4(O1) axes in adjacent cellobiose units are aligned at angles of equal but opposite sign with respect to the x 3 axis, the rotation of plane ABDE about the O1–O4(O1) axis corresponds to a rotation of the helical chain about the helical (x 3 ) axis.
This is shown in Fig. 10a which shows that the cellulose chains appear as tilted ‘rod’ segments (terminated by C6 atoms) interconnected by hydrogen bonds when projected onto the x 1–x 2 plane. Tilt angles δ 1 and δ 2, previously referred to in Fig. 6, are defined by the angle the cellulose ‘rods’ in the corner and center chains make with the x 2 axis in the x 1–x 2 projection, respectively (positive values correspond to anti-clockwise rotation). The CVFF3 model predicts values for the undeformed structure of δ 1 = 17.2° and δ 2 = −6.7°. The magnitudes of δ 1 and δ 2 are predicted to increase with increasing tensile strain along the x 3 direction (Fig. 10b). In other words, each cellulose chain is predicted to rotate about its axis in response to a uniaxial load applied along x 3.
a Projection of the structure of cellulose Iβ in the x 1–x 2 plane, defining tilt angles δ 1 and δ 2 as the angle the C6···C6 length projected in the plane makes with the x 2 axis for the corner chain and center chain, respectively. b Predicted variation in the magnitudes of δ 1 and δ 2 with strain in the x 3 direction (CVFF3 model)
Cellulose chains in adjacent sheets are predicted to be connected by C4–H···O2 bonds (Fig. 6c), whereas inter-chain bonding within a sheet occurs via O6–H···O3 hydrogen bonds (Fig. 6b). This is consistent with previous reports showing no hint of inter-sheet O–H···O hydrogen bonds, and cellulose sheets held together by C–H···O bonds and hydrophobic interactions (Finkenstadt and Millane 1998; Nishiyama et al. 2002; Claffey and Blackwell 1976). The length between the (donor) C4–H in the center chain and O2 (accepter) in the corner chain is predicted to remain constant at 2.491 Å as stress is applied along the x 3 direction (Table 4). A slight decrease in the distance between the donor hydrogen and acceptor oxygen is predicted with increasing applied stress for the intra-sheet O6–H···O3 hydrogen bond (d(H···A) decreases from 2.643 to 2.631 Å as stress increases in the range −2 < σ3 < +2 GPa). The C6···C6 distances defining the rod segments in Fig. 9a increase slightly with increasing tensile stress along x 3 for both the corner and center chains, consistent with the predicted increase in glycosidic bridging angle τ.
Chain unfolding in the x 1–x 3 plane
The projection of the cellulose Iβ structure in the x 1–x 3 plane is presented in Fig. 11a, showing the covalently bonded chains aligned along the x 3 axis. The bridging O1 atoms are labeled for clarity. The projected structure can be characterized by a zigzag framework connecting the O1 bridging atoms along each chain. The angle the projected O1···O4(O1) distance makes with the x 3 axis in the x 1–x 3 plane (defined as α 1 and α 2 for the corner and center chains, respectively—Fig. 11a) is predicted to decrease with increasing tensile strain in the loading (x 3) direction for both the corner and center chains, as shown in Fig. 11b. The cellulose chains are, then, also predicted to unfold along x 3 in the x 1–x 3 plane in response to a uniaxial tensile load applied along x 3.
Discussion
In this work, molecular mechanics has been used to predict the structure and elastic properties of single-crystal cellulose Iβ. The CVFF force field has been found to reproduce the lattice parameters, bond structure and hydrogen bond structure reasonably well. In the undeformed state the CVFF force field predicts positive on-axis Poisson’s ratios. The on-axis Poisson’s ratios are all predicted to be positive and remain virtually unchanged when a triaxial stress is applied in order for the predicted lattice parameters to reproduce exactly the experimentally determined values. The positive Poisson’s ratios are consistent with reported values for crystalline cellulose from normally grown wood, which have been attributed to the presence of the amorphous lignin-hemicellulose matrix (Peura et al. 2006).
Applying a stress along the x 1 direction, to simulate swelling along this direction, leads to the predicted appearance of negative values of the major Poisson’s ratios in the x 1–x 3 plane. This is consistent with the previous experimental measurement of a negative ν 31 Poisson’s ratio in kraft cooked Norway spruce, in which the removal of lignin and hemicelluloses during cooking leads to the swelling of the crystallites in the x 1 direction (Peura et al. 2006). The values of ν 31 = −0.559 and −0.406 from the slope of the transverse strain vs axial strain curve and the 2nd derivative of the energy expression (Table 3), respectively, compare with the experimental average values of ν 31 in the ranges −0.26 to −1.17 (before yield point) and −0.86 to −1.05 (after yield point) (Peura et al. 2006). The results suggest an alternative or additional mechanism for auxetic behavior to the microfibril non-alignment and cell–cell wall layer shearing interactions proposed by Peura et al. (2006).
The swelling simulation in CVFF3 employed a stress along the x 1 direction to simulate swelling since it is expected that the inter-plane direction is most affected by removal of the hemicellulose-lignin matrix and presence/absence of moisture (Zabler et al. 2010). On the face of it the employed stress of 0.8 GPa is a very large stress to use since the theoretical tensile strength of crystalline cellulose is ~2 GPa along the chain (x 3) direction (Mark 1967), for example. However, 0.8 GPa is within the range of stress magnitudes employed in the CVFF2 model to bring the CVFF force field unit-cell length predictions in line with experiment. Hence caution should be applied when considering the absolute value of stress employed in the swelling simulation.
The amount of swelling due to the kraft cooking process is not clear from Peura et al. (2006). For comparison, a 0.6 % expansion in a during dehydration of crystalline cellulose has been reported (Zabler et al. 2010), and a 5 % expansion in a occurs on heating cellulose Iβ to the transition to high temperature cellulose I (Wada et al. 2010). The expansion in the CVFF3 simulation (relative to the CVFF1 simulation) reported here (Table 1) is 7 %. In this work we have been concerned with the effects of swelling on the mechanical properties of cellulose Iβ. More sophisticated modelling treatments for simulating swelling than those presented here have been reported including, for example, molecular dynamics simulations of small microcrystallites of cellulose Iβ in aqueous solution (Matthews et al. 2006, 2012).
The CVFF1 and CVFF2 Young’s moduli (Table 3) are in agreement with previous axial and transverse Young’s moduli ranges from the literature of 134–220 GPa (Sakurada et al. 1962; Gillis 1969; Tashiro and Kobayashi 1991; Salmén 2004; Diddens et al. 2008) and 15–27.2 GPa (Salmén 2004; Diddens et al. 2008), respectively. The CVFF3 energy minimizations indicate the effect of swelling of the a lattice parameter has little effect on the Young’s modulus in the chain direction (E 3) but reduces the transverse Young’s moduli (by an order of magnitude for the amount of swelling considered in the models).
The mechanism responsible for the negative ν 31 response has been explored by examining the evolution of the crystallographic structure in energy minimizations employing a uniaxial stress in the x 3 direction. The cellobiose chains are predicted to undergo rotation in the x 1–x 2 plane (transverse to chain axis and loading (x 3) direction—Fig. 10). The C4–H…O2 inter-sheet interaction distance was found to remain constant with applied stress along the x 3 direction and, therefore, effectively acts as a rigid spacer unit between the rotating cellobiose chains. This enables the development of a conceptual model providing a mechanistic explanation for the auxetic response. In the conceptual model the projection of the structure in the x 1–x 2 plane is simplified in a first approximation to an array of rotatable rigid rods (projected cellobiose chains) connected by a series of intra-layer and inter-layer inextensible spacers (projected O–H···O and C4–H···O2 interaction distances, respectively). This is shown in Fig. 12 where the rigid spacers corresponding to the projected O–H···O intra-layer distances connect adjacent rigid rods in a corner-to-corner manner [one bottom corner to one top corner in the untilted (δ = 0) configuration (Fig. 12b)]. The projected C4–H···O2 rigid spacers are connected to the ‘corner sheet’ rods at a corner adjacent to the connected ‘center sheet’, and to the ‘center sheet’ rods at a fixed location on the edge facing the connected ‘corner sheet’. The untilted configuration shown in Fig. 12b possesses a rectangular unit-cell in the x 1 –x 2 plane.
a Projection of the CVFF3 model structure in the x 1–x 2 plane. Conceptual model of a network of rotatable rigid rods interconnected by inextensible spacers mimicking the projected CVFF3 structure in the x 1–x 2 plane: b no rotation of rigid rods, c intermediate rotation of the rigid rod units and d high rotation of the rigid rod units
If it is assumed that the angle the inter-sheet rigid spacer makes with the center sheet rigid rod (assumed perpendicular in Fig. 12) remains constant irrespective of the tilt (rotation) of the rigid rods, then cooperative rotation of the rigid rod units by angle δ with respect to the x 2 axis leads to the structure shown in Fig. 12c, with a concomitant shearing of the unit cell in the x 1–x 2 plane. This is consistent with the monoclinic unit-cell and tilted chain orientations predicted by the undeformed CVFF3 model (Fig. 12a). Increasing the rigid rod rotation (tilt angle δ) further causes an increase in lattice parameter a and a decrease in lattice parameter b and, therefore, expansion and contraction of the structure along the x 1 and x 2 directions, respectively (Fig. 12d). Figure 10 shows that such rigid rod rotation occurs in response to a tensile stress applied in the x 3 direction perpendicular to the plane of the structure (σ3 > 0), and so this corresponds to negative and positive values for ν 31 and ν 32, respectively, as predicted in the force field-based energy minimizations (Table 3; Fig. 8). Similarly, applying a compressive load along the chain axis to the structure in Fig. 12c would tend to remove the rigid rod tilt (i.e. tend towards the structure in Fig. 12b) resulting in contraction and expansion of the structure along the x 1 and x 2 directions, respectively, consistent with the CVFF3 model predictions in Fig. 7.
Clearly the 2D interpretation presented in Fig. 12 is a simplification of the cellulose Iβ system. Whilst the force field energy minimizations indicate inter-sheet C4–H···O2 interactions act as rigid spacers in 3D (Table 4), a slight reorientation of this interaction length is also predicted such that the projected C4–H···O2 distance in the x 1–x 2 plane increases slightly with increasing tensile stress along x 3 (the models indicate an increase in the projected length of ~0.2 % for an applied strain along x 3 of ~1 %). The projected C4–H···O2 distance is aligned most closely with the x 1 axis and so the increase in the projected length provides an increase in x 1 additional to that from x 1–x 2 chain rotation, reinforcing the negative value of ν 31. Similarly, the projected O–H···O intra-layer interaction distance, most closely aligned with the x 2 axis, decreases in the x 1–x 2 plane with increasing tensile stress (by ~0.1 % for an applied strain of ~1 %), giving an additional decrease in x 2 to that from x 1 to x 2 chain rotation to reinforce the positive value of ν 32.
The prediction of chain tilting and inter-layer hydrogen bonds due to swelling along the x1 direction in an infinite crystal of cellulose Iβ in this work has also been predicted in Molecular Dynamics simulations of small microcrystallites of cellulose Iβ in aqueous solution using the CHARMM and GLYCAM force fields (Matthews et al. 2006; Matthews et al. 2012). Structures with tilts and rotating units have previously been identified as leading to auxetic behavior. Examples include rotation of tetrahedral sub-units in inorganic tetrahedral framework systems such as the α-cristobalite polymorph of crystalline silica (Yeganeh-Haeri et al. 1992; Alderson and Evans 2002), and in certain zeolitic structures (Grima et al. 2000). Rotating units have also been proposed in ‘nodule-fibril’ models for auxetic microporous polymers (Evans and Caddock 1989) and, at the molecular level, in auxetic liquid crystal polymers (He et al. 1998). In the polymer cases, the rotation of the units has been reported in the plane containing the loading direction. This work identifies rotation of tilted units in the plane transverse to the molecular chain axis and loading direction as a mechanism for auxetic response in crystalline polymeric systems.
The orientation of the cellobiose chain in the x 1–x 2 plane and the identification of the role of rotation of these chains about the x 3-axis is analogous to the mechanism proposed for anisotropic (including negative) thermal expansion in pentacene crystals (Haas et al. 2007). The tilt angle identified in this work is analogous to the herringbone angle describing the packing of the assumed rigid pentacene molecules. With increasing temperature, the increase of the herringbone angle and the increasingly dominant vibrations about the long molecular axis cause a distinctly anisotropic expansion in the a–b plane, similar to that described in Fig. 12. The vibrating molecules at the corners of the pentacene unit cell interact with the one in the center, pushing each other further apart in one unit-cell direction as the vibration amplitude grows with temperature, with a concomitant contraction in the other lattice parameter giving rise to a negative coefficient of thermal expansion in this direction. In other words, the two principal directions in the x 1–x 2 plane undergo opposite expansion/contraction in response to thermal loading in pentacene crystals, whereas in cellulose Iβ crystals this mechanism appears to be triggered by uniaxial mechanical loading along the x 3 direction.
Interestingly, cellulose Iβ also displays anisotropic thermal expansion which becomes more dramatic upon phase transition to high temperature cellulose I (Wada et al. 2010). As noted above, high temperature cellulose I displays significant swelling of the a lattice parameter (relative to cellulose Iβ) which undergoes expansion upon further heating, accompanied by a contraction of the b lattice parameter. These are the same responses as for a tension applied along the chain axis in the CVFF3 model presented here. Molecular dynamics simulations (CHARMM and GLYCAM06 force fields) predict the presence of tilted chains and inter-layer hydrogen bonds in high temperature cellulose I (Matthews et al. 2011). Taken together these suggest a mechanistic link between the thermal expansion and Poisson’s ratio responses in high temperature cellulose I and kraft cooked cellulose Iβ, respectively.
It is tempting to compare the projected zig-zag framework connecting the O1 bridging atoms along each chain and interconnecting C4–H···O2 inter-sheet interactions in the x 1–x 3 plane (Fig. 11a) with a 2D re-entrant hexagonal honeycomb structure. Deformation of a re-entrant hexagonal honeycomb by rotation of the ribs forming the honeycomb, corresponding to a reduction in honeycomb angle α (i.e. unfolding of the zig-zag structure along the x 3 direction) for a tensile stress in the x 3 direction, is known to produce a negative value for ν 31 (Evans et al. 1995; Gibson et al. 1982; Masters and Evans 1996). The molecular mechanics energy minimizations presented here predict an unfolding of the molecular chains along the loading x 3 axis (Fig. 11b) consistent with this mechanism. However, the models also indicate the projection of the O1···O1 distance in the x 1–x 3 plane increases with increasing tensile stress along x 3 (projected distance increases by ~0.7 % for loading strain of ~0.9 %). This corresponds to stretching of the oblique ribs in a re-entrant hexagonal honeycomb, which is known to lead to a positive value of ν 31 (Masters and Evans 1996). From the analytical model expressions for a re-entrant hexagonal honeycomb (Masters and Evans 1996), the magnitude of change in projected O1···O1 length would appear to be sufficient to overcome the zig-zag unfolding mechanism driving the auxetic response.
This work has identified mechanisms of chain rotation and chain unfolding, and the crucial role of secondary bonding, in realizing auxetic response at the molecular chain level in a naturally-occurring macromolecular system. It is expected this will provide impetus to the further design and development of molecular-engineered synthetic auxetic polymers.
Conclusion
In this work we have attempted to interpret the structural evolution of the 3D structure of crystalline cellulose Iβ through consideration of key structural features in 2D projections. It is clear that the effects of bond stretching and reorientation of the 3D structure complicate an interpretation of the mechanisms responsible for auxetic behavior in such systems via a consideration of 2D projections. Nevertheless we have identified here two potential mechanisms operating in crystalline cellulose Iβ: namely rotation of cellobiose chains transverse to the loading x 3 direction, and unfolding of the chains along the loading direction. The former mechanism appears to be the most likely of the two mechanisms to be responsible for the auxetic effect predicted by the molecular mechanics energy minimizations. In both mechanisms the presence of secondary (hydrogen) bonding between chains, perpendicular to the chain/loading direction, appears to be crucial in realizing auxetic behavior.
References
Alderson A, Alderson K (2007) Auxetic materials. Proc Inst Mech Eng Part G J Aerosp Eng 221:565–576
Alderson KL, Evans KE (1992) The fabrication of microporous polyethylene having a negative Poisson’s ratio. Polymer 33:4435–4438
Alderson A, Evans KE (2002) Molecular origin of auxetic behavior in tetrahedral framework silicates. Phys Rev Lett 89:225503-1
Alderson KL, Pickles AP, Neale PJ, Evans KE (1994) Auxetic polyethylene: the effect of a negative Poisson’s ratio on hardness. Acta Metall Mater 42:2261–2266
Alderson KL, Webber RS, Mohammed UF, Murphy E, Evans KE (1997) An experimental study of ultrasonic attenuation in microporous polyethylene. Appl Acoust 50:23–33
Alderson KL, Alderson A, Smart G, Simkins VR, Davies PJ (2002) Auxetic polypropylene fibres Part 1—manufacture and characterisation. Plast Rubbers Compos 31:344–349
Alderson A, Davies PJ, Williams MR, Evans KE, Alderson KL, Grima JN (2005) Modelling of the mechanical and mass transport properties of auxetic molecular sieves: an idealised organic (polymeric honeycomb) host-guest system. Mol Simul 31:897–905
Asensio JL, Martin-Pastor M, Jimenez-Barbero J (1995) The use of CVFF and CFF91 force fields in conformational analysis of carbohydrate molecules. Comparison with AMBER molecular mechanics and dynamics calculations for methyl α-lactoside. Int J Biol Macromol 17:137–148
Atalla RH, Van der Hart DL (1984) Native cellulose: a composite of two distinct crystalline forms. Science 223:283–285
Baughman RH, Galvão DS (1993) Crystalline network with unusual predicted mechanical and thermal properties. Nature 365:735–737
Bazooyar F, Momany FA, Bolton K (2012) Validating empirical force fields for molecular-level simulation of cellulose dissolution. Comput Theor Chem 984:119–127
Caddock BD, Evans KE (1989) Microporous materials with negative Poisson’s ratios. II. Mechanisms and interpretation. J Phys D Appl Phys 22:1877–1882
Choi JB, Lakes RS (1992) Nonlinear properties of metallic cellular materials with a negative Poisson’s ratio. J Mater Sci 27:5375–5381
Claffey W, Blackwell J (1976) Electron diffraction of valonia cellulose. A quantitative interpretation. Biopolymers 15:1903–1915
Diddens I, Murphy B, Krisch M, Müller M (2008) Anisotropic elastic properties of cellulose measured using inelastic X-ray scattering. Macromolecules 41:9755–9759
Dri FL, Hector LG Jr, Moon RJ, Zavattieri PD (2013) Anisotropy of the elastic properties of crystalline cellulose Iβ from first principles density functional theory with Van der Waals interactions. Cellulose 20:2703–2718
Dri FL, Wu X, Moon RJ, Martini A, Zavattieri PD (2015) Evaluation of reactive force fields for prediction of the thermo-mechanical properties of cellulose Iβ. Comput Mater Sci 109:330–340
Eichhorn SJ, Davies GR (2006) Modelling the crystalline deformation of native and regenerated cellulose. Cellulose 13:291–307
Evans KE (1990) Tailoring the negative Poisson’s ratio. Chem Ind 20:654–657
Evans KE (1991) The design of doubly curved sandwich panels with honeycomb cores. Compos Struct 17:95–111
Evans KE, Alderson A (2000) Auxetic materials: functional materials and structures from lateral thinking. Adv Mater 12:617–624
Evans KE, Caddock BD (1989) Microporous materials with negative Poisson’s ratio: II. Mechanisms and interpretation. J Phys D Appl Phys 22:1883–1887
Evans KE, Nkansah M, Hutchison IJ, Rogers SC (1991) Molecular network design. Nature 353:124
Evans KE, Alderson A, Christian FR (1995) Auxetic two-dimensional polymer networks: an example of tailoring geometry for specific mechanical properties. J Chem Soc Faraday Trans 91:2671–2680
Finkenstadt VL, Millane RP (1998) Crystal structure of valonia cellulose Iβ. Macromolecules 31:7776–7783
Foley BL, Tessier MB, Woods RJ (2012) Carbohydrate force fields. Wiley Interdiscip Rev Comput Mol Sci 2(4):652–697
Franke M, Magerle R (2011) Locally auxetic behavior of elastomeric polypropylene on the 100 nm length scale. ACS Nano 5:4886–4891
French AD (2014) Idealized powder diffraction patterns for cellulose Polymorphs. Cellulose 21:885–896
Friis EA, Lakes RS, Park JB (1988) Negative Poisson’s ratio polymeric and metallic materials. J Mater Sci 23:4406–4414
Gibson LJ, Ashby MF, Schajer GS, Robertson CI (1982) The mechanics of three-dimensional. Cellular materials. Proc R Soc Lond A382:25–42
Gillis PP (1969) Effect of hydrogen bonds on the axial stiffness of crystalline native cellulose. J Polym Sci Part A-2 7:783–794
Greaves GN, Greer AL, Lakes RS, Rouxel T (2011) Poisson’s ratio and modern materials. Nat Mater 10:823–837
Grima JN, Jackson R, Alderson A, Evans KE (2000) Do zeolites have negative Poisson’s ratios. Adv Mater 12:1912–1918
Grima JN, Alderson A, Evans KE (2005) Auxetic behaviour from rotating rigid units. Phys Status Solidi B 242:561–575
Guvench O, Greene SN, Kamath G, Brady JW, Venable RM, Pastor RW, Mackerell Jr AD (2008) Additive empirical force field for hexopyranose monosaccharides. J Comput Chem 29:2543–2564
Haas S, Batlogg B, Besnard C, Schiltz M, Kloc C, Siegrist T (2007) Large uniaxial negative thermal expansion in pentacene due to steric hindrance. Phys Rev B Condens Matter Mater Phys 76:205203-1–205203-5
Hagler AT, Dauber P, Lifson S (1979a) Consistent force field studies of intermolecular forces in hydrogen-bonded crystals. 3. The C=O…H–O hydrogen bond and the analysis of the energetics and packing of carboxylic acids. J Am Chem Soc 101:5131–5141
Hagler AT, Lifson S, Dauber P (1979b) Consistent force field studies of intermolecular forces in hydrogen-bonded crystals. 2. A benchmark for the objective comparison of alternative force fields. J Am Chem Soc 101:5122–5130
Hardy BJ, Sarko A (1993) Conformational analysis and molecular dynamics simulation of cellobiose and larger cellooligomers. J Comput Chem 7:831–847
He C, Liu P, Griffin AC (1998) Toward negative Poisson’s ratio polymers through molecular design. Macromolecules 31:3145–3147
Homans SW (1990) A molecular mechanical force field for the conformational analysis of oligosaccharides: comparison of theoretical and crystal structures of Manα1-3Manβ1-4GlcNAc. Biochemistry 29:9110–9118
Howell B, Prendergast P, Hansen L (1991) Acoustic behaviour of negative Poisson’s ratio materials. DTRC-SME-91/01, David Taylor Research Centre, Annapolis
Josefsson G, Tanem BS, Li Y, Vullum PE, Gamstedt EK (2013) Prediction of elastic properties of nanofibrillated cellulose from micromechanical modeling and nano-structure characterization by transmission electron microscopy. Cellulose 20:761–770
Keskar NR, Chelikowsky JR (1992) Negative Poisson ratios in crystalline SiO2 from 1st-principles calculations. Nature 358:222–224
Kirschner KN, Yongye AB, Tschampel SM, Gonzáles-Outeiriño J, Daniels CR, Foley BL, Woods RJ (2008) GLYCAM06: a generalizable biomolecular force field. Carbohydrates. J Comput Chem 29:622–655
Kroon-Batenburg LMJ, Bouma B, Kroon J (1996) Stability of cellulose structures studied by MD simulations. Could mercerized cellulose II be parallel? Macromolecules 29:5695–5699
Lakes RS (1987) Foam structures with a negative Poisson’s ratio. Science 235:1038–1040
Lins RD, Hünenberger PH (2005) A new GROMOS force field for hexopyranose-based carbohydrates. J Comput Chem 26:1400–1412
Mark RE (1967) Cell wall mechanics of tracheids. Yale University Press, New Haven, p 310
Masters IG, Evans KE (1996) Models for the elastic deformation of honeycombs. Compos Struct 35:403–422
Matthews JF, Skopec CE, Mason PE, Zuccato P, Torget RW, Sugiyama J, Himmel ME, Brady JW (2006) Computer simulation studies of microcrystalline cellulose Iβ. Carbohydr Res 341:138–152
Matthews JF, Bergenstrahle M, Beckham GT, Himmel ME, Nimlos MR, Brady JW, Crowley MF (2011) High-temperature behavior of cellulose I. J Phys Chem B 115:2155–2166
Matthews JF, Beckham GT, BergenstrÅhle-Wohlert M, Brady JW, Himmel ME, Crowley MF (2012) Comparison of cellulose Iβ simulations with three carbohydrate force fields. J Chem Theory Comput 8:735–748
Mayo SL, Olafson BD, Goddard WA III (1990) A generic force field for molecular simulations. J Phys Chem 94:8897–8909
Mazeau K, Heux L (2003) Molecular dynamics simulations of bulk native crystalline and amorphous structures of cellulose. J Phys Chem B 107:2394–2403
Miyamoto H, Schnupf U, Crowley MF, Brady JW (2016) Comparison of the simulations of cellulosic crystals with three carbohydrate force fields. Carbohydr Res 422:17–23
Nakamura K, Wada M, Kuga S, Okano T (2004) Poisson’s ratio of cellulose Iβ and cellulose II. J Polym Sci Part B Polym Phys 42:1206–1211
Nishiyama Y, Langan P, Chanzy H (2002) Crystal structure and hydrogen-bonding system in cellulose Iβ from synchrotron X-ray and neutron fiber diffraction. J Am Chem Soc 124:9074–9082
Nkansah MA, Evans KE, Hutchinson IJ (1994) Modelling the mechanical properties of an auxetic molecular network. Mod Simul Mater Sci Eng 2:337–352
Peura M, Grotkopp I, Lemke H, Vikkula A, Laine J, Müller M, Serimaa R (2006) Negative Poisson ratio of crystalline cellulose in Kraft cooked Norway spruce. Biomacromolecules 7:1521–1528
Rappé AK, Casewit CJ, Colwell KS, Goddard WA, Skiff WM (1992) UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J Am Chem Soc 114:10024–10035
Ravirala N, Alderson A, Alderson KL, Davies PJ (2005) Expanding the range of auxetic polymeric products using a novel melt-spinning route. Phys Status Solidi B 242:653–664
Rigby D, Sun H, Eichinger BE (1997) Computer simulations of poly(ethylene oxide): force field, PVT diagram and cyclization behaviour. Polym Int 44:311–330
Sakurada I, Nukushina Y, Ito T (1962) Experimental determination of the elastic modulus of crystalline regions in oriented polymers. J Polym Sci 57:651–660
Salmén L (2004) Micromechanical understanding of the cell-wall structure. Comptes Rendus Biol 327:873–880
Scarpa F, Pastorino P, Garelli A, Patsias S, Ruzzene M (2005) Auxetic compliant flexible PU foams: static and dynamic properties. Phys Status Solidi B 242:681–694
Siebert H-C, Reuter G, Schauer R, von der Lieth C-W, Dabrowski J (1992) Solution conformations of GM3 gangliosides containing different sialic acid residues as revealed by NOE-based distance mapping, molecular mechanics, and molecular dynamics calculations. Biochemistry 31:6962–6971
Simon I, Glasser L, Scheraga HA, Manley RSJ (1988) Structure of cellulose. 2. Low-energy crystalline arrangements. Macromolecules 21:990–998
Stenberg N, Fellers C (2002) Out-of-plane Poisson’s ratios of paper and paperboard. Nordic Pulp Paper Res J 17:387–394
Sun H (1998) COMPASS: an ab initio forcefield optimized for condensed-phase applications-overview with details on alkane and benzene compounds. J Phys Chem B 102:7338–7364
Sun H, Mumby SJ, Maple JR, Hagler AT (1994) An ab initio CFF93 all-atom force-field for polycarbonates. J Am Chem Soc 116:2978–2987
Sun H, Ren P, Fried JR (1998) The COMPASS force field parameterization and validation for phosphazenes. Comput Theor Polym Sci 8:229–246
Tanpichai S, Quero F, Nogi M, Yano H, Young RJ, Lindström T, Sampson WW, Eichhorn SJ (2012) Effective Young’s modulus of bacterial and microfibrillated cellulose fibrils in fibrous networks. Biomacromolecules 13:1340–1349
Tashiro K, Kobayashi M (1991) Theoretical evaluation of 3-dimensional elastic-constants of native and regenerated celluloses-role of hydrogen-bonds. Polymer 32:1516–1526
Van der Hart DL, Atalla RH (1984) Studies of microstructure in native celluloses using solid-state carbon-13 NMR. Macromolecules 17:1465–1472
Verma P, Shofner ML, Griffin AC (2014) Deconstructing the auxetic behavior of paper. Phys Status Solidi B 251:289–296
Wada M, Hori R, Kim U-J, Sasaki S (2010) X-ray diffraction study on the thermal expansion behavior of cellulose Iβ and its high-temperature phase. Polym Degrad Stab 95:1330–1334
Yeganeh-Haeri Y, Weidner DJ, Parise JB (1992) Elasticity of α-cristobalite: a silicon dioxide with a negative Poisson’s ratio. Science 257:650–652
Zabler S, Paris O, Burgert I, Fratzl P (2010) Moisture changes in the plant cell wall force cellulose crystallites to deform. J Struct Biol 171:133–141
Acknowledgments
Part of this work has been funded through a doctoral studentship from the Northwest Composites Centre in the UK.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yao, Y.T., Alderson, K.L. & Alderson, A. Modeling of negative Poisson’s ratio (auxetic) crystalline cellulose Iβ . Cellulose 23, 3429–3448 (2016). https://doi.org/10.1007/s10570-016-1069-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10570-016-1069-9