Introduction

Extensional rheometry of polymeric, nanoparticulate and associating fluids has been a subject of interest for many researchers for last three decades following the realization that the deformation regimes in many industrial and biological processes have a significant extensional component (e.g. coating, atomization, flow through porous media and sensory perception in the case of food products) (Duxenneuner et al. 2008; Patruyo et al. 2002). Extensional deformation is encountered whenever a fluid undergoes a change in its cross-sectional area of flow. This includes but is not limited to flow through converging channels, capillary entrance flows and free surface capillary thinning (Gonzalez et al. 2005). Aqueous solutions of biopolymers and their derivatives, owing to their commercial use have to undergo abovementioned extensional deformations and therefore are subjects of interest with regards to their extensional rheological properties.

For fluids with shear viscosity <103 Pa s, Capillary break-up extensional rheometry (CaBER) has received much attention during the past few years (Tripathi et al. 2000; Tirtaatmadja et al. 2006; McKinley and Tripathi 2000; Kheirandish et al. 2008; Tripathi et al. 2006; Plog et al. 2005; Arnolds et al. 2010). In CaBER, a fluid filament is subjected to step-strain and the mid-plane diameter of the filament undergoing capillary driven thinning is recorded as a function of time (Fig. 1). The user has little control over the elongational flow kinematics and the extensional strain rate is self selected by the balance between capillary, elastic, inertial and viscous forces. For elastic fluids, the diameter decays exponentially whereas for Newtonian fluids (and the viscoelastic fluids in which the polymer chains have been stretched as much as possible during the elastocapillary thinning) the filament diameter decays linearly. The rate constants associated with the exponential and linear capillary thinning allow the determination of an extensional relaxation time λ E (timescale for viscoelastic stress growth) and quasi-steady state terminal extensional viscosity η E respectively. CaBER measurements are relatively time-efficient and require less sample volume (<1 ml) compared to the techniques such as capillary extrusion (Cogswell 2003), opposed jet flow (Patruyo et al. 2002) and filament stretching rheometry (FiSER) (Bhardwaj et al. 2007). It is noteworthy that Cross-slot rheometry also offers some of the abovementioned advantages of CaBER, and has been used for cellulosic fluids (Sharma et al. 2015) and hyaluronic acid solutions (Haward et al. 2013; Haward 2014). From the perspective of processability, breaking up of an initially stable fluid filament is a process which has commercial applications such as spraying and atomization of pesticides, applying paints and adhesives, coating and food processing operations e.g. container filling (McKinley 2005b).

CaBER technique has been used in the past for Newtonian fluids (Mckinley and Tripathi 2000), shear-thinning viscoelastic fluids (Tripathi et al. 2006; Clasen et al. 2006b; Rodd et al. 2005), non-shear-thinning viscoelastic fluids, i.e. Boger fluids (Plog et al. 2005; Campo-Deano et al. 2011; Anna and McKinley 2001), and yield stress fluids (McKinley 2005a, b; Niedzwiedz et al. 2009) CaBER measurements for a number of systems containing biopolymers and their derivatives in aqueous media have been reported in the past literature, most notably for xanthan (Stelter et al. 2002), hydroxypropyl ether guar (Duxenneuner et al. 2008), methyl hydroxyethyl cellulose (HEC) (Plog et al. 2005), alginate (Storz et al. 2010; Rodriguez-Rivero et al. 2014), scleroglucan (Japper-Jaafar et al. 2009), cellulose acetate + PEO solutions (Chen et al. 2008), cellulose in an ionic liquid 1-ethyl-3-methylimidazolium acetate (Haward et al. 2012) (Michud et al. 2015), DNA (Chevallier 2009), cornstarch-water suspension (Bischoff White et al. 2010), galactomannan (Bourbon et al. 2010), casein/waxy maize starch (Chan et al. 2009) and dilute ethyl HEC solutions (Sharma et al. 2015). In the present study, extensional rheology of HEC solutions has been investigated with the help of CaBER.

The CaBER instrument records the mid-plane filament diameter using a laser sheet micrometer, presupposing that the filament necking takes place in mid-plane. However, if the filament neck is located somewhere other than the mid-plane, the measurements recorded by the laser sheet micrometer are not reliable. Also, flow instabilities such as ‘bead-on-string’ are often encountered during capillary thinning experiments. These instabilities refer to the growth of satellite fluid droplet(s) connected to either of or both the fluid hemispheres through the filament. The formation of so called ‘bead-on-string’ structures in the capillary thinning of filaments and jets has been investigated extensively (Chang et al. 1999; Stelter et al. 2000; Li and Fontelos 2003; Clasen et al. 2006a). ‘Bead-on-string’ flow instabilities in uniaxial extensional flows have been reported to be primarily caused by either (1) inertia or (2) elasticity.

Rodd et al. (2005) observed that the capillary thinning of low viscosity (η 0  < 0.070 Pa s) fluids with low elasticity is predominantly inertio-capillary in nature. As the pinch-off process is much faster owing to the capillary forces being much stronger compared to the viscous forces, very high elongational deformation rates are attained. At such rates, the inertial stresses dominate over visco-capillary and elasto-capillary stresses, resulting into the so-called ‘bead(s)-on-string’ formation. This effect immediately follows the cessation of step-stretch applied by CaBER and is usually accompanied by the oscillations of the hemispherical fluid reservoirs at the endplates. It is very hard to observe a distinctive elastocapillary thinning (exponential decay of the filament) in such filaments and the determination of λ E is often not possible (Rodd et al. 2005).

Fig. 1
figure 1

The endplates of CaBER with sample a before and b after the step-stretch

Full size image

An alternative explanation of the ‘bead(s)-on-string’ effect can be given by elastic instabilities (Oliveira and McKinley 2005). Chang et al. (1999) predicted using the slender filament equations derived for a FENE (finitely extensible nonlinear elastic) dumbbell model that the accumulated viscoelastic stresses near the mid-filament neck of a thinning filament render it unstable to mechanical wave-like perturbations. This often triggers flow instability and “elastic recoil” of the polymer chain at the neck near the break-up event. Such local relaxation of elastic stresses leads to the formation of a bead which is connected to the hemispherical fluid reservoirs located at the endplates by (a) thinner and cylindrical filament(s). The polymer molecules are relaxed inside the bead where surface tension dominates, whereas in the filament the polymer molecules are highly stretched and are dominated by viscoelastic stress. Elastocapillary thinning continues in the secondary filament giving rise to another bead, which is connected to one of the hemispherical reservoirs by tertiary filament. Such hierarchical process (also referred to as iterated stretching) repeats itself within the limits of polymer extensibility, which is infinite for Oldroyd-B fluids (Oliveira and McKinley 2005). For real polymeric fluids, elastocapillary thinning is truncated by the finite extensibility of polymer chains, leaving the possibility of the formation of finite number of beads. Also, several criteria have been suggested for the possibility of such flow instability, including extensibility parameters for polymer chains and dimensionless numbers. This phenomenon has been reported experimentally for a flexible polymer such as PEO (Arnolds et al. 2010; Oliveira and McKinley 2005; Oliveira et al. 2006; Sattler et al. 2008), emulsions (Erni et al. 2009), human saliva (Sattler et al. 2012), and for the systems with rigid polymers such as xanthan gum solution drop falling under gravity (Smolka and Belmonte 2006) and DNA suspensions (Juarez and Arratia 2011).

However, since the filament in the vicinity of the midplane is no longer axisymmetric, the observed data following the bead formation cannot be considered reliable for evaluating λ E and/or η E . Also, since cellulosic polymers are widely used as rheology modifiers, an understanding of this flow instability for the systems containing cellulosic polymers is very important due to their potential applications in the commercial processes such as roll-coating, fertilizer spraying, paint-leveling, bottle-filling, misting and inkjet printing (Clasen et al. 2006a; Oliveira and McKinley 2005). These processes have a significant component of free surface extensional deformation and the presence of droplets could potentially affect the quality of the end product. However, according to the best of our knowledge, elastic instabilities such as iterated stretching have never been reported in the past literature for any system containing cellulosic polymers.

In order to identify such flow instabilities, high-speed imaging of the filament decay is essential. Many of the studies concerning biopolymers mentioned above did not provide the high-speed photographic images of their CaBER experiments, which made it very difficult to verify if the filament diameter is smallest at the mid-plane (thereby rendering the use of mid-filament diameter for the analysis questionable) and to identify inertial/elastic flow instabilities, e.g. ‘bead-on-string’. The images provided by Duxenneuner et al. (2008) for the capillary thinning of hydroxypropyl ether guar solutions clearly indicate the presence of a ‘bead-on-string’ instability prior to the break-up, but this effect was not mentioned by the authors in their description of the images. In the present study, an elastic ‘bead-on-string’ instability observed in the CaBER experiment for HEC solutions has been reported using high-speed photographic image analysis and discussed in detail.

During CaBER experiments, step-stretch conditions can significantly affect the subsequent capillary thinning in a number of respects. A larger step-strain results in a smaller initial filament diameter and early break-up of the filament (Miller et al. 2009). Also, higher stretch speed has shown to stabilize the filament (i.e. increase the maximum length at which the filament exists following the step-stretch) of the fluids composed of casein + waxy maize starch (Chan et al. 2009). These factors eventually affect the rate constants associated with elastocapillary (the exponent) and viscocapillary thinning (the slope of the line) of the filament, and hence the determination of λ E and η E . Hence, a comprehensive study of complex fluids with CaBER should include the dependency of λ E and η E on different step-stretch conditions.

However, most studies concerning CaBER measurements of biopolymers mentioned above have used only one step-stretch profile for the experiments. For synthetic polymers, Miller et al. (2009) have reported that the capillary thinning of 1.0 g dl−1 aqueous solution of PAA is not significantly sensitive to the step-stretch parameters, while the polymer blends (PIB + PDMS) and solutions of wormlike micelles exhibit sensitivity (Miller et al. 2009; Kim et al. 2010). In the present study, various step-stretch profiles have been used for the rheometry of an HEC solution and the corresponding parameters related to extensional rheology obtained from the data analysis have been found to be sensitive towards step-stretch parameters.

Capillary thinning of a filament of viscoelastic fluid is governed by the dominant balance of capillarity, inertia, as well as elastic and viscous forces. The relative magnitudes of these forces can be expressed by the respective characteristic timescales (discussed in detail in the “Theory” section). Different dimensionless groups (Deborah, Ohnesorge and Elastocapillary numbers) can be derived using these characteristic timescales. The dimensionless groups are often used to describe the overall nature of the process. However, most literature regarding capillary break-up extensional rheometry of biopolymer related systems lack a detailed force balance analysis of the results.

This study aims to investigate the capillary thinning of semi-dilute HEC solutions with high-speed imaging. The dependency of temporal evolution of filament diameter (and hence the derived parameters λ E and η E ) on the step-stretch parameters i.e. step strain and stretch speed has been studied. The ‘bead-on-string’ elastic flow instability observed during the filament thinning has been discussed in detail.

Theory

Capillary break-up extensional rheometry

CaBER is a rheometrical technique in which, as opposed to most other rheometrical techniques, neither stress nor deformation rate are applied but rather the deformation rates at different stages of the experiment are self-selected by means of force balance between capillary force and other forces such as inertia, elasticity and viscosity. Nevertheless, rheologically important parameters such as stress, strain and strain rate can indeed be calculated by observing the temporal evolution of filament diameter with time and the value of surface tension by means of the following equations suggested by the past literature pioneering experimental development of the technique (McKinley and Tripathi 2000; Anna and McKinley 2001; Stelter et al. 2002; Kolte and Szabo 1999).

$$\varepsilon = 2\ln \left( {\frac{{D_{0} }}{D(t)}} \right)$$
(1)

Here ε is the extensional Hencky strain acquired by the filament, D 0 is the plate diameter and D(t) is the filament diameter at a given time t. The time derivative of Hencky strain gives the effective extensional strain rate:

$$\dot{\varepsilon } = 2 \frac{{d\ln \left( {\frac{{D_{0} }}{D(t)}} \right)}}{dt} = \frac{ - 2}{D(t)} \left( {\frac{d D(t)}{dt}} \right)$$
(2)

The effective capillary stress at mid-filament is given as:

$$\tau = \frac{2\sigma }{D(t)}$$
(3)

Here σ is the surface tension of the fluid sample which is measured separately. Hence the apparent extensional viscosity is described as the ratio of stress and strain rate, i.e. Eqs. 3 and 2.

$$\eta_{E,app} = \frac{\tau }{{\dot{\varepsilon }}} = \frac{ - \sigma }{{\left( {\frac{d D(t)}{dt}} \right)}}$$
(4)

It can be noticed from the Eqs. 2 and 4 that the rate of diameter decay is an important factor in capillary breakup extensional rheometry (CaBER). Newtonian and viscoelastic fluids have distinctively different filament thinning profiles. For Newtonian fluids, the elastic stresses are insignificant and hence the extensional flow is primarily caused by a viscocapillary balance (McKinley and Tripathi 2000; Entov and Hinch 1997). The filament radius decreases linearly with a slope of −σ/η S where η S is the shear viscosity of the Newtonian fluid. This filament decay can be described by the following expression:

$$D(t) = 0.1418 \left( {\frac{\sigma }{{\eta_{S} }}} \right) \left( {t_{b} - t} \right)$$
(5)

Here t b is the filament breakup time. The term σ/η S has a dimension of m s−1 and is termed as capillary velocity (V). Capillary velocity V is used to calculate capillary number Ca to describe the importance of capillarity in free-surface flows of Newtonian fluids. However, by its definition, Ca remains unity during the viscocapillary thinning in CaBER because V is self-selected by the fluid as the ratio σ/η S . The constant prefactor has been introduced by Papageorgiou (1995).

$$Ca = \frac{{\eta_{s} V}}{\sigma } = 1$$
(6)

From Eq. 7, the effective strain rate during viscocapillary thinning appears to increase with time due to decreasing filament diameter.

$$\dot{\varepsilon } = \frac{2}{D(t)} \left( {\frac{\sigma }{{\eta_{S} }}} \right)$$
(7)

However, in case of Oldroyd-B viscoelastic liquids (Kolte et al. 1997) with a single relaxation time, the filament follows an exponential decay profile in which the dynamics of the filament drainage are controlled by elastocapillary balance, as described in Eq. 8. Here D 1 is the mid-filament diameter immediately following the step-stretch.

$$D(t) = \left( {\frac{{GD_{1}^{4} }}{\sigma }} \right)^{1/3} \exp \left( {\frac{ - t}{{3\lambda_{E} }}} \right)$$
(8)

Oldroyd-B fluids are models which treat dilute polymer solutions as the suspensions of dumbbells. These dumbbells do not interact with one another and are made of two point masses (beads) connected by a Hookean spring. Upon deformation of the fluid, these dumbbells experience the solvent drag without slip and the spring gets stretched. These infinitely stretchable springs impart elastic stress to the fluid. Provided all the dumbbells have springs with identical force constants, the fluid exhibits a single relaxation time (Clasen et al. 2006a).

Analysis of the data collected enables the determination of λ E , the characteristic time governing the elasto-capillary thinning (Entov and Hinch 1997; Liang and Mackley 1994) and G, the elastic modulus. Although the constant λ E with the dimension of time has been often mentioned in the literature as a ‘relaxation time’ it is different than the time constants associated with stress relaxation following cessation of steady shear. λ E is in fact related to the viscoelastic stress growth as the filament radius approaches zero. This constant is of a wide commercial interest in industrial operations with capillary break-up, such as spraying, mould-filling, jetting etc. (Rodd et al. 2005).

Using Eqs. 2 and 8, the effective extensional strain rate during exponential filament decay can be expressed as an explicit function of the relaxation time λ E . This implies that the extensional strain rate in the region of elastocapillary thinning is constant and self-selected by the fluid.

$$\dot{\varepsilon } = \frac{2}{{3\lambda_{E} }}$$
(9)

Weissenberg number, as defined by the product of strain rate and relaxation time exceeds the critical value of Wi = ½ for the coil stretch transition in uniaxial flow which ensures that the elastic stress in the filament is balanced by the capillary pressure (Entov and Hinch 1997).

$$Wi = \dot{\varepsilon }\lambda_{E} = \frac{2}{3}$$
(10)

Even though the exponential thinning continues indefinitely in the numerical simulations, in practice the finite extensibility of polymer chains limits the elastocapillary stress growth (Stelter et al. 2002). The polymer coils, undergoing strong deformation, get stretched during the extensional flow and induce localized anisotropy in the microstructure at the mid-filament. The filament thinning followed by the elongation of chains is dominated by viscocapillary balance in a quasi-steady state. The polymer chains, however, do not necessarily have to undergo full extension up to their contour length. It has been shown that the quasi-steady state is already achieved when the polymer chains are extended to about 1/10th of their full contour length (Yarin 1993).

Force balance, characteristic timescales and dimensionless numbers

Despite of a comprehensive data analysis to obtain the parameters discussed above, a true systematic understanding of extensional flows of complex fluids can be very difficult due to various types of forces controlling the overall process. These forces include capillarity, viscous forces, inertia and gravity as well as the elasticity arising from the microstructural deformation within complex fluids. Out of the forces listed above, the relative magnitudes of relevant parameters control the overall nature of the process, and hence it is impossible to describe the process based on any one of them.

A good approach to this problem is to define dimensionless groups which compare the magnitudes of different parameters involved in the process and hence allow us to classify and compare the nature of flows. In a typical CaBER experiment, the filament thinning driven by capillarity is resisted by viscous, inertial and elastic forces. The dominant balance of forces can be determined by comparing different timescales associated with them (Rodd et al. 2005).

Viscous break-up timescale t v

For Newtonian fluids with no inertia or elasticity, the filament decay and subsequent breakup is entirely governed by the viscocapillary force balance. In Eq. 5, the break-up time t b is identical to t V . At D(t) = 0, i.e. filament breakup, the break-up timescale can be defined as:

$$t_{V} = t_{b} = 0.1418 \frac{{\eta_{0} R_{0} }}{\sigma }$$
(11)

Here η 0 is the so-called zero-shear rate viscosity of the fluid and R 0 is the endplate radius containing the cylindrical sample which acts as a characteristic length scale in free-surface flows such as capillary thinning in CaBER.

Rayleigh and inertial timescale t R and t i

For an inviscid and inelastic fluid, the filament decay is completely dependent on the inertio-capillary balance. The characteristic time arising from such balance is defined as the Rayleigh timescale (McKinley 2005b).

$$t_{R} = \sqrt {\frac{{\rho R_{0}^{3} }}{\sigma }}$$
(12)

Here ρ is the fluid density. The Rayleigh timescale is related to the break-up time of an inviscid and inelastic jet (t i ) by the following relationship (Rodd et al. 2005):

$$t_{i} = 1.95 t_{R}$$
(13)

Extensional relaxation time λ E

When the elastic stresses due to the elongation of the polymer chains in a filament undergoing decay dominate the viscous stresses arising due to the solvent, the exponential thinning as per the Eq. 8 corresponding to the relaxation time λ E takes place. Unlike the other timescales discussed above, λ E does not ideally relate to the filament break-up time and is ideally independent of the geometry used. Also, it is not a true relaxation time as in context of stress relaxation but a timescale for viscoelastic stress growth.

Deborah number De

In order to compare the relative magnitudes of both λ E and t R , their ratio is defined as the Deborah number (De).

$$De = \frac{{\lambda_{E} }}{{t_{R} }} = \frac{{\lambda_{E} }}{{\sqrt {\frac{{\rho R_{0}^{3} }}{\sigma }} }}$$
(14)

The Eq. 14 suggests that the non-Newtonian effects become more dominant in the free-surface flows such as CaBER at lower characteristic length scales (McKinley 2005b).

Ohnesorge number Oh

Ohnesorge number compares the relative magnitude of viscous (t v ) and Rayleigh (t R ) timescales:

$$\frac{{t_{V} }}{{t_{R} }} = \frac{{\left( {0.1418 \eta_{0} R_{0} /\sigma } \right)}}{{\left( {\sqrt {\rho R_{0}^{3} /\sigma } } \right)}} = \frac{{0.1418 \eta_{0} }}{{\sqrt {\rho R_{0} \sigma } }} = 0.1418 Oh$$
(15)

Elastocapillary number Ec

The collective importance of elastic and capillary stresses to that of the viscous stresses is measured by Elastocapillary number, which can be defined using either λ E and t V , or De and Oh (McKinley 2005b).

$$Ec = \frac{De}{Oh} = \frac{{\lambda_{E} }}{{\left( {t_{V} /0.1418} \right)}} = \frac{{\lambda_{E} \sigma }}{{\eta_{0} R_{0} }}$$
(16)

It is again apparent that the non-Newtonian effects become more relevant with diminishing length-scales.

Materials and methods

Hydroxyethyl cellulose solutions

HEC was supplied under the brand name of Natrosol HEC 250 MR by Hercules Aqualon (now Ashland) with a quoted molecular mass of M w  = 720,000 Da in the literature provided with the product. The MS (molecular substitution) value from the product literature provided by the supplier is 2.5.

1.0, 1.5 and 2.0 g dl−1 (% w/w) solutions of HEC were prepared by mixing the powder with 0.1 M sodium nitrate and 10−3 M sodium azide prepared in deionized water. The mixtures were mixed using a roller mixer for 24 h. All solutions then were stored at 21 °C (room temperature) and were used within 48 h of preparation.

Density of all solutions was measured using a 25 ml calibrated specific gravity bottle at 22 ± 0.1 °C. Owing to the relatively small quantities of HEC dissolved in the solutions, the densities were very similar for all concentrations and were considered to be constant at 997 ± 0.5 kg m−3 for all the solutions of HEC.

Shear rheometry

The shear viscosity was measured at 0.01–1000 s−1 range of shear rate with 30 data points using AR-2000 (TA instruments) controlled stress rheometer fitted with a 2° steel cone-and-plate geometry with 60 mm diameter. The solvent trap was employed to delay drying out of the samples. The sample was subjected to pre-shearing for 180 s at 3 s−1 shear rate followed by 180 s of equilibration time. Each shear rate was applied for 45 s and the average shear stress and normal force during last 15 s were measured. The reproducible nature of all experiments was verified by repeating them. For some samples, the flow curve experiments were repeated with longer time for each shear rate to confirm the steady state.

Tensiometry

The surface tension of all the samples was measured using a surface Tensiometer K8 (Kruss, Germany) and a platinum DuNuoy ring with 1 cm radius. The viscosities of all the samples were low enough not to cause appreciable interference during surface tension measurements. The measured surface tension values have been given in Table 2.

Capillary break-up extensional rheometry

The extensional rheometry experiments were performed on capillary break-up extensional rheometer (CaBER 1) supplied by Thermo Haake. The endplates with diameter D 0 = 4 mm initially separated by 2 mm (aspect ratio = 0.5) were used for the measurements. This aspect ratio and plate size were chosen with an attempt of restricting Bond Number Bo = ρgR 2/σ to less than 1. This value of Bond Number indicates the dominance of surface tension over gravity to facilitate the formation of a stable cylindrical bridge between the endplates (Rodd et al. 2005).

For 1.0, 1.5 and 2.0 g dl−1 solutions, a drop of test fluid was loaded between the plates using a syringe and a gauge. The absence of air bubbles inside the fluid sample was confirmed. The step-strain was adjusted to 1.49 Hencky strain using the micrometer screw provided. The upper plate was moved up with an exponentially increasing velocity within 0.05 s. The evolution of the filament diameter was recorded as a function of time with the laser micrometer as a part of CaBER assembly. Photron MC-1 high-speed camera was used for capturing the videos and images of the filament thinning at 1000 frames s−1.

In order to examine the sensitivity of CaBER measurements to the step-stretch parameters, experiments were performed on 1.5 g dl−1 solution employing three different step-strains: 1.25, 1.50 and 1.75. Within each of the step-strain, the three strike times (the timescale during which the step-stretch takes place) of 0.06, 0.08 and 0.10 s were applied during which the upper plate moved upwards with a constant velocity. The reason for choosing to move the plate with constant velocity instead of exponentially increasing velocity is due to the observation of an overshoot in the actuator owing to the velocity of the upper plate being very high near the end of its final position during an exponential strike. At the final position, the plate and the liquid bridge moving with high velocity stop suddenly. As a result, an inertial oscillation moves across the filament bridge from the upper to the lower plate which causes a temporary disruption in the measurement of filament diameter and might also affect the subsequent thinning.

All experiments (shear and extensional rheometry, surface tension measurement) were performed at 25 °C. The image analysis for diameter measurement was performed using Adobe Photoshop CS software.

Size exclusion chromatography

The molecular mass M W of the HEC sample was measured to be about 7.01 × 105 ± 0.3 % Da through aqueous size exclusion chromatography coupled with multi-angle laser light scattering. The sample was dissolved in 0.1 M NaNO3 + 10−3 M NaN3 and filtered through Milipore 0.45 μm filter. The flow rate of the mobile phase was 0.5 ml min−1 through Suprema mixed bed column containing nearly monodisperse beads of polyhydroxymethacrylate copolymer. Results were treated using Zimm method. Manually measured value of refractive index increment (dn/dc = 0.107) using Optilab DSP differential refractometer was used in the calculation.

The Radius of gyration \(( {\langle {R_{g}^{2} } \rangle }^{{^{1/2} }})\) was calculated using the following Zimm equation by plotting KC/R θ against sin2(θ/2).

$$\frac{Kc}{{R_{\theta } }} = \left( {\frac{1}{M} + 2A_{2} c} \right) \left( {1 + \frac{{16\pi^{2} n_{0}^{2} \left\langle {R_{g}^{2} } \right\rangle }}{{3\lambda_{0}^{2} }} \sin^{2} \frac{\theta }{2}} \right)$$
(17)

In the above expression, K is an optical constant, c is the concentration, R θ is the excess Rayleigh ratio, θ is the scattering angle, n 0 is the solvent refractive index, λ 0 is the wavelength of light and A 2 is the second virial coefficient indicating the thermodynamic solvent quality. The constant K and the excess Rayleigh ratio R θ can be defined as:

$$K = \frac{{2\pi^{2} n_{0}^{2} }}{{N_{A} \lambda_{0}^{4} }} \left( {\frac{dn}{dc}} \right)^{2}$$
(18)

Here, N A is the Avogadro number and dn/dc is the refractive index increment for the polymer–solvent system, which is measured independently via differential refractometry.

$$R_{\theta } = \frac{{\left( {I_{\theta } - I_{\theta , solvent} } \right)r^{2} }}{{I_{0} V}} = f \frac{{E_{\theta } - E_{\theta , solvent} }}{{E_{laser} }}$$
(19)

I θ and I θ, solvent are the scattered light intensity of the solution and the solvent respectively. V is the solution volume and r is the distance between the detector and the scattering volume. Instrumentally, however, R θ is determined by E θ, E θ,solvent and E laser , the detector signal voltages of the solution, solvent and laser respectively. The value of \(\langle {R_{g}^{2} } \rangle^{{^{1/2} }}\) manifests the perturbed dimensions of the polymer coil. The parameter called characteristic ratio (C ∞ ) compares \(\langle {R_{g}^{2} } \rangle^{{^{1/2} }}\) to the unperturbed dimensions, hence quantifying the apparent chain stiffness.

$$C_{\infty } = \frac{{6\left\langle {R_{g}^{2} } \right\rangle }}{{Nb^{2} }}$$
(20)

Here b is the length of a repeating unit of a polymer chain and N is the degree of polymerization.

The extensibility of a polymer coil decreases with the increasing stiffness of the backbone. Finite extensibility parameter (L 2) can be defined as below:

$$L^{2} = 3\left( {\frac{{j \sin^{2} \left( {{\raise0.7ex\hbox{$\theta $} \!\mathord{\left/ {\vphantom {\theta 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right) M}}{{C_{\infty } M_{u} }}} \right)^{{2\left( {1 - \nu } \right)}}$$
(21)

Here j is the number of bonds present in a repeating unit across the bridge connecting two neighboring repeating units on each side (taken 4 for the cellulose repeating unit). θ is the bond angle between two consecutive repeating units. M and M u are the molecular masses of the polymer and the repeating unit respectively, and ν is the excluded volume exponent. There has been at least one report in the literature that the above equation may overpredict experimentally measured values of L 2 (Szabo et al. 2012).

Based on the above experiments, some of the properties of the HEC sample are summarized in Table 1.

Table 1 Parameters describing HEC sample
Full size table

Results and discussion

Shear rheology

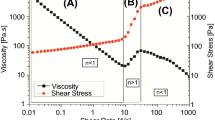
Figure 2 shows the steady shear viscosity data of all three HEC solutions fitted with the following equation referred to as Cross model:

$$\frac{{\eta - \eta_{\infty } }}{{\eta_{0} - \eta_{\infty } }} = \frac{1}{{1 + \left( {\gamma^{o} \tau } \right)^{m} }}$$
(22)

Here η is the steady shear viscosity, η 0 and η ∞ are the so called zero-shear rate viscosity and infinite-shear rate viscosity respectively, τ is the characteristic time for microstructural change under applied strain conditions and m is the power-law exponent of the shear thinning region (Cross 1965).

Fig. 2
figure 2

The shear viscosity of 1.0 g dl−1 (open square), 1.5 g dl−1 (open circle) and 2.0 g dl−1 (open triangle) HEC solutions plotted against shear strain rate. The red lines represent the fits of Cross model for obtaining zero shear viscosity. (Color figure online)

Full size image

CaBER experiments

The mid-plane diameters of the filaments of 1.0, 1.5 and 2.0 g dl−1 solutions of HEC undergoing capillary driven thinning are plotted in Fig. 3 against elapsed time where t = 0 corresponds to the cessation of exponential step-stretching the filament. The measurements obtained from the in-built laser micrometer are in a good agreement with those obtained using image analysis. The filament undergoing thinning remains adequately axiosymmetric according to Fig. 4 which justifies the use of the mid-filament diameter as the representative of the thinning process. A “knee” can be observed in the plots for 1.5 and 2.0 g dl−1 samples with a duration of ~0.01 s immediately after the cessation of step-stretch and prior to the beginning of the elastocapillary drainage, indicating very slow decay of the filament within the region immediately following the cessation of step-stretch. The straight red lines represent the fit according to Eq. 8 within the region of exponential decay of the filament. The exponent has been utilized to calculate the extensional relaxation time λ E , which determines the effective self-selected extensional strain rate during the elastocapillary thinning.

Fig. 3
figure 3

The diameter of thinning filaments obtained using laser micrometer (open symbols) and image analysis (closed symbols) of 1.0 g dl−1 (squares), 1.5 g dl−1 (circles) and 2.0 g dl−1 (triangles) HEC solutions plotted against time. The red lines and blue lines represent the exponential fit to the data corresponding to the elastocapillary thinning and the linear fit to the data corresponding to the viscocapillary thinning respectively. The initial diameters have been marked with ‘a’ for all three concentrations and their images are displayed in Fig. 4. (Color figure online)

Full size image
Fig. 4
figure 4

Filament thinning of 1.0, 1.5 and 2.0 g dl−1 HEC solutions at different times. The red lines indicate mid-filament plane where the diameter is measured using in-built laser micrometer. The corresponding data points have been marked in Fig. 4. Six images for each concentration represent several important events during capillary thinning. (Color figure online)

Full size image

The blue lines represent the fit of Eq. 5 describing viscocapillary thinning which follows the elastocapillary thinning once the polymer chains cannot be extended further. The parameters obtained using the fits of Eqs. 8 and 5 have been given in Table 2.

Table 2 Parameters obtained from the surface tension and capillary thinning measurements of the HEC solutions at three different concentrations
Full size table

Bead-on-string flow instability

For all three concentrations, the diameter values close to the break-up event have not been taken into account in the data analysis by Eq. 5 due to a ‘bead-on-string’ flow instability shown in Fig. 4. The temporal evolution of the filament diameter during viscocapillary thinning for all three concentrations has been plotted against time separately in Fig. 5 with a linear–linear scale. The images corresponding to certain significant events during capillary thinning (i.e. cessation of step-stretch, flow instability and filament break-up) have been shown in Fig. 4. All the HEC samples under investigation were observed to form only one bead prior to the break-up event.

Fig. 5
figure 5

The diameter versus time data corresponding to the viscocapillary thinning has been plotted on a linear–linear axes graph for 1.0 (squares), 1.5 (circles) and 2.0 (triangles) g dl−1 HEC solutions. The onset of viscocapillary thinning, the onset of flow instability and the filament break-up event for each concentration have been marked with ‘b’, ‘c’ and ‘d’. The blue lines represent linear fit to the data between the line segment ‘bc’ according to Eq. 5. (Color figure online)

Full size image

As discussed in the introduction, these flow instabilities can be explained using either inertial or elastic effects. In the past literature, several criteria related to the fluid properties and the capillary thinning have been identified to be associated with the type of ‘bead-on-string’ instability.

Rodd et al. (2005) reported that it is possible to observe a ‘bead-on-string’ flow instability immediately following the cessation of step-stretch of a fluid filament (low viscosity PEO solutions) with Oh ≪ 1. Also, the apparent absence of the region of exponential filament decay makes it very difficult to calculate λ E and shows that the elastic effects are very weak (De ≪ 1). With capillary and inertial forces dominating over viscous and elastic forces, the fluid hemispheres attached to each plate undergo oscillation with a characteristic timescale proportional to t R (Rodd et al. 2005). However, the data corresponding to the filament decay in Fig. 3 for all three concentrations contain easily recognizable regions of exponential thinning, and hence the elastic effects are not insignificant. This is further confirmed by the dimensional analysis performed later in this paper where 0.44 ≤ De ≤ 8.78. The intermediate range of Ohnesorge number (0.63 ≤ Oh ≤ 14.14) indicates that the filament decay is not completely dominated by inertio-capillary forces, as opposed to the data reported by Rodd et al. (2005).

An alternative explanation of such ‘bead-on-string’ instabilities have been given by Chang et al. (1999) as well as Oliveira and McKinley (2005). The accumulated viscocapillary stress at the filament neck renders the filament unstable to mechanical perturbations near the break-up event. The elongated polymer coils may eventually undergo ‘elastic recoil’ to generate ‘bead-on-string’ structures. Chang et al. (1999) and Oliveira and McKinley (2005) proposed key conditions to be met by certain physical parameters (i.e. De, Oh, viscosity ratio S = η s /η 0 where η S is the solvent viscosity, and the finite extensibility parameter L 2 indicating the ratio of maximum extended length to the equilibrium length of polymer coils) for the possibility of such elastic instability. They proposed De ≫ 1 to ensure sufficient elastic effects, S ≠ 0 or 1 for an intermediate viscosity ratio and L 2 ≫ 1 to ensure that the iterated nature of elastic elongation and recoil processes is not truncated by limited molecular extensibility.

In order to calculate these values (given in Table 3) for the systems being investigated in this study, some of the values from Table 2 were used.

Table 3 Dimensionless groups and other parameters calculated for HEC
Full size table

As it is apparent from Table 2, the value of L 2 remains much above 1, as the criteria defined by Chang et al. (1999) and Oliveira and McKinley (2005), as does the value of S unequal to 0 and 1 according to Table 3. However, De for 1.0 g dl−1 sample remains below 1, as opposed to those criteria. In a later publication, it was theoretically shown that systems with De < 1 are also prone to ‘bead-on-string’ instability (Bhat et al. 2010).

In Fig. 5, the data points after the onset of flow-instability have been excluded from the calculation of linear fits for all three concentrations as the observed flow instability cannot be classified as viscocapillary thinning. However, it is noteworthy that the extended lines for data fit still remain in good agreement with the observed data within the region of flow instability for 1.0 and 1.5 g dl−1 solutions but not for the 2.0 g dl−1 solution.

Effect of step-stretch parameters

In CaBER experiments, the capillary thinning is often influenced by the applied conditions of step-stretch (Miller et al. 2009). After the cessation of step-stretch, the initial diameter D 1 is influenced by the stretch ratio L f /L 0 (where L f is the final height and L 0 is the initial height of the sample) according to the following “reverse squeeze flow” solution (Anna and McKinley 2001; McKinley and Sridhar 2002):

$$\left( {\frac{{D_{0} }}{{D_{1} }}} \right)^{4/3} = \left( {\frac{{L_{f} }}{{L_{0} }}} \right)$$
(23)

According to Eq. 23, D 1 decreases with increasing step-strain. Moreover, D 1 decreases further with increasing stretch-time as the fluid across the filament drains under the influence of gravity. The variation in D 1 influences the elastocapillary thinning and the filament break-up time. Hence the parameters such as λ E and η E which are derived from the exponential and linear decay of the filament respectively, vary appreciably with the stretch profile. The results of CaBER experiments should therefore be interpreted and compared in the context of the applied step-stretch profile.

The variation in the exponent of elastocapillary filament decay and the slope of viscocapillary filament decay (according to Eqs. 8 and 5 respectively) with the step-stretch parameters can be observed in Table 4. The D 1 values for all strike times within a step strain are lower compared to the calculated D 1 as per Eq. 23, indicating significant axial flow under gravity. The exponent for elastocapillary thinning generally tends to decrease with decreasing D 1. Also the slope of linear filament decay generally tends to increase with decreasing filament break-up time.

Table 4 The initial filament diameter D 1 following the cessation of step-stretch, the filament breakup time t b , the exponent values calculated from the exponential fit for the data in elastocapillary thinning region and the slope calculated from the linear fit for the data in viscocapillary thinning region for 1.5 g dl−1 HEC solutions at various step-stretch conditions
Full size table

The temporal evolution of filament diameter of three different CaBER experiments with same stretch time but different step-strain is plotted in Fig. 6a. The data points acquired following the onset of ‘bead-on-string’ flow instability have been neglected during the analysis. However, according to Fig. 6b, the neglected data nevertheless seems to be in agreement with the linear fit. It is evident from the data fits (red and blue lines) from both Fig. 6a, b that the rate constants associated with both exponential and linear filament decay vary with step-stretch profile. It is thus apparent that the parameters derived from these rate constants also vary with step-stretch parameters. In Fig. 7, the variation in λ E and η E has been plotted with relevant error bars describing the reproducibility of the experiments.

Fig. 6
figure 6

a Diameter versus time data for 1.5 g dl−1 HEC solution using 60 ms stretch time and different step-Hencky strain values such as 1.25 (triangles), 1.50 (circles) and 1.75 (squares) on a log-linear plot. The red and blue lines indicate the exponential and linear fits to the data corresponding to elastocapillary and viscocapillary thinning. b The segments with viscocapillary thinning and flow instability taken from the curves displayed in a on a linear–linear plot. The graph legend is similar to that of a. The red circles indicate the onset of flow instability and the subsequent diameter values have not been taken into account in fitting the straight line. (Color figure online)

Full size image
Fig. 7
figure 7

Extensional relaxation time λ E (red squares with error bars) and steady state extensional viscosity η E (blue squares with error bars) measured within the region of viscocapillary thinning is plotted against different strike times for different values of initially applied step strains. The dotted lines guide the eyes. Error bars represent one standard deviation. (Color figure online)

Full size image

The variation in η E is relatively small but significant, whereas λ E strongly depends upon the step-stretch conditions according to Fig. 7. Also, λ E decreases with increasing step-strain while η E decreases. Miller et al. (2009) found that while the step-stretch parameters affected the measurement of extensional viscosity and relaxation time of wormlike micelle solutions and PIB/PDMS polymer blends, similar measurements for 1.0 g dl−1 aqueous solution of polyacrylamide were insensitive towards the stretch conditions (Miller et al. 2009).

Thus, even though the capillary drainage of the filaments of complex fluids is dominated by the balance of capillary, elastic, inertial and viscous forces in CaBER, it is apparently important to determine the sensitivity of parameters such as η E and λ E to step-stretch profiles in CaBER measurements. However, according to the best of our knowledge, there have been no reports in the literature about the sensitivity of capillary thinning of polysaccharide solutions to the step-stretch conditions in CaBER measurements.

Dimensionless groups

Dimensionless groups such as De for various polymeric systems reported in the past literature and HEC have been plotted in Fig. 8 against their corresponding Oh. The straight lines on the plot indicate various values for Ec = De/Oh. For 1.5 g dl−1 HEC solution with different step-stretch profiles, the variation in De is observed while Oh remain constant. This is obvious because the calculation of Oh involves neither η E nor λ E .

Fig. 8
figure 8

Deborah number as a function of Ohnesorge number for HEC solutions (black star) measured during this study and various other systems from past literature such as PEO (open square) (Arnolds et al. 2010), alginate (black square) (Storz et al. 2010), hydroxypropyl ether guar (black hexagon) (Duxenneuner et al. 2008), scleroglucan (black circle) (Japper-Jaafar et al. 2009), methyl hydroxyethyl cellulose with different molecular mass distribution (open triangle) (Plog et al. 2005), cellulose in an ionic liquid (black triangle) (Haward et al. 2012), methacrylic acid + acrylic acid + ethyl acrylate copolymer (open circle) (Kheirandish et al. 2008) and DNA (black rhombus) (Chevallier 2009). For 1.5 g dl−1 HEC solution, the data points (red star) calculated using a range of step-stretch profiles have been plotted. The straight lines indicate different values of elastocapillary numbers ranging from 0.01 to 100. Error bars represent one standard deviation. (Color figure online)

Full size image

Rodd et al. (2005) suggested that for a polymer solution with either of the conditions, i.e. λ E  < 0.001 s or η 0 < 0.070 Pa s, the inertial effects dominate over the elastic/viscous effects and CaBER measurement will not be possible (Rodd et al. 2005). These parameters corresponded to the dimensionless groups De < 1 and Oh < 0.14. These restrictions were referred to as the “operability diagram”. McKinley et al. (2005) proposed that CaBER tests become impractical for the polymer solutions with De < 1 and Oh < 1 (McKinley 2005a). However, many data points in Fig. 8 correspond to De < 1 and Oh < 1. Moreover, η 0 of hydroxypropyl ether guar solutions at various concentrations ranged from 0.0012 to 0.596 Pa s which included four concentrations with η 0  < 0.070 Pa.s. Duxenneuner et al. (2008) reported that all of these solutions exhibited elastocapillary thinning according to Eq. 8 and the calculation of λ E was possible.

This can be explained by the fact that the characteristic length scale (i.e. plate radius R 0) used to calculate the characteristic timescales and consecutively “global” values of De and Oh does not consider the continuous filament thinning. Hence with the diminishing length scale (i.e. filament diameter) the inertial effects become increasingly less important and the “local” De and Oh increase. Also, since the parameters related to extensional rheology of a non-Newtonian fluid cannot be determined using its shear rheology data, the predictions about the feasibility of CaBER experiments using η 0 should be made carefully.

However, these dimensionless groups are nevertheless useful for determining the dominant balance of forces in the flow. The Ec being a ratio of De to Oh indicates the dominant effect in the filament thinning process. For Ec below and above unity, the filament thinning and necking is viscously-dominated and elastically-dominated respectively (Clasen et al. 2006b; McKinley 2005a). While it is evident from Fig. 8 that elastocapillary thinning can occur for a measurable duration even when Ec < 1, the transition from the viscocapillary balance (immediately after the step-strain) to the elastocapillary balance shifts to later times with decreasing Ec.

In Fig. 8, the Ec of HPG and PEO solutions increases with concentration while that of the HEC, methacrylic acid + acrylic acid + ethyl acrylate copolymer and cellulose in the ionic liquid 1-ethyl-3-methylimidazolium acetate solutions remain almost constant with their concentration. Decreasing Ec with increasing concentration is apparently counter-intuitive because stronger elastic effects (with higher λ E ) are expected with increasing concentration. However, in certain systems the increase in viscosity is greater than the increase in relaxation time. This phenomenon has been previously observed for polystyrene in diethyl phthalate (Clasen 2010) and PEO in water (Sachsenheimer et al. 2014).

Conclusion

Capillary break-up extensional rheology of HEC solutions was investigated at three different concentrations (1.0, 1.5 and 2.0 g dl−1) and the parameters such as steady state terminal extensional viscosity and extensional relaxation time were determined. The high-speed imaging of filament thinning process showed flow instability (i.e. ‘bead-on-a-string’) near the filament break-up event. It was proposed that this flow instability emerged from “elastic recoil” of polymer chains subsequently causing thinning of the “secondary filament” formed between the “bead” from elastic recoil and the hemispheres of the liquid bridge. This phenomenon has been reported for the first time for any cellulosic system. While many other polymeric systems may also exhibit this effect, widespread use of cellulose ethers as rheology modifiers makes such findings commercially relevant.

The sensitivity of CaBER measurements to step-stretch parameters for cellulosic systems was also reported for the first time. 1.5 g dl−1 HEC solution was examined by applying three different timescales for step-strain within each of the three step-strains with different magnitude. It was observed that the step-stretch profiles influenced the rate constants associated with exponential and linear decay of the filament as well as the filament break-up time. The variation in these rate constants affected the extensional relaxation time and the steady state extensional viscosity. The relaxation time was observed to decrease and the extensional viscosity was observed to increase with increasing step-strain. The ‘reverse squeeze flow’ solution was applied to various step-strains and the theoretical initial diameter values for various step-strains were calculated and compared with the observed values.

Different characteristic timescales (inertial, elastic and viscous) which are important for capillary thinning and breakup were discussed. The force balance as described by the dimensionless numbers (Deborah, Ohnesorge and Elastocapillary) derived from these timescales was explained.

De was plotted against Oh for a variety of biopolymers and synthetic polymers from the previous literature and the HEC solutions examined in this study. The variation of Ec with concentration for different systems was explained using the competing effects of extensional relaxation time and viscosity increasing with the concentration.