Abstract
We consider the Keplerian distance d in the case of two elliptic orbits, i.e., the distance between one point on the first ellipse and one point on the second one, assuming they have a common focus. The absolute minimum \(d_{\textrm{min}}\) of this function, called MOID or orbit distance in the literature, is relevant to detect possible impacts between two objects following approximately these elliptic trajectories. We revisit and compare two different approaches to compute the critical points of \(d^2\), where we squared the distance d to include crossing points among the critical ones. One approach uses trigonometric polynomials, and the other uses ordinary polynomials. A new way to test the reliability of the computation of \(d_{\textrm{min}}\) is introduced, based on optimal estimates that can be found in the literature. The planar case is also discussed: in this case, we present an estimate for the maximal number of critical points of \(d^2\), together with a conjecture supported by numerical tests.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The distance d between two points on two Keplerian orbits with a common focus, that we call Keplerian distance, appears in a natural way in Celestial Mechanics. The absolute minimum of d is called MOID (minimum orbital intersection distance), or simply orbit distance in the literature, and we denote it by \(d_{\textrm{min}}\). It is important to be able to track \(d_{\textrm{min}}\), and actually all the local minimum points of d, to detect possible impacts between two celestial bodies following approximately these trajectories, e.g., an asteroid with the Earth (Milani et al. 2001, 2005), or two Earth satellites (Rossi et al. 2020). Moreover, the information given by \(d_{\textrm{min}}\) is useful to understand observational biases in the distribution of the known population of NEAs, see Gronchi and Valsecchi (2013). Because of the growing number of Earth satellites (e.g., the mega constellations of satellites that are going to be launched, see Arroyo-Parejo et al. 2021) and discovered asteroids, fast and reliable methods to compute the minimum values of d are required.
The computation of the minimum points of d can be performed by searching for all the critical points of \(d^2\), where considering the squared distance allows us to include trajectory-crossing points in the results.
There are several papers in the literature concerning the computation of the critical points of \(d^2\), e.g., Sitarski (1968), Dybczynski et al. (1986), Kholshevnikov and Vassiliev (1999), Gronchi (2002), Gronchi (2005), Baluyev and Kholshevnikov (2005). Some authors also propose methods for a fast computation of \(d_{\textrm{min}}\) only, e.g., Wisniowski and Rickman (2013), Hedo et al. (2018).
We will focus on an algebraic approach for the case of two elliptic trajectories, as in Kholshevnikov and Vassiliev (1999), Gronchi (2002). In Kholshevnikov and Vassiliev (1999), the critical points of \(d^2\) are found by computing the roots of a trigonometric polynomial g(u) of degree 8, where u is the eccentric anomaly parametrizing one of the trajectories. The polynomial g(u) is obtained by the computation of a Groebner basis, implying that generically we cannot solve this problem by a polynomial with a smaller degree. In Gronchi (2002), resultant theory is applied to a system of two bivariate ordinary polynomials, together with the discrete Fourier transform, to obtain (generically) a univariate polynomial of degree 20 in a variable t, with a factor \((1+t^2)^2\) leading to 4 pure imaginary roots that are discarded, so that we may have at most 16 real roots. Note that the trigonometric polynomial g(u) of degree 8 corresponds to an ordinary polynomial of degree 16 in the variable t through the transformation \(t=\tan (u/2)\). These methods were extended to the case of unbounded conics with a common focus in Baluyev and Kholshevnikov (2005), Gronchi (2005).
In this paper, we revisit the computation of the critical points of \(d^2\) for two elliptic trajectories by applying resultant theory to polynomial systems written in terms of the eccentric or the true anomalies. We obtain different methods using either ordinary or trigonometric polynomials. Moreover, we are able to compute via resultant theory the 8-th degree trigonometric polynomial g(u) found by Kholshevnikov and Vassiliev (1999), and its analogue using the true anomalies (see Sects. 4, 5). Some numerical tests comparing these methods are presented. We also test the reliability of the methods by taking advantage of the estimates for the values of \(d_{\textrm{min}}\) introduced in Gronchi and Valsecchi (2013) when one trajectory is circular. For the case of two ellipses, since we do not have such estimates for \(d_{\textrm{min}}\), we use the optimal bounds for the nodal distance \(\delta _{\textrm{nod}}\) derived in Gronchi and Niederman (2020).
After introducing some notation in Sect. 2, we deal with the problem using eccentric anomalies and ordinary polynomials in Sect. 3. In Sects. 4 and 5, we describe other procedures employing trigonometric polynomials and, respectively, eccentric or true anomalies. Some numerical tests and the reliability of our computations are discussed in Sect. 6. Finally, we present results for the maximum number of critical points in the planar problem in Sect. 7 and draw some conclusions in Sect. 8. Additional details of the computations can be found in the Appendix.
2 Preliminaries
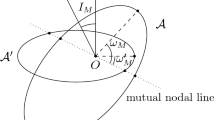
Let \({{\mathcal {E}}}_1\) and \({{\mathcal {E}}}_2\) be two confocal elliptic trajectories, with \({{\mathcal {E}}}_i\) defined by the five Keplerian orbital elements \(a_i,e_i,i_i,\Omega _i,\omega _i\). We introduce the Keplerian distance
where \({{\mathcal {X}}}_1,{{\mathcal {X}}}_2\in \mathbb {R}^3\) are the Cartesian coordinates of a point on \({{\mathcal {E}}}_1\) and a point on \({{\mathcal {E}}}_2\), corresponding to the vector \(V=(v_1,v_2)\), where \(v_i\) is a parameter along the trajectory \({{\mathcal {E}}}_i\). In this paper we will parametrize the orbits either with the eccentric anomalies \(u_i\) or with the true anomalies \(f_i\).
Let \((x_1,y_1)\) and \((x_2,y_2)\) be Cartesian coordinates of two points on the two trajectories, each in its respective plane. The origin for both coordinate systems is the common focus of the two ellipses. We can write
with
where
If we use the eccentric anomalies \(u_i\), we have
for \(i=1,2\), while with the true anomalies \(f_i\) we have
Note that
and set
3 Eccentric anomalies and ordinary polynomials
We look for the critical points of the squared distance \(d^2\) as a function of the eccentric anomalies \(u_1, u_2\), that is we consider the system
where \(\nabla d^2 = \bigl (\frac{\partial d^2}{\partial u_1}, \frac{\partial d^2}{\partial u_2}\bigr )\). We can write
where
System (3) can be written as
with
Following (Gronchi 2002), we can transform (4) into a system of two bivariate ordinary polynomials in the variables t, s through
Then, (4) becomes
where
and
Let
be the Sylvester matrix related to (5). From resultant theory (Cox et al. 1992) we know that the complex roots of \(\det (S_0(t))\) correspond to all the t-components of the solutions \((t, s)\in \mathbb {C}^2\) of (5). The determinant \(\det (S_0(t))\) is in general a polynomial of degree 20 in t. We notice that it can be factorized as
with
where
Therefore, to find the t-components corresponding to the critical points, we can look for the solutions of \(\det ({\hat{S}})=0\), which in general is a polynomial equation of degree 16. We can follow the same steps explained in Gronchi (2005, Sect. 4.3) to obtain the coefficients of the polynomial \(\det ({\hat{S}})\) by an evaluation/interpolation procedure based on the discrete Fourier transform. Then, the method described in Bini (1997) is applied to compute its roots. We substitute each of the real roots t of \(\det ({\hat{S}})\) in (5) and use the first equation \(p(t,s)=0\) to compute the two possible values of the s variable. Finally, we evaluate q at these points (t, s) and choose the value of s that gives the evaluation with the smallest absolute value.
3.1 Angular shifts
To improve the numerical stability of the method we introduce angular shifts. Define a shifted angle \({v_1 = u_1-s_1}\), for some \(s_1\in [0,2\pi )\), and let
Then, system (4) becomes
The coefficients \({\tilde{\alpha }}, {\tilde{\beta }}, {\tilde{\gamma }}, {\tilde{A}}, {\tilde{B}}, {\tilde{D}}\) are written in Appendix A. If \(T_0(z)\) is the Sylvester matrix related to (10) we get
with
where
We find the values of z by solving the polynomial equation \(\det ({\hat{T}})=0\), which again has generically degree 16. We compute the values of \(v_1\) from (9) and shift back to obtain the \(u_1\) components of the critical points. Substituting in (4) and applying the angular shift \(u_2=v_2+s_2\), we consider the system
where the first equation corresponds to the first equation in (4), and
For each value of \(u_1\), we compute two solutions for \(\cos v_2\), \(\sin v_2\) and the corresponding values of \(\cos u_2\), \(\sin u_2\). We choose between them by substituting in the second equation in (4).
4 Eccentric anomalies and trigonometric polynomials
To work with trigonometric polynomials, we write system (3) as
where
Inserting relation
into \(\cos ^2u_1+\sin ^2u_1-1 = 0\) and into the first equation in (12), we obtain
We call \(p_1\), \(p_2\) the two trigonometric polynomials appearing on the left-hand side of (14). The Sylvester matrix of \(p_1\) and \(p_2\) is
We define
which corresponds to the resultant of \(p_1\), \(p_2\) with respect to \(\cos u_1\) and is a trigonometric polynomial in \(u_2\) only. The \(u_2\) component of each critical point satisfies \(\mathscr {G}(u_2)=0\).
Proposition 1
We can extract a factor \(\beta ^2\) from \(\det \mathscr {S}\).
Proof
Using simple properties of determinants, we can write \(\det \mathscr {S}\) as a sum of different terms. The terms independent from \(\beta \) in this sum are given by
and both determinants are 0. The linear terms in \(\beta \) are given by
and this sum is 0, because the two determinants are opposite. Therefore, \(\mathscr {G}(u_2)\) is made by terms of order higher than 1 in \(\beta \). It results
where
Their explicit expressions read
\(\square \)
The trigonometric polynomial
has total degree 8 in the variables \(\cos u_2\), \(\sin u_2\), and corresponds to the polynomial g introduced in Kholshevnikov and Vassiliev (1999) with Groebner bases theory. For this reason, generically, there is no polynomial of smaller degree giving all the \(u_2\) components of the critical points of \(d^2\).
We now explain the procedure to reduce the problem to the computation of the roots of a univariate polynomial. Set
where
We find that
for some polynomial coefficients \(g_j\) such that
Then, we consider the polynomial system
Using relations
obtained from the second equation in (15), we can substitute \(\mathfrak {g}\) in system (15) with
where
We can also write
with
Note that a and b have degree 7 and 8, respectively. We eliminate y from system
by computing the resultant \(\mathfrak {u}(x)\) of the two polynomials with respect to y, and obtain
which is a univariate polynomial of degree 16.
Each of the real roots x of \(\mathfrak {u}\), with \(|x|\le 1\), is substituted into the equation \(\tilde{\mathfrak {g}}(x,y) = 0\) to get the value of y. Finally, we evaluate \(\alpha ,\beta ,\gamma ,\mu ,\nu \) at the computed pairs (x, y) and solve system (12) by computing the values of \(\cos u_1\) and \(\sin u_1\) from (14) and (13), respectively.
4.1 Finding the roots of \(\mathfrak {u}\) with Chebyshev’s polynomials
To compute the roots of the polynomial \(\mathfrak {u}(x)\) in a numerically stable way, we need to express \(\mathfrak {u}\) in a basis ensuring that the roots are well-conditioned functions of its coefficients. This can be achieved using Chebyshev’s polynomials (Noferini and Pérez 2017) in place of the standard monomial basis.
In the monomial basis, we have
for some coefficients \(p_j\). The same polynomial can be written as
where \(T_j\) are Chebyshev’s polynomials, recursively defined by
which are a basis for the vector space of polynomials of degree at most n. The coefficients \(c_j\) are obtained from the \(p_j\) as follows. Setting
we have
with
where the integer coefficients \(a_{ij}\) are determined from relations (19). We invert A by the following procedure. Define
Equation (20) becomes
with
where \(N^n=0\), that is N is a nilpotent matrix of order n. Relation
implies that the inverse of \(\tilde{A}\) is
Let us introduce the vectors
made by the coefficients of the polynomials in (17), (18), and the diagonal matrix
From (20) and (21) we can write
so that
Therefore, the relation between the coefficients \(c_j\) and \(p_j\) is given by
Searching for the roots of \(\mathfrak {u}(x)\) corresponds to computing the eigenvalues of an \(n\times n\) matrix \(\mathscr {C}\), called colleague matrix (Good 1961). We use the form of the colleague matrix described in Casulli and Robol (2021):
The computation of the roots of a polynomial using the colleague matrix and a backward stable eigenvalue algorithm, such as the QR algorithm, is backward stable, provided that the 2-norm of the polynomial is moderate (see Noferini and Pérez 2017).
5 True anomalies and trigonometric polynomials
The same steps described in Sect. 4 can be applied to look for the critical points of the squared distance function expressed in terms of the true anomalies \(f_1\), \(f_2\). Note that using true anomalies allows to deal with both bounded and unbounded trajectories (Sitarski 1968; Gronchi 2005).
We write the system
as
where
We also set
so that
Inserting relation
into \(\cos ^2f_1+\sin ^2f_1-1 = 0\) and into the second equation of (23), we obtain
As in Sect. 4, we consider the Sylvester matrix of the two polynomials in (25)
and define
that we are able to factorize. In particular, we can write
where
with
We can show that \(h(f_2)\) has degree 8 in \((\cos f_2, \sin f_2)\). The related computations are displayed in Appendix B.
Let us set
where
We find that
for some polynomial coefficients \(h_j\) such that
Then, we consider the system
Proceeding as in Sect. 4, we can substitute \(\mathfrak {h}(x,y)\) with
with
where
We apply resultant theory to eliminate the dependence on y as in Sect. 4 and obtain a univariate polynomial \(\mathfrak {v}\) of degree 16. The real roots of \(\mathfrak {v}\) with absolute value \(\le 1\) correspond to the values of \(\cos f_2\) we are searching for. We compute \(\sin f_2\) from (28) and substitute \(\cos f_2\) and \(\sin f_2\) in (25). Finally, \(\cos f_1\) and \(\sin f_1\) are found by solving (25) and using (24).
5.1 Angular shifts
Also for the method presented in this section, we consider the application of an angular shift. If we define the new shifted angle \(v_2\) by
for some \(s_2\in [0,2\pi )\), the coefficients of the polynomial (26) written in terms of \(v_2\) are derived following the computations of Appendix C. Then, following a procedure analogous to Sect. 5, we find the values of \(v_2\) and shift back to get \(f_2\). Finally, we can apply an angular shift also to the angle \(f_1\) when solving system (25). Defining the shifted angle as
for \(s_1\in [0,2\pi )\), system (25) becomes
where
with \(\alpha , \beta , \gamma , \kappa , \lambda , \mu , \nu \) defined at the beginning of this section.
6 Numerical tests
We have developed Fortran codes for each of the methods presented in this paper. We denote these methods with (OE, OES, TE, TEC, TT, TTS), see Table 1. Moreover, we denote by (OT) the method presented in Gronchi (2005). Numerical tests have been carried out for pairs of bounded trajectories to compare the different methods.
Taking the NEA catalogue available at https://newton.spacedys.com/neodys/, we applied these methods to compute the critical points of the squared distance between each NEA and the Earth, and between all possible pairs of NEAs. We applied a few simple checks to detect errors in the results:
-
Weierstrass check (W): for each pair of trajectories we have to find at least one maximum and one minimum point;
-
Morse check (M): for each pair of trajectories, let N be the total number of critical points, and M and m be the number of maximum and minimum points, respectively. Then (assuming \(d^2\) is a Morse function) we must have \(N=2(M+m)\);
-
Minimum distance check (\(d_{\textrm{min}}\)): we sample the two trajectories with k uniformly distributed points each (we used \(k=10\)), and compute the distance between each pair of points. We check that the minimum value of d computed through this sampling is greater than the value of \(d_{\textrm{min}}\) obtained with our methods.
For each method a small percentage of cases fail due to some of the errors above. However, in our tests, for each pair of orbits, at least one method passes all three checks.
The angular shifts (see Sects. 3.1, 5.1) allow us to solve the majority of detected errors for the methods of Sects. 3 and 5 without shift (OE, TT). Applying a shift could also be a way to solve most of the errors detected by the method of Sect. 4 (TE, TEC).
Some data on the detected errors for each method are reported in Table 1. Here, we show the percentages of cases failing some of the three checks described above. We note that the NEA catalogue contains 31,563 NEAs with bounded orbits (to the date of February 25, 2023). Therefore, for the NEA–Earth test we are considering 31,563 pairs of orbits, while for the NEA–NEA test the number of total pairs is 498,095,703. From Table 1, we see that the method TE is improved with Chebyshev’s polynomials (TEC). In the same way, the methods OE, TT are improved by applying angular shifts in case of detected errors (OES, TTS). Indeed, the method TTS turns out to be the most reliable for the computation of \(d_{\textrm{min}}\).
Two additional ways to check in particular the computation of \(d_{\textrm{min}}\) are discussed below.
6.1 Reliability test for \(d_{\textrm{min}}\)
Although all the presented methods allow us to find all the critical points of \(d^2\), we are particularly interested in the correct computation of the minimum distance \(d_{\textrm{min}}\). For this reason, we introduce two different tests to check whether the computed values of \(d_{\textrm{min}}\) are reliable.
The first test is based on the results of Gronchi and Valsecchi (2013), where the authors found optimal upper bounds for \(d_{\textrm{min}}\) when one orbit is circular. Let us denote with \({{\mathcal {A}}}_1\) and \({{\mathcal {A}}}_2\) the two trajectories. Assume that \({{\mathcal {A}}}_2\) is circular with orbital radius \(r_2\), and call \(q_1,e_1,i_1,\omega _1\) the pericenter distance, eccentricity, inclination and argument of pericenter of \({{\mathcal {A}}}_1\). Moreover, set
where we used \(q_{\textrm{max}}=1.3\), which is the maximum perihelion distance of near-Earth objects. Then, for each choice of \((q_1,\omega _1)\in {{\mathcal {D}}}\) we have
where \(\delta (q_1,\omega _1)\) is the distance between \({{\mathcal {A}}}_1\) and \({{\mathcal {A}}}_2\) with \(e_1=1, i_1=\pi /2\):
with \(\xi =\xi (q,\omega )\) the unique real solution of
We compare this optimal bound with the maximum values of \(d_{\textrm{min}}\) computed with the method OE, for a grid of values in the \((q_1,\omega _1)\) plane. The results are reported in Fig. 1. Here, we see that the maximum values of \(d_{\textrm{min}}\) obtained through our computation appear to lie on the grey surface corresponding to the graph of \(\displaystyle {\max _{{\mathcal {C}}}d_{\textrm{min}}(q_1,\omega _1)}\) defined in (31). This test confirms the reliability of our computations. Similar checks were successful with all the methods of Table 1.
To test our results also in case of two elliptic orbits, we consider the following bound introduced in Gronchi and Niederman (2020) for the nodal distance \(\delta _{\textrm{nod}}\) defined below. Let

where \(q_2\), \(e_2\) are the pericenter distance and eccentricity of \({{\mathcal {A}}}_2\), and  ,
,  are the mutual arguments of pericenter (see Gronchi and Niederman 2020).
are the mutual arguments of pericenter (see Gronchi and Niederman 2020).
We introduce the ascending and descending nodal distances

The (minimal) nodal distance \(\delta _{\textrm{nod}}\) is defined as
Set
For each choice of \((q_1,\omega _1)\in {{\mathcal {D}}}\), defined as in (30), we have

where, denoting by \(Q_2\) the apocenter distance of \({{\mathcal {A}}}_2\) and by \(p_2 = q_2(1+e_2)\) its conic parameter,
with
and
We compare the computed values of \(d_{\textrm{min}}\) with the bound (34) on the maximum nodal distance. The results are displayed in Fig. 2 where, for four different values of \(e_2\), the grey surface represents the bound of Gronchi and Niederman (2020), while the black dots correspond to the maximum value of \(d_{\textrm{min}}\) for a grid in the \((q_1,\omega _1)\) plane computed with the method OE. Since the value of \(\delta _{\textrm{nod}}\) is always greater than or equal to the value of \(d_{\textrm{min}}\), for the test to be satisfied, we need all the black dots to fall below or lie on the grey surface. From Fig. 2, we see that this is indeed what happens.
Similar checks done with the methods OT, OE, OES, TT, TTS were successful.
7 The planar case
Let us consider the case of two coplanar conics parametrized by the true anomalies \(f_1\), \(f_2\). Then, \((f_1, f_2)\) is a critical point of \(d^2\) iff \(d^2(f_1, f_2)=0\) or the tangent vectors
to the first and second conic at \({{\mathcal {X}}}_1(f_1)\) and \({{\mathcal {X}}}_2(f_2)\), respectively, are parallel. If one trajectory, say the second one, is circular, then the tangent vector \(\varvec{\tau }_2\) is orthogonal to the position vector \({{\mathcal {X}}}_2\) for any value of \(f_2\). Therefore, to find critical points that do not correspond to trajectory intersections, it is enough to look for values of \(f_1\) such that \(\textbf{r}_1\cdot \varvec{\tau }_1=0\). By symmetry, we can write
that is we can assume \(\omega _1 = 0\). Thus, up to a multiplicative factor, we have
so that
is satisfied iff \(f_1 = 0,\pi \). Therefore, in general, we have the four critical points
We may have at most two additional critical points that correspond to trajectory intersections, see Gronchi and Tommei (2007, Sect. 7.1). In conclusion, the maximum number of critical points with a circular and an elliptic trajectory in the planar case is 6.
We consider now the case of two ellipses. The position vectors can be written as
and
Up to a multiplicative factor, we have
The critical points that do not correspond to trajectory intersections are given by the values of \(f_1, f_2\) such that \(\varvec{\tau }_1, \varvec{\tau }_2\) are parallel and both orthogonal to \({{\mathcal {X}}}_2-{{\mathcal {X}}}_1\). These two conditions lead to the system

Multiplying (35) by \(r_2\) and subtracting (36) we get
Equations (35) and (37) can be written as

Level curves of the squared distance for the case reported in Table 2. The position of the critical points is highlighted: saddle points are represented by black asterisks, while the red and blue crosses correspond to maximum and minimum points, respectively
where
From (38) we obtain
which is replaced into relation \(\cos ^2f_2+\sin ^2f_2-1=0\) to give
Moreover, after replacing in (40)
which follows from (39), we obtain
Since
the trigonometric polynomial in (41) has, in general, degree 5 in \(\cos f_1\), \(\sin f_1\). Therefore, we cannot have more than 10 critical points which do not correspond to trajectory intersections. Then, the maximum number of critical points of \(d^2\) (including intersections) for two elliptic orbits in the planar case is at most 12. However, we remark that this bound has never been reached in our numerical tests, where we got at most 10 critical points that we think is the maximum number. This conjecture adds a new question to Problem 8 in Albouy et al. (2012).
In Table 2, we write a set of orbital elements giving 10 critical points. We draw the level curves of \(d^2\) in Fig. 3, as function of the eccentric anomalies \(u_1, u_2\), where the position of each critical point is highlighted: we use an asterisk for saddle points, and crosses for local extrema. Finally, the critical points, the corresponding values of d and their type (minimum, maximum, saddle) are displayed in Table 3.
8 Conclusions
In this work, we investigate different approaches for the computation of the critical points of the squared distance function \(d^2\), with particular care for the minimum values. We focus on the case of bounded trajectories. Two algebraic approaches are used: the first employs ordinary polynomials, the second trigonometric polynomials. In both cases, we detail all the steps to reduce the problem to the computation of the roots of a univariate polynomial of minimal degree (that is 16, in the general case). The different methods are compared through numerical tests using the orbits of all the known near-Earth asteroids. We also perform some reliability tests of the results, which make use of known optimal bounds on the orbit distance. Finally, we improve the theoretical bound on the number of critical points in the planar case, and refine the related conjecture.
References
Albouy, A., Cabral, H.E., Santos, A.A.: Some problems on the classical N-body problem. Cel. Mech. Dyn. Ast. and MNRAS. 113(4), 369–375 (2012)
Arroyo-Parejo, C.A., Sanchez-Ortiz, N., Dominguez-Gonzalez, R.: Effect of mega-constellations on collision risk in space. In: 8th European Conference on Space Debris. ESA Space Debris Office (2021)
Baluyev, R.V., Kholshevnikov, K.V.: Distance between two arbitrary unperturbed orbits. Cel. Mech. Dyn. Ast. and MNRAS 91(3–4), 287–300 (2005)
Bini, D.A.: Numerical computation of polynomial zeros by means of Aberth method. Numer. Algorithms 13, 179–200 (1997)
Casulli, A., Robol, L.: Rank-structured QR for Chebyshev rootfinding. SIAM J. Matrix Anal. Appl. 42(3), 1148–1171 (2021)
Cox, D., Little, J., O’Shea, D.: Ideals, Varieties, and Algorithms. Springer, New York (1992)
Dybczynski, P.A., Jopek, T.J., Serafin, R.A.: On the minimum distance between two Keplerian orbits with a common focus. Cel. Mech. Dyn. Ast. and MNRAS 38, 345–356 (1986)
Good, I.: The colleague matrix, a Chebyshev analogue of the companion matrix. Q. J. Math. Oxford Ser. 2(12), 61–68 (1961)
Gronchi, G.F.: On the stationary points of the squared distance between two ellipses with a common focus. SIAM J. Sci. Comput. 4(1), 61–80 (2002)
Gronchi, G.F.: An algebraic method to compute the critical points of the distance function between two Keplerian orbits. Cel. Mech. Dyn. Ast. and MNRAS 93(1), 297–332 (2005)
Gronchi, G.F., Niederman, L.: On the nodal distance between two Keplerian trajectories with a common focus. Cel. Mech. Dyn. Ast. and MNRAS 132(5), 1–29 (2020)
Gronchi, G.F., Tommei, G.: On the uncertainty of the minimal distance between two confocal keplerian orbits. Discrete Contin. Dyn. Syst. B 7(4), 755–778 (2007)
Gronchi, G.F., Valsecchi, G.B.: On the possible values of the orbit distance between a near-Earth asteroid and the Earth. Mon. Not. R. Astron. Soc. 429, 2687–2699 (2013)
Hedo, J.M., Ruíz, M., Peláez, J.: On the minimum orbital intersection distance computation: a new effective method. MNRAS 479(3), 3288–3299 (2018)
Kholshevnikov, K.V., Vassiliev, N.N.: On the distance function between two Keplerian elliptic orbits. Cel. Mech. Dyn. Ast. and MNRAS. 75, 75–83 (1999)
Milani, A., Chesley, S.R., Chodas, P.W., Valsecchi, G.B.: Asteroid Close Approaches: Analysis and Potential Impact Detection. In: Bottke, W.F., Cellino, A., Paolicchi, P., Binzel, R.P. (eds.) ASTEROIDS III, pp. 55–69. Arizona University Press, Tucson (2001)
Milani, A., Chesley, S.R., Sansaturio, M.E., Tommei, G., Valsecchi, G.B.: Nonlinear impact monitoring: line of variation searches for impactors. Icarus 173(2), 362–384 (2005)
Noferini, V., Pérez, J.: Chebyshev rootfinding via computing eigenvalues. Math. Comput. 86(306), 1741–1767 (2017)
Rossi, A., Petit, A., McKnight, D.: Short-term space safety analysis of LEO constellations and clusters. Acta Ast. 175, 476–483 (2020)
Sitarski, G.: Approaches of the parabolic comets to the outer planets. Acta Ast. 18(2), 171–195 (1968)
Wisniowski, T., Rickman, H.: Fast geometric method for calculating accurate minimum orbit intersection distances (MOIDs). Acta Ast. 63, 293–307 (2013)
Acknowledgements
We wish to thank Leonardo Robol for his useful comments and suggestions. The authors have been partially supported through the H2020 MSCA ETN Stardust-Reloaded, Grant Agreement n. 813644. The authors also acknowledge the project MIUR-PRIN 20178CJA2B “New frontiers of Celestial Mechanics: theory and applications” and the GNFM-INdAM (Gruppo Nazionale per la Fisica Matematica).
Funding
Open access funding provided by Università di Pisa within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
A: Coefficients of shifted polynomials for the method with ordinary polynomials and eccentric anomalies
The coefficients of system (10) are
B: Factorization of \(\mathscr {H}(f_2)\)
Let
and define
Proposition 2
We can extract the factor \(\beta ^2(1+e_2\cos f_2)^2\) from \(\det \mathscr {T}\).
Proof
We first prove that we can extract the factor \(\beta ^2\).
Noting that
we consider
We can write \(\det \mathscr {T}\) as a sum of terms where the only one that is independent on \(\beta \) is
which is equal to 0, as previously proved at the beginning of Proposition 1. The terms that are linearly dependent on \(\beta \) are given by
and their sum is equal to 0, because the two determinants are opposite. Therefore, \(\mathscr {H}(f_2)\) is made by terms of degree higher than 1 in \(\beta \). Thus, we can write
where
We have
Remark 1
\(\mathscr {H}(f_2)/\beta ^2\) is a trigonometric polynomial of degree 10 in \((\cos f_2\), \(\sin f_2)\).
Then, we show that \(\xi ^2 = (1+e_2\cos f_2)^2\) is a factor of \(\mathscr {H}(f_2)/\beta ^2\). For this purpose, using the definitions of \(\alpha \), \(\beta \), \(\nu \), \(\lambda \), \(\tilde{\alpha }\), \(\tilde{\beta }\), \(\tilde{\lambda }\) given in Sect. 5, we write
The factor \(\beta ^2\) can be extracted from \((\mathfrak {D}_1+\mathfrak {D}_2+\mathfrak {D}_3)/\beta ^2\), therefore also \(\xi ^2\) is a factor of this polynomial. Consider now \(\mathfrak {D}_4/\beta ^2\) and write it as
Noting that
and
where we used the expressions of \(\alpha \), \(\lambda \), \(\nu \) in (43), (44), (45) and the definition of \(\eta \) in (42), we prove that \(\xi ^2\) factors \(\mathfrak {D}_4/\beta ^2\).
Finally, using relation (46) and
we show that also \(\mathfrak {D}_5/\beta ^2\) contains the factor \(\xi ^2\). \(\square \)
The trigonometric polynomial
is of degree 8 in \((\cos f_2\), \(\sin f_2)\).
C: Angular shift for trigonometric polynomials
Let
with \(x = \cos u, y = \sin u\) and \({{\mathcal {K}}}\subset \mathbb {N}\times \mathbb {N}\) (non-negative 2-index integers) be a trigonometric polynomial. We wish to write p(x, y) in terms of the variables (z, w), where
Writing \(c_\alpha \), \(s_\alpha \) for \(\cos \alpha \), \(\sin \alpha \), respectively, we have
so that we obtain
If
introducing the coefficients
we can write

where
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gronchi, G.F., Baù, G. & Grassi, C. Revisiting the computation of the critical points of the Keplerian distance. Celest Mech Dyn Astron 135, 48 (2023). https://doi.org/10.1007/s10569-023-10161-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10569-023-10161-4