Single-averaged model for analysis of frozen orbits around planets and moons

Abstract

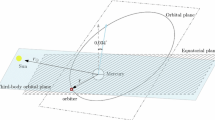
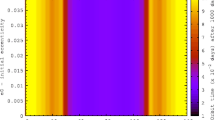
Let us consider the restricted three-body problem. Analysis of the orbital motion of a spacecraft around planets or moons is presented taking into account the nonsphericity of the primaries and the perturbations coming from a third body in an elliptical and inclined orbit. In the specific case of a spacecraft designed to explore a planet, moon or asteroid, it is noteworthy the increasing use of the averaging methods. This is a very powerful technique to simulate, very fast, the main effects caused by the disturbers on the dynamics of the spacecraft. In this work, we focus on the averaged methods applied in different conditions. Some comparisons are presented between the single-averaged, double-averaged models and the complete model, that is, the unaveraged model based on direct integration of the Cartesian (x, y, z) coordinates. This unaveraged model is quite necessary as it provides all the requirements to validate the performance and evaluate the usefulness of the averaged models for each specific problem. In the first part of this paper, we describe briefly some well-known techniques to obtain the averaged model considering the nonsphericity of the primary as well as the perturbation due to the third body. On the other hand, this is a opportunity to mention some misprints and typos problems, in the literature related to this subject. We compared the performance of single- and double-averaging models, keeping the x–y–z unaveraged model as the baseline of reference. The case of a high lunar orbit (Nie et al. in Celest Mech Dyn Astron 131(29):1–31, 2019) considering the perturbation of the Earth seems to be instructive. Single-average model is more accurate than the double-average model in the analysis of the eccentricity evolution, but in some cases of the inclination evolution, the three models agree and the average models are both very accurate. When comparing the results, eventual typos were detected in some works related to the literature of this subject. In the second part of this paper, we detached some aspects of the dynamics of a probe around Mercury (Sect. 5) involved in frozen orbit (FO) and in "quasi-frozen orbit", (quasi-FO). Due to the interesting gravitational field of the planet and its proximity to the Sun, this is an important problem. Recently, many papers, not only on pure dynamics but on gravitational field of Mercury, have been published, according to references listed in this work. An exhaustive investigation on FO using double-averaging model was reported in Tresaco et al. (Celest Mech Dyn Astron 130(9):1–26, 2018). In this paper we revisit this problem, using x–y–z-model as a primary source of results. After a number of experiments, it was possible to use confidently the single averaging in many cases, for instance, in searching "quasi-FO" for Mercury planet. Although we do not include the effect of the radiation pressure, a number of our simulations can be compared with those given in Tresaco et al. (2018).

Appendices

Appendix A

To apply the average, we use known equations of the celestial mechanics, which are:

$$\begin{aligned}&\begin{array}{l} \sin (f)=(\sqrt{1-e^2}\sin (\nu ))/(1-e\cos (\nu )), \end{array} \end{aligned}$$

(19)

$$\begin{aligned}&\begin{array}{l} \cos (f)=(\cos (\nu )-e)/(1-e\cos (\nu )), \end{array} \end{aligned}$$

(20)

$$\begin{aligned}&\begin{array}{l} r/a=1-e\cos (\nu ), \end{array} \end{aligned}$$

(21)

$$\begin{aligned}&\begin{array}{l} dl=(1-e\cos (\nu ))d\nu , \end{array} \end{aligned}$$

(22)

where l is the mean anomaly of the space vehicle.

Now replacing Eqs. (3), (19), (20) and (21) in Eq. (2), the average is made using Eq. (22).

For the mean anomaly ($l_{\odot }$) of the third body to appear explicitly in Eq. (4), we use the following expansions given by Eqs. (23), (24) and (25) (see Murray and Dermott 1999).

$$\begin{aligned}&\begin{array}{l} {[{\frac{a_{\odot }}{{ r_{\odot }}}}]}^{3}=1+3\,e_{\odot }\cos \left( { l_{\odot }} \right) +3/2 \,{e_{\odot }}^{2} \left( 1+3\,\cos \left( 2\,{ l_{\odot }} \right) \right) , \end{array} \end{aligned}$$

(23)

$$\begin{aligned}&\begin{array}{l} \sin {f_{\odot }}=\sin \left( { l_{\odot }} \right) +e_{\odot }\sin \left( 2\,{ l_{\odot }} \right) +{e_{\odot }}^{2 } \left( {\frac{9\,\sin \left( 3\,{ l_{\odot }} \right) }{8}}-{\frac{7\, \sin \left( { l_{\odot }} \right) }{8}} \right) , \end{array} \end{aligned}$$

(24)

$$\begin{aligned}&\begin{array}{l} \cos {f_{\odot }}=\cos \left( { l_{\odot }} \right) +e_{\odot } \left( \cos \left( 2\,{ l_{\odot }} \right) -1 \right) +{e_{\odot }}^{2} \left( {\frac{9\,\cos \left( 3\,{ l_{\odot }} \right) }{8}}-{\frac{9\,\cos \left( { l_{\odot }} \right) }{8}} \right) . \end{array} \end{aligned}$$

(25)

The well-known formulas of the two-body problem connecting true and mean anomaly (Brouwer and Clemence 1961) is used:

$$\begin{aligned}&\displaystyle a/r=(1+e\cos (f))/(1-e^2),\end{aligned}$$

(26)

$$\begin{aligned}&\displaystyle dl= \frac{1}{\sqrt{1-e^2}}\frac{r^2}{a^2}df. \end{aligned}$$

(27)

Appendix B

The disturbing potential due to the third body in an elliptical and inclined orbit, obtained via the single-averaged model, is written in the form

$$\begin{aligned} R2_{SA}=&{\frac{255 k n_{\odot }^{2}{a}^{2}}{256}} ( {\frac{7 e_{\odot }{e}^{2} ( { c_{\odot }}-1 ) ^{2} ( c-1 ) ^{2}\cos ( -{ l_{\odot }}+2 g-2 h-2 \lambda _{\odot }+4 { h_{\odot }} ) }{17}} \\&+{\frac{7 e_{\odot }{e}^{2} ( { c_{\odot }}-1 ) ^{2} ( 1+c ) ^{2}\cos ( {l_{\odot }}+2 g+2 h+2 \lambda _{\odot }-4 { h_{\odot }} ) }{17}}\\&- 1/17 e_{\odot }{e}^{2}( 1+{ c_{\odot }} ) ^{2} ( c-1 ) ^{2}\cos ( 2g-2 h+2 \lambda _{\odot }-{ l_{\odot }} ) \\&- 1/17 e_{\odot }{e}^{2} ( { c_{\odot }}-1) ^{2} ( c-1 ) ^{2}\cos ( { l_{\odot }}+2 g-2 h-2\lambda _{\odot }+4 { h_{\odot }} ) \\&- 1/17 e_{\odot }{e}^{2} ( 1+{ c_{\odot }}) ^{2} ( 1+c ) ^{2}\cos ( { l_{\odot }}+2 g+2 h-2\lambda _{\odot } ) \\&- 1/17 e_{\odot }{e}^{2} ( { c_{\odot }}-1 ) ^{2}( 1+c ) ^{2}\cos ( -{ l_{\odot }}+2 g+2 h+2 \lambda _{\odot }-4{ h_{\odot }} ) \\&+ {\frac{7 e_{\odot }{e}^{2} ( 1+{ c_{\odot }} ) ^{2}( 1+c ) ^{2}\cos ( -{ l_{\odot }}+2 g+2 h-2 \lambda _{\odot }) }{17}}\\&-{\frac{5 ( { c_{\odot }}-1 ) ^{2}{e}^{2}( {e_{\odot }}^{2}-2/5 ) ( 1+c ) ^{2}\cos ( 2 g+2h+2 \lambda _{\odot }-4 { h_{\odot }} ) }{17}}\\&+ {\frac{7 e_{\odot }{e}^{2}( 1+{ c_{\odot }} ) ^{2} ( c-1 ) ^{2}\cos ( 2 g-2 h+2\lambda _{\odot }+{ l_{\odot }} ) }{17}}\\&- {\frac{5 {e}^{2} ( {e_{\odot }}^{2}-2/5)( 1+{ c_{\odot }} ) ^{2} ( 1+c ) ^{2}\cos ( 2 g+2 h-2 \lambda _{\odot } ) }{17}}\\&- {\frac{5 ( { c_{\odot }}-1 ) ^{2} ( c-1 ) ^{2}{e}^{2} ( {e_{\odot }}^{2}-2/5) \cos ( 2 g-2 h-2 \lambda _{\odot }+4 { h_{\odot }} ) }{17}}\\&-{\frac{5 ( c-1 ) ^{2}{e}^{2} ( {e_{\odot }}^{2}-2/5 )( 1+{ c_{\odot }} ) ^{2}\cos ( 2 g-2 h+2 \lambda _{\odot }) }{17}}\\&+{e_{\odot }}^{2}{e}^{2} ( { c_{\odot }}-1 ) ^{2} ( c-1 ) ^{2}\cos ( -2 { l_{\odot }}+2 g-2 h-2 \lambda _{\odot }+4 {h_{\odot }} )\\&+{e_{\odot }}^{2}{e}^{2} ( 1+{ c_{\odot }} ) ^{2} ( 1+c) ^{2}\cos ( -2 { l_{\odot }}+2 g+2 h-2 \lambda _{\odot } ) \\&+{e_{\odot }}^{2}{e}^{2} ( 1+{ c_{\odot }} ) ^{2} ( c-1 ) ^{2}\cos ( 2 { l_{\odot }}+2 g-2 h+2 \lambda _{\odot } ) \\&+{e_{\odot }}^{2}{e}^{2}( { c_{\odot }}-1 ) ^{2} ( 1+c ) ^{2}\cos ( 2{ l_{\odot }}+2 g+2 h+2 \lambda _{\odot }-4 { h_{\odot }} )\\&+{\frac{108 {e_{\odot }}^{2} ( ( {c}^{2}+1 ) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}+{c}^{2}-5/3 ) ( {e}^{2}+2/3 ) \cos ( 2 {l_{\odot }} ) }{85}}\\&- {\frac{18 {e}^{2}{e_{\odot }}^{2} ( ( {c}^{2}-1 ) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}+{c}^{2}-1) \cos ( 2 g+2 { l_{\odot }} ) }{17}}\\&+2 {e}^{2}( ( {c}^{2}-1 ) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}-{c}^{2}+1 ) {e_{\odot }}^{2}\cos ( -2 { l_{\odot }}-2\lambda +2 {h_{\odot }}+2 g ) \\&+{\frac{14 {e}^{2} ( ( {c}^{2}-1) {{ c_{\odot }}}^{2}+ 2 {s}^{2}{{ s_{\odot }}}^{2}-{c}^{2}+1 ) e_{\odot }\cos ( -{ l_{\odot }}-2 \lambda _{\odot }+2 { h_{\odot }}+2 g ) }{17}}\\&+2 {e}^{2} ( ( {c}^{2}-1 ) {{ c_{\odot }}}^{2}\\&+{s}^{2}{{s_{\odot }}}^{2}-{c}^{2}+1 ) {e_{\odot }}^{2}\cos ( 2 { l_{\odot }}+2 \lambda _{\odot }-2{ h_{\odot }}+2 g ) \\&- {\frac{18 {e}^{2}{e_{\odot }}^{2} ( ( {c}^{2}-1 ) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}+{c}^{2}-1) \cos ( 2 g-2 { l_{\odot }} ) }{17}}\\&-{\frac{10 {e}^{2} ( {e_{\odot }}^{2}-2/5 ) ( ( {c}^{2}-1 ) {{c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}-{c}^{2}+1 ) \cos ( 2\lambda _{\odot }-2 { h_{\odot }}+2 g ) }{17}}\\&-{\frac{12 {e}^{2} ( {e_{\odot }}^{2}+2/3 ) ( ( {c}^{2}-1 ) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}+{c}^{2}-1 ) \cos ( 2 g) }{17}}\\&-2/17 {e}^{2} ( ( {c}^{2}-1 ) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}-{c}^{2}+1 ) e_{\odot }\cos ( { l_{\odot }}-2 \lambda _{\odot }+2{ h_{\odot }}+2 g ) \\&- {\frac{12 {e}^{2}e_{\odot } ( ( {c}^{2}-1) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}+{c}^{2}-1 )\cos ( -{ l_{\odot }}+2 g ) }{17}}\\&+ {\frac{14 {e}^{2} (( {c}^{2}-1 ) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}-{c}^{2}+1 ) e_{\odot }\cos ( { l_{\odot }}+2 \lambda _{\odot }-2 { h_{\odot }}+2 g) }{17}}\\&- {\frac{10 {e}^{2} ( {e_{\odot }}^{2}-2/5 )( ( {c}^{2}-1 ) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}-{c}^{2}+1 ) \cos ( -2 \lambda _{\odot }+2 { h_{\odot }}+2 g) }{17}}\\&- {\frac{12 {e}^{2}e_{\odot } ( ( {c}^{2}-1 ){{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}+{c}^{2}-1 ) \cos ({ l_{\odot }}+2 g ) }{17}}\\&- 2/17 {e}^{2} ( ( {c}^{2}-1) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}-{c}^{2}+1 ) e_{\odot }\cos ( -{ l_{\odot }}+2 \lambda _{\odot }-2 { h_{\odot }}+2 g ) \\&+ {\frac{28e_{\odot }s{ s_{\odot }} {e}^{2} ( { c_{\odot }}-1 ) ( c-1 )\cos ( 2 g-2 \lambda _{\odot }+3 { h_{\odot }}-{ l_{\odot }}-h ) }{17}}\\&+ {\frac{216 { c_{\odot }} { s_{\odot }} {e_{\odot }}^{2}sc ( {e}^{2}+2/3 )\cos ( h-{ h_{\odot }}+2 { l_{\odot }} ) }{85}}\\&+{\frac{28 e_{\odot }s{s_{\odot }} {e}^{2} ( 1+{ c_{\odot }} ) ( c-1 ) \cos ( { l_{\odot }}+2 g+2 \lambda _{\odot }-{ h_{\odot }}-h ) }{17}}\\&+ {\frac{28e_{\odot }s{ s_{\odot }} {e}^{2} ( 1+{ c_{\odot }} ) ( 1+c )\cos ( 2 g-2 \lambda _{\odot }+{ h_{\odot }}-{ l_{\odot }}+h ) }{17}}\\&- {\frac{36 {e_{\odot }}^{2}s{ s_{\odot }} {e}^{2}{ c_{\odot }} ( c-1 ) \cos ( 2 g-h+{ h_{\odot }}-2 { l_{\odot }} ) }{17}}\\&- {\frac{36 {e_{\odot }}^{2}s{ s_{\odot }} {e}^{2}{ c_{\odot }} ( 1+c ) \cos ( 2 g-{h_{\odot }}+h-2 { l_{\odot }} ) }{17}}\\&- {\frac{24 e_{\odot }{ c_{\odot }} s{ s_{\odot }} {e}^{2} ( c-1 ) \cos ( 2 g+{ h_{\odot }}-h+{ l_{\odot }} )}{17}}\\&+ {\frac{144 { c_{\odot }} { s_{\odot }} e_{\odot }sc ( {e}^{2}+2/3) \cos ( -{ h_{\odot }}+h+{ l_{\odot }} ) }{85}}\\&+{\frac{28 e_{\odot }s{ s_{\odot }} {e}^{2} ( { c_{\odot }}-1 ) ( 1+c ) \cos ( 2 g+2 \lambda _{\odot }-3 { h_{\odot }}+{ l_{\odot }}+h ) }{17}}\\&-{\frac{20 {e}^{2} ( {e_{\odot }}^{2}-2/5 ) ( 1+{ c_{\odot }} ) {s_{\odot }} s ( 1+c ) \cos ( 2 g-2 \lambda _{\odot }+{ h_{\odot }}+h) }{17}}\\&- {\frac{24 e_{\odot }{ c_{\odot }} s{ s_{\odot }} {e}^{2} ( 1+c) \cos ( 2 g-{ h_{\odot }}+h-{ l_{\odot }} ) }{17}}\\&- {\frac{24 e_{\odot }{ c_{\odot }} s{ s_{\odot }} {e}^{2} ( 1+c ) \cos ( {l_{\odot }}+2 g-{ h_{\odot }}+h ) }{17}}\\&- {\frac{4 e_{\odot }s{ s_{\odot }} {e}^{2}( 1+{ c_{\odot }} ) ( 1+c ) \cos ( 2 g-2\lambda _{\odot }+{ h_{\odot }}+{ l_{\odot }}+h ) }{17}}\\&+{\frac{216 { c_{\odot }} {s_{\odot }} {e_{\odot }}^{2}sc ( {e}^{2}+2/3 ) \cos ( -{ h_{\odot }}+h-2 { l_{\odot }} ) }{85}}\\&- {\frac{24 {e}^{2} ( {e_{\odot }}^{2}+2/3) { c_{\odot }} { s_{\odot }} s ( 1+c ) \cos ( 2 g-{h_{\odot }}+h ) }{17}}\\&- {\frac{24 e_{\odot }{ c_{\odot }} s{ s_{\odot }} {e}^{2}( c-1 ) \cos ( 2 g+{ h_{\odot }}-h-{ l_{\odot }} ) }{17}}\\&- {\frac{4 e_{\odot }s{ s_{\odot }} {e}^{2} ( { c_{\odot }}-1 ) ( c-1) \cos ( 2 g-2 \lambda _{\odot }+3 { h_{\odot }}+{ l_{\odot }}-h ) }{17}}\\&+ {\frac{144 { c_{\odot }} { s_{\odot }} e_{\odot }sc ( {e}^{2}+2/3 )\cos ( -{ l_{\odot }}-{ h_{\odot }}+h ) }{85}}\\&- {\frac{36 {e_{\odot }}^{2}s{s_{\odot }} {e}^{2}{ c_{\odot }} ( c-1 ) \cos ( 2 g+{ h_{\odot }}-h+2 { l_{\odot }} ) }{17}}\\&- {\frac{36 {e_{\odot }}^{2}s{ s_{\odot }} {e}^{2}{c_{\odot }} ( 1+c ) \cos ( 2 g-{ h_{\odot }}+h+2 { l_{\odot }}) }{17}}\\&- {\frac{4 e_{\odot }s{ s_{\odot }} {e}^{2} ( { c_{\odot }}-1) ( 1+c ) \cos ( 2 g+2 \lambda _{\odot }-3 { h_{\odot }}-{l_{\odot }}+h ) }{17}}\\&- {\frac{4 e_{\odot }s{ s_{\odot }} {e}^{2} ( 1+{c_{\odot }} ) ( c-1 ) \cos ( -{ l_{\odot }}+2 g+2 \lambda _{\odot }-{ h_{\odot }}-h ) }{17}}\\&+4 {e_{\odot }}^{2}s{ s_{\odot }} {e}^{2} ( { c_{\odot }}-1 ) ( c-1 ) \cos ( 2 g-2 \lambda _{\odot }+3 { h_{\odot }}-2 { l_{\odot }}-h )\\&+4 {e_{\odot }}^{2}s{ s_{\odot }} {e}^{2} ( 1+{ c_{\odot }}) ( c-1 ) \cos ( 2 { l_{\odot }}+2 g+2 \lambda _{\odot }-{ h_{\odot }}-h ) \\&+4 {e_{\odot }}^{2}s{ s_{\odot }} {e}^{2} ( { c_{\odot }}-1) ( 1+c ) \cos ( 2 { l_{\odot }}+2 g+2 \lambda _{\odot }-3{ h_{\odot }}+h \\&+4 {e_{\odot }}^{2}s{ s_{\odot }} {e}^{2} ( 1+{ c_{\odot }}) ( 1+c ) \cos ( -2 { l_{\odot }}+2 g-2 \lambda _{\odot }+{ h_{\odot }}+h ) \\&-{\frac{6 e_{\odot }{e}^{2} ( { c_{\odot }}-1 )( 1+{ c_{\odot }} ) ( 1+c ) ^{2}\cos ( 2 g+2h-2 { h_{\odot }}-{ l_{\odot }} ) }{17}}\\&-{\frac{9 {e_{\odot }}^{2}{e}^{2}( { c_{\odot }}-1 ) ( 1+{ c_{\odot }} ) ( c-1) ^{2}\cos ( 2 g-2 h+2 { h_{\odot }}-2 { l_{\odot }} ) }{17}}\\&-6/5 ( { c_{\odot }}-1 ) ^{2} ( c-1 ) {e_{\odot }}^{2}( 1+c ) ( {e}^{2}+2/3 ) \cos ( 2 { l_{\odot }}+2 \lambda _{\odot }-4 { h_{\odot }}+2 h )\\&-{\frac{6 e_{\odot }{e}^{2} ( {c_{\odot }}-1 ) ( 1+{ c_{\odot }} ) ( 1+c ) ^{2}\cos ( 2 g+2 h-2 { h_{\odot }}+{ l_{\odot }} ) }{17}}\\&-{\frac{42( { c_{\odot }}-1 ) ^{2} ( c-1 ) e_{\odot } ( 1+c) ( {e}^{2}+2/3 ) \cos ( { l_{\odot }}+2 \lambda _{\odot }-4{ h_{\odot }}+2 h ) }{85}}\\&-{\frac{9 {e_{\odot }}^{2}{e}^{2} ( {c_{\odot }}-1 ) ( 1+{ c_{\odot }} ) ( 1+c ) ^{2}\cos ( 2 g+2 h-2 { h_{\odot }}-2 { l_{\odot }} ) }{17}}\\&-{\frac{6 e_{\odot }{e}^{2} ( { c_{\odot }}-1 ) ( 1+{ c_{\odot }} ) ( c-1 ) ^{2}\cos ( -{ l_{\odot }}+2 g-2 h+2 { h_{\odot }} ) }{17}}\\&+{\frac{6 ( { c_{\odot }}-1 ) ^{2} ( c-1 )( {e_{\odot }}^{2}-2/5 ) ( 1+c ) ( {e}^{2}+2/3) \cos ( 2 \lambda _{\odot }-4 { h_{\odot }}+2 h ) }{17}}\\&+{\frac{6 ( { c_{\odot }}-1 ) ^{2} ( c-1 ) e_{\odot } (1+c ) ( {e}^{2}+2/3 ) \cos ( -{ l_{\odot }}+2\lambda _{\odot }-4 { h_{\odot }}+2 h ) }{85}}\\&-{\frac{6 e_{\odot }{e}^{2} ( {c_{\odot }}-1 ) ( 1+{ c_{\odot }} ) ( c-1 ) ^{2}\cos ( { l_{\odot }}+2 g-2 h+2 { h_{\odot }} ) }{17}}\\&-{\frac{9 {e_{\odot }}^{2}{e}^{2} ( { c_{\odot }}-1 ) ( 1+{ c_{\odot }} )( 1+c ) ^{2}\cos ( 2 g+2 h-2 { h_{\odot }}+2 { l_{\odot }}) }{17}}\\&-{\frac{9 {e_{\odot }}^{2}{e}^{2} ( { c_{\odot }}-1 )( 1+{ c_{\odot }} ) ( c-1 ) ^{2}\cos ( 2 g-2h+2 { h_{\odot }}+2 { l_{\odot }} ) }{17}}\\&-{\frac{168 c ( 1+{c_{\odot }} ) s ( {e}^{2}+2/3 ) { s_{\odot }} e_{\odot }\cos ( -{l_{\odot }}-2 \lambda _{\odot }+{ h_{\odot }}+h ) }{85}}\\&-{\frac{24 c ( {c_{\odot }}-1 ) s ( {e}^{2}+2/3 ) { s_{\odot }} {e_{\odot }}^{2}\cos ( 2 { l_{\odot }}+2 \lambda _{\odot }-3 { h_{\odot }}+h ) }{5}}\\&+{\frac{24c ( { c_{\odot }}-1 ) s ( {e}^{2}+2/3 ) { s_{\odot }} e_{\odot }\cos ( 2 \lambda _{\odot }-3 { h_{\odot }}-{ l_{\odot }}+h ) }{85}}\\&+{\frac{24 c ( 1+{ c_{\odot }} ) s ( {e_{\odot }}^{2}-2/5 ) ( {e}^{2}+2/3 ) { s_{\odot }} \cos ( -2 \lambda _{\odot }+{ h_{\odot }}+h) }{17}}\\&+{\frac{144 c{ c_{\odot }} s ( {e}^{2}+2/3 ) {s_{\odot }} ( {e_{\odot }}^{2}+2/3 ) \cos ( -{ h_{\odot }}+h )}{85}}\\&+{\frac{24 c ( 1+{ c_{\odot }} ) s ( {e}^{2}+2/3) { s_{\odot }} e_{\odot }\cos ( { l_{\odot }}-2 \lambda _{\odot }+{ h_{\odot }}+h) }{85}}\\&-{\frac{24 { c_{\odot }} ( c-1 ) s{e}^{2}{s_{\odot }} ( {e_{\odot }}^{2}+2/3 ) \cos ( 2 g+{ h_{\odot }}-h) }{17}}\\&-{\frac{168 c ( { c_{\odot }}-1 ) s ( {e}^{2}+2/3 ) { s_{\odot }} e_{\odot }\cos ( 2 \lambda _{\odot }-3 { h_{\odot }}+{ l_{\odot }} +h ) }{85}}\\&+{\frac{24 c ( { c_{\odot }}-1 ) s ( {e_{\odot }}^{2}-2/5 ) ( {e}^{2}+2/3 ) { s_{\odot }} \cos ( 2\lambda _{\odot }-3 { h_{\odot }}+h ) }{17}}\\&-{\frac{24 c ( 1+{ c_{\odot }}) s ( {e}^{2}+2/3 ) { s_{\odot }} {e_{\odot }}^{2}\cos ( -2{ l_{\odot }}-2 \lambda _{\odot }+{ h_{\odot }}+h ) }{5}}\\&+{\frac{6 ( 1+{c_{\odot }} ) ^{2} ( c-1 ) ( 1+c ) ( {e_{\odot }}^{2}-2/5 ) ( {e}^{2}+2/3 ) \cos ( 2 h-2\lambda _{\odot } ) }{17}}\\&+{\frac{6 ( 1+{ c_{\odot }} ) ^{2}( c-1 ) ( 1+c ) ( {e}^{2}+2/3 ) e_{\odot }\cos ( { l_{\odot }}+2 h-2 \lambda _{\odot } ) }{85}}\\&-6/5 ( 1+{c_{\odot }} ) ^{2} ( c-1 ) ( 1+c ) ( {e}^{2}+2/3 ) {e_{\odot }}^{2}\cos ( -2 { l_{\odot }}+2 h-2 \lambda _{\odot }) \\&-{\frac{42 ( 1+{ c_{\odot }} ) ^{2} ( c-1 ) ( 1+c ) ( {e}^{2}+2/3 ) e_{\odot }\cos (-{ l_{\odot }}+2 h-2 \lambda _{\odot } ) }{85}}\\&+{\frac{72}{85}} (( {c}^{2}+1 ) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}+{c}^{2}-5/3 ) ( e_{\odot }\cos ( { l_{\odot }} ) +1/2 {e_{\odot }}^{2}+1/3 ) ( {e}^{2}+2/3 ) \\&-{\frac{20}{17}} ( { c_{\odot }}-1 ) ( 1+c ) s ( {e_{\odot }}^{2}-2/5 ) {e}^{2}{s_{\odot }} \cos ( 2 g+2 \lambda _{\odot }-3 { h_{\odot }}+h ) \\&+{\frac{54}{85}} ( { c_{\odot }}-1 ) ( 1+{ c_{\odot }} ) ( c-1) ( 1+c ) ( {e}^{2}+2/3 ) {e_{\odot }}^{2}\cos ( -2 { h_{\odot }}+2 h-2 { l_{\odot }} ) \\&-{\frac{6}{17}} ( {c_{\odot }}-1 ) ( 1+{ c_{\odot }} ) ( c-1 ) ^{2}{e}^{2} ( {e_{\odot }}^{2}+2/3 ) \cos ( 2 g-2 h+2 { h_{\odot }}) \\&-{\frac{6}{17}} ( { c_{\odot }}-1 ) ( 1+{ c_{\odot }}) ( 1+c ) ^{2}{e}^{2} ( {e_{\odot }}^{2}+2/3 )\cos ( 2 g+2 h-2 { h_{\odot }} ) \\&-{\frac{12}{5}} (( {c}^{2}+1 ) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}-{c}^{2}-1 ) ( {e}^{2}+2/3 ) {e_{\odot }}^{2}\cos ( -2 {l_{\odot }}-2 \lambda _{\odot }+2 { h_{\odot }} ) \\&-{\frac{84}{85}} ( ( {c}^{2}+1 ) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}-{c}^{2}-1) ( {e}^{2}+2/3 ) e_{\odot }\cos ( -{ l_{\odot }}-2 \lambda _{\odot }+2 { h_{\odot }} ) \\&+{\frac{12}{85}} ( ( {c}^{2}+1) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}-{c}^{2}-1 )( {e}^{2}+2/3 ) e_{\odot }\cos ( { l_{\odot }}-2 \lambda _{\odot }+2 {h_{\odot }} ) \\&+{\frac{12}{17}} ( ( {c}^{2}+1 ) {{ c_{\odot }}}^{2}+2 {s}^{2}{{ s_{\odot }}}^{2}-{c}^{2}-1 ) ( {e_{\odot }}^{2}-2/5) ( {e}^{2}+2/3 ) \cos ( -2 \lambda _{\odot }+2 {h_{\odot }} ) \\&+{\frac{54}{85}} ( { c_{\odot }}-1 ) ( 1+{c_{\odot }} ) ( c-1 ) ( 1+c ) ( {e}^{2}+2/3 ) {e_{\odot }}^{2}\cos ( -2 { h_{\odot }}+2 h+2 { l_{\odot }} ) \\&+{\frac{36}{85}} ( { c_{\odot }}-1 ) ( 1+{ c_{\odot }} )( c-1 ) ( 1+c ) ( {e}^{2}+2/3 ) e_{\odot }\cos ( -2 { h_{\odot }}+2 h-{ l_{\odot }} ) \\&+{\frac{36}{85}}( { c_{\odot }}-1 ) ( 1+{ c_{\odot }} ) ( c-1) ( 1+c ) ( {e}^{2}+2/3 ) e_{\odot }\cos (-2 { h_{\odot }}+2 h+{ l_{\odot }} ) \\&-{\frac{20}{17}} ( 1+{ c_{\odot }}) ( c-1 ) s ( {e_{\odot }}^{2}-2/5 ) {e}^{2}{s_{\odot }} \cos ( 2 g+2 \lambda _{\odot }-{ h_{\odot }}-h ) \\&-{\frac{20}{17}}( { c_{\odot }}-1 ) ( c-1 ) s ( {e_{\odot }}^{2}-2/5) {e}^{2}{ s_{\odot }} \cos ( 2 g-2 \lambda _{\odot }+3 { h_{\odot }}-h) \\&+{\frac{36}{85}} ( { c_{\odot }}-1 ) ( 1+{ c_{\odot }}) ( c-1 ) ( 1+c ) ( {e}^{2}+2/3) ( {e_{\odot }}^{2}+2/3 ) \cos ( -2 { h_{\odot }}+2 h) ), \end{aligned}$$

where $c_{\odot }=\cos (i_{\odot })$ and $s_{\odot }=\sin (i_{\odot })$.

Appendix C

Now, a second average is applied to obtain the double-averaged disturbing potential in elliptical and inclined orbit, to eliminate the short-period terms of the disturbing body. For this, it is necessary to perform algebraic manipulations where we used known equations of celestial mechanics (see Brouwer and Clemence 1961), namely Eqs. (28) and (29).

$$\begin{aligned}&\begin{array}{l} {{\frac{a_{\odot }}{{r_{\odot }}}}}=(1+e_{\odot }\cos (f_{\odot }))/(1-e_{\odot }^2), \end{array} \end{aligned}$$

(28)

$$\begin{aligned}&\begin{array}{l} dl_{\odot }= \frac{1}{\sqrt{1-e_{\odot }^2}}\frac{r_{\odot }^2}{a_{\odot }^2}df_{\odot }. \end{array} \end{aligned}$$

(29)

Using Eqs. (4), (28) and (29), after some algebraic manipulations, we get

$$\begin{aligned} \begin{array}{l} R_{2DA}=\frac{9\mu '{n_{\odot }}^{2} {a}^{2}}{8( 1-{e_{\odot }}^{2})^{3/2}}( 10/3\cos ( -2{h_{\odot }}+2g+2h) {e}^{2}AC\\ \qquad + 10/3\cos ( 2{h_{\odot }}+2g-2h) {e}^{2}BD+10/3E{e}^{2}( A-C) \cos ( 2g-{h_{\odot }}+h ) \\ \qquad +10/3E{e}^{2}( B-D) \cos ( 2g+{h_{\odot }}-h) + 2( {e}^{2}+2/3)( AB+CD) \times \\ \qquad \cos ( 2h-2{h_{\odot }}) -2( {e}^{2}+2/3) ( A+B-C-D) E\cos ( -{h_{\odot }}+h) \\ \qquad + 10/3{e}^{2}( AD+BC-{E}^{2}) \cos ( 2g) \\ \qquad +( {e}^{ 2}+2/3)( {A}^{2}+{B}^{2}+{C}^{2}+{D}^{2}+2{E}^{2}-2/3)). \end{array} \end{aligned}$$

(30)

From Brouwer and Clemence (1961), we know that in the double-averaged process the pericenter argument of the third body is eliminated from the disturbing potential, see, for example, a recent demonstration of this fact given by Yokoyama (1999) and Celletti et al. (2017). Now, making $i_{\odot }= 0$, $e_{\odot }=0$ in Eq. (30), we obtain the double-averaged equation in planar and circular orbit. After algebraic manipulations, we check that the simplified equation is in agreement with Nie et al. (2019) (equation 67), Yokoyama (2002) and Broucke (2003).