Representation of the gravitational potential of a level ellipsoid by a simple layer

Abstract

A closed-form expression is obtained for the density of a simple layer, equipotential to an oblate level ellipsoid of revolution in an outer space. The potential of any level spheroid of positive mass with the inward direction of the attracting force on its surface can be represented in this way. A family of density functions defined within the whole volume of a level ellipsoid of revolution is found. Several density examples are considered.

Appendix

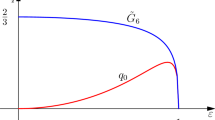
The function $H(\varepsilon )$ defined by (19) decreases on the interval [0, 1]. Let us express the dependence of H on $\varepsilon$ explicitly and make sure that its derivative is negative,

$$\begin{aligned}&H(\varepsilon ) = \frac{1}{\varepsilon ^5} \left( 3(2\varepsilon ^4 - 15\varepsilon ^2 + 9)\sqrt{1 - \varepsilon ^2}\arcsin \varepsilon - \right. \left. 8\varepsilon ^5 + 18\varepsilon ^3 - 9\varepsilon \right) , \\&\begin{aligned} H'(\varepsilon )&= \frac{3}{\varepsilon ^6} \left( 3(4\varepsilon ^2 - 5)\sqrt{1 - \varepsilon ^2}\arcsin \varepsilon + 2\varepsilon ^5 - 17\varepsilon ^3 + 15\varepsilon \right) \\ {}&= \frac{3\sqrt{1-\varepsilon ^2}}{\varepsilon ^7} \left( (15 - 2\varepsilon ^2)\sqrt{1-\varepsilon ^2} - 3(5 - 4\varepsilon ^2)\frac{\arcsin \varepsilon }{\varepsilon }\right) . \end{aligned} \end{aligned}$$

Let us expand the square root and the arcsine into series up to the fourth degree of $\varepsilon ^2$:

$$\begin{aligned} \begin{aligned}&(15 - 2\varepsilon ^2)\sqrt{1-\varepsilon ^2} - 3(5 - 4\varepsilon ^2)\frac{\arcsin \varepsilon }{\varepsilon } \\&\quad < (15 - 2\varepsilon ^2)\left( 1 - \frac{\varepsilon ^2}{2} - \frac{\varepsilon ^4}{8} - \frac{\varepsilon ^6}{16} - \frac{5\varepsilon ^8}{128}\right) - 3(5 - 4\varepsilon ^2)\left( 1 + \frac{\varepsilon ^2}{6} + \frac{3\varepsilon ^4}{40} + \frac{5\varepsilon ^6}{112} + \frac{35\varepsilon ^8}{1152}\right) \\&\quad =\varepsilon ^6\left( \frac{85}{192}\varepsilon ^2 - \frac{8}{21}\varepsilon - \frac{16}{35}\right) . \end{aligned} \end{aligned}$$

The maximum of the quadratic trinomial in the last expression is attained at $\varepsilon =1$ and equals $-2657/6720$.