Ellipsoidal equilibrium figure and Cassini states of rotating planets and satellites deformed by a tidal potential in the spatial case

Abstract

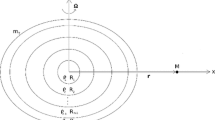
The equilibrium figure of an inviscid tidally deformed body is the starting point for the construction of many tidal theories such as Darwinian tidal theories or the hydrodynamical Creep tide theory. This paper presents the ellipsoidal equilibrium figure when the spin rate vector of the deformed body is not perpendicular to the plane of motion of the companion. We obtain the equatorial and the polar flattenings as functions of the Jeans and the Maclaurin flattenings, and of the angle $\theta$ between the spin rate vector and the radius vector. The equatorial vertex of the equilibrium ellipsoid does not point toward the companion, which produces a torque perpendicular to the rotation vector, which introduces terms of precession and nutation. We find that the direction of spin may differ significantly from the direction of the principal axis of inertia C, so the classical approximation ${\mathsf {I}}\varvec{\omega } \approx C\varvec{\omega }$ only makes sense in the neighborhood of the planar problem. We also study the so-called Cassini states. Neglecting the short-period terms in the differential equation for the spin direction and assuming a uniform precession of the line of the orbital ascending node, we obtain the same differential equation as that found by Colombo (Astron J 71:891, 1966). That is, a tidally deformed inviscid body has exactly the same Cassini states as a rotating axisymmetric rigid body, the tidal bulge having no secular effect at first order.

Appendices

Appendix 1: Gravitational potentials

1.1 Potential of a homogeneous ellipsoid at an internal point

The potential generated for the homogeneous ellipsoid on its surface, in the reference system $\mathcal {F}_\mathcal {B}$ fixed to the principal axes of inertia, is (see Kellogg 1929)

$$\begin{aligned} V_\mathrm{m} = V_0 + A_xX^2 + A_yY^2 + A_zZ^2, \end{aligned}$$

(36)

where $V_0$, $A_x$, $A_y$ and $A_z$ are constants. The constants $A_{x_i}$ are

$$\begin{aligned} A_x= & {} \frac{3Gm}{4R^3} \alpha \int _0^\infty \frac{\hbox {d}t}{(1+\alpha t)\sqrt{(1+\alpha t)(1+\beta t)(1+t)}} \nonumber \\ A_y= & {} \frac{3Gm}{4R^3} \beta \int _0^\infty \frac{\hbox {d}t}{(1+\beta t) \sqrt{(1+\alpha t)(1+\beta t)(1+t)}} \nonumber \\ A_z= & {} \frac{3Gm}{4R^3} \int _0^\infty \frac{\hbox {d}t}{(1+t)\sqrt{(1+\alpha t)(1+\beta t)(1+t)}}, \end{aligned}$$

(37)

where R and m is the mean radius and the mass of the primary, G is the gravitational constant, and

$$\begin{aligned} \alpha =\frac{c_\mathrm{m}^2}{a_\mathrm{m}^2}=1-\epsilon _\rho -2\epsilon _z; \qquad \beta =\frac{c_\mathrm{m}^2}{b_\mathrm{m}^2}=1+\epsilon _\rho -2\epsilon _z. \end{aligned}$$

(38)

Hence, the contribution to the equilibrium equations, neglecting terms of order 2 in the flattenings, is

$$\begin{aligned} \chi _X[V_\mathrm{m}]=\frac{1}{X}\frac{\partial V_\mathrm{m}}{\partial X}- \frac{\alpha }{Z}\frac{\partial V_\mathrm{m}}{\partial Z}= & {} \frac{4Gm}{5R^3} \left( \frac{\epsilon _\rho }{2}+\epsilon _z\right) \nonumber \\ \chi _Y[V_\mathrm{m}]=\frac{1}{Y}\frac{\partial V_\mathrm{m}}{\partial Y}-\frac{\beta }{Z}\frac{\partial V_\mathrm{m}}{\partial Z}= & {} \frac{4Gm}{5R^3} \left( -\frac{\epsilon _\rho }{2}+\epsilon _z\right) . \end{aligned}$$

(39)

1.2 Tidal potential

The potential due to the tide is Lambeck (1980)

$$\begin{aligned} \nabla V_\mathrm{tid} = \frac{GM}{r^3}\left[ \varvec{X}-\frac{3(\varvec{X}\cdot \varvec{r})\varvec{r}}{r^2}\right] . \end{aligned}$$

(40)

Using that $\varvec{r}=r\sin {\theta _r}\widehat{X}+r\cos {\theta _r}\widehat{Z}$ and $\varvec{X}=X\widehat{X}+Y\widehat{Y}+Z\widehat{Z}$, we obtain

$$\begin{aligned} \nabla V_\mathrm{tid} = \frac{GM}{r^3} \left( \begin{array}{ccc} X(1-3\sin ^2{\theta _r}) - 3Z\sin {\theta _r}\cos {\theta _r} \\ Y \\ - 3X\sin {\theta _r}\cos {\theta _r}+Z(1-3\cos ^2{\theta _r}) \end{array} \right) . \end{aligned}$$

(41)

Hence, the contribution to the equilibrium equations, neglecting terms of order 2 in the flattenings, is

$$\begin{aligned} \chi _X[V_\mathrm{tid}]=\frac{1}{X}\frac{\partial V_\mathrm{tid}}{\partial X}-\frac{\alpha }{Z}\frac{\partial V_\mathrm{tid}}{\partial Z}= & {} \frac{4Gm}{5R^3}\epsilon _J \left[ \cos {2\theta _r} +\left( \frac{X}{Z}-\frac{Z}{X}\right) \frac{\sin {2\theta _r}}{2}\right] \nonumber \\ \chi _Y[V_\mathrm{tid}]=\frac{1}{Y}\frac{\partial V_\mathrm{tid}}{\partial Y}- \frac{\beta }{Z}\frac{\partial V_\mathrm{tid}}{\partial Z}= & {} \frac{4Gm}{5R^3}\epsilon _J \left[ \frac{1+\cos {2\theta _r}}{2} +\frac{X}{Z}\frac{\sin {2\theta _r}}{2}\right] , \end{aligned}$$

(42)

where

$$\begin{aligned} \epsilon _J = \frac{15MR^3}{4mr^3} \end{aligned}$$

(43)

is the equatorial flattening of a Jeans ellipsoid.

Appendix 2: The spatial resulting ellipsoid as a simple geometric composition

In this appendix, we demonstrate that, at the first order in flattenings, the simple geometric composition of the Jeans and the Maclaurin ellipsoids results in the same triaxial ellipsoid calculated in Sects. 2 and 3. In this way, the geometric sum of the heights of Jeans and the Maclaurin, each of these ellipsoids with a different axis of symmetry, produces a triaxial ellipsoid with the same flattenings and the same orientation of the equilibrium ellipsoid in the spatial case. This peculiar result is a consequence of the linearity of the deformations when they are small enough.

If $\delta \rho (\widehat{\theta },\widehat{\varphi })$, $\delta \rho _\mathrm{tid}(\widehat{\theta },\widehat{\varphi })$ and $\delta \rho _\mathrm{rot}(\widehat{\theta },\widehat{\varphi })$ are the distances of the surface point of the equilibrium ellipsoid, the Jeans ellipsoid and the Maclaurin ellipsoid, respectively, of coordinates $\widehat{\varphi }$ (longitude) and $\widehat{\theta }$ (co-latitude) in the body reference frame $\mathcal {F}_\mathcal {B}$ to the sphere of radius R, we use the expressions

$$\begin{aligned} \delta \rho = \delta \rho _\mathrm{tid}+\delta \rho _\mathrm{rot}, \end{aligned}$$

(44)

which is valid in the first order in flattenings. In order to proceed, we need to describe $\delta \rho$, $\delta \rho _\mathrm{tid}$ and $\delta \rho _\mathrm{rot}$ in the reference frame $\mathcal {F}_\mathcal {B}$.

We start with the description of the resulting ellipsoid $\delta \rho$. The semiaxes of this ellipsoid can be written as

$$\begin{aligned} a_\mathrm{m} = R\Big (1+\frac{\epsilon _\rho }{2}+\frac{\epsilon _z}{3}\Big ); \qquad b_\mathrm{m} = R\Big (1-\frac{\epsilon _\rho }{2}+\frac{\epsilon _z}{3}\Big ); \qquad c_\mathrm{m} = R\Big (1-\frac{2\epsilon _z}{3}\Big ), \end{aligned}$$

(45)

where $\epsilon _\rho$ and $\epsilon _z$ are the equatorial and the polar flattenings, in principle unknown and that we want to obtain. Equations (45) are equivalent, at the first order in flattenings, to those used in Eq. (8) and are valid, at the first order in flattenings, for any triaxial ellipsoid. (They are just consequences of the definitions used.)

The equation of surface of this homogeneous triaxial ellipsoid in $\mathcal {F}_\mathcal {B}$ is:

$$\begin{aligned} 1 = \frac{X^2}{a_\mathrm{m}^2}+\frac{Y^2}{b_\mathrm{m}^2}+\frac{Z^2}{c_\mathrm{m}^2}. \end{aligned}$$

(46)

If we use the semiaxes given by Eq. (45), the spherical coordinates

$$\begin{aligned} X=\rho \sin {\widehat{\theta }} \cos {\widehat{\varphi }}; \qquad Y=\rho \sin {\widehat{\theta }} \sin {\widehat{\varphi }}; \qquad Z=\rho \cos {\widehat{\theta }}, \end{aligned}$$

(47)

and expanding to the first order in the flattenings, we obtain

$$\begin{aligned} \rho (\widehat{\theta },\widehat{\varphi })=R\Big (1+\frac{\epsilon _\rho }{2}\sin ^2{\widehat{\theta }}\cos {2\widehat{\varphi }}+\epsilon _z\Big (\frac{1}{3}-\cos ^2{\widehat{\theta }}\Big )\Big ). \end{aligned}$$

(48)

Fig. 7

Polar section of the equilibrium spheroid corresponding to the tide generated by M on m (left) and corresponding to the rotation (right)

For the case of the tidal deformation $\delta \rho _\mathrm{tid}$, we use the Jeans ellipsoid (left panel of Fig. 7), where the equatorial and the polar flattenings are:

$$\begin{aligned} \epsilon _\rho ^{(\mathrm tid)} = \epsilon _J; \qquad \epsilon _z^{(\mathrm tid)} = \frac{\epsilon _J}{2}. \end{aligned}$$

(49)

Hence, the semiaxes of this ellipsoid can be written as

$$\begin{aligned} a_\mathrm{tid} = R\Big (1+\frac{2\epsilon _J}{3}\Big ); \qquad b_\mathrm{tid} = c_\mathrm{tid} = R\Big (1-\frac{\epsilon _J}{3}\Big ). \end{aligned}$$

(50)

The equation of surface of this homogeneous ellipsoid, in a reference frame $\mathcal {F}_r$ where the semiaxes $a_\mathrm{tid}$, $b_\mathrm{tid}$ and $c_\mathrm{tid}$ are aligned to the coordinates axes $X'_\mathrm{tid}$, $Y'_\mathrm{tid}$ and $Z'_\mathrm{tid}$, respectively, is:

$$\begin{aligned} 1 = \frac{X_\mathrm{tid}^{'2}}{a_\mathrm{tid}^2}+\frac{Y_\mathrm{tid}^{'2}}{b_\mathrm{tid}^2}+\frac{Z_\mathrm{tid}^{'2}}{c_\mathrm{tid}^2}. \end{aligned}$$

(51)

It is important to note that $X'_\mathrm{tid}$ is pointing toward the companion.

If $(X_\mathrm{tid},Y_\mathrm{tid},Z_\mathrm{tid})$, defining by

$$\begin{aligned} X_\mathrm{tid}=\rho _\mathrm{tid} \sin {\widehat{\theta }} \cos {\widehat{\varphi }}; \qquad Y_\mathrm{tid}=\rho _\mathrm{tid} \sin {\widehat{\theta }} \sin {\widehat{\varphi }}; \qquad Z_\mathrm{tid}=\rho _\mathrm{tid} \cos {\widehat{\theta }}, \end{aligned}$$

(52)

are the coordinates of the point $(X'_\mathrm{tid},Y'_\mathrm{tid},Z'_\mathrm{tid})$ in $\mathcal {F}_\mathcal {B}$, thus, using the rotation matrix around the second axis ${\mathsf {R}}_2(\delta )$, we obtain

$$\begin{aligned} X'_\mathrm{tid}= & {} X_\mathrm{tid}\cos {\delta }+Z_\mathrm{tid}\sin {\delta }\nonumber \\ Y'_\mathrm{tid}= & {} Y_\mathrm{tid} \nonumber \\ Z'_\mathrm{tid}= & {} -X_\mathrm{tid}\sin {\delta }+Z_\mathrm{tid}\cos {\delta }. \end{aligned}$$

(53)

Expanding to the first order in the flattenings, we obtain

$$\begin{aligned} \rho _\mathrm{tid}(\widehat{\theta },\widehat{\varphi })= & {} R\Big (1+\frac{\epsilon _J}{2}\frac{1+\cos {2\delta }}{2}\sin ^2{\widehat{\theta }}\cos {2\widehat{\varphi }}-\frac{3\epsilon _J}{4}\Big (\frac{1}{3}-\cos {2\delta }\Big )\Big (\frac{1}{3}-\cos ^2{\widehat{\theta }}\Big )\nonumber \\&\qquad +\frac{\epsilon _J}{4}\sin {2\delta }\sin {2\widehat{\theta }}\cos {\widehat{\varphi }}\Big ) \end{aligned}$$

(54)

For the case of the rotational deformation $\delta \rho _\mathrm{rot}$, we use the Maclaurin ellipsoid (right panel of Fig. 7), where the equatorial and the polar flattenings are:

$$\begin{aligned} \epsilon _\rho ^{(\mathrm rot)} = 0; \qquad \epsilon _z^{(\mathrm rot)} = \epsilon _M; \end{aligned}$$

(55)

thus, the semiaxes of this ellipsoid are

$$\begin{aligned} a_\mathrm{rot} = b_\mathrm{rot} = R\Big (1+\frac{\epsilon _M}{3}\Big ); \qquad c_\mathrm{rot} = R\Big (1-\frac{2\epsilon _M}{3}\Big ). \end{aligned}$$

(56)

The equation of surface of Maclaurin ellipsoid, in a reference frame $\mathcal {F}_\omega$ where the semiaxes $a_\mathrm{rot}$, $b_\mathrm{rot}$ and $c_\mathrm{rot}$ are aligned to the coordinates axes $X''_\mathrm{rot}$, $Y''_\mathrm{rot}$ and $Z''_\mathrm{rot}$, respectively, is:

$$\begin{aligned} 1 = \frac{X_\mathrm{rot}^{''2}}{a_\mathrm{rot}^2}+\frac{Y_\mathrm{rot}^{''2}}{b_\mathrm{rot}^2}+\frac{Z_\mathrm{rot}^{''2}}{c_\mathrm{rot}^2}. \end{aligned}$$

(57)

In this case, $Z''_\mathrm{rot}$ is parallel to the spin rate vector $\varvec{\omega }$.

If $(X_\mathrm{rot},Y_\mathrm{rot},Z_\mathrm{rot})$, defining by

$$\begin{aligned} X_\mathrm{rot}=\rho _\mathrm{rot} \sin {\widehat{\theta }} \cos {\widehat{\varphi }}; \qquad Y_\mathrm{rot}=\rho _\mathrm{rot} \sin {\widehat{\theta }} \sin {\widehat{\varphi }}; \qquad Z_\mathrm{rot}=\rho _\mathrm{rot} \cos {\widehat{\theta }}, \end{aligned}$$

(58)

are the coordinates of the point $(X''_\mathrm{rot},Y''_\mathrm{rot},Z''_\mathrm{rot})$ in $\mathcal {F}_\mathcal {B}$, thus, using the rotation matrix ${\mathsf {R}}_2(\theta +\delta -\pi /2)$, we obtain

$$\begin{aligned} X''_\mathrm{rot}= & {} X_\mathrm{rot}\sin {\theta _\mathcal {B}}-Z_\mathrm{rot}\cos {\theta _\mathcal {B}}\nonumber \\ Y''_\mathrm{rot}= & {} Y_\mathrm{rot} \nonumber \\ Z''_\mathrm{rot}= & {} X_\mathrm{rot}\cos {\theta _\mathcal {B}}+Z_\mathrm{rot}\sin {\theta _\mathcal {B}}, \end{aligned}$$

(59)

where $\theta _\mathcal {B}=\theta +\delta$.

Expanding to the first order in the flattenings, we obtain

$$\begin{aligned} \rho _\mathrm{rot}(\widehat{\theta },\widehat{\varphi })= & {} R\Big (1-\frac{\epsilon _M}{2}\frac{1+\cos {2\theta _\mathcal {B}}}{2}\sin ^2{\widehat{\theta }}\cos {2\widehat{\varphi }}+\frac{3\epsilon _M}{4}\Big (\frac{1}{3}-\cos {2\theta _\mathcal {B}}\Big )\Big (\frac{1}{3}-\cos ^2{\widehat{\theta }}\Big )\nonumber \\&\qquad -\frac{\epsilon _M}{4}\sin {2\theta _\mathcal {B}}\sin {2\widehat{\theta }}\cos {\widehat{\varphi }}\Big ). \end{aligned}$$

(60)

Finally, using Eqs. (44), (48), (54) and (60), by identification of the terms with same trigonometric arguments we obtain three equations for the flattenings $\epsilon _\rho$ and $\epsilon _z$ and the angle $\delta$:

$$\begin{aligned} \epsilon _\rho= & {} \frac{\epsilon _J-\epsilon _M}{2}+\frac{1}{2}\Big (\epsilon _J\cos {2\delta }-\epsilon _M\cos {2\theta _\mathcal {B}}\Big )\nonumber \\ \epsilon _z= & {} \frac{\epsilon _M-\epsilon _J}{4}+\frac{3}{4}\Big (\epsilon _J\cos {2\delta }-\epsilon _M\cos {2\theta _\mathcal {B}}\Big )\nonumber \\\nonumber \\ 0= & {} \epsilon _J\sin {2\delta }-\epsilon _M\sin {2\theta _\mathcal {B}}. \end{aligned}$$

(61)

The system of Eq. (61) is the same as that found in Sect. 3 (Eq. 11). Hence, the solution for the equatorial flattening for the polar flattening and for the angle of orientation is the same

$$\begin{aligned} \epsilon _\rho= & {} \frac{\epsilon _J-\epsilon _M}{2}+\frac{1}{2}\sqrt{\epsilon _J^2+\epsilon _M^2-2\epsilon _J\epsilon _M\cos {2\theta }}\nonumber \\ \epsilon _z= & {} \frac{\epsilon _M-\epsilon _J}{4}+\frac{3}{4}\sqrt{\epsilon _J^2+\epsilon _M^2-2\epsilon _J\epsilon _M\cos {2\theta }}, \end{aligned}$$

(62)

and

$$\begin{aligned} \cos {2\delta }=\frac{\epsilon _J-\epsilon _M\cos {2\theta }}{\sqrt{\epsilon _J^2+\epsilon _M^2-2\epsilon _J\epsilon _M\cos {2\theta }}};\qquad \sin {2\delta }=\frac{\epsilon _M\sin {2\theta }}{\sqrt{\epsilon _J^2+\epsilon _M^2-2\epsilon _J\epsilon _M\cos {2\theta }}}. \end{aligned}$$

(63)

Appendix 3: The ${\mathsf {B}}$-matrices

In this section, we show the derivation of the formulas of ${\mathsf {B}}_J$ and ${\mathsf {B}}_M$ matrices presented by Eq. (18), in Sect. 4. These matrices represent the non-dimensional form of the moment of quadrupole matrix (see Ragazzo and Ruiz, 2017) due to the rotational and the tidal deformation.

For this reason, we proceed by presenting the expressions for the principal moments of inertia $A<B<C$. From Eq. (8), the principal moments of inertia can be expressed in terms of the equatorial and the polar flattenings $\epsilon _\rho$ and $\epsilon _z$, respectively, and of the mean body radius $R=\root 3 \of {a_\mathrm{m}b_\mathrm{m}c_\mathrm{m}}$ of a general triaxial ellipsoid with semi-axes $a_\mathrm{m}<b_\mathrm{m}<c_\mathrm{m}$ as:

$$\begin{aligned} A= & {} \frac{1}{5}m(b_\mathrm{m}^2+c_\mathrm{m}^2) \approx I_0 \left( 1-\frac{\epsilon _\rho }{2}-\frac{\epsilon _z}{3}\right) \nonumber \\ B= & {} \frac{1}{5}m(a_\mathrm{m}^2+c_\mathrm{m}^2) \approx I_0 \left( 1+\frac{\epsilon _\rho }{2}-\frac{\epsilon _z}{3}\right) \nonumber \\ C= & {} \frac{1}{5}m(a_\mathrm{m}^2+b_\mathrm{m}^2) \approx I_0 \left( 1+\frac{2\epsilon _z}{3}\right) , \end{aligned}$$

(64)

where $I_0=\frac{2}{5}mR^2$. It is important to note that the rightmost expression in Eq. (64) is a linearization, so despite being valid for a general triaxial ellipsoid, it is only valid for ellipsoids with small flattening.

In the case in which only the deformation due to the tides is considered, the primary takes the shape of a Jeans ellipsoid (left panel of Fig. 7), where its equatorial vertex is pointing toward the companion and its equatorial and polar flattenings are:

$$\begin{aligned} \epsilon _\rho ^{(\mathrm tid)} = \epsilon _J; \qquad \epsilon _z^{(\mathrm tid)} = \frac{\epsilon _J}{2}. \end{aligned}$$

(65)

Thus, replacing Eq. (65) in Eq. (64), we obtain the principal moments of inertia of the Jeans ellipsoid:

$$\begin{aligned} A_\mathrm{tid} = R\Big (1-\frac{2\epsilon _J}{3}\Big ); \qquad B_\mathrm{tid} = C_\mathrm{tid} = R\Big (1+\frac{\epsilon _J}{3}\Big ). \end{aligned}$$

(66)

Hence, the inertia tensor, in a reference frame $\mathcal {F}_r$ where the semiaxes $a_\mathrm{tid}$, $b_\mathrm{tid}$ and $c_\mathrm{tid}$ are aligned to the coordinates axes $X'_\mathrm{tid}$, $Y'_\mathrm{tid}$ and $Z'_\mathrm{tid}$ (defined in the above appendix), respectively, is

$$\begin{aligned} {\mathsf {I}}_{\mathcal {F}_r}^\mathrm{tid} = I_0(\mathbb {I}-{\mathsf {B}}_{\mathcal {F}_\omega }^{(J)}), \end{aligned}$$

(67)

where the ${\mathsf {B}}_{\mathcal {F}_r}^{(J)}$ matrix in reference frame $\mathcal {F}_r$ is:

$$\begin{aligned} {\mathsf {B}}_{\mathcal {F}_r}^{(J)}= & {} \frac{\epsilon _J}{r^2}\left( \begin{array}{ccc} \frac{2}{3}r^2 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad -\frac{1}{3}r^2 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad -\frac{1}{3}r^2 \end{array} \right) . \end{aligned}$$

(68)

On the other hand, it is important to note that the radius vector $\varvec{r}_{\mathcal {F}_r}$ in reference frame $\mathcal {F}_r$ has the simple form:

$$\begin{aligned} \varvec{r}_{\mathcal {F}_r}=\left( \begin{array}{c} r \\ 0 \\ 0 \end{array} \right) . \end{aligned}$$

(69)

In order to describe the matrix ${\mathsf {B}}_J$ in a general inertial reference frame $\mathcal {F}_0$, we define the rotation matrix ${\mathsf {S}}$ as

$$\begin{aligned} {\mathsf {S}}= & {} {\mathsf {R}}_3(\varphi _0){\mathsf {R}}_2(\theta _0-\pi /2)=\left( \begin{array}{ccc} \sin {\theta _0}\cos {\varphi _0} &{} \quad -\sin {\varphi _0} &{} \quad -\cos {\theta _0}\cos {\varphi _0} \\ \sin {\theta _0}\sin {\varphi _0} &{} \quad \cos {\varphi _0} &{} \quad -\cos {\theta _0}\sin {\varphi _0} \\ \cos {\theta _0} &{} \quad 0 &{} \quad \sin {\theta _0}\end{array} \right) , \end{aligned}$$

(70)

where $\theta _0,\varphi _0$ are the co-latitude and the longitude of the companion with respect to $\mathcal {F}_0$.

${\mathsf {R}}_2$ and ${\mathsf {R}}_3$ represent the rotation matrices around the second and third axis, respectively:

$$\begin{aligned} {\mathsf {R}}_2(\alpha ) = \left( \begin{array}{ccc} \cos {\alpha } &{} \quad 0 &{} \quad \sin {\alpha } \\ 0 &{} \quad 1 &{} \quad 0 \\ -\sin {\alpha } &{} \quad 0 &{} \quad \cos {\alpha } \end{array} \right) ; \qquad {\mathsf {R}}_3(\alpha ) = \left( \begin{array}{ccc} \cos {\alpha } &{} \quad -\sin {\alpha } &{} \quad 0 \\ \sin {\alpha } &{} \quad \cos {\alpha } &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 1\end{array} \right) . \end{aligned}$$

(71)

Therefore, inertia tensor and the radius vector in ${\mathcal {F}_0}$ are

(72)

and

$$\begin{aligned} \varvec{r}_{\mathcal {F}_0}\;\buildrel \hbox { def}\over {\,=\;}\varvec{r}= & {} {\mathsf {S}}\varvec{r}_{\mathcal {F}_r}=\left( \begin{array}{ccc} r\sin {\theta _0}\cos {\varphi _0} \\ r\sin {\theta _0}\sin {\varphi _0} \\ r\cos {\theta _0} \end{array} \right) = \left( \begin{array}{c} x \\ y \\ z \end{array} \right) , \end{aligned}$$

(73)

respectively.

Therefore, the matrix ${\mathsf {S}}{\mathsf {B}}_{\mathcal {F}_r}^{(J)}{\mathsf {S}}^{-1}$ is ${\mathsf {B}}_{\mathcal {F}_0}^{(J)}\;\buildrel \hbox { def}\over {\,=\;}{\mathsf {B}}_J$ in reference frame $\mathcal {F}_0$:

$$\begin{aligned} {\mathsf {B}}_J= & {} {\mathsf {S}}{\mathsf {B}}_{\mathcal {F}_r}^{(J)}{\mathsf {S}}^{-1}\nonumber \\= & {} \frac{\epsilon _J}{r^2}\left( \begin{array}{ccc} r^2 \sin ^2{\theta _0} \cos ^2{\varphi _0}-\frac{1}{3}r^2 &{} \quad r^2\sin ^2{\theta _0}\sin {\varphi _0}\cos {\varphi _0} &{} \quad r^2\cos {\theta _0}\sin {\theta _0}\cos {\varphi _0} \\ r^2\sin ^2{\theta _0}\sin {\varphi _0}\cos {\varphi _0} &{} \quad r^2 \sin ^2{\theta _0} \sin ^2{\varphi _0}-\frac{1}{3}r^2 &{} \quad r^2\cos {\theta _0}\sin {\theta _0}\sin {\varphi _0} \\ r^2\cos {\theta _0}\sin {\theta _0}\cos {\varphi _0} &{} \quad r^2\cos {\theta _0}\sin {\theta _0}\sin {\varphi _0} &{} \quad r^2 \cos ^2{\theta _0}-\frac{1}{3}r^2 \end{array} \right) \nonumber \\= & {} \frac{\epsilon _J}{r^2}\left( \begin{array}{ccc} x^2-\frac{1}{3}r^2 &{} \quad xy &{} \quad xz \\ yx &{} \quad y^2-\frac{1}{3}r^2 &{} \quad yz \\ zx &{} \quad zy &{} \quad z^2-\frac{1}{3}r^2 \end{array} \right) = \frac{\epsilon _J}{r^2}\Big (\varvec{r}\otimes \varvec{r}-\frac{r^2}{3}\mathbb {I} \Big ). \end{aligned}$$

(74)

In the case in which only the deformation due to the rotation is considered, the primary takes the shape of a Maclaurin ellipsoid (right panel of Fig. 7), where its axial axis of symmetry is parallel to the angular velocity vector and its equatorial and polar flattenings are:

$$\begin{aligned} \epsilon _\rho ^{(\mathrm rot)} = 0; \qquad \epsilon _z^{(\mathrm rot)} = \epsilon _M. \end{aligned}$$

(75)

Thus, replacing Eq. (75) in Eq. (64), we obtain the principal moments of inertia of the Maclaurin ellipsoid:

$$\begin{aligned} A_\mathrm{rot} = B_\mathrm{rot} = I_0\Big (1-\frac{\epsilon _M}{3}\Big ); \qquad C_\mathrm{rot} = I_0\Big (1+\frac{2\epsilon _M}{3}\Big ). \end{aligned}$$

(76)

Hence, the inertia tensor, in a reference frame $\mathcal {F}_\omega$ where the semiaxes $a_\mathrm{rot}$, $b_\mathrm{rot}$ and $c_\mathrm{rot}$ are aligned to the coordinates axes $X''_\mathrm{rot}$, $Y''_\mathrm{rot}$ and $Z''_\mathrm{rot}$ (defined in the above appendix), respectively, is

$$\begin{aligned} {\mathsf {I}}_{\mathcal {F}_\omega }^\mathrm{(rot)} = I_0(\mathbb {I}-{\mathsf {B}}_{\mathcal {F}_\omega }^{(M)}) \end{aligned}$$

(77)

where the ${\mathsf {B}}_{\mathcal {F}_\omega }^{(M)}$ matrix in reference frame $\mathcal {F}_\omega$ is:

$$\begin{aligned} {\mathsf {B}}_{\mathcal {F}_\omega }^{(M)}= & {} \frac{\epsilon _M}{\omega ^2}\left( \begin{array}{ccc} \frac{1}{3}\omega ^2 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad \frac{1}{3}\omega ^2 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad -\frac{2}{3}\omega ^2 \end{array} \right) . \end{aligned}$$

(78)

On the other hand, it is important to note that the angular velocity vector $\varvec{\omega }_{\mathcal {F}_\omega }$ in reference frame $\mathcal {F}_\omega$ has the simple form:

$$\begin{aligned} \varvec{\omega }_{\mathcal {F}_\omega }=\left( \begin{array}{c} 0 \\ 0 \\ \omega \end{array} \right) . \end{aligned}$$

(79)

In order to describe the matrix ${\mathsf {B}}_M$ in a general inertial reference frame $\mathcal {F}_\omega$, we define the rotation matrix ${\mathsf {R}}$ as

$$\begin{aligned} {\mathsf {R}}= & {} {\mathsf {R}}_3(\psi ){\mathsf {R}}_1(J) =\left( \begin{array}{ccc} \cos {\psi } &{} \quad -\cos {J}\sin {\psi } &{} \quad \sin {J}\sin {\psi } \\ \sin {\psi } &{} \quad \cos {J}\cos {\psi } &{} \quad -\sin {J}\cos {\psi } \\ 0 &{} \quad \sin {J} &{} \quad \cos {J} \end{array} \right) , \end{aligned}$$

(80)

where J is the inclination of the equatorial plane of the primary (defined as the plane perpendicular to the angular velocity vector) with respect to the $x_0-y_0$ inertial plane, and $\psi$ is the longitude of the ascending node of the rotational equator.

${\mathsf {R}}_1$ and ${\mathsf {R}}_3$ represent the rotation matrices around the first and third axis, respectively:

$$\begin{aligned} {\mathsf {R}}_1(\alpha ) = \left( \begin{array}{ccc} 1 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad \cos {\alpha } &{} \quad -\sin {\alpha } \\ 0 &{} \quad \sin {\alpha } &{} \quad \cos {\alpha } \end{array} \right) . \end{aligned}$$

(81)

Therefore, inertia tensor and the angular velocity vector in ${\mathcal {F}_0}$ are

$$\begin{aligned} {\mathsf {I}}_{\mathcal {F}_0}^\mathrm{(rot)}\;\buildrel \hbox { def}\over {\,=\;}{\mathsf {I}}_\mathrm{rot}= & {} {\mathsf {R}}{\mathsf {I}}_{\mathcal {F}_\omega }^\mathrm{(rot)}{\mathsf {R}}^{-1}\nonumber \\= & {} I_0\big (\mathbb {I}-{\mathsf {R}}{\mathsf {B}}_{\mathcal {F}_\omega }^{(M)}{\mathsf {R}}^{-1}\big ), \end{aligned}$$

(82)

and

$$\begin{aligned} \varvec{\omega }_{\mathcal {F}_0}\;\buildrel \hbox { def}\over {\,=\;}\varvec{\omega }= & {} {\mathsf {R}}\varvec{\omega }_{\mathcal {F}_\omega }=\left( \begin{array}{ccc} \omega \sin {J}\sin {\psi } \\ -\omega \sin {J}\cos {\psi } \\ \omega \cos {J} \end{array} \right) = \left( \begin{array}{c} \omega _x \\ \omega _y \\ \omega _z \end{array} \right) , \end{aligned}$$

(83)

respectively.

Therefore, the matrix ${\mathsf {R}}{\mathsf {B}}_{\mathcal {F}_\omega }^{(M)}{\mathsf {R}}^{-1}$ is ${\mathsf {B}}_{\mathcal {F}_0}^{(M)}\;\buildrel \hbox { def}\over {\,=\;}{\mathsf {B}}_M$ in reference frame $\mathcal {F}_0$:

$$\begin{aligned} {\mathsf {B}}_M= & {} {\mathsf {R}}{\mathsf {B}}_{\mathcal {F}_\omega }^{(M)}{\mathsf {R}}^{-1}\nonumber \\= & {} \frac{\epsilon _M}{\omega ^2}\left( \begin{array}{ccc} \frac{1}{3}\omega ^2 -\omega ^2 \sin ^2{J} \sin ^2{\psi } &{} \quad \omega ^2\sin ^2{J}\sin {\psi }\cos {\psi } &{} \quad -\omega ^2\cos {J}\sin {J}\sin {\psi } \\ \omega ^2\sin ^2{J}\sin {\psi }\cos {\psi } &{} \quad \frac{1}{3}\omega ^2 -\omega ^2 \sin ^2{J} \cos ^2{\psi } &{} \quad \omega ^2\cos {J}\sin {J}\cos {\psi } \\ -\omega ^2\cos {J}\sin {J}\sin {\psi } &{} \quad \omega ^2\cos {J}\sin {J}\cos {\psi } &{} \quad \frac{1}{3}\omega ^2 -\omega ^2 \cos ^2{J} \end{array} \right) \nonumber \\= & {} \frac{\epsilon _M}{\omega ^2}\left( \begin{array}{ccc} \frac{1}{3}\omega ^2 -\omega _x^2 &{} \quad -\omega _x\omega _y &{} \quad -\omega _x\omega _z \\ -\omega _y\omega _x &{} \quad \frac{1}{3}\omega ^2 -\omega _y^2 &{} \quad -\omega _y\omega _z \\ -\omega _z\omega _x &{} \quad -\omega _z\omega _y &{} \quad \frac{1}{3}\omega ^2 -\omega _z^2 \end{array} \right) = \frac{\epsilon _M}{\omega ^2}\Big (\frac{\omega ^2}{3}\mathbb {I} - \varvec{\omega }\otimes \varvec{\omega }\Big ). \end{aligned}$$

(84)

Finally, and as a consequence of the linearity of the deformations shown in the previous section (that is, when these deformations are small enough for the linear expansions in the flattening to be valid), the inertial tensor of a body deformed by the action of the tides and the rotation in the inertial reference frame $\mathcal {F}_0$ can be written as the sum of the two components presented in this section:

$$\begin{aligned} {\mathsf {I}}_{\mathcal {F}_0}\;\buildrel \hbox { def}\over {\,=\;}{\mathsf {I}} = I_0(\mathbb {I}-{\mathsf {B}}_J-{\mathsf {B}}_M). \end{aligned}$$

(85)