Abstract
We describe a comprehensive model for systems locked in the Laplace resonance. The framework is based on the simplest possible dynamical structure provided by the Keplerian problem perturbed by the resonant coupling truncated at second order in the eccentricities. The reduced Hamiltonian, constructed by a transformation to resonant coordinates, is then submitted to a suitable ordering of the terms and to the study of its equilibria. Henceforth, resonant normal forms are computed. The main result is the identification of two different classes of equilibria. In the first class, only one kind of stable equilibrium is present: the paradigmatic case is that of the Galilean system. In the second class, three kinds of stable equilibria are possible and at least one of them is characterised by a high value of the forced eccentricity for the ‘first planet’: here, the paradigmatic case is the exo-planetary system GJ-876, in which the combination of libration centres admits triple conjunctions otherwise not possible in the Galilean case. The normal form obtained by averaging with respect to the free eccentricity oscillations describes the libration of the Laplace argument for arbitrary amplitudes and allows us to determine the libration width of the resonance. The agreement of the analytic predictions with the numerical integration of the toy models is very good.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Multi-resonant planetary problems are extremely interesting both for theory and applications. The prototypical example is given by the system composed of Jupiter and its first three Galilean satellites, Io, Europa and Ganymede. The satellites are phase-locked into the so-called Laplace resonance (Ferraz-Mello 1979; Murray and Dermott 1999). This implies the ratio 4:2:1 of the mean motions and a fixed value of the relative precession of the peri-Joves of Io and Europa. Another well-known example is GJ-876 (Rivera et al. 2010) which is an exo-planetary system with the same multi-resonant structure. Other extrasolar systems with the same mean motion resonances are under investigation (Morbidelli 2013; Pichierri et al. 2019) in the ever-growing census of these systems (see, for example, Fabrycky et al. 2014). However, multi-resonant systems are not so common (Batygin 2015) even with more general resonant combinations (Gallardo et al. 2016), implying complex general questions about their origin and stability, in particular in the case of compact systems.
The motion of the Galilean system is characterised by a regular behaviour: out of the four resonant angles combining longitudes and arguments of peri-Joves, three are librating with small amplitudes and one is rotating (Showman and Malhotra 1997) with almost constant angular velocity. On the other hand, the same resonant angle is reported to have a chaotic evolution in the case of GJ-876 (Batygin et al. 2015; Nelson et al. 2016). It is therefore important to understand the structure of the regular part of phase space and the possible origins of chaotic dynamics. Moreover, the long-term evolution of these systems is affected by dissipative effects (Yoder and Peale 1981; Batygin and Morbidelli 2013b; Pichierri et al. 2019): actually, in the Galilean system, the coupling between tides and the internal dynamics plays an essential role in the approach to the resonance and its subsequent evolution. The fundamental work of Yoder and Peale Yoder and Peale (1981) introduced an analytical model, and subsequent studies (Henrard 1983; Malhotra 1991; Showman and Malhotra 1997; Lari et al. 2020) have extended the treatment with semi-analytical or numerical methods. To have a simple but reliable model for the conservative dynamics may offer clues to investigate also the cases in which non-conservative effects have different origins like in protoplanetary disks.
The purpose of this work is to elaborate on the following two problems:
-
1.
All analytical and numerical computations so far (Lieske 1977; Hadjidemetriou and Michalodimitrakis 1981; Musotto et al. 2002; Lainey et al. 2004a, b) show that the Laplace resonance is quite stable but at the same time very sensitive to the values of orbital elements. The first question is therefore to be able to predict the extent of the resonance domain, that is to devise a reduction process able to identify and compute the width of the resonance in terms of the parameters of the system.
-
2.
The Laplace status of the Galilean satellites is very well understood and described in terms of three combination angles librating around an equilibrium value: however, these equilibrium values (or their symmetric equivalent) are clearly different from those reported for the GJ-876 system (Rivera et al. 2010; Nelson et al. 2016). This discrepancy raises issues concerning the stability of this configuration. The second question we want to address refers therefore to the possibility of predicting the location and nature of the equilibria in terms of the parameters of the system, in order to interpret the status of this and other possible configurations.
As said above, there is a fourth combination angle which could also librate but is observed to rotate in the real Galilean system. The configuration in which all four combinations librate is known as de Sitter equilibrium (de Sitter 1931; Broer and Hanßmann 2016; Broer and Zhao 2017; Celletti et al. 2018). Therefore, another question related to point 2 above is why the observed systems are not in the de Sitter equilibrium and how to predict the possible regular/chaotic regimes of the involved arguments. The model we study is strictly related to the classical basic ones, starting from the seminal works of Sinclair Sinclair (1975) and Ferraz-Mello Ferraz-Mello (1979) and elaborated mainly by Henrard Henrard (1982, 1984) and Malhotra Malhotra (1991). It closely follows the applications done in (Celletti et al. 2018; Paita et al. 2018) and generalised in (Celletti et al. 2019). The substantial difference in the present approach is to modify the choice of variables adapted to the resonance and to convert the system to a slowly perturbed chain of forced harmonic oscillators.
Actually, the study of mean-motion resonances is one of the pillars of Celestial Mechanics (Poincaré 1902; Schubart 1964; Wisdom 1980; Henrard and Lemaître 1983) which should now be standard textbook material (Murray and Dermott 1999; Morbidelli 2002; Ferraz-Mello 2007). However, the intricacies of resonant dynamics often require dedicated expansions and coordinate transformations (Henrard et al. 1986; Moons 1994; Michtchenko et al. 2006; Batygin and Morbidelli 2013a; Pichierri et al. 2018) for perturbative applications. We have endeavoured to find a framework better suited to first-order multi-resonant planetary problems. The main advantage is to have a suitable action conjugated with the Laplace argument to be used in the construction of a resonant normal form. This leads to a direct evaluation of the libration frequency and of the resonance width. Moreover, with this coordinate choice it is easier to analyse the forced equilibria by finding an efficient strategy to locate additional solutions with respect to the classical ones (de Sitter 1931; Sinclair 1975).
We validate this approach by applying it to the two reference systems mentioned above, the Galilean satellites and the GJ-876 system. They result in two toy models limited to second-order expansions in the eccentricities so to reduce as much as possible mathematical complexity. The Galilean case is already described quite faithfully at first order and possible discrepancies between predictions of the model and observations are only quantitative; they can be reduced with higher-order expansions. In the exo-planetary instance, the first-order model is able to predict several peculiarities: in particular, the different nature of the Laplace dynamics (when compared to the Galilean system) and the high values of the forced eccentricities. However, the reported libration centres are correctly predicted by the model only when including second-order terms in the eccentricities.
The plan of the paper is as follows: in Sect. 2 is presented the basic starting Hamiltonian model; in Sect. 3 the truncated series of the model is set with a suitable book-keeping order and are determined its equilibrium solutions; in Sect. 4 are computed the Laplace normal form and its variants; in Sect. 5 the model is applied to observed systems; in Sect. 6 conclusions are drawn.
2 The simplified starting model
We consider a 1 + 3-body self-gravitating system in which three ‘planets’ of mass \(m_k, k=1,2,3\) are orbiting around a ‘star’ \(m_0\) with mean motions close to the ratios \(n_1 / n_2 = n_2 / n_3 = 2\). We work in modified Delaunay variables
and, in the usual case of small eccentricities, almost always we will assume that
Using a Jacobi coordinate system (Henrard 1984), the Kepler part of the Hamiltonian is given by
where \(a_k \) are the semi-major axes, the \(L_k\) are defined as
and
with \(M_0=Gm_0\) and
In order to implement normalisation, it is useful to expand the Keplerian part as follows (Batygin and Morbidelli 2013a)
\({\overline{L}}_k\) are three ‘nominal’ values of the first actions and
are evaluated at nominal values. Exactly resonant mean motions such that
would provide the set of resonant nominal actions, but we remark that the choice of nominal elements is rather arbitrary and we could as well choose not strictly resonant mean motions. Pros and cons of these choices have been the subject of detailed analyses in several papers devoted to mean-motion resonances for which we refer to Batygin and Morbidelli Batygin and Morbidelli (2013a) and references therein.
The disturbing function, as usual in the general case of first-order resonances (Ferraz-Mello 1979; Batygin and Morbidelli 2013b; Papaloizou 2015), is limited to the first-order terms in the expansion in the eccentricities \(e_k\). After averaging with respect to the non-resonant angles, we keep the terms in the following sum:
where the coefficients \({B_0}\) and \(f_k\) are defined as
and the \(b_{s}^{(j)}(\rho )\) are the Laplace coefficients (Murray and Dermott 1999), with the ratios \(\rho _{ik}=\overline{a}_i / \overline{a}_k, (i,k=1,2,3)\) usually fixed at their nominal values. We will scale physical units by choosing units of time and length such that \(Gm_0=1\) and \(a_1=1\), and therefore, it is natural to introduce the parameters
2.1 Henrard–Malhotra variables
We assume that the disturbing function is expressed in terms of modified Delaunay variables. With an aim to investigate the Laplace resonance, it is customary to use the followingFootnote 1Henrard–Malhotra coordinate transformation \((L_k, P_k, \lambda _k, p_k) \longrightarrow (Q_{\alpha }, q_{\alpha }), \alpha =1,\ldots ,6,\) (Henrard 1984; Malhotra 1991),
which takes into account the resonant combinations of the angles. The list of the old L-actions in terms of the new ones is
With this transformation, the model can be expressed as
where it is made clear that now the dependence on the new angles is such that \(q_5,q_6\) are cyclic and therefore \(Q_5,Q_6\) are integrals of motion (\(Q_6\) is the total angular momentum). Among the non-trivial momenta \(Q_a, \; a=1,\ldots ,4\), the first three, being equal to the \(P_k\), are ‘small’ quantities. From (16) it is evident that \(Q_4\) is instead of the order of \(L_2\). We are therefore led to introduce also nominal valuesFootnote 2 for the \(P_k\), say \({\overline{P}}_k\), such that
where \( {\widehat{Q}}_4\) is ‘small’. Accordingly, the three terms in the Hamiltonian (22) can be written as
In the linear part, \(H_0^{HM}\), the new frequencies
appear. The quadratic part \(H_1^{HM}\) accounts for the nonlinear dependence on the actions. In the third term, the angle-dependent part \(H_2^{HM}\), the nominal values of the \(L_k\) are used so that, using (8–11), the coupling parameters
are introduced.
2.2 Modified Henrard–Malhotra variables
The basic structure of the model is that sketched above: we have a Hamiltonian which is the sum of the Keplerian expansion up to second order and a coupling part depending also on resonant combination angles. The magnitude of these terms is ordered in a natural way and the resonant angles determine the form of the canonical transformation to variables adapted to the resonance. However, the transformation introduced in Henrard (1984) is not unique: in the paper on his version of the model on the tidal evolution of the Galilean satellites, Henrard Henrard (1983) himself uses a different form of the action conjugated to new cyclic angles and therefore to different choices of the conserved actions. For our model, we will instead employ a modified Henrard–Malhotra (MHM) coordinate system in which the momentum \(Q_4\), whose dynamical meaning is a little obscure, is replaced by
which is more naturally associated with the conjugate angle \(\lambda =q_4\). Using for simplicity the same notation of the previous section for the unchanged variables, the MHM coordinate set is given by
where the new angles are
Now we have
and the angles \(q_5^M,q_6^M\) are again cyclic with the same associated integrals of motion \(Q_5,Q_6\) as before in the original transformation. In the MHM coordinate set, the list of the old L-actions in terms of the new ones is
By using the MHM set and introducing the ‘angular momentum deficit’ (Laskar 1997, 2000; Laskar and Petit 2017)
the three terms in the Hamiltonian (22) now are
In the resonant part, with a slight abuse of notation, we have left the standard ‘third’ combination angle \(q_3\) in place of \(q_3^M - q_4\). In the linear part, \(H_0^M\), the new frequencies
appear. These new frequencies seem odd if compared with (27–28), in which the resonant combinations of mean motions are varied exclusively in terms of the small quantities \({\overline{P}}_k\). \(\kappa _1^M,\kappa _4^M\) rather depend on the ‘large’ quantities \( {\overline{L}}_k, Q_5, Q_6 \). This apparent shortcoming is due to the fact that, in the modified transformation, we did not impose the condition that the fourth momentum is a small quantity obtained by a variation analogous to the introduction of \( {\widehat{Q}}_4\). The advantage of this choice roots into the special dynamical role played by the new momentum as will appear clear in the following. Therefore, we keep the definition of these frequencies by taking into account that the issue refers to the role of \(Q_5, Q_6 \) themselves. Being them integrals of motion, they can be considered as arbitrary parameters of the model. However, the initial conditions of a given solution fix the value of the integrals of motion, and we are interested essentially in initial conditions which are sufficiently close to the resonance. A simple choice could be that of fixing the integrals at nominal values of the elements. However, in the implementation of the model this turns out to be over-restrictive, since it places the unperturbed system at exact resonance producing, as we see in the following, the dynamical instability of the perturbed one. In order to be able to explore the proximity to the resonance, we have found that the best choice is that of fixing nominal resonant values for the mean motions used in the Keplerian expansion, but to leave free the values of \(Q_5, Q_6 \) as they are fixed by realistic initial conditions. In this way, (45–46) take the simplified form
2.3 Poincaré variables
By using Poincaré variables \(x_k, y_k \; (k=1,2,3)\) defined as
the angular momentum deficit can be written as
Hamiltonian (22) is then changed into
where, for the MHM coordinate set, we get
and we have introduced the shorthand symbols:
3 Book-keeping order of the modified model and its equilibria
Hamiltonian (51) has a nice ‘perturbed oscillators’ form which promises to be quite simple to use. This setting is reminiscent of that proposed by Sagnier (1975) and Brown (1977). However, in order to proceed with the analysis of the dynamics it is useful to perform an appropriate book-keeping of the various terms. At the basis of every perturbative approach, there is a decision about the relative weight of small terms defining the perturbation. Here there are at least two sources of ‘smallness’: the ratio of masses of the orbiting bodies over that of the central body and the eccentricities. The model can be considered of first order with respect to both: therefore, in order to simplify things, a unique order parameter is used, making care of pointing out possible cases in which this is no more consistent.
3.1 Book-keeping order
We see that, in principle, the following hierarchy can be established among variables and control parameters (from now on, to lighten notation, we suppress the M index, except for the angle \(q_3^M\) which is important to distinguish from the original \(q_3\)):
-
Zero-order quantities \(\Lambda ; \kappa _1, \kappa _4, \eta _k, k=1,2,3;\)
-
First-order quantities \(x_k, y_k; \alpha , \beta _1, \beta _2, \gamma ;\)
-
Second-order quantities \(Q_k = \left( x_k^2 + y_k^2 \right) /2.\)
The order can be represented by the power of a book-keeping parameter, say \(\sigma \): so a term of Nth-order is multiplied by the label \(\sigma ^N\). In view of this ordering, we rearrange the model Hamiltonian in the following form:
with
It is then useful to write the equations of motion
where the symplectic form
has been exploited, for each order term. Coherently with the book-keeping introduced above, we can write the series:
At zero order, we get:
At first order, equations (62) are:
and at second order, we can consider only
3.2 De Sitter equilibria
Let us denote with \(X_k,Y_k,\Lambda _E,\lambda _E\) the equilibrium values of the \(x_k, y_k\) and the pair \(\Lambda ,\lambda \), assuming a series in \(\sigma \) also for these quantities.
We immediately find a simple approximation of the de Sitter equilibria in the form of the zero-order solution to \(\dot{\lambda }^{(0)} = 0\) provided by (69)
and to \( \dot{x}_k^{(1)} = \dot{y}_k^{(1)}=0\) given by (7071727374)–(75):
with, respectively, \(\lambda _E^{(0)}=\pi \) and \(\lambda _E^{(0)}=0\). (We will see that the first case plays a special role.) The new ‘slow’ frequency
has been introduced and readily, the first-order correction for \(\Lambda _E,\lambda _E\) is obtained from (76) and from (77), with vanishing left-hand side at equilibrium:
In these expressions, where different signs appear, they, respectively, correspond either to \(\lambda =\pi \) (those with the upper sign) or to \(\lambda =0\) (lower sign): we keep this convention in all results obtained in the following. We have also to remark that \(\omega \) is usually smaller than \(\kappa _1, \kappa _4\): however, even smaller characteristic frequencies will appear in the process of normalisation, so that we could better say that \(\omega \) is semi-slow. Moreover, we assume overall that \(\omega \) does not vanish: this excludes the singular occurrence of exact resonance and is justified by the stability analysis implemented in the following subsection. The higher-order correction \(x_j^{(3)}\) can be obtained by solving the third-order equations
At equilibrium, they give
These solutions can be interpreted as the equilibrium values of the \(x_k, y_k\) providing the forced eccentricities. The zero-order terms (79–84) are dominant, so their sign allows us to identify the libration centres (if any) for the resonant combinations. Since the coupling parameters \(\alpha ,\beta _1,\beta _2,\gamma \) have definite signs (Batygin and Morbidelli 2013b) for any reasonable combination of physical quantities, it is the sign of \(\omega \) which produces different possibilities: this result agrees with what was already obtained by de Sitter de Sitter (1931) and Sinclair Sinclair (1975), and in the following we will refer to these solutions as de Sitter–Sinclair equilibria. The updated solutions can therefore be written in the form
where
We can, however, inquire about a possibility not included in this perturbative approach: one (or more) of the forced eccentricities can be so big to violate the book-keeping hierarchy assumed above. In this respect, we have to consider the case that also this quantity must be taken as a zero-order term in the book-keeping parameter and we are required to take into account also second-order terms in the eccentricities. These are described by the quadratic form (Henrard 1982; Malhotra 1991; Showman and Malhotra 1997; Celletti et al. 2019)
where the multi-indexes \(x^n = x_1^{n_1}x_2^{n_2}x_3^{n_3}, y^m = y_1^{m_1}y_2^{m_2}y_3^{m_3}\) are used and the \(\alpha _{\ell nm}\) are coupling constants, first order in the mass ratios, suitable generalisations of (293031)-(32). In other words, we can look for additional solutions to the three equations
where (90) has been inserted into the equilibrium conditions still considering the \(X_k\) as unknown and shorthand notation has been used for the non-vanishing coupling constants. In order to test this possibility, let us assume that there exist additional equilibrium solutions with, for example, \(X_1 \gg X_2,X_3\). By using this condition in (92), we get
where now only \({\varvec{\alpha }}\) and \(\alpha _2\), defined as
are assumed to be small parameters. This cubic can indeed have three real solutions if its discriminant is positive and they can be explicitly written down (Lemaître 2010). However, in view of the structure of the equation, we can proceed in a simpler way, looking now for solutions of the form
To order zero in \(\sigma \), we get the three solutions
and
The first of these provides again \(X_1^{(1)} = \alpha /\omega \), namely (7980) already obtained above. But, if the argument of the square root is positive, we obtain two new solutions:
Since, recalling (55–57) and the definition in (95), K is always positive, the necessary condition for these new solutions is strictly
whereas we recall that the de Sitter–Sinclair solution allowed for both signs of \(\omega \). With this result plugged in the other two equations (93) and (94) (still under the assumption \(X_1 \gg X_2,X_3\)) we get the new solutions
and
to be, respectively, added to (8182) and (83). In every cases, the equilibrium value of the \(Y_k\) is still zero. The relevant coupling constants appearing in the new solutions are
where \(f_3\) is defined in (96) and
We remark that exact solutions of the cubic can be explicitly computed. However, this would still be an incomplete representation of the whole set whose algebraic expression is very involved. Moreover, in order to not overload the notation, we have considered together solutions corresponding to both \(\lambda =\pi \) and \(\lambda =0\). In practice, a direct numerical solution of the equilibrium equations will be performed specifying to which kind of equilibrium one is referring to. What is important now is to highlight the existence of additional possible equilibria with respect to the well-known de Sitter–Sinclair ones. We will refer to these new equilibria as new de Sitter solutions. We will see later if they actually play some relevant role.
3.3 Stability of the de Sitter equilibria
A stability analysis of these equilibria can be performed with standard techniques and compared with other numerical (Hadjidemetriou and Michalodimitrakis 1981; Yoder and Peale 1981) and analytical (Sinclair 1975; Broer and Zhao 2017) studies. Collectively denoting with z the set \((x_k, y_k,\Lambda ,\lambda )\), we consider the linear Hamiltonian equations providing the variational system (Yoder and Peale 1981)
Looking for solutions of the form
we have to compute the eigenvalues of the Hamiltonian matrix in (107). The case of the first class of de Sitter–Sinclair equilibria (78)–(84) can be treated explicitly. We have to compute the eigenvalues of the matrix
Like before, where different signs appear, they, respectively, correspond either to \(\lambda =\pi \) (upper sign) or to \(\lambda =0\) (lower sign). The eigenvalues \(\mu _a, \, a=1,\ldots ,8,\) are the solutions of the characteristic equation
which has the form
The explicit expression of the solution is too cumbersome to be reproduced here. However, the stability property can still be described working only with the determinant of the matrix itself which is
A pair of eigenvalues \(\pm i \omega \) is already factored out in (109). Three other pairs remain, which, for a Hamiltonian matrix, are either pure imaginary or real and opposite. Therefore, a sufficient condition for instability is that the determinants are negative: in practice, this condition is also necessary, because only one pair of real eigenvalues appear in standard cases. By using (7980)–(84) the determinants in the two cases can be rewritten as
It is straightforward to check that \( \beta _1 \beta _2 <0\) for every reasonable choice of parameters; therefore, a sufficient condition for instability is
in the first case (\(\lambda =\pi \)) and \(\omega < \omega _U\) in the second case. We remark that these findings agree with Sinclair Sinclair (1975) results. The analytical evaluation of the instability transition in the case of the new de Sitter equilibria is much more involved. However, direct numerical computation of the eigenvalues can be easily performed to predict the stability properties of the additional solutions.
4 Normal forms
4.1 Previous attempts at normalisation
A 4-DOF multi-resonant system shows intricate dynamics. There have been some previous works producing simplified models. We first mention the works by Ferraz-Mello Ferraz-Mello (1979),Malhotra Malhotra (1991) and Showman and Malhotra Showman and Malhotra (1997), in which a quite general model for the Galilean system (including dissipation) is presented and solved in terms of ‘variational’ solutions. Averaging methods have been henceforth applied in several variants (Batygin et al. 2015; Martí et al. 2016; Lari 2018). However, they always result in non-integrable systems and, in the end, worth of numerical evaluations only.
A more effective approach is that of constructing a ‘normal form’ which captures the resonant dynamics by means of a near-identity canonical transformation. This is usually generated by enforcing the commutation of the new Hamiltonian with a predefinite integrable part. With suitable assumptions and restrictions, integrability can be extended to the normal form itself. Extending integrability breaks when more than one exact resonances are present, although an approximate integrable Hamiltonian can be constructed in some cases (Hadden 2019), so even in the multi-resonant case a resonant normal form provides several useful information.
A remarkable attempt is due to Henrard Henrard (1984) who constructed a normal form by eliminating all angles but the Laplace argument \(\lambda \). His aim was to have an analytical tool to explore models of capture in which the libration of the Laplace argument may not necessarily be small. We observe that, even without an explicit statement, Henrard’s normal form in (Henrard 1984) is constructed by expanding around the de Sitter equilibrium. Analogously, in (Celletti et al. 2018; Paita et al. 2018) we have constructed a normal form in which all angles are eliminated, except \(q_3\): this choice was dictated by the objective of enlightening the apparently important role played by this angle in determining the nature of the dynamics. However, the resonant dynamics are effectively better described when considering the \(\Lambda -\lambda \) plane and therefore here we pursue Henrard’s approach but with two important differences: the use of the modified variable set and a completely symbolic approach not limited to the numerical data of the Galilean system.
4.2 Laplace normal form
Once obtained the two sets of equilibria with
we can address the investigation of the dynamics around them. The best strategy for this is to normalise the Hamiltonian by eliminating ‘fast’ angles. In analogy with Henrard’s approach, we do not limit the construction to the neighbourhood of the equilibrium but allow for large amplitude librations. Therefore, considering as a reference the ‘standard’ approximate \(\pi ,\Lambda _E^{(0)}\) equilibrium provided by (78), we only perform the translation
The model Hamiltonian can then be rewritten as
where \(\Gamma \) is the angular momentum deficit introduced in (41) and \(H_{res}\) is the resonant coupling part of (44).
The \(\omega \) frequency is associated with the free eccentricity oscillations. We assume it to be ‘fast’ with respect to the libration of the Laplace argument. We can therefore normalise with respect to the ‘isotropic oscillator’
by removing the dependence of the Hamiltonian on fast angles. Resonant combinations cannot be removed and actually produce interesting phenomena like ‘beats’ in the eccentricities. However, they appear only at order higher than two and, in case, they can be included by imposing equilibrium values for resonant angles different from \(\lambda \). A preliminary analysis of their role is performed in the following subsection.
For the sake of completeness we briefly recall some aspects of resonant normalisation. A given set of frequencies \(\kappa _a, a=1,\ldots ,n\) is resonant if
The vectors \(\{{ \ell }^{\ (b)}\}\) provide the resonant module; the minimum of \(||{\ell }^{\ (b)}||-1, \, b=1,\ldots ,m\) gives the order of the resonance. \(H_I\) is fully isotropic in the space of frequencies, so \(m=3\) and the first-order resonant module is given by the vectors:
We construct the resonant normal form by enforcing the commutation of the terms in the new Hamiltonian with \(H_I\). The ‘Laplace normal form’ is constructed by implementing a Lie transform with resonant module spanned by the vectors (114) (Efthymiopoulos 2011). Using primes to denote the new variables, the first-order normalisation gives the following Hamiltonian
The construction around the other equilibrium \(\lambda =0\) would lead to the same function with the positive sign in front of the cosine term. The transformed angular momentum deficit can be denoted as
and, in this approximation, is a conserved quantity. We are therefore led to investigate the reduced Laplace Hamiltonian
It provides a first-order approximation of the libration frequency around the reference \(\lambda =\pi \) equilibrium
and an approximate resonance width given by
These results are analogous to those derived by Quillen Quillen (2011) in her general treatment of pure three-body resonances.
The dynamics of the nonlinear oscillators is given by
where the frequency
gives the free eccentricity oscillations. \(\omega \) is therefore the first-order approximation of \(\omega _\mathrm {free}\) at the equilibrium value \(\Lambda =\Lambda _E\). It is worthwhile to remark that, the smaller the value of \(\omega \) the larger the resonance width. On the other hand, a lower bound for \(|\omega |\) is provided by (111). We can add a general result by observing that, when inserting in (120) the appropriate definitions and the equilibrium results obtained above, we get
We see that, by choosing exactly resonant nominal values, namely such that \({\overline{n}}_1 = 2 {\overline{n}}_2 = 4 {\overline{n}}_3\), \(\omega _\mathrm {free}\) vanishes and so does \(\omega \) if the nominal choice \(Q'_k=0\) is done.
Higher-order evaluations of these quantities can be performed by means of higher-order normal forms. Explicit algebraic expressions are cumbersome and will be reported in a forthcoming publication (Celletti et al. 2021). Numerical values for a more accurate modelling of the Laplace libration in the Galilean system are provided in the Appendix. It is interesting to compare this normal form with that obtained in the pioneering work by Henrard Henrard (1984). Apparently, Henrard normal form was constructed by suppressing free eccentricities (see the next subsection) and therefore locating the system in a de Sitter equilibrium. This clearly does not prevent an accurate evaluation of the libration frequency of the Laplace argument but leads to an incomplete description of all the aspects of the dynamics of the Laplace resonance.
4.3 Forced and free eccentricity oscillations
Let us now collectively denote the canonical coordinates as \(W=(Q,\Lambda ,q,\lambda )\). The original coordinates are given by a series of the form \(\sum _{k} \sigma ^k W_k\) such that, in terms of the new normalising coordinates, they are given by
The first two generating functions of the Laplace normal form are
and \(\chi _2=0\), so that, to second order we get
where the free eccentricity oscillations are
and the amplitudes \(a_k\) are fixed by initial conditions.
These relations show how the transformation to the Laplace normal form, aimed at removing non-resonant terms depending on \(q_k\), automatically shifts the eccentricity vectors to the forced equilibria (apart for the slow modulation due to \(\lambda \)), a nice feature already exploited in the approach by Henrard (1984).
4.4 Higher-order Resonant normalisation
The resonant normal forms allows us to investigate additional slow phenomena associated with beats among resonant terms. To evaluate them, the model (24)–(26) expressed in the original Henrard–Malhotra coordinate performs better because the frequency vector is not degenerate, breaking the isotropy of the linear oscillator. For the frequencies appearing in \(H_0\) (see (24)), the resonant module is now given by the two vectors:
The procedure based on the Lie transform approach now produces the following Hamiltonian (again, for the sake of simplicity, we leave the same symbols for the new normalising variables):
with
In the linear part, the frequencies appear to be amended by the following coefficients:
The quadratic part has the same form (25) as in the original Hamiltonian. The resonant part is characterised by the two resonant combinations \(q_1 - q_2\) and \(q_2 - q_3 - q_4\) and the two coefficients
The simplification offered by the normal form is evident when considering that the dimensionality of the system is reduced from 4 to only 2 degrees of freedom. In fact, we recognise the existence of the two additional formal integrals
and \(\Gamma \), the angular momentum deficit already introduced in (41).
By means of the canonical transformation \((Q_a, q_a) \longrightarrow (R_1,R_2,\mathscr {E},\Gamma ,r_1,r_2,e_1,e_2)\)
the resonant normal form can be written as
where
The normal form \(K_R (R_1,R_2,r_1,r_2)\) can be used to investigate the dynamics on longer timescales than those associated with the libration of the Laplace arguments. For example, in the case of the Galilean satellites, on timescales of the order of \(50000 \div 100000\) days, on which we see modulations of the eccentricities due to the resonance. On the other side, we deduce that the Laplace normal form model of the previous subsection, implementing the inverse transformation in Poincaré variables, is good for the short-time dynamics of the libration of the Laplace arguments.
4.5 Detuning the exact resonant dynamics
Secular precessions (e.g. due to the quadrupole) break the exact resonance. However, nonlinear coupling restores the resonant behaviour slightly changing libration frequencies. In order to describe additional precessional effects, we can add to \(H_{Kep}\) a secular part depending on the \(Q_k\) to include in the model the effects due to the oblateness of the central body and, possibly, the averaged motion of other bodies (‘Callisto’). The main effects due to the quadrupole of the central body can be described by a term
where \(J_2\) is the quadrupole coefficient and \(R_J\) is the radius of the central body (‘Jupiter’).
In place of (42), the linear part of the expansion can now be written as
where
are the detuned frequencies. The corrections are usually small; therefore, the normalisation can be implemented in the same way as above by keeping resonant combinations in a detuned resonant normal form (Pucacco et al. 2008). The unperturbed part is a slightly anisotropic oscillator of the form
where the semi-slow frequencies are defined as natural generalisations of (121). As a meaningful example, in the Appendix is discussed the Galilean case when the oblateness of Jupiter is included in the model.
5 Applications
In the present section, we substantiate the results obtained above. First we give a resume of the outcomes of the simplified model and the associated normal form. Afterwards, we apply those results to the two most representative systems: the Galilean satellites of Jupiter and the extra-solar system GJ-876. Happily, these two examples are in a certain sense paradigmatic since each of them represents a general type of Laplace configurations.
5.1 Summary of the results
We can summarise the main outcome of the previous sections by recalling the main ingredients of the Laplace resonance dynamics. We assume an ideal system composed of a main spherical body \(m_0\) and three point masses \(m_j\) located on three nominal orbits assuring mean motion resonance, fixing in this way the semi-major axes. An analogous approach is usually adopted in investigating two-body mean-motion resonances (Batygin and Morbidelli 2013a, b). Recalling (11) and (12), the system parameters are therefore:
which give:
In this way, in view of (5), mean motions \(n_j\) and \(\eta _j\) are specified determining in turn the A, B, C introduced in (5556)–(57) and the coupling constants defined in (293031)–(32). We remark that these nominal values are used as ‘seeds’ to compute reference quantities specifying the models. In particular, the trivial choice \({\overline{P}}_j = 0, j=1,2,3\) produces in practice reliable models as a more accurate choice would do when based on actual elements. However, this choice combined with the nominal resonant \({\overline{L}}_j\) given above, would give, recalling (121), a vanishing value for the frequency of the free eccentricity and a singularity in the Laplace libration. Since the model is completely defined by specifying the values of the two conserved momenta \(Q_5, Q_6\) of (17)–(18), we can chose initial conditions in a domain which is implicitly defined by \(|\omega |>\omega _U\) to comply with (111) but small enough to get a finite size for the resonance width.
Osculating values of \(L_j, Q_j\) are then obtained by exploiting the results of Sects. 3 and 4. The forced eccentricities are computed by using the solutions (91) or/and (97)–(100) to get
and the libration centres can be evaluated by looking at the sign of the \(X_j\) so that:
The equilibrium solution (90) and the libration frequency (118) of the Laplace argument can henceforth be obtained. Finally, by using the forced values in (159), the libration width (119) can be evaluated.
5.2 The case of the Galilean system
As a benchmark for these results, we use an idealised version of the Galilean system, namely a mock-up of the actual system of the satellites of Jupiter with which to compare our predictions. We remark that this exercise has a pure pedagogic value and is not aimed at an accurate reconstruction of the system. It is well known that, for a good description of the Galilean satellite dynamics, we have to include at least the oblateness of the planet and to expand the disturbing function up to second order in the eccentricities (Yoder and Peale 1981; Henrard 1984; Malhotra 1991; Paita et al. 2018). However, for the sake of understanding the qualitative aspects, the present simplified model is sufficient: for more accurate quantitative results we refer to the detuned resonant normal form illustrated in the Appendix.
In Table 1 we can see a comparison between nominal actual element values of the Galilean system and corresponding values obtained with the procedure outlined above: as said, this is just to have an idea of how far our toy model is from the actual system. Using these values, the two frequencies turn out to be
taking into account the time scale implicit in the choice of unit (\(\omega =1/T\), with time unit = 1.7714 days). They, respectively, correspond to the periods
These values are in very good agreement with those obtained from numerical solutions with the toy model (for more accurate values concerning the ‘true’ Galilean system, see Table 4). The equilibrium value at the centre of libration of \(\Lambda \) computed with (90) is
The value corresponding to nominal values is 0.0100872. The resonance width (in agreement with (119)) is
This result shows how small is the domain of the resonance and provides a strong condition for the architecture of the system. In fact, we can conjecture that, for some physical reason (e.g. dissipative long-term effects due to tidal interactions), the semi-major axes could be quite different from those observed but the combination among the \(L_j\)-s given by \(\Lambda \) remains close to the equilibrium value. For the sake of completeness, we provide a preliminary evaluation of the forced eccentricity when considering also the contribution of the quadrupole of Jupiter and expanding up to second order in the eccentricities (Celletti et al. 2021).
Using the first-order solution (91), the standard de Sitter equilibrium
is stable: using (111) we get \(\omega _U = -0.0064\), which can be compared with the numerical outcome by Yoder and Peale (1981) that, when converted to our units, is \(-0.0068\). The eigenvalues of the matrix (108) of the variational system are in fact
Their product gives the determinant (110) in the case with upper signs. They give two frequencies very close to those above in (163) and two others with periods of \(\sim 540\) and \(\sim 735\) days which can be traced in the evolution of the eccentricities of the toy model. We observe that, in this framework, the rotation regime of \(q_3\) is possible if the amplitude of the free eccentricity of Ganymede is sufficiently high. It is worthwhile to remark that, even in this case (which is what happens in the real system), the libration regime is still possible (Lari et al. 2020). Therefore, the libration around the de Sitter–Sinclair equilibrium can be a feasible outcome of the future long-term evolution of the Galilean system.
The ‘anti-de Sitter’ equilibrium
is unstable: the eigenvalues of the matrix of the variational system (their product gives the determinant (110) with lower signs) are now
As a matter of fact, condition (98) is never satisfied so the additional solutions (97)-(100) do not apply in the context of Galilean dynamics.
5.3 The case of the GJ-876 system
The system Gliese-Jahreiß 876 (GJ-876 hereafter) plays a very important role in the now 25-years long history of exoplanets studies. It was the first case of detection of mean motion resonance outside our Solar System (Marcy et al. 2001) and the first instance of multi-mean motion resonance among three planets (Rivera et al. 2010). It is very close (4.689 parsec) and therefore radial velocity and photometric data are of very good quality. In Table 2 we list the nominal elements reported in Nelson et al. (2016) in the framework of a fit which appears to favour small relative inclinations among the planets: a coplanar model is therefore adequate. Semi-major axes and eccentricities are given with very high precision, with the large value \(e_1=0.2531\) for the first planet in the resonant chain, planet-c, a Jupiter-like with a period of 30 days. A second gas-giant, planet-b (the first to be discovered) has a period of 61 days and finally there is a Uranus-like object, planet-e with a period of 124.5 days. There is also an internal super-Earth with a period of 2 days not trapped in resonance.
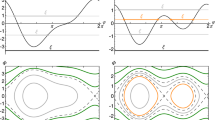
In the context of the present theory, the system exhibits several puzzling aspects which we are going to discuss in what follows. The claim of a system in Laplace resonance is out of question. However, when the configuration is examined, we see that the combination of libration centres is at odds with respect to the equilibria corresponding to de Sitter–Sinclair solutions, notwithstanding the unclear evidence for the behaviour of \(q_3\). In fact, the third resonant angle apparently rotates according to Rivera et al. (2010) but is found librating around \(\pi \) by Martí et al. (2013). Then, is reported to be evolving chaotically in Nelson et al. (2016); however, in this same work the Authors refer also to a chaotic behaviour of \(q_4\) which appears to conflict with their own plots. In addition, in the same work, the claim of the description of the chaotic motion of \(q_3\) found in Batygin et al. (2015), is attributed to \(q_4\). We remark that, while the outcome concerning \(q_3\) appears convincing, it is quite notable to deduce the evolution of the 3-body combination \(q_4\) with a 2-planet model. Anyway, the solutions provided by the de Sitter–Sinclair theory predict not only a mismatch in the reported equilibrium value of the resonant angles but, what is more, very different values of the forced eccentricities. However, the quality of the observational data is so good, at least for planet-b and planet-c, that there should be little doubts about the architecture of the system. As can be seen in Table 2, the libration centres of \(q_1, \ q_2\) and \( q_4\) are found, in the most recent reference (Nelson et al. 2016 ), all to be zero. On the ground of the results obtained here, we can state that the new de Sitter solution denoted as \(X^{(2)}(0)\) provides both the correct architecture and good predictions of the dynamical quantities.
In passing, we observe that the solution denoted as \(X^{(1)}(0)\) is interesting in its own: it is the complementary case with respect to the Galilean solution seen above. It is produced by the condition \(\omega >0\) so that the libration centre \(q_4=0\) turns out to be stable and so the sequence is in this case \(q_1 = \pi , \ q_2 = 0 , \ q_3 =0, \ q_4 = 0\). This configuration is considered by Sinclair (1975) relevant for the Uranian satellites and has also been discussed by Yoder and Peale (1981) in the context of Galilean dynamics as a possible end-state under dissipative effects. It is, however, ruled out for GJ-876. Rather, the new de Sitter solutions envisaged here provide quite reliable values for the forced eccentricities: in particular, the solution \(X^{(2)}(0)\) is stable and reproduces the observed configuration \(q_1 = 0, \ q_2 = 0 , \ q_3 =\pi , \ q_4 = 0\). On the other side, the complementary solution \(X^{(3)}(0)\) is again stable but has the same configuration of \(X^{(1)}(0)\) f or the Uranian system.
The second new de Sitter solution \(X^{(2)}(0)\) predicts values of the forced eccentricities quite close to the observed ones and provides additional convincing dynamical predictions. Triple conjunctions are allowed (Rivera et al. 2010) with planet-c and -b at periastron (\(\lambda _1=\lambda _2=\varpi _1=\varpi _2=0\)) and planet-e at apastron (\(\lambda _3=0,\varpi _3=\pi \)). By computing the eigenvalues of the stability matrix, we get
giving, with the proper units of time, a precession of nodes of \(-0.12\) degrees/day and a period of the Laplace libration of 2750 days. These predictions are quite close to the observed value \(-0.11\) degrees/day and 2800 days reported by Rivera et al. (2010).
In both cases of equilibrium solutions \(X^{(2)}(0)\) and \(X^{(3)}(0)\), the free eccentricity of planet-e ( as large as almost 100% of the forced one (Rivera et al. 2010; Nelson et al. 2016)), produces a non-librating evolution of \(q_3\). For the greatest majority of reasonable initial condition, \(q_3\) displays a ‘nodding’ behaviour, namely the tendency to repeat patterns of bounded libration for several cycles followed by one or more cycles of circulation (Ketchum et al. 2013). Since apparently this happens in a random way, we may guess a stable chaotic behaviour even if most probably in a small region of phase space. The theoretical and numerical analyses of the system have highlighted the chaotic dynamics (Martí et al. 2013; Batygin et al. 2015) and diffusion (Martí et al. 2016) in the system. However, dynamical stability arguments are invoked to speak of stable chaos for which it is reasonable to deduce a dynamical stationary state with well definite, albeit with large amplitude, libration centres. We can only remark that these emerge quite clearly in the framework of the model and appear to be fully compatible with the data analysis.
6 Conclusions
We have described a comprehensive model for systems locked in the Laplace libration. The framework is that of the simplest possible dynamical structure based only on the resonant coupling truncated at second order in the eccentricities. The analytic model is then constructed by a suitable ordering of the terms in the expansion of the Hamiltonian, the study of their equilibria and the computation of resonant normal forms. The agreement of the analytic predictions with the numerical integration of the toy model is very good.
The main result is that of discriminating between two different classes of equilibria, according to the sign of the frequency of the free eccentricity oscillations. In the first class, only one kind of stable equilibrium is possible: the paradigmatic case is that of the Galilean system, for which a fair reconstruction of the dynamics is achieved when including the quadrupole of the Jovian potential by constructing a detuned resonant normal form. In the second class, three kinds of stable equilibria are possible and, at least one of them, is characterised by a high value of the forced eccentricity for the ‘first planet’: here, the paradigmatic case is the exo-planetary system GJ-876.
In the case of the Galilean system, we point out that the resonant normal forms may offer useful insights into the evolution of the system under non-conservative perturbations. Concerning GJ-876, we are presented with a dynamical configuration with some unexpected features (e.g. triple conjunctions of the three planets) which are faithfully reconstructed by the new stable equilibria predicted by the model. Here too, the basic Hamiltonian model truncated at second order provides a solid basis for the investigation of mechanisms of capture to or exit from the resonance.
Notes
The notations are slightly different from the usual ones: in the following we adopt almost systematically the ‘capital-lower case’ convention for momenta and coordinates.
Here, we can consider ‘nominal’ initial conditions: however, a possible choice (made for example by Henrard 1984) is that of considering nominal circular orbits so that \({\overline{P}}_k = 0\).
References
Batygin, K.: Capture of planets into mean-motion resonances and the origins of extrasolar orbital architectures. Mon. Not. R. Astron. Soc. 451, 2589–2609 (2015)
Batygin, K., Morbidelli, A.: Analytical treatment of planetary resonances. Astron. Astrophys. 556, A28 (2013a)
Batygin, K., Morbidelli, A.: Dissipative divergence of resonant orbits. Astron. J. 145, 1 (2013b)
Batygin, K., Deck, K.M., Holman, M.J.: Dynamical Evolution of Multi-resonant systems: the Case of GJ876. Astron. J. 149, 167–182 (2015)
Broer, H.W., Hanßmann, H.: On Jupiter and his Galilean satellites: librations of de sitter’s periodic motions. Indag. Math. 27, 1305–1336 (2016)
Broer, H.W., Zhao, L.: De Sitter’s theory of Galilean satellites. Celest. Mech. Dyn. Astron. 127, 95–119 (2017)
Brown, B.: The long period behavior of the orbits of the Galilean satellites of Jupiter. Celest. Mech. 16, 229–259 (1977)
Celletti, A., Karampotsiou, E., Lhotka, C., Pucacco, G., Volpi, M.: The dynamics of the Laplace resonance: long term dissipative evolution. preprint (2021)
Celletti, A., Paita, F., Pucacco, G.: The dynamics of the de Sitter resonance. Celest. Mech. Dyn. Astron. 130, 15 (2018)
Celletti, A., Paita, F., Pucacco, G.: The dynamics of Laplace-like resonances. Chaos 29, 033111 (2019)
de Sitter, W.: Jupiter’s galilean satellites. Mont. Not. R. Astron. Soc. 91, 706–738 (1931)
Efthymiopoulos, C.: Canonical perturbation theory; stability and diffusion in Hamiltonian systems: applications in dynamical astronomy. Third La Plata International School on Astronomy and Geophysics, Edited by P.M. Cincotta, C.M. Giordano, and C. Efthymiopoulos, Asociación Argentina de Astronomia Workshop Series 3, 3–146 (2011)
Fabrycky, D.C., Lissauer, J.J., Ragozzine, D., Rowe, J.F., Agol, E., et al.: Architecture of Kepler’s Multi-transiting systems: II new investigations with twice as many candidates. Astrophys. J. 790, 146 (2014)
Ferraz-Mello, S.: Dynamics of the Galilean Satellites: An Introductory Treatise. Universidade de Sāo Paulo, Instituto Astronomico e Geofisico (1979)
Ferraz-Mello, S.: Canonical Perturbation Theories. Degenerate Systems and Resonance, Springer Science and Business Media, New York (2007)
Gallardo, T., Coito, L., Badano, L.: Planetary and satellite three body mean motion resonances. Icarus 224, 83–98 (2016)
Hadden, S.: An integrable model for the dynamics of planetary mean-motion resonances. Astron. J. 158, 238–251 (2019)
Hadjidemetriou, J.D., Michalodimitrakis, M.: Periodic Planetary-type Orbits of the General 4-body problem with an application to the satellites of jupiter. Astron. Astrophys. 93, 204–211 (1981)
Henrard J.: Orbital Evolution of the Galilean Satellites: The Conservative Model, Proceedings of the Sao Paulo Conference, The motion of Planets and Natural and Artificial Satellites, Edited by S. Ferraz-Mello and P. E. Nacozy, Reidel, Dordrecht, pp 233–244 (1982)
Henrard, J.: Orbital evolution of the galilean satellites: capture into resonance. Icarus 53, 55–67 (1983)
Henrard, J.: Libration of Laplace’s argument in the Galilean satellites theory. Celest. Mech. 34, 255–262 (1984)
Henrard, J., Lemaître, A.: A second fundamental model for resonance. Celest. Mech. 30, 197–218 (1983)
Henrard, J., Lemaître, A., Milani, A., Murray, C.D.: The reducing transformation and apocentric librators. Celest. Mech. Dyn. Astron. 38, 335–344 (1986)
Ketchum, J.A., Adams, F.C., Bloch, A.M.: Mean motion resonances in exoplanet systems: an investigation into nodding behavior. Astrophys. J. 762, 71 (2013)
Lainey, V., Duriez, L., Vienne, A.: New accurate ephemerides for the Galilean satellites of Jupiter (I). Astron. Astrophys. 420, 1171–1183 (2004a)
Lainey, V., Duriez, L., Vienne, A.: New accurate ephemerides for the Galilean satellites of Jupiter (II). Astron. Astrophys. 427, 371–376 (2004b)
Lainey, V., Duriez, L., Vienne, A.: Synthetic representation of the Galilean satellites’ orbital motions from L1 ephemerides. Astron. Astrophys. 456, 783–788 (2006)
Lari, G.: A semi-analytical model of the Galilean satellites’ dynamics. Celest. Mech. Dyn. Astron. 130, 50 (2018)
Lari, G., Saillenfest, M., Fenucci, M.: Long-term evolution of the Galilean satellites: the capture of Callisto into resonance. Astron. Astrophys. 639, A40 (2020)
Laskar, J.: Large scale chaos and the spacing of the inner planets. Astron. Astrophys. 317, L75–L78 (1997)
Laskar, J.: On the Spacing of Planetary Systems. Phys. Rev. Lett. 84, 3240 (2000)
Laskar, J., Petit, A.C.: AMD-stability and the classification of planetary systems. Astron. Astrophys. 605, A72 (2017)
Lemaître, A.: Resonances: Models and captures. Lect. Notes Phys. 790, 1–62 (2010)
Lieske, J.H.: Theory of Motion of Jupiter’s Galilean Satellites. Astron. Astrophys. 56, 333–352 (1977)
Malhotra, R.: Tidal Origin of the Laplace Resonance and the Resurfacing of Ganymede. Icarus 94, 399–412 (1991)
Marcy, G.W., Butler, R.P., Fischer, D., Vogt, S.S., Lissauer, J.J., Rivera, E.J.: A pair of resonant planets orbiting GJ 876. Astrophys. J. 556, 296 (2001)
Martí, J.G., Giuppone, C.A., Beaugé, C.: Dynamical analysis of the Gliese-876 Laplace resonance. Mon. Not. R. Astron. Soc. 433, 928–934 (2013)
Martí, J.G., Cincotta, P.M., Beaugé, C.: Chaotic diffusion in the gliese-876 planetary system. Mon. Not. R. Astron. Soc. 460, 1094–1105 (2016)
Michtchenko, T.A., Beaugé, C., Ferraz-Mello, S.: Stationary orbits in resonant extrasolar planetary systems. Celest. Mech. Dyn. Astron. 94, 411–432 (2006)
Moons, M.: Extended Schubart averaging. Celest. Mech. Dyn. Astron. 60, 173–186 (1994)
Morbidelli, A.: Planets, Stars and Stellar Systems. Volume 3, Solar and Stellar Planetary Systems, 63 (2013)
Morbidelli, A.: Modern Celestial Mechanics. Taylor and Francis, Florida (2002)
Murray, C.D., Dermott, S.F.: Solar system dynamics. Cambridge University Press, Cambridge, UK (1999)
Musotto, S., Varadi, F., Moore, W., Schubert, G.: Numerical simulations of the orbits of the galilean satellites. Icarus 159, 500–504 (2002)
Nelson, B.E., Robertson, P.M., Payne, M., et al.: An empirically derived three-dimensional laplace resonance in the gliese-876 planetary system. Month. Not. R. Astron. Soc. 455, 2484–2499 (2016)
Paita, F., Celletti, A., Pucacco, G.: Element history of the Laplace resonance: a dynamical approach. Astron. Astrophys. 617, A35 (2018)
Papaloizou, J.C.B.: Three body resonances in close orbiting planetary systems: tidal dissipation and orbital evolution. Int. J. Astrobiol. 14, 291–304 (2015)
Pichierri, G., Morbidelli, A., Crida, A.: Capture into first-order resonances and long-term stability of pairs of equal-mass planets. Celest. Mech. Dyn. Astron. 130, 54 (2018)
Pichierri, G., Batygin, K., Morbidelli, A.: The role of dissipative evolution for three-planet, near-resonant extrasolar systems. Astron. Astrophys. 625, A7 (2019)
Poincaré, H.: Les solutions pèriodique et le planète du type d’Hécuba. Bull. Astron. 19, 177–198 (1902)
Pucacco, G., Boccaletti, D., Belmonte, C.: Quantitative predictions with detuned normal forms. Celest. Mech. Dyn. Astron. 102, 163 (2008)
Quillen, A.C.: Three-body resonance overlap in closely spaced multiple-planet systems. Mon. Not. R. Astron. Soc. 418, 1043–1054 (2011)
Rivera, E.J., Lissauer, J.J., Butler, R.P., et al.: The Lick-Carnegie Exoplanet Survey: a Uranus-mass fourth planet for GJ 876 in an extrasolar Laplace configuration. Astrophys. J. 719, 890–899 (2010)
Sagnier, J.L.: A new theory of the Galilean satellites of Jupiter. Celest. Mech. 12, 19–25 (1975)
Schubart, J.: Long-period effects in nearly commensurable cases of the restricted three-body problem. Smithson. Astrophys. Obs. Spec. Rep. 149, 1–36 (1964)
Showman, A.P., Malhotra, R.: Tidal evolution into the laplace resonance and the resurfacing of ganymede. Icarus 127, 93–111 (1997)
Sinclair, A.T.: The orbital resonances amongst the Galilean satellites of Jupiter. Mon. Not. R. Astron. Soc. 171, 59–72 (1975)
Wisdom, J.: The resonance overlap criterion and the onset of stochastic behavior in the restricted three-body problem. Astron. J. 85, 1122–1133 (1980)
Yoder, C.F., Peale, S.J.: The Tides of Io. Icarus 47, 1–35 (1981)
Acknowledgements
This work has been performed with the support of the Italian Space Agency, under the ASI Contract n. 2018-25-HH.0 (Scientific Activities for JUICE, C/D phase): my deep thanks to the whole Juice teams of Roma Tor Vergata and Roma la Sapienza. I also acknowledge fruitful discussions with C. Efthymiopoulos, S. Ferraz-Mello, H. Hanßmann and A. Morbidelli and the partial support from INFN (Sezione di Roma II) and GNFM-INdAM.
Funding
Open access funding provided by Università degli Studi di Roma Tor Vergata within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the topical collection on Exoplanet Dynamics.
Editors: Alessandro Morbidelli, Kleomenis Tsiganis and Alessandra Celletti.
Appendix: Higher-order normal form for the Galilean system
Appendix: Higher-order normal form for the Galilean system
In this appendix we provide a preliminary computation of a high-order Laplace normal form for the Galilean system. In order to get reliable quantitative predictions, the starting model is improved with respect to the toy model of Subsect. 5.2 with the inclusion of:
-
1.
The oblateness of Jupiter, represented by (Lainey et al. 2004a)
$$\begin{aligned} J_2 = 1.4783 \times 10^{-2}, \quad R=71398 \; {\mathrm{km}}, \end{aligned}$$to be used in the evaluation of the secular precessions as described in Subsect. 4.5
-
2.
A second-order expansion in the eccentricities of the resonant coupling terms as given, for example, in Celletti et al. (2018) with Laplace coefficients computed for the specific semi-axes ratio corresponding to the de Sitter–Sinclair solution.
With the addition of the contribution due to the oblateness as in (154), the semi-slow frequencies become
(tu/T, 1 tu = 1.7714 days) so that the linear part of the Hamiltonian is expressed like that in (155). The corresponding corrections used in the equilibrium solutions of Subsect. 3.2 lead to the eccentricities listed in Table 1 under the denomination ‘de Sitter–Sinclair (analytical with \(J_2\))’.
The normal form at order N can be written as a series of the form
At each intermediate order \(2 \le n \le N\), the coordinates \(\mathbf{Q},\mathbf{q}\), with
have to be intended as new variables but for ease of notation are denoted with the same symbol. The norm of the integer vectors
at each order must comply with the conditions
so that the normal form has the D’Alembert character only with respect to the eccentricity vectors. The coefficients \(a^{(n)}_{\mathbf{s},\mathbf{k}}\) are functions of the \(\omega _j\) and of the parameters \(\alpha ,\beta _1,\beta _2,\gamma \).
Here, we are interested in finding more accurate predictions for the libration frequencies and the resonance width. Therefore, we compute the normal form at the Sinclair–de Sitter equilibrium obtaining a series of the form
In Table 3 we display its coefficients in a form that can be directly compared with the analogous series computed by Henrard (1984). The resonance width turns out to be further reduced with respect to the value of the toy model and now amounts to
The libration periods (\(T_j, \, j=1,2,3; T_L\)) are listed in Table 4: in the second column are reported the values computed with the sixth-order normal form (171), showing the improvement of the present model with respect to (164); in the third, are listed the periods obtained by averaging the outcomes of numerical integration of the Hamiltonian model described above; in the fourth are given the corresponding values obtained by Lainey et al. (2006) from a Fourier analysis of their accurate L-1 ephemerides (Lainey et al. 2004b).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pucacco, G. Normal forms for the Laplace resonance. Celest Mech Dyn Astr 133, 11 (2021). https://doi.org/10.1007/s10569-021-10008-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10569-021-10008-w