Probabilistic data association: the orbit set

Abstract

This paper presents a novel method to obtain the solution to the initial orbit determination problem for optical observations as a continuum of orbits—namely the orbit set—that fits the set of acquired observations within a prescribed accuracy. Differential algebra is exploited to analytically link the uncertainty in the observations to the state of the orbiting body with truncated power series, thus allowing for a compact analytical description of the orbit set. The automatic domain splitting tool controls the truncation error of the polynomial approximation by patching the uncertainty domain with different polynomial expansions, effectively creating a mesh. The algorithm is tested for different observing strategies to understand the working boundaries, thus defining the region for which the admissible region is necessary to extract meaningful information from observations and highlight where the new method can achieve a smaller uncertainty region, effectively showing that for some observing strategies it is possible to extract more information from a tracklet than the attributable. Consequently, the method enables comparison of orbit sets avoiding sampling when looking for correlation of different observations. Linear regression is also implemented to improve the uncertainty estimation and study the influence of the confidence level on the orbit set size. This is shown both for simulated and real observations obtained from the TFRM observatory.

1 Introduction

Determining the state of resident space objects (RSOs) is crucial to maintain a collision-free environment in space, predict space events and allow uninterrupted delivery of services from operational satellites. New observing technologies are now capable of detecting objects which were too small or too far away to be observed in the past, thus delivering many more observations than before. This, coupled with the ever-growing number of RSOs, calls for more efficient methods able to deal with the amount of data produced (Hussein et al. 2014). Furthermore, when performing survey campaigns, the selected schedule and/or visibility constraints often result in short-arc observations (Tommei et al. 2007) with long observing gaps, which do not allow for precise orbit determination during a single passage of the object over an observing station. Indeed, being the detections very close in time, little is known about the geometry of the orbit. Thus, for each set of observations—namely a tracklet—there is more than one orbit that complies with the acquired data, as shown in Fig. 1a. The set of admissible solutions corresponding to a single tracklet is here called the orbit set (OS). To reduce the uncertainty on the solution and pinpoint the correct orbit associated with the observation, one needs other independent observations of the same object as sketched in Fig. 1b. The main challenge in this, however, is to determine whether two or more observations pertain to the same object, thus whether they are correlated, since the objects are unknown when observed. This is the problem of data association, where one has to look for a common solution in the two OSs generated by the observations, as shown in Fig. 1c and d. The aim of this paper is thus to determine a compact formulation of the OS so that the intersection of two or more uncertainty volumes can be easily found and calculated. In the literature, the admissible region (AR) is the most known approach to deal with too-short arcs where classical methods for initial orbit determination (IOD) fail. Developed by Milani et al. (2004), the method gathers all the information available from the tracklet in a four-dimensional vector called Attributable and determines the set of ranges and range rates achievable by posing physical constrains: when setting a maximum eccentricity and a minimum and maximum semi-major axis for the orbit, one can bound the values for the range $\rho$ and range rate $\dot{\rho }$, effectively determining the constraints for the two-dimensional region in the $(\rho ,\dot{\rho })$-plane. For each point in the plane, then, the state of the object is defined. Figure 2 shows the AR for a too-short arc simulated from object 36830.¹ The constraints are found by substituting the boundary semi-major axis and eccentricity in the equations for energy and angular momentum (DeMars and Jah 2013). The method, however, does not consider any uncertainty in the observations, in that it is completely deterministic and discretizes the AR to perform data association. In the last years a probabilistic approach is becoming more popular: here the AR is described as a bi-variate uniform probability density function (PDF), where, thus, each point of the constrained plane has the same probability to represent the real observation. Although more complete because it easily allows for the inclusion of uncertainties in observations, measurements and timing—as described by Worthy III and Holzinger (2015a)—this approach also poses some new difficulties. Indeed, Worthy III and Holzinger (2015b) describe the constraints for the variables transformations and conclude that in general it is very difficult to transform a PDF if the transformation function is not linear or the PDF is not Gaussian (Park and Scheeres 2006), and both assumptions usually do not hold for the IOD case. This problem is not found in the deterministic approach, where a function may be expressed in another state without any restriction. Different authors follow the probabilistic approach, such as Armellin and Di Lizia (2016), Fujimoto (2013), DeMars and Jah (2013). All three of them use a different approach: the first paper uses differential algebra (DA), the second one maps the AR into Delaunay variables, while the third uses Gaussian mixture methods (GMMs), where a generic PDF over the AR is approximated as the sum of Gaussian PDFs.

Fig. 1

Initial uncertainty region, precise determination of the orbit with new observations of the same object and example of correlated and uncorrelated observations

Fig. 2

Admissible region for a too-short arc of observed object 36830

This paper wants to first and foremost identify the range of observing strategies for which the AR is the only way to extract meaningful information from a too short and/or too uncertain tracklet. To do so, a new technique to perform IOD based on DA is developed and its working boundary tested. In the new formulation, uncertainty is described in six dimensions to avoid the problems of the probabilistic AR and the set of viable states come directly from the observations properties rather than some a priori physical constraints. The DA approach, furthermore, would allow for an analytical treatment of the region, thus avoiding the sampling used in the deterministic AR approach. An in-depth analysis of the uncertainty size for different orbital regimes, accuracy and separation is then carried out in order to discriminate when the AR is actually necessary and when instead more information can be retrieved than that stored in the attributable. Lastly, the effects of polynomial regression on the observations and IOD output are studied.

The paper is organized as follows. Section 2 contains all the relevant mathematical tools to build the algorithm. The theory of the method, called differential algebra initial orbit determination (DAIOD), is described in Sect. 3 taking advantage of all the mathematical blocks described in Sect. 2. Results are shown in Sect. 4, while conclusions and future work are contained in Sect. 5.

2 Mathematical background

This section contains all the building blocks for the DAIOD algorithm. Section 2.1 describes the basics of DA, Sect. 2.2 describes the linear regression implementation to treat optical observations, and lastly Sects. 2.3 and 2.4, respectively, describe Gauss’ and Lambert’s algorithms.

2.1 Differential algebra

This work makes use of DA, a computing technique that uses truncated power series (TPS) instead of numbers to represent variables (Armellin and Di Lizia 2016). By substituting the classical implementation of real algebra with the implementation of a new algebra of Taylor polynomials, any deterministic function f of v variables that is $\mathcal {C}^{k+1}$ in the domain of interest $[-1,1]^v$ is expanded into its Taylor polynomial up to an arbitrary order k with limited computational effort (Berz 1986, 1987). The notation for this is: $f \approx \mathcal {T}_f^{(k)}$. Similar to algorithms for floating point arithmetic, various algorithms were introduced in DA, including methods to perform composition of functions, to invert them, to solve nonlinear systems explicitly and to treat common elementary functions (Berz 1999). Ultimately, this technique allows for the definition of analytical solutions of complicated systems of equations which normally require numerical techniques to be solved.

2.1.1 Expansion of the solution of parametric implicit equations

An important feature of DA is the expansion of the solution of parametric implicit equations. Suppose one has to find the solution of a classical implicit equation:

$$\begin{aligned} f(x) = 0. \end{aligned}$$

(1)

Several well-known algorithms are available to do so, such as Newton’s. Suppose an explicit dependence on a parameter p can be highlighted in the previous function f, which leads to the parametric implicit equation

$$\begin{aligned} f(x, p) = 0. \end{aligned}$$

(2)

DA techniques can effectively handle this problem by identifying the function x(p) in terms of its k-th order Taylor expansion with respect to the parameter p:

$$\begin{aligned} x(p) = \mathcal {T}_x^{(k)} (p). \end{aligned}$$

(3)

The DA-based algorithm to solve Eq. (2) is now explained. The first step is to consider a reference value of the parameter p and to compute the solution x by means of a classical numerical method, such as Newton’s method. Variable x and parameter p are then initialized as k-th order DA variables. By evaluating function f in DA, one obtains the k-th order expansion of f with respect to x and p:

$$\begin{aligned} f = \mathcal {T}_f^{(k)} ( x, p), \end{aligned}$$

(4)

The superscript indicating the polynomial order will be dropped in the following equations for clarity purpose. A constant order k is to be implied. The map is then partially inverted through a built-in DA routine, which returns

$$\begin{aligned} x = \mathcal {T}_x ( f, p). \end{aligned}$$

(5)

As the goal is to compute the k-th order Taylor expansion of the solution x(p) of Eqs. (2), (5) is evaluated for $f = 0$

$$\begin{aligned} x = \mathcal {T}_x ( f=0, p) = \mathcal {T}_x (p). \end{aligned}$$

(6)

The map thus expresses how a variation of the parameter p affects the solution x as a k-th order Taylor polynomial, all the while imposing $f=0$. Although a classical numerical method is necessary to start the computation, the advantage is the final map obtained: whenever one needs to investigate the sensitivity of the output with respect to parameter p, one can perform simple function evaluations rather than other numerical computations. In this paper, one can assume x to be the state of the object, which depends on the observations and their variation (respectively, parameter p and $\delta p$), such that the six angles define an orbit (the condition $f=0$). The accuracy of the approximation depends on both the order k of the Taylor expansion and the displacement $\delta p$ from the reference value of the parameter. Thus, a careful analysis is always mandatory to tune the expansion order to assure that Eq. (6) is sufficiently accurate for the entire range of p we are interested in.

2.1.2 The automatic domain splitting tool

An alternative solution to the tuning of the expansion order and range of domain of interest is the use of the automatic domain splitting (ADS) tool. The ADS estimates the truncation error of a TPS, pinpoints the variable that most affects it and halves the initial domain along that variable, when the truncation error exceeds a fixed tolerance. The tool then evaluates a new Taylor expansion for each of the two new domains. The process is repeated until all TPS obtained lie on a region within the set tolerance. The output is then a mesh of domains and respective TPS, whose union corresponds to the initial DA set. Figure 3 shows an example: here the Gaussian function and the tenth-order single polynomial approximation are shown, respectively, in Fig. 3a and c, where the error between real function and polynomial approximation is shown to grow unbounded when getting further from the expansion point. Figure 3b and d, on the other hand, respectively, shows the mesh created by the ADS and the error between the real function and the set of polynomials used to patch the domain. Here, the error is controlled up to the specific tolerance $e = 10^{-5}$.

Fig. 3

Example of ADS applied to Gaussian function (Pirovano et al. 2017)

The most crucial problem within the tool is the estimation of the error between the real function and the TPS that approximates it. The theory behind the error estimation function is explained in Wittig et al. (2015). The ADS needs two more inputs in addition to the DA domain, which are the maximum allowed truncation error $e_r$ and the maximum number of splits N. The latter is introduced to avoid unnecessary splits that create domains too small to be relevant. The tool can be used for any function, for example, Wittig et al. (2014) were the first ones to use it to accurately propagate uncertainty. Figure 4 shows the flowchart of the tool.

Fig. 4

Flowchart for the ADS tool

2.2 Linear regression of observations

A list of observed angles in consecutive epochs for a single object is called tracklet. Tracklets usually contain three or more observations, each observation being made of a right ascension $\alpha$, a declination $\delta$, a precision $\sigma$ and a time of observation t. To account for sensor-level errors, the precision of the observation can be modelled as white noise and thus be considered as a Gaussian random variable with zero mean and $\sigma$ standard deviation (Poore et al. 2016):

$$\begin{aligned} \mathbf{Y} \sim \mathcal {N}(\mathbf{y} , \varSigma ), \end{aligned}$$

(7)

where, for the case of optical observations analysed in this paper, the observed values $\mathbf{y}$ are the right ascension $\alpha$ and the declination $\delta$, while $\varSigma$ is a diagonal matrix containing the variances $\sigma ^2$. When performing IOD, three independent observations are needed, and to exploit the full length of the tracklet, the first, middle and last observations are usually used. However, this means that some data are left unused, when the tracklet contains more than three observations. To take advantage of all observations, some kind of regression can be performed and exploited to reduce the overall uncertainty. For example, when tracklets are too short, information about the orbit’s curved path is very scarce and thus it can sometimes be linearly approximated, which is actually the basis of the attributable approach by Milani et al. (2004). This happens especially in the case of geostationary Earth orbits (GEOs), where the apparent null motion with respect to the observatory enhances the problem of gaining information about the orbit. In this case, the distribution of the right ascension and declination can be linearly regressed with respect to time, following the well-known linear regression equation $\hat{\varvec{Y}} = \hat{\varvec{\beta }}_0 + \hat{\varvec{\beta }}_1 \varvec{X}$:

$$\begin{aligned} \left[ \begin{array}{c} \hat{\alpha } \\ \hat{\delta } \end{array}\right] = \left[ \begin{array}{c} \hat{\alpha }_0 \\ \hat{\delta }_0 \end{array}\right] + \left[ \begin{array}{c} \hat{\dot{\alpha }} \\ \hat{\dot{\delta }} \end{array}\right] t. \end{aligned}$$

(8)

In case of different precisions within the same tracklet, weights can be constructed as the inverse of the square precision: $w = \sigma ^{-2}$. Regression can be conveniently performed at the central time of observation (C): it will be shown that in this case the resulting slope and intercept are uncorrelated. The four-dimensional vector containing the estimated values $(\hat{\alpha }_C,\hat{\delta }_C, \hat{\dot{\alpha }}, \hat{\dot{\delta }})$ is the attributable from the admissible region approach. The quantity

$$\begin{aligned} T = \frac{\hat{\beta }-\beta }{s_{\hat{\beta }}} \sim t_{N-2} \end{aligned}$$

(9)

is known to be distributed as a Student’s T (Casella and Berger 2001), where $\hat{\beta }$ stands for any of the four estimated coefficients that constitute the attributable, N is the number of fitted parameters and $s_{\hat{\beta }}$ is standard estimate (SE) of the coefficient $\hat{\beta }$. The covariance of the attributable is a diagonal matrix whose elements can be written as a function of N, the root mean square error (RMSE) of the regression $s_{\hat{Y}}$ and the tracklet length $\varDelta t$

$$\begin{aligned} \varSigma _{\left( \hat{\beta }_0, \hat{{\beta }_1}\right) } = s_{\hat{Y}} \left( \begin{array}{cc} \dfrac{1}{N} &{} \quad 0\\ 0&{}\quad \dfrac{12}{N(N+1)(N-1) \varDelta t^2} \end{array} \right) , \end{aligned}$$

(10)

where $(\hat{\beta }_0, \hat{{\beta }_1}) = \lbrace (\hat{\alpha }_C, \hat{\dot{\alpha }}), (\hat{\delta }_C ,\hat{\dot{\delta }})\rbrace$. This result is obtained by considering the covariance definition

$$\begin{aligned} \varSigma _{\left( \hat{\beta }_0, \hat{{\beta }_1}\right) } = s_{\hat{Y}}^2 (H^\mathrm{T} H)^{-1} = s_{\hat{Y}}^2 \left( \begin{array}{c c} \dfrac{\sum _i x_i^2}{N \sum _i x_i^2 -\left( \sum _i x_i\right) ^2} &{} - \dfrac{\sum _i x_i}{ N \sum _i x_i^2 -\left( \sum _i x_i\right) ^2}\\ - \dfrac{\sum _i x_i}{ N \sum _i x_i^2 -\left( \sum _i x_i\right) ^2}&{} \dfrac{N}{N \sum _i x_i^2 -\left( \sum _i x_i\right) ^2} \end{array} \right) \end{aligned}$$

(11)

where $H_i = [ 1 \quad t_i-t_C]$. Remembering that we are performing regression at the central time of observation, differently from Fujimoto and Alfriend (2015) who perform it at $t=t_0$, the following holds:

• $\sum _i x_i = 0$ and thus $\overline{x} = 0$. This is exploited to obtain a diagonal matrix, thus uncorrelated coefficients.

• $\sum _i x_i^2 =\sum \nolimits _{i=- \frac{N-1}{2}}^{\frac{N-1}{2}}\varDelta t^2i^2 = 2 \varDelta t^2 \sum \nolimits _{i=1}^{\frac{N-1}{2}} i^2 = \dfrac{1}{12}N(N+1)(N-1) \varDelta t^2$.

The same conclusion was reached by Siminski (2016) and Maruskin et al. (2009) (after rearranging the equations with different variables). Taking one step forward, it is possible to infer statistical properties of the fitted observations starting from the attributable. Indeed, being the fitted values a linear composition of the estimated coefficients, their variance is:

$$\begin{aligned} \varSigma _{\hat{Y}_i} = H_i \, \varSigma _{\left( \hat{\beta }_0, \hat{{\beta }_1}\right) } \, H_i^\mathrm{T}. \end{aligned}$$

(12)

It is thus possible to define a confidence interval (CI) of the fitted observations. This is the interval within which the true value can be found with confidence level $\alpha$. It can be constructed through $\varSigma _{\hat{Y}_i}$ and the Student’s T quantiles:

$$\begin{aligned} \hbox {CI:}\quad \left[ \hat{Y} \pm t_{\frac{\alpha }{2},n-2} \cdot \sqrt{\hbox {diag}(\varSigma _{\hat{Y}})} \right] \end{aligned}$$

(13)

where $\alpha$ is the confidence level. This statistical manipulation of data usually achieves a much smaller uncertainty on the observed angles, given that more information is used and is thus beneficial to the process of IOD in that a smaller uncertainty volume needs to be taken into account. This, however, only holds when linear approximation is valid: depending on the p-value of the statistics, one may decide either to add higher-order terms to the regression or work with raw data instead. Whenever linear regression is found beneficial, fitted observations are used instead of raw observations and consequently the confidence interval is chosen over the $3\sigma$ uncertainty from the instrument precision. Figure 5 summarizes the regression showing the observations (dots), the mean prediction (solid line) and the CI (dashed lines).

Fig. 5

Regression for the right ascension $\alpha$ centred at the central time of observation. Values are amplified by a factor 1000 for clarity purpose (Pirovano et al. 2018)

2.3 Gauss’ algorithm

Gauss’ algorithm takes as input three times of observations $(t_1, t_2, t_3)$, the positions of the observatory at these times ($\varvec{R}_1, \varvec{R}_2, \varvec{R}_3)$ and the direction cosine vectors $(\hat{\varvec{\rho }}_1 \hat{\varvec{\rho }}_2 \hat{\varvec{\rho }}_3)$. The algorithm then estimates the slant ranges $(\rho _1, \rho _2,\,\rho _3)$ in order to obtain the object positions

$$\begin{aligned} \varvec{r}_\text {i} = \varvec{R}_\text {i} + \rho _\text {i}\, \hat{\varvec{\rho }}_\text {i}, \qquad \hbox { where } i =1,2,3 \end{aligned}$$

(14)

in two-body dynamics. The description of this algorithm can be found in Curtis (2015). The quality of the solution degrades when the arc is too long, due to the approximations considered, and when it is extremely short, due to the geometry of the problem. For our method, we use the solution of the Gauss’ algorithm to obtain an initial estimate for the slant ranges.

2.4 Lambert’s algorithm

Lambert’s algorithm takes as input two position vectors, the $\varDelta t$ between them and the gravitational parameter, and gives as output the velocity vectors. Thus, the algorithm produces the state of the object at two different epochs, following Keplerian dynamics. Since it is not possible to solve the problem analytically, as outlined in Vallado and McClain (2001), several methods were created in the past. For the work at hand, the C++ implementation by Izzo (2014) has been used, after updating it to be able to accept both double precision and DA variables.

3 DAIOD Algorithm

This section describes the DAIOD algorithm, which takes advantage of the mathematical blocks described in Sect. 2. The algorithm was firstly defined and used in Armellin et al. (2012). The latest variations which are implemented in this paper were firstly introduced in Pirovano et al. (2017) and later exploited by Principe et al. (2017) to obtain a first estimate of the state for orbit determination of tracks. The DAIOD algorithm takes as input the optical observation of an object and gives as output the TPS of the object state at the central time of the observation, depending on the six-dimensional uncertainty of the observations considered. Depending on the length of the observation and measurement accuracy, fitted observations defined in Sect. 2.2 may be used instead of raw data.

The choice of introducing a different method to perform IOD came from the necessity to not only obtain a point solution, but also a converging map in the neighbourhood. Section 4.2 will compare the DAIOD algorithm against Gooding’s method and a slight variation of it. All three methods converge to the same nominal solution but have different behaviours towards the map expansions, where the DAIOD results a more attractive choice. Gauss’ algorithm is firstly exploited to obtain an initial estimate of the object position at $t_1, t_2$ and $t_3$. The observatory state can be retrieved through SPICE (Acton 1996),² while the direction cosines are found through the observation angles:

$$\begin{aligned} \hat{\varvec{\rho }}_\text {i} = \begin{bmatrix} \cos \delta _\text {i} \cos \alpha _\text {i} \\ \cos \delta _\text {i} \sin \alpha _\text {i} \\ \sin \delta _\text {i} \end{bmatrix} \end{aligned}$$

(15)

where $i = 1, 2, 3$ refers to the observation epochs (Curtis 2015).

The output of the Gauss’ algorithm is an estimate for the position vectors $\varvec{r}_\text {1}, \varvec{r}_\text {2}$ and $\varvec{r}_\text {3}$. Having the position vectors, it is then possible to compute the velocities through Lambert’s algorithm: indeed, given two position vectors and the $\varDelta t$ between them, Lambert’s algorithm produces the velocity vectors as output. This means that by computing Lambert’s algorithm twice—from $t_1$ to $t_2$ and from $t_2$ to $t_3$—one should be able to retrieve the three state vectors. However, given the simplifications performed within Gauss’ algorithm, the equality of the two velocity vectors $\varvec{v}_\text {2}^{-}$ and $\varvec{v}_\text {2}^{+}$ is not ensured, as sketched in Fig. 6a. To fix this problem and obtain the dependency between state and observations uncertainty, a two-step Lambert’s solver is implemented. The first step finds the $\delta \varvec{\rho } = \left( \delta \rho _{t_1}, \, \delta \rho _{t_2},\, \delta \rho _{t_3}\right)$ necessary to ensure that $\varvec{v}_2^{-} - \varvec{v}_2^{+} = \varvec{0}$. Once the three ranges are forced to be part of the same orbit, as sketched in Fig. 6b, the second step determines the new solution $(\varvec{r}_2, \, \varvec{v}_2)$ as a function of the observation angle variations $\delta \varvec{\alpha }$ and $\delta \varvec{\delta }$. This last step returns an analytical description of the state variation due to variations in the observations, where point values can be found just by means of function evaluations. Analysing the neighbourhood of the solution is indeed essential because the observations are not free of errors, and hence, they allow for a range of solutions rather than a single point. This final function encloses all possible orbits that fit the observations within a certain precision; hence, it is the OS, the set of admissible solutions corresponding to a single tracklet.

Fig. 6

First Lambert’s step of DAIOD algorithm

The first Lambert’s routine is started by initializing the output of Gauss’ algorithm as DA variable, that is $\varvec{\rho }_0 = [\rho _{t_1} \,\rho _{t_2} \,\rho _{t_3} ]$. In this way, the output of Lambert’s algorithm is a vectorial function that depends on the variations of the slant ranges starting from the nominal solution given by Gauss’ algorithm. In particular,

$$\begin{aligned} {\left\{ \begin{array}{ll} \varvec{v}_2^{-} = \mathcal {T}_{\varvec{v}_2^{-}} \left( \rho _{t_1}, \, \rho _{t_2}\right) \\ \varvec{v}_2^{+} = \mathcal {T}_{\varvec{v}_2^{+}} \left( \rho _{t_2}, \, \rho _{t_3}\right) . \end{array}\right. } \end{aligned}$$

(16)

With the goal of solving the discontinuity in $t_2$, the $\varDelta \varvec{v}$ between the left and right velocities is calculated:

$$\begin{aligned} \varDelta \varvec{v} = \varvec{v}_2^{+}-\varvec{v}_2^{-} = \mathcal {T}_{\varvec{v}} \left( \rho _{t_1}, \, \rho _{t_2}, \, \rho _{t_3}\right) . \end{aligned}$$

(17)

The equation is made of a constant residual $\varDelta \varvec{v}_\mathrm{res} \ne 0$—as highlighted in Fig. 6a—and a function of the slant ranges. By forcing $\varDelta \varvec{v} = \varvec{0}$, one has to solve a system of three equations in three unknowns to find the $\delta \varvec{\rho }$ necessary to obtain it. Newton method for DA explained in Sect. 2.1.1 is used here: $\varvec{\rho }_{0}$ is indeed the tentative solution, $\varDelta \varvec{v}-\varDelta \varvec{v}_\mathrm{res}$ is function f, and $\varvec{\rho }$ is variable $\varvec{x}$. Thus, we need to calculate the variation $\varDelta x$ such that $f = 0$. To do so, we firstly partially invert Eq. (17) by exploiting DA routines:

$$\begin{aligned} \varDelta \varvec{v} = \mathcal {T}_{\varDelta \varvec{v} } \left( \varvec{\rho } \right) \qquad \rightarrow \qquad \varvec{\rho } = \mathcal {T}_{ \varvec{\rho }} \left( \varDelta \varvec{v}\right) \end{aligned}$$

(18)

and then evaluate the new map for $\varDelta \varvec{v} = \varvec{0}$, thus finding the variation needed:

$$\begin{aligned} \varDelta \varvec{\rho } = \mathcal {T}_{ \varvec{\rho }} \left( \varDelta \varvec{v} = \varvec{0} \right) . \end{aligned}$$

(19)

Once the variation is summed to the initial guess, one obtains:

$$\begin{aligned} \varvec{\rho }_{1} = \varvec{\rho }_{0} + \varDelta \varvec{\rho } = \mathcal {T}_{\varvec{\rho }} (\varvec{\rho }) . \end{aligned}$$

(20)

Since the change in the slant range also modifies the velocity vectors, Eqs. (16–20) are placed in a while-loop that stops once $\Vert \varvec{\rho }_{i+1} - \varvec{\rho }_{i} \Vert < \varvec{\epsilon }_\rho$, where i is the number of iterations. The constant part of the resulting map, here called $\varvec{\rho }_{L}$, allows for the definition of the state of a satellite whose orbit intersects the three starting observations within the prescribed accuracy $\varvec{\epsilon }_\rho$. However, the final Taylor expansion depends on the slant ranges, as seen in Eq. (20). This is not useful, since one wants the solution in terms of the observations deviation. For this reason, the second step of the Lambert’s solver is implemented by initializing the six observed angles as DA variables. The values used for the angles are either the raw observation data from the observatory or the fitted values from the regression, while their maximum variation $(\varDelta \varvec{\alpha }, \varDelta \varvec{\delta })$ is, respectively, either $3\varvec{\sigma }$—the Gaussian CIs given by the precision of the raw observation—or the Student’s T CIs for the fitted values from linear regression (Sect. 2.2). At this point, the position vector at central time of observation is initialized as:

$$\begin{aligned} \varvec{r}_i = \varvec{R}_i + \rho _{L1} \cdot \hat{\varvec{\rho }}_i\left( \alpha _i, \delta _i \right) = \mathcal {T}_ {\varvec{r}_i} \left( \alpha _i, \delta _i \right) , \quad \hbox {for } i=1,2,3 \end{aligned}$$

(21)

where the DA direction cosines are found by plugging the six DA angles into Eq. (15). Once the three position vectors are given to the Lambert’s algorithm in couples, $\varDelta \varvec{v}_2 = \mathcal {T}_{\varDelta \varvec{v}_2} \left( \varvec{\alpha }, \varvec{\delta }\right)$. This time partial inversion cannot be performed, since nine DA variables would be needed: six angular variables (parameter p) and three position variables (variable x). The use of nine variables is avoided for two reasons: firstly, once the inversion is computed, three DA variable would be left unused, but still be weighing on the algorithm performance and secondly an increase in the number of variables produces an influential increase in computational and storage requirement (Berz 1986).

Thus, differently from Armellin et al. (2012), a simple first-order DA Newton’s scheme is used to compute $\varvec{\rho } = \mathcal {T}_{\varvec{\rho }} \left( \varvec{\alpha }, \varvec{\delta }\right)$:

$$\begin{aligned} \mathcal {T}_{\varvec{\rho }_{i+1}}\left( \varvec{\alpha }, \varvec{\delta }\right) = \mathcal {T}_{\varvec{\rho }_i}\left( \varvec{\alpha }, \varvec{\delta }\right) - J_{\varDelta \varvec{\text {v}}(\varvec{\rho }_\text {0})}^{-1} \, \cdot \mathcal {T}_{\varDelta \varvec{v}}\left( \varvec{\alpha }, \varvec{\delta }\right) , \end{aligned}$$

(22)

where the Jacobian $J_{\varDelta \mathbf{v }(\varvec{\rho }_\text {0})}$ is easily retrieved as the linear part of Eq. (20). Here, the assumption is made that the Jacobian does not change in the loop. The iteration is carried out until $i = k$, thus until the highest order of the DA variable is reached. The result is the state of the satellite at central time as a map on the domain defined by the six DA angles:

$$\begin{aligned} f_\mathrm{IOD} \approx \mathcal {T}_\mathrm{IOD}:\left( \varvec{\alpha },\varvec{\delta } \right) \subset \mathbb {R}^6 \, \rightarrow \, \left( \varvec{r}_2,\varvec{v}_2 \right) \subset \mathbb {R}^6. \end{aligned}$$

(23)

An important outcome of this method is that one not only obtains the point solution, but can also easily calculate its variation within the CI designated by means of functions evaluations and observe polynomial dependencies. The solution is thus the OS we wanted to compactly define.

However, polynomial approximations are only valid for neighbouring variations of the nominal solution, as highlighted in Sect. 2.1.1. This implies that one single TPS may not be able to cover the entire initial domain. For this reason, the ADS described in Sect. 2.1.2 is applied to the algorithm. If necessary, the initial domain is thus split until the precision of the map reaches a defined tolerance $\varvec{\epsilon }_r$. Equation (24) shows the final function:

$$\begin{aligned} f_{\mathrm{IOD}+\mathrm{ADS}} = \bigcup _j\mathcal {T}_j: \left( \varvec{\alpha },\varvec{\delta } \right) _j \subset \mathbb {R}^6 \, \rightarrow \, \left( \varvec{r}_2,\varvec{v}_2 \right) _j \subset \mathbb {R}^6. \end{aligned}$$

(24)

The entire process supposes an initial good estimate from the Gauss’ algorithm and the presence of an elliptical solution to the Lambert’s algorithm for every point considered within the CI. However, this may not be the case for too-short observations and very uncertain observations. For the first case, the initial estimate from Gauss may be poor due to scarce knowledge of the orbit and thus impede the loop on Lambert’s algorithm to converge for a point solution, while for the latter case, supposing the availability of a point solution, a too large uncertainty may include re-entering or hyperbolic solutions, which thus would make the expansion routine fail when looking for an elliptical solution.

An important variable to be chosen is the order of the Taylor polynomials. The order has a considerable impact on the number of monomials in the Taylor representation and thus on the computation time. On the other hand, the lower the order of the polynomial is, the smaller the domain of validity of the expansion is, thus requiring more splits. The ADS also imposes the requirement of at least a third-order polynomial to accurately estimate the truncation error. Thus, a trade-off between computing time for polynomial operations and splitting routine has to be made, with the constraint of a lower bound. The optimal order for this algorithm was found to be 6.

4 Results

This section presents the results achieved by applying the DAIOD algorithm to observations obtained with different strategies, both real and simulated.

As a first result to appreciate the double-step approach to the IOD problem, Fig. 7a shows the variation in slant range that is achieved with the differential correction in Lambert’s algorithm starting from the initial solution through Gauss’ algorithm to solve the discontinuity in velocity at central time of observation depicted in Fig. 7b. The plot is composed of 100 simulations for each observing strategy. As small as it may seem, the correction ensures continuity for the velocity vector at the central time of observation and it is thus fundamental to retrieve the orbit of the orbiting body. As expected, the correction is independent of the uncertainty of the observation, as it only considers the geometry of it. This can be seen especially for longer observations, while for shorter observations the lower success rate of the algorithm affects the results.

Fig. 7

Initial discontinuity and differential correction to solve it during the Gauss–Lambert routine

Section 4.1 tests the validity of the DAIOD algorithm for strategies that differ in precision and length of observation. For these tests observations were simulated. Section 4.2 compares the OS as obtained through Lambert’s or Gooding’s algorithms. Section 4.3 analyses the effects of linear regression on synthetic observations, while Section 4.4 shows the effects of the truncation error control performed by the ADS on real observations. Although results were obtained as 6D polynomial functions, they are shown as 2D projections on the AR for clarity and comparison purposes. The OS is also compared against the arbitrary direction (AD) method, which makes use of the line of variations (LOV).

4.1 Validity of DAIOD algorithm

The DAIOD algorithm is sensitive to two main variations in the observations: the tracklet length and the uncertainty of the observation. The former contains information about the curve nature of the orbit; thus, the shorter the tracklet is, the lesser is known about it, increasing the range of possible solutions. The latter directly influences the size of the OS by defining a larger initial uncertainty domain. This section addresses this sensitivity and analyses the working boundary of the DAIOD algorithm, building on results presented in Pirovano et al. (2018). This analysis is necessary to analyse a wide range of different surveying strategies. The ranges for tracklets length and uncertainty were taken from Dolado et al. (2016) and adapted to also accommodate the strategy adopted by Siminski et al. (2014) and Zittersteijn et al. (2015). In particular, when surveying the sky, the range for the track length considered was $[0.33{:}14] \deg$ in arc length. This scaled to an observing time of [40 : 3, 600] in GEO and [5,285] in LEO. The uncertainty spanned [0.25, 50] arcsec. The tests were run on GEO object 33595 and LEO object 27869, with simulated observations taken from an hypothetical optical instrument at TFRM observatory starting on 2016 JAN 11 00:04:47.82. Each observation was simulated 100 times using the ephemerides of the object created with SPICE and adding white noise as defined in Eq. (7). Two different outputs need to be analysed: the quality of the point-wise solution and the success rate for the DAIOD algorithm. The point-wise solution was achieved by correcting the Gauss’ solution through Lambert’s algorithm, obtaining $\varvec{\rho }_L$ at the end of Eq. (20).

Fig. 8

DAIOD success rate and quality of point-wise solution for raw LEO, raw GEO and regressed GEO data

Figure 8a and b shows the results for the LEO case, where only a small portion of the observing strategy area does not ensure $100\%$ success rate. This happens when the point-wise solution error is roughly above $5\%$. This behaviour can be compared to that of the GEO observation depicted in Fig. 8c and d. One can clearly see that for the same observing strategy the point-wise solution obtained is poorer and the success rate lower. This is due to the apparent motion of the object with respect to the observing station: for a given tracklet length, more information about the orbit can be inferred from a LEO orbit than from a GEO orbit. Furthermore, Fig. 8c highlights three macro-areas with radically different results: the lower triangle where the algorithm never failed (precise long observations), the upper triangle where the algorithm rarely worked (short and very uncertain observations) and the diagonal belt with a success rate around 80–90%. The reason for failure is the following: the shorter and more uncertain the observation was, the more unreliable the Gauss’ solution fed to the Lambert’s algorithm was. This led to non convergence of the iterative process to refine the state of the object thus falling within hyperbolic orbits and not allowing for a solution. This can also be noticed in Fig. 8d where the distance of the DAIOD point-wise solution from the TLE is shown. Whenever the success rate started dropping in Fig. 8c, the distance of the point solution from the real observation exceeded $5\%$, in accordance with Fig. 8a, and went above $10\%$ for very low values of the success rate. The behaviour noted in Fig. 8a–d determines the overall success rate of the DAIOD+ADS algorithm depicted in Fig. 10a and b. The algorithm unsurprisingly failed where the DAIOD failed, but also in the neighbouring belt. In this region, a point-wise solution was available, but it was the map solution that could not be computed. This was due to solutions of the expansions falling into hyperbolic or re-entering orbits. Indeed, Fig. 10b shows a range uncertainty $\sim 10^4$ km on the verge of failure, which is of the same order of magnitude as the solution.

4.2 DAIOD versus Gooding

To be able to iteratively correct the preliminary solution and obtain an orbit—and its neighbouring variation—out of the six observation angles, it is necessary to work with algorithms that allow the observations to be treated by couples, such that one can implement a differential correction by imposing constraints. Algorithms such as Gibb’s take as input the three observations and retrieve the velocity vector geometrically starting from Gauss’ equations, thus not correcting the preliminary solution for the simplifications in the equations. Gooding’s algorithm, on the other hand, allows for such a differential correction since it checks the state at the central time of observation against the Lambert’s solution obtained with the boundary observations. The point-wise and map expansion solutions for this method have thus been compared against the DAIOD algorithm to test the efficiency.

Two different implementations of Gooding’s algorithm have been considered: the original one where one wants to set to zero the projections of the position vector on the true line of sight and a modified version where the residuals for the central observations are considered instead.

For the point-wise solution a first-order DA expansion was chosen, such that it would match the Newton–Raphson scheme in Gooding’s algorithm. The algorithms were tested with object 36830, whose observations were simulated from the TFRM observatory with uncertainty $\sigma =1$ arcsec. Several observations evenly spaced 30 seconds apart were obtained, thus having $\varDelta \theta = 0.25$ degree as the smallest arc length. All three algorithms delivered the same point-wise solution for the different arc-lengths, the DAIOD and modified Gooding being the fastest and the original Gooding only being slightly slower. This proved that the three algorithms were interchangeable to obtain the point-wise solution.

When introducing the map expansion, however, the original Gooding did not reach convergence: the map rapidly diverged when considering order higher than 2. This is because the rotation matrix needed to calculate the components of the residuals becomes singular when reaching convergence, not allowing for map inversion to obtain the higher-order terms of the polynomial expansion. Hence, the modified version was introduced. The modified Gooding and DAIOD were then compared by computing the point-wise solution and map expansion in DA framework, also including the ADS, to understand the difference in error growth and failure boundary. The methods performed almost equally, having the same failure boundaries and delivering the same point-wise solution and uncertainty size, as can be seen in the map evaluation in Fig. 9. However, the Gooding’s algorithm always had to perform more splits to maintain the same accuracy on the output; the number of splits in Fig. 9 is indeed, respectively, 8 and 11. This can be explained by the simpler form of the DAIOD residuals with respect to the Gooding’s algorithm, the former involving difference between Cartesian components of velocity vectors, while the latter the evaluation of sines and cosines, notably difficult to handle in DA framework. This transformation goes directly in matrix J which is then inverted and included in Eq. (22).

Fig. 9

Point evaluation and splits comparison between DAIOD and DA-based Gooding’s algorithm

4.3 Regression versus raw data

Given the very short nature of the observed tracklets and the apparent null motion of the satellite with respect to the observing stations, the trails associated with the GEO observations usually behave linearly, as underlined in Siminski (2016). Building on the mathematical description defined in Sect. 2.2, linear regression was thus implemented on raw GEO data. In this section, results on simulated observations are presented to understand the influence it had on both the point-wise solution and the dimension of uncertainty for varying length and precision of the tracklet, thus allowing for a comparison with Fig. 8c and d. Figure 8e and f shows results for, respectively, the success rate for the point-wise IOD and distance from TLE when fitted observations were considered instead of raw. Success rate reached $100\%$ for any type of tracklet analysed, and the distance from the TLE solution was never above $10^2$ km. This clearly shows that regression was beneficial to identify a more accurate point solution; indeed, a point solution was always available. Once the improvement of the point-wise solution was proved, the map uncertainty analysis was carried out. To assess the influence that the regression had on the tracklets, the DAIOD+ADS algorithm was performed on regressed data with $1\%$ and $5\%$ CIs. Logically, the more confidence was given to the observations, the smaller the uncertainty on the map was expected to be. Figure 10 depicts the success rate of the DAIOD+ADS algorithm (on the left) and the uncertainty size (on the right). The dashed rectangle includes the TFRM observing strategy, while the circle represents the strategy adopted by Zittersteijn et al. (2015) for the ZimSMART telescope. The presence of known observing strategies in the plots helps the reader understand the change in behaviour due to the regression and choice of confidence. The white line ($\varDelta \rho \simeq 16,000$ km) shows the contour level that corresponds to the size of the largest range uncertainty for the AR. Again, the constraints were $a_\mathrm{min} = 20,000$ km, $a_\mathrm{max} = 60,000$ km, $e_\mathrm{max} = 0.75$.

It is to be underlined that linear regression was not always necessary, as for very long tracklets nonlinearities were non-negligible and thus higher-order terms would have been necessary for the regression. Thus, whenever the p value of the regression was consistent, regression was not performed and raw data were kept. This observation is in accordance with findings from Siminski (2016).

If on the one side the regression clearly improved the point-wise solution for the DAIOD algorithm, the success rate for the DAIOD+ADS algorithm and the size of the uncertainty region were also dependent on the confidence in the observations: the more confidence was given to the observations, the more the failure boundary was pushed towards the north-western part of the plot, when looking at the left column of Fig. 10. This can be noticed in Eq. (13); indeed, $\varDelta Y_i$ depends on both $\varSigma _i$ and t, respectively, the variance and the quantile chosen. Thus, a smaller uncertainty in the angles directly influenced the initial domain, which in return defined the range of the state uncertainty. Regression was able to attenuate the residuals of raw data due to inclusion of more information, thus allowing for a smaller uncertainty, but it is the choice of the CI that mainly drove the size of $\varDelta \varvec{\alpha }_{\hbox {CI}}$ and $\varDelta \varvec{\delta }_{\hbox {CI}}$.

However, the optimal value for this variable can only be found when looking at the success rate of data association: too little confidence may impede the calculation of a solution, while too much confidence may exclude the real solution from the map and thus cause false uncorrelations. Therefore, a careful tuning of the confidence level may optimize the search for correlations avoiding unnecessarily large uncertainties all the while keeping a low rate of false uncorrelations.

Nevertheless, there is still an area of strategies that cannot be handled by the DAIOD+ADS algorithm with enough reliability. Indeed, even with a $5\%$ CI the AR approach remains more attractive for the area containing the ZimSMART strategy, for example. This calls for alternative DA-based methods that build on the AR to treat the observations uncertainty; preliminary results for association based on a DA-based AR are included in Pirovano et al. (2019). This analysis was thus able to define the working environment of the DAIOD+ADS algorithm, showing that it can better constrain the IOD uncertainties for some observing strategies, while it fails for others.

Fig. 10

DAIOD+ADS success rate and range uncertainty for raw and regressed data. Dashed rectangle is TFRM strategy, circle is ZimSMART strategy, and white line is AR approach (Pirovano et al. 2018)

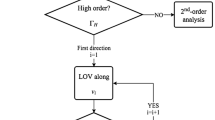
When IOD on raw data is feasible, a second approach that considers all observations in a track is the least squares (LS). The size of the OS obtained with fitted data was then checked against the confidence region with the same confidence level. A DA-based LS has been used followed by the computation of the 2D confidence region. For this purpose, one of the methods proposed in Principe et al. (2019) has been implemented, that is the arbitrary direction (AD). This algorithm takes as input the point solution for the LS and finds the gradient extremal (GE) (Hoffman et al. 1986) also known as LOV (Milani et al. 2005) along $\varvec{v}_1$, which is the main direction of uncertainty of the orbit determination problem. Then, assuming nonlinearities along $\varvec{v}_2$ are negligible, and the algorithm samples the second main direction of uncertainty as a straight line. For this approach DA is especially useful since functions are already available as polynomials. The simulated track had 10 observations evenly spaced every 40 seconds with 1 arcsec accuracy. Figure 11 shows that both the AD and the OS with fitted data can achieve comparable uncertainty regions, much smaller than the OS with raw data. The advantage of the AD is that it can work with tracks in GEO as short as 280 s (Principe et al. 2019), while the DAIOD algorithm could handle up to 360 s long tracklets. On the other hand, performing a LS results in the loss of the functional dependency on the input uncertainty, which is the link to the physical world and only deals with the statistics of residuals. Keeping a polynomial representation of the OS allows to compare different OSs by means of function evaluations to find the area of input values which overlap, thus proving correlation and obtaining a new method for data association as opposed to, for example, the Mahalanobis distance. This new method for data association is part of our current research.

Fig. 11

Comparison between the uncertainty regions on the range and range rate plane for IOD with raw and fitted data and for AD

4.4 DAIOD+ADS and regression on TFRM observations

The results presented in this section were obtained with real observations taken with the Fabra-ROA telescope at Montsec (TFRM), where tracklets were 8 to 14 minutes long with 1 to 4 arcsec precision and observations were retrieved every 2 minutes. This survey campaign obtained 1 to 2 observations of the same objects on consecutive nights. Given the large number of observations in a single tracklet, it was possible to construct the AR with the first three as in Fig. 2 and then sequentially update the AR with each new observation in the tracklet. This method was introduced in Principe et al. (2017) for the update of the confidence region associated with a track and now adjusted to the AR approach for tracklets containing more than three observations. The resulting uncertainty region was compared to the OS and AD approaches in the range–range rate domain. Considering a $3\sigma$ uncertainty on raw observations, the confidence level for fitted observations and confidence region were chosen accordingly. Three different observations were considered: a long precise observation in GEO, a long imprecise observation in GEO and a short precise observation in geostationary transfer orbit (GTO). The tracklets retrieved by the TFRM for GEO observations were 14 minutes long, the precise one having a 1 arcsec precision, while the imprecise one a 2 arcsec precision. The tracklet retrieved for the GTO observation was 8 minutes long with 1 arcsec precision. The length of the tracklets was dictated by the data received by TFRM. However, given the more pronounced relative motion of the GTO satellites with respect to the observatory, more information about the curved path of the orbit was obtained. This allowed for a similar final uncertainty between GTOs and GEOs, despite the shorter observation time. Figures 12a, 13a and 14a show the absolute error for the polynomial approximation with ADS, imposing the threshold for position and velocity truncation errors to be, respectively, 1 km and 1 m/s on each coordinate. These constraints were used for all the computations within the paper. The grey boxes show the estimated extremities of the polynomial expansions calculated in DA with a polynomial bounder. The red boxes are the pruned AR. The sequential update of the AR brings to a comparable uncertainty region, however, with much larger uncertainty in the range rate. One can see that the OS in Fig. 13a exceeds the physical limit of $a=50000$ km imposed on the AR thus having a much larger uncertainty in the range. A possible workaround to avoid it and reduce the OS size is to update the OS by eliminating the sub-domains for which the bounds on semi-major axis and eccentricity fall outside the general AR. Indeed, given a polynomial expression for each sub-domain, it is possible to obtain the bounds on the orbit in any coordinate system. Comparing Fig. 12a with Fig. 13a, one can notice that the imprecise observations originated a much larger uncertainty region. This followed logically from the definition of the OS in Eq. (24). It can be appreciated that in the precise cases depicted in Figs. 12a and 14a the ADS never had to split the domain as one single expansion was able to represent the entire uncertainty of the region. Lastly, in all cases the state of the satellite retrieved through the two-line elements (TLEs)³ was contained in the uncertainty region.

Fig. 12

OS, AR and AD for precise GEO observation from TFRM observatory

Fig. 13

OS+ADS, AR and AD for imprecise GEO observation from TFRM observatory

Fig. 14

OS, AR and AD for precise GTO observation from TFRM observatory

All results obtained with DAIOD are also compared to the AD. Figures 12b, 13b and 14b show the uncertainty regions projected on the range–range rate plane. Both methods find comparable areas and when linear regression is feasible the resulting OS is even smaller, as already highlighted in Fig. 11. While for the AD sampling along the LOV is necessary to follow the nonlinear development of the uncertainty, the DAIOD algorithm automatically found the same region with no point-wise sampling. Furthermore, DAIOD+ADS took 0.8 s for the single polynomial expansions and 56.3 s for the split case depicted in Fig. 13. The AD on the other hand took 113.7 s, 132.3 s and 115.08 s, respectively, for each of the three cases analysed, on top of the IOD and LS computation time. It has to be noted, however, that the AD was implemented in MATLAB and not yet optimized for efficiency. Lastly, a comparison between DA and point-wise approach from the computational point of view is outlined. A single-point solution for IOD took $10^{-3}$ s, while computing the mesh of maps took $\sim 10^0-10^1$ s depending on the number of splits. However, when comparing two OSs to perform data association, several samples are necessary. In Pirovano et al. (2018) $10^5$ samples were necessary due to the very small intersection volume, while Fujimoto and Scheeres (2012) considered $10^5$ to $10^7$ points to sample the AR. This raised the time necessary for the point-wise approach to at least $10^{2}$ s, while performing $10^{5}$ function evaluations took less than a second, thus keeping the full computation below 1  min. The strength of DA is thus clear: when in need for lots of point-wise evaluations, the computational load of creating the map is acceptable to then save time performing function evaluations. This will come in handy when looking for intersecting OSs, which can just be performed as a series of function evaluations, rather than point-wise propagated states retrieved with IOD. Furthermore, partial derivatives between input and output variables are available through the high-order analytical map. This is a key strength of the algorithm: target functions for the data association problem are usually very steep making sampling-based methods not easy to be implemented. In Pirovano et al. (2018) a subset sampling method was implemented due to failure of the classical Monte Carlo to find the intersecting volume. The functional description enables the straightforward implementation of association algorithms based on, for example, bounding and optimization. Lastly, once the functional relation from observations to states is accurately represented, one could analyse the uncertainty mapping between the two spaces. Three approaches have been studied so far in DA: Monte Carlo function evaluation (Armellin et al. 2010), polynomial approximation of the statistical moments (Valli et al. 2014) and polynomial mapping of the probability density function (Armellin and Di Lizia 2016).

As a final test for regression and confidence level, results for TFRM observations with and without regression are shown for different confidence levels. Figure 15 shows the OS of two GEO observations from the TFRM observatory. On the left, the OSs are computed with raw data, while on the right the same is done with fitted data. These plots show the influence of the confidence level on the OS.

Fig. 15

DAIOD+ADS for raw and regressed data from real observations from TFRM

One can appreciate two main outcomes from these plots: regressed data produce a smaller uncertainty region for the same confidence level and their OSs have a concentric behaviour. The first outcome is already highlighted in Fig. 10, indeed by performing a linear regression the uncertainty considered was shrunk and the ADS did not have to perform as many splits. A clear improvement is seen especially in the range uncertainty. The latter outcome is a direct result of the improvement of the point-wise solution, as highlighted in Fig. 8e and f. Overall, one can clearly see the OSs shrank whenever more confidence was given to the observations. However, this may result in the real observation falling out of the uncertainty region if too much confidence is given, as one can see for the highest confidence in Fig. 15c, where the real value is on the border of the uncertainty region. If this confidence level were kept, the association routine may return low probability of correlation. On the other side, if a too large uncertainty were considered, the probability calculation could become computationally expensive.

5 Conclusions

This paper analysed a novel method to perform angles-only IOD, which is the initial estimate of the state of a satellite given six independent angular observations. Building on the Gauss’ solution, the algorithm found the differential correction to improve it by imposing continuity in the velocity vector at central time of observation through the use of two Lambert’s solvers. Once the nominal solution was found, the DAIOD method exploited DA to analytically find the set of orbits that fit the three angular observations with uncertainty, namely the OS. Due to the polynomial nature of the solution, the truncation error had to be controlled: the ADS tool estimated the truncation error and created a mesh of Taylor expansions to accurately describe the entire domain. The final algorithm for IOD was thus called DAIOD+ADS. After testing the usefulness of the ADS for the truncation error control, one further result was obtained for the computation time: indeed, the effort to compute a polynomial map was alleviated when performing several function evaluations, which was much faster than performing single IOD solutions. Thus, the advantage of DA can be appreciated when lots of evaluations are needed, together with the knowledge of the relationship between input and output, clearly stated in the polynomial structure.

The sensitivity of the algorithm to tracklet length and observations uncertainty was then analysed, for both point-wise solution and map expansion. As expected, the longer and more precise the tracklet was, the higher the DAIOD success rate and point-wise solution quality were. It was found that the algorithm could handle LEO and GTO orbits more easily than GEO: this was due to the information about curvature contained in the tracklets which allowed the algorithm to obtain a smaller uncertainty on the output given the same type of observation. The DAIOD+ADS algorithm was also affected by these performances, failing where the DAIOD failed, as expected, but also in the neighbouring region, due to solutions of the map expansion falling into hyperbolic orbits. Then, linear regression on the tracklet was introduced. This dramatically increased the success rate and quality of the point-wise solution. It also improved the size of the map uncertainty, although it was also linked to the confidence level chosen for the data CI. The more confidence was given to the data, the smaller the overall final uncertainty was with an increase in the success rate of the algorithm. However, the choice of the confidence level cannot be carried out independently and needs to be carefully tuned for the data association problem: it needs to be the optimal value that allows for the description of the OS, while keeping low the rate of false uncorrelations—i.e. wrongly non associating observations of the same object. Nevertheless, there is an area of observing strategies, among which there was one specific known real observing strategy, where the algorithm could not provide a reliable IOD solution with accurate uncertainty quantification. The AR approach is thus the most suitable way to deal with such observation strategies. A working boundary for DAIOD+ADS could thus be defined.

The algorithm proposed in this paper is a novel method that takes into account six-dimensional uncertainty in the observations to build a six-dimensional region of solutions—the OS, differently from the AR approach, which fixes four values and then constrains two degrees of freedom and the AD, where a LS is performed and the confidence region is based on residuals. For several observing strategies the proposed approach provides a better description of the IOD uncertainty with respect to the AR approach, showing that there may be more information in the tracklet than that contained in the attributable. However, it has a limited working environment, as for very short and/or very uncertain tracklets, the AR still provides better results. An immediate update of the DAIOD algorithm will be the introduction of physical constraints as in the AR to update the OS by eliminating those sub-domains where the bounds on semi-major axis and eccentricity fall outside the constrained region.

The algorithm most important feature is the ability to represent the OS as a polynomial function of the observation uncertainty, thus making clear the influence of the observations on the output and keeping an analytical approach rather than point-wise sampling, as found in the literature. The analytical description will also enable the straightforward implementation of association algorithms based on bounding and optimization as opposed to sampling. This is the main difference as opposed to the AD solution, which provides a similar uncertainty region but relies on sampling and does not have an analytical dependency on input variables.

The next step of this work foresees the development and implementation of the data association algorithm to analyse multiple OSs and look for intersecting volumes to prove correlation. This part includes the implementation of a DA+ADS numerical propagator to keep an analytical description of the flow. In this framework the optimal confidence level will also be determined. Furthermore, a DA-based treatment of the AR is being thought of to solve the problem of the very short tracklets that the DAIOD+ADS algorithm cannot handle. In this way one would exploit the strength of the AR without giving up analytical representation and uncertainty in the observations. For this type of observations, an efficient DA-based multi-target tracking solver is being studied.