Analytical stability in the Caledonian Symmetric Five-Body Problem

Abstract

In this paper, we develop an analytical stability criterion for a five-body symmetrical system, called the Caledonian Symmetric Five-Body Problem (CS5BP), which has two pairs of equal masses and a fifth mass located at the centre of mass. The CS5BP is a planar problem that is configured to utilise past–future symmetry and dynamical symmetry. The introduction of symmetries greatly reduces the dimensions of the five-body problem. Sundman’s inequality is applied to derive boundary surfaces to the allowed real motion of the system. This enables the derivation of a stability criterion valid for all time for the hierarchical stability of the CS5BP. We show that the hierarchical stability depends solely on the Szebehely constant $C_0$ which is a dimensionless function involving the total energy and angular momentum. We then explore the effect on the stability of the whole system of varying the relative sizes of the masses. The CS5BP is hierarchically stable for $C_0 > 0.065946$. This criterion can be applied in the investigation of the stability of quintuple hierarchical stellar systems and symmetrical planetary systems.

1 Introduction

The five-body system considered in this paper is frequently hierarchical in structure. In hierarchical N-body systems, the masses involved can be divided into subgroups. The relative motion of the subgroups is dominated by their gravitational interaction with one another. Within each subgroup, the relative motion of the masses is dominated by their gravitational interaction with other masses in that subgroup. The subgroups themselves may be likewise divisible into further subgroups in a recursive fashion.

Analytical studies of the stability of hierarchical systems, of three or more bodies, are challenging because of the greater number of variables involved with increasing numbers of bodies and the limitation of just 10 integrals that exist in the gravitational N-body problem. The utilisation of symmetries and/or neglecting the masses of some of the bodies compared to others can simplify the dynamical problem and enable global analytical stability conditions to be derived. These symmetric and restricted few-body systems with their analytical stability criteria can then provide useful information on the stability of the general few-body system when near symmetry or the restricted situation.

Even with symmetrical reductions, analytical stability derivations for four- and five-body problems are rare. In the general three-body problem, Marchal and Saari (1975) and Zare (1976, 1977) derived a stability criterion. For this the energy H and angular momentum c, combine to produce a critical value $c^2 H_{{\mathrm{crit}}}$, which governs the closing of phase space into topologically separate subregions. Different hierarchical arrangements of the system exist in different subregions of the space of real motion. For values of $c^2H > c^2 H_{{\mathrm{crit}}}$, gaps appear in real motion space so that it is physically impossible to go from one hierarchical subregion to another.

In two papers by Loks and Sergysels (1985), and Sergysels and Loks (1987), the three-body $c^2 H$ stability criterion was extended to the general four-body problem. Sundman’s inequality for N bodies was applied to the four-body problem in generalised Jacobi coordinates and zero-velocity surfaces were derived in three-dimensional space. The zero-velocity surfaces define the limits of the three-dimensional regions in which motion can take place.

Sweatman (2002, 2006) analyses the linear stability of a collinear symmetrical four-body system where the masses are mirror images about the centre of mass. These Schubart-like orbits are stable for some mass ratios but unstable for others.

Roy and Steves (2000) and Steves and Roy (2001) developed a symmetrically restricted four-body problem called the Caledonian Symmetric Four-Body Problem (CSFBP). The CSFBP is a planar problem with time symmetry and rotational symmetry about the centre of mass. These authors derived an analytical stability criterion valid for all time, showing that the hierarchical stability of the CSFBP depends solely on a parameter which is a dimensionless function of energy, angular momentum, total mass of the system and the gravitational constant. They called this parameter the Szebehely Constant, $C_0$. The stability criterion has been verified numerically by Széll et al. (2004c). The relationship between the chaotic behaviour of the phase space of the CSFBP and its global stability is analysed by Széll et al. (2004a, 2004b).

More recently, Gong and Liu (2016) derived a stability criterion for the coplanar four-body problem utilising the surfaces of zero velocity and the concepts of Hill stability. They use the criterion to study the Hill stability of the Sun–Jupiter–Ganymede–Callisto system. Chopovda and Sweatman (2018) studied a family of CSFBP symmetric periodic four-body orbits, and their stability, in the plane.

The Caledonian Symmetric Five-Body Problem (CS5BP) is obtained from the CSFBP by adding a fifth, stationary mass at the centre of mass of the system (Shoaib 2004). Alternatively, we may consider the CSFBP as a subset of the CS5BP problem in which the central stationary mass is of negligible mass in relation to the other masses. Some preliminary, primarily numerical, stability results for the CS5BP are presented by Shoaib et al. (2008). In the present paper, we develop a general analytical stability criterion for the CS5BP and investigate how variation of the masses effects the stability of the whole CS5BP system.

In Sect. 2, we define the CS5BP. The equations of motion, the force function and energy integral are given in Sect. 3. The constraints on the system and the regions of allowed motion are considered in Sects. 4, 5 and 6.

The Szebehely constant, $C_0$, is a function of the total energy and angular momentum. In Sect. 7, we explain its role in determining the topological stability of the phase space. This topological stability is explored in Sect. 8, for a range of mass ratios of central body and symmetric pairs. We conclude in Sect. 9.

2 Definition of the Caledonian Symmetric Five-Body Problem (CS5BP)

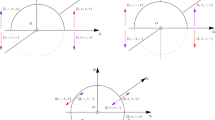
The CS5BP consists of two symmetrical pairs of masses orbiting a stationary central mass. Figures 1 and 2 , respectively, show the initial configuration of the CS5BP and the coplanar configuration at some later time t. We note there is a difference with the previous notation and scaling for the CSFBP. This is detailed in Appendix A.

The CS5BP utilises both past–future symmetry and dynamical symmetry. Past–future symmetry occurs when the dynamical system passes through a mirror configuration. This is a special arrangement of all the bodies so that every velocity vector is perpendicular to all the position vectors from the centre of mass of the system (Roy and Ovenden 1955). The motion after the mirror configuration at $t = 0$ is a mirror image of the motion before $t = 0$.

By additionally ensuring that the two bodies on one side of the centre of mass are balanced symmetrically by the two bodies on the other side of the centre of mass, we gain dynamical symmetry. The evolving orbital motion of the bodies therefore always forms a parallelogram of variable size and orientation.

We assign the five bodies to be point masses $m_{i}~i=0\ldots 4$. With respect to the centre of mass, the position and velocity vectors of the bodies are given by $\mathbf {r}_{i}$ and $V_i=\dot{\mathbf {r}}_{i}$, respectively, $i=0\ldots 4$. The CS5BP has the following conditions:

• 1. $m_0$ is stationary at the centre of mass of the system. Two symmetrically moving pairs are formed by $m_1$ with $m_3$ and $m_2$ with $m_4$, so that

  $$\begin{aligned} m_1=m_3, \qquad m_2=m_4 \end{aligned}$$

  (1)

  and

  $$\begin{aligned} \mathbf {r}_1=-\mathbf {r}_3,\qquad \mathbf {r}_2=-\mathbf {r}_4,\qquad \mathbf {{r}_0=0}, \nonumber \\ \dot{\mathbf {r}}_1=-\dot{\mathbf {r}}_3,\,\qquad \dot{\mathbf {r}}_2=-\dot{\mathbf {r}}_4, \qquad \dot{\mathbf {r}}_0=\mathbf {0}. \end{aligned}$$

  (2)

  These remain valid for all time.

• 2. To ensure past–future symmetry, the initial configuration, $t = 0$, is arranged so that the masses are collinear and all their velocity vectors are perpendicular to all their position vectors (cf. Fig. 1). So initially

  $$\begin{aligned} \mathbf {r}_1\times \mathbf {r}_2=0, \qquad \mathbf {r}_1\cdot \dot{\mathbf {r}}_1=0, \qquad \mathbf {r}_2\cdot \dot{\mathbf {r}}_2=0 . \end{aligned}$$

  (3)

In this paper, we study the coplanar CS5BP and therefore can simplify the velocity vectors further to the coplanar case.

Fig. 1

Initial configuration of the CS5BP (Shoaib et al. 2008)

The total mass of the system is

$$\begin{aligned} M=m_0+2\left( m_1+m_2\right) . \end{aligned}$$

(4)

We introduce mass ratios $\mu _0=\frac{m_0}{M}$, $\mu _1=\frac{m_1}{M}$, $\mu _2=\frac{m_2}{M}$, so then Equation (4) becomes

$$\begin{aligned} \mu _0+2\left( \mu _1+\mu _2\right) =1 \end{aligned}$$

(5)

and we note that

$$\begin{aligned} 0\le \mu _0\le 1, \ \ 0\le \mu _1, \mu _2\le 0.5 . \end{aligned}$$

(6)

3 The equations of motion, the force potential function and the energy integral

The equations of motion for the general five-body system are

$$\begin{aligned} m_{i}\ddot{\mathbf {r}}_{i}=\nabla _{i}U,\qquad i=0,1,2,3,4, \end{aligned}$$

(7)

where U is the force potential function given by

$$\begin{aligned} U = G \sum _{i=0}^4\sum _{j=i+1}^4 \frac{m_im_j}{r_{ij}}, \end{aligned}$$

(8)

${\nabla }_{i}=\mathbf {i}\frac{\partial }{\partial x_{i}}+ \mathbf {j}\frac{\partial }{\partial y_{i}}+\mathbf {k}\frac{\partial }{ \partial z_{i}}, \text { }\mathbf {i,j,k}$ are unit vectors along the rectangular axes $O_{x},O_{y},O_{z}$, respectively, and ${r}_{ij}={|\mathbf {r}}_i-{\mathbf {r}}_j|.$ The centre of mass of the system O is at rest and is located at the origin. $x_{i},y_{i},z_{i}$ are the rectangular coordinates of $m_{i}$.

Using the symmetry conditions of Eq. (2), the force potential function U (Eq. (8)) becomes

$$\begin{aligned} U= & {} G\left[ 2m_0\left( \frac{m_1}{ r_1}+\frac{m_2}{r_2}\right) +\frac{1}{2}\left( \frac{m_1^2}{r_1}+\frac{m_2^2}{r_2} \right) \right. \nonumber \\&\left. +2m_1m_2\left( \frac{1}{r_{12}}+\frac{1}{\sqrt{2\left( r_1^2+r_2^2\right) -r_{12}^2}}\right) \right] . \end{aligned}$$

(9)

Fig. 2

Configuration of the coplanar CS5BP for $t > 0$ (Shoaib et al. 2008)

The energy $H=T - U$, where T is the kinetic energy. Since $\ m_0$ is stationary, it is not involved in the kinetic energy T. Similarly, its fixed location at the centre of mass means that it is absent from the angular momentum c and the moment of inertia I. Therefore

$$\begin{aligned} T = m_1\dot{r}_1^2+m_2\dot{r}_2^2, \qquad I = 2\left( m_1r_1^2+m_2r_2^2\right) \end{aligned}$$

(10)

and

$$\begin{aligned} H= & {} \left( m_1\dot{r}_1^2+m_2\dot{r}_2^2\right) \nonumber \\&-G\left[ 2m_0\left( \frac{m_1}{r_1}+\frac{m_2}{r_2}\right) +\frac{1}{2}\left( \frac{m_1^2}{r_1}+\frac{m_2^2}{r_2} \right) \right. \nonumber \\&\left. +2m_1m_2 \left( \frac{1}{r_{12}} +\frac{1}{\sqrt{2\left( r_1^2+r_2^2\right) -r_{12}^2}} \right) \right] . \end{aligned}$$

(11)

The energy has a constant value $H=-E_0$, so that $E_0$ will be positive for a gravitationally bound system. (A gravitationally bound system is one where it is impossible for all the masses to escape, i.e. at least two masses must remain close to one another.) Alongside the mass ratios $\mu _{i}$, we introduce the dimensionless variables $\rho _1$, $\rho _2$ and $\rho _{12}$, and dimensionless time $\tau$, where:

$$\begin{aligned} \rho _1=\frac{E_0r_1}{GM^2}\;;\quad \rho _2= \frac{E_0r_2}{GM^2}\;;\quad \rho _{12}=\frac{E_0r_{12}}{GM^2} { \;;\quad \tau =\frac{{E}_{{0}}^{{3/2}}{t}}{{GM}^{{5/2}}}.} \end{aligned}$$

So now, dividing by $E_0$, Eq. (11) becomes

$$\begin{aligned} -1= & {} \mu _1\left( \frac{d\rho _1}{d\tau }\right) ^2+\mu _2\left( \frac{d\rho _2}{d\tau }\right) ^2 -2\mu _0\left( \frac{\mu _1}{\rho _1}+\frac{\mu _2}{\rho _2}\right) \nonumber \\&-\frac{1}{2}\left( \frac{\mu _1^2}{\rho _1} +\frac{\mu _2^2}{\rho _2}\right) -\frac{2\mu _1\mu _2}{\rho _{12}} -\frac{2\mu _1\mu _2}{\sqrt{2\left( \rho _1^2+\rho _2^2\right) -\rho _{12}^2}} . \end{aligned}$$

(12)

4 The boundary surface for real motion

For the CSFBP, Steves and Roy (2001) show how the region of real motion can be progressively constrained with boundaries arising from the kinematic constraints, the surfaces of zero velocity using the energy integral, and finally the surfaces of separation using Sundman’s Inequality. A similar approach can be used in the CS5BP.

Because of dynamical symmetry, only the motions of $m_1$ and $m_2$ are needed to determine the motion of the whole CS5BP system. Their positions are fully described by providing the distances $r_1$, $r_2$ and $r_{12}$. The regions of possible motion of the bodies $m_1$ and $m_2$ can therefore be displayed as a boundary surface in the corresponding three-dimensional space in the dimensionless coordinates $\rho _1$, $\rho _2$, and $\rho _{12}$.

An arbitrary point $(\rho _1,\rho _2,\rho _{12})$ in this space has the following kinematic constraints

$$\begin{aligned} |\rho _1-\rho _2|\le \rho _{12}\le \rho _1+\rho _2 . \end{aligned}$$

(13)

Quintuple collision, the simultaneous collision of all five bodies, corresponds to the origin of the $\rho _1\rho _2\rho _{12}$ space. Apart from this, there are four distinct types of two- and three-body collisions that may occur:

• 1. 12 Collision. If $\rho _{12}=0$, then $m_1$ collides with $m_2$, and $m_3$ collides with $m_4$. The inequalities (13) are only satisfied when $\rho _2=\rho _1$.

• 2. 14 Collision. If $\rho _{12}=\sqrt{2(\rho _1^2+\rho _2^2)}$, then $m_1$ collides with $m_4$, and $m_2$ collides with $m_3$. The inequalities (13) are only satisfied when $\rho _1=\rho _2$ and so $\rho _{12}=2\rho _1$.

• 3. 13 Collision. If $\rho _1=0$ then $m_1$, $m_3$ and $m_0$ collide in the centre. The inequalities (13) are only satisfied when $\rho _{12}=\rho _2$.

• 4. 24 Collision. If $\rho _2=0$ then $m_2$, $m_4$ and $m_0$ collide in the centre. The inequalities (13) are only satisfied when $\rho _{12}=\rho _1$.

For real motion, the kinetic energy must be greater than or equal to zero ($U+H\ge 0$). This provides zero-velocity surfaces that further constrain and bound the region of real motion. Real motion for the CS5BP takes place in four tube-like regions of the $\rho _1\rho _2\rho _{12}$ space (Fig. 3). This is similar to the special case of the CSFBP (Roy and Steves 2000). Near the origin, the four tubes connect forming a region in which strong interplay between all of the bodies occurs. Each tube begins near the origin, contains the line corresponding to one of the four distinct types of two- and three-body collisions and corresponds to a particular five-body hierarchy. The four hierarchies are:

• 1. 12 Hierarchy. A double binary hierarchy where $m_1$ and $m_2$ orbit their centre of mass $C_{12}$ and $m_3$ and $m_4$ orbit their centre of mass $C_{34}$. The centres of mass $C_{12}$ and $C_{34}$ orbit each other about $m_0$ at the centre of mass of the five-body system. The 12 hierarchy is the allowed motion in the tube located along $\rho _1= \rho _2,\rho _{12}=0.$

• 2. 14 Hierarchy. A double binary hierarchy where $m_1$ and $m_4$ orbit their centre of mass $C_{14}$ and $m_2$ and $m_3$ orbit their centre of mass $C_{23}$. The centres of mass $C_{14}$ and $C_{23}$ orbit each other about $m_0$ at the centre of mass of the five-body system. The 14 hierarchy is the allowed motion in the tube located along $\rho _1= \rho _2,\rho _{12}=2\rho _1.$

• 3. 13 Hierarchy. A single trinary hierarchy where $m_1$ and $m_3$ orbit $m_0$ at their centre of mass as a central trinary, i.e. they form a three-mass group at the centre of the system. The other masses $m_2$ and $m_4$ orbit around this trinary. The 13 hierarchy is the allowed motion in the tube located along $\rho _1=0$ and the $\rho _2\rho _{12}$ plane.

• 4. 24 Hierarchy. A single trinary hierarchy where $m_2$ and $m_4$ orbit $m_0$ at their centre of mass as a central trinary. The other masses $m_1$ and $m_3$ orbit around this trinary. The 24 hierarchy is the allowed motion in the tube located along $\rho _2=0$ and the $\rho _1\rho _{12}$ plane.

Fig. 3

General tube-like structure of the surfaces of zero velocity for the CS5BP. (This figure is based on the corresponding CSFBP diagram of Roy and Steves (2000)

A further sculpting of the $\rho _1 \rho _2 \rho _{12}$ space for real motion can be found using the generalised Sundman inequality (Muller 1986; Roy 2005).

$$\begin{aligned} U+H\ge \frac{c^2}{2I}. \end{aligned}$$

(14)

This inequality (14) further decreases the space available for real motion. It introduces forbidden regions near the origin.

For the CS5BP, the inequality (14) can be written solely in terms of $r_1$, $r_2$ and $r_{12}$

$$\begin{aligned}&G\left[ 2m_0\left( \frac{m_1}{r_1}+\frac{m_2}{r_2}\right) + \frac{1}{2}\left( \frac{m_1^2}{r_1}+\frac{m_2^2}{r_2} \right) + \frac{2m_1m_2}{r_{12}} \ \ \ \ \right. \nonumber \\&\quad \left. + \frac{2m_1m_2}{\sqrt{2\left( r_1^2+r_2^2\right) -r_{12}^2}} \right] \ge \frac{c^2}{4(m_1r_1^2+m_2r_2^2)}+E_0. \end{aligned}$$

(15)

We introduce the mass ratios $\mu _{i}$, the dimensionless variables $\rho _1$, $\rho _2$ and $\rho _{12}$, and a new dimensionless quantity

$$\begin{aligned} C_0=\frac{c^2E_0}{G^2M^{5}}, \end{aligned}$$

(16)

called the Szebehely constant (Steves and Roy 2001), and divide by $E_0$ (we assume $E_0 \ne 0$). Then, our version of Sundman’s inequality (15) becomes

$$\begin{aligned}&2\mu _0\left( \frac{\mu _1}{\rho _1}+\frac{\mu _2}{\rho _2}\right) +\frac{1}{2}\left( \frac{\mu _1^2}{\rho _1}+\frac{\mu _2^2}{\rho _2}\right) +\frac{2\mu _1\mu _2}{\rho _{12}} \ \ \nonumber \\&\quad +\frac{2\mu _1\mu _2}{\sqrt{2\left( \rho _1^2+\rho _2^2\right) -\rho _{12}^2}} \ge \frac{C_0}{4\left( \mu _1\rho _1^2+\mu _2\rho _2^2\right) }+1. \end{aligned}$$

(17)

Recall that, if the mass ratios $\mu _0$ and $\mu _1$ are known, then mass ratio $\mu _2$ is determined by equation (5). Thus, for a CS5BP system, with given values of $\mu _0$ and $\mu _1$ and Szebehely constant (i.e. angular momentum and energy combination) $C_0$, equations (17) and (13) define a surface in dimensionless $\rho _1 \rho _2 \rho _{12}$ coordinate space that confines the possible motion.

If any region of the accessible $\rho _1 \rho _2 \rho _{12}$ space is totally disconnected from any other, then the hierarchical arrangement of the system in that region cannot physically evolve into the hierarchical arrangements possible in the other regions of real motion. Thus, a CS5BP system existing in that hierarchical arrangement would be hierarchically stable for all time. The topology or disconnectedness of the accessible $\rho _1 \rho _2 \rho _{12}$ space, that is contained within the boundary surface given by (17) and (13), can therefore provide a stability criterion for the system.

5 Determining the regions of allowed motion in the CS5BP

In this section, we further develop explicit formulae for the boundary surface of real motion. These will enable us to draw the surface and identify the critical points for which the topology, and therefore the hierarchical stability of the system, changes.

It is useful to parameterise the surface in terms of the variables

$$\begin{aligned} y_{i}=\frac{\rho _{i}}{\rho _{n}}, \text { for } i=1,2, \text { and }x_{12}=\frac{\rho _{12}}{\rho _{n}}, \end{aligned}$$

(18)

where $\rho _{n}=\max (\rho _1,\rho _2)$. This allows us to study the phase space in two parts.

• Case (i): if $\rho _1\ge \rho _2$, then $\rho _{n}=\rho _1$; $y_1=1$; $y_2=\frac{\rho _2}{\rho _1}$ and $x_{12}=\frac{\rho _{12}}{\rho _1}$.

• Case (ii): if $\rho _2\ge \rho _1$, then $\rho _{n}=\rho _2$; $y_2=1$; $y_1=\frac{\rho _1}{\rho _2}$ and $x_{12}=\frac{\rho _{12}}{\rho _2}$.

In the new variables, Sundman’s inequality takes the form

$$\begin{aligned}&\frac{1}{\rho _n}\left[ 2\mu _0\left( \frac{\mu _1}{y _1}+\frac{\mu _2}{y _2}\right) +\frac{1}{2}\left( \frac{\mu _1^2}{y _1}+\frac{\mu _2^2}{y _2}\right) +\frac{2\mu _1\mu _2}{x _{12}} \right. \nonumber \\&\quad \left. +\frac{2\mu _1\mu _2}{\sqrt{2\left( y _1^2+y _2^2\right) -x _{12}^2}}\right] \ge \frac{1}{\rho _n^2} \frac{C_0}{4\left( \mu _1y _1^2+\mu _2y_2^2\right) }+1 \end{aligned}$$

(19)

and the kinematic constraints (13) become

$$\begin{aligned} |y_1-y_2|\le x_{12}\le y_1+y_2 . \end{aligned}$$

(20)

Taking the equality sign in (19), we obtain the following quadratic equation which defines the boundary surface between real and imaginary motion,

$$\begin{aligned} \rho _{n}^2-A\rho _{n}+B=0, \end{aligned}$$

(21)

where

$$\begin{aligned} A= & {} 2\mu _0\left( \frac{\mu _1}{y_1}+\frac{\mu _2}{y_2}\right) +\frac{1}{2}\left( \frac{\mu _1^2}{y_1}+\frac{\mu _2^2}{y_2}\right) \nonumber \\&+2\mu _1\mu _2\left( \frac{1}{x_{12}}+\frac{1}{\sqrt{2\left( y_1^2+y_2^2\right) -x_{12}^2}}\right) , \end{aligned}$$

(22)

and

$$\begin{aligned} B=\frac{C_0}{4\left( \mu _1y_1^2+\mu _2y_2^2\right) }. \end{aligned}$$

(23)

The solution of the above quadratic equation (21) is

$$\begin{aligned} \rho _{n}=\frac{1}{2}\sqrt{\frac{C}{\mu _1y_1^2+\mu _2y_2^2}}\left( 1\pm \sqrt{1-\frac{C_0}{C }}\right) , \end{aligned}$$

(24)

where

$$\begin{aligned} C=A^2\left( \mu _1y_1^2+\mu _2y_2^2\right) , \end{aligned}$$

(25)

a function of $y_1$, $y_2$ and $x_{12}$. Thus for Case (i), $\rho _1 \ge \rho _2$, when $y_1=1$,

$$\begin{aligned} \rho _1=\frac{1}{2}\sqrt{\frac{C}{\mu _1+\mu _2y_2^2}}\left( 1\pm \sqrt{1-\frac{C_0}{C}}\right) , \end{aligned}$$

(26)

where

$$\begin{aligned} C= & {} \left( \mu _1+\mu _2y_2^2\right) \times \left[ 2\mu _0\left( \mu _1+\frac{\mu _2}{y_2}\right) \right. \nonumber \\&+ \frac{1}{2}\left( \mu _1^2+\frac{\mu _2^2}{y_2^2}\right) \nonumber \\&+\left. 2\mu _1\mu _2 \left( \frac{1}{x_{12}}+\frac{1}{\sqrt{2\left( 1+y_2^2\right) -x_{12}^2}}\right) \right] ^2, \end{aligned}$$

(27)

with the constraints, from (18) and (20),

$$\begin{aligned} 0\le y_2\le 1 \qquad 1-y_2\le x_{12}\le 1+y_2 . \end{aligned}$$

(28)

For a given $\rho _1$, the values of $\rho _2$ and $\rho _{12}$ can be reconstructed by

$$\begin{aligned} \rho _2=y_2\rho _1\qquad \rho _{12}=x_{12}\rho _1. \end{aligned}$$

(29)

For Case (ii), $\rho _2 \ge \rho _1$, we can proceed similarly. The calculation is essentially the same as for Case (i) but with the indices 1 and 2 exchanged.

These cases, (i) and (ii), provide an explicit set of formulae for determining points $(\rho _1,\rho _2,\rho _{12})$ on the boundary surface. For Case (i), the parameters $y_2$ and $x_{12}$ are varied within the constraints (28). For Case (ii), there are similar constraints for $y_1$ and $x_{12}$. In the two cases, $y_2$ and $y_1$, respectively, are the gradients of straight lines through the origin O in the $\rho _1\rho _2$ plane. Further, $x_{12}$ is the gradient of a straight line through the origin O in either the $\rho _1\rho _{12}$ or the $\rho _2\rho _{12}$ plane.

In the CSFBP, Steves and Roy (2001) found that, as $C_0$ is increased, forbidden regions near the origin grow to the point where they meet the boundary walls of the tubes, resulting in disconnected regions. This is also the case for the CS5BP.

6 The projection of the space of real motion into the $\rho _1\rho _2$ plane

A useful tool, for assessing the connectivity of the regions of motion, is the projection of the extreme values of the boundary surface of real motion onto the $\rho _1\rho _2$ plane (Steves and Roy 2001; Shoaib et al. 2008).

6.1 Maximum extension of the real motion projected in $\rho _1 \rho _2$ space

Equation (13) and its equivalent in the new variables (20) give the extreme values of $\rho _{12}$ and $x_{12}$, respectively. The intersection of the kinematic constraints with the boundary surface (24) gives curves when projected onto the $\rho _1 \rho _2$ plane. These display the four tubes as three arms. The two tubes located near $\rho _1\approx \rho _2$ lie one on top of the other in the projection, giving one arm near $\rho _1\approx \rho _2$.

The projection curves of the maximum widths of the tubes can be found by substituting the equalities of (20) into the boundary surface (24). Both limits $x_{{12}_{+}}=y_1+y_2$ and $x_{{12}_{-}}=|y_1-y_2|$ give the same equations, indicating that the maximum widths at the $x_{{12}_{+}}$ upper location and the $x_{{12}_{-}}$ lower location are identical.

We find the equations giving the maximum projections in the two cases. For Case (i), $\rho _1 \ge \rho _2$, the behaviour of C depends solely on $y_2$, and we write $C=C_e(y_2)$. Then, Eq. (24) becomes

$$\begin{aligned} \rho _1=\frac{1}{2}\sqrt{\frac{C_{e}(y_2)}{\mu _1+\mu _2y_2^2}}\left( 1\pm \sqrt{1-\frac{C_0}{C_{e}(y_2)}}\right) , \end{aligned}$$

(30)

where

$$\begin{aligned} C_{e }(y_2)= & {} \left( \mu _1+\mu _2y_2^2\right) \left[ 2\mu _0\left( \mu _1+\frac{\mu _2}{y_2}\right) \right. \nonumber \\&\left. +\frac{1}{2} \left( \mu _1^2+\frac{\mu _2^2}{y_2}\right) +4\mu _1\mu _2\frac{1}{1-y_2^2} \right] ^2. \end{aligned}$$

(31)

The corresponding variable $\rho _2$ is given by

$$\begin{aligned} \rho _2=y_2\rho _1. \end{aligned}$$

(32)

As before, Case (ii), $\rho _2 \ge \rho _1$, is essentially the same as Case (i) but with the indices 1 and 2 exchanged. We have

$$\begin{aligned} \rho _2=\frac{1}{2}\sqrt{\frac{C_{e}^{\prime }(y_1)}{\mu _1y_1^2+\mu _2}}\left( 1\pm \sqrt{1-\frac{C_0}{C_{e}^{\prime }(y_1)}}\right) , \end{aligned}$$

(33)

where

$$\begin{aligned} C_{e }^{\prime }(y_1)= & {} \left( \mu _1y_1^2+\mu _2\right) \left[ 2\mu _0\left( \frac{\mu _1}{y_1}+\mu _2\right) \right. \nonumber \\&\left. +\frac{1}{2}\left( \frac{\mu _1^2}{y_1}+\mu _2^2\right) +4\mu _1\mu _2\frac{1}{ 1-y_1^2}\right] ^2 \end{aligned}$$

(34)

and $\rho _1=y_1\rho _2$.

Fig. 4

$\mu _0=\mu _1=\mu _2=0.2$ (the 5-body equal masses case): a, b: the projection of the boundary surface onto the $\rho _1\rho _2$ plane (a) $C_0=R_1=0.0392219$ (b) $C_0=R_4=0.0655514$ (given by Eqs. (30) and (32) for $\rho _1 \ge \rho _2$); c, d: The corresponding cross sections of the boundary surface in the vertical $\rho _1\rho _{12}$ plane ($\rho _1=\rho _2$) (c) $C_0=R_1=0.0392219$ (d) $C_0=R_4=0.0655514$. The forbidden regions, where motion is impossible, are shaded black

Figure 4a, b shows two examples of such projections for a given $\mu _0$, $\mu _1$ and $C_0$. (Recall that there are only two independent mass ratios required since $\mu _0+2(\mu _1+\mu _2)=1$.) In Fig. 4a, $C_0=R_1$, which is the critical minimum value at which the regions of real motion (the tubes in Fig. 3) first become disconnected within the junction where the four tubes connect. In Fig. 4b, $C_0=R_4$, which is the critical value at which the three-dimensional regions of real motion, become fully disconnected. (We discuss the values $R_1, \ldots , R_4$ in more detail in Sect. 7.)

Real motion can only take place within the four-tube structure, which has been projected onto the white arms shown. For $C_0 \ne 0$, a forbidden region (black) exists at the origin, which grows as $C_0$ is increased to meet the forbidden region surrounding the exterior of the arms. Orbits in the $\rho _2<<\rho _1$ arm are in the 24 hierarchy. Likewise, those in the $\rho _2\approx \rho _1$ arm are in either the 12 or 14 hierarchies. Orbits within the $\rho _1<<\rho _2$ arm are in the 13 hierarchy. The connectedness of the three arms in Fig. 4a, for $C_0=0.0392219$, indicates that it is possible to change from one hierarchical arrangement to another. Figure 4b gives the projection for $C_0=C_{{\mathrm{crit}}}=0.0655514$, a critical value, at which the regions of real motion become disconnected. In Sect. 7, we give the derivation of this critical value $C_{{\mathrm{crit}}}$. For $C_0>C_{{\mathrm{crit}}}$, the arms are completely disconnected. No movement is permitted between different hierarchies. The system is therefore hierarchically stable.

6.2 The minima of the boundary surface of real motion projected in $\rho _1 \rho _2$ space

The minima of the boundary surface also provide information on the three-dimensional shape of the surface. Projection of the curves indicating where the minima are located in the $\rho _1\rho _2$ plane are useful in identifying when, as $C_0$ is increased, forbidden regions first appear within the boundary surface. Motion is still possible from one hierarchy to another but now this has to avoid the forbidden region within the junction where the four tubes connect.

For example, Fig. 4c and d shows the cross section of the boundary surface in the vertical $\rho _1\rho _{12}$ plane ($\rho _1=\rho _2$) for the five-body equal mass case. These figures have the same values of $\mu _0$, $\mu _1$ and $C_0$, and correspond to, Fig. 4a, b, respectively. Orbits in the $\rho _{12}\approx 2\rho _{1}$ arm (corresponding to the upper central tube) are in the 14 hierarchy. This arm has an upper boundary of the line $\rho _{12}=2\rho _{1}$ corresponding to the 14 collision described in Sect. 4, collision case (ii). Orbits in the $\rho _{12}\approx 0$ arm (corresponding to the lower central tube) are in the 12 hierarchy. The line $\rho _{12}=0$ corresponds to the 12 collision described in Sect. 4, collision case (i).

Figure 4c gives the cross section for $C_0=R_1=0.0392219$. In three dimensions, real motion is still possible by moving around the forbidden point visible in the two-dimensional cross section. Figure 4d gives the cross section for $C_0=R_4=0.0655514$. Both Fig. 4c, d shows that regions of allowed motion (white) exist, forming the $\rho _{12}\approx 2\rho _1$ arm (upper central tube) beyond the forbidden zone at the origin.

Steves and Roy (2001) considered the special case of the four-body equal-mass CSFBP, with a zero central mass. For $C_0$ values corresponding to the minimum for the boundary surface, they showed that it was necessary to pass through a 13 or a 24 hierarchy (Fig. 3, side tubes) in order to move between the double binary 14 and 12 hierarchies (Fig. 3, upper central tube to the lower central tube).

For a given $y_1,y_2$, the minima of $\rho _n$ with respect to $x_{12}$ occur at $x_{12}=\sqrt{y_1^2+y_2^2}$. We find the projection of the minima onto the $\rho _1 \rho _2$ plane in the two cases. For Case (i), $\rho _1 \ge \rho _2$, Eq. (24) becomes

$$\begin{aligned} \rho _1=\frac{1}{2}\sqrt{\frac{C_{m}(y_2)}{\mu _1+\mu _2y_2^2}}\left( 1\pm \sqrt{1-\frac{C_0}{C_{m}(y_2)}}\right) , \end{aligned}$$

(35)

where

$$\begin{aligned} C_{m }(y_2)= & {} \left( \mu _1+\mu _2y_2^2\right) \left[ 2\mu _0\left( \mu _1+\frac{\mu _2}{y_2}\right) \right. \nonumber \\&\left. +\frac{1}{2}\left( \mu _1^2+\frac{\mu _2^2}{y_2}\right) + 4\frac{\mu _1\mu _2}{\sqrt{1+y_2^2}} \right] ^2. \end{aligned}$$

(36)

For Case (ii), $\rho _2 \ge \rho _1$, equation (24) becomes

$$\begin{aligned} \rho _2=\frac{1}{2}\sqrt{\frac{C_{m}^{\prime }(y_1)}{\mu _1y_1^2+\mu _2}}\left( 1\pm \sqrt{1-\frac{C_0}{C_{m}^{\prime }(y_1)}}\right) , \end{aligned}$$

(37)

where

$$\begin{aligned} C_{m }^{\prime }(y_1)= & {} \left( \mu _1y_1^2+\mu _2\right) \left[ 2\mu _0\left( \frac{\mu _1}{y_1}+\mu _2\right) \right. \nonumber \\&\left. +\frac{1}{2}\left( \frac{\mu _1^2}{y_1}+\mu _2^2\right) +4\frac{\mu _1\mu _2}{ \sqrt{y_1^2+1}}\right] ^2. \end{aligned}$$

(38)

7 The Szebehely ladder and Szebehely constant

Through the projections in the $\rho _1\rho _2$ plane given by the maximum extensions and the minima of the boundaries of real motion in $\rho _1\rho _2\rho _{12}$ space, we can study the topology of the boundary surfaces and thus gain knowledge on the hierarchical stability of the system. The topology changes as $C_0$ increases. The critical values of $C_0$ at which the space becomes disconnected therefore provide a stability criterion.

The value of $\rho _n(y_1,y_2)$, for the maximum extensions and the minima projections, explicitly depends on the value of the appropriate C-function: $C_e$, $C_e^{\prime }$, $C_m$ or $C_m^{\prime }$. The function $\rho _n$ has two real roots, a single repeated real root or two conjugate imaginary roots, if that C-function is greater than, equal to or less than $C_0$, respectively.

The quantities $C_e(y_2)$, $C_e^{\prime }(y_1)$,$C_m(y_2)$, $C_m^{\prime }(y_1)$ therefore give information on the point at which the topology of the projections changes. The critical changes occur when the C-value is equal to $C_0$, the single repeated real root solution. For example, $C_e$ can be evaluated for the range of $y_2$ from 0 to 1. (Recall that $y_2$ is the gradient of a straight line through the origin O in the $\rho _1\rho _2$ plane.) The minimum value of $C_e(y_2)=C_e^{{\mathrm{min}}}$ is the first value of $C_0$, as it is increased, where there is only one solution ($\rho _1,\rho _2$) to the maximum projection curve. For $C_0>C_e^{{\mathrm{min}}}$, there are no solutions ($\rho _1,\rho _2$) and the projection becomes disconnected indicating the presence of a stable system.

The minima of the four C-functions, each of which indicate a point of change in the topology, can be thought of as the rungs of a ladder, that Steves and Roy (2001) call the Szebehely ladder. The rungs of the ladder, $R_1=C_m^{{\mathrm{min}}}$, $R_2=C_m^{\prime {\mathrm{min}}}$, $R_3=C_e^{{\mathrm{min}}}$ and $R_4=C_e^{\prime {\mathrm{min}}}$, solely depend on the masses of the system. They are invariant under other changes to the initial conditions, the angular momentum c, or energy H of the system.

Fig. 5

Szebehely Ladder for $\mu _0=0.1$ $\mu _1=0.15$ and $\mu _2=0.30$

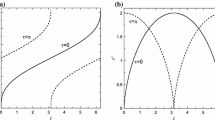
Both $y_1$ and $y_2$ are between 0 and 1. Therefore, we may plot relations $C_{e}(y_2)$, $C_{e}^{\prime }(y_1)$, $C_{m}(y_2)$, $C_{m}^{\prime }(y_1)$ in the same figure C against y. Figure 5 shows the curves of the four C-functions for the case $\mu _0=0.1$ $\mu _1=0.15$ and $\mu _2=0.30$. From the definitions of the C-functions, in equations (31), (34), (36) and (38), we deduce that all the C-functions tend to infinity as the y-value tends to zero and further both the ratio of $C_e$ to $C_m$ and the ratio of $C_e^{\prime }$ to $C_m^{\prime }$ tend to one. Additionally, $C_e$ and $C_e^{\prime }$ tend to infinity, and their ratio tends to one, as the y-value tends to one. Finally, both $C_m$ and $C_m^{\prime }$ tend to the value

$$\begin{aligned} \left( \mu _1+\mu _2\right) \left[ 2\mu _0\left( {\mu _1}+\mu _2\right) +\frac{1}{2}\left( {\mu _1^2}+\mu _2^2\right) +2\sqrt{2} (\mu _1\mu _2)\right] ^2, \end{aligned}$$

(39)

as the y-value tends to one. This is 0.0336682 for the example (Fig. 5).

The rungs of the Szebehely ladder are formed by the minima of the four curves. The system’s stability depends on the location of its Szebehely constant $C_0$ with respect to these rungs. Thus, when

• 1. $C_0>R_1$, there is a region of forbidden motion near the origin within the boundary surface for $\rho _1\ge \rho _2$. This partially blocks the junction between the four tubes.

• 2. $C_0>R_2$, there is a region of forbidden motion near the origin within the boundary surface for $\rho _2\ge \rho _1$. This partially blocks the junction between the four tubes.

• 3. $C_0>R_3$, the arms in the projection of the maximum extensions for $\rho _1\ge \rho _2$ are disconnected and the 24 hierarchy is stable.

• 4. $C_0>R_4$, the arms in the projection of the maximum extensions for $\rho _2\ge \rho _1$ are disconnected and the 13 hierarchy is stable.

When $C_0>$ max$(R_3,R_4)$, all arms are disconnected and the system is hierarchically stable.

• 1. If $\mu _2>\mu _1$, then $R_4>R_3>R_2>R_1$.

• 2. If $\mu _1>\mu _2$, then $R_3>R_4>R_1>R_2$.

• 3. If $\mu _1=\mu _2$, then $R_2=R_1$ and $R_3=R_4$.

Therefore the critical value of $C_0$ at which the whole system becomes hierarchically stable for all time is

$$\begin{aligned} C_{{\mathrm{crit}}}=\max (R_3,R_4)=\left\{ \begin{array}{c} R_3=C_{e}^{{\mathrm{min}}}\qquad \text {if }\mu _1>\mu _2 \\ R_4=C_{e}^{\prime {\mathrm{min}}} \qquad \text {if }\mu _2>\mu _1 \end{array} \right. . \end{aligned}$$

(40)

$\mu _1=\mu _2$ is the special case of equal masses where $C_0> C_{{\mathrm{crit}}}=R_3=R_4$ gives total hierarchical stability at one critical point. Otherwise, hierarchical stability occurs in two stages $C_0>C_{{\mathrm{crit}}_1}=R_3$ and $C_0>C_{{\mathrm{crit}}_2}=R_4$. If $\mu _0=0$, then we have the special case of the CSFBP discussed by Steves and Roy (2001).

We now present several examples, for a range of mass ratios, to illustrate how rungs of the Szebehely ladder can be computed solely from $\mu _0$, $\mu _1$. Then using the value of the Szebehely constant $C_0$ for the system, which depends on the initial conditions, the hierarchical stability of the system can be determined.

8 The stability of the CS5BP systems with a range of different mass ratios

8.1 The equal mass CS5BP

The equal-mass CS5BP has $\mu _0=\mu _1=\mu _2=0.2$. In this case, there exist only two rungs of the Szebehely ladder; since $C_m=C_m^{\prime }$ and $C_e=C_e^{\prime }$, viz.

$$\begin{aligned} C_{m }(y)= & {} \frac{1}{5}\left( 1+y^2\right) \left[ \frac{1}{10}\left( 1+ \frac{1}{y}\right) +\frac{4}{25\sqrt{1+y^2}}\right] ^2, \end{aligned}$$

(41)

$$\begin{aligned} C_{e }(y)= & {} \frac{1}{5}\left( 1+y^2\right) \left[ \frac{1}{10}\left( 1+ \frac{1}{y}\right) +\frac{4}{25\left( 1-y^2\right) }\right] ^2 , \end{aligned}$$

(42)

where $0\le y\le 1$.

The minimum values of $C_{m }(y)$ and $C_{e }(y)$ form the two rungs of the Szebehely Ladder. The minimum values of $C_{m }$ and $C_{e }$ are $R_1=0.039222$ and $R_4=0.065551$, respectively. $R_1$ and $R_4$ occur at $y=1$ and $y=0.472$, respectively.

Figure 4a shows the projection of the maximum extensions for $C_0=R_1$. The phase space remains connected but a small forbidden region exists near the origin. This forbidden region grows as $C_0$ is increased until at $C_0=R_4$, at the highest rung of the ladder, the phase space becomes disconnected (cf. Fig. 4b). The five-body equal-mass CS5BP is hierarchically stable for values of $C_0$ greater than $R_4=0.065551$.

8.2 Four equal masses with a varying central mass $\mu _0$

In this case there is only one independent mass ratio since, from (5), $\mu _1=\mu _2=\frac{1}{4}(1-\mu _0)$. Only two rungs of the Szebehely ladder exist as $C_{m}=C_{m}^{\prime }$ and $C_{e}=C_{e}^{\prime }$. Thus,

$$\begin{aligned} C_{m}= & {} \mu _1\left( 1+y^2\right) \left[ \left( 2\mu _0\mu _1+\frac{\mu _1^2}{2} \right) \left( 1+\frac{1}{y}\right) +\frac{4\mu _1^2}{\sqrt{1+y^2}}\right] ^2, \end{aligned}$$

(43)

$$\begin{aligned} C_{e}= & {} \mu _1\left( 1+y^2\right) \left[ \left( 2\mu _0\mu _1+\frac{\mu _1^2}{2} \right) \left( 1+\frac{1}{y}\right) +\frac{4\mu _1^2}{\left( 1-y^2\right) }\right] ^2. \end{aligned}$$

(44)

Figures 6 and 7 show the projections of the maximum extensions onto the $\rho _1\rho _2$ plane for two typical cases:

• 1. A small central mass; $\mu _0=0.01,\mu _1=\mu _2=0.2475$ (Fig. 6);

• 2. A large central mass; $\mu _0=0.96,\mu _1=\mu _2=0.01$ (Fig. 7).

In each figure, the two values $C_0=R_1$ and $C_0=R_4$ have been selected.

Fig. 6

$\mu _0=0.01, \mu _1=\mu _2=0.2475$: The projection of the boundary surface onto the $\rho _1\rho _2$ plane at (a) $C_0=R_1=0.0295707$ (b) $C_0=R_4=0.048036$. The forbidden regions, where motion is impossible, are shaded black

For CS5BPs with a small central mass, the central arms $\rho _1\approx \rho _2$ are relatively broader than the side arms. This suggests that such systems are most likely to be moving in double binary hierarchies of type 12 and 14 (cf. Fig. 6).

In contrast, CS5BPs with large central bodies have relatively broader side arms ($\rho _1\approx 0$ and $\rho _2\approx 0$). This suggests that the single trinary hierarchies 13 and 24 will be dominant (cf. Fig. 7).

Fig. 7

$\mu _0=0.96, \mu _1=\mu _2=0.01$: The projection of the boundary surface onto the $\rho _1\rho _2$ plane at (a) $C_0=R_1=0.0000301$ (b) $C_0=R_4=0.0000323$. The forbidden regions, where motion is impossible, are shaded black

To study the effect on the relative sizes of the arms of real motion, the fifth central body ($m_0$) is varied in mass from 0 to 1 while maintaining the other masses equal in size. Figure 8 shows the projections for $C_0= 0$ and for a range of $\mu _0$.

For $\mu _0=0$ to 0.2, i.e. a small central mass, the double binary hierarchies dominate, with single trinary hierarchies more prevalent as $\mu _0$ increases beyond 0.2. At $\mu _0=0.2$, i.e. the five-body equal-mass case, the areas of real motion are of relatively equal sizes for the double binary and single trinary hierarchies, suggesting neither is dominant. When comparing the area of real motion available for $\mu _0=0$ (the four-body equal-mass case), with that of $\mu _0=0.2$ (the five-body equal-mass case), we see that the addition of a fifth body of equal mass at the centre increases the area of real motion between single trinary and double binary hierarchies. Thus, it most likely increases the chance of moving from one hierarchy to another, and this makes the five-body equal mass system more hierarchically unstable, as would be expected.

Fig. 8

Projections of the boundary surfaces onto the $\rho _1\rho _2$ plane for $C_0=0$, $\mu _1=\mu _2$ and a range of $\mu _0$ from 0 to 0.96

For $\mu _0=0.2~$to 1, i.e. a larger central mass, single trinary hierarchies dominate, with double binary hierarchies becoming virtually non-existent for $\mu _0$ close to 1. If $\mu _0$ is close to 1, then the system could be considered as a star with four planets or else a planet with four satellites. In such situations, it is highly unlikely that the four small bodies will form two binary pairs orbiting the central body.

Fig. 9

Critical values of $C_0$, namely $C_{{\mathrm{crit}}}$, at which the CS5BP becomes hierarchically stable as a function of $\mu _0$, when $\mu _1=\mu _2$

The critical value of $C_0$ at which the system becomes hierarchically stable for all time is given by (40). The quantities $R_3$ and $R_4$ are purely functions of $\mu _0$ and $\mu _1$. For $\mu _1=\mu _2$, they are functions only of $\mu _0$. Figure 9 plots these critical values as a function of $\mu _0$. For $C_0>C_{{\mathrm{crit}}}(\mu _0)$, hierarchical stability is guaranteed. Figure 9 shows that $C_{{\mathrm{crit}}}(\mu _0)$ has a maximum of 0.065667 at $\mu _0=0.183$. Thus if $C_0>0.065667$, all CS5BP’s with $\mu _1=\mu _2$ will be hierarchically stable. The figure also shows that the four-body case of equal masses (i.e. $\mu _0=0$) will always be hierarchically stable when $C_0>0.045$.

8.3 Non-equal masses, i.e. $\mu _0\ne \mu _1\ne \mu _2\ne \mu _0$

With $\mu _0\ne \mu _1\ne \mu _2\ne \mu _0$, we now have two independent mass ratios $\mu _0,\mu _1$, since $\mu _2=\frac{1}{2}(1-\mu _0)-\mu _1$. We also have four separate rungs of the Szebehely ladder, i.e. $C_{m }\ne C_{m }^{\prime }$ and $C_{e}\ne C_{e}^{\prime }$, as illustrated in Fig. 5.

Fig. 10

$\mu _0< \mu _1 < \mu _2,\mu _0=0.01$, $\mu _1=0.195,$ $\mu _2=0.3$. The projection of the boundary surface onto the $\rho _1-\rho _2$ plane at (a) $C_0=R_3= 0.0439109$ (b) $C_0=R_4= 0.046941$. The forbidden regions, where motion is impossible, are shaded black

Figures 10 and 11 give two typical examples of projections for first $\mu _0<\mu _1<\mu _2$ (Fig. 10); and second $\mu _2<\mu _0<\mu _1$ (Fig. 11). In each figure, two values $C_0=R_3$ and $C_0=R_4$ have been selected to show the two stages of increasing hierarchical stability. For example, in Fig. 10, $\mu _1<\mu _2$, therefore, when $R_3<C_0<R_4$, the arm $\rho _2\approx 0$ becomes disconnected first and any system in a 24 hierarchy will be stable. If the system is in a different hierarchy (12, 13, or 14), it is still free to change to any other hierarchy except for the 24 hierarchy. See Fig. 10a. Once $C_0>R_4$, all arms become disconnected and the system is hierarchically stable for all hierarchical arrangements and for all time (cf. Fig. 10b).

Fig. 11

$\mu _2< \mu _0 < \mu _1$, $\mu _1=0.3,$ $\mu _2=0.1$ and $\mu _0=0.2.$ The projection of the boundary surface onto the $\rho _1-\rho _2$ plane at (a) $C_0=R_4= 0.0501$ (b) $C_0=R_3= 0.0553$. The forbidden regions, where motion is impossible, are shaded black

Note that, as in Fig. 11, when $\mu _1>\mu _2$ the arm $\rho _1\approx 0$ becomes disconnected first. Thus for $R_4<C_0<R_3$, any system in a 13 hierarchy will be hierarchically stable. Once $C_0>R_3$, all arms become disconnected and the system is hierarchically stable for all time (cf. Fig. 11b).

The quantity $C_{{\mathrm{crit}}}$, the critical value of $C_0$ at which the whole system becomes stable, is given by equation (40). This is a function of only $\mu _0$ and $\mu _1$. Figure 12 plots these critical values as a function of $\mu _0$ and $\mu _1$. There is a symmetry due to the interchangeability of $\mu _1$ and $\mu _2$. Figure 13 shows the cross section through this surface at the value $\mu _0=0.2$. For $C_0>C_{{\mathrm{crit}}}$, hierarchical stability is guaranteed for all time. The maximum value of $C_{{\mathrm{crit}}}$ is approximately 0.065946 which occurs at the two symmetrical points $(\mu _0,\mu _1)=(0.184,0.218)$ and $(\mu _0,\mu _1)=(0.184,0.190)$. Thus, if $C_0>0.065946$, then all CS5BP, regardless of their mass ratios, will be hierarchically stable. The $C_{{\mathrm{crit}}}$ stability criterion was verified numerically by Shoaib et al. (2008). Note that Fig. 12 shows that, as the central mass $\mu _0$ increases towards 1, the critical value $C_{{\mathrm{crit}}}$ reduces to 0, indicating that there will be hierarchical stability for a greater range of systems of different $C_0$,with a large central mass.

Fig. 12

Critical values of $C_0$, namely $C_{{\mathrm{crit}}}$, at which the CS5BP becomes hierarchically stable as a function of $\mu _0$ and $\mu _1$

Fig. 13

Critical values of $C_0$, namely $C_{{\mathrm{crit}}}$, at which the CS5BP becomes hierarchically stable as a function of $\mu _1$, when $\mu _0=0.2$

9 Conclusions

In this paper, we have investigated the hierarchical stability of the Caledonian Symmetric Five-Body Problem (CS5BP). The analytical stability criterion derived for the five-body system shows that the hierarchical stability depends solely on the Szebehely Constant, $C_0$, a function of the total energy and angular momentum of the system.

Sundman’s inequality is used to define a surface, in dimensionless coordinate space, that confines regions of real motion. As $C_0$ is increased the effect is to disconnect the regions of real motion of systems with different hierarchical arrangements. This can be visualised in projections onto two dimensions. In the special case of four equal masses, orbiting the central mass $(\mu _1=\mu _2)$, total hierarchical stability occurs when $C_0>C_{{\mathrm{crit}}}$ where $C_{{\mathrm{crit}}}=R_3=R_4$ is one critical point. Otherwise, for non-equal pairs of masses orbiting the central mass, the hierarchical stability occurs in two stages as the $C_0$ of the system is increased. In the first stage, $C_0>C_{{\mathrm{crit1}}}$ produces hierarchical stability for a single trinary. At the second stage, $C_0>C_{{\mathrm{crit2}}}$, the whole system is hierarchically stable for all time, i.e. any CS5BP system existing in a particular hierarchy cannot evolve into any other hierarchy.

The effect of adding a central body to the four-body symmetrical problem and increasing its mass $\mu _0$ from 0 to 1 represents the change from the four-body equal-mass case (a stellar cluster) to a large central body with four infinitesimal masses orbiting a central body (a planetary system). The projections showing the regions of real motion indicate that, for a small central mass (stellar cluster) double binary hierarchies dominate, and for a large central mass (planetary system) single trinary hierarchies dominate. The addition of a fifth central body of equal mass to the other four masses has the effect of increasing the projected area of real motion between single trinary and double binary hierarchies near the origin. This suggests that the chances of moving from one hierarchy to another have increased, making the five-body equal-mass system more hierarchically unstable than the four-body equal-mass system.

The critical value $C_{{\mathrm{crit}}}$, at which the system becomes hierarchically stable for all time, depends only on the mass ratios $\mu _0$ and $\mu _1$ of the five-body system. The maximum value of $C_{{\mathrm{crit}}}$ across all mass ratios is 0.065946, indicating that, for $C_0$ greater than this maxima, all CS5BP, regardless of their mass ratios, will be hierarchically stable for all time. All CSFBP, regardless of their mass ratios, will be hierarchically stable for all time if $C_0>0.045.$

The analytical stability criterion based on the Szebehely Constant $C_0$ has proven a powerful tool in understanding the hierarchical evolution of the CS5BP and its subsystem the CSFBP. The analysis provides not only information on the levels of energy and angular momentum needed for hierarchical stability of the system for all time, but also information on the dominant hierarchy types expected when hierarchies are able to evolve from one to another.

Dedication The authors would like to dedicate this paper to Professor Archie E Roy (1924–2012). He was a leading inspiration to many in Celestial Mechanics and a cherished friend in exploring the wonders of the Caledonian Symmetric problems.

Difference of notation with Steves and Roy (2000, 2001) explained

• 1. Roy and Steves (2000) began numbering their CSFBP in numerical order 1234, thus the symmetric pairs were (1) $P_1$ and $P_4$ and (2) $P_2$ and $P_3$.

  In this current work, it was realised that when the four-body problem was generalised to a higher number of bodies, mathematically it would be advantageous to label the bodies so that the first body in a symmetric pair is numbered j where $1\le j\le n$, and the second body in the pair is numbered $n+j$, where 2n is the total number of bodies in the system. For the four- and five-body problems, this meant the symmetric pairs became: (1) $P_1$ and $P_3$ and (2) $P_2$ and $P_4$. Table 1 compares the original notation for the CSFBP (Roy and Steves 2000; Steves and Roy 2001; Széll et al. 2004a, b, c) with the current notation corresponding to the present paper.

• 2. For the CSFBP, Steves and Roy (2001) only require two different masses m and M, one for each pair of bodies. They, therefore, need only one mass ratio to describe the whole system. Thus in the four-body symmetrical system, $\mu$ (the mass ratio) is defined as $\mu =m/M$. When more than four bodies are included in the problem, it is easier to use a more general system of mass ratios. Thus, $\mu _i$ is chosen to be the ratio of the ith body to the total mass of the system $\sum m_i$. Therefore, we have a scaling difference between the Steves and Roy original notation and the present paper’s notation and

  $$\begin{aligned} \mu _1=\frac{\mu }{\left( 2\mu +2\right) } \qquad \mu _2=\frac{1}{\left( 2\mu +2\right) }, \end{aligned}$$

  (45)

  where $\mu =m/M$ as defined by Steves and Roy (2001). Hence for $\mu =1$, i.e. the equal-mass four-body problem, we have $\mu _1=0.25$, $\mu _2=0.25$ and $\mu _0=0.$

• 3. For the same reasons as above, we have a scaling difference for the Szebehely Constant $C_0$ for which we give the following conversion formula

  $$\begin{aligned} C_{A}=\left( 2\mu +2\right) ^5 C_{S}, \end{aligned}$$

  (46)

  where $C_{A}$ is the Szebehely Constant given by Steves and Roy and $C_{S}$ is the Szebehely Constant given in the present paper.

Table 1 Modified labelling of hierarchies