Abstract
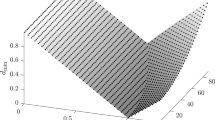
We obtain a lower bound of the distance function (MOID) between two noncoplanar bounded Keplerian orbits (either circular or elliptic) with a common focus. This lower bound is positive and vanishes if and only if the orbits intersect. It is expressed explicitly, using only elementary functions of orbital elements, and allows us to significantly increase the speed of processing for large asteroid catalogs. Benchmarks confirm high practical benefits of the lower bound constructed.









Similar content being viewed by others
Notes
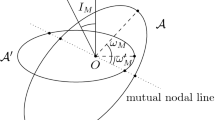
It is easy to see that \(\ell <0\) if and only if \(\mathcal {E}\) and \(\mathcal {E}'\) are linked, whereas \(\ell >0\) if and only if \(\mathcal {E}\), \(\mathcal {E}'\) are unlinked. The case of zero \(\ell \) corresponds to intersection and vice versa. Thus, with the help of the function \(\ell \) one can quickly find out which topological configuration the orbits \(\mathcal {E}\) and \(\mathcal {E}'\) have. See Kholshevnikov and Vassiliev (1999a) for more details.
Note that the equality \(\cos I=\mathbf {Z}\cdot \mathbf {Z}'=\cos i\cos i'+\sin i\sin i'\cos (\varOmega -\varOmega ')\) defines the angle I uniquely, since \(0<I<\pi \).
A more precise calculation should take into account, for example, accompanying file IO operations.
Indeed, if the planes of confocal ellipses are far from coplanar configuration, then the line segment representing the MOID most likely (especially when e, \(e'\) are small) is located near the mutual line of nodes. It follows that \(\rho \) and \(\sigma \) are expected to approach each other (\(\sigma /\rho \) tends to unity) as the orbital configuration approaches the perpendicular one. Further, the function \(C(e, e', I)\) in (16) obviously increases when \(I\rightarrow \pi /2\) (provided e and \(e'\) are hold fixed), which means that \(\tau \) is also expected to increase as \(I\rightarrow \pi /2\).
References
Armellin, R., Di Lizia, P., Berz, M., Makino, K.: Computing the critical points of the distance function between two Keplerian orbits via rigorous global optimization. Celest. Mech. Dyn. Astron. 107, 377–395 (2010)
Baluev, R.V., Mikryukov, D.V.: Fast error-controlling MOID computation for confocal elliptic orbits. Astron. Comput. 27, 11–22 (2019)
Crowell, R.H., Fox, R.H.: Introduction to Knot Theory. Springer, Berlin (1963)
Dybczyński, P.A., Jopek, T.J., Serafin, R.A.: On the minimum distance between two Keplerian orbits with a common focus. Celest. Mech. 38, 345–356 (1986)
Gellert, W., Gottwald, S., Hellwich, M., Kästner, H., Küstner, H.: The VNR Concise Encyclopedia of Mathematics, 2nd edn. Van Nostrand Reinhold, New York (1989)
Gronchi, G.F.: On the stationary points of the squared distance between two ellipses with a common focus. SIAM J. Sci. Comput. 24(1), 61–80 (2002)
Gronchi, G.F.: An algebraic method to compute the critical points of the distance function between two Keplerian orbits. Celest. Mech. Dyn. Astron. 93, 295–329 (2005)
Hedo, J.M., Ruíz, M., Peláez, J.: On the minimum orbital intersection distance computation: a new effective method. Mon. Not. R. Astron. Soc. 479(3), 3288–3299 (2018)
Kholshevnikov, K.V., Titov, V.B.: Two-Body Problem: The Tutorial. St. Petersburg State University Press, St. Petersburg (2007) (in Russian)
Kholshevnikov, K.V., Vassiliev, N.N.: On linking coefficient of two Keplerian orbits. Celest. Mech. Dyn. Astron. 75, 67–74 (1999a)
Kholshevnikov, K.V., Vassiliev, N.N.: On the distance function between two Keplerian elliptic orbits. Celest. Mech. Dyn. Astron. 75, 75–83 (1999b)
Sitarski, G.: Approaches of the parabolic comets to the outer planets. Acta Astron. 18(2), 171–195 (1968)
Vassiliev, N.N.: Determining of critical points of distance function between points of two Keplerian orbits. Bull. Inst. Theor. Astron. 14(5), 266–268 (1978)
Zheleznov, N.B., Kochetova, O.M., Kuznetsov, V.B., Medvedev, Yu.D., Chernetenko, Yu.A., Shor, V.A.: Ephemerides of minor planets for 2018. St. Petersburg, Inst. Appl. Astron. (2017)
Acknowledgements
We are grateful to Professor K. V. Kholshevnikov for the statement of the problem, for important remarks and for his help in preparing the manuscript. We also express our gratitude to A. Ravsky for valuable discussion, as well as anonymous reviewers, whose constructive and valuable comments greatly helped the authors to improve the manuscript. All calculations made in the work were conducted by means of the equipment of the Computing Centre of Research Park of Saint Petersburg State University. This work is supported by the Russian Science Foundation Grant No. 18-12-00050.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
This research did not involve human participants.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: The distance between two V-sets
Appendix: The distance between two V-sets
The proof of the following lemma is very simple and therefore is omitted.
Lemma
Let \(\mathcal {S}_1, \mathcal {S}_2\subset \mathbb {R}^3\) be two arbitrary sets satisfying the following three conditions:
-
(i)
\(\rho (\mathcal {S}_1, \mathcal {S}_2)>0\).
-
(ii)
There are two points \(Q_1\in \mathcal {S}_1\) and \(Q_2\in \mathcal {S}_2\) such that \(\rho (\mathcal {S}_1, \mathcal {S}_2)=Q_1Q_2\).
-
(iii)
The pair \((Q_1, Q_2)\) is the only element of a set \(\mathcal {S}_1\times \mathcal {S}_2\) that gives \(\rho (\mathcal {S}_1, \mathcal {S}_2)=Q_1Q_2\).
Then, for any two subsets \(\mathcal {S'}_1\subset \mathcal {S}_1\) and \(\mathcal {S'}_2\subset \mathcal {S}_2\) such that \(\mathcal {S'}_1\ni Q_1\) and \(\mathcal {S'}_2\ni Q_2\) one always has \(\rho (\mathcal {S'}_1, \mathcal {S'}_2)=\rho (\mathcal {S}_1, \mathcal {S}_2)\).
For example, if two points M and N lie on skew lines m and n, respectively, and satisfy \(\rho (m, n)=MN\), then for any two rays \(m'\) and \(n'\) (open or closed, no matter) such that \(m'\subset m\), \(n'\subset n\), \(m'\ni M\), \(n'\ni N\) we have \(\rho (m', n')=\rho (m, n)\).
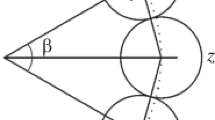
Consider again two two-dimensional closed half-planes \(\alpha \subset \{z\geqslant 0\}\) and \(\beta =\{y\geqslant 0; z=0\}\) that form a dihedral angle in \(\mathbb {R}^3\) with the plane angle J satisfying \(0<J\leqslant \pi /2\) (see Fig. 10). In the positive side of the axis Ox draw points A and B such that \(OA<OB\). Given any positive acute angles \(\psi \) and \(\varphi \), define in the face \(\alpha \) a V-set \(\mathcal {V}_1\) with a vertex A and an exterior angle \(\psi \), and in the face \(\beta \) construct a V-set \(\mathcal {V}_2\) with a vertex B and an exterior angle \(\varphi \) (see Fig. 10). Decompose boundaries of \(\mathcal {V}_1\) and \(\mathcal {V}_2\) into four closed rays \(a', a'', b', b''\), where \(a', a''\subset \mathcal {V}_1\), \(b', b''\subset \mathcal {V}_2\), in such a way that \(a'', b'\) both intersect the plane \(\{x=0\}\). Further, draw two straight lines a, b such that \(a\supset a'\) and \(b\supset b'\). The line a defines in the plane of \(\mathcal {V}_1\) a closed half-plane \(\mathcal {P}_1\) that (completely) contains \(\mathcal {V}_1\). Similarly, define a closed half-plane \(\mathcal {P}_2\) with the edge b such that \(\mathcal {P}_2\supset \mathcal {V}_2\) (see Fig. 10). Our aim is to prove that
First of all, draw two points \(H\in a\) and \(G\in b\) that give \(\rho (a, b)=HG\). It is easy to check that under the conditions
we always have \(H_z, G_y>0\). This yields \(H\in a'\), \(G\in b'\), and hence, we can write
The distance between half-planes \(\mathcal {P}_1\) and \(\mathcal {P}_2\) is equal to the distance between their edges a and b. This fact results from elementary similarity and continuity considerations (\(AB\rightarrow 0\) implies \(\rho (\mathcal {P}_1, \mathcal {P}_2)\rightarrow 0\)). See text for the strict proof
Further, show that \(\mathcal {P}_1\) and \(\mathcal {P}_2\) satisfy all conditions of lemma. For this, we prove that
and verify that a pair (H, G) is the only element of a set \(\mathcal {P}_1\times \mathcal {P}_2\) satisfying (25). Fix any pair \((Q_1, Q_2)\in \mathcal {P}_1\times \mathcal {P}_2\) distinct from the pair \((H, G)\in \mathcal {P}_1\times \mathcal {P}_2\). It suffices to prove that \(Q_1Q_2>HG\). There are three possibilities.
-
(A)
\(Q_1\in a\), \(Q_2\in b\).
-
(B)
One of the points \(Q_1, Q_2\) is interior for the half-plain containing it, while another is boundary one.
-
(C)
\(Q_1\notin a\), \(Q_2\notin b\).
Consider case (A). Since straight lines a and b are skew, one concludes \(Q_1Q_2>HG\).
Consider case (B). Let, for example, \(Q_1\notin a\), \(Q_2\in b\) (see Fig. 10). Through the point \(Q_1\) draw a straight line \(c\parallel a\) and denote by C a point where c (dashed in Fig. 10) meets the axis Ox. We have
and therefore \(Q_1Q_2>HG\).
Case (C) differs from case (B) only in that we have to draw auxiliary straight lines in both half-planes \(\mathcal {P}_1\) and \(\mathcal {P}_2\).
We see that \(\mathcal {P}_1\) and \(\mathcal {P}_2\) satisfy all conditions of lemma. In view of (24) by lemma we conclude that
which finally implies (23).
Rights and permissions
About this article
Cite this article
Mikryukov, D.V., Baluev, R.V. A lower bound of the distance between two elliptic orbits. Celest Mech Dyn Astr 131, 28 (2019). https://doi.org/10.1007/s10569-019-9907-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10569-019-9907-3