Abstract
A closed-form first-order perturbation solution for the attitude evolution of a triaxial space object in an elliptical orbit is presented. The solution, derived using the Lie–Deprit method, takes into account gravity-gradient torque and is facilitated by an assumption of fast rotation of the object. The formulation builds on the earlier implementation of Lara and Ferrer, which assumes a circular orbit. The previously presented work—which assumes spin about an object’s axis of maximum inertia—is further extended by the explicit presentation of the transformations required to apply the solution to an object spinning about its axis of minimum inertia. Additionally, several numerical analyses are presented to more completely assess the utility of the solution. These studies (1) validate the elliptical solution, (2) assess the impact of varying the small parameter of the perturbation procedure, (3) analyze the assumption of fast rotation, and (4) apply the solution to the common and important scenario of a tumbling rocket body.














Similar content being viewed by others
Notes
The transformations between Andoyer variables and the Lara–Ferrer solution variables are given in “Appendix C.”
The angle \(\mu \) defines the orientation of the \(\varvec{i}_1 \varvec{i}_2\) plane. The angle \(\nu \) defines the orientation of the \(\varvec{ij}\) plane.
The conjugate momenta of \(\phi \) and h are identical.
In the development of the equations of the second averaging, all solution variables are doubly transformed. Following the convention of Lara and Ferrer (2013), the double-prime notation is not used explicitly to improve readability.
The results presented in the current work are obtained using explicit perturbation transformations for both forward and backward transformations. For example, \(\xi ' = \xi '' + \delta \xi \), with \(\delta \xi \) expressed in terms of double-prime variables, and \(\xi '' = \xi ' - \delta \xi \), with \(\delta \xi \) expressed in terms of single-prime variables. The results presented by Lara and Ferrer (2013) were obtained using only the \(\xi '' \rightarrow \xi '\) and \(\xi ' \rightarrow \xi \) transformation equations. In those works, the inverse transformations were performed by solving the forward transformation equations implicitly. The differences between the explicit and implicit solutions are insignificant at the scale of Figs. 4 and 5.
Eccentricity is zero in these scenarios.
The brightness of an SO, as measured by an observer on Earth, may change over time, in large part due to the presentation of different surfaces with unique reflectance properties to the observer and to the Sun. A flash period is the time between consecutive maxima in the observed brightness of an SO. Under the assumption of a cylindrical SO whose top and bottom share common reflectance properties—which are different from those of the sides—a flash period approximates one half of the rotational period of the SO (Pontieu 1997).
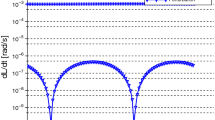
Absolute differences are used rather than relative differences because such a plot would be distorted by large relative differences when N passes through zero.
The nominal value of the small parameter of the perturbation procedure for the rocket body example is \(\epsilon ^2 = 3.855 \times 10^{-5}\).
Abbreviations
- \(\bar{\varvec{q}}\) :
-
Quaternion describing attitude of body-fixed frame with respect to inertial orbital frame
- \(\epsilon , \epsilon _{ell}\) :
-
Small parameter of perturbation procedure for circular and elliptical orbit cases, respectively
- \(\lambda , \mu , \nu , \Lambda , M, N\) :
-
Andoyer variables
- \(\mathcal {H}\) :
-
Hamiltonian for fast-rotating space object
- \(\mathcal {K},S\) :
-
Singly and doubly averaged Hamiltonians, respectively
- \(\mathrm {am} \left( u | m \right) \) :
-
Jacobi amplitude function with input parameter m and argument u
- \(\mathrm {F} \left( \Psi | m \right) , \mathrm {E} \left( \Psi | m \right) , \Pi \left( f, \Psi | m \right) \) :
-
Incomplete elliptic integrals of the first, second, and third kinds, respectively, with input parameter m and argument \(\Psi \). f is the characteristic.
- \(\mathrm {K} (m), \mathrm {E} (m), \Pi \left( f | m \right) \) :
-
Complete elliptic integrals of the first, second, and third kinds, respectively, with input parameter m. f is the characteristic.
- \(\mathrm {sn} \left( u | m \right) , \mathrm {cn} \left( u | m \right) , \mathrm {dn} \left( u | m \right) \) :
-
Jacobi elliptic functions with input parameter m and argument u
- \(\mu _*\) :
-
Gravitational parameter of central body
- \(\Phi \) :
-
Hamiltonian of unperturbed rotating triaxial rigid body
- \(\theta \) :
-
True anomaly
- \(\varvec{\omega }\) :
-
Angular velocity vector of body-fixed frame with respect to inertial orbital frame, expressed in body-fixed frame
- \(\varvec{J}\) :
-
Space object inertia tensor
- \(\varvec{R}\) :
-
Transformation matrix from inertial orbital frame to body-fixed frame
- \(\varvec{r}_B\) :
-
Position vector of mass center of space object with respect to mass center of central body, expressed in body-fixed frame
- \(\xi \) :
-
Any element of the solution variable set
- a :
-
Semimajor axis
- A, B, C :
-
Principal moments of inertia of space object; \(A \le B \le C\)
- \(c_I\) :
-
\(\cos {I}\); \(\cos ^2 I = H^2/G^2\)
- e :
-
Eccentricity
- I :
-
Inclination of plane orthogonal to rotational angular momentum with respect to inertial orbital frame
- J :
-
Inclination of equatorial plane of rigid body with respect to plane orthogonal to rotational angular momentum
- \(l, g, h, \tau , L, G, H, T\) :
-
Lara–Ferrer solution variables
- M :
-
Magnitude of rotational angular momentum
- \(M_0\) :
-
Mean anomaly
- n :
-
Mean motion
- r :
-
Distance between mass centers of primary body and space object
- \(r_p, r_a\) :
-
Periapsis and apoapsis distances, respectively
- \(s_I\) :
-
\(\sin {I}\)
- t :
-
Time
- U :
-
Gravity-gradient potential for fast-rotating space object
- W, V :
-
Generating functions of first and second Lie transformations, respectively
- x, y, z :
-
Subscripts representing vector components
- Z, f, m, u, \(\Delta \), \(\Psi \), \(\phi \), \(\kappa \) :
-
Intermediate variables used to simplify form of solution
References
Arribas, M., Elipe, A.: Attitude dynamics of a rigid body on a Keplerian orbit: a simplification. Celest. Mech. Dyn. Astron. 55, 243–247 (1993). https://doi.org/10.1007/BF00692512
Boccaletti, D., Pucacco, G.: Theory of Orbits 2: Perturbative and Geometrical Methods. Springer, New York, pp. 2, 28–36, 40–44, 69–80, 125–178 (1999)
Brouwer, D.: Solution of the problem of artificial satellite theory without drag. Astron. J. 64(1274), 378–396 (1959). https://doi.org/10.1086/107958
Castronuovo, M.M.: Active space debris removal-a preliminary mission analysis and design. Acta Astronaut. 69, 848–859 (2011). https://doi.org/10.1016/j.actaastro.2011.04.017
Celletti, A.: Stability and Chaos in Celestial Mechanics, pp. 83–88. Springer-Praxis, Berlin (2006)
Cochran, J.E.: Effects of gravity-gradient torque on the rotational motion of a triaxial satellite in a precessing elliptic orbit. Celest. Mech. 6, 127–150 (1972). https://doi.org/10.1007/BF01227777
Curtis, H.: Orbital Mechanics for Engineering Students. Elsevier, Butterworth-Heinemann, Burlington, MA, pp. 435–437, 530–533 (2005)
De Pontieu, B.: Database of photometric periods of artificial satellites. Adv. Space Res. 19(2), 229–232 (1997). https://doi.org/10.1016/S0273-1177(97)00005-7
Deprit, A.: Free rotation of a rigid body studied in the phase plane. Am. J. Phys. 35, 424–428 (1967). https://doi.org/10.1119/1.1974113
Deprit, A.: Canonical transformations depending on a small parameter. Celest. Mech. 1, 12–30 (1969). https://doi.org/10.1007/BF01230629
Deprit, A., Elipe, A.: Complete reduction of the Euler–Poinsot problem. J. Astronaut. Sci. 41(4), 603–628 (1993)
Edelen, D.G.B.: Construction of autonomous canonical systems when the Hamiltonian depends explicitly on time. Int. J. Eng. Sci. 26(6), 605–608 (1988). https://doi.org/10.1016/0020-7225(88)90057-2
Ferrer, S., Lara, M.: Families of canonical transformations by Hamilton–Jacobi–Poincare equation. Application to rotational and orbital motion. J. Geometric. Mech. 2(3), 223–241 (2010). https://doi.org/10.3934/jgm.2010.2.223
Früh, C., Jah, M.K.: Attitude and orbit propagation of high area-to-mass ratio (HAMR) objects using a semi-coupled approach. J. Astronaut. Sci. 60(1), 32–50 (2014). https://doi.org/10.1007/s40295-014-0013-1
Fukushima, T.: Simple, regular, and efficient numerical integration of rotational motion. Astron. J. 135(6), 2298–2322 (2008). https://doi.org/10.1088/0004-6256/135/6/2298
Hatten, N., Russell, R.P.: A semianalytical technique for six-degree-of-freedom space object propagation. In: 27th AAS/AIAA Space Flight Mechanics Meeting, San Antonio, TX (2017)
Heard, W.B.: Rigid Body Mechanics: Mathematics, Physics and Applications, pp. 88–145. Wiley-VCH, Weinheim (2006)
Holland, R.L., Sperling, H.J.: A first-order theory for the rotational motion of a triaxial rigid body orbiting an oblate primary. Astron. J. 74(3), 490–496 (1969). https://doi.org/10.1086/110826
Hoots, F.R., Roehrich, R.L.: Spacetrack Report No. 3: Models for Propagation of NORAD Element Sets. Technical Report, U. S. Air Force Aerospace Defense Command, Colorado Springs, CO (1980)
ISC Kosmotras, : Dnepr User’s Guide, 2nd edn. ISC Kosmotras, Moscow (2001)
Lara, M., Ferrer, S.: Closed form integration of the Hitzl–Breakwell problem in action-angle variables. Adv. Astronaut. Sci. 145, 27–39 (2012a)
Lara, M., Ferrer, S.: Complete closed form solution of a tumbling triaxial satellite under gravity-gradient torque. Adv. Astronaut. Sci. 143, 255–274 (2012b)
Lara, M., Ferrer, S.: Closed form perturbation solution of a fast rotating triaxial satellite under gravity-gradient torque. Cosm. Res. 51(4), 289–303 (2013). https://doi.org/10.1134/S0010952513040059
Lara, M., Fukushima, T., Ferrer, S.: Ceres’ rotation solution under the gravitational torque of the Sun. Mon. Not. R. Astron. Soc. 415, 461–469 (2011). https://doi.org/10.1111/j.1365-2966.2011.18717.x
Le Fevre, C., Morand, V., Delpech, M., Gazzino, C., Henriquel, Y.: Integration of coupled orbit and attitude dynamics and impact on orbital evolution of space debris. In: AAS/AIAA Space Flight Mechanics Meeting, Williamsburg, VA (2015)
Levin, E., Pearson, J., Carroll, J.: Wholesale debris removal from LEO. Acta Astronaut. 73, 100–108 (2012). https://doi.org/10.1016/j.actaastro.2011.11.014
McCants, M.: Mike McCants’ BWGS PPAS Page (2016). https://www.prismnet.com/~mmccants/bwgs/index.html. Accessed on 29 June 2016
NASA: NASA space science data coordinated archive. (2016). http://nssdc.gsfc.nasa.gov/nmc/masterCatalog.do?sc=2009-041B. Accessed June 2016
Ojakangas, G.W., Anz-Meador, P., Cowardin, H.: Probable rotation states of rocket bodies in low Earth orbit. In: 13th Annual Advanced Maui Optical and Space Conference, Maui, HI (2012)
Pelivan, I., Theil, S.: Higher accuracy modelling of gravity-gradient induced forces and torques. In: AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO (2006)
Sadov, I.A.: The action-angle variables in the Euler–Poinsot problem. J. Appl. Math. Mech. 34(5), 922–925 (1970). https://doi.org/10.1016/0021-8928(70)90077-8
Santoni, F., Cordelli, E., Piergentili, F.: Determination of disposed-upper-stage attitude motion by ground-based optical observations. J. Spacecr. Rockets 50(3), 701–708 (2013). https://doi.org/10.2514/1.A32372
Van der Ha, J.C.: Perturbation solution of attitude motion under body-fixed torques. Acta Astronaut. 12(10), 861–869 (1985). https://doi.org/10.1016/0094-5765(85)90103-1
Wetterer, C.J., Jah, M.K.: Attitude determination from light curves. J. Guid. Control Dyn. 32(5), 1648–1651 (2009). https://doi.org/10.2514/1.44254
Woodburn, J., Tanygin, S.: Efficient numerical integration of coupled orbit and attitude trajectories using an Encke type correction algorithm. In: AAS/AIAA Astrodynamics Specialist Conference, Quebec City (2001)
Yanagisawa, T., Kurosaki, H.: Shape and motion estimate of LEO debris using light curves. Adv. Space Res. 50(1), 136–145 (2012). https://doi.org/10.1016/j.asr.2012.03.021
Zanardi, M.C., Vilhena de Moraes, R.: Analytical and semi-analytical analysis of an artificial satellite’s rotational motion. Celest. Mech. Dyn. Astron. 75, 227–250 (2000). https://doi.org/10.1023/A:1008358801859
Zanardi, M.C., Moreira, L.S.: Analytical attitude propagation with non-singular variables and gravity gradient torque for spin stabilized satellite. Adv. Space Res. 40, 11–17 (2007). https://doi.org/10.1016/j.asr.2007.04.047
Zanardi, M.C., Quirelli, I.M.P., Kuga, H.K.: Analytical attitude prediction of spin stabilized spacecrafts perturbed by magnetic residual torque. Adv. Space Res. 36, 460–465 (2005a). https://doi.org/10.1016/j.asr.2005.07.020
Zanardi, M.C., Vilhena De Moraes, R., Cabette, R.E.S., Garcia, R.V.: Spacecraft’s attitude prediction: solar radiation torque and the Earth’s shadow. Adv. Space Res. 36, 466–471 (2005b). https://doi.org/10.1016/j.asr.2005.01.070
Acknowledgements
This work was funded, in part, by a Phase II SBIR from the Air Force Research Laboratory, contract FA9453-14-C-0295, under a subcontract from Emergent Space Technologies, Inc. The authors would also like to gratefully acknowledge fruitful correspondence with Martin Lara, as well as the comments of the anonymous referees.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest Statement
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Appendices
Appendix A: Spin about axis of minimum inertia
As presented in Lara and Ferrer (2013), the transformation from Andoyer variables to fully reduced action-angle variables (“solution variables”) is only applicable to an object spinning about its axis of maximum inertia. However, rotation about the axis of minimum inertia may be considered by revising the transformation procedure as follows. Transformed variables are denoted by a subscript T.
The problem is reorganized such that the axis of minimum inertia is aligned most closely with the body z-axis. Under the assumption \(A \le B \le C\),
The transformed values are then converted to Andoyer variables (Celletti 2006), and transformation to action-angle variables proceeds identically to the case of spin about the maximum inertia axis. When evaluating the analytical solution, the transformed moments of inertia must be used. Further, it must be remembered that the resulting attitude solutions do not describe the orientation of the original body-fixed frame with respect to the inertial frame. For example, once the result is calculated in (transformed) action-angle variables and converted to a (transformed) angular velocity vector and rotation matrix, Eqs. (26)–(28) must be applied to obtain the \(\varvec{\omega }\) and \(\varvec{R}\) of the original body-fixed frame with respect to the original inertial frame.
Appendix B: Original Lara–Ferrer equations for a circular orbit
In Sect. 2, the equations of the perturbation solution for the elliptical orbit case that are the same or only slightly modified from the original circular case are omitted in the interest of reducing clutter in the presentation of the solution. For completeness, however, the relevant equations are given in this appendix. The corresponding equations in the text of the paper in which the solution for a circular orbit is described (Lara and Ferrer 2013) are referenced when appropriate; equations from Lara and Ferrer (2013) are denoted as “L–F Eq. (X),” where X is the equation number in Lara and Ferrer (2013). It is emphasized that these equations are the original equations, applicable to circular orbits only. The revisions described in Sect. 2 of the present paper must be performed in order to achieve validity for eccentric orbits.
To simplify the form of the solution, Lara and Ferrer (2013) define the auxiliary variables f (L–F Eq. (11)), m (L–F Eq. (12)), and \(\Delta \) (L–F Eq. (5)) as
L–F Eq. (18) gives the torque-free Hamiltonian in solution variables:
L–F Eqs. (27) and (30) give variable relationships necessary for performing calculations:
L–F Eq. (49) gives the Hamiltonian for gravity-gradient-perturbed rotation, simplified by the assumption of fast rotation, in Andoyer variables:
Meanwhile, the disturbing potential in solution variables is given by L–F Eq. (59), with u defined in L–F Eq. (76):
The full fast-rotating Hamiltonian in solution variables is given by L–F Eq. (60):
where \(\Phi \) is given by Eq. (32), n is the orbital mean motion, H is the conjugate momentum of h, and U is given by Eq. (37).
The \(H_{0,2}\) contribution to the averaged Hamiltonian of the first Lie–Deprit transformation is given by L–F Eq. (65), with the auxiliary variable \(\kappa \) defined in L–F Eq. (66):
The \(W_2\) term of the generating function of the first Lie–Deprit transformation is given by L–F Eq. (67). Calculations are facilitated by L–F Eqs. (68) and (35), which give \(Z \left( \Psi | m \right) \) and \(\Psi \), respectively:
L–F Eqs. (77)–(82) give the variable transformations for the first Lie–Deprit transformation, which averages over the angle l:
where (L–F Eq. (75))
Appendix C: Transformations between Andoyer and action-angle variables
In this appendix, the transformations between Andoyer variables (\(\lambda \), \(\mu \), \(\nu \), \(\Lambda \), M, N) and the action-angle variables or Lara–Ferrer solution variables (l, g, h, \(\tau \), L, G, H, T) are described (Ferrer and Lara 2010; Lara and Ferrer 2013). The transformation from Andoyer variables to solution variables is accomplished via
where \(\Psi \) is calculated using
The transformation from solution variables to Andoyer variables is performed using
where \(\Psi \) is given by Eq. (44).
It is noted that no transformations are required for \(\tau \) and T because these variables are associated with the use of the extended phase space rather than the rotational state of the body.
Rights and permissions
About this article
Cite this article
Hatten, N., Russell, R.P. The eccentric case of a fast-rotating, gravity-gradient-perturbed satellite attitude solution. Celest Mech Dyn Astr 130, 71 (2018). https://doi.org/10.1007/s10569-018-9864-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10569-018-9864-2