1 Introduction

Solar sails are an alternative form of spacecraft propulsion which use solar radiation pressure to push the spacecraft through space (McInnes 1999a). Conventional thrusters are replaced by a large, reflective membrane surface onto which the incoming solar photons transfer their momentum, accelerating the spacecraft. This provides a solar sail with an essentially unlimited supply of fuel and allows it to undertake missions that spacecraft with conventional propulsion would find impossible (McInnes 1999b).

Although the concept and mathematics behind solar sails was introduced in the 1950s (Garwin 1958), it is only in the past few years that we have finally seen the first solar sail launched. The successful demonstration of the IKAROS solar sail mission (Tsuda et al. 2011), launched in 2010 by the Japan Aerospace Exploration Agency (JAXA), has spurred on more mission concepts with both the Planetary Society (2014) and Surrey Space Centre (2014) set to launch solar sail technology demonstration and deorbiting missions in 2016.

While the majority of the objects in the solar system lie within a few degrees of the ecliptic plane, there are a significant number of objects that do not. These include Pluto, the Heliopause and minor bodies in the asteroid belt and Kuiper Belt, with many of these objects having an inclination of tens of degrees with respect to the ecliptic. Sending spacecraft to these objects is therefore challenging due to the large delta-v required to change a spacecraft’s inclination. Gravitational assists are often used but this will place constraints on mission launch dates and can result in highly complex trajectories. Solar sails are able to solve this problem since the continuous source of photons allows them to change their inclination without any fuel. Solar sail use in these sorts of missions has been investigated numerically by Dachwald (2003, 2004) using evolutionary neurocontrol optimization techniques. However despite this inclination change advantage, three-dimensional heliocentric orbits are still poorly understood from an analytical point of view.

Early research focussed on the two-dimensional equations of motion and the solutions to these equations. Tsu (1959), London (1960) and Bacon (1959) all investigated the only known exact analytical solution; the logarithmic spiral solution. Bacon’s work was actually concerned with continuous thrust spacecraft, not specifically solar sails, although the results were directly applicable. The work of Van Der Ha and Modi (1978) then provided one of the few analytical insights into three-dimensional heliocentric solar sail orbits. It was shown that the in-plane perturbations could be uncoupled from the orientation of the orbital plane via a choice of independent variable. Exact solutions were found for the three-dimensional logarithmic spiral case with the inclination found to exhibit periodic behaviour. Series approximations were required to investigate the long term behaviour of a solar sail for non-logarithmic orbits. In terms of the orbital angles, the behaviour of the inclination and true latitude were investigated for near-circular initial orbits. The use of the independent variable here to uncouple the equations will form the basis of the approximate solution presented here.

This was followed by several papers over the following decades, most notably by Sauer (2000), Leipold (1999) and Vulpetti (1996, 1997, 1999), that used numerical methods to examine high performance solar sails and missions to the outer solar system. These studies in particular showed the enormous potential of solar sails. Missions to the outer solar system, including missions requiring significant inclination changes, could be accomplished in much shorter time scales than with conventional propulsion. Perturbation effects such as the Poynting–Robertson effect have also been studied in relation to these types of missions by (Kezerashvili and Vázquez-Poritz 2011, 2013), showing decreased Heliocentric distance. Further examination of heliocentric orbits were almost entirely numerical.

Current research is heavily focussed on solar sails in the Earth–Sun or Earth–Moon circular restricted three-body problem. A large number of papers have been published on the use of a solar sail to generate and control artificial Lagrange points (McInnes et al. 1994; McInnes and Macdonald 2005; Macdonald et al. 2007; Waters and McInnes 2007, 2008a, b; Farres and Jorba 2008). While solar sails in previously reviewed studies have used large solar sails as a propulsion system for highly non-Keplerian orbits and deep space missions, current research uses much smaller solar sails for near-Earth missions. Now with larger solar sails set to be launched, focus is starting to shift back to the heliocentric solar sail orbits that dominated early research.

More recently, a geometric tool, the hodograph, has been used to analyse solar sail orbits. The hodograph is essentially a visualization of the tangential and radial velocity and it’s mathematical treatment and usage in Keplerian orbits and orbital transfers were discussed by Szebehely (1964) and Battin (1999). It was first shown by Wokes et al. (2008) that the four-dimensional planar dynamics of a fixed Sun angle solar sail can be reduced down to a two-dimensional problem using the transformation to the hodograph. Trajectories could then be classified as either spiral, angular momentum reversal or hyperbolic based on the selection of initial conditions in this two-dimensional hodograph phase space. This was the first time the long term behaviour of two-dimensional heliocentric solar sail orbits had been described using an analytical model and we seek to build upon this work here by extending their approach to three-dimensional orbits.

This paper will combine the hodograph results with the early work of Van Der Ha and Modi (1978) to present a full analytical description of three-dimensional heliocentric solar sail orbits. Although further work has been done on the angular momentum reversal trajectory Zeng et al. (2011), for this work the initial conditions near the logarithmic spiral orbit where chosen, as this is relevant to Earth escape orbits as their initial conditions are close to the logarithmic spiral. We extend the work of Van der Ha and Modi to include the longitude of ascending node and classify the possible long term behaviour of a fixed angle solar sail into distinct categories. Sections 2 and 3 will introduce the fixed angle solar sail and detail the hodographs use in trajectories. Section 4 derives the three-dimensional equations of motion showing how the hodograph solution couples with the orientation of the orbital plane. In Sect. 5 we demonstrate how the rotational symmetry of a heliocentric orbit allows us to simplify the equations of motion considerably by showing that any two orbits with identical hodograph parameters can be mapped to one another. We use this result in Sect. 6 to derive a complete analytical description of solar sail orbits near the logarithmic spiral initial conditions.

2 Force model for a fixed angle solar sail

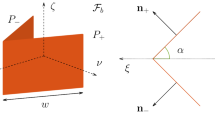
In this section, we present a simple model for the forces on a fixed angle solar sail due to solar gravitational force and solar radiation pressure. Perturbation effects, such as the Poynting–Robertson effect as discussed in the introduction, will not be considered here. First, the definition of a fixed angle in three dimensions is provided. Let \(\varvec{\hat{r}}\) be the radial unit vector connecting the Sun and solar sail and \(\varvec{\hat{n}}\) the unit vector pointing normal to the sail. For a perfectly reflecting sail, a photon striking the sail will transfer double the momentum of a perfectly absorbing sail, with all the force directed along \(\varvec{\hat{n}}\). The incident angle is the angle between the radial vector and sail normal vector and is denoted as \(\alpha \). Following McInnes (1999a), we also define a secondary angle, known as the clock angle \(\delta \) which is defined as the angle between the angular momentum vector and the sail normal projected onto the plane formed by \(\varvec{\hat{h}}\) and \(\varvec{\hat{\lambda }} = \varvec{\hat{r}} \times \varvec{\hat{h}}\). Figure 1 shows these angles.

Fig. 1
figure 1

Diagram showing how the sail angles \(\alpha \) and \(\delta \) are defined in the orbital plane

Full size image

Following the derivation of McInnes (1999a), we have that the acceleration due to solar radiation pressure is given by

$$\begin{aligned} \mathbf {a_{SRP}}&= \beta \frac{\mu }{r^2} (\varvec{\hat{r}} \cdot \varvec{\hat{n}} )^2 \varvec{\hat{n}} \end{aligned}$$
(1)
$$\begin{aligned}&= \beta \frac{\mu }{r^2} \cos ^2\alpha \varvec{\hat{n}} \end{aligned}$$
(2)

where r is the radial distance, \(\mu \) the standard gravitational parameter and \(\beta \) is a dimensionless parameter signifying the ratio of solar radiation force to gravitational force. We define \(\beta \) as

$$\begin{aligned} \beta = \frac{\varvec{F}_{\textit{SRP}}}{\varvec{F}_{{\textit{grav}}}} = \frac{L_s}{2 \pi \mu c} \end{aligned}$$
(3)

where \(L_s\) is the solar luminosity at 1AU, equal to \(3.839 \times 10^{26}W\) and c the speed of light. Defining \(\varvec{\hat{\lambda }} = \varvec{\hat{r}} \times \varvec{\hat{h}}\), the sail normal vector can then be written as

$$\begin{aligned} \varvec{\hat{n}} = \cos \alpha \varvec{\hat{r}} + \sin \alpha \sin \delta \varvec{\hat{\lambda }} + \sin \alpha \cos \delta \varvec{\hat{h}}. \end{aligned}$$
(4)

A fixed angle solar sail is then one for which the components of the sail normal vector are constant along \(\varvec{\hat{r}}\), \(\varvec{\hat{\lambda }}\) and \(\varvec{\hat{h}}\). Including solar gravity, the total acceleration can be written as

$$\begin{aligned} \mathbf {a} = \frac{\mu }{r^2}(k_1 \varvec{\hat{r}} + k_2 \varvec{\hat{\lambda }} + k_3 \varvec{\hat{h}}) \end{aligned}$$
(5)

where

$$\begin{aligned} k_1&= -1 + \beta \cos ^3\alpha \end{aligned}$$
(6)
$$\begin{aligned} k_2&= \beta \cos ^2\alpha \sin \alpha \sin \delta \end{aligned}$$
(7)
$$\begin{aligned} k_3&= \beta \cos ^2\alpha \sin \alpha \cos \delta . \end{aligned}$$
(8)

3 The hodograph

The hodograph is a mathematical tool for looking at spacecraft velocity. In this section we provide a derivation along with an example. Following Wokes et al. (2008), the equations of motion for a fixed angle solar sail in a two-dimensional heliocentric orbit are given as

$$\begin{aligned} \ddot{r} - \frac{h^2}{r^3}&= k_1\frac{\mu }{r^2} \end{aligned}$$
(9)
$$\begin{aligned} \dot{h}&= \frac{\mu }{r}k_2 \end{aligned}$$
(10)
$$\begin{aligned} \dot{\psi }&= \frac{h}{r^2} \end{aligned}$$
(11)

where r is the radial distance, \(h = r^2 \dot{\psi }\) the angular momentum and \(\dot{r}\) the radial velocity. In this two-dimensional case, \(\psi \) is just the true anomaly. This is however not true for the three-dimensional case as will be discussed later. We then use a change of variables in order to derive the hodograph reduction. Let

$$\begin{aligned} v = \frac{h^2}{\mu r}, \quad w = \frac{h}{\mu }\dot{r} \end{aligned}$$
(12)

where v and w are non-dimensional. Taking the derivative of v and w with respect to \(\psi \) (denoted as \('\) throughout this paper), we get

$$\begin{aligned} v'&= 2k_2 - w \end{aligned}$$
(13)
$$\begin{aligned} w'&= k_2\frac{w}{v} + v + k_1. \end{aligned}$$
(14)

We see then that the hodograph transformation reduces the system from four-dimensional down to two-dimensional as the derivatives of v and w only depend on v and w. The full planar dynamics can be recovered by including either the radial distance or magnitude of angular momentum, since a choice of one of these allows the other to be found through the equation for v. From Battin (1999), the eccentricity can also be written as

$$\begin{aligned} e = \sqrt{(v - 1)^2 + w^2}. \end{aligned}$$
(15)

We also normalize the variables such that \(\mu = 1\), the initial radial distance is 1 and one time unit is \(2\pi \). From Eq. (12), the differential equations for r and h along with their initial conditions are then

$$\begin{aligned} r'&= \frac{w}{v}r, \quad r(0) = 1 \end{aligned}$$
(16)
$$\begin{aligned} h'&= \frac{k_2}{v}h, \quad h(0) = \sqrt{v_0}. \end{aligned}$$
(17)

This \(v-w\) system of equations exhibit two equilibrium points, \((\tilde{v}_1, \tilde{w})\) and \((\tilde{v}_2, \tilde{w})\) where

$$\begin{aligned} \tilde{v}_{1,2}&= \frac{-k_1}{2} \left( 1 \mp \sqrt{1 - 8 \left( \frac{k_2}{k_1} \right) ^2 } \right) \end{aligned}$$
(18)
$$\begin{aligned} \tilde{w}&= 2 k_2. \end{aligned}$$
(19)

These correspond to the logarithmic spiral trajectories when \(\beta \ne 0\). When \(\beta =0\), the system reduces to Keplerian motion. In the hodograph phase space this is represented by a family of circles centred at \(v=1\), \(w=0\) with the radius being the eccentricity of the orbit. As such, a Keplerian orbit with zero eccentricity is simply the point (1, 0) in the phase space. This can be considered a realistic starting condition for a solar sail that has been released on an Earth escape orbit assuming the Earth is on a circular orbit around the Sun at 1AU. In order to develop analytical approximations for the full three-dimensional solar sail dynamics, we will first need to find approximations for v and w as their differential equations are not solvable analytically. Approximate solutions for the behaviour of v and w near \(\tilde{v}_2\) can be found using a linear approximation. Let \(v = \tilde{v}_2 + x\), \(w = \tilde{w} + y\) and

$$\begin{aligned} a = \frac{k_2}{2\tilde{v}_2} \end{aligned}$$

where x and y are small deviations away from the equilibrium point. To first order, and neglecting any \(a k_2\) terms, we find that

$$\begin{aligned} x'&= -y \end{aligned}$$
(20)
$$\begin{aligned} y'&= x + 2ay. \end{aligned}$$
(21)

Using polar coordinates centred at \((\tilde{v}_2, \tilde{w}_2)\), we define the initial conditions on the hodograph plane \(v_0\) and \(w_0\) as

$$\begin{aligned} v_0&= \tilde{v}_2 + \rho _0 \cos \theta _0 \end{aligned}$$
(22)
$$\begin{aligned} w_0&= \tilde{w} + \rho _0 \sin \theta _0 \end{aligned}$$
(23)

where \(\theta _0\) is measured anti-clockwise from the horizontal nullcline and \(\rho _0\) is the distance from the equilibrium point \(\tilde{v}_2\), as shown in Fig. 2.

Fig. 2
figure 2

Illustration of \(\rho _0\) and \(\theta _0\)

Full size image

Solving Eqs. (20) and (21) then yields the following solutions for v and w

$$\begin{aligned} v&= \tilde{v}_2 + \rho _0 \cos (\psi + \theta _0)\mathrm {e}^{a \psi } \end{aligned}$$
(24)
$$\begin{aligned} w&= \tilde{w} + \rho _0 \sin (\psi + \theta _0)\mathrm {e}^{a \psi }, \end{aligned}$$
(25)

To complete the description of the in-plane trajectories, we will also derive the approximation for h as this is simpler than solving the equation for \(r'\). By substituting the above approximation for v into Eq. (17) and performing an expansion of 1 / v in terms of \(\rho _0\), we find that

$$\begin{aligned} h = \sqrt{v}_0 \mathrm {exp} \left[ \frac{k_2}{\tilde{v}_2^2} \left( \tilde{v}_2 \psi - \rho _0 \sin (\psi + \theta _0) \mathrm {e}^{a \psi } \right) \right] . \end{aligned}$$
(26)

From this we can recover r and so the complete dynamics of the two-dimensional solar sail orbit can be expressed in terms of \(\psi \).

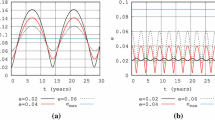
We show the accuracy of the v, w and h approximation in Fig. 3 by comparing the numerical solution of the equations of motion with our approximations for different values of \(\beta \). We choose the initial values of v, w and h to be \(v_0=1\), \(w_0=0\) and \(h_0=1\) to represent an Earth escape orbit. We let \(\beta \) range from 0.001 to 0.1 with \(\alpha = \arctan (1/\sqrt{2})\), \(\delta = 1\) and compare the solutions for an orbit lasting approximately 35 years. This value of alpha is chosen to maximize the tangential force (McInnes 1999b) and will be used throughout this paper. We use \(\beta =0.1\) as the maximum value here as this is twice what current technology will allow and so will exaggerate any errors. The mean error is calculated by summing the absolute value of the difference between the numerical solution and approximation at each integration step and dividing by the number of time steps, while the maximum error is simply the largest error recorded at any time step over a whole orbit. In doing this we can see that the approximations of v and w retain their accuracy well over this time period, with the maximum error being of order \(10^{-3}\).

Fig. 3
figure 3

Error in v, w and h for given sail lightness factor

Full size image

4 Equations of motion

In this section we derive the full equations of motion for a solar sail in a three-dimensional heliocentric orbit. Define an inertial coordinate system \(\varvec{\hat{e}}_{x}\), \(\varvec{\hat{e}}_{y}\), \(\varvec{\hat{e}}_{z}\) such that the spacecraft is initially situated on the \(\varvec{\hat{e}}_{x}\) axis and the \(\varvec{\hat{e}}_{z}\) axis is aligned with the initial angular momentum vector. The unit vectors \(\varvec{\hat{r}}\), \(\varvec{\hat{\lambda }}\) and \(\varvec{\hat{h}}\), as described in Sect. 2, form a non-uniformly rotating coordinate system with respect to this inertial system, we refer to this rotating system as the orbital frame. The orbital frame, and hence the orientation of the orbital plane, is described using the classical orbital elements; the longitude of ascending node, \(\varOmega \), the inclination i and the true latitude \(\lambda = \omega + \nu \) where \(\omega \) is the longitude of periapsis and \(\nu \) the true anomaly. We refer to these three angles as the orbital angles. The orbital frame can be written in terms of the inertial coordinate system using three consecutive Euler rotations as follows

$$\begin{aligned} \begin{pmatrix} \varvec{\hat{r}} \\ \varvec{\hat{\lambda }} \\ \varvec{\hat{h}} \end{pmatrix} = \varvec{R} \begin{pmatrix} \varvec{\hat{e}}_{x} \\ \varvec{\hat{e}}_{y} \\ \varvec{\hat{e}}_{z} \end{pmatrix} \end{aligned}$$
(27)

where \(\varvec{R}\) is a matrix representing a 3–1–3 rotation using the angles \(\varOmega \) followed by i and finally \(\lambda \). The angular velocity is then defined as

$$\begin{aligned} \varvec{\dot{R}} \varvec{R}^T = \begin{pmatrix} 0 &{} -\omega _z &{} \omega _y \\ \omega _z &{} 0 &{} -\omega _x \\ -\omega _y &{} \omega _x &{} 0 \end{pmatrix} \end{aligned}$$

with the components given by

$$\begin{aligned} \omega _x&= -\sin {\lambda }\sin {i}\frac{d\varOmega }{dt} - \cos {\lambda }\frac{di}{dt} \end{aligned}$$
(28)
$$\begin{aligned} \omega _y&= -\cos {\lambda }\sin {i}\frac{d\varOmega }{dt} + \sin {\lambda }\frac{di}{dt} \end{aligned}$$
(29)
$$\begin{aligned} \omega _z&= -\frac{d\lambda }{dt} - \cos {i}\frac{d\varOmega }{dt}. \end{aligned}$$
(30)

The goal now is to find alternative expressions for these components and so compute the derivatives of the orbital angles. From the definition of angular momentum for a perturbed three-dimensional orbit as given by Brouwer and Clemence (1961), we have that

$$\begin{aligned} h = r^2 \left( \frac{d\lambda }{dt} + \cos {i}\frac{d\varOmega }{dt} \right) = r^2 \dot{\psi } \end{aligned}$$
(31)

and hence \(\omega _z = -h/r^2\). We will now derive the torque vector \(\varvec{\tau }\) in two different ways. Doing this allows a comparison of components which will lead to alternative expressions for \(\omega _x\) and \(\omega _z\). First, simply consider the definition of the torque vector which is \(\varvec{\tau } = \varvec{r} \times \varvec{F}\) with \(\varvec{F}\) the force on the solar sail. We find the force from the acceleration given by Eq. (5) and hence the torque is

$$\begin{aligned} \varvec{\tau } = \frac{\mu }{r} \left( k_2 \varvec{\hat{h}} - k_3 \varvec{\hat{\lambda }} \right) . \end{aligned}$$

However, the torque can also be written as the derivative of the angular momentum and so we have \(\varvec{\tau } = \dot{\varvec{h}}\) and hence

$$\begin{aligned} \varvec{\tau } = \frac{d}{dt} \left( h \varvec{\hat{h}} \right) = \dot{h} \varvec{\hat{h}} + h \varvec{\dot{\hat{h}}}. \end{aligned}$$
(32)

Using the rotation matrix \(\varvec{R}\) from Eq. (27), we find the time derivative of the angular momentum unit vector in the rotating coordinate system to be

$$\begin{aligned} \varvec{\dot{\hat{h}}} = -\omega _y \varvec{\hat{r}} + \omega _x \varvec{\hat{\lambda }}. \end{aligned}$$
(33)

Substituting this into Eq. (32), we then compare the unit vectors components to find that \(\omega _y = 0\) and

$$\begin{aligned} \omega _x = -\frac{\mu }{rh}k_3 = -\frac{h k_3}{r^2 v}. \end{aligned}$$
(34)

Now, by combining Eqs. (28–30) with Eq. (34), \(\omega _z = -h/r^2\) and \(\omega _y = 0\), we can rearrange to solve for the derivatives of the orbital angles. By changing the independent variable to \(\psi \), a factor \(h/r^2\) can be removed from the derivatives and therefore we derive the following set of differential equations

$$\begin{aligned} \frac{dv}{d\psi }&= 2k_2 - w \nonumber \\ \frac{dw}{d\psi }&= k_2\frac{w}{v} + v + k_1 \nonumber \\ \frac{dh}{d\psi }&= \frac{k_2}{v}h \nonumber \\ \frac{d\lambda }{d\psi }&= 1 - \frac{\sin {\lambda }}{\tan {i}}\frac{k_3}{v} \nonumber \\ \frac{di}{d\psi }&= \cos {\lambda }\frac{k_3}{v} \nonumber \\ \frac{d\varOmega }{d\psi }&= \frac{\sin {\lambda }}{\sin {i}}\frac{k_3}{v}. \end{aligned}$$
(35)

These six equations then fully describe the solar sail’s three-dimensional orbit, with the in-plane dynamics being described by the first three equations, and the orientation of the orbital plane and position of the solar sail in that plane described by the final three. For completeness, we use the definition of the hodograph variables from Battin (1999) to derive the argument of periapsis as

$$\begin{aligned} \omega = \lambda - \nu = \lambda - \arctan \frac{w}{v - 1}. \end{aligned}$$
(36)

The benefit of these equations is that they neatly split the kinematics and dynamics, with the orbital angles being coupled to the hodograph variables only through v. The problems with the equations are the singularities at \(i=0\), caused by the longitude of ascending node being undefined for a planar orbit. This causes problems when trying to find approximate solutions as \(\lambda \) and \(\varOmega \) change rapidly for small inclination values. In the next section we’ll describe how we solve this problem by showing that the orbit generated by any initial set of orbital angles can be mapped to any other orbit with different orbital angles.

5 Rotational symmetry of the problem

There are six variables that are required to recover the full dynamics, giving us a six dimensional solution space. However, with both gravitational force and solar radiation pressure being dependent only on r and not the orientation in space, the problem admits rotational symmetry. We now use this to reduce the complexity of the solution space.

Let \(F_1\) denote an inertial frame. Consider an orbit with some arbitrary initial conditions, as measured in this frame, to be

$$\begin{aligned} (v_0, w_0, r_0, \lambda _1(0), i_1(0), \varOmega _1(0)). \end{aligned}$$
(37)

Let \(F_2\) denote a second inertial frame which measures the initial conditions for the same orbit as

$$\begin{aligned} (v_0, w_0, r_0, \lambda _2(0), i_2(0), \varOmega _2(0)) \end{aligned}$$
(38)

with \(v_0\), \(w_0\) and \(r_0\) identical in both sets of initial conditions. Although both of these frames will measure the orbital angles differently as the orbit evolves, there is in fact only a single unique orbit here. Through rotational symmetry, it is possible to use some transformation to map the orbital angles measured by one inertial frame onto the orbital angles measured by another inertial frame. The question is then,

If, at some point in time, the orbital angles, as measured in frame \(F_1\), are \(\lambda _1\), \(i_1\) and \(\varOmega _1\), what are the orbital angles as measured in frame \(F_2\)?

Solving this will mean that we need only consider the dynamics of a single set of initial conditions for the orbital angles. Other orbits with arbitrary initial conditions can be obtained from this by applying rotations. There is a constant rotation matrix, R, defining the transformation from \(F_1\) to \(F_2\) which can be written as

$$\begin{aligned} R = R_z(\lambda )R_x(i)R_z(\varOmega ). \end{aligned}$$
(39)

Taking the unit vectors of \(F_1\) as coordinate axis of the identity matrix. The unit vectors of \(F_2\), denoted as \(\varvec{\hat{x}}_2\), \(\varvec{\hat{y}}_2\) and \(\varvec{\hat{z}}_2\) are then the row vectors of R. The unit vectors of the orbital frame can be written as

$$\begin{aligned} \begin{pmatrix} \varvec{\hat{r}} \\ \varvec{\hat{\lambda }} \\ \varvec{\hat{h}} \end{pmatrix} = R_z(\lambda _1) R_x(i_1) R_z(\varOmega _1) F_1. \end{aligned}$$
(40)

Figure 4 illustrates the relationship between \(F_1\), \(F_2\) and the orbital frame.

Fig. 4
figure 4

Relationship between the two inertial frames and the orbital frame

Full size image

We can now calculate the orbital angles, as measured in \(F_2\), to be the following

$$\begin{aligned} \cos \lambda _2&= \frac{\varvec{n}}{\mid \varvec{n} \mid } \cdot \varvec{\hat{r}} \nonumber \\ \cos i_2&= \varvec{\hat{z}}_2 \cdot \varvec{\hat{h}} \nonumber \\ \cos \varOmega _2&= \varvec{\hat{x}}_2 \cdot \frac{\varvec{n}}{\mid \varvec{n} \mid } \end{aligned}$$
(41)

where

$$\begin{aligned} \varvec{n} = \varvec{\hat{z}}_2 \times \varvec{\hat{h}} \end{aligned}$$
(42)

is the vector in the direction of the longitude of the ascending node. The orbital angles in \(F_2\) can now be written in terms of only the orbital angles in \(F_1\). As a final reduction in complexity, we choose the initial radial distance to be unity. The three dimensional solar sail orbit is then defined only in terms of the initial hodograph variables, as any other orbit can be found through the rotation method described above. The initial condition solution space has therefore been reduced from six variables to two. These are supplemented by the sail parameters \(\alpha \), \(\delta \) and \(\beta \).

6 Analytic description of orbits near the log spiral

The rotational symmetry and angle mapping in Eq. (41) mean that if the equations of motion are solved for one set of initial orbital angles, they are solved for all sets. Consider an initial set of orbital angles

$$\begin{aligned} \lambda _0&= 0 \end{aligned}$$
(43)
$$\begin{aligned} i_0&= 90^{\circ } \end{aligned}$$
(44)
$$\begin{aligned} \varOmega _0&= 0. \end{aligned}$$
(45)

With these initial conditions, the equations of motion given in Eq. (35) can be simplified. Assume that the variation in the inclination is small enough such that

$$\begin{aligned} \sin i \approx 1, \quad \frac{1}{\tan i} \approx 0. \end{aligned}$$
(46)

Using the approximation of the hodograph variables in Eq. (24) the differential equation for \(\lambda \) then becomes \(\lambda ' = 1\) and hence, with \(\lambda (0) = 0\), we find that

$$\begin{aligned} \lambda = \psi . \end{aligned}$$
(47)

Combining this with a first order expansion of 1 / v from Eq. (24), we obtain the following differential equations for the inclination and longitude of ascending node:

$$\begin{aligned} \frac{di}{d\psi }&= \cos {\psi }\frac{k_3}{\tilde{v}_2}\left( 1 - \rho _0\cos (\psi + \theta _0)\mathrm {e}^{a\psi }/\tilde{v}_2 \right) \\ \frac{d\varOmega }{d\psi }&= \sin {\psi }\frac{k_3}{\tilde{v}_2}\left( 1 - \rho _0\cos (\psi + \theta _0)\mathrm {e}^{a\psi }/\tilde{v}_2 \right) . \end{aligned}$$

Solving this yields the following solutions

$$\begin{aligned} i&= \frac{\pi }{2} + \frac{k_3}{\tilde{v}_2} \sin \psi + C_1 \left( \mathrm {e}^{a \psi } - 1 \right) \end{aligned}$$
(48)
$$\begin{aligned} \varOmega&= \frac{k_3}{\tilde{v}_2} - \frac{k_3}{\tilde{v}_2} \cos \psi - C_2 \left( \mathrm {e}^{a \psi } - 1 \right) \end{aligned}$$
(49)

where

$$\begin{aligned} C_1 = -\frac{k_3 \rho _0 \cos \theta _0}{2 \tilde{v}_2^2 a} = \frac{1}{\tan \delta } \left( \frac{\tilde{v}_2 - v_0}{\tilde{v}_2} \right) \end{aligned}$$
(50)

and

$$\begin{aligned} C_2 = -\frac{k_3 \rho _0 \sin \theta _0}{2 \tilde{v}_2^2 a} = \frac{1}{\tan \delta } \left( \frac{\tilde{w} - w_0}{\tilde{v}_2} \right) . \end{aligned}$$
(51)

To recover the full three-dimensional orbit, we can use either the radial distance or angular momentum derived earlier. The equations of motion are now solved for the given initial conditions meaning the analytic solution for any initial condition can be found through rotational symmetry. As an example to demonstrate the accuracy of the above solution, we use the same parameters as in Sect. 3 and compare the numerical solution and the approximate solution with \(\beta \) ranging from 0 to 0.1 (Fig. 5).

Fig. 5
figure 5

Error in \(\lambda \), inclination and \(\varOmega \) for given sail lightness factor

Full size image
Fig. 6
figure 6

Long term behaviour of orbital angles in \(90^{\circ }\) inclination frame

Full size image

We can see from Eqs. (48–51) that the long term behaviour of the orbital angles can be described simply in terms of \(v_0\) and \(w_0\). The general behaviour for both angles is an oscillation around the initial condition with \(\tilde{v}_2 - v_0\) and \(\tilde{w} - w_0\) determining in which direction the drift away from this happens. For the inclination this neatly splits the hodograph phase space into two regions; \(v_0 < \tilde{v}_2\) and \(v_0 > \tilde{v_2}\). Similarly for the longitude of ascending node the two regions are; \(w_0 < \tilde{w}\) and \(w_0 > \tilde{w}\). The benefit of using this \(90^{\circ }\) inclination frame is then apparent as the long term behaviour of a solar sail can be determined from one of four regions in the hodograph phase space which are found by combining the inclination and longitude of ascending node regions. As the problem admits rotational symmetry, there will also be four regions describing the behaviour of the angles in any other arbitrary frame. For the \(90^{\circ }\) inclination frame, the behaviour is illustrated in Fig. 6. The initial conditions used to obtain these results were \(v_0 = \tilde{v}_2 \,+\, 0.1 \cos \theta \) and \(w_0 = \tilde{w} \,+\, 0.1 \sin \theta \) for \(\theta \in \{45^{\circ }, 135^{\circ }, 225^{\circ }, 315^{\circ }\}\) with the sail parameters being \(\beta = 0.2\), \(\alpha = \arctan (1/\sqrt{2})\) and \(\delta = 1\).

7 Conclusions

This paper introduces an analytical approximation to three-dimensional solar sail orbits for trajectories starting close to the logarithmic spiral. It was shown that, by choosing a frame in which the initial inclination was \(90^{\circ }\), the equations of motion could be simplified considerably and accurate approximations to the orbital angles made. The rotational symmetry of the problem then allowed us to transform this approximation into any other inertial frame and hence solutions for any initial set of orbital angles could be found. The use of the \(90^\circ \) inclination frame allowed the hodograph phase space to be divided into four distinct regions with each having a different long term behaviour for the inclination and longitude of ascending node. The general behaviour of these angles was shown to be an oscillation combined with a slowly increasing deviation away from the initial value, driven by the sail orientation and the distance from the logarithmic spiral initial condition.